黄金分割的正确计算方法

黄金分割取点技巧
黄金分割是一种常见的数学比例关系，常用在美术设计、摄影构图、股市分析等领域。

以下是一些黄金分割取点的技巧：
1. 确定起点和终点：首先，需要确定你要分割的起点和终点。

这可以是图片的任意两个点，也可以是线段的两个端点。

2. 计算分割点：根据黄金分割的比例关系，计算出分割点的位置。

黄金分割的比例关系是，因此，可以用以下公式计算分割点的位置：
分割点 = (终点 - 起点) × + 起点
3. 确定黄金分割点：将计算出的分割点与起点和终点进行比较，确定黄金分割点的位置。

一般来说，黄金分割点位于起点和分割点的中点和分割点和终点的中点。

4. 验证分割效果：最后，可以验证分割的效果。

可以通过对比分割前后的效果，来评估黄金分割点是否有效地提高了视觉效果或表现力。

需要注意的是，黄金分割只是一种参考方法，并不是万能的。

在实际应用中，还需要结合具体的情况进行调整和修改。

同时，对于不同领域的应用，黄金分割的比例关系也可能有所不同，需要根据实际情况进行调整。

黄金分割点比例
黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值约为0.618。

这个比例被公认为是最能引起美感的比例，因此被称为黄金分割。

在古希腊时期，有一天毕达哥拉斯走在街上，在经过铁匠铺前他听到铁匠打铁的声音非常好听，于是驻足倾听。

他发现铁匠打铁节奏很有规律，这个声音的比例被毕达哥拉斯用数学的方式表达出来。

把一条线段分割为两部分，使较大部分与全长的比值等于较小部分与较大的比值，则这个比值即为黄金分割。

其比值是根号五减一的差除以二，近似值为0.618，通常用希腊字母Ф表示这个值。

上升上涨压力＝21．97＋（34．31－ 21．97）1．618＝42元 该股在今年二月份摸高至45元后回落， 投资者在42元可以从容卖出获利。 该股走势说明了如果对黄金分割掌握 透彻，可以成功利用它来捕捉黑马。使 用时要注意。
1、买点在回调到0．618处比较 安全，回调到0．382处对于激进 型投资者较适合，稳健型投资者 还是选择回调到0．618处介入。
黄金分割的正确计算方法
股市数学技巧:黄金分割的正确 计算方法
1．6182，黄金分割在个股当中 的应用方式有一派观点认为是：直接从 波段的低点加上0．382倍、0．618倍、 1．382倍、1．618倍……作为其涨升压 力。或者直接从波段的高点减去0．382 倍及0．618倍，作为其下跌支撑。
另一派观点认为不应以波段的高 低点作为其计算基期。而应该以 前一波段的涨跌幅度作为计算基 期，黄金分割的支撑点可分别用 下述公式计算：
1、某段回档高点支撑＝某段终 点－（某段终点－某段最低点） 0．382 2、某段低点支撑＝某段终点 －（某段终点－某段最低点） 0．618
如果要计算目标位：则可用下列 公式计算 3、前段最低点（或最高点） ＝（前段最高点－本段起涨点） 1．382（或1．618） 上述公式有四种计算方法，根 据个股不同情况分别应用。
2、卖点在涨升1．382处比较保 守，只要趋势保持上升通道，可 选择涨升1．618处卖出。
案例分析托普软件（000583）
该股的走势颇为符合黄金分割原 则，1999年3月份，该股从 14．31元起步，至6月底，该股 拉升到34．31元，完成这一波的 涨升，随后我们来看该股的支撑 价位：
根据公式：下跌低点支撑＝34．31－ （34．31－14．35）0．618＝22元事实 上该股1999年11月份回调最低点为 22．48元，误差极小，投资者只要在22 元一线附近吸纳，就可以找到获利机会。 目标价位也可通过公式计算。

黄金分割的正确计算方法1．618减去基数1，得0．618，1再减去0．618得0．382，黄金分割在个股当中的应用方式有一派观点认为是：直接从波段的低点加上0．382倍、0．618倍、1．382倍、1．618倍……作为其涨升压力。

或者直接从波段的高点减去0．382倍及0．618倍，作为其下跌支撑。

另一派观点认为不应以波段的高低点作为其计算基期。

而应该以前一波段的涨跌幅度作为计算基期，黄金分割的支撑点可分别用下述公式计算：(抄底不可盲目，要抓住真正机会！)1、某段回档高点支撑＝某段终点－（某段终点－某段最低点）0．3822、某段低点支撑＝某段终点－（某段终点－某段最低点）0．618如果要计算目标位：则可用下列公式计算3、前段最低点（或最高点）＝（前段最高点－本段起涨点）1．382（或1．618）上述公式有四种计算方法，根据个股不同情况分别应用。

案例分析托普软件（000583）该股的走势颇为符合黄金分割原则，1999年3月份，该股从14．31元起步，至6月底，该股拉升到34．31元，完成这一波的涨升，随后我们来看该股的支撑价位：根据公式：下跌低点支撑＝34．31－（34．31－14．35）0．618＝22元事实上该股1999年11月份回调最低点为22．48元，误差极小，投资者只要在22元一线附近吸纳，就可以找到获利机会。

目标价位也可通过公式计算。

上升上涨压力＝21．97＋（34．31－21．97）1．618＝42元该股在今年二月份摸高至45元后回落，投资者在42元可以从容卖出获利。

该股走势说明了如果对黄金分割掌握透彻，可以成功利用它来捕捉黑马。

使用时要注意。

1、买点在回调到0．618处比较安全，回调到0．382处对于激进型投资者较适合，稳健型投资者还是选择回调到0．618处介入。

2、卖点在涨升1．382处比较保守，只要趋势保持上升通道，可选择涨升1．618处卖出。

[晓漠孤烟]-- 黄金分割率数学家法布兰斯在１３世纪写了一本书，关于一些奇异数字的组合。

黄金分割知识总结
黄金分割是一个数学术语，它是指将一个线段分成两部分，使得其中一部分与原线段的比例等于另一部分与这部分的比例。

这个比例被认为是最美的比例之一，因此在艺术、建筑、设计等领域中得到了广泛的应用。

黄金分割的数学表达式为：较长线段是较短线段与原线段的比例中项。

在黄金分割中，较长线段和较短线段的长度可以通过以下公式计算：
较长线段= (√5 + 1) / 2 * 原线段
较短线段= 原线段- 较长线段
黄金分割在数学中有很多有趣的性质和应用。

它与斐波那契数列有着密切的联系，因为斐波那契数列中的任何一个数字都可以表示为前两个数字之和。

斐波那契数列在自然界中也有很多奇妙的应用，例如植物的花瓣排列和动物的生长周期等。

此外，黄金分割还被广泛应用于艺术、建筑和设计等领域。

例如，在建筑中，黄金分割被用来确定窗户、门和建筑物线条的位置和大小，以使建筑物看起来更加协调和美观。

在绘画和摄影中，黄金分割也被用来确定构图和画面布局的最佳位置。

总之，黄金分割是一个非常有趣和有用的数学概念，它不仅在数学中有广泛的应用，还在艺术、建筑和设计等领域中发挥着重要的作用。

黄金分割点比例公式计算过程
公式为(√5-1)/2，黄金比又称黄金律，是指事物各部分间一定的数学比例关系，即
将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1∶0.，即长段为全段的0.。

主要特点
黄金比例就是一种数学上的比例关系。

黄金比例具备严苛的比例性、艺术性、人与自
然性，蕴含着多样的美学价值。

应用领域时通常挑0. ，就像是圆周率在应用领域时挑
3.14一样。

黄金矩形(golden rectangle)的长宽之比为黄金分割率，换言之，矩形的长边为短边1.倍。

黄金分割率和黄金矩形能够给画面带来美感，令人愉悦。

在很多艺术品以及小自然中都能够找出它。

希腊雅典的帕撒神农庙就是一个较好的例子。

而超过·芬奇的《维特鲁威人》合乎黄金矩形。

《蒙娜丽莎》中蒙娜丽莎的脸也合乎
黄金矩形，《最后的晚餐》同样也应用领域了该比例布局。

三角形的黄金比
正五边形对角线连满后发生的所有三角形，都就是黄金分割三角形。

黄金分割三角形有一个特殊性，所有的三角形都可以用四个与其本身全等的三角形来
生成与其本身相似的三角形，但黄金分割三角形是唯一一种可以用5个而不是4个与其本
身全等的三角形来生成与其本身相似的三角形的三角形。

由于五角形的顶角是36度，这
样也可以得出黄金分割的数值为2sin18°（即2*sin(π/10)）。

将一个正五边形的所有对角线连接起来，所产生的五角星里面的所有三角形都就是黄
金分割三角形。

线段黄金分割点公式
线段黄金分割点公式，也被称为黄金分割比或黄金分割比例，是一种常用的数学工具，可用于寻找线段中的黄金分割点。

黄金分割，又称为黄金比例，是指将一条线段分割成两段，使整条线段的长度与较长部分的长度之比等于较长部分与较短部分之比。

这个比值约等于1.618，常用希腊字母φ（phi）表示。

根据线段黄金分割点公式，我们可以计算出黄金分割点在
线段上的位置。

设线段的长度为L，黄金分割点距离线段起点
的距离为x，则根据公式：
L / x = x / (L - x) = 1.618
将上述公式进行简化，我们可以得到二次方程：
x^2 - 1.618xL + L^2 = 0
通过解这个二次方程，我们可以得到黄金分割点在线段上
的位置。

常见的求解方法包括配方法、求根公式或者使用计算机软件进行数值计算。

使用黄金分割点公式可以帮助我们在绘画、摄影、设计等
领域中进行构图的优化。

人眼往往更喜欢黄金比例所呈现的比例关系，因此在布局和设计中使用黄金分割点可以创造出更具吸引力和美感的作品。

值得注意的是，黄金分割点公式只是一种计算工具，并不
意味着黄金分割点一定是最优解。

在实际应用中，我们可以根据需求和审美来灵活运用，以达到最佳的效果。

线段黄金分割点公式是一种能够帮助我们找到黄金分割点
的数学工具。

了解这个公式可以帮助我们在艺术创作和设计中更好地运用黄金分割的美学原理。

初中黄金分割点公式
初三数学黄金分割公式是是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

其比值是一个无理数，用分数表示为√5减1除以2，取其前三位数字的近似值是0点618，由于按此比例设计的造型十分美丽，因此称为黄金分割，也称为中外比。

这个分割点就叫做黄金分割点，通常用Φ表示，这是一个十分有趣的数字，以0点618来近似表示，通过简单的计算就可以发现1减0点618除以0点618约等于0点618，即一条线段上有两个黄金分割点。

黄金分割黄金分割又称黄金律，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为1∶0.618或1.618∶1，即长段为全段的0.618。

0.618被公认为最具有审美意义的比例数字。

上述比例是最能引起人的美感的比例，因此被称为黄金分割。

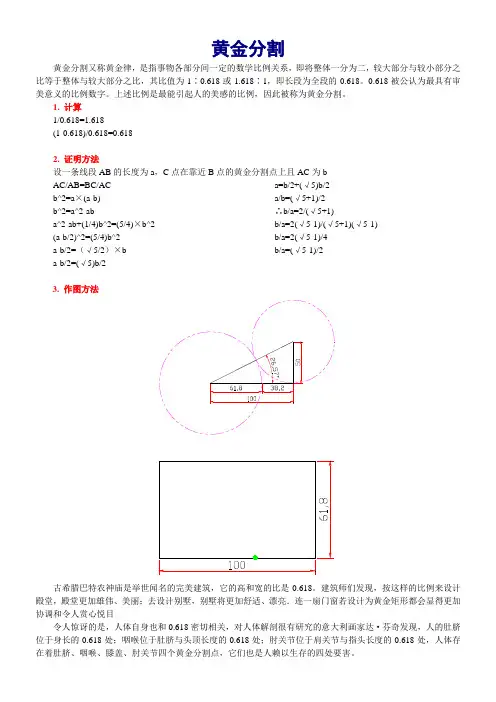
1. 计算1/0.618=1.618(1-0.618)/0.618=0.6182. 证明方法设一条线段AB的长度为a，C点在靠近B点的黄金分割点上且AC为bAC/AB=BC/ACb^2=a×(a-b)b^2=a^2-aba^2-ab+(1/4)b^2=(5/4)×b^2 (a-b/2)^2=(5/4)b^2a-b/2=（√5/2）×ba-b/2=(√5)b/2 a=b/2+(√5)b/2a/b=(√5+1)/2∴b/a=2/(√5+1)b/a=2(√5-1)/(√5+1)(√5-1) b/a=2(√5-1)/4b/a=(√5-1)/23. 作图方法古希腊巴特农神庙是举世闻名的完美建筑，它的高和宽的比是0.618。

建筑师们发现，按这样的比例来设计殿堂，殿堂更加雄伟、美丽；去设计别墅，别墅将更加舒适、漂亮．连一扇门窗若设计为黄金矩形都会显得更加协调和令人赏心悦目令人惊讶的是，人体自身也和0.618密切相关，对人体解剖很有研究的意大利画家达·芬奇发现，人的肚脐位于身长的0.618处；咽喉位于肚脐与头顶长度的0.618处；肘关节位于肩关节与指头长度的0.618处，人体存在着肚脐、咽喉、膝盖、肘关节四个黄金分割点，它们也是人赖以生存的四处要害。

养生专家指出要抓住健康的黄金分割点人体黄金分割点人体是这世界上最杰出的艺术品，从面部到身体都遵循黄金分割率。

以人的面部来说，脸的宽度和长度比值为0.618时，为最完美的脸型；上身长和下身长的比值为0.618时，是最协调的身材。

我们的牙齿、耳朵、宽度和长度的比值也都近似0.618。

黄金分割的公式和计算嘿，说起黄金分割，这可是个挺有趣的数学概念。

咱们先来讲讲黄金分割的公式。

简单来说，黄金分割点是把一条线段分割为两部分，较大部分与整体部分的比值等于较小部分与较大部分的比值。

这个比值约为 0.618 。

如果设线段的全长为 1 ，较长段为 x ，那公式就是：x / 1 = ( 1 - x ) / x ，通过解方程就能得到 x 约等于 0.618 。

那在实际计算中怎么用呢？我给您举个例子哈。

比如说，有一幅画，您想把它的上下比例弄得好看，符合黄金分割。

假设这画的高度是 100 厘米，那按照黄金分割，上面部分大约就是 38.2 厘米，下面部分大约就是 61.8 厘米，这样看起来就会更舒服、更美观。

再比如说，建筑师在设计建筑的时候，也会用到黄金分割。

像有些高楼大厦，从整体的外观比例，到窗户的分布，都可能藏着黄金分割的影子。

我之前去参观过一个新建成的图书馆，那建筑的外观比例简直绝了。

从远处看，整个大楼的高度和宽度之间，就像是被一只神奇的手按照黄金分割的比例塑造出来的。

走近一看，每一层楼窗户的分布，还有大门和整个建筑立面的比例，都有着黄金分割的韵味。

当时我就感叹，这设计师真是把黄金分割运用得炉火纯青，让这栋建筑不仅仅是一个实用的场所，更是一件精美的艺术品。

还有啊，在摄影中也能用到黄金分割。

您拍照的时候，如果把主体放在画面大约 0.618 的位置，照片往往会更有吸引力。

有一次我和朋友出去旅游，看到一处特别美的风景，我就想拍下来。

一开始怎么拍都觉得差点意思，后来我突然想到黄金分割，调整了拍摄的构图，把那最吸引人的部分放在了画面的黄金分割点上，哇，拍出来的效果就是不一样，朋友看了都赞不绝口。

在日常生活中，咱们的衣服设计、家具的尺寸比例等等，都可能会用到黄金分割。

就连一些音乐的节奏和旋律，有时候也会遵循黄金分割的规律，给人一种特别和谐、美妙的感觉。

所以说啊，黄金分割这东西，虽然听起来有点神秘，但其实就在咱们身边，影响着咱们生活的方方面面。

黄金分割点计算公式黄金分割点计算公式是指根据黄金分割比例，通过一定的数学计算来确定两个数之间的黄金分割点。

黄金分割比例是指将一个整体分割为两部分，使其中一部分与整体的比值等于另一部分与其中一部分的比值。

这个比值通常被称为黄金分割比例或黄金比例，其近似值为1.618。

黄金分割点的计算公式可以用数学符号表示为：黄金分割点 = 总长度× 黄金分割比例例如，假设总长度为L，黄金分割比例为1.618，则黄金分割点可以表示为L × 1.618。

在实际应用中，黄金分割点的计算可以用于各种领域，如美学、设计、金融等。

下面将分别介绍其中的应用。

1. 美学：黄金分割点的计算可用于绘画、摄影等艺术领域。

艺术家可以通过将画布或照片按照黄金分割比例进行分割，将重要的元素放置在黄金分割点上，从而使作品更加美观和吸引人。

2. 设计：在设计领域，黄金分割点的计算可以用于平面设计、建筑设计等。

设计师可以根据黄金分割点的位置来布局元素，使设计更加和谐和平衡。

3. 金融：在金融领域，黄金分割点的计算可以用于技术分析。

技术分析是一种通过研究历史价格和交易量数据来预测未来价格走势的方法。

通过将价格波动按照黄金分割比例进行分割，分析师可以找到可能的支撑位和阻力位，从而做出更准确的交易决策。

除了以上应用外，黄金分割点的计算在其他领域也有一定的应用。

例如，在生物学中，黄金分割点的计算可以用于研究植物的生长规律；在运动学中，黄金分割点的计算可以用于优化运动员的动作表现等。

需要注意的是，黄金分割点的计算公式只是一种工具，其结果并不一定是绝对正确或最优的。

在实际应用中，还需要结合具体情况和经验来进行判断和决策。

黄金分割点的计算公式是一种用于确定两个数之间黄金分割点的数学工具。

它在美学、设计、金融等领域有广泛的应用，并可以帮助人们更好地理解和利用黄金分割比例。

通过合理地运用黄金分割点的计算公式，我们可以创造出更美观、更和谐的作品，也可以做出更准确的决策。

黄金分割点的公式黄金分割点的公式是指在数学和美学中常用的一种比例关系公式，用于划分成两个部分时，使其比例恰到好处，达到美感的效果。

这个公式是由古希腊数学家欧几里得在其著作《几何原本》中提出的。

黄金分割点的公式可以用一个简洁的比例表示：a/b = (a+b)/a = φ，其中φ是黄金分割比例，约等于1.618。

黄金分割点的公式在建筑、绘画、设计等领域被广泛运用。

在建筑设计中，黄金分割点的公式被用来确定建筑物的比例和比例尺寸，以创造出更加和谐和美观的空间。

例如，古希腊的帕台农神庙就采用了黄金分割点的比例来设计柱廊和建筑的各个部分，使整个建筑具有均衡和谐的视觉效果。

在绘画领域，黄金分割点的公式被用来确定画面的构图和元素的位置。

根据黄金分割点的原理，将画面分为两部分，使其中一部分的长度与整个画面的长度之比等于黄金分割比例。

这样可以使画面更加平衡和美观。

著名画家达·芬奇就是运用黄金分割点的公式来构图的。

他在绘画中经常运用黄金分割点来安排人物的位置、景物的摆放和线条的走势，以创造出具有动态和谐感的画面效果。

在设计领域，黄金分割点的公式被用来确定设计元素的比例和位置。

无论是平面设计还是产品设计，黄金分割点都能帮助设计师创造出更加美观和平衡的作品。

例如，在网页设计中，可以将网页的主要内容放置在黄金分割点的位置，使用户的视线更容易聚焦在重要的部分上。

除了在艺术领域，黄金分割点的公式还被应用于金融和自然科学领域。

在金融领域，黄金分割点的比例被用来进行技术分析，预测价格的变化趋势。

在自然科学领域，黄金分割点的公式也被用来研究自然界的规律，例如植物的生长、动物的形态等。

黄金分割点的公式在数学和美学中具有重要的地位。

它被广泛运用于建筑、绘画、设计等领域，帮助人们创造出更加和谐、美观的作品。

黄金分割点的公式不仅仅是一种数学工具，更是一种追求美感和平衡的表达方式。

通过运用黄金分割点的公式，人们可以创造出更加优雅和富有吸引力的作品，提升作品的艺术价值。

黄金分割点公式黄金分割点也称金分割点，是指两个数字之间的比例，它们总是成比例，具有非常特殊的数学意义，它可以在许多领域里发挥重要作用。

例如，黄金分割点的原理和应用被广泛用于艺术设计、建筑学、电影分析、美学等领域。

而且，它还被广泛应用于图形用户界面（GUI）、照片编辑、网页设计等，从而形成了一种重要的设计标准。

黄金分割点的计算方法并不复杂，它的数学表达式是：F = a + b / (1+a/b)，其中a和b分别表示两个数字的比例。

计算出的结果，即F，就是两个数字之间的黄金分割点。

从古至今，黄金比例已经被广泛应用于艺术的创作中。

例如，古建筑永恒的原则，古希腊音乐的比例，音乐理论中的比例，作曲家和画家都在某种程度上使用了黄金比例，把它作为创作的基础。

古希腊建筑师和雕塑家对它的运用也很深刻。

甚至比较远古的一些艺术形式都在一定程度上使用了黄金比例。

古希腊的哲学家、数学家和科学家们还发现，黄金比例在许多自然界中都有非常显著的表现。

例如，解剖学家发现，人体的多个器官、骨骼构造、血管等都具有黄金比例结构。

甚至花瓣、叶子也有黄金比例结构。

人们也惊叹于黄金比例在动物身形中的典型表现，尤其是蝴蝶翅膀、鱼体等等。

事实上，大自然中随处可见黄金比例的踪迹，这从某种程度上证明了黄金比例的确是自然界的客观规律之一。

除此之外，黄金比例还在多种不同的设计领域中得到了广泛的应用，例如印刷、平面设计、照片编辑、影像分析、图形界面设计等。

设计师们一般都是通过在尺寸和外形等方面，将实体物体按照黄金比例结构进行划分和组织，从而达到视觉上最佳的效果。

尤其是在平面设计和照片编辑中，使用黄金比例的灵活性、简洁性以及极强的审美价值，让设计师们受益匪浅。

同时，黄金比例也可以被应用于图形用户界面的设计，以便让用户更容易和更快速地浏览、使用和理解操作界面。

GUI设计中，使用黄金比例还可以让控件、框架、按钮和菜单等，自然、简单地组合在一起，而且，通过使用黄金比例，可以让控件和框架看起来更加合理、整洁、完美。

黄金分割算法详解(一)黄金分割算法详解什么是黄金分割算法？黄金分割算法指的是一种数学算法，可以将一条线段分成两部分，使得其中一部分与全长之比等于另一部分与这部分之比。

这个比例的值是1:1.618。

黄金分割算法的历史黄金分割算法最早出现在公元前500年的希腊文化中，被广泛应用于建筑、艺术、音乐等领域。

黄金分割比例被认为可以使设计更加和谐美观。

黄金分割算法的应用黄金分割算法在现代设计中仍然被广泛应用。

包括网页设计、平面设计、产品设计等领域。

在网页设计中，黄金分割比例可以用来平衡不同元素之间的空间关系，使得页面看起来更加整齐有序。

黄金分割算法的计算方法黄金分割算法的计算方法是根据下列公式：x / a = a / (x - a)其中，a 是线段的一部分，x 是整个线段的长度。

将公式进行简化得到：x^2 = ax + a^2将此公式移项得：x^2 - ax - a^2 = 0求根公式为：x = (1 + √5) / 2 * a或：x = (1 - √5) / 2 * a其中，√5 表示5的平方根。

总结黄金分割算法是一种古老且经典的数学算法，它在现代设计中仍然被广泛应用。

了解黄金分割算法的计算方法和应用，有助于设计出更加美观和协调的作品。

如何应用黄金分割算法黄金分割算法可以应用于各种设计中，例如：网页设计在网页设计中，黄金分割算法可以应用于设计网页布局、文本框、按钮等，以实现平衡美观的设计。

例如，比例1:1.618可以用于确定网页主体内容宽度。

平面设计在平面设计中，黄金分割算法可以应用于设计海报、名片、杂志等，以确保设计中各个元素在相对大小和位置上达到最佳协调效果。

产品设计在产品设计中，黄金分割算法可以应用于设计产品外形、尺寸、比例等，以实现优美的外观和使用体验。

建议在应用黄金分割算法时，需要结合实际情况进行调整和变化，而不是僵化地遵守1:1.618比例。

设计师需要根据需要在不同场景下设置不同的比例。

结论黄金分割算法是一种重要的设计思想，可以应用于设计方方面面，提升作品的整体质量和美感。

黄金分割点两个比例公式黄金分割点是一个充满神秘和美的概念，以其简洁的比例和无限的可能性，在建筑、艺术、设计、科学、数学等领域发挥着重要的作用。

本文将介绍黄金分割点的定义、历史、应用领域以及两个比例公式，希望能为读者进一步认识这个神秘而又充满智慧的概念。

一、定义和历史黄金分割点指的是一种比例关系，通常表示为a:b=b:(a+b)，其中a、b是两个长度或数量，而a+b是它们的总和。

这个比例关系在古代埃及、希腊、罗马等文明中都有广泛应用，被认为是一种特殊、意义深远的比例。

在西方文化中，它经常被称之为“黄金比例”或“神圣比例”。

黄金分割点最早的应用可以追溯到古希腊数学家欧几里德的著作《几何原本》中。

欧几里德在该书中提出了黄金分割点的定义和性质，并应用到许多几何学问题中。

他的这一发现在后来成为了欧几里德几何学中的一个基本概念。

在文艺复兴时期，黄金分割点再次引起了人们的关注。

意大利画家达芬奇在他的画作中经常运用黄金分割点来创造对称美和平衡感。

德国数学家费马则在研究数论和几何学时，发现了黄金分割点的一些性质，如黄金角、黄金直角三角形等。

此外，黄金分割点还被广泛应用于音乐、建筑、设计等领域中。

二、应用领域黄金分割点的应用领域非常广泛，它不仅是一种数学概念，更是艺术、科学、建筑、设计等领域中的重要元素。

1、艺术领域黄金分割点在艺术领域中被广泛应用。

在绘画、雕塑、摄影等中，经常使用黄金分割点来组合画面元素，创造出对称美和平衡感。

著名画家马蒂斯曾说：“在艺术中，黄金分割点是创意和美的灵魂。

”很多经典艺术品都采用了黄金分割点的结构，例如米开朗基罗的雕塑《大卫像》、莫奈的画作《睡莲》等。

2、建筑领域黄金分割点在建筑领域中被广泛运用。

建筑师经常使用黄金分割点来设计建筑结构、布局、比例等，以增强建筑的美感和稳定性。

例如，希腊万神殿的柱子高度就采用了黄金分割点的比例。

3、设计领域在设计领域中，黄金分割点也是一种重要的元素。

许多设计师使用黄金分割点来调整线条、形状、空间等元素的比例和位置，以达到和谐、美观、舒适的效果。