《乘法公式的复习课》案例
- 格式:doc
- 大小:874.50 KB
- 文档页数:6

拒绝盲从——“乘法公式复习课”教学案例背景:复习课在教学中并不讨人喜欢,因为复习课的教学内容往往如同把已学的知识进行“回炉”,学生缺少了首次学习知识的新鲜感;复习课的教学方式僵化、呆板,一般都是“整理+练习”的板块结构,教师组织复习时,大多是一厢情愿机械地对所学知识进行简单的重复、堆积、罗列,学生缺乏主动性······因此,与新授课相比,师生都不钟情复习课,教师讲得累,学生听得累。
那么,复习课是否就因复习内容的旧、方式的死而无法“美容”从而吸引学生呢?复习课非得有复习课的模式吗?笔者以《乘法公式复习课》这一案例来述说复习课教学有时也应拒绝盲从,不拘泥于传统教学模式。
情景描述:(师课前已分给学生所需的学具)打破传统复习课教学模式,教学一开始,不再是立即告诉学生这节上的是乘法公式的复习课,而是从游戏引入:师:同学们,你们喜欢网络游戏吗?学生异口同声道:“喜欢。
”回答在意料之中,我微笑地说:“今天,老师就带大家进入网络拼图游戏。
”屏幕上出示当时最流行的网络游戏画面。
此时,我发现学生们的注意力开始集中,连平时上课精神涣散的个别学生也聚精会神。
片断一:师:拼一拼,现在如图正方形①一个,正方形②一个和长方形③两个,请你用它们拼成一个正方形。
学生一听说拼图,个个劲头十足,课堂气氛活跃,每个学生都积极参与到动手拼图之中。
师:谁能把你的作品展示在黑板上?大家反应非常踊跃。
一生上台展示后,我乘胜追击,因势利导:“你能根据所拼图的面积关系验证乘法公式吗?”一生站起来:(a+b)²=a²+2ab+b²反应快的同学情不自禁赞叹道:“好样的。
”反应较慢的则一露出迷茫的眼神,这时一位平时好问但成绩不好的学生问道:”老师,为什么可以验证乘法公式?“生:因为拼好后的大正方形边长为a+b ,面积则为(a+b )²,若看成4部分面积和,则为a²+2ab+b²,所以正好验证了完全平方和公式(a+b )²=a²+2ab+b²。

《乘法复习课》一、教学目标1.知识与技能:(1)使学生进一步理解和掌握乘法的意义,熟练掌握乘法的基本运算方法。
(2)使学生能够熟练地进行乘法计算,提高计算速度和准确性。
2.过程与方法:(1)通过复习乘法的基本概念,培养学生的逻辑思维能力和抽象思维能力。
(2)通过解决实际问题,提高学生运用乘法知识解决实际问题的能力。
3.情感态度与价值观:(1)培养学生对数学的兴趣和热爱,增强学生克服困难的信心。
(2)培养学生团结协作的精神,提高学生的合作意识。
二、教学内容1.乘法的意义和基本运算方法2.乘法口诀和乘法计算3.乘法在实际问题中的应用三、教学过程1.导入(5分钟)(1)教师通过提问方式引导学生回顾乘法的意义和基本运算方法。
(2)学生回答问题,教师给予点评和指导。
2.讲解(15分钟)(1)教师详细讲解乘法的意义和基本运算方法,强调乘法与加法的联系和区别。
(2)教师通过实例讲解乘法口诀和乘法计算的方法,引导学生掌握乘法计算技巧。
3.练习(15分钟)(1)学生独立完成练习题,巩固乘法的基本概念和计算方法。
(2)教师对学生的练习进行点评和指导,纠正错误,解答疑问。
4.应用(10分钟)(1)教师提出实际问题,引导学生运用乘法知识解决问题。
(2)学生分组讨论,共同解决问题,教师给予指导和评价。
5.总结(5分钟)(1)教师对本节课的内容进行总结,强调重点和难点。
(2)学生分享学习心得,提出改进意见和建议。
四、作业布置1.完成课后练习题,巩固乘法的基本概念和计算方法。
2.预习下节课的内容,提前了解乘法在实际问题中的应用。
五、教学反思本节课通过复习乘法的基本概念和计算方法,培养了学生的逻辑思维能力和抽象思维能力。
通过解决实际问题,提高了学生运用乘法知识解决实际问题的能力。
在教学中,要注意关注学生的学习情况,及时给予指导和帮助,确保学生能够熟练掌握乘法知识。
同时,要注重培养学生的合作意识和团队精神,提高学生的综合素质。
重点关注的细节是“讲解(15分钟)”,特别是教师如何详细讲解乘法的意义和基本运算方法,以及如何通过实例讲解乘法口诀和乘法计算的方法,引导学生掌握乘法计算技巧。



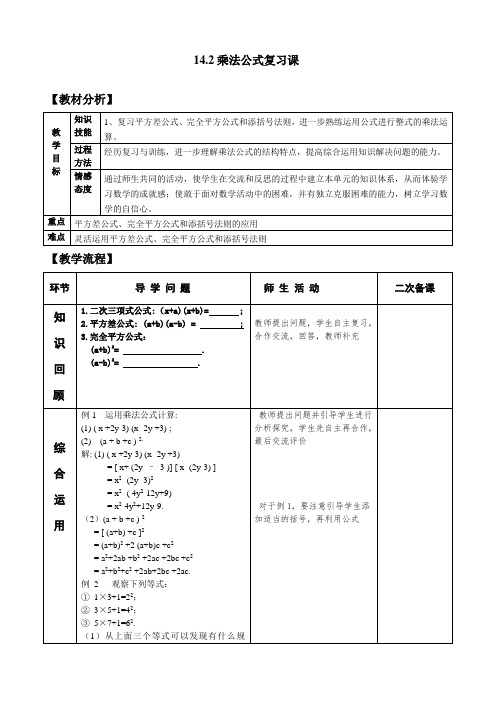
《乘法公式复习课》导学案枣阳市第六中学王军【复习目标】⑴、复习平方差公式、完全平方公式的应用;⑵、经历复习与训练,进一步理解乘法公式的结构特点,提高综合运用知识解决问题的能力;⑶、敢于面对数学活动中的困难,并有独立克服困难的能力,树立学习数学的自信心。
【复习重点】平方差公式、完全平方公式和快速公式的应用。
【复习难点】灵活运用平方差公式、完全平方公式和快速公式。
【复习过程】二、合作交流,探究方法类型一:应用公式1、下列各式:A、(x+y)(-x-y);B、(x-y)(-x-y);C、(2a+3b)(3b-2a) D 、(2X-3Y)(2Y+3X).可以用平方差公式计算的有();可以用完全平方公式计算的()2、下列各式中,运算结果是 x2-36y2的是( )A、(-6y-x)(6y-x)B、(-6y+x)(6y-x)C、(x+4y)(x-9y)D、(-6y+x)(-6y-x)3、想一想:(1)、(2x-y)(_____)=4x2-y2(2)、(b-a)(_____)=a2-b2(3)、4x2-12xy+(____)=(______)2 (4)、(-3x-2)(_____)=4-9x24、试一试:(相信你能行!)①、 a4-(a-b)(a+b)(a2-b2)②、(m+n+1)(m+n-1)-(m+n)2 ③、(2x+3y)2- (2x-3y)25、比一比,谁最快6、考一考:⑴、⑵、1022三、基础训练应用拓展:类型二:公式变形1、若x2-y2=44,x-y=4,则x+y=2、a2+b2-ab+ =(a+b )23、(a+b)2=(a-b)2+4、已知(a+b)2=9,(a-b)2=5 ,则 a2+b2= ab=5、请你认真填一填:已知a+b=-7,ab=10,则 (1)、a2+b2=_____,(2)、 ab2+a2b=_______6、若 (a+1)2+b2-8b+16=0求 3(a-b)的值。
1、 平方差、完全平方公式的熟练掌握。
2.能运用公式进行简单的计算。
重点:公式特征分析与公式的熟练运用难点:根据图形转化数学公式以及用图形表达公式 教学过程设计:布置作业课堂小结形成技能公式固化公式内化课堂小测→→→→→教学过程:一、课堂小测:填空:(1).平方差公式: (a +b)(a -b)=______________(2)完全平方和公式: (a +b)2=_____________ ;(3)完全平方差公式: (a -b)2=______________ (4)( )(-2x-3y)=2294y x - (5)(3a-2b)( )=224129b ab a +-二、公式内化练习1:指出下列各式中的错误,并加以改正:(1) 122)12(22+-=-a a a (4) (3a+2)(3b-2)=9ab-4(2) 14)12(22+=+a a (5) (0.5+a)(-a+0.5)=25.02-a(3) 12)1(22--=--a a a (6) (-x-1)(x+1)=12-x三、运用与提升:例题1:先化简,再求值:(1)(x +2y )(x -2y )-(2x -y )(-2x -y ), 其中x =8,y =-8;(2) [(x -y)2+(x+y)(x -y)]÷2x ,其中x=3,y=-1.5.例题2、(1)已知已知:的值)(的值)(试求2222b a )2()1(:,2,7+-==+b a ab b a (2)已知()72=+b a ,ab=2,求22b a +的值例题3下面计算是否正确?若不正确,写出正确的计算过程和计算结果。
99999999110000)1100)(1100()1100)(110)(110()1100)(110)(110)(110(100011011122222222=-=+-=++-=+++-=⨯⨯四、巩固与练习 1.计算(1)、 498×502 (2)、 2253539447+⨯+2. 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x ,y 表示矩形的长和宽(x >y),则下列关系式中不正确的是( )A. x+y=12B. x -y=2C. xy=35D. 14422=+y x五、课堂小结:符号语言,公式左边与右边的特点,转化,整体思想。
教师学科教案[ 20 – 20 学年度第__学期]任教学科:_____________任教年级:_____________任教老师:_____________xx市实验学校乘法公式的复习(1)光明初级中学 杜颜教学目标1.通过学生自主练习以及教师点拨,进一步理解平方差公式和完全平方公式。
2.能够正确、熟练地运用公式。
3.在练习过程中体会数学的“整体”思想和“化归”思想。
教学重点能够正确、熟练地运用公式。
在练习过程中体会数学的“整体”思想和“化归”思想。
教学难点在练习过程中体会数学的“整体”思想和“化归”思想。
教学过程一、引入(上节课,我们已经复习了多项式乘以多项式的运算,那么现在我们来做一组练习。
)练习1计算: (32)(23)a b a b +- (32)(32)a b a b +-(2)(3)a b a b -- (2)(2)a b a b --公式,在适合的情况下使用乘法公式可以使计算得以简化。
(板书课题)二、复习公式结构练习2计算:① 11()()22a b a b +- ② 2(30.1)m n + ③ ()()x y x y ++ ④ 22(2)x y -(板书公式,分析结构。
)三、应用与巩固练习3计算:① 11()()22a b a b -+- ② (44)()a b a b +- 总结:如果遇到不能直接使用乘法公式的情况,可以尝试进行转化。
练习4计算:① 11()()22a b a b --- ② 21()2a b -+ ③ 11()()22a b b a -++ ④ 21()2a b -- 总结:善于使用“整体思想”考虑问题可以更快的实现“转化”目标。
四、巩固与提高练习5计算:(说说你的解题思路。
)① 2()a b c ++ ② 2)32(z y x +-③ ()()b c a a b c ++--- ④ ))((z y x z y x -+++⑤ )14)(14(+--+y x y x ⑥ )32)(32(d b y x d b y x -+++-+总结:对于两项以上的多项式乘法再应该重视“整体思想”的应用,体会化归思想。
乘法口诀复习课教案(共5篇)第一篇:乘法口诀复习课教案数学游乐园教学目标:1、通过复习使学生知道乘法的意义与各部分的名称。
熟记1~9的乘法口诀,能熟练地口算9以内的两个数相乘。
2、学生会根据乘法的意义解决一些简单的实际问题。
3、培养学生良好的学习习惯和数学能力。
教学重点、难点:熟记1---9的乘法口诀并能正确计算。
根据乘法的意义解决一些简单的实际问题。
教学过程:一、创设情境,激发兴趣谈话:(出示游乐园)同学们,你们都去过游乐园,那里很好玩吧?今天,老师要带大家去一个特殊的游乐园(出示幻灯片)——数学游乐园玩一玩,想去吗?那让我们出发吧!板书课题:数学游乐园二、检查口诀,铺垫主题谈话:可是,我们要想进游乐园,必须过乘法口诀的关,游乐园的门才会自动打开。
你们愿意挑战吗?(1)乘火车背诵口诀同学们可真棒啊!乘法口诀说的这么流利,.但游乐园的门还没开.好像不太相信你们的真本领,所以他想让老师和你们对口令.你们敢吗?谁想好了就可以直接抢答.(师说口令,生抢答)(2)师生对口诀谈话:刚才同学们表现的非常踊跃。
不知不觉,游乐园的门已经打开,让我们进去玩玩吧。
三、巧设游戏,启迪思维1、跷跷板先让我们来玩跷跷板吧(出示跷跷板)每组跷跷板的两边各有一句乘法口诀,你能很快地说出两个乘法算式吗? 七八五十六四六二十四五七三十五八九七十二(八九七十二中两个因数分别是几)你还能举出因数不同的乘法算式吗?你能举出两个因数相同的乘法算式吗?你们真厉害,跷跷板对于你们来说很简单了,让我们继续往前行。
随着熙熙攘攘的人群来到了竞技馆,好热闹啊,原来是魔术表演,快让我们来加入吧。
(出示幻灯)2、魔术表演(1)我会变魔术。
同学们请你们随意说出一个两位数,将这个两位数的十位数字与个位数字相乘,并算出结果,如果结果又是一个两位数,再将这个两位数的十位数字和个位数字相乘,最后得的结果肯定是小于10的数,不信我们试一试。
如,一位学生说:“59”,另一位学生则口算:5×9=45→4×5=20→2×0=0学生说,老师可以在黑板上板书。
拒绝盲从——“乘法公式复习课”教学案例背景:复习课在教学中并不讨人喜欢,因为复习课的教学内容往往如同把已学的知识进行“回炉”,学生缺少了首次学习知识的新鲜感;复习课的教学方式僵化、呆板,一般都是“整理+练习”的板块结构,教师组织复习时,大多是一厢情愿机械地对所学知识进行简单的重复、堆积、罗列,学生缺乏主动性······因此,与新授课相比,师生都不钟情复习课,教师讲得累,学生听得累。
那么,复习课是否就因复习内容的旧、方式的死而无法“美容”从而吸引学生呢?复习课非得有复习课的模式吗?笔者以《乘法公式复习课》这一案例来述说复习课教学有时也应拒绝盲从,不拘泥于传统教学模式。
情景描述:(师课前已分给学生所需的学具)打破传统复习课教学模式,教学一开始,不再是立即告诉学生这节上的是乘法公式的复习课,而是从游戏引入:师:同学们,你们喜欢网络游戏吗?学生异口同声道:“喜欢。
”回答在意料之中,我微笑地说:“今天,老师就带大家进入网络拼图游戏。
”屏幕上出示当时最流行的网络游戏画面。
此时,我发现学生们的注意力开始集中,连平时上课精神涣散的个别学生也聚精会神。
片断一:师:拼一拼,现在如图正方形①一个,正方形②一个和长方形③两个,请你用它们拼成一个正方形。
学生一听说拼图,个个劲头十足,课堂气氛活跃,每个学生都积极参与到动手拼图之中。
师:谁能把你的作品展示在黑板上?大家反应非常踊跃。
一生上台展示后,我乘胜追击,因势利导:“你能根据所拼图的面积关系验证乘法公式吗?”一生站起来:(a+b )²=a²+2ab+b²反应快的同学情不自禁赞叹道:“好样的。
”反应较慢的则一露出迷茫的眼神,这时一位平时好问但成绩不好的学生问道:”老师,为什么可以验证乘法公式?“生:因为拼好后的大正方形边长为a+b ,面积则为(a+b )²,若看成4部分面积和,则为a²+2ab+b²,所以正好验证了完全平方和公式(a+b )²=a²+2ab+b²。
我进一步提出疑问:“你们能根据这一幅拼图的面积关系验证另一条完全平方公式吗?”(学生思考片刻,纷纷举手抢着要回答)生:这个拼图中红色部分正方形边长为a-b ,面积则为(a-b )²,如果看成大正方形面积减去两个长a ,宽为b 的长方形的面积,则多减了一个边长为b 的正方形,所以还要加上这个小正方形的面积,所以是a²-2ab+b²,因此正好验证了完全平方差公式(a-b )²=a²-2ab+b²。
我对他们的积极思考。
发言给予肯定。
趁热打铁,我出示一道数形结合的综合运用题:如图,已知a+b=3,a ·b=1,求a²+b²的值。
[为了能让学生了解一些代数式的几何意义,为他们今后学习数学打下了些基础,我用数形结合方法向学生出示这样一个问题:][1]你能用图来解释a²+b²这个代数式的几何奥秘吗?[2]还有其他求面积的方法吗?[3]你能根据以上提示写出一个代数恒等式吗? 学生陷入沉思,一会儿,有一位学生站起来发言(激动地忘记了举手):“老师,我想出来,a²+b²表示边长分别a 、b 的两个正方形面积之和,并且这两个正方形面积也可以看成最大正方形面积减去两个相同的长方形面积。
所以代数恒等式为:a²+b²=(a+b )²–2ab 。
因此题目中的a²+b²的值也可以根据这个恒等式求出来,得数为7。
”生2(插嘴):根据完全平方和公式就马上能推出a²+b²=(a+b )²–2ab(对于他们的回答,我无懈可击,心理很是得意,同学们个个备受鼓舞。
)此时,我趁机引导:“同理a²+b²=(a –b )²···?”生七嘴八舌道:“a²+b²=(a –b )²+2ab ”片断二:如图:①是一个长为2a ,宽为2b 的正方形,沿虚线剪开,均分成4块长方形,然后按a ba b aab图②的形状拼成一个正方形。
动手操作,请讨论以下问题:[1]在图②中,空白正方形边长是多少?[2]在图②中,请你用两种不同的方法表示空白正方形的面积。
你能从中得到怎样的代数恒等式?[3]你还能根据图②写出其它代数恒等式吗?(开始,全班都在动手操作,过一会儿,同学们有的一个在想,有的和同桌在小声讨论。
)[这个练习我考虑了很久,因为它不仅能训练学生的数形结合能力,而且能进一步理解完全平方和与完全平方差的关系。
但是,是给出图形要学生写代数式,还是给出代数式要学生拼图呢?后者显然更难,最后决定给出图形要学生写代数式。
但是,是像前面给出提示让学生写代数恒等式呢?还是放手让学生写呢?因为考虑到学生水平,最后采用提示一种,其余放开手让学生发挥。
结果学生反馈时出现了4种很好的思维:]学生1说:空白正方形边长为(a –b ),面积为(a –b )²,如果空白部分看成大正方形面积减去小正方形的面积,则面积为(a+b )²–4ab ,因此(a –b )²=(a+b )²–4ab 。
学生2不甘示弱,马上举手回答:“根据求大正方形的面积两种方法,可以写出(a+b )²=(a –b )²+4ab 这个代数恒等式。
”(这两个代数恒等式虽差不多,但思路不一样,我还是及时表扬了他们,学生的情绪更加高涨,纷纷举手想说出自己的看法。
)学生3肯定地说:“从求四个长方形面积和的两种方法中,我们写出代数恒等式(a+b )²–(a –b )²=4ab ”学生4说:“我也是求大正方形面积,不过我跟前面的同学不一样的分法,我是把大正方形看成三个长方形的和,所以得到的代数恒等式为(a+b )²=(a+b )(a –b)+2b (a+b )”片断三:如图,(1)你能将它剪成两部分然后拼写一个长方形吗?(2)若能,你能用两种方法求你所拼成的长方形面积吗?b a ab b(学生自发采用四人小组合作方式动手操作,讨论交流,课堂气氛迅速活跃起来,看得出学生的思维状态非常活跃。
)“哪组能派个代表上来演示作个汇报?”我适时地问道。
生1:这个图形面积可看作两个长方形面积的差,即a²–b²我沿这条线剪开拼成一个长方形,这个长方形为(a+b),宽为(a–b),所以a²–b² =(a+b)(a–b)。
生2:我是沿这条线剪开,拼成一个长方形,这个长方形(b+a),宽为(a–b),所以a²–b² =(a+b)(a–b)。
师:“太棒了,你们很会学习。
”(成功的喜悦即红了他们的小脸,他们自觉地进入下一个探索。
)[为了培养学生从写会这个问题到会通过它解决其他问题的意识和能力,我创设了下面一个探索题。
]①②1、如图①是由2个边长分别为100和99的正方形重叠得到的,求图中阴影部分的面积。
(对于这一题学生很容易解决)。
2、如图②中若由100个边长为100、99、98、……,2、1的正方形重叠而成的,那么,按这种方式重叠,而成的阴影部分面积是____,对这题,我以为学生理解可能会有些困难,可学生的反应非常不错片断四:[希望学生在思维方面能有所拓展,我设计了具有一定的挑战性和开放性的练习。
] “你能用以下3个正方形和6个不同的长方形拼成一个更大的正方形,”(没有重叠,没有空白)并能根据这个大正方形的两种不同面积法写出代数恒等式吗?“我带着期待眼光问。
(a+b+c)²=a²+b²+c²+2ab+2ac+2bc(一下子,整个班静悄悄,陷入思考之中,似乎他们感觉到此题有难度,按惯例自发组成小小组合作探索。
过了一会儿,有一小组举起了手,随后过了片刻,又有几小组举起了手。
)我让第一个举手的小组代表展示并汇报,这学生果然不负众望,很出色地完成了任务。
“很会思考。
”我对他的展示及汇报表示了充分地肯定,其他学生也报以掌声,不少学生脸上充满了自信。
”(下课钟声即将敲响,我们的课也在小记者采访同学学习收获中结束了。
)教学研究:1、课后反思:新课程强调学习方式的转变,要求学习方式由单一性转向多样性,让学生在读中学、玩中学、听中学,在思考中学习、游戏中学习、合作中学习,让学生了解和掌握更多的学习方式,让身体更多的器官参与学习,从而获得学习中的乐趣与全面和谐的发展。
的确,新课程的实施给教师提出了全新的挑战。
但大部分的教师新课程的理念都只体现在新授课中,我个人认为,复习课中也应有新课程理念的体现。
本课通过拼图游戏贯穿整节课,复习痕迹淡化,在拼图复习乘法公式及其变形,又在拼图中学习根据图形列代数恒等式的能力,并从中体会数形结合的奥秘。
整节课学生都是在拼图游戏中复习旧知,在合作探索中理解旧知,一扫以往复习的沉闷。
在此我的思考是“复习课与新授课可以融合,可以是新的不新、旧的不旧,新中有旧、旧中有新。
”2、与同行讨论的问题:(1)本课的设计调动学生的积极性的同时,由于时间问题,知识能力目标是否会受到影响?(2)是否有必要把本课设计分成两节复习课,对每个知识点再纵向深入复习,对每个知识点再添加几个巩固应用?(3)本课内容通过动手拼图游戏展开教学,使学生对乘法公式及变形的复习依旧兴趣盎然,可有些复习课因内容性质所限,难以使教学变得新颖时,采到怎样的教学方法能尽量提高学生的复习兴趣?。