西安交大流体力学上机实验

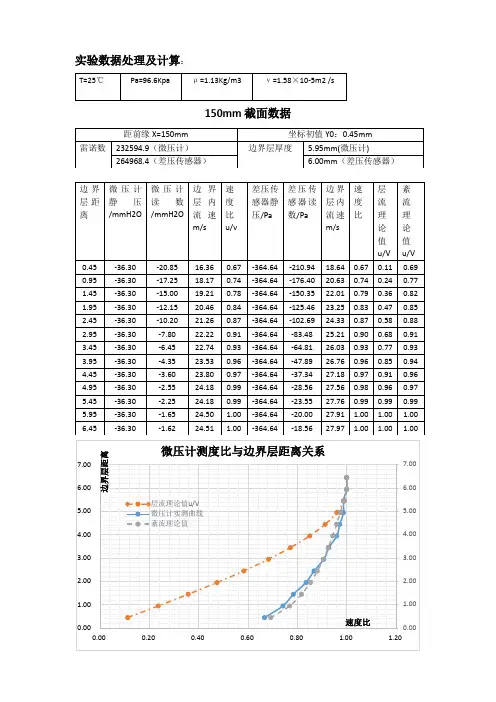
实验数据处理及计算：
150mm截面数据
250mm截面数据
数据结果分析：
1.由雷诺数判断流态：
临界雷诺数Re=3∗10
流态判断：150mm截面为层流流动
250mm截面为层流向紊流过度区域2.根据边界层的速度分布判断流态：
由绘制的曲线分析，实测曲线均与紊流理论曲线吻合较好。

判断结果为：150mm截面、250mm截面均为紊流流态
3.根据边界层厚度判断流态：
层流：δ=5∗√υx
V
紊流：δ=0.37*υ1
5*x
由以上数据判断结果为：150mm截面流态为：紊流250mm截面流态为：紊流
实验总结与思考：
通过如上三种方法认为，通过实验，该平板模型在实验流场中，150mm截面处与250mm界面处均为紊流流态。

原因可能是风洞中流速过快，以及1截面选择过于靠后，因而测不到或测得层流流态。

建议下次试验对100mm截面进行测试。

思考题：
1.流体的流动状态受到哪些因素的影响？
答：Re=LVρ/μ,影响因素有特征长度L，,流速u,流体密度ρ,流体粘度μ.而温度会影响流体的粘度和密度。

2.为何层流和紊流呈现不同的速度分布规律？
答：两种状态和流动的雷诺数雷诺数小,意味着流体流动时各质点间的粘性力占主要地位,流体各质点平行于管路内壁有规则地流动,呈层流流动状态.雷诺数大,意味着惯性力占主要地位,流体呈紊流流动状态。

流体力学上机实验报告一、 实验问题描述该算例是一个二维的导流管分析，分析一个雷诺数为400的层流情况，所用二、 分析方法及假定用FLUID141单元来作二维分析，本算例作了如下分析：雷诺数为400的假想流的层流分析，分析时假定进口速度均匀，并且垂直于进口流场方向上的流体速度为零。

在所有壁面上施加无滑移边界条件（即所有速度分量都为零）；假定流体不可压缩，并且其性质为恒值，在这种情况下，压力就可只考虑相对值，因此在出口处施加的压力边界条件是相对压力为零。

分析时，流场为层流，着可以通过雷诺数来判定，其公式为：R e =ρvD ℎμ三、 几何尺寸及流体性质进口段长度 4 m 进口段高度 2 m 过渡段长度 2m 出口段高度 2 m 出口段长度 4 m 假设流体密度 1 Kg/m3 假设流体粘性 0.01Kg/m -s ； 空气密度 1.205 Kg/m3 空气粘性 1.8135*10-5 Kg/m -s 进口速度 2.0 m/s 出口压力 0 nt/m2四、 分析过程1. 进入ANSYS参见ANSYS Operation Guide进口 出口过渡段 流体流动方向外壁面内壁面2. 设置分析选择1）进入Main Menu>Preference2）点取FLOTRAN CFD项3）点取OK3.定义单元类型1）进入Main Menu>Preprocessor> Element Type>Add/Edit/Delete2）点取Add3）在弹出菜单的左框中点取FLOTRAN CFD，右框中点取2D FLOTRAN 1414）点取OK5）点取Close4.生成分析区域的几何面1）生成进口段，进入Main Menu>Preprocessor>-Modeling-Create>-Areas- Rectangle>By Dimensions2）在弹出菜单中的相应区域输入以下值：X1处输入0X2处输入4Y1处输入0Y2处输入23）点取Apply4）生成出口段，再在上面弹出菜单中输入以下值：X1处输入6X2处输入12Y1处输入0Y2处输入25）点取OK6）在工具栏（Toolbar）窗口中点取SAVE_DB7）进入Main Menu>Preprocessor>-Modeling-Create>Lines>Tan to 2 Lines 8）点取左侧矩形的右面一条线作为第一条切线，再在点取菜单中点取OK 9）点取该线的上端点作为第一切点，再在点取菜单中点取OK10）点取右侧矩形的左面一条线作为第二条切线，再在点取菜单中点取OK11）点取该线的上端点作为第二切点，再在点取菜单中点取OK12）在点取菜单中点取Cancel。

《流体力学》课程实验指导书袁守利编汽车工程学院2005年9月前言1.实验总体目标、任务与要求1)学生在学习了《流体力学》基本理论的基础上，通过伯努利方程实验、雷诺实验、阻力综合实验和动量方程实验，实现对基本理论的验证。

2）通过实验，使学生对水柱（水银柱）、U型压差计、毕托管、孔板流量计、文丘里流量计等流体力学常用的测压、测流量装置的结构、原理和使用有基本认识。

2.适用专业热能与动力工程3.先修课程《流体力学》相关章节。

4.实验项目与学时分配5. 实验改革与特色根据实验内容和现有实验条件，在实验过程中，采取学生自己动手和教师演示相结合的方法，力求达到较好的实验效果。

实验一阻力综合实验一、实验目的1．观察和测试流体稳定地在等直管道中流动及通过阀门时的能量损失情况；2．掌握管道沿程阻力系数和局部阻力系数的测定方法；3．熟悉流量的测量和测定文丘里及孔板流量计的流量系数；4．熟悉毕托管的使用。

二、实验条件阻力综合实验台三、实验原理1．实验装置：图一阻力综合实验台结构示意图1.水泵电机2.水泵3.循环储水箱4.计量水箱5.孔板及比托管实验管段进水阀6.阀门阻力实验管段进水阀7. D=14mm沿程阻力实验管段进水阀8.D=14mm沿程阻力实验管段9. 阀门阻力实验管段10.孔板流量计11. 比托管12. 测阻阀门13.测压管及测压管固定板14. D=14mm沿程阻力实验管段出水阀15阀门阻力实验管段出水阀16. 孔板及比托管实验管段出水阀17.文丘里实验管段出水阀18. D=10mm沿程阻力实验管段出水阀19.管支架20. D=10mm沿程阻力实验管段21. 文丘里流量计22排水阀门2.工作原理阻力综合实验台为多用途实验装置，利用这种实验台可进行下列实验：A 、阻力实验。

1）. 两种不同直径管路的沿程阻力实验。

2）.阀门局部阻力实验。

B 、孔板流量计流量系数和文丘里流量计流量系数的测定方法。

C 、皮托管测流速和流量的方法。

一、 选择题(略) 二、 判断题(略) 三、 简答题1.等压面是水平面的条件是什么？:①连续介质 ② 同一介质 ③ 单一重力作用下.2. 同一容器中装两种液体，且21ρρ〈，在容器侧壁装了两根测压管。

试问：图中所标明的测压管中液面位置对吗？为什么？C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器解：不对，（右测压管液面要低一些，从点压强的大小分析） 3. 图中三种不同情况，试问：A-A 、B-B 、C-C 、D-D 中哪个是等压面？哪个不是等压面？为什么？：（ a ）A-A 是 （b ）B-B 不是 （c ）C-C 不是， D-D 是。

四、作图题(略)五、计算题(解题思路与答案)1. 已知某点绝对压强为80kN/m 2，当地大气压强p a =98kN/m 2。

试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。

解： 用水柱高表示（1）该点绝对压强：8.16mH 2o （2）该点相对压强：-1.84mH 2o（3）该点真空压强：1.84mH 2o用水银柱高表示（1）该点绝对压强：599.1mm H g（2）该点相对压强：-135.4 mm H g （3）该点真空压强：135.4 mm H g2. 一封闭水箱自由表面上气体压强p 0=25kN/m 2，h 1=5m ，h 2＝2m 。

求A 、B 两点的静水压强。

解：由压强基本公式ghp p ρ+=0求解A p = 7.551 mH 2o (74 kN/m 2) B p = 4.551 mH 2o (44.6 kN/m 2)3 如图所示为一复式水银测压计，已知m 3.21=∇，m 2.12=∇，m5.23=∇，m 4.14=∇，m5.15=∇(改为3.5m)。

试求水箱液面上的绝对压强0p ＝？解：①找已知点压强(复式水银测压计管右上端)②找出等压面③计算点压强,逐步推求水箱液面上的压强0p.: 0p=273.04 kN/m24 某压差计如图所示，已知H A=H B=1m，ΔH=0.5m。

《计算流体力学》上机实验报告班级：姓名：学号：北京航空航天大学流体力学研究所上机实验名称两平行平板间不可压缩流体绕物体的平面无旋流动一、实验目的通过具体算例，熟悉和掌握使用CFD方法获取给定流场的流动参数。

二、实验内容、方法及步骤1.流动问题描述如下图所示，考虑在平行放置的两平板之间流过的理想不可压缩流体绕方形物体的平面无旋流动。

2.求解区域H；绕流物体是边长为2的正方形，设两平行平板之间的距离为6L。

根据流动的对称性，可取流上游来流入口位置与物体中心的距离为3动区域的四分之一作为求解区域，如下图所示。

3. 控制方程对于不可压缩流体的平面无旋流动，流函数 在区域 内满足Laplace 方程22220xy4. 边界条件（1）OABC 是一条流线，规定0OABC；（2）对 OE 上任意一点 0,P y ，有Py ；（3） ED 也是一条流线，所以2EDH ； （4）根据对称性，在 CD 上有0CDx。

5. 定解问题对于这里考虑的流动，可用下述定解问题来描述22220 , 0 , , , 20 , x yOABC y OE HED CDx在 内在上在上在上在 上6. 求解区域的离散化 － 计算网格将单位长度等分成n 份，记1h n ，于是求解区域沿x 方向可划分成M L n 个网格，用0,1,2,3,,j M 来标记；沿y 方向可划分成2HNn 个网格，用0,1,2,3,,k N 来标记。

这些网格点可分成三类：（1）当 01j L n 且 0k N ，或者当 1L njM 且 n k N 时，网格点落在流场内部，称为内点。

这些网格点上的流函数需通过求解方程组来计算； （2）当 1Ln j M 且 0k n 时，网格点落在正方形物体内部，网格点上不存在流场，无需计算；（3）其余的网格点落在流场的边界上，称为边界点。

这些网格点上的流函数直接由边界条件给定，也无需计算。

7. 定解问题的离散化 － 差分格式Laplace 方程22220xy的差分近似为1,,1,,1,,122220j kj k j kj k j k j k hh边界条件0x的差分近似为,1,0j kj kh8. 内点上流函数的计算－ 迭代算法在实际的计算中，内点的数量非常多，计算流函数需要求解大型的代数方程组。

φ1 − φ2 E= （φ1 + φ2）2
三、计算过程
用 MATLAB 编写计算程序，取网格步长 ∆x = ∆y = 0.1m 。 1、第一类边界条件 （1）运行程序 1（见附录 1） ，得到等温边界条件下计算墙角温度分布图：
图 4 等温边界条件下计算等温线分布（左图中每两条线间隔为三摄氏度） 运行程序 2（见附录 2） ，得到等温边界条件下实测墙角温度分布图：
s1=0; for i=2:11 s1=s1+(30-T(i,2))*0.53; end for j=2:15 s1=s1+(30-T(11,j))*0.53; end s1=s1+(30-T(1,2))*0.53/2+(30-T(11,16))*0.53/2
%墙角外侧换热量
s2=0; for i=2:6 s2=s2+T(i,5)*0.53; end for j=7:15 s2=s2+T(8,j)*0.53; end s2=s2+T(1,5)*0.53/2+T(8,16)*0.53/2+T(7,5)*0.53/2+T(8,6)*0.53/2 %墙角内侧换热量 s=2*(s1+s2) %单位长度墙壁的总换热量 e=abs(s1-s2)/((s1+s2)/2)
图3
内节点和绝热边界
图 3 所示的内节点和绝热边界节点方程如下： 内节点：
⎡(t −t )∆x (t −t )∆x (t −t )∆y (t −t )∆y⎤ ΦN +ΦS +ΦE +ΦW = λ⋅1⋅ ⎢ i, j+1 i, j + i, j−1 i, j + i+1, j i, j + i−1, j i, j ⎥ = 0 ∆y ∆y ∆x ∆x ⎣ ⎦

流体力学上机实验报告题6-27强度为 24 m2/s 的点源位于坐标原点，与速度为 10m/s沿x正向的均匀流动叠加。

求复合流动滞止点到坐标原点的距离：该流动可以表示的绕流物体的形状及在θ=π/2 和3π/2 处物体外廓线之间的距离；θ=π/2 处物体外廓线上的速度。

分析：复合流动的速度势函数与流函数分别为Φ=10r cosθ+242πln rΨ=10r sinθ+242πθ流线方程为C=10r sinθ+242πθ势流速度场为V r=10r cosθ+242πrVθ=−10sinθ当θ=π2时V r=6.366m/s, Vθ=−10m/s则当Vr=0时，X=r=−0.382m外轮廓线所对应方程为12=10r sinθ+242πθ则在θ=π2，3π2之间时：外轮廓线距离为1.2m下面采用EXCEL工具绘制轮廓线：图中A代表θ，B代表X值，C代表Y值B= (1.2-0.38217*A)/TAN(A)C==1.2-0.38217*A所绘图像如下题7-36设有一虹吸管，其装置如图所示，设管径为 150mm.试求通过该管的流量。

已知水温为10 ℃，Δ=1mm,ξ弯头= 0.4 ,ξ进口= 1.0 。

分析：根据题意列出伯努利方程：p1ρg +z1+V122g=p2ρg+z2+V222g+ℎLT根据题意代入数据得：ℎLT=3−V22 2g考虑沿程和局部水力损失：ℎLT=(f ld+1+2∗0.4)V222g整理得：58.86=（70f+2.8）V22雷诺数Re有：Re=ρV2D μ当温度是10摄氏度时：ρ=999.7kg/m3,μ=1.307*10-3 N*s/m2 则整理上述方程代入数据可得：Re=114730√58.8670f+2.8根据科尔布鲁克公式1√f =−2.0lg (∆D⁄3.7+2.51Re√f)由上式即可构成迭代循环。

其中，对于循环初值，由,在大雷诺数条件下可在莫迪图上查出f 的初值为0.033.最后由Q=AV=πD＾2V/4可解得流量值。

其他系统西安交通大学---流体力学所有答案应用总流伯努利方程解题时，两个断面间一定是缓变流，方程才成立。

答案是：错误液体在重力场中作加速直线运动时，其自由面与重力和惯性力的合力处处正交。

答案是：错误液滴内的压强比大气压小。

（答案是：错误相邻两流线的函数值之差，是此两流线间的单宽流量。

（）答案是：正确相对静止状态的等压面一定也是水平面。

答案是：错误相对静止状态的等压面可以是斜面或曲面。

答案是：正确温度升高液体的表面张力系数增大。

答案是：错误温度升高液体的表面张力系数增大答案是：错误通过一个曲面上的体积流量与法向速度有关。

答案是：正确声音传播过程是一个等熵过程。

答案是：正确如果流场中若干流体微团无绕自身轴线旋转运动，刚称为无旋流动。

答案是：错误气体的粘性随温度的升高而增大。

答案是：正确普朗特混合长度理论建立了脉动速度与时均速度梯度之间的关系。

答案是：正确平面无旋流动既存在流函数又存在势函数。

平面流只存在流函数，无旋流动存在势函数。

答案是：正确牛顿流体的粘性切应力与速度梯度，即角变形速率成正比。

答案是：正确马赫线是超音速流动中被扰动和未扰动区域的分界线。

答案是：正确流体质点只有质量没有大小答案是：错误流体静止或相对静止状态的等压面一定是水平面。

答案是：错误流体的粘滞性随温度变化而变化，温度升高粘滞性减少；温度降低粘滞性增大。

（）答案是：错误流体的静压是指流体的点静压。

答案是：正确理想流体定常流动，流线与等势线重合。

答案是：错误静止流体中任意点的压强与方向无关。

答案是：正确静止的流体中任意一点的各个方向的压强值均相等。

答案是：正确恒定流是迁移加速度为零。

答案是：错误附面层外的流体流动时理想无旋流动。

（）答案是：正确附面层内的流体流动是粘性有旋流动。

答案是：正确附面层分离只能发生在增压减速区。

对于无旋流动，其速度势函数满足拉普拉斯方程的必要条件是流动定常。

答案是：错误对于不可压缩流体的平面流动，存在着流函数。

研究生课程介绍课程编码：091002课程名称：计算方法(A)Computational Methods (A)学分：3课内总学时数：72上机（实验）学时数：18课程内容简介：本课程讲授电子计算机上使用的各种基本的数值计算方法, 如插值法, 最小二乘法, 最佳一致逼近, 数值微积分, 方程求根法, 线性与非线性代数方程组解法, 矩阵特征值与特征向量求法, 常微分方程初值问题的解法, 求解数理方程定解问题的差分法, 有限元法等. 书中重点讨论了各种计算方法的构造原理和使用, 对稳定性, 收敛性, 误差估计等也作了适当讨论. 本课程适合于计算数学专业以外的理工科各专业研究生学习。

先修课：高等数学, 线性代数, C 语言或FORTRAN 语言参考书目：1. 邓建中,刘之行编, 计算方法，西安交通大学出版社，2002执笔人：梅立泉、李乃成、高静审定人：彭济根课程编码：091003课程名称：计算方法（B）Computational Methods (B)学分：3课内总学时数：54上机（实验）学时数：48课程内容简介：由于现代计算机技术的迅速发展，数值方法已成为科学研究的最重要的手段之一。

本课程在介绍数值计算的基本问题，包括浮点数、误差形成等的基础上，主要介绍：线性方程组的直接解法与迭代解法、离散数据的连续化处理（包括多项式插值、分段插值和最小二乘法）、数值积分和数值导数、非线性方程解法简介、常微分方程数值解法、以及最优化方法简介。

通过听课与相应的上机练习等途径，理解数值方法的形成原理，掌握最基本的数值方法，了解采用数值方法时应注意的主要问题，为以后在科研和工程技术工作中设计算法、应用数值软件进行数值计算奠定必要的基础。

先修课：高等数学、线性代数、算法语言（Fortran、C、C++、或Matlab 等）参考书目：1.凌永祥、陈明逵编，计算方法教程（第二版）西安交通大学出版社，2005执笔人：黄昌斌、苏剑、马军审定人：彭济根课程名称：工程优化方法及其应用Engineering Optimization Methods and Its Applications学分：2课内总学时数：40上机（实验）学时数：课程内容简介：讲述工程优化的数学基础，凸集、凸函数、凸规划的基本概念与基本理论；突出非线性规划各类算法的共性分析及其在计算机上可实现的步骤，并指出每类算法中所包含各种常用和著名算法；简介工程中常用到的几类特殊规划，如：线性规划、二次规划、几何规划和多目标规划的基本概念、常用和最新算法；简介工程优化设计应用实例（包括建立优化模型，根据模型特点构造或选用相适应的算法、计算流程图）。

工程流体力学实验报告实验一流体静力学实验实验原理在重力作用下不可压缩流体静力学基本方程或(1.1)式中：z被测点在基准面的相对位置高度；p被测点的静水压强，用相对压强表示，以下同；p0水箱中液面的表面压强；γ液体容重；h被测点的液体深度。

另对装有水油（图1.2及图1.3）U型测管，应用等压面可得油的比重S0有下列关系：(1.2)据此可用仪器（不用另外尺）直接测得S0。

实验分析与讨论1.同一静止液体内的测管水头线是根什么线？测压管水头指，即静水力学实验仪显示的测管液面至基准面的垂直高度。

测压管水头线指测压管液面的连线。

实验直接观察可知，同一静止液面的测压管水头线是一根水平线。

<0时，试根据记录数据，确定水箱内的真空区域。

2.当PB，相应容器的真空区域包括以下三部分：(1)过测压管2液面作一水平面，由等压面原理知，相对测压管2及水箱内的水体而言，该水平面为等压面，均为大气压强，故该平面以上由密封的水、气所占的空间区域，均为真空区域。

(2)同理，过箱顶小水杯的液面作一水平面，测压管4中，该平面以上的水体亦为真空区域。

(3)在测压管5中，自水面向下深度某一段水柱亦为真空区。

这段高度与测压管2液面低于水箱液面的高度相等，亦与测压管4液面高于小水杯液面高度相等。

3.若再备一根直尺，试采用另外最简便的方法测定γ最简单的方法，是用直尺分别测量水箱内通大气情况下，管5油水界面至水面和油水界面至油面的垂直高度h和h0，由式，从而求得γ0。

4.如测压管太细，对测压管液面的读数将有何影响？设被测液体为水，测压管太细，测压管液面因毛细现象而升高，造成测量误差，毛细高度由下式计算式中，为表面张力系数；为液体的容量；d为测压管的内径；h为毛细升高。

常温(t=20℃)的水，=7.28dyn/mm，=0.98dyn/mm。

水与玻璃的浸润角很小，可认为cosθ=1.0。

于是有(h、d单位为mm)一般来说，当玻璃测压管的内径大于10mm时，毛细影响可略而不计。

流体力学上机报告班级：能动05姓名：赵凯学号100311346-27强度为242m /s 的点源位于坐标原点，与速度为10m/s 沿x 正向的均匀流动叠加。

求复合流动滞止点到坐标原点的距离：该流动可以表示的绕流物体的形状及在θ=π/2和3π/2处物体外廓线之间的距离；θ=π/2处物体外廓线上的速度。

推导如下：强度为242m /s 的点源流函数为：Ψ=π224θ10m/s 沿x 正向的均匀流动流函数为：Ψ=10rsin θ二者叠加后流动的流函数即为Ψ=π224θ+10rsin θ则V r =θψ∂∂r =θπcos 10224+rV θ=-r∂∂ψ=θsin 10−对于滞止点需满足{00==θV V r 解得r=0.382mθ=π−即滞止点到原点的距离为0.382m绕流物体形状的方程即为Ψ=1224θ+10rsinθ=12即π2当θ=π/2时，r=0.6θ=3π/2时，r=0.6所以b=1.2m当θ=π/2，r=-0.6时=6.366m/s,VrV=10m/s.θ根据流线方程即绕流物体形状方程应用Excel软件解得散点数据后，应用origin软件画出流线和绕流物体形状如下图所示：7-36设有一虹吸管，其装置如图所示，设管径为150mm.试求通过该管的流量。

已知水温为10℃，Δ=1mm,4.0=弯头ξ,0.1=进口ξ。

推导如下：在自由界面与管道出口间列伯努利方程：LT h gp z g V g p z g V +++=++ρρ2222112122（1）其中1V =0,;1z =-1,2z =-4;1p =2p =a p .gD L f h LT2V 2(22）进口弯头ξξ++=（2）联立（1），（2）即可解得12)(2212+++−=进口弯头ξξDLf z zg V （3）又υD V 2Re =（4）Re 51.27.3/log(0.21f D f+∆−=（5）由式（3）（4）（5）即可构成迭代循环。

西安交通大学一、试验目的概率论部分1.了解matlab软件的基本命令与操作；2.熟悉matlab用于描述性统计的基本菜单操作及命令；3.会用matlab求密度函数值、分布函数值、随机变量分布的上下侧分位数。

数理统计部分1.熟悉matlab进行参数估计、假设检验的基本命令与操作.2.掌握用matlab生成点估计量值的模拟方法3.会用matlab进行总体数学期望和方差的区间估计。

4.会用matlab进行单个、两个正态总体均值的假设检验。

5.会用matlab进行单个、两个正态总体方差的假设检验。

二、试验问题实验五、随机变量综合试验实验内容1. 产生(6),(10),F(6,10)和t(6)四种随机数，并画出相应的频率直方图；2. 在同一张图中画出了N(0,1)和t(6)随机数频率直方图，比较它们的异同；3. 写出计算上述四种分布的分布函数值和相应上侧分位点命令.实验七、对统计中参数估计进行计算机模拟验证实验内容：1.产生服从给定分布的随机数，模拟密度函数或概率分布；2.对分布包含的参数进行点估计，比较估计值与真值的误差；3. 对分布包含的参数进行区间估计，行区间估计，可信度。

三、实验源程序及结果实验5源程序：% 清空内存，清空输出屏幕clc;clear;% 首先是指数分布n = normpdf(-2::14,6);% 绘制频率直方图plot(-2::14,n,'color','r','linewidth',2);ylabel('概率密度');title('正态分布概率密度');% t分布h1 = figure;t = tpdf(-3::3,6);plot(-3::3,t,'color','g','linewidth',2);ylabel('对应频率');title('t分布频率密度');% F分布h2 = figure;f = fpdf(0::10,6,10);plot(0::10,f,'color','k','linewidth',2); ylabel('对应频率');title('F分布频率直方图');% 卡方分布h3 = figure;ka = chi2pdf(0::15,6);plot(0::15,ka,'color','y','linewidth',2); ylabel('对应频率');title('卡方分布频率直方图');% 再来绘图h4 = subplot(2,1,1);y1=normpdf(-10::10,0,1);plot(-10::10,y1,'color','b','linewidth',2); title('N(0,1)');h5 = subplot(2,1,2);t1 = tpdf(-10::10,6);plot(-10::10,t1,'color','r','linewidth',2);%上侧分位数norminv,0,1)tinv,6)chi2inv,6)finv,6,10)运行结果：正态分布T分布F分布N(0,1)和t(6)随机数频率直方图四种分布的分布函数值和相应上侧分位点实验7源程序：% 以正太分布为例% 清空内存，清空输出屏幕clc;clear;y=normrnd(10,1,10000,1);ymin=min(y);ymax=max(y);x=linspace(ymin,ymax,80);yy=hist(y,x);yy=yy/10000;bar(x,yy);grid;xlabel('(a)¸概率密度分布直方图 ');phat=mle(y,'distribution','norm','alpha',%对分布函数参数进行区间估计，并估计区间的可信度 [mu,sigma,m_ci,s_si]=normfit(y,运行结果：正态分布概率密度分布直方图得到估计参数m =σ =由上可知估计的m = ，而实际是 10。

1.1 连续介质假说
连续介质方法失效场合 火箭穿越大气层边缘，此时微观特征尺度接近宏观特征尺度； 研究激波结构，此时宏观特征尺度接近微观特征尺度。
流体质点
1.1 连续介质假说
由确定流体分子组成的流体团，流体由流体质点连续无间隙 地组成，流体质点的体积在微观上充分大，在宏观上充分小。
流体质点是流体力学研究的最小单元。
控制体
流场中某一确定的空间区域，其边界称控制面。流体可以通过控制面流进流 出控制体，占据控制体的流体质点随时间变化。 为了在欧拉参考系中推导控制方程，通常把注意力集中在通过控制体的流体 上，应用质量、动量和能量守恒定律于这些流体，即可得到欧拉参考系中的 基本方程组。
通常力学和热力学定律都是针对系统的，于是需要在拉格朗日参考系下推导 基本守恒方程，而绝大多数流体力学问题又是在欧拉参考系下求解的，因此 需要寻求联系两种参考系下场变量及其导数的关系式
ur lim(vrm) V m
lim(m)
V V
在微观上充分大，宏观上充分小。
连续介质方法的适用条件
1 L3 n
1.1 连续介质假说
n为单位体积的分子数（特征微观尺度是分子自由程）， L为最小宏观尺度。
在通常温度和压强下，边长2微米的立方体中大约包含2×108个气 体分子或2×1011液体分子；在日常生活和工程中，绝大多数场合 均满足上述条件，连续介质方法无论对气体和液体都适用。
连续介质方法
把流体看作连续介质，而忽略分子的存在，假设场变量（速度、密 度、压强等）在连续介质的每一点都有唯一确定的值，连续介质遵 守质量、动量和能量守恒定律。从而推导出场变量的微分方程组。 流体力学采用连续介质的方法
连续介质方法
1.1 连续介质假说

西安交⼤概率论上机实验报告西安交通⼤学概率论实验报告概率论与数理统计上机实验报告⼀、实验内容使⽤MATLAB 软件进⾏验证性实验，掌握⽤MATLAB 实现概率统计中的常见计算。

本次实验包括了对⼆维随机变量，各种分布函数及其图像以及频率直⽅图的考察。

1、列出常见分布的概率密度及分布函数的命令，并操作。

2、掷硬币150次，其中正⾯出现的概率为0.5，这150次中正⾯出现的次数记为X ，(1) 试计算45=X 的概率和45≤X 的概率；(2) 绘制分布函数图形和概率分布律图形。

3、⽤Matlab 软件⽣成服从⼆项分布的随机数，并验证泊松定理。

4、设22221),(y x e y x f +-=π是⼀个⼆维随机变量的联合概率密度函数，画出这⼀函数的联合概率密度图像。

5、来⾃某个总体的样本观察值如下，计算样本的样本均值、样本⽅差、画出频率直⽅图。

A=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 2220 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13 14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16 19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28 19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18 18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33 08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24 17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18]6. 利⽤Matlab 软件模拟⾼尔顿板钉试验。