哈尔滨工业大学理论力学第七版第10章 动量定理
- 格式:ppt
- 大小:966.50 KB
- 文档页数:28



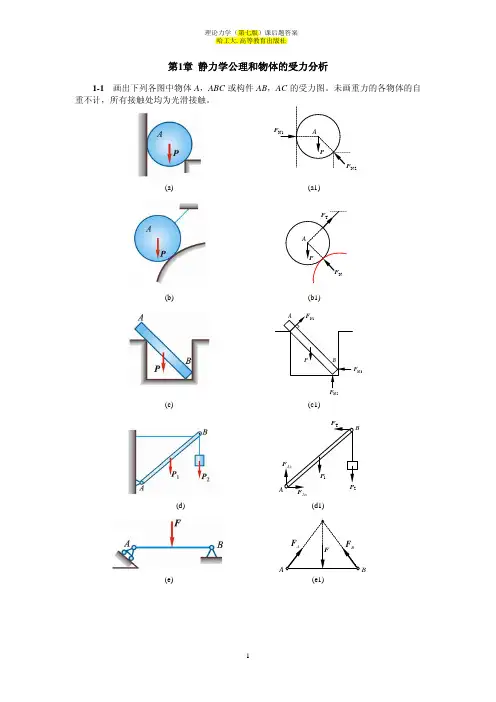
yOyO第十章 质心运动定理 动量定理 习题解[习题10-1] 船A 、B 的重量别离为kN 4.2及kN 3.1,两船原处于静止间距m 6。
设船B 上有一人,重N 500,使劲拉动船A ,使两船靠拢。
若不计水的阻力,求当两船靠拢在一路时,船B 移动的距离。
解:以船A 、B 及人组成的物体系统为质点 系。
因为质点系在水平方向不受力。
即:0=∑ixF,设B 船向左移动了S 米, 则A 船向右移动了6-S 米。
由质点系的动量定理得:t v m m v m B B A A x F 0])([=--人+0])([=-人B B A A v m m v m + B B A A v m m v m )(人+= B B A A v m m v m )(人+=tsm m t s m B A)(6人+=- s m m s m B A )()6(人+=-s s )5.03.1()6(4.2+=-s s )5.03.1()6(4.2+=- s s 3)6(4=- )(43.3724m s ==[习题10-2] 电动机重1P ,放置在滑腻的水平面上,还有一匀质杆,长L 2,重2P ,一端与电动机机轴固结,并与机轴的轴线垂直,另一端则刚连一重3P 的物体,设机轴的角速度为ω(ω为常量),开始时杆处于铅垂位置而且系统静止。
试求电动机的水平运动。
rC 3C v →y解:以电动机、匀质杆和球组成的质点系为研究对象。
其受力与运动分析如图所示。
匀质杆作平面运动。
→→→+=1212C C C C v v v ωl v r C =212cos C x C v t l v -=ωω→→→+=1313C C C C v v v ωl v r C 23=13cos 2C x C v t l v -=ωω因为质点系在水平方向上不受力,所以0==∑ix x F F由动量定理得:t F v t l m v t l m v m x C C C =--+-+-0)]cos 2()cos ([111321ωωωω 00)]cos 2()cos ([111321=--+-+-C C C v t l m v t l m v m ωωωω 111132)cos 2()cos (C C C v m v t l m v t l m =-+-ωωωω 11113322cos 2cos C C C v m v m t l m v m t l m =-+-ωωωω 1)(cos 2cos 32132C v m m m t l m t l m ++=+ωωωωt m m m m m l v C ωωcos )(321321+++=At m m m m m l dtdx C ωωcos )(321321+++=tdt m m m m m l dx C ωωcos )(321321+++=tdt m m m m m l x C ωωcos )(321321⎰+++=)(cos )(321321t td m m m m m l x C ωω⎰+++=t m m m m m l x C ωsin )(321321+++=t P P P P P l x C ωsin )(321321+++=这就是电动机的水平运动方程。






《理论力学》课程教学大纲(开实验2个)Theoretical Mechanics学时:64 学分: 3层次:本科适用专业:机械设计、机电、汽车服务类等第一部分大纲说明一、课程性质、目的和培养目标《理论力学》是工科大学的一门重要的技术基础课。
它既是各门后续力学课程的理论基础,又是一门具有完整体系并继续发展着的独立的学科,而且在许多工程技术领域中有着广泛的应用。
本课程的任务是使学生掌握质点,质点系和刚体机械运动(包括平衡)的基本规律和研究方法,初步学会运用这些理论和方法去分析、解决实际问题,为学习后续课程和有关的科学技术打好基础。
结合本课程的特点,使学生的逻辑思维能力(包括推理、分析、综合等能力)、表达能力(包括运用文字和图象等的能力)、计算能力,以及解决实际问题的能力(把一些简单工程实物抽象为力学模型,进行数学描述,应用力学原理求解)得到训练与提高。
二、课程的基本要求第一篇:静力学(20学时)基本要求:熟悉力、力矩和力偶的基本概念及其性质,熟练地计算力的投影,力对点之矩和力对轴之矩。
熟悉各种常见约束的性质,能熟练地取分离体并画出受力图。
掌握各种类型力系的简化方法,熟悉简化结果,能熟练地计算主矢和主矩。
能应用平衡条件和各种类型的平衡方程求解单个物体和物体系统的平衡问题。
对平面一般力系的平衡问题,能熟练地选取分离体和应用各种形式的平衡方程求解,掌握求解简单桁架、组合桁架内力的节点法和截面法。
掌握计算物体重心的各种方法。
理解滑动摩擦、摩擦力的概念,能求解考虑摩擦时简单的物体系统平衡问题。
了解滚动摩擦的概念、超静定问题概念。
第二篇:运动学(22学时)基本要求:掌握描述点的运动的矢量法、直角坐标法、自然坐标法及各种方法下点的运动轨迹、运动方程、速度和加速度。
熟悉刚体平动、刚体定轴转动的概念,能求解转动刚体的角速度、角加速度,转动刚体上各点的速度和加速度。
掌握运动合成和分解的基本概念和方法,熟练掌握点的速度合成定理,牵连运动为平动、定轴转动时的加速度合成定理及应用。