多抽样率窄带滤波器的设计及实现

DSP C54X 窄带中频抽样的实现1 引言本文在讨论基本的带通抽样定理基础上，分析欠抽样率对带通信号采样的频谱搬移特点，同时结合对普通的AM 调幅接收机中频信号的采样、滤波与处理，以获得基带的语音信号。

这种用软件进行信号处理的技术有助于深入理解带通抽样滤波的理论，并为软件无线电接收数据信号提供理论与实践依据。

本文讨论的中频窄带抽样实现的基本框图如图1 所示。

带通抽样定理是Nyquist 抽样定理的进一步扩展。

Nyquist 抽样定理的基本意义是：一个频率限带信号x(t)，其频带限制在（0，fh）内，如果用fs=2fh 的采样频率对x(t)进行等间隔抽样，得到的离散信号x(n)=x(nTs)，那么x(t)信号将被所得到的采样值x(n)所确定，抽样后的信号频谱不发生混叠，因此可以用滤波器恢复原始的限带信号x(t)，该信号是零频附近的基带信号。

而实际接收的无线电信号绝大多数是一个有中心频率的限带信号，并且满足信号带宽与中心频率之比远远小于1（B/fo1）的条件，即中心频率fo 远高于信号所携带频谱宽度，根据基本抽样定理知道，此时抽样频率fs2fo，这样不仅要求高性能的AD 转换器，而且高速的抽样数据又大大的加剧了DSP 的信号处理负担。

为了让DSP 有足够的时间去处理实时的信号，当前主要的方法有两种：（1）直接降低抽样率；（2）进行高速抽样，然后采用抽取方法降低抽样率。

本文采用的是直接降低抽样率的方法。

那么降低抽样率是否会产生信号混叠等问题呢？这由带通抽样理论来回答。

带通抽样定理：设一个频率限带信号x(t)，其频带限制在（fL，fH）内，如果采样频率fs 满足：其中n 取值是满足fs≥2B(B=fH-fL）的最大整数值（0，1，2,...），此时用fs 进行等间隔抽样的x(nTs)能准确的确定原始信号x(t)。

并确定带通信号的中心频率，那么。

这个表达式表示：当抽样频率确定后，有许多频率（或带通信号）在满足以上表达式所取的n 值条件下,可以产生同一个频率（或同一个带通信号）；同样对于确定的fo 通过选择不同的n 来确定fs。

中文译文多采样率滤波器的设计基于多采样的滤波器设计方法可以用来设计具有较窄过渡带或具有较窄或较宽通带的有限脉冲响应滤波器。

这些有限脉冲响应滤波器一般来说是不能作为普通时不变有限脉冲响应滤波器来实际设计和应用，因为他们的结构非常长。

下列所示的滤波器类型可以用多采样率滤波器设计技术设计：●窄带低通滤波器●窄带带通滤波器●窄带高通滤波器●宽带高通滤波器●宽带低通滤波器●窄带带阻滤波器用于滤波器设计的多采样信号处理：多采样率信号处理包括在一个系统中使用不同采样速率以获得较高的计算效率，但在一个使用单一固定采样速率的系统中是不可能获得的。

举个例子，考虑下面的低通滤波器：抽样速率50khz通带截止频率800hz阻带截止频率1khz通带最大波动0.1db阻带最小衰耗60.0db这个滤波器如果用标准帕克斯-麦克莱伦算法来设计则需要681个单元。

然而，采样速率变为2500hz，，滤波器仅需要35 组的值。

这就引出了改变抽样速率到一个较小的抽样速率（即抽取）的概念;然后滤出这个信号改变它的抽样速率到原来的抽样速率（即插值）。

降低采样速率需要在抽取到较低采样率前加一个抗混叠滤波器。

增加采样率需要在插值以后叠加一个镜像滤波器。

这两个滤波器必须使用规范的原始低通滤波器。

为了实现计算增益的最大化，这两个滤波器必须工作在降低的采样频率上。

这篇文章将向你展示怎样获得期望的计算增益。

回到我们的例子，在25至1效率计算增益可以实现。

由于通带边缘以一个固定的抽样速率趋向于零，计算效率将趋于无穷大。

抽取抽样速率以M因子的减小可以由此方法获得：舍去每M-1个采样点或相似的保持每个Mth采样点。

当每M个输入采样点舍去M-1个点时就会使原始采样率以M 因子减小，这也将引起高于半抽取速率的输入频谱输延拓至基带到乃奎斯特频率部分。

为了减小这种影响，输入的信号必须经过低通滤波器以滤除输出频谱部分中一些频率成分,这部分需要在接下来的信号处理步骤中抗混叠. 抽取处理的一个好处是，低通滤波器可被设计运行在锐减的采样率上.而不是采用有限脉冲响应滤波器结构工作在较高的输入频率上,而且应当注意到的是与M-1相关联的舍去的采样点不需要计算.设x(m) 是输入信号, h(k), 0 <= k <= K 是低通滤波器的单位脉冲响应, z(m)是在M 因子抽取前的输出信号.则:z(m) = ∑=K0k h(k)x(m – k) 1-1现在,设输出信号经过抽取器y(r) = z(rM)即抽样速率以M 因子的速率减小。

滤波器设计与实现方法总结滤波器是信号处理中常用的工具，用于降低或排除信号中的噪声或干扰，保留所需的频率成分。

在电子、通信、音频等领域中，滤波器发挥着重要作用。

本文将总结滤波器的设计与实现方法，帮助读者了解滤波器的基本原理和操作。

一、滤波器分类滤波器根据其频率特性可分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

它们分别具有不同的频率传递特性，适用于不同的应用场景。

1. 低通滤波器低通滤波器将高频信号抑制，只通过低于截止频率的信号。

常用的低通滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。

设计低通滤波器时，需要确定截止频率、阻带衰减和通带波动等参数。

2. 高通滤波器高通滤波器将低频信号抑制，只通过高于截止频率的信号。

常见的高通滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。

设计高通滤波器时，需要考虑截止频率和阻带衰减等参数。

3. 带通滤波器带通滤波器同时允许一定范围内的频率通过，抑制其他频率。

常用的带通滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。

设计带通滤波器时，需要确定通带范围、阻带范围和通带波动等参数。

4. 带阻滤波器带阻滤波器拒绝一定范围内的频率信号通过，允许其他频率信号通过。

常见的带阻滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。

设计带阻滤波器时，需要确定阻带范围、通带范围和阻带衰减等参数。

二、滤波器设计方法1. 传统方法传统的滤波器设计方法主要基于模拟滤波器的设计原理。

根据滤波器的频率特性和参数要求，可以利用电路理论和网络分析方法进行设计。

传统方法适用于模拟滤波器设计，但对于数字滤波器设计则需要进行模拟到数字的转换。

2. 频率抽样方法频率抽样方法是一种常用的数字滤波器设计方法。

它将连续时间域的信号转换为离散时间域的信号，并利用频域采样和离散时间傅立叶变换进行设计。

频率抽样方法可以实现各种类型的数字滤波器设计，包括有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器。

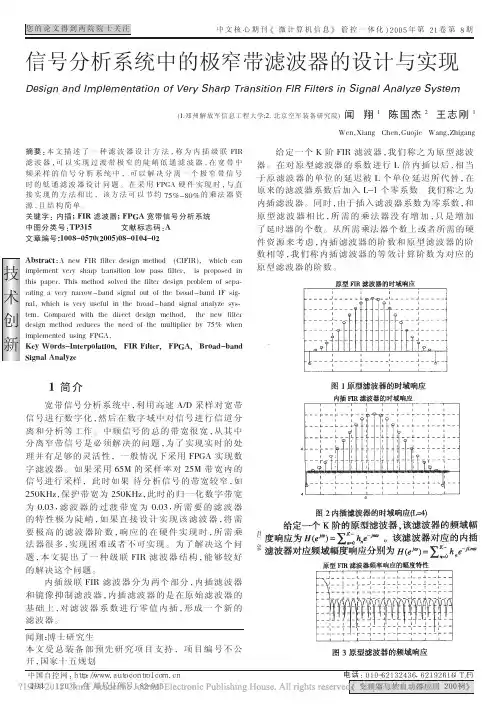
带通滤波器设计方法之三：窄带耦合谐振器设计法窄带带通滤波器可以使用耦合技术进行设计。

这个设计方法很简单，就是用耦合元件，即电感或电容，将调谐于相同谐振频率的并联协整电路连接起来。

这个设计方法的理论基础是，假定耦合元件对于带通滤波器的通带频率具有不变的阻抗。

由于电容在直流点将产生谐振零点，所以，滤波器的通带的低频一边稍微陡一些，也就是说，滤波器的阻带衰减在低端比高端要好一些；反之，如使用电感耦合，则滤波器的通带的高端稍微陡一些，滤波器的阻带衰减高端比低端要好一些。

窄带滤波器的设计步骤如下：1、计算所要设计的滤波器的通带Q值：Qbp = f/ BW3dB2、由给出的表中选择和，以选择滤波器的形式和复杂度；Q 1 = Qbp× q1Qn= Qbp× qnKxy= kxy/ Qbp3、由源和负载求出合适的电感值；R S = ωLQ1RL= ωLQn4、决定总的节点电容；C J = 1 / ( ω2L )耦合电容由下式计算：C xy = KxyCJ5、决定并联谐振电路的电容C 1 = CJ－ C12C2= CJ－ C12－ C23C7= CJ－ C67－ C786、对源和负载进行阻抗变换，以使所设计的滤波器符合源和负载的技术要求。

例：设计一只带通滤波器，其中心频率为100kHz，3dB带宽为±2.5kHz，35dB衰减为±12.5kHz。

1、判断该滤波器的技术要求是否属于窄带带通滤波器；2、根据所给出的带通滤波器的技术要求，求出该滤波器的矩形系数，即：（阻带宽度）/（通带宽度）；由此，根据相关的列线图求出该滤波器所需要的阶数为4；3、在k和q参数表中找出对应于阶数4的k和q值：q1= 0.233q4= 2.240k12= 2.530k23= 1.175k34= 0.644该滤波器的通带Q值为：Qbp = f/ BW3dB= 100kHz / 5kHz = 20解归一化，每个k除以Q，每个q乘以Q，我们得到：Q1 = 4.66 Q4= 44.8 K12= 0.1265 K23= 0.05875 K34= 0.03224、我们选择电感为L = 2.5mH，则源和负载为：RS = 7.32kΩ RL= 70.37kΩω = 2пf5、总的节点电容是;CJ= 1013pF 计算出耦合电容为：C1 = CJ－ C12= 884.9pFC2 = CJ－ C12－ C23= 825.4pFC3 = CJ－ C23－ C34= 920.9pFC4 = CJ－ C34= 980.4pF6、最后的电路如下图所示。

窄带光滤波器的设计和制备窄带光滤波器（Narrowband Optical Filters）是一种光学器件，它可以选择性地透过一定波长范围内的光，并将其他波长的光进行屏蔽。

设计和制备窄带光滤波器是光学领域的一个重要分支，其应用涉及到光学通信、生物医学、光学成像等领域。

一、窄带光滤波器的工作原理窄带光滤波器基于光学干涉原理，通过将多个传输光学元件叠加组合，来实现对单一波长区域的滤波。

其基本构成包括反射膜、透镜或反射器等光学元件。

光线进入光滤波器后，会在反射膜之间发生多次反射，并在光路长度与波长之间的干涉效应下，达到波长分离效应。

二、窄带光滤波器的设计窄带光滤波器的设计需要考虑到一系列因素，如过渡带宽、透过率、群延时等。

其中，过渡带宽是指光滤波器从透过光到屏蔽光的过渡区域的宽度。

在实际应用中，需要尽量压缩过渡带宽，以提高光滤波器的频率选择性和抑制不必要的噪声。

透过率是指光滤波器在滤波波长处的透过比例。

需要根据具体应用要求，选择适当的透过率，并保证其稳定性和重现性。

群延时则是指光滤波器对光的传输时间的影响，需要控制其误差范围，避免影响光学系统的整体性能。

三、窄带光滤波器的制备窄带光滤波器的制备通常有两种方法：热蒸汽沉积和离子束溅射。

其中，热蒸汽沉积法是一种可以在大范围内制备滤波器的方法，它通过将材料放在加热的舟中蒸发，并在反射膜表面上沉积一层厚度大约为几分之一波长的物质。

不同的蒸发材料和蒸发速率可以控制反射膜的反射光谱和透过特性。

离子束溅射法则是一种由高能离子束击打目标材料表面，在反射膜上形成各种薄膜材料的技术，可以获得分子厚度水平的非常均匀的薄膜。

这种技术也可以实现多层蒸发，用于制备多波段滤波器。

四、窄带光滤波器的应用窄带光滤波器的应用十分广泛，其中最重要的是在光学通信中的应用。

利用窄带光滤波器可以实现波分复用技术，将不同数据流在不同波长处传输，提高信号传输效率和携带能力。

此外，在生物医学和光学成像领域，窄带光滤波器还可以被用于分离不同颜色的荧光信号、实现图像识别和目标检测等应用。

窄带滤波器的设计与DSP实现
石青春;陈侠;杨琳
【期刊名称】《电子器件》
【年(卷),期】2009(032)004
【摘要】基于多抽样率数字信号处理原理,设计窄带FIR滤波器,并在DSP芯片上实现.阐述了实现窄带FIR滤波器的两种特殊的滤波器(积分梳状滤波器和半带滤波器)的原理和设计方法,利用Matlab中的FDATOOL工具箱,能够快速地设计出符合各级性能要求的滤波器,利用Matlab/Simulink中的工具箱,全部采用图形化的编程模式,自动生成DSP源代码.结论为窄带FIR滤波器采用抽样率转换多级实现的方法,有效地降低了滤波器的节数,自动生成的DSP源代码能在DSP芯片上正常运行.【总页数】4页(P774-777)
【作者】石青春;陈侠;杨琳
【作者单位】杭州电子科技大学电子信息学院,杭州,310018;中国电子科技集团第50研究所,上海,200063;中国电子科技集团第50研究所,上海,200063
【正文语种】中文
【中图分类】TN911.7
【相关文献】
1.基于TMS320C64x DSPs的MPEG-4实时编码器设计与实现 [J], 李群迎;张晓林;刘荣科;姚远
2.基于McBSP实现DSPs与串行AD/DA的接口设计 [J], 杨雪;牟燕妮
3.信号分析系统中的极窄带滤波器的设计与实现 [J], 闻翔;陈国杰;王志刚
4.信号分析系统中的极窄带滤波器的设计与实现 [J], 闻翔;陈国杰;王志刚
5.多抽样率窄带滤波器的设计及实现 [J], 张小英;李敏
因版权原因，仅展示原文概要，查看原文内容请购买。

第 31卷第5期电子科技大学学报 Vol.31No.5 2002年10月Journal of UEST of China Oct. 20022002年4月25日收稿* 男31岁硕士生多抽样率频率抽样FIR数字滤波器设计谭小刚*(电子科技大学自动化工程学院成都 610054)【摘要】采用多抽样率方法设计频率抽样FIR数字滤波器，可以获得性能优异的滤波器，以消除心电信号ECG中的基线漂移和工频干扰，对目前类似滤波器存在的截止频率不易控制、通带和阻带纹波过大、工频阻带过窄、易受工频波动干扰或消除基线漂移时对ECG的低频部分削得过多等问题，提出了一个较好的解决办法。

相对于IIR滤波器或模拟滤波器避免了因非线性相位滤波带来的失真问题。

关键词 多抽样率； 频率抽样FIR数字滤波器； 基线漂移； 工频干扰中图分类号TN713+.7; TP391Design of Multirate Frequency-sampling FIR Digital FilterTan Xiaogang(College of Automation Engineering,,UEST of China Chengdu 610054)Abstract This paper presents the design of frequency_sampling FIR digital filter based on multirate conception for removal of base_line wander and power_line interference from the ECG .We can design high performance digital filter which can be used to resolve the problems involvingpresent filters, such as difficulty of controlling cutoff frequency ,large ripple in stop_band andpass_band, too narrow stop bandwidth for removing power_line interference, sensitivity to thefluctuation of power frequency, or the low frequency part of the ECG being cut off too much whenremoving base_line wander. This scheme can also avoid distortion resulting from non-linear filtering when compared with IIR digital filter or analog filter.Key words multirate; frequency_sampling FIR digital filter; base_line wander;power_line interference在生物医学工程中，心电信号ECG因其反映了人体心脏电活动而受到重视。