最新吊装平衡梁受力计算

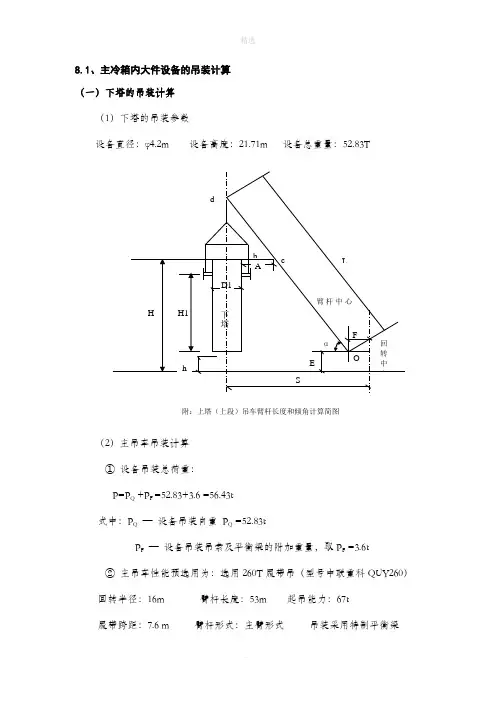
8.1、主冷箱内大件设备的吊装计算（一）下塔的吊装计算（1）下塔的吊装参数设备直径：φ4.2m 设备高度：21.71m 设备总重量：52.83T附：上塔（上段）吊车臂杆长度和倾角计算简图（2）主吊车吊装计算①设备吊装总荷重：P=P Q +P F =52.83+3.6 =56.43t式中：P Q—设备吊装自重P Q =52.83tP F—设备吊装吊索及平衡梁的附加重量，取P F =3.6t②主吊车性能预选用为：选用260T履带吊（型号中联重科QUY260）回转半径：16m 臂杆长度：53m 起吊能力：67t履带跨距：7.6 m 臂杆形式：主臂形式吊装采用特制平衡梁钩头选用160t/100t吊钩，钩头重量为2.8吨吊车站位：冷箱的西面③臂杆倾角计算：α=arc cos（S－F）/L = arc cos（16-1.5）/53 =74.12°式中：S —吊车回转半径：选S=16mF —臂杆底铰至回转中心的距离，F=1.5mL —吊车臂杆长度，选L=53m④净空距离A的计算：A=Lcosα－（H－E）ctgα－D/2=53cos74.12°－(36.5-2) ctg74.12°－5/2=2.1m式中：H —设备吊装时距臂杆最近的最高点b至地面的高度，选H=36.5mE —臂杆底铰至地面的高度，E=2mD —设备直径：D=4.2m，取D=5 m以上计算说明所选的吊车性能能满足吊装需求⑤主吊车吊装能力选用校核：吊装总荷重/起吊能力=P/Q=56.43/67=84.22%经过校核，选用的主吊车能够满足吊装要求。

（3）溜尾吊车的吊装计算①受力计算F=（9-1）×52.83=21.44t21.71-1-1②溜尾吊车的选择辅助吊车选用为：75T汽车吊臂杆长度：12m；回转半径：7m；起吊能力：36t；吊装安全校核：因为21.44t〈36t，所以75T汽车吊能够满足吊装要求。

（二）、上塔（上段）的吊装计算（1）上塔上段的吊装参数设备直径：φ3.6m 设备高度：11.02m 设备重：17.35T 安装高度：45米附：吊装臂杆长度和倾角计算简图（2）主吊车吊装计算①设备吊装总荷重：P=P Q +P F=17.35+3.6=20.95t式中：P Q—设备吊装自重P Q =17.35tP F—设备吊装吊索及平衡梁的附加重量，取P F =3.6t②主吊车性能预选用为：选用260T履带吊（型号中联重科QUY260）回转半径：16m 主臂杆长度：59m 副臂杆长度：27m 起吊能力：55t履带跨距：7.6 m 臂杆形式：主臂＋塔式副臂，主臂角度不变85度，钩头选用160t/100t吊钩，钩头重量为2.8吨副臂起落吊装采用特制平衡梁, 主吊车站位于冷箱的西面③主臂角度不变85度，副臂杆倾角计算：C=16-F-59coc85°=16-1.5-59coc85°=9.34mγ=β-（90°-α）=arcSin(C/27)-(90°-85°)= arcSin(9.34/27)-5°= 15.24°式中：γ—副臂杆倾角，为副臂中心线与主臂中心线夹角S —吊车回转半径：选S=16mF —臂杆底铰至回转中心的距离，F=1.5m主臂杆长度：59m 副臂杆长度：27mα—为主臂角度不变85度④净空距离A的计算：A=C-［H-(59*Sinα+E)］tanβ－D/2=9.34－［74-(59*Sin85°+2)］tan20.24－4/2 =2.46m式中：H —设备吊装时距臂杆最近的最高点b至地面的高度，选H=74mE —臂杆底铰至地面的高度，E=2 mD —设备直径D=3.6m, 取D=4 m以上计算说明所选的吊车性能能满足吊装需求。

起重吊装简易计算公式(一)
起重吊装简易计算公式
1. 垂直吊装公式
•计算物体的重力：
–重力（N）= 质量（kg） x 重力加速度（m/s^2）
–例：一块重1000 kg的物体在地球上的重力：
•重力 = 1000 kg x m/s^2 = 9800 N
•计算起重机选配：
–起重机吨位（T）= 重力（N）/ 1000
–例：需要起吊重力为9800 N的物体，选择起重机吨位：•吨位 = 9800 N / 1000 = T (即10 T)
2. 水平吊装公式
•计算侧向力（只针对固定角度）：
–侧向力（N）= 重力（N） x tan(角度）
–例：物体重力为9800 N，角度为30度时的侧向力：
•侧向力 = 9800 N x tan(30度) = 9800 N x = N
•计算水平力（只针对固定角度）：
–水平力（N）= 重力（N） x sin(角度）
–例：物体重力为9800 N，角度为30度时的水平力：
•水平力 = 9800 N x sin(30度) = 9800 N x = 4900 N
3. 吊杆长度计算（尺规公式）
•计算吊杆长度（只针对水平吊装）：
–吊杆长度（m）= 半径长度（m） x 正弦(角度）
–例：半径长度为5米，角度为60度时的吊杆长度：
•吊杆长度 = 5m x sin(60度) =
结论
以上列举了起重吊装中的一些常用的简易计算公式，包括垂直吊装和水平吊装的计算公式以及吊杆长度的计算公式。

这些公式能够帮助工程师和操作人员进行起重吊装的初步计算和选择，以确保吊装过程的安全和可靠性。

吊车吊装计算公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]、主冷箱内大件设备的吊装计算 （一）下塔的吊装计算（1）下塔的吊装参数设备直径：φ 设备高度： 设备总重量：（2）主吊车吊装计算 ① 设备吊装总荷重： P=P Q +P F =+ =式中：P Q — 设备吊装自重 P Q =P F — 设备吊装吊索及平衡梁的附加重量，取P F = ② 主吊车性能预选用为：选用260T 履带吊（型号中联重科QUY260）回转半径：16m 臂杆长度：53m 起吊能力：67t附：上塔（上段）吊车臂杆长度履带跨距： m 臂杆形式：主臂形式吊装采用特制平衡梁钩头选用160t/100t吊钩，钩头重量为吨吊车站位：冷箱的西面③臂杆倾角计算：α=arc cos（S－F）/L = arc cos（）/53 =°式中：S —吊车回转半径：选S=16mF —臂杆底铰至回转中心的距离，F=L —吊车臂杆长度，选L=53m④净空距离A的计算：A=Lcosα－（H－E）ctgα－D/2=°－°－5/2=式中：H —设备吊装时距臂杆最近的最高点b至地面的高度，选H=E —臂杆底铰至地面的高度，E=2mD —设备直径：D=，取D=5 m以上计算说明所选的吊车性能能满足吊装需求⑤主吊车吊装能力选用校核：吊装总荷重/起吊能力=P/Q=67=%经过校核，选用的主吊车能够满足吊装要求。

（3）溜尾吊车的吊装计算①受力计算F=（9-1）×=②溜尾吊车的选择辅助吊车选用为：75T汽车吊臂杆长度：12m；回转半径：7m；起吊能力：36t；吊装安全校核：因为〈36t，所以75T汽车吊能够满足吊装要求。

（二）、上塔（上段）的吊装计算（1）上塔上段的吊装参数设备直径：φ设备高度：设备重：安装高度：45米附：吊装臂杆长度和倾角计算简图（2）主吊车吊装计算①设备吊装总荷重：P=PQ +PF=+=式中：PQ —设备吊装自重 PQ=PF —设备吊装吊索及平衡梁的附加重量，取PF=②主吊车性能预选用为：选用260T履带吊（型号中联重科QUY260）回转半径：16m 主臂杆长度：59m 副臂杆长度：27m 起吊能力：55t履带跨距： m 臂杆形式：主臂＋塔式副臂，主臂角度不变85度，钩头选用160t/100t吊钩，钩头重量为吨副臂起落吊装采用特制平衡梁, 主吊车站位于冷箱的西面③主臂角度不变85度，副臂杆倾角计算：C=16-F-59coc85°=°=γ =β-（90°-α）=arcSin(C/27)-(90°-85°)= arcSin27)-5°= °式中：γ—副臂杆倾角，为副臂中心线与主臂中心线夹角S —吊车回转半径：选S=16mF —臂杆底铰至回转中心的距离，F=主臂杆长度：59m 副臂杆长度：27mα—为主臂角度不变85度④净空距离A的计算：A=C-［H-(59*Sinα+E)］tanβ－D/2=－［74-(59*Sin85°+2)］－4/2 =式中：H —设备吊装时距臂杆最近的最高点b至地面的高度，选H=74mE —臂杆底铰至地面的高度，E=2 mD —设备直径D=, 取D=4 m以上计算说明所选的吊车性能能满足吊装需求。

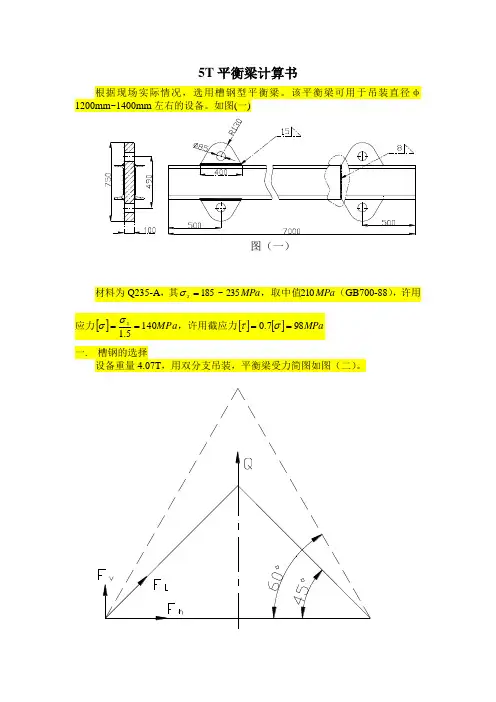
5T 平衡梁计算书 根据现场实际情况，选用槽钢型平衡梁。

该平衡梁可用于吊装直径φ1200mm~1400mm 左右的设备。

如图(一)图（一）材料为Q235-A ，其MPa MPa s 210235~185，取中值=σ（GB700-88），许用一. 槽钢的选择设备重量4.07T ，用双分支吊装，平衡梁受力简图如图（二）。

分支拉力L F 平衡梁的夹角为)60~45(︒︒α，计算取︒55，吊重Q=4.07T 计算吊重动计K Q Q ⋅=44.12.12.121=⨯=⨯=K K K 动其中 1K 为冲击系数，2K 为不均匀系数 故 Q 计=4.07×1.44=5.86TF V =Q/n=5.86/2=2.93TF L = (Q 计/n)×1/sin a=3.57TF h =F V /tan a=2.05T槽钢为只受轴力作用。

根据强度条件确定槽钢的横截面积为A ≥F h /[σ]=(2.05×1000×9.806)/(140×106)m 2=1.44cm 2选用16a 型槽钢，截面积为21.95×2=43.9cm 2，满足要求。

二. 吊耳板的验算 ：如图(三):在断面A1B1处，b=20cm ，δ=3cmσ1=(Q 计/2)/b δ=4.79 MPa在断面A2B2处，b=16cm （偏保守），δ=3cm ，d=8cmσ2=(Q 计/2)/(b-d)δ=11.97 MPa在断面A3B3处，D=2R=16cm ，d=8cm ，δ=3cm 按拉漫公式验算： σ=(Q 计/2)/d δ=11.97 MPaσ3=σ(D 2+d 2)/ (D 2-d 2)=19.95 MPa吊索方向最大拉应力：σL =F L /((D-d) δ)=14.59 MPa []σ<，满足要求。

三. 焊缝的验算：对平衡梁受力分析知：焊缝（左侧吊耳）主要承受如图示方向的作用力 其剪切力为=⨯-⨯=3201054251h h F F P 96.63T 32010542511⨯-⨯=h h F F P =-34.87T (即1P 方向应向右) 上边焊缝承受弯距较下边的大，故只校验上边焊缝即可m N F M h •=⨯⨯⨯⨯=⨯=-23.72672105.10806.9100058.705.82m N l h M f f M .872.5910)2255(24.123.7267264.16622=⨯⨯-⨯⨯⨯==-τ m N l h P f .358.66102)2255(27.0806.9100063.967.04=⨯⨯⨯-⨯⨯⨯⨯==-剪τ式中： f h ——焊缝厚度l ——焊缝总计算长度，等于焊缝实际长度减去2f h[]ττττ MPa M 376.89358.66872.592222=+=+=剪，安全。

按机动起重设备拉板类设计规定安全系数K=4设计标准
【屈服应力】 =367.5MPa . K=367.5/61.6=5.965﹥(K)安全
三：钢丝绳计算：
吊具安装吊装作业时采用 双股钢丝绳双吊索选用双绳兜吊。吊具由四个支座即四个吊点承载160T.每个吊点承载40T(4000000N).
钢丝绳破断拉力=40*6=240T(安全载重系数取值为6)
平衡吊具计算书
编制
校对
审核
一 现场采用二组吊具同时平稳起吊。吊具计算公式按单组平衡吊具计算。
如图一
单组吊具图（二）
二：荷载：
横梁吊耳板尺寸
39m箱梁重160T分配至每端为80T(800000N);按最重者验算受力。考虑1.2倍安全系数储备，800000N*1.2=960000N.单组吊具则要求吊具具备负重96T的能力。
轴截面惯性矩：W=0.1* =172800mm(销轴直径 )
轴最大弯曲应力： =M/W=80850000/172800=467.88MPa
抗拉强度：【 】=1080MPa/467.88MPa=2.3﹥【K】安全
钢丝绳破断拉力总和=240/0.82=292.6（换算系数取值0.82）
钢丝绳破断拉力总和：S破=292.6吨，动载系数1.05偏载系数1.1钢丝绳计算拉力:Smax=40t*动载系数*偏载系数=46.2t钢丝绳安全系数：n≧6，钢丝绳使用系数：0.92 机械效率：0.98. 实际安全系数：n=292.6*0.92*0.98*2/46.2=11.4﹥【6】安全
根据现场使用受力尺寸：四根销轴承载力为160T每根销轴承载40T,根据机动起重销轴类设计规定安全系数值K=1.75按单根销轴需承载P=40*1.75=70T
P=70T=700000N

简单吊梁的承载力计算公式在工程建设中，吊梁是一种常见的结构形式，用于支撑和承载各种重物。

在设计和施工过程中，需要对吊梁的承载力进行合理的计算，以确保其安全可靠地使用。

本文将介绍简单吊梁的承载力计算公式，帮助工程师和施工人员更好地理解和应用这一重要的知识点。

简单吊梁是指由两个支点支撑的横梁结构，通常用于起重和吊装作业。

在计算其承载力时，需要考虑吊梁本身的重量以及所承载的物体的重量，以确保吊梁不会发生过载而造成安全事故。

下面我们将介绍简单吊梁的承载力计算公式及其应用方法。

首先，我们需要了解吊梁的基本参数，包括长度、材质、截面形状等。

这些参数将直接影响吊梁的承载能力。

在实际工程中，通常会根据具体情况选择合适的吊梁材质和截面形状，以满足承载要求。

根据梁的基本理论，我们可以得到简单吊梁的承载力计算公式如下：P = Wl^2 / 8I。

其中，P表示吊梁的最大承载力，单位为牛顿（N）；W表示吊梁的自重，单位为牛顿（N）；l表示吊梁的长度，单位为米（m）；I表示吊梁的惯性矩，单位为米的四次方（m^4）。

根据这个公式，我们可以看到吊梁的承载力与其长度的平方成正比，与其惯性矩的倒数成正比，与其自重成反比。

这也说明了在设计吊梁时，需要尽量减小其自重，增大其惯性矩，以提高其承载能力。

在实际应用中，我们可以通过这个公式来计算吊梁的最大承载力，从而确定其合理的使用范围。

在计算时，需要考虑吊梁的实际工作环境和工况，以及所承载物体的重量和重心位置，以确保计算结果的准确性和可靠性。

除了上述的简单吊梁承载力计算公式外，我们还可以通过有限元分析等现代计算方法来进一步优化吊梁的设计和计算。

这些方法可以更精确地考虑吊梁的各种受力情况和边界条件，从而得到更合理的设计方案。

总之，简单吊梁的承载力计算是工程设计和施工中的重要环节，直接关系到吊梁的安全可靠性。

通过合理应用承载力计算公式和现代计算方法，可以更好地设计和使用吊梁，确保工程施工的顺利进行和安全运行。

位于B处吊耳的拉力（支座反力）：RB=1041.6 KN,
最大弯矩：Mmax=1034.77 KN.m，位置：X=4.596m;
该处应力：σ=M/W=1034.77 KN.m/15262.57cm3=67.80MPa
安全系数：n1=σb/σ= 216 MPa /67.80 MPa = 3.19
吊耳剪切应力：τ=RB/A=1041.6KN / 0.023 m2= 45.29MPa
附图一
附图二
3.结论
根据上述两种装载方式的计算结果可知：
吊架的结构强度在两种装载方式下均满足要求。
四、安全措施及建议
1.第一种装载方式的安全系数明显比第二种高，建议采取第一种装载方式。
2.吊架的上盖板与纵、横向梁的焊接仅为间断焊，须用碱性焊条补成双面连续焊。
3.由于试验载荷的增加，本吊架配备的钢丝绳、卸扣也需加大，其安全系数应不低于2.0。（破断力不低于1042KN，每个吊耳至少配双根钢丝绳，这样每根钢丝绳破断力不低于721KN。）
安全系数：n2=τb/τ=151.2 MPa /45.29 MPa = 3.34
2.第二种装载方式：(详见附图二)
1)所有载荷均布于4只吊耳之间。
由附图二可知：
载荷1：Q1=352.1875 KN/m X 5.76mX 9.8 tf /KN =207tf;
位于吊耳处的拉力（支座反力）：RA=RB=1014.30KN;
2)1000X1500X425钢锭20块分2~3层叠加均布于4只吊耳之间。
由附图一可知：
载荷1：Q1=116.51KN/m X 9.0m X 9.8 tf /KN=107 tf,
载荷1：Q2=170.14 KN/m X 5.76m X 9.8 tf /KN =100tf;

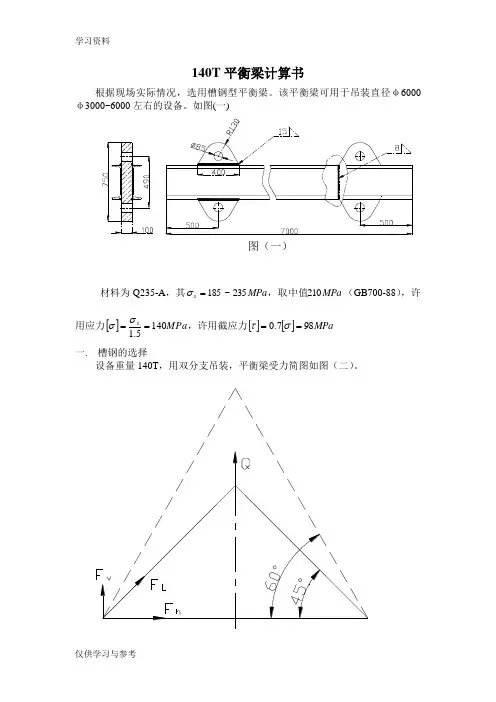
140T 平衡梁计算书根据现场实际情况，选用槽钢型平衡梁。

该平衡梁可用于吊装直径φ6000φ3000~6000左右的设备。

如图(一)图（一）材料为Q235-A ，其MPa MPa s 210235~185，取中值=σ（GB700-88），许用应力[]MPa s1405.1==σσ，许用截应力[][]MPa 987.0==στ一. 槽钢的选择设备重量140T ，用双分支吊装，平衡梁受力简图如图（二）。

分支拉力L F 平衡梁的夹角为)60~45(︒︒α，计算取︒55，吊重T Q 140= 计算吊重动计K Q Q ⋅=44.12.12.121=⨯=⨯=K K K 动其中 1K 为冲击系数，2K 为不均匀系数故 T Q 6.20144.1140=⨯=计。

T n Q F v 8.10026.201=== T n Q F L 054.12355sin 126.201sin 1=︒⋅=⋅=α计T F F v h 581.70tan /==α槽钢为只受轴力作用。

根据强度条件确定槽钢的横截面积为[]22643.4910140806.91000581.70cm m F A h =⨯⨯⨯=≥σ 选用32b 型槽钢，截面积为222.11021.55cm cm =⨯，满足要求。

二. 吊耳板的验算 ：如图(三):在断面A1B1处，b=55cm ，δ=10cmMPa Pa b Q 98.1710105512806.910006.2011241=⨯⨯⨯⨯⨯=⋅=-δσ计在断面A2B2处，b=26cm （偏保守），δ=10cm ，d=10cmMPa Pa d b Q 78.611010)1026(12806.910006.201)(1242=⨯⨯-⨯⨯⨯=-⋅=-δσ计在断面A3B3处，D=2R=26cm ，d=10cm ，δ=10cm 按拉漫公式验算：MPa Pa d Q 63.9910101012806.910006.201124=⨯⨯⨯⨯⨯=⋅=-δσ计 MPa d D d D 22.1341026102637.117222222223=--⨯=-+=σσ 吊索方向最大拉应力：MPa Pa d D F L L 42.751010)1026(806.91000054.123))/((4=⨯⨯⨯-⨯⨯=⋅-=-δσ[]σ<，满足要求 三. 焊缝的验算：对平衡梁受力分析知：焊缝（左侧吊耳）主要承受如图示方向的作用力 其剪切力为=⨯-⨯=3201054251h h F F P 96.63T 32010542511⨯-⨯=h h F F P =-34.87T (即1P 方向应向右) 上边焊缝承受弯距较下边的大，故只校验上边焊缝即可m N F M h •=⨯⨯⨯⨯=⨯=-23.72672105.10806.9100058.705.82m N l h M f f M .872.5910)2255(24.123.7267264.16622=⨯⨯-⨯⨯⨯==-τ m N l h P f .358.66102)2255(27.0806.9100063.967.04=⨯⨯⨯-⨯⨯⨯⨯==-剪τ式中： f h ——焊缝厚度l ——焊缝总计算长度，等于焊缝实际长度减去2f h[]ττττπMPa M 376.89358.66872.592222=+=+=剪，安全。

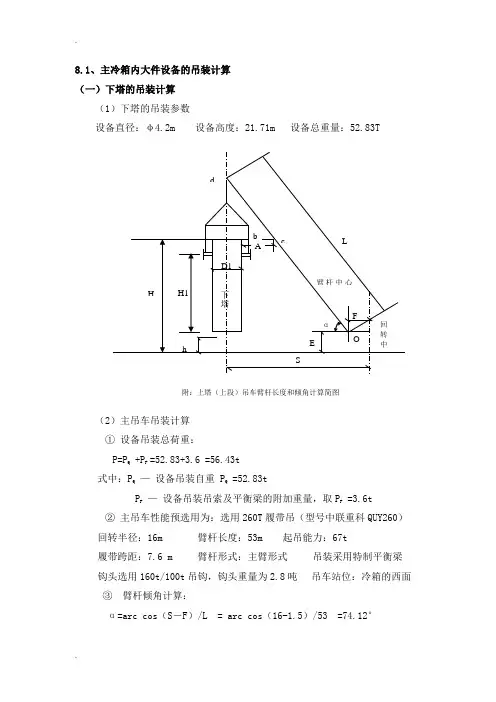
8.1、主冷箱内大件设备的吊装计算 （一）下塔的吊装计算（1）下塔的吊装参数设备直径：φ4.2m 设备高度：21.71m 设备总重量：52.83T（2）主吊车吊装计算 ① 设备吊装总荷重： P=P Q +P F =52.83+3.6 =56.43t 式中：P Q — 设备吊装自重 P Q =52.83tP F — 设备吊装吊索及平衡梁的附加重量，取P F =3.6t ② 主吊车性能预选用为：选用260T 履带吊（型号中联重科QUY260） 回转半径：16m 臂杆长度：53m 起吊能力：67t 履带跨距：7.6 m 臂杆形式：主臂形式 吊装采用特制平衡梁 钩头选用160t/100t 吊钩，钩头重量为2.8吨 吊车站位：冷箱的西面 ③ 臂杆倾角计算：α=arc cos （S －F ）/L = arc cos （16-1.5）/53 =74.12°HAD1hb c F OEα回 转 中 心臂杆中心LdS附：上塔（上段）吊车臂杆长度和倾角计算简图H1下塔式中：S — 吊车回转半径：选S=16mF — 臂杆底铰至回转中心的距离，F=1.5m L — 吊车臂杆长度，选L=53m ④ 净空距离A 的计算： A=Lcos α－（H －E ）ctg α－D/2=53cos74.12°－(36.5-2) ctg74.12°－5/2=2.1m式中：H — 设备吊装时距臂杆最近的最高点b 至地面的高度，选H=36.5mE — 臂杆底铰至地面的高度，E=2m D — 设备直径：D=4.2m ，取D=5 m以上计算说明所选的吊车性能能满足吊装需求 ⑤ 主吊车吊装能力选用校核：吊装总荷重/起吊能力=P/Q=56.43/67=84.22% 经过校核，选用的主吊车能够满足吊装要求。

（3）溜尾吊车的吊装计算① 受力计算 F=② 溜尾吊车的选择（9-1）×52.8321.71-1-1=21.44tQ26M1.0m 1m9mQG21.71mF 附：下塔溜尾吊车受力计算简图辅助吊车选用为：75T汽车吊臂杆长度：12m；回转半径：7m；起吊能力：36t；吊装安全校核：因为21.44t〈36t，所以75T汽车吊能够满足吊装要求。

建筑力学梁承受力计算公式在建筑工程中，梁是一种常见的结构元件，用于承担横向荷载和弯矩。

梁的设计和计算是建筑工程中非常重要的一部分，其中梁的承受力计算是其中的关键步骤之一。

在本文中，我们将讨论建筑力学梁承受力计算的公式和方法。

梁的承受力计算涉及到多个因素，包括梁的几何形状、材料特性、荷载情况等。

在进行承受力计算时，通常需要考虑梁的弯曲、剪切、挠曲等多种受力情况。

下面我们将分别介绍这些受力情况下的承受力计算公式和方法。

1. 弯曲。

当梁受到集中力或均布力作用时，会产生弯曲。

在弯曲情况下，梁的受力状态可以用弯矩来描述。

根据弯矩的定义，我们可以得到梁的弯曲应力和弯曲应变的公式。

在一般情况下，梁的弯曲应力和弯曲应变可以用以下公式来计算：弯曲应力σ = M y / I。

弯曲应变ε = σ / E。

其中，M为弯矩，y为受力点到截面重心的距离，I为截面惯性矩，E为材料的弹性模量。

通过这些公式，我们可以计算出梁在弯曲情况下的应力和应变，从而评估其受力情况。

2. 剪切。

除了弯曲外，梁在受到横向力作用时还会产生剪切。

剪切力会导致梁产生剪切应力和剪切变形。

在计算剪切力时，我们可以使用以下公式：剪切应力τ = V Q / (I b)。

其中，V为剪切力，Q为截面偏心距，b为截面宽度。

通过这个公式，我们可以计算出梁在剪切情况下的应力，从而评估其受力情况。

3. 挠曲。

除了弯曲和剪切外，梁在受到荷载作用时还会产生挠曲。

挠曲会导致梁产生挠曲变形和挠曲应力。

在计算挠曲时，我们可以使用以下公式：挠曲应力σ = M y / W。

其中，M为弯矩，y为受力点到截面重心的距离，W为截面模量。

通过这个公式，我们可以计算出梁在挠曲情况下的应力，从而评估其受力情况。

在实际工程中，梁通常会同时受到多种受力情况的作用，因此需要综合考虑这些受力情况下的影响。

在进行梁的承受力计算时，我们通常会根据实际情况综合考虑弯曲、剪切、挠曲等多种受力情况，并采用适当的方法进行计算。

有限公司市天然气综合利用及调峰项目设备E-401及K-501吊装方案编制：审核：审批：中国化学工程第建设有限公司二O一五年十一月目录一、编制说明二、编制依据三、工程概况四、施工前准备五、钢绳吊索选择及校验计算、平衡梁的制作及校验六、吊装方法、吊车的选择及摘钩七、吊装安全质量保证体系八、安全技术措施九、劳动力安排计划十、主要工机具及手段用料十一附图一：E-401吊装平、立平面图附图二：K-501吊装平、立平面图附图三：350t及500t汽车吊吊装性能表一、编制说明：市天然气综合利用及调峰项目液化工艺装置区内主换热器E-401重99.77t，冷剂压缩机K-501电机重量48t，撬块重量43.4t。

该吊装方案专门为这三台设备编制。

二、编制依据2.1《化工工程建设起重施工规范》HGJ2012.2《中、低压化工设备施工及验收规范》HGJ2092.3《现场设备、工业管道焊接工程施工及验收规范》GBJ2362.4 SH/T3536-2011《石油化工工程起重施工规范》2.5设备图纸三、工程概况设备详细技术参数如下：四、施工前准备4.1该施工方案涉及到的设备施工图及其它安装技术资料应齐全。

4.2构件到货齐全，并附有质量说明书。

设备经验收合格，并办理完相关交接出库手续。

4.3现场基础验收合格，场地平整完毕。

4.4 由于厂区内为湿陷黄土地质，为保证大型吊车能够顺利进场且保证站位安全，我单位将准备对火炬区周围设计图纸中未进行地基处理的区域，进行地基处理，以保证吊装安全。

4.4.1地基处理主要施工方法吊装场地（吊车站位及行走路线等）先用300mm厚的泥石进行铺设，用6t压路机进行压实。

然后在泥石上面铺设100mm厚的碎石，再次用压路机做压实处理。

压实系数λc 应为0.94-0.97。

碾压次数以达到要求密实度为准，一般不少于4遍。

泥石及碎石铺设选用装载机及人力共同作业。

4.4.2地基铺设平面图（吊车站位及行走路线等）：见工艺装置区地基铺设平面图4.5施工方案已经有关部门批准，技术交底已进行。

一、Spreader bar selection (refer to drawing T3510-Lifting Sketch-3)a、平衡梁选择（参见图T3510-吊装草图-3）The spreader bar uses the steel pipe ofφ219×8, material=20#, length=3.8m, mechanics specialty is F=5300mm2,rotating radius isr=74.48 mm平衡梁选用φ219×8的钢管,材质20#,长3.8米,其力学特性为截面积F=5300mm2，回转半径r=74.48 mmSpreader bar pulling isP2= P1cos19.5=Q/2 =120.68/2tP2=64.19t=629062NP2----------吊装梁所受正压力平衡梁受力为P2= P1cos19.5=Q/2 =120.68/2tP2=64.19t=629062NSpreader bar slightness ratio: λ=μl/r=3800/74.48=51.02平衡梁细长比: λ=μl/r=3800/74.48=51.02From above u-----length factor. Two ends hinge u=1L----Supporting girder length L=3.8m上式中u-----长度系数、两端铰支u=1L-----支撑梁长L=3.8m折减系数Φ=1.018-0.0023*51.02=0.9Reduction coefficientΦ=1.018-0.0023*51.02=0.9Spreader bar stress[σ]= P2/(ΦF)= 629062/ (0.9×5300)=131N/mm2 平衡梁应力为[σ]= P2/(ΦF)= 629062/(0.9×5300)=131N/mm2Bend limit of steel tube isσs=245.15N/mm2Take safety factor n=1.8 钢管的屈服极限为:σs=245.15N/mm2取安全系数n=1.8[δ] = δs /n =245.15/1.8 = 136.19N/mm2＞σb、两端夹板钢板计算钢板所受应力δ=P2/A=629062N/102050 mm2=6.16N/ mm2δ-----钢板所受压应力N/ mm2P2----吊装梁所受正压力NA------受压面积mm2钢板δ=20 Q235 的屈服极限为:σs=225N/mm2取安全系数n=1.8[δ] = δs /n =225/1.8 = 125N/mm2＞δ,钢板满足要求.C、对夹螺栓的计算F1=G/2+f=G/2sin70F1-----钢丝绳受力64.19T=629062Nf--------钢丝绳受摩擦力f=F2*ζ+n*N*ζ*2N--------螺栓对钢丝绳的压力(t)ζ-------钢丝绳在钢板上摩擦系数ζ=0.2n--------螺栓数量选4套G/2sin70-G/2=G/2ctg70*0.2+4*N*0.2*2N=2.3T选用M20的螺栓，4套；查表得M20的螺栓旋紧螺母时螺栓对钢板的压力大小为2.5T。

3.5.2场地基础的处理1．在吊机定位，吊机作业周围的其他钢结构设备基础暂缓施工，待设备吊装结束后进行施工。

2．300吨吊机的每个支腿与处理过的路基上放上四块双面路基板，在此路基板上再设置300吨吊机的专用路基板。

3．300吨吊机与150吨吊行车范围及设备进场的场地道路应加固处理，采用换垫层法使其具有一定的地耐力，开挖一定的面积，开挖深度约1米，以除去松软的回填土，挖至老土为准，再在上面铺设大石块约800毫米厚，并用压路机压实压平，然后再在大石块上铺约200毫米厚，再用压路机来回数次的压实压平，表面一定要处理平整，具体要求详见(图8)。

4．150吨履带吊的定位与行走区域范围场地道路处理后，并在处理过的路基上要铺设双面路基板，以增强和扩大地基的承载能力和受力面。

5．根据吊机的有关资料及设备重量和吊索的重量300吨吊机每个支腿最大的承载148吨。

P1+P2+P3+P4+P5+P64（79+120+124.9+1+3.8+0.34）/ 4 = 329/4=82.3吨P1：主吊机的自重量79吨P2：主吊机的配重重量120吨P3：设备的重量124.9吨P4：吊索具的重量1吨P5：吊钩的重量 3.8吨P6：设备群座支撑用钢管的重量Ø219×10 0.34吨3.6吊机性能选用详见氧氯化反应器吊装立面图（6、7）3.6.1主吊机选用DEMAG-TC2000型300吨桁架式汽车吊。

1)吊装总重量的计算G1.设备重量G1 =124.9吨2.吊钩重量G2 =3.8吨3.主吊索具的重量Ø60.5-6×37-170 G3 =1.027吨4.群座支撑钢管的重量Ø219×10 G4 =0.35吨5.底部吊索具的重量Ø56-6×37-170 G5 =0.23吨6.卸扣的重量75吨级5只G6 =0.72吨7.吊梁重量G7=1.5吨8.G=G1+G2+G3+G4+G5+G6+G7=132.5吨符合吊机性能要求。

梁的受力计算
强度
抗弯强度
考虑钢材部分截面的发展塑性
单向弯曲：
双向弯曲：
抗剪强度
局部承压强度
折算应力
刚度
原因：
刚度不足是会出现过大的挠度使人感觉不安全，同时有可能引起过大的震动使附着物脱落；吊车如果挠度过大，可能影响吊车的正常工作，因此要对梁的最大挠度和相对最大挠度加以限制。

计算公式：
注意问题
梁的刚度属于正常的使用极限状态，所以在计算时采用荷载标准值。

整体稳定
整体稳定的概念
弯矩增加到使受压翼缘的弯曲应力达到某一数值，梁在偶然横向干扰力的作用下突然离开最大刚度平面向内侧弯曲，并伴随扭转此时若弯矩增加，则侧向弯扭变形将迅速增加，梁失去继续承受荷载的能力，次种现象称为梁丧失整体失稳。

提高整体稳定的有效措施
有效措施是加大梁的侧向抗弯强度和抗扭强度，以及增加受压翼缘侧向支承点以减少侧向在自由度。

整体稳定的计算公式
单向受弯：
双向受弯：
用计算整体稳定的条件
局部稳定
梁受压翼缘的局部稳定限值条件
工字形，T形梁的受压翼缘自由外伸宽度与厚度之比为：
箱形截面梁受压翼缘在两腹板间宽度与厚度之比：
梁腹板的局部稳定
2.腹板在纯弯曲作用下失稳
当腹板四周受均匀剪力同时考虑翼缘对腹板的弹性嵌固得：。