比尔定律
- 格式:doc
- 大小:196.17 KB
- 文档页数:5

比尔-朗伯定律光吸收系数
比尔-朗伯定律(Beer-Lambert law),又称作比尔定律
(Beer's law)或伯-朗伯定律(Lambert's law),是描述光在
某一物质中吸收的规律。
它的数学表达式为:
A = ε * c * L
其中,A代表吸光度(Absorbance),ε代表光吸收系数(Molar absorptivity),c代表溶液中物质的摩尔浓度(Molar concentration),L代表光路长度(Path length)。
光吸收系数(Molar absorptivity)是一个物质本身的性质,表
示单位浓度、单位光路长度下物质对光的吸收能力。
光吸收系数与物质的化学结构和电子跃迁有关,不同物质的光吸收系数不同。
光吸收系数可以通过实验测量得到,以便定量分析物质的浓度。
在实验中,通过测量样品的吸光度A,已知光路长度L和光
吸收系数ε,可以计算出样品的摩尔浓度c。
需要注意的是,比尔-朗伯定律在某些条件下可能不成立,例
如溶液浓度过高、光路长度过长等情况会引起吸光度的非线性增加。
在实际应用中,需要对样品进行适当稀释或者选择合适的测量条件以满足线性关系。

比尔定律成立的条件比尔定律是指在计算机科学中,处理器性能的提升速度远远超过了内存访问速度的提升速度。
它是由英特尔公司创始人之一戈登·摩尔提出的。
根据比尔定律,处理器的性能每18个月翻倍,而内存访问速度则只能每10年翻倍一次。
比尔定律的成立条件如下:1. 处理器的性能提升速度快于内存访问速度的提升速度。
这是比尔定律的核心条件。
处理器的性能提升包括提高时钟频率、增加核心数量、改善指令集等方面,而内存访问速度的提升主要通过增加带宽和降低延迟来实现。
2. 处理器和内存之间的数据传输存在瓶颈。
由于处理器的性能提升速度快于内存访问速度的提升速度,导致处理器在等待数据从内存中读取时会出现空闲时间。
这种空闲时间会导致处理器的利用率下降,影响整体系统的性能。
3. 程序的性能瓶颈主要集中在内存访问上。
由于处理器的性能提升速度快于内存访问速度的提升速度,导致程序的性能瓶颈主要集中在内存访问上。
如果程序的性能瓶颈主要集中在处理器上,那么比尔定律就不成立。
4. 内存层次结构的设计能够提高访问效率。
为了缓解比尔定律带来的性能瓶颈,计算机系统采用了多级缓存和虚拟内存等技术来改善内存访问效率。
多级缓存可以减少处理器访问内存的次数,提高访问效率;虚拟内存可以将磁盘作为扩展内存使用,减少内存的访问需求。
5. 高效的并行计算能够提高处理器的利用率。
由于比尔定律带来的空闲时间,提高处理器的利用率成为提升系统性能的关键。
并行计算可以将多个任务同时执行,提高处理器的利用率。
并行计算可以通过多核处理器、多线程和分布式计算等方式实现。
比尔定律的成立条件包括处理器的性能提升速度快于内存访问速度的提升速度,处理器和内存之间存在数据传输瓶颈,程序的性能瓶颈主要集中在内存访问上,内存层次结构的设计能够提高访问效率,高效的并行计算能够提高处理器的利用率。
只有在满足这些条件的情况下,比尔定律才能成立。
比尔定律的成立意味着处理器的性能提升速度远远快于内存访问速度的提升速度,这对计算机系统的设计和优化提出了挑战,也为计算机科学领域带来了许多机遇和发展空间。

比尔定律(Beer-Lambert Law)是分光光度法的基本定律,又称郎伯一比尔定律,描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系。
比尔定律的数学表达式为:I=I0e-kcC,其中I为透射光强度,I0为入射光强度,C为吸光物质的浓度,k为吸光系数,与入射光波长、吸光物质的吸光特性以及溶剂和温度等因素有关。
比尔定律适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔定律表明,光被吸收的量正比于光程中产生光吸收的分子数目。
光通过溶液后强度减弱的程度,与入射光强、溶液浓度和厚度的乘积成正比。
然而,比尔定律只在溶液浓度较小时成立,浓度很大时,分子对光的吸收本领受四周邻近分子的影响很大,分子间的相互影响不能忽略,比尔定律不再成立。

伯(Lambert)定律阐述为:光被透明介质吸收的比例与入射光的强度无关;在光程上每等厚层介质吸收相同比例值的光。
目录编辑本段定义朗伯比尔定律又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
光被吸收的量正比于光程中产生光吸收的分子数目。
公式及参数意义log( Io/I)= εCl (1—4)公式中Io和I分别为入射光及通过样品后的透射光强度;log(Io/I)称为吸光度(ab—sorbance)旧称光密度(optical density);C为样品浓度;l为光程;ε为光被吸收的比例系数。
当浓度采用摩尔浓度时,ε为摩尔吸收系数。
它与吸收物质的性质及入射光的波长λ有关。
当产生紫外吸收的物质为未知物时,其吸收强度可用表示:(1—5)公式中C为lOOml溶液中溶质的克数;b为光程,以厘米为单位;A为该溶液产生的紫外吸收;表示lcm光程且该物质浓度为lg/lOOmL时产生的吸收。
朗伯—比尔定律数学表达式A=lg(1/T)=Kbc(A为吸光度,T为透射比,是透射光强度比上入射光强度c为吸光物质的浓度b 为吸收层厚度)物理意义当一束平行单色光垂直通过某一均匀非散射的吸光物质时,与其吸光度A与吸光物质的浓度c及吸收层厚度b成正比.朗伯-比耳定律成立的前提(1) 入射光为平行单色光且垂直照射.(2) 吸光物质为均匀非散射体系.(3) 吸光质点之间无相互作用.(4) 辐射与物质之间的作用仅限于光吸收,无荧光和光化学现象发生.比尔-朗伯定律维基百科,自由的百科全书(重定向自比尔-朗伯定律)比尔-朗伯定律(Beer–Lambert law),又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。

比尔—朗伯定律数学表达式【最新版】目录1.比尔 - 朗伯定律的概述2.比尔 - 朗伯定律的数学表达式3.比尔 - 朗伯定律的应用4.总结正文1.比尔 - 朗伯定律的概述比尔 - 朗伯定律,又称为比尔定律,是由英国物理学家威廉·比尔(William Hyde Wollaston)和德国物理学家约瑟夫·朗伯(Joseph von Fraunhofer)于 19 世纪先后发现的一个物理定律。
该定律主要描述了黑体辐射强度与温度之间的关系。
黑体辐射是指一个物体在热力学平衡状态下,以电磁波形式发射出的热辐射。
2.比尔 - 朗伯定律的数学表达式比尔 - 朗伯定律的数学表达式为:I = (1/c) * εσ * (1/T^4) * ∫(0 至∞) [f(频率,温度) * (e^(h *频率/kT) - 1)]其中:I 代表黑体辐射强度;c 代表光速;εσ代表黑体表面的发射率;T 代表黑体温度;h 代表普朗克常数;k 代表玻尔兹曼常数;频率代表电磁波的频率;f(频率,温度) 代表黑体在频率和温度下的辐射强度。
3.比尔 - 朗伯定律的应用比尔 - 朗伯定律在物理学、天文学和工程领域具有广泛的应用。
例如,在热力学研究中,它可以用来研究物体在不同温度下的热辐射特性;在天文学中,它可以用来分析恒星表面的辐射特性,从而推测恒星的温度、半径等参数;在工程领域,比尔 - 朗伯定律被应用于红外热像仪、太阳能电池等设备的设计和优化。
4.总结比尔 - 朗伯定律是一个描述黑体辐射强度与温度之间关系的重要定律,其数学表达式为 I = (1/c) * εσ * (1/T^4) * ∫(0 至∞) [f(频率,温度) * (e^(h *频率/kT) - 1)]。

朗伯 - 比尔定律
朗伯-比尔定律(Lambert's-Beer's Law)是一种描述光线通过介质中吸收和散射的表现的定律。
该定律是由瑞士数学家约翰·海因里希·朗伯(Johann Heinrich Lambert)和德国化学家奥古斯特·比尔(August Beer)独立发现的。
根据朗伯-比尔定律,当光束通过一个透明介质时,它的强度将会随着介质中物质的浓度而减弱。
该定律可以表示为:A = εcl,其中A是透过率(或吸光度),ε是摩尔吸光系数,c是溶液或气体中溶质的浓度,l是光路的长度。
这个定律的实际应用非常广泛。
在分析化学中,通过测量溶液中某种物质吸收光线的强度变化,可以确定其浓度。
这是许多光谱分析方法的基础,例如紫外-可见吸收光谱法和红外光谱法。
此外,朗伯-比尔定律还可以用于测量大气中的污染物浓度、血液中的氧含量以及其他许多化学和生物学的应用中。
总的来说,朗伯-比尔定律是光学和化学分析领域中的重要定律,它描述了光在介质中被吸收的行为,并且提供了确定物质浓度的方法。

朗伯一比尔(Lam阮m Beer)定律当入射光波长一定时,待测溶液的吸光度4与其浓度和液层厚度成正比,即k为比例系数,与溶液性质、温度和入射波长有关。
Lam阮k Beer定律是分光光度定量分析的基础。
当浓度以g/L表示时,称k为吸光系数,以a表示,即A = abc当浓度以mol/L表示时,称k为摩尔吸光系数,以8表示,即A = 8 bc比耳定律成立的前提条件是:(1)入射光是单色光;(2)吸收发生在均匀的介质中;(3)吸收过程中,吸收物质互相不发生作用透射率定义:T 取值为0.0 %〜100.0 % 全部吸收T = 0.0 % 全部透射T = 100.0 %吸光度与透射率-也尸=KCb = A 以百分透光度和吸光度分别对溶液浓度作图得一条通过原点的直线和一条指数曲线根据比尔定律,在理论上,吸光度对溶液浓度作图所得的直线的截距为零,斜率为kb 。
实 际上,吸光度与浓度的关系有时是非线性的,或者不通过原点,这种现象称为偏离比尔定 律。
引起偏离比尔定律的因素样品吸光度4与光程b 总是成正比。
但当b 一定时,4与c 并不总是成正比,即 偏离L-B 定律!这种偏离由样品性质和仪器决定。
1. 样品性质影响a ) 稀溶液。
待测物高浓度--吸收质点间隔变小一质点间相互作用一对特定辐射的吸收能力 发生变化---8变化;b ) 稳定溶液。
试液中各组份的相互作用,如缔合、离解、光化反应、异构化、配体数目改 变等,会引起待测组份吸收曲线的变化;c ) 溶剂的影响:对待测物生色团吸收峰强度及位置产生影响;d ) 均匀溶液。
胶体、乳状液或悬浮液对光的散射损失。
2. 仪器因素仪器因素包括光源稳定性以及入射光的单色性等。
3)入射光的非单色性:不同波长的光所产生的吸收不同,可导致测定偏差。
假设入射光由测量波长气和干扰气波长组成,据疏纣定律,溶液对在气 和气的光的吸光度分别为:A = 1它一0* =£ bc ^-^(x ) = e ^bc A Tg W ) =8.bc 或叩)=e &, x D Ix x IxX 1 I 2 - 综合前两式,得I _i !— ______ L _i ! __________A = 1g 0( x ) 0(/) = 1g 0( x ) 0(/) I +1 I 10-£ bc + I 10-£ bcx i0( x ) 0(/) 。

比尔沙发定律
朗伯比尔定律又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律,是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔-朗伯定律是比色分析及分光光度法的理论基础。
光被吸收的量正比于光程中产生光吸收的分子数目。
比尔—朗伯定律数学表达式:A=lg(1/T)=Kbc。
物理意义是当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度A与吸光物质的浓度c及吸收层厚度b成正比,而与透光度T成反相关。


朗伯-比尔定律原理朗伯-比尔定律(Lambert's Beer Law),也被称为比尔-朗伯定律,是一种描述光在透明介质中吸收的现象的定律。
这个定律是由德国科学家约翰·海因里希·朗伯和法国科学家皮埃尔·比尔于19世纪初提出的。
朗伯-比尔定律在化学、光学、分析化学和生物医学等领域有广泛的应用。
朗伯-比尔定律可以用下面的公式表示:A = εlc其中,A是物质溶液的吸光度(absorbance),ε是摩尔吸光度(molar absorptivity),l是光程(path length),c是溶液的浓度。
根据朗伯-比尔定律,当光通过一个透明介质时,光的强度会随着介质中吸收物质的浓度增加而减弱。
这是因为介质中的吸收物质会吸收部分光的能量,使光的强度降低。
吸收物质的浓度越高,吸收的光的能量就越多,光的强度减弱的程度也就越大。
摩尔吸光度(ε)是一个物质的固有属性,表示单位浓度下该物质对光的吸收能力。
摩尔吸光度越大,说明物质对光的吸收能力越强。
不同物质的摩尔吸光度是不同的,这也是朗伯-比尔定律可以用于定量测量物质浓度的基础。
光程(l)是光在透明介质中传播的距离,一般以厘米作为单位。
光程越长,光通过介质时被吸收的能量就越多,光的强度减弱的程度也就越大。
溶液的浓度(c)是指单位体积溶液中溶质的质量或摩尔数。
浓度越高,溶液中的吸收物质的数量就越多,光通过溶液时被吸收的能量也就越多。
朗伯-比尔定律可以用于分析化学中测量溶液中吸收物质浓度的定量分析方法,这种方法被称为分光光度法。
在分光光度法中,通过测量物质溶液的吸光度,再利用朗伯-比尔定律的公式,就可以计算出溶液中物质的浓度。
朗伯-比尔定律在生物医学领域也有广泛的应用。
例如,血红蛋白是血液中的一种重要成分,可以通过测量血红蛋白溶液的吸光度,利用朗伯-比尔定律的公式,计算出血红蛋白的浓度。
这对于临床诊断和疾病监测具有重要意义。
总之,朗伯-比尔定律是描述光在透明介质中吸收现象的定律。
比尔-朗伯定律光吸收系数摘要:1.比尔- 朗伯定律的概述2.光吸收系数的定义和计算方法3.比尔- 朗伯定律与光吸收系数的关系4.比尔- 朗伯定律在实际应用中的意义正文:一、比尔- 朗伯定律的概述比尔- 朗伯定律,又称比尔定律,是由约翰·亨利·朗伯和威廉·斯蒂芬·比尔两位科学家于1852 年提出的。
该定律主要描述了物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系。
这一定律为光吸收现象的研究和应用提供了理论基础,被广泛应用于化学、环境科学、生物学等领域。
二、光吸收系数的定义和计算方法光吸收系数是一个物质在单位浓度、单位厚度和单位光路长度条件下,对某一波长光吸收能力的量度。
光吸收系数用字母ε表示,单位为升/(摩尔·厘米)。
光吸收系数可以通过比尔- 朗伯定律进行计算。
三、比尔- 朗伯定律与光吸收系数的关系比尔- 朗伯定律表明,吸光物质对某一波长光的吸收程度与吸光物质的浓度及其液层厚度成正比。
具体数学表达式为:A = εbc,其中A 表示吸光度,ε表示光吸收系数,b 表示吸光物质的浓度,c 表示吸光物质的液层厚度。
由此可知,光吸收系数是比尔- 朗伯定律中一个重要的参数。
四、比尔- 朗伯定律在实际应用中的意义比尔- 朗伯定律在许多领域具有重要的实际应用价值。
例如,在环境监测中,通过测量污染物的光吸收系数,可以推算出污染物的浓度,从而为环境污染治理提供依据。
在生物学中,比尔- 朗伯定律可用于研究生物体内某些物质的吸收和代谢过程。
在化学分析中,光吸收系数被广泛应用于各种化学物质的定量分析。
朗伯比尔定律的公式及符号含义朗伯比尔定律(Lambert-Beer Law),又称为比尔定律(Beer's Law)或者比尔-朗伯定律(Beer-Lambert Law),是化学和物理领域中常用的定律。
此定律描述了溶液中光线吸收的强度与光路长度及物质浓度间的关系。
公式:A = εcl符号意义:A:溶液中吸收的光线强度ε:摩尔消光系数c:溶液中物质的浓度l:光路长度该定律的前提是光线穿过溶液的路径和光线进入溶液前的强度相等。
这个定律在分析学、光谱学、环境科学、药物学以及生化学等领域有着广泛应用。
朗伯比尔定律的由来:朗伯-比尔-虎克实验。
1802年,比尔通过实验发现,溶液吸收的光线强度与光路长度成正比例关系。
后来,朗伯(Lambert)在1820年左右又发现,在某些物质中,光线被吸收的程度与该物质的浓度成正比例关系。
这两个实验在后来被整合成了朗伯比尔定律。
应用:1. 分析学:通过比较吸收光谱中溶液与纯溶剂的光谱,可以确定其中某个物质的浓度。
2. 光谱学:朗伯比尔定律解释了吸收光谱强度与物质浓度之间的关系。
根据该定律,不同波长的光线被物质吸收的程度不同,所以可以通过吸收光谱来确定分子的结构。
3. 环境科学:朗伯比尔定律被应用于环境科学中的水体、大气、土壤等领域。
通过分析水或大气中某种物质的浓度,可以推断出该物质的源头或是环境的状况。
4. 生物医学:通过分析吸收光谱,可以确定人体或者其他生物体内某种物质的浓度,如葡萄糖、蛋白质、激素等。
5. 化学工业:朗伯比尔定律被用于监控化学反应中反应物与产物之间的浓度变化,以保证反应的正常进行。
此外,该定律还被用于测定某种化学物质的含量以及检测污染物浓度。
总之,朗伯比尔定律可以被广泛地应用于物理、化学、生物学等领域,为科学研究和工业应用提供了有力的支持。
比尔-朗伯定律比尔-朗伯定律(Beer–Lambert law),又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
概述一束单色光照射于一吸收介质表面,在通过一定厚度的介质后,由于介质吸收了一部分光能,透射光的强度就要减弱。
吸收介质的浓度愈大,介质的厚度愈大,则光强度的减弱愈显著,其关系为:其中:∙:吸光度;∙:入射光的强度;∙:透射光的强度;∙:透射比,或称透光度;∙:系数,可以是吸收系数或摩尔吸收系数,见下文;∙:吸收介质的厚度,一般以 cm 为单位;∙:吸光物质的浓度,单位可以是 g/L 或 mol/L。
比尔-朗伯定律的物理意义是,当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度与吸光物质的浓度及吸收层厚度成正比。
当介质中含有多种吸光组分时,只要各组分间不存在着相互作用,则在某一波长下介质的总吸光度是各组分在该波长下吸光度的加和,这一规律称为吸光度的加合性。
系数:∙当介质厚度以 cm 为单位,吸光物质浓度以 g/L 为单位时,用表示,称为吸收系数,其单位为。
这时比尔-朗伯定律表示为。
当介质厚度以 cm 为单位,吸光物质浓度以 mol/L 为单位时,用表示,称为摩尔吸收系数,其单位为。
这时比尔-朗伯定律表示为。
两种吸收系数之间的关系为:。
历史物质对光吸收的定量关系很早就受到了科学家的注意并进行了研究。
皮埃尔·布格(Pierre Bouguer)和约翰·海因里希·朗伯(Johann Heinrich Lambert)分别在1729年和1760年阐明了物质对光的吸收程度和吸收介质厚度之间的关系;1852年奥古斯特·比尔(August Beer)又提出光的吸收程度和吸光物质浓度也具有类似关系,两者结合起来就得到有关光吸收的基本定律——布格-朗伯-比尔定律,简称比尔-朗伯定律。
伯(Lambert)定律阐述为:光被透明介质吸收的比例与入射光的强度无关;在光程上每等厚层介质吸收相同比例值的光。
目录编辑本段定义朗伯比尔定律又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
光被吸收的量正比于光程中产生光吸收的分子数目。
公式及参数意义log( Io/I)= εCl (1—4)公式中 Io和I分别为入射光及通过样品后的透射光强度;log(Io/I)称为吸光度(ab—sorbance)旧称光密度(optical density);C为样品浓度;l为光程;ε为光被吸收的比例系数。
当浓度采用摩尔浓度时,ε为摩尔吸收系数。
它与吸收物质的性质及入射光的波长λ有关。
当产生紫外吸收的物质为未知物时,其吸收强度可用表示:(1—5)公式中 C为lOOml溶液中溶质的克数;b为光程,以厘米为单位;A为该溶液产生的紫外吸收;表示lcm光程且该物质浓度为lg/lOOmL时产生的吸收。
朗伯—比尔定律数学表达式A=lg(1/T)=Kbc(A为吸光度,T为透射比,是透射光强度比上入射光强度 c为吸光物质的浓度 b 为吸收层厚度)物理意义当一束平行单色光垂直通过某一均匀非散射的吸光物质时,与其吸光度A与吸光物质的浓度c及吸收层厚度b成正比.朗伯-比耳定律成立的前提(1) 入射光为平行单色光且垂直照射.(2) 吸光物质为均匀非散射体系.(3) 吸光质点之间无相互作用.(4) 辐射与物质之间的作用仅限于光吸收,无荧光和光化学现象发生.比尔-朗伯定律维基百科,自由的百科全书(重定向自比尔-朗伯定律)比尔-朗伯定律(Beer–Lambert law),又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
朗伯-比尔定律是光吸收的基本定律
朗伯-比尔定律(Lambert-Beer law)是光吸收的基本定律。
该定律描述了光线通过一定浓度的溶液、气体或固体时被吸收的量与透射的光线强度之间的关系。
根据该定律,光通过介质中被吸收的量与介质的浓度成正比,并与光线通过后溶液、气体或固体的厚度成指数关系。
即当浓度增加时,吸收量也增加,而通过的透射光强度下降。
该定律可表示为:A = εlc
其中,A表示吸光度(absorbance),即被测溶液、气体或固体吸收光线的程度;ε表示摩尔吸光系数(molar absorptivity),即浓度为1mol/L的溶液吸光度为1的能力;l表示光通过介质的厚度(path length);c表示溶液、气体或固体的浓度。
比尔-朗伯定律比尔-朗伯定律,通常被称为比尔定律,是指在透明溶剂中发色团的吸光度随着样品池光程以及发色团浓度的变化而呈线性变化。
比尔定律是对描述光与物质的相互关系的麦克斯韦远场方程的简化描述。
事实上,比尔定律对一系列发色团、溶剂和浓缩物品而言都是非常精确的定律,在定量光谱学中被广泛运用。
吸光度通过分光光度计度量,这需要通过一束波长是λ的平行光束,光束要穿过一个类似平面的厚平板,该材料与光束垂直。
对液体而言,样品保存在一个叫做样品池的光学平面透明的容器里。
吸光度(Aλ)的计算是入射光穿过样品(I)的光能与入射在样品(I)表面的光能的比率。
Aλ= -log (I/I0)比尔定律遵从:A λ= ελbcc =波长λ的发色团的分子吸收率或消光系数(1M溶液的1cm厚样品的光密度),ελ 是溶液和材料的特性。
b = 样品路径(厘米)c =样品中化合物浓度,摩尔浓度 (mol L-1)在吸收度实验中,光束不仅通过发色团衰减,也通过从空气和样品之间的界面反射、样品和小型管之间的界面反射、以及溶液的吸收而衰减。
各因素可以分别量化,但常常当光束通过样品“空白”或“基准”或参考样品时,这些因素被通过定义I0的方式被去除了。
(例如,充满溶液但发色团浓度为0的小型管被用做”空白”。
)许多因素可以影响比尔定律的有效性。
它通常通过测量一系列标准的吸光度的方式用来检测发色团比尔定律的线性。
这种校准也可以去除实验、设备以及一批试剂中的误差。
(比如光程未知的样品池)。
紫外可见分光光度法——光的吸收定律一. Lambert-Beer 定律——光吸收基本定律“ Lambert-Beer 定律” 是说明物质对单色光吸收的强弱与吸光物质的浓度(c)和液层厚度(b)间的关系的定律,是光吸收的基本定律,是紫外-可见光度法定量的基础。
Lambert定律——吸收与液层厚度(b)间的关系Beer 定律——吸收与物质的浓度(c)间的关系“ Lambert-Beer 定律”可简述如下:当一束平行的单色光通过含有均匀的吸光物质的吸收池(或气体、固体)时,光的一部分被溶液吸收,一部分透过溶液,一部分被吸收池表面反射;设:入射光强度为 Io,吸收光强度为Ia,透过光强度为It,反射光强度为Ir,则它们之间的关系应为:Io = Ia + It + Ir (4)若吸收池的质量和厚度都相同,则 Ir 基本不变,在具体测定操作时 Ir 的影响可互相抵消(与吸光物质的 c及 b 无关)上式可简化为: Io= Ia +It (5)实验证明:当一束强度为 I0 的单色光通过浓度为 c、液层厚度为 b 的溶液时,一部分光被溶液中的吸光物质吸收后透过光的强度为 It ,则它们之间的关系为:称为透光率,用 T % 表示。
比尔-朗伯定律[编辑]
(重定向自比尔定律)
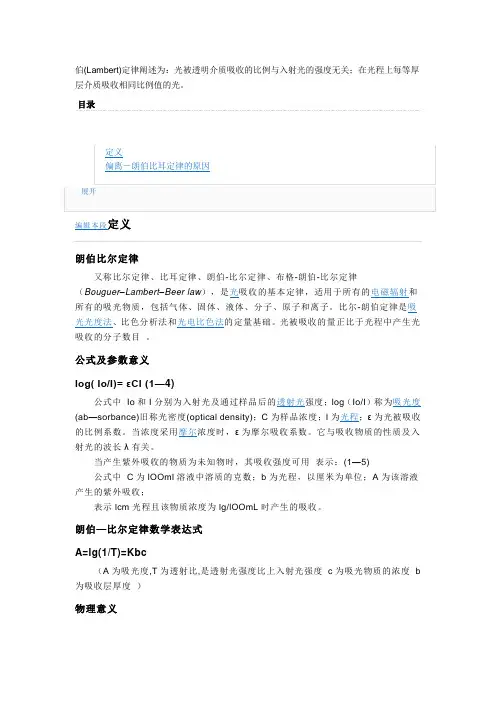
比尔-朗伯定律的一个例子:绿色激光射入罗丹明6B溶液中,激光的光强逐渐减弱。
比尔-朗伯定律(Beer–Lambert law),又称比尔定律、比耳定律、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。
比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
概述[编辑]
一束单色光照射于一吸收介质表面,在通过一定厚度的介质后,由于介质吸收了一部分光能,透射光的强度就要减弱。
吸收介质的浓度愈大,介质的厚度愈大,则光强度的减弱愈显著,其关系为:
其中:
∙ :吸光度;
∙ :入射光的强度;
∙ :透射光的强度;
∙ :透射比,或称透光度;
∙ :系数,可以是吸收系数或摩尔吸收系数,见下文;
∙ :吸收介质的厚度,一般以 cm 为单位; ∙
:吸光物质的浓度,单位可以是 g/L 或 mol/L 。
比尔-朗伯定律的物理意义是,当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度 与
吸光物质的浓度 及吸收层厚度 成正比。
当介质中含有多种吸光组分时,只要各组分间不存在着相互作用,则在某一波长下介质的总吸光度是各组分在该波长下吸光度的加和,这一规律称为吸光度的加合性。
系数
:
∙
当介质厚度 以 cm 为单位,吸光物质浓度 以 g/L 为单位时, 用 表示,称为吸
收系数,其单位为。
这时比尔-朗伯定律表示为。
∙ 当介质厚度 以 cm 为单位,吸光物质浓度 以 mol/L 为单位时, 用 表示,称为
摩尔吸收系数,其单位为。
这时比尔-朗伯定律表示为。
两种吸收系数之间的关系为:。
历史[编辑]
物质对光吸收的定量关系很早就受到了科学家的注意并进行了研究。
皮埃尔·布格(Pierre Bouguer )和约翰·海因里希·朗伯(Johann Heinrich Lambert )分别在1729年和1760年阐明了物质对光的吸收程度和吸收介质厚度之间的关系;1852年奥古斯特·比尔(August Beer )又提出光的吸收程度和吸光物质浓度也具有类似关系,两者结合起来就得到有关光吸收的基本定律——布格-朗伯-比尔定律,简称比尔-朗伯定律。
推导[编辑]
假设一束强度为
的平行单色光(入射光)垂直照射于一块各向同性的均匀吸收介质表面,在通过厚度
为 的吸收层(光程)后,由于吸收层中质点对光的吸收,该束入射光的强度降低至
,称为透射光强
度。
物质对光吸收的能力大小与所有吸光质点截面积的大小成正比。
设想该厚度为 的吸收层可以在垂直
于入射光的方向上分成厚度无限小的多个小薄层 ,其截面积为 ,而且每个薄层内,含有吸光质点的
数目为 个,每个吸光质点的截面积均为 。
因此,此薄层内所有吸光质点的总截面积。
假设强度为 的入射光照射到该薄层上后,光强度减弱了 。
是在小薄层中光被吸收程度的量
度,它与薄层中吸光质点的总截面积
以及入射光的强度 成正比,也就是
负号表示光强度因吸收而减弱,k1为比例系数。
假设吸光物质的浓度为c,则上述薄层中的吸光质点数为
代入上式,合并常数项并设,经整理得
对上式进行定积分,则有
上式中称为吸光度();而透射光强度与入射光强度之间的比值称为透射比,或称透光度(),其关系为:
(请注意本段中透射光强度的符
号与首段中的符号不同)
即比尔-朗伯定律。
前提[编辑]
比尔-朗伯定律的成立是有前提的,即:
1.入射光为平行单色光且垂直照射;
2.吸光物质为均匀非散射体系;
3.吸光质点之间无相互作用;
4.辐射与物质之间的作用仅限于光吸收过程,无荧光和光化学现象发生。
根据比尔-朗伯定律,当吸收介质厚度不变时,与之间应该成正比关系,但实际测定时,标准曲线常会出现偏离比尔-朗伯定律的现象,有时向浓度轴弯曲(负偏离),有时向吸光度轴弯曲(正偏离)。
造成偏离的原因是多方面的,其主要原因是测定时的实际情况不完全符合使比尔-朗伯定律成立的前提条件。
物理因素有:
1.非单色光引起的偏离;
2.非平行入射光引起的偏离;
3.介质不均匀引起的偏离;
化学因素有:
1.溶液浓度过高引起的偏离;
2.化学反应(如水解、解离)引起的偏离;
化学分析[编辑]
比尔-朗伯定律可以用于通过分光光度法,以分析混合物的性质。
这种方法不需要对于样品进行过多的预操作。
例如测定血浆中胆红素的浓度。
纯胆红素的光谱是已经确定了的,因此它的摩尔吸收系数也是确定的。
需要测量两个波长的光的吸收情况,其中第一个是胆红素特定的波长,而另一个则是为了修正可能存在的干涉。
从而可以得到浓度c = A修正 / κ。
再例如,在一个更复杂的例子中,溶液中有两种溶质,浓度分别为c1和c2。
此时,单位长度下,任何波长λ的吸光度为:
因此,如果对两个波长进行测量,则可以得到两个方程,形成一个二元一次方程组。
此时只要知道两个波长下,两个溶质的摩尔吸收系数κ1和κ2,那么就可以求出它们的浓度c1和c2。
如果溶液中有更多溶质,也可以通过这种方法求出各溶质的浓度。
如果有n种溶质,只需要测量n个波长下的吸收度即可。
这种方法广泛应用于红外光谱学和近红外光谱学,用以分析聚合物降解和氧化。
6微米下,羰基的吸收度十分容易测量,因此聚合物的氧化程度也很溶液得到。
大气中的比尔-朗伯定律[编辑]
比尔-朗伯定律也可应用于大气当中,用以描述阳光和星光通过大气时的衰减状况。
此时,除了吸收之外,还要考虑大气散射。
大气中的比尔-朗伯定律的形式为:
其中,
∙代表光深度,其下标x所对应物质分别为:
∙指浮质(能吸收和散射);
∙指均匀混合气体(主要是二氧化碳()和氧分子(),仅吸收);
∙指二氧化氮,主要有城市污染产生(仅吸收);
∙指水蒸气(吸收);
∙指臭氧(仅吸收);
∙指氧分子()和氮分子()的瑞利散射(导致天空的蓝色)。
代表大气光学质量因子。
若被观测物处于一个比较小的天顶角,则大气光学质量(英语:airmass)约等于。
[1]
这条方程可以用于反推浮质的光学厚度,这对于卫星图像的修正和计算浮质在大气中的角色都十分重要。
当光穿过大气层时,空气的密度并非常量,因此原方程应作以下修正:
其中z是在大气中走过的路程,其它符号在上文已有定义。
[2]这在上面大气方程中的每一个里面已经考虑。