下载文档原格式
MATLAB课程设计基于MATLAB的直流电机双闭环调速系统的设计与仿真班级：自动化12-2姓名：学号：目录一、目录-----------------------------------------------------------1二、前言-----------------------------------------------------------2三、设计目的及要求--------------------------------------------3四、设计题目及参数--------------------------------------------3五、设计内容过程-----------------------------------------------31.计算电流和转速反馈系数-----------------------------------------32.电流环的动态校正过程--------------------------------------------33.转速环的动态校正过程--------------------------------------------94.建立转速电流双闭环直流调速系统的Simulink仿真模型，对上述分析设计结果进行仿真-------------------------------------14六、设计总结---------------------------------------------------18七、参考文献---------------------------------------------------19二、前言：控制系统理论与技术是现代科学技术的主要内容，以经广泛应用于航空与航天工业、电力工业、核能工业、石油工业、化学工业及冶金工业等众多学科和工程技术领域，并且具有经济、安全、快捷、优化设计和预测的特殊功能等优点，在非工程系统（如社会、管理、经济等系统）中，由于其规模及复杂程度巨大，直接实验几乎不可能，这是通过仿真技术的应用可以获得对系统的某种超前认识，因此仿真技术已经成为对控制系统进行分析、设计和综合研究中很有效的手段。
第36卷第2期2016年5月桂林理工大学学报Journal of Guilin University of TechnologyVol . 36 No . 2 May 2016文章编号：1674 -9057(2016)02 -0378 -05doi ：10. 3969/j . issn . 1674 -9057. 2016. 02. 032基于MATLAB 的双闭环直流调速系统建模与仿真刘胜前，张烈平，孙旋，钟志贤(桂林理工大学机械与控制工程学院，广西桂林541004)摘要：结合转速、电流双闭环直流调速系统的系统结构和电路组成，使用仿真软件Simulink 对双闭环直 流调速系统电流环进行建模仿真。
结果表明：阻尼系数越大，超调量越大，上升时间越短，当阻尼系数为0.5时，电流环性能达到最优。
在电流环性能最优时：空载运行条件下，系统稳定转速随给定电压变小而 变小；额定负载条件下，通过较长上升时间，达到额定转速。
抗扰性检验表明，该系统抗扰性较强。
关键词：负反馈；双闭环；直流调速系统；Simulink中图分类号：TP 273文献标志码：A在生产和生活中，各种电机的快速起动、制动 事关工业生产效率和人们的生活质量，基于电力电 子技术的不断发展，对于调速系统的起动时间、制动响应等性能指标要求也越来越高。
由于直流调 速系统技术比较成熟，多年以来一直是自动调速系 统的主要形式，普遍应用于冶金、地质、土建、轻 工业等领域[1]。
相比开环调速系统，闭环调速系 统的各项性能指标更优[2]。
如果对于系统的动态 性能要求较高，要求系统可以快速的起、制动，尤 其是在突然施加负载的情况下，速降很小，那么就 需要应用转速、电流双闭环直流调速系统[3]。
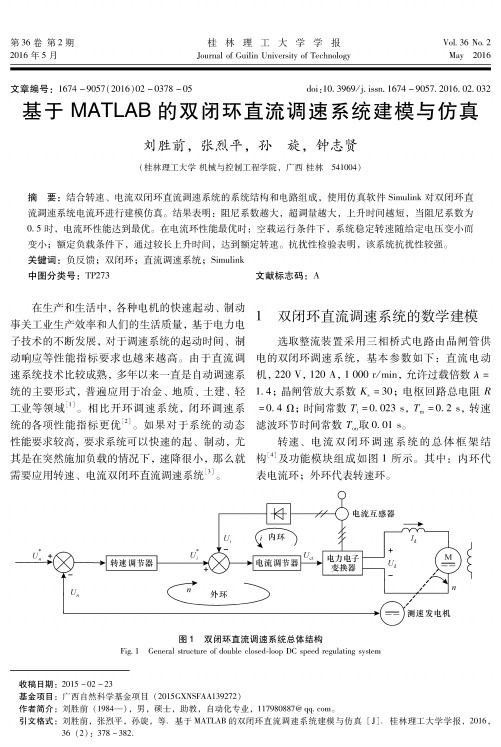
1双闭环直流调速系统的数学建模选取整流装置采用三相桥式电路由晶闸管供电的双闭环调速系统，基本参数如下：直流电动 机，220 V ，120 A , 1 000 r /min ，允许过载倍数 A = 1.4;晶闸管放大系数& =30;电枢回路总电阻只 =0.4 11;时间常数 L =0.023 s ，r m =0.2 s ，转速 滤波环节时间常数7^取〇.〇1 S。
、基于matlab的直流双闭环调速系统设计与仿真前言在直流双闭环调速系统设计中，在理论设计基础上根据实际系统运行情况作参数的调整是系统设计调试过程必不可少的一部分。
原因在于系统的实际参数，往往与理论设计时所用的值有一定的误差，而且系统某些环节非线性因素影响会使系统在理论设计参数后并不能立即获得理想的调速性能，因此需要通过调试过程才能获得理想性能。
传统的调试方法不仅增加系统的设计与调试强度而且不易产生预期结果。
matlab/simulink仿真平台是基于模型化图形组态的动态系统仿真软件，利用这种仿真工具可以不运行实际系统，只要在计算机上建立数字仿真模型，模仿被仿真对象的运行状态及其随时间变化的过程。
通过对数字仿真模型的运行过程的观察和设计，得到被仿真系统的仿真输出参数和基本特征，以此来估计和推断实际系统的真实参数和真实性。
而且可以非常方便地完成调试过程且能十分直观地得到系统输出波形。
利用matlab/simulink仿真工具有效地对直流调速系统进行参数调试，可以非常直观地观察电动机电流和转速响应情况进行静态和动态分析，是目前国际上广泛流行的工程仿真技术。
本文利用matlab仿真工具对直流调速系统进行仿真分析，通过仿真方法来调整理论设计所得的参数，找出系统调节器的最佳参数，仿真结果可以用来指导实际系统的设计。
直流调速系统的理论设计1.1 系统组成及要求本文研究的对象为电流转速双闭环直流调速系统，其系统动态结构框图如图1 所示，系统参数如下：电动机：V U N 220=；A I N 136=；rpm n N 1460=；rpm v C e /132.0=； 允许过载倍数： 5.1=λ；三相桥式整流装置放大倍数：40=s K ；电枢回路总电阻： Ω=∑5.0R ；时间常数： s T l 03.0=；ss T m 18.0=，电流反馈系数：A V /05.0=β； 转速反馈系数：rpm V /07.0=α。
基于Matlab的双闭环调速系统设计报告目录一、摘要 (2)二、总体方案设计 (3)1、控制原理2、控制结构图三、参数计算 (5)1、静态参数设计计算2、动态参数设计计算四、稳定性分析 (8)1、基于经典自控理论得分析2、利用MATLAB辅助分析A、利用根轨迹分析B、在频域内分析奈氏曲线：bode图利用单输入单输出仿真工具箱分析用Simulink仿真五、系统校正 (14)1、系统校正的工具2、调节器的选择3、校正环节的设计4、限流装置的选择六、系统验证 (15)1、分析系统的各项指标2、单位阶跃响应3、Simulink仿真系统验证系统运行情况七、心得体会 (20)八、参考文献 (20)一、摘要运动控制课是后续于自动控制原理课的课程，是更加接近本专业实现应用的一门课程。
直流电动机具有良好的起、制动性能，宜于在大范围内平滑调速，在许多需要调速和快速正反向的电力拖动领域中得到了广泛的应用。
由于直流拖动控制系统在理论上和实践上都比较成熟，而且从控制的角度来看，它又是交流拖动控制系统的基础。
所以加深直流电机控制原理理解有很重要的意义。
本设计首先进行总体系统设计，然后确定各个参数，当明确了系统传函之后，再进行稳定性分析，在稳定的基础上，进行整定以达到设计要求。
另外，设计过程中还要以matlab为工具，以求简明直观而方便快捷的设计过程。
二、总体方案设计1、控制原理根据设计要求，所设计的系统应为单闭环直流调速系统，选定转速为反馈量，采用变电压调节方式，实现对直流电机的无极平滑调速。
所以，设计如下的原理图：图1、单闭环直流调速系统原理图转速用与电动机同轴相连的测速电机产生的正比于转速的电压信号反馈到输入端，再与给定值比较，经放大环节产生控制电压，再通过电力电子变换器来调节电机回路电流，达到控制电机转速的目的。
这里，电压放大环节采用集成电路运算放大器实现，主电路用晶闸管可控整流器调节对电机的电源供给。
所以，更具体的原理图如下：图2、单闭环直流调速系统具体原理图2、控制结构图有了原理图之后，把各环节的静态参数用自控原理中的结构图表示，就得到了系统的稳态结构框图。
基于Matlab 的双闭环直流调速系统仿真一、双闭环直流调速系统的组成及要求为了实现转速和电流两种负反馈分别起作用，在系统中设置了两个调节器，分别调节转速和电流，二者之间实行串级连接，即把转速调节器的输出当作电流调节器的输入，再用电流调节器的输出去控制晶闸管整流器的触发装置。
从闭环结构上看，电流调节环在里面，叫做内环；转速环在外面，叫做外环。
这样就形成了转速、电流双闭环调速系统。
该双闭环调速系统的两个调节器ASR 和ACR 一般都采用PI 调节器。
因为PI 调节器作为校正装置既可以保证系统的稳态精度，使系统在稳态运行时得到无静差调速，又能提高系统的稳定性；作为控制器时又能兼顾快速响应和消除静差两方面的要求。
一般的调速系统要求以稳和准为主，采用PI 调节器便能保证系统获得良好的静态和动态性能。
图1直流双闭环调速系统动态结构图图中 、—转速给定电压和转速反馈电压、—电流给定电压和电流反馈电压ASR —转速调节器ACR —电流调节器TG —测速发电机TA —电流互感器UPE —电力电子变换器本文研究的对象为电流转速双闭环直流调速系统，其系统动态结构框图如图1 所示，系统参数如下：电动机：V U N 220=；A I N 136=；rpm n N 1460=；rpm v C e /132.0=； 允许过载倍数： 5.1=λ；三相桥式整流装置放大倍数：40=s K ；电枢回路总电阻： Ω=∑5.0R ；时间常数： s T l 03.0=，ss T m 18.0=；电流反馈系数：A V /05.0=β；转速反馈系数：rpm V /07.0=α。
二、系统仿真根据理论设计结果，构建直流双闭环调速系统的仿真模型，如图2 所示。
图2 直流双闭环调速系统的仿真模型仿真结果：在启动过程中，转速调节器ASR将经历不饱和、饱和、退饱和三个阶段，因此整个启动过程分为三个阶段。
▪第一阶段是电流上升阶段,由于转速变化慢，转速调节器很快饱和――饱和时转速环相当于开环，ASR输出限幅值。
基于matlab的双闭环直流调速系统仿真及参数进化设计本文基于matlab平台，设计了一个双闭环直流调速系统，并通过参数进化算法对其进行优化设计，以提高系统的性能和稳定性。
一、双闭环直流调速系统的基本结构和参数双闭环直流调速系统包括基本结构和控制回路两个部分。
其基本结构如下图所示： /β ，则电流环便等效成单位负反馈系统。
3） 小惯性环节近似处理由于T s 和 T 0i 一般都比T l 小得多，可以当作小惯性群而近似地看作是一个惯性环节，其时间常数为T ∑i = T s + T oi 简化的近似条件为ois ci 131T T ≤ω电流环结构图最终简化成图。
b 电流调节器结构的选择 1) 典型系统的选择：从稳态要求上看，希望电流无静差，以得到理想的堵转特性，采用 I 型系统就够了。
从动态要求上看，实际系统不允许电枢电流在突加控制作用时有太大的超调，以保证电流在动态过程中不超过允许值，而对电网电压波动的及时抗扰作用只是次要的因素，为此，电流环应以跟随性能为主，应选用典型I 型系统 2) 电流调节器选择电流环的控制对象是双惯性型的，要校正成典型 I 型系统，显然应采用PI型的电流调节器，其传递函数可以写成ss K s W i i i ACR )1()(ττ+=K i — 电流调节器的比例系数；τi — 电流调节器的超前时间常数3) 校正后电流环的结构和特性为了让调节器零点与控制对象的大时间常数极点对消，选择则电流环的动态结构图便成为图a 所示的典型形式，其中a) 动态结构图:b) 开环对数幅频特性c. 电流调节器的参数计算电流调节器的参数有：K i 和 τi ，其msT l8i==τRK K K i siI τβ=中 τi 已选定，剩下的只有比例系数 K i ， 可根据所需要的动态性能指标选取。
MATLAB双闭环直流调速系统的工程设计与仿真双闭环直流调速系统是一种常见的控制系统，在工业中被广泛应用于电机的调速。
本文将针对MATLAB中的双闭环直流调速系统进行工程设计与仿真。
1.系统架构设计双闭环直流调速系统主要由速度环和电流环组成。
速度环主要负责控制电机的速度，通过比较给定速度和实际速度，产生速度偏差。
电流环主要控制电机的电流，通过比较给定电流和实际电流，产生电流偏差。
速度环和电流环形成了一个闭环控制系统，可以使得电机在速度和电流方面达到我们所要求的目标。
2.系统建模在MATLAB中，可以使用Simulink进行系统建模。
首先，需要建立电机的数学模型，包括机械模型、电磁模型和电气模型。
电机的机械模型可以使用转矩方程来描述，电磁模型可以使用电压方程来描述，电气模型可以使用网路方程来描述。
然后，将这些模型通过各个子系统进行连接，并进行参数设置。
最后，通过连接速度环和电流环的闭环控制系统，完成整个系统的建模。
3.控制器设计在MATLAB中，可以使用PID控制器进行控制器的设计。
首先，通过调节PID控制器的参数，使得系统的过渡过程满足我们对速度和电流的要求。
然后，使用增量PID算法对控制器进行改进，减小控制误差。
最后，通过将速度控制器与电流控制器进行串联，完成双闭环控制系统的设计。
4.系统仿真在MATLAB中，可以使用Simulink进行系统的仿真。
首先，设置仿真时间和步长，并进行仿真参数设置。
然后，通过给定输入信号，例如阶跃信号，观察系统的输出响应。
通过调整控制器的参数，观察系统的响应特性，包括超调量、稳定时间和稳态误差等。
最后，通过对仿真数据的分析，检验系统是否满足我们的设计要求。
总结：MATLAB提供了丰富的工具和函数，可以帮助我们进行双闭环直流调速系统的工程设计与仿真。
通过建立系统模型、设计控制器并进行仿真分析，可以快速有效地完成系统设计。
同时，可以通过调整参数和算法对系统进行优化，使得系统的性能更加稳定和可靠。
