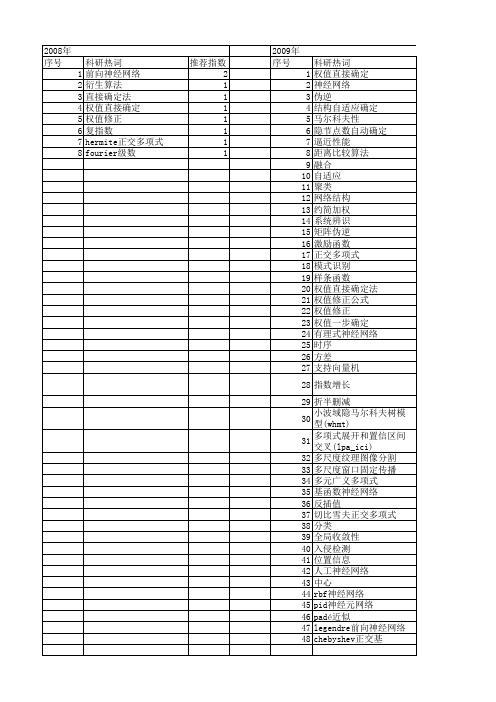
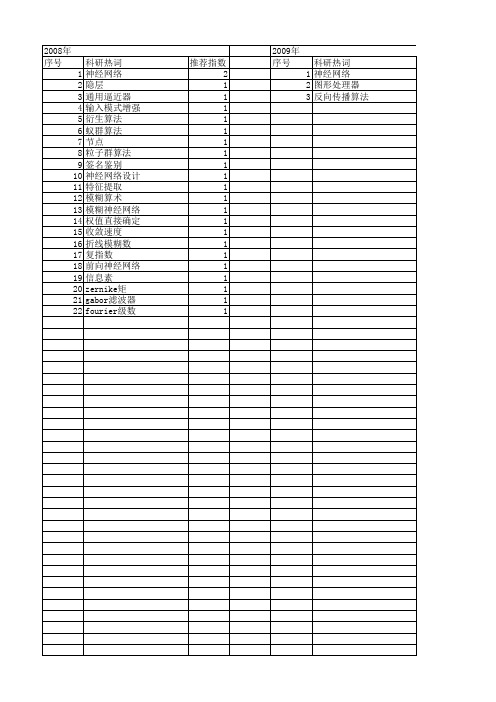
Hermite正交基前向神经网络的权值直接确定法

神经网络模型中的权重调整算法神经网络是一种复杂的计算模型，可以模拟人类大脑的神经系统。

神经网络的训练过程通常包括两个阶段：前向传播和反向传播。

在前向传播过程中，信号从输入层到输出层进行传递，每一层都通过激活函数计算输出。

在反向传播过程中，误差从输出层向输入层进行传播，通过权重的调整来最小化误差。

神经网络模型中的权重调整算法主要包括以下几种：1. 梯度下降算法梯度下降算法是一种常见的权重调整算法，它的基本思想是沿着误差函数的负梯度方向进行权重的更新。

具体来说，假设神经网络的误差函数为E(w)，其中w表示权重向量。

那么在每一次迭代中，梯度下降算法通过以下公式更新权重：w = w - α * ∇E(w)其中α表示学习率，∇E(w)表示误差函数E(w)关于权重向量w 的梯度。

梯度下降算法的优点是简单易用，但存在可能陷入局部最优解的问题。

2. 拟牛顿法拟牛顿法是一种更为高效的权重调整算法，它使用拟牛顿矩阵来近似海森矩阵，从而更快地收敛到全局最优解。

拟牛顿法的基本思想是通过迭代更新拟牛顿矩阵H来更新权重向量w。

具体来说，假设神经网络的误差函数为E(w)，Hk表示在第k次迭代时的拟牛顿矩阵，dk表示Hk的逆矩阵与梯度向量的乘积，那么权重向量w在第k+1次迭代时的更新规则为：w(k+1) = w(k) - α * dk拟牛顿法的优点是收敛速度快，但相应地也需要更多的计算资源。

3. 随机梯度下降算法随机梯度下降算法是梯度下降算法的一种变体，它在每一次迭代中只使用一个样本进行权重的更新。

这种算法的优点是每次迭代速度快，缺点是可能会导致权重的震荡，同时也需要设置一个较小的学习率。

4. 自适应学习率算法自适应学习率算法是一种根据当前情况自动调整学习率的算法。

这种算法通常会监控每次迭代的代价函数值，如果代价函数值下降较慢，就会减小学习率；反之，如果代价函数值下降较快，就会增大学习率。

这种算法的优点是能够自动适应不同的情况，但缺点是需要不断地监控代价函数值，增加了计算量。

数据融合在电力系统中的应用摘要：为了提高工作效率、减少数据冗余和冲突性，需要将多个系统的关键数据进行融合。

本文根据实际情况，选择数据融合的方式，设计电力数据融合系统，将多个体系来源的数据进行分类融合处理，得到比单一来源更加完善、全面的数据、提高了数据的有效性和可信度。

关键词：数据融合系统；有效性；可信度0引言随着智能电网的不断发展以及信息化技术的逐渐提升，电力系统也应该向智能化和信息化方向发展。

目前，电力系统电力公司内部通常有多个业务系统同时并存，不同的系统由于开发时间节点、开发公司及开发背最等诸多历史原因，导致这些信息系统分别独立运行，或者仅有少量体系简单整合，这给体系的良好运转带来极大挑战。

而且，不同体系中的数据既有交互，又有重叠，但又因特定业务系统的要求不同，其数据内容亦存在一定的不一致性，使数据提取及统一口径造成一定的统计难度。

针对以上问题，为了提高工作效率、减少数据冗余和冲突性，需要将多个业务系统来源的数据进行分类融合处理，根据实际情况，选择数据融合的方式，设计电力数据融合系统，将多个业务系统来源的数据进行分类融合处理，得到比单一来源更加完善、全面的数据、提高了数据的有效性和可信度。

１数据融合方案电网数据广泛分布、种类众多，包括实时数据、历史数据、文本数据、多媒体数据、时同序列数据等各类结构化，半结构化数据以及非结构化数据。

电力数据来源广泛化，分为内部数据和外部数据，电网内部数据主要来源于发电，输电、变电、配电、用电、调度六大环节相关业务系统；外部数据包括可反映经济、社会、政策、气象、用户特征、地理环境等影响电网规划和运行的数据。

因此，为了融合所需的不同业务系统的关键数据，包括企业用电数据，设备状态监测数据，地理空间、气象数据等，现有两种电力数据融合系统设计方案可供选择。

1.1业务整合业务整合方案需要将所有的业务系统进行重新设计为单一系统。

优点：统一入口、统一出口、无冗余、无数据冲突。

权重确定方法
权重确定方法是指用于计算矩阵或网络中每个元素相对于其他元素的权值的方法。

以下是几种常见的权重确定方法:
1. 自适应法:自适应法是一种基于机器学习的方法,它使用内部学习算法根据输入数据中的信息来更新权重。

这种方法通常用于优化网络的性能和泛化能力。

自适应法包括自编码器、对抗生成网络和生成对抗网络。

2. 前馈神经网络法:前馈神经网络法是一种基于神经网络结构的方法,它使用神经网络结构中的权重和偏置来更新网络中的自适应参数。

前馈神经网络法的优点是具有鲁棒性,可以在各种输入下保持稳定的性能。

3. 最小二乘法:最小二乘法是一种常用的优化方法,它用于求解网络中的权重矩阵。

最小二乘法通过最小化损失函数来寻找最优的权重矩阵。

4. 人工设计法:人工设计法是一种基于经验和专业知识的方法,它通过与其他方法相结合来寻找最优的权重矩阵。

这种方法通常需要专家的知识和经验,并且具有一定的不确定性。

5. 随机初始化法:随机初始化法是一种随机选择权重矩阵的方法。

这种方法可以保证网络的随机性和鲁棒性,并且可以避免陷入局部最优解。

随机初始化法通常用于小样本学习或初始化权重矩阵存在问题的网络。

牛顿方法的用导一致性张雨浓;陈宇曦;付森波;肖林【摘要】导数及其使用是一种重要的数学工具与方法,在数值方法研究中起着十分重要的作用,很多经典数值计算方法理论中都涉及了对导数的运用.作为常用的数值方法,牛顿方法大量利用了求导的思想.通过归纳牛顿迭代法的显性用导特性和牛顿插值多项式的隐性用导特性,得到牛顿方法的用导一致性.%Derivatives and their use as an important mathematical tool and method plays an important role in the research of numerical methods. In addition,many classical numerical methods involve the use of derivatives. Being commonly-used.Newton methods exploit the idea of using derivatives extensively. By summing up the explicit use of derivatives in Newton iteration method and the implicit use of derivatives in Newton interpolation polynomial, the consistency of using derivatives in Newton methods is thus illustrated.【期刊名称】《甘肃科学学报》【年(卷),期】2012(024)002【总页数】4页(P5-8)【关键词】牛顿迭代法;牛顿插值多项式;用导一致性【作者】张雨浓;陈宇曦;付森波;肖林【作者单位】中山大学信息科学与技术学院,广东广州510006;中山大学信息科学与技术学院,广东广州510006;中山大学信息科学与技术学院,广东广州510006;中山大学信息科学与技术学院,广东广州510006【正文语种】中文【中图分类】O241.4随着当今科学技术的快速发展，计算机在自然科学和社会科学的各个领域发挥着举足轻重的作用，导数及其使用作为数值方法研究的一种工具和方法日渐被研究者所重视.以下从牛顿迭代法和牛顿插值多项式两个方面探讨牛顿方法所体现的用导一致性现象.17世纪英国数学家牛顿开展了对牛顿迭代法的研究工作：他基于二项式定理，推导出牛顿迭代法的基本表达形式.18世纪英国数学家辛普森从微积分的角度给出了牛顿迭代法的现代表达形式[1].由于每次迭代都需要求出和利用函数导数值，因此求导和用导成为牛顿迭代法的一个重要特征.定理1 设f∈C2[a，b]，且存在数p∈ [a，b]，满足f（p）＝0.如果f′（p）≠0，则存在一个数δ＞0，对任意初始近似值p0∈[p－δ，p＋δ]，使得由如下迭代定义的序列pk（k＝1，2，…）收敛到p[1－8]：pk ＝g（pk－1）＝pk－1－f（pk－1）／f′（pk－1）. （1）设在几何上y＝f（x）是一曲线[2－6]，如图1所示.它与x轴的交点的横坐标p为方程的根，假设已给出一个近似根p0，我们用曲线在点（p0，f（p0））处的切线逼近该曲线.令p1是该切线与x轴交点的横坐标，由图1可见，p1对根的近似比p0的效果要好.由此可以写出切线L的表达式为整理上式可得用以上方法，利用一系列的切线与x轴的交点来逐步逼近曲线y＝f （x）与x轴的交点，即可得到p2，p3，…，pk，…，最终使序列｛pk｝收敛到p，它正是局部线性化与迭代法结合产生的方法.对比式（1）和式（2）可以发现，它们在表达形式上是一致的.可见，式（1）就是牛顿迭代法对函数几何模型迭代求解的一个函数表达式.它是建立在对函数图形求解切线斜率的基础上，得出比初始选取点更接近方程根的一系列点，在精度要求范围内经过有限次迭代求出函数根的近似值.牛顿迭代法中还要求近似根p0的选取必须充分靠近真正根p，这可以通过泰勒多项式进行分析.即用泰勒级数展开，可得[1，2，4]用x＝p代入式（3），并利用f （p）＝0，可得如果p0足够逼近p，则式（4）中的最后一项比前两项的和要小得多，因此可以将最后一项（非线性项）忽略，这样便得到牛顿迭代公式比较发现，式（5）的结果与式（2）一样，它们都要求近似根的选取充分靠近真实根.因此从泰勒级数展开式的角度再次体现牛顿迭代式对一阶导数的适当应用，证明了牛顿迭代法几何上的斜率分析法的正确性和有效性.通过上述对泰勒级数展开式的分析，体现了牛顿迭代法的求导和用导特性.由式（1）可见，牛顿迭代法中每次迭代都需要求一次导数，因此需要一种与牛顿法的收敛速度差不多快的方法且不用计算f′（x）.我们可以用函数值的差商近似导数，那么每次的迭代只需计算两次f（x），这就是割线法的思想.可以证明它在单根上的收敛阶R≈1.618 033 989，与收敛阶为2的牛顿迭代法差不多快[1－8]. 设曲线f（x）的图形如图2中所示[2，5，6]，经过点（p，0），即p为函数f （x）的一个根.（p0，f（p0））和（p1，f（p1））是靠近点（p，0）的两个已知初始点.定义p2为经过两个初始点的直线与x轴的交点的横坐标，则p2比p0或p1更接近p.由式（6）整理可得到因此，根据以上两点的迭代公式可得到一般式为这个迭代表达式被称为求解非线性方程的割线法公式.假设割线法中所选取的两个点（p0，f（p0））和（p1，f（p1））无限逼近，则理论而言，过这两个点得到的割线将无限逼近于函数在该处的切线.因此牛顿迭代法其实可以看作割线法的一种极限情况.而在这个极限情况下，从割线法的角度来看，牛顿迭代法同样体现了牛顿方法的求导和用导特征.以下给出n维非线性方程组的牛顿迭代法求解方法，并同时观察和分析牛顿方法的求导和用导思想在高维非线性方程组求解时的运用.由p2、p1和p0可得到以下方程：设考虑的非线性方程组问题为[4－6，8]其中函数f1，f2，…，fn在某解p的邻域D内具有二阶连续偏导数，列向量x定义为x ＝ [x1，x2，…，xn]T，则该非线性方程组的牛顿迭代式为[4－6，8]其中pk 代表第k次迭代向量值（k＝1，2，3，…），雅可比矩阵J满足Jij ＝∂fi／∂xj，i，j∈ ｛1，2，…，n｝.对比可见式（8）与式（1）基本上是一致的.在保证函数可微的前提下，牛顿方法从一维非线性方程求解扩展到n维非线性方程组求解，其中的一维求导和用导对应地变成了求取和利用一阶偏导数而已（最终形成具有明显的牛顿方法求导和用导特征的雅可比矩阵J，从形式上看，其相当于一维牛顿迭代式（1）中的导数f′）. 插值多项式是插值的一种重要方法.常见的插值多项式有拉格朗日多项式、牛顿多项式和切比雪夫多项式等.牛顿多项式因其在增加节点时具有“承袭性”[1－8]，避免了多项式的重新构建，因此更为简单和适用，具有明显更大的优势，从而成为一种更为实用的插值多项式数值算法.定理2 设目标函数f在n＋1个节点x0，x1，…，xn 上的值f（x0），f（x1），…，f（xn）为已知，存在惟一的至多n次的多项式Nn（x），具有插值性质f（xi）＝Nn（xi），其中i＝0，1，2，…，n.该多项式的牛顿形式为[2，5，6]式（9）即被称为基于点x0，x1，…，xn 的牛顿插值多项式.推论1 设Nn（x）是上述定理中给出的牛顿插值多项式[2，5]，并用来逼近目标函数f（x），即如果f∈Cn＋1[a，b]，则对每个x∈ [a，b]，对应地存在（a，b）内的数c＝c（x），使得误差项形如从式（11）能够看出，在对函数f（x）逼近的误差项的给出中，涉及到了函数高阶导数，即使用了目标函数f（x）在c＝c（x）处的n＋1阶导数f（n＋1）（c），因此牛顿方法的求导和用导思想在估计牛顿插值多项式的误差项时也得到了有效的使用.我们引入如下差商的概念，并同时观察牛顿插值多项式对导数的运用情况.定义1 设目标函数f关于xi的零阶差商f[xi]为f 在xi 的值[4，5，9，10]：由零阶差商出发可以归纳地定义各阶差商，其中f关于xi＋1 与xi 的一阶差商记作f[xi＋1，xi].且有以下关系：一般而言，设f 关于xi＋k，…，xi＋1，xi 的k 阶差商为根据上述牛顿插值多项式和差商的定义，可以求得式（9）中的系数如下：即牛顿插值多项式的系数可以用如下一般式确定：即牛顿插值多项式每一项的系数ck（k＝0，1，2，…，n）等于目标函数f（x）对应阶的差商.另外，通过对差商与牛顿插值多项式的余项分析还可以得到以下关系.定理3 设目标函数f在[a，b]上存在n＋1阶导数，且x0，x1，…，xn ∈ [a，b]，则存在c∈ [a，b]满足[4]从定义1和定理3可见：导数，具体就是差商的一种带权极限，所以差商本身就包含了求导和用导的思想.牛顿迭代法是建立在对切线求斜率（导数）的基础上的，且在迭代过程中需要显式地计算出来.假设割线法中所选取的两个点无限逼近，则过这两个点得到的割线将无限逼近于函数在该处的切线（即导数），因此牛顿迭代法其实可以看作是割线法的一种极限情况，而这个极限过程体现了牛顿类方法的求导和用导特征.当牛顿迭代法推广高维非线性方程组求解时，在表达式的整体形式上保持了一维非线性方程求解的特征，而对函数求偏导数形成的雅可比矩阵则对应了一维非线性方程求解的函数导数项，其中雅可比矩阵正体现了牛顿方法在求解非线性方程组中的求导和用导特征.牛顿插值多项式项数随节点增加而“承袭性”地增加，因此不需要重构该插值多项式.这一方便性远远高于拉格朗日插值多项式.牛顿插值多项式虽然看上去与函数的求导没什么关系，但经过仔细观察和推敲便可发现，其中使用的差商与导数是有密切关系的.导数其实就是差商的一种带权极限，所以在求解牛顿插值多项式的系数过程中处处隐性地用到了导数.另外，由差商与导数的关系，可以将牛顿插值多项式的误差项以差商的形式写为：其进一步体现了求导和用导思想在估计和求解牛顿插值多项式误差余项过程中的具体运用.可见，不论是牛顿迭代法求解非线性方程（组）还是牛顿插值多项式的构造，在它们的计算和扩展中均使用到了求导和用导思想.通过以上对牛顿迭代法和牛顿插值多项式的分析可见，牛顿方法广泛运用求导和用导思想，比如函数的几何分析、函数的泰勒展开式、插值函数系数和误差项的求取等等.在这些问题中，导数的运用使得牛顿法在同类数值算法中占据优势.当今各个科学领域的研究中，人们已经离不开对求导和用导思想和方法的运用，比如文献[11]关于一阶微分公式的研究，以及文献[12-17]关于神经网络和神经动力学的研究.显然，倘若这些研究失去了导数的辅助，将使其陷入困境甚至无法进行.此外，牛顿方法的用导一致性现象也说明，在数值方法的研究中，要善于利用求导工具进行数值计算方法的设计和优化；在研究新的数值算法时可从多方面加强对求导和用导思想方法的运用.【相关文献】[1]McNAMEE J M.Numerical Methods for Roots of Polynomials[M].London：Elsevier，2007.[2]John H M，Kurtis D F.数值方法（MATLAB版）[M].周璐，陈渝，钱方，等译.北京：电子工业出版社，2009.[3]李庆扬，峰杉白，关治.数值计算原理[M].北京：清华大学出版社，2000.[4]Jaan K.Numerical Methods in Engineering with Matlab[M].Cambridge：Cambridge University Press，2005.[5]李建良，蒋勇，汪光先.计算机数值方法[M].南京：东南大学出版社，2000.[6]Gerald Recktenwald（USA）.数值方法和 MATLAB实现与应用[M].伍卫国，万群，张辉，等译.北京：机械工业出版社，2009.[7]关治，陆金甫.数值方法[M].北京：清华大学出版社，2006.[8]冯康.数值计算方法[M].北京：科学出版社，1981.[9]《现代应用数学手册》编委会.现代应用数学手册：计算与数值分析卷[M].北京：清华大学出版社，2005.[10]Nicholas J H.Accuracy and Stability of Numerical Algorithms[M].SecondEdition.Washington：Society for Industrial and Applied Mathematics，2002.[11]张雨浓，郭东生，徐思洪，等.未知目标函数之一阶数值微分公式验证与实践[J].甘肃科学学报，2009，21（1）：13-18.[12]张雨浓，陈扬文，易称福，等.Hermite正交基前向神经网络的权值直接确定法[J].甘肃科学学报，2008，20（1）：82-86.[13]Zhang Yunong，Li Zhan，Li plex-valued Zhang Neural Network for Online Complex-valued Time-varying Matrix Inversion[J].Applied Mathematics and Computation，2011，217（24）：10 066-10 073.[14]Yunong Zhang，Yiwen Yang，Ning Tan，etal.Zhang Neural Network Solving forTime-varying Full-rank Matrix Moore-Penrose Inverse[J].Computing，2011，92（2）：97-121.[15]Zhang Yunong，Xiao Lin，Ruan Gongqin，etal.Continuous and Discrete Time Zhang Dynamics for Time-varying 4th Root Finding[J].Numerical Algorithms，2011，57（1）：35-51.[16]Yunong Zhang，Yiwen Yang，Gongqin Ruan.Performance A-nalysis of Gradient Neural Network Exploited for Online Time-varying Quadratic Minimization and Equality-constrained Quadratic Programming[J].Neurocomputing，2011，74（10）：1 710-1 719.[17]Zhang Yunong，Yi Chenfu，Guo Dongsheng，parison on Zhang Neural Dynamics and Gradient-based Neural Dynamics for Online Solution of Nonlinear Time-varying Equation[J].Neural Computing and Applications，2011，20（1）：1-7.。

神经网络中的正交化方法神经网络是一种强大的人工智能工具，其已经被广泛应用于机器学习、自然语言处理、计算机视觉等领域中。

而神经网络中的正交化方法在最近的研究中被认为是一种非常有用的技术。

本文将着重探讨神经网络中的正交化方法及其应用。

一、什么是正交化方法？在数学中，正交化是一种常见的操作，在向量空间中，可以将一个向量集合投影到相互垂直的向量上，这样的操作可以使得投影后的向量空间更加稳定和可控。

正交化方法已经被广泛应用于信号处理、图像处理和计算机视觉等领域中。

在神经网络中，使用正交化方法可以帮助神经网络更好地学习复杂的特征，提高神经网络的性能和稳定性。

二、如何正交化神经网络？正交化方法可以应用于神经网络的不同层级，包括输入层、隐藏层和输出层。

下面将重点介绍两种常见的神经网络正交化方法，一种是SVD正交方法，另一种是Gram-Schmidt正交方法。

1.SVD正交方法SVD正交方法是一种基于矩阵分解的方法，它可以将一个矩阵分解为三个子矩阵的乘积，其中包括一个正交矩阵。

通过对神经网络的权重矩阵进行SVD分解后，可以得到一组新的正交矩阵，这些正交矩阵可以代替原来的权重矩阵，使得神经网络的性能有所提升。

2.Gram-Schmidt正交方法Gram-Schmidt正交方法基于向量组的正交化，每次选择一个新的向量，然后将其投影到之前的所有向量上，去除与之前向量的重合部分，得到一个新的正交向量。

重复此过程，直到向量组的所有成员都通过正交化的处理得到。

这种方法可以应用于神经网络的权重矩阵中，通过对权重矩阵的列向量进行Gram-Schmidt正交化后，得到一组新的正交矩阵，这些正交矩阵可以代替原来的权重矩阵，使得神经网络更具有稳定性和较好的性能。

三、正交化方法在神经网络中的应用正交化方法在神经网络中的应用非常广泛，特别是在深度学习中更是如此。

正交化方法可以帮助神经网络更好地学习抽象的特征，提高分类和识别的准确性。

正交化方法还可以帮助解决神经网络中出现的梯度消失、梯度爆炸等问题，提高模型的鲁棒性和鲁棒性。