离散数学(3.7复合关系与逆关系)

离散数学(Discrete Mathematics)
张捷
1
第三章
集合与关系
（Sets and Relations)
3.1 集合及其运算(Sets & Operations with sets) 3.2 序偶与笛卡尔积(Ordered Pairs & Cartesian Product) 3.3 关系 (Relations) 3.4 关系的性质(The Propeties of Relations) 3.5 复合关系与逆关系(Compound Relations & Inverse Relations) 3.6 关系的闭包运算(Closure Operations)
3 0 0 1 0 4 1 2 1 0 0 M 3 1 4 1 0 0
2
2 1 1 2 0 M 1 3 0 4 1
2 3
0 0 1 0 M 1 2 0 1
1 1 1 2 1 3 0 4 1
2 3 0 0 0 1 1 0 0 0
n 经 过 长 为 n 的 路 能 够 到 达 的 结 点 ， 这 些 结 点 在
的关系图构造出 的关系图： 的 关系 图 中 的 每 一 结 ，找出 a点 ai从 i 指向它们。
的关系图中，边必须由 ai
例10 试利用构造 2和 3。
n （3）利用关系图求复合关系
设 是有限集A上的关系，则复合关系 2 也是A上的关 系，由复合关系的定义，对于任意的 ai , a j A ，当且仅 当 ak A 存在，使得 ai ak ， ak a j 时，有 a 2a 。 反映在关系图上，这意味着，当且仅当在 的关系图 ak 中有某一结点 ak 存在，使得有边由 a i 指向 ak ，且有 2 j 边由 指向 时，在 的关系图中有边从 aa ai 指 a j a k j 向 。 2
(1)
则必存在 x A, z C , 使x1 2 z ， 从而 y B,
使
x1 y, y2 z, 故 y ran1 ,且 y dom2 , 2 ，这就与 所以 y ran1 dom ran1 dom2 矛盾。
定理3.5.4
(1) 设
0 1 1 0 0 0 1 0 1 0 0 0
根据定理3.5.5
0 1 M M 0 0
1 0 0 0
0 1 1 0
M 2
因此
2 {a, a, a, c, b, b, b, c, b, d , c, c, c, d }
（1）根据复合关系的定义求复合关系 例5中求复合关系采用的就是这种方法。
又例如 下面的关系图给出了从集合A到B的关系 1 和从B到C的关系 2 2
1 2 {2,2, 2,3, 3,1}
（2）运用关系矩阵的运算求复合关系 •布尔运算
其加法和乘法运算定义如下
00+0=0 0 , 00+1=1+0=1+1=1
{ 1,3 , 2,4 , 4,2 }
1 2 { 1,2 , 2,4 , 3,3 , 1,3 , 4,2 }. 1 2 { 2,4 }. 1 2 { 1,2 , 3,3 }. 1 2 {1,2, 3,3, 1,3, 4,2}.
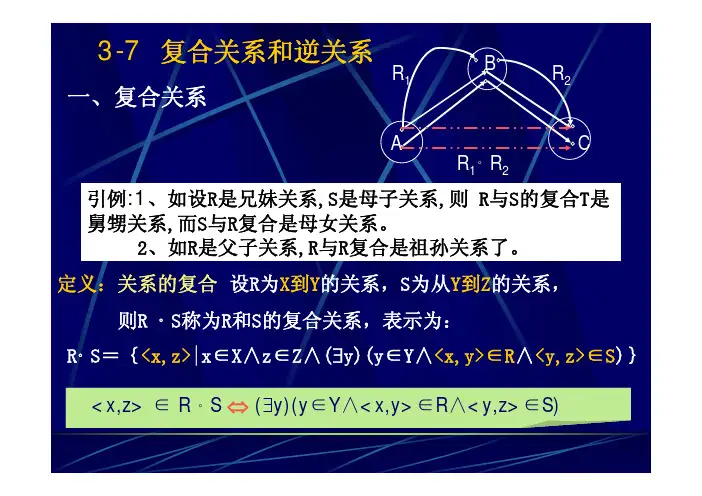
3.5.2 复合关系 (Compound Relations)
3 {2,4, 1,5, 2,6, 3,6} 1 2 {2,3, 2,2, 4,1}
到 A3 的关系，…， n 是一由 An 到An1 的关系，则不
2 是由A 一般地，若 1 是一由 A 到 A 的关系， 2 2 1
加括号的表达式 1 2 n ， 唯一地表示一由A1
设 C到D的关系
则A到C的关系
因此
因此 所以
( 1 2 ) 3 {2,6, 2,4, 4,5} 2 3 {2,5, 3,4, 3,6, 4,6} 1 ( 2 3 ) {2,6, 2,4, 4,5} ( 1 2 ) 3 1 ( 2 3 )
3.5 复合关系与逆关系(Compound Relations &
Inverse Relations) 3.5.1 关系的并、交、补及对称差运算 3.5.2 逆关系(Inverse Relations) 3.5.3 复合关系 (Compound A B Relations)

AB

第三章 集合与关系(Sets & Relations)
I A IB
例4
以例2中的关系
从关系图，可得
I A 1 1 , 1 I B 1
定理3.5.3 设 1 是由A到B的关系， 2 是由B到C的关系，
则有
证:
dom( 1 2 ) dom1 (2) ran( 1 2 ) ran2 (3) 若ran1 dom2 , 则1 2 (3)反设 1 2 ,
1 0 0 0
0 1 1 0
0 1 0 0 1 0 0 0
0 1 0 0
1 1 1 0
0 0 1 1 1 0 0 0
1 0 0 0
1 1 1 0
1 1 1 0
因此
3 {a, b, a, c, a, d , b, a, b, c, b, d , c, c, c, d }
到 A 的关系，在计算这一关系时，可以运用结合 n1
律将其中任意两个相邻的关系先结合。
特别,当A A A A ， 1 2 n 1 2 n1
时，复合关系 简记作 n ，它也是集 A
上的一个关系。
3. 求复合关系的几种方法
3.5.1 关系的并、交、补及对称差运算
定理 3.5.1 若 R 与 S 都是集合 A 到集合 B 的关 系，则 R∪S,R∩S,R-S,R, R S 均为 A
到 B的关系。 1 2 {( 2,4)}
例1
则
11 {21, 2{( ,1 2 ,4 , 33 ,3 2 设 ,2 ), ( ,3 )}}，
系的复合运算。 由定义可知:
1 2 { a, c (a A) (c C) b((b B) (a1b) (b2c))}
例2 2 关系。
设 1 是由A {1,2,3,4, } 到 B {2,3,4} 是由 B 到 C {3,5,6} 的关系。
( 1 2 ) 3 ( 1 3 ) ( 2 3 )
例5
A {1,2,3,4} ， B {2,3,4} ， C {1,2,3} , D {4,5,6} . A到B的关系 1 {2,4, 2,3, 4,2} B到C的关系 2 { 2,1, 3,2, 4,3}
11 1
例如
1 1 1 , 0 1 1 0 0 0 0
(1 0 0) (0 1) (111) (0 0 0) (11) 1
• 关系矩阵的乘积
对两个关系矩阵求其乘积时，其运算法则与一般 矩阵的乘法是相同的，但其中的加法运算和乘法运 算应改为布尔加和布尔乘。 例6 设 M 1 和 M 2是两个关系矩阵
与例6比较得
M 1 2 M 1 M 2
例8
设 A {a, b, c, d } ，A上的关系
{a, b, b, a, c, c, c, d , b, c} 2 3 试求 和 。 解 作出的关系矩阵 a b c d
a 0 b 1 M c 0 d 0
的
分别定义为：
1 { a, b | a b 6} { 2,4 , 3,3 , 4,2 }
2 { b, c | b整除c} { 2,6 , 3,3 , 3,6 }
于是复合关系
1 2 { 3,3 , 3,6 , 4,6 }
例3
设 A B C 是所有人的集合
1 是由A到B的关系， 2 是由B到C的关系，
3是由C到D的关系，则有
(2)设
( 1 2 ) 3 1 ( 2 3 ) 1 是由A到B的关系， 2 , 3 是由B到C的关系，
2 是由A到B的关系， 3 是由B到C的关系，
则有
(3)设 1 , 则有
1 ( 2 3 ) ( 1 2 ) ( 1 3 )
1 { a, b | a, b A, a是b的兄弟 }
2 { b, c | b, c A, b是c的父亲 }
于是复合关系
} 1 2 { a, c | a, c A, a是c的叔伯
2. 关系复合运算的性质
定理3.5.2 设
是由集合A到B的关系，则
1 为例， 1 { 2,4 , 3,3 , 4,2 }
1 是由A到B的关系， 2 是由B到C的 关系，则 1和 2 的复合关系是一个由 A到C的关系， 用 1 2表示，定义为：当且仅当存在元素 b B，
定义3.5.1 设 使得 a b ， b
1
1. 复合关系的定义
时，有a( 1 2 )c 。 c 2
这种由 1 和 2 求复合关系 1 2 的运算称为关

i
j
ai
ai
ak
aj
aj
类似地，对于任意正整数n，当且仅当在 的 关系图中存在n-1个结点 ak , ak ,, ak ,使得有 1 2 n1
边由 ai
时，在

指向 ak
n
1
,由 ak
1
指向 ak
2
，…a 由 k
的关系图中，有边由结点
n
a i 指向a j 。
n1
指向 a
j
根据 对 于