建筑力学课后答案解析 2

填空一1、对于作用在刚体上的力，力的三要素是大小、方向、作用点°2、力对矩心的矩，是力使物体绕矩心转动效应的度量:。

3、杆件变形的基本形式共有轴向拉伸（压缩）变形、弯曲、剪切和扭转四种。

4、轴力是指沿着杆件轴线.的内力。

5、轴向拉伸（压缩）的正应力大小和轴力的大小成_1£112_,规定受拉为正,受压为负。

6、两端固定的压杆，其长度系数是一端固定、一端自由的压杆的4倍。

7、细长压杆其他条件不变，只将长度增加一倍，则压杆的临界应力为原来的0.25倍。

8、在力法方程中，主系数恒一大于零。

9、力矩分配法的三个基本要素为转动刚度、分配系数和传递系数】0、梁的变形和抗弯截面系数成一^比。

11、结构位移产生的原因有荷载作用、温度作用、支座沉降等。

填空二1、在任何外力作用下，大小和形状保持不变的物体称_刚体o2、2、力是物体之间相互的机械作用o这种作用会使物体产生两种力学效果分别是—外效果和—内效果o3、力的三要素是力的大小、力的方向、—力的作用点4、4、加减平衡力系公理对物体而言、该物体的_外_效果成立。

5、一刚体受不平行的三个力作用而平衡时，这三个力的作用线必_汇交于一6、使物体产生运动或产生运动趋势的力称荷载（主动力）7、约束反力的方向总是和该约束所能阻碍物体的运动方向相反8、柔体的约束反力是通过_接触点，其方向沿着柔体_中心线的拉力。

9、平面汇交力系平衡的必要和充分的几何条件是力多边形自行封闭10、平面汇交力系合成的结果是一个合力o合力的大小和方向等于原力系中各力的—矢量和°11力垂直于某轴、力在该轴上投影为_零12、ZX=0表示力系中所有的力在_X轴上的投影的_代数和____________为'■>O13、力偶对作用平面内任意点之矩都等于_力偶矩14、力偶在坐标轴上的投影的代数和_为零o15、力偶对物体的转动效果的大小用_力偶矩表示。

16、力可以在同一刚体内平移，但需附加一个力偶o力偶矩等于—原力对新作用点之矩。

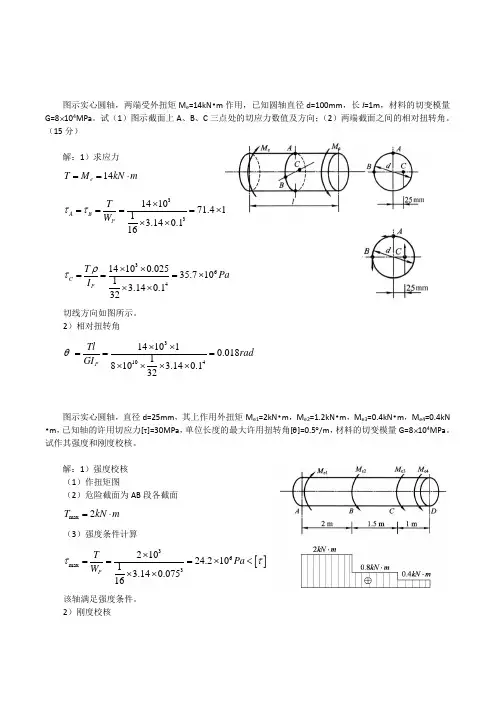
图示实心圆轴，两端受外扭矩M e =14kN •m 作用，已知圆轴直径d=100mm ，长l =1m ，材料的切变模量G=8⨯104MPa 。

试（1）图示截面上A 、B 、C 三点处的切应力数值及方向；（2）两端截面之间的相对扭转角。

（15分）解：1）求应力14e T M kN m ==⋅363141071.4101 3.140.116A B PT PaW ττ⨯====⨯⨯⨯36414100.02535.7101 3.140.132C PT Pa I ρτ⨯⨯===⨯⨯⨯切线方向如图所示。

2）相对扭转角3104141010.0181810 3.140.132P Tl rad GI θ⨯⨯===⨯⨯⨯⨯图示实心圆轴，直径d=25mm ，其上作用外扭矩M e1=2kN •m ，M e2=1.2kN •m ，M e3=0.4kN •m ，M e4=0.4kN •m ，已知轴的许用切应力[τ]=30MPa ，单位长度的最大许用扭转角[θ]=0.5︒/m ，材料的切变模量G=8⨯104MPa 。

试作其强度和刚度校核。

解：1）强度校核 （1）作扭矩图（2）危险截面为AB 段各截面max 2T kN m =⋅（3）强度条件计算[]36max321024.2101 3.140.07516PT Pa W ττ⨯===⨯<⨯⨯该轴满足强度条件。

2）刚度校核[]3max1041802101800.46/1 3.14810 3.140.07532P T m GI θθπ⨯=⨯=⨯=<⨯⨯⨯⨯该轴满足刚度条件。

求桁架结点C 的水平位移，各杆EA 相同。

解：（一）求载荷作用下的轴力。

见图。

（二）求C 点作用水平单位力的轴力。

见图。

（三）求位移122221(221)2222222222C F FaF a F a a EA EA ⎡⎤⎛⎫⎛⎫+∆=⨯⨯+-⨯-⨯+⨯⨯⨯=⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦求桁架结点1的竖向位移，两下弦抗拉（压）刚度为2EA ，其他各杆抗拉（压）刚度为EA 。

建筑力学与结构王洪波张蓓第3版课后题答案1．结构按几何形状分为哪几种？答案：结构的类型是多种多样的，按照几何特征区分：（1）杆件结构（2）薄壳结构和（3）实体结构。

2．关于材料的基本假设有哪些？答案：（1）连续、均匀性假设。

即认为构成变形固体的物质无空隙地充满了固体所占的几何空间，内部各处的材料是均匀分布的。

（2）各向同性假设。

即认为变形固体内部各方向的力学性能完全相同，对这类材料从不同方向作理论分析时得到相同的结论。

（3）小变形假设即认为构件的变形与其原尺寸相比通常很小，可以忽略不计。

3．荷载可简化为哪几种？答案：作用在结构上的荷载根据作用范围大小通常简化为集中荷载和分布荷载。

4．结构或构件的承载能力是什么？答案：强度、刚度和稳定性称为构件的承载能力。

5．杆件变形的基本形式是什么？答案：杆件在外力的作用下的变形是多种多样的，并且比较复杂，但都可以归结为以下四种基本变形。

（1）轴向拉伸或压缩变形；（2）剪切变形；（3）扭转变形；（3）弯曲6．建筑力学与结构主要研究什么问题？答案：建筑力学与结构是一门紧密联系工程实际的技术基础课，其主要研究对象是建筑物中的结构或构件。

7．实际物体没有刚体，为什么还要提出刚体这一概念？答案：刚体是指在外力的作用下不变形的物体。

任何物体在力的作用下都将发生变形，但在工程实际中许多物体的变形都非常微小，对于讨论物体的平衡问题影响很小，因此研究物体受力而平衡的问题时可将物体看成是不变形的刚体。

8．结构计算简图大致需要简化哪些方面？答案：工程中的实际结构都是比较复杂的，计算时往往对结构进行简化、结构计算简图大致需要简化以下几个方面（1）结构体系的简化。

（2）构件的简化。

（3）结点与支座的简化。

（4）荷载的简化。

模块1静力学基本知识一、思考题1.作用力与反作用力公理和二力平衡公理的区别？答案：作用力与反作用力是分别作用在两个相互作用的物体上的，并且两个力的性质相同，作用力和反作用力经常用F和F&#039;表示。

建筑力学复习题一、判断题（每题1分，共150分，将相应的空格内，对的打“√”，错的打’“×”）第一章静力学基本概念及结构受力分析1、结构是建筑物中起支承和传递荷载而起骨架作用的部分。

（√）2、静止状态就是平衡状态。

（√）3、平衡是指物体处于静止状态。

（×）4、刚体就是在任何外力作用下，其大小和形状绝对不改变的物体。

（√）5、力是一个物体对另一个物体的作用。

（×）6、力对物体的作用效果是使物体移动。

（×）7、力对物体的作用效果是使物体的运动状态发生改变。

（×）8、力对物体的作用效果取决于力的人小。

（×）9、力的三要素中任何一个因素发生了改变，力的作用效果都会随之改变。

（√）10、既有大小，又有方向的物理量称为矢量。

（√）11、刚体平衡的必要与充分条件是作用于刚体上两个力大小相等，方向相反。

（×）12、平衡力系就是合力等于零的力系。

（√）13、力可以沿其作用线任意移动而不改变对物体的作用效果。

（√）14、力可以在物体上任意移动而作用效果不变。

（×）15、合力一定大于分力。

（×）16、合力是分力的等效力系。

（√）17、当两分力的夹角为钝角时，其合力一定小于分力。

（√）18、力的合成只有唯一的结果。

（√）19、力的分解有无穷多种结果。

（√）20、作用力与反作用力是一对平衡力。

（×）21、作用在同一物体上的三个汇交力必然使物体处于平衡。

（×）22、在刚体上作用的三个相互平衡力必然汇交于一点。

（√）23、力在坐标轴上的投影也是矢量。

（×）24、当力平行于坐标轴时其投影等于零。

（×）25、当力的作用线垂直于投影轴时，则力在该轴上的投影等于零。

（√）26、两个力在同一轴的投影相等，则这两个力相等。

（×）27、合力在任意轴上的投影，等于各分力在该轴上投影的代数和。

（√）28、力可使刚体绕某点转动，对其转动效果的度量称弯矩。

第1章一、分析简答题1. 不正确。

因为合力不仅与分力的大小有关，还和分力的方向有关。

满足平行四边形法则，即表示合力的平行四边形对角线不一定比表示分力的边长。

2. 无关系。

3. 不一定平衡。

4. 二力平衡公理，对变形体，此条件只是平衡的必要条件而不充分；加减平衡力系公理，对变形体加减平衡力系后，不改变其运动状态，而会使物体产生形变。

5. 二力平衡：BC S 与'CB S ，AC S 与'AC S ； 作用力与反作用力；CA S 与'CA S ， CB S 与'CB S 。

第2章一、分析简答题 1. 不能。

2. 无关。

3. 无影响。

4. 重心的坐标改变，重心的位置不变化。

5. 不一定。

6. 利用力矩的性质，用钉锤增加了力臂，从而即省力又达到工作目的。

7. 相同点：都产生转动效应。

不同点：力矩对物体的转动效应与矩心的位置有关，力偶对物体的转动效应与矩心的位置无关。

8. 不一定相等。

9. 不能。

10. 不能。

二、分析计算题1．kN F x 101= 01=y F ()m kN F M o ⋅-=501 kN F x 07.72-= kN F y 07.72-= ()02=F M o kN F x 53= kN F y 66.83= ()m kN F M o ⋅=32.373 2． )(a FL )(b 0 )(c αsin FL - )(d Fb - )(e ()r L F +- )(f βsin 22b L F + 3．()mm kN 501⋅-=T O M ()mm kN 252⋅-=T O M4．()m N F F M ⋅='60, ()m N P P M ⋅-='69, m N M ⋅-=9 5． m N M ⋅=3002 6．kN P 200= 7． kN F 1.72=8．82.45=R kN ︒=11.79α =A M 4350 mm kN ⋅9 （1）0=R ()R L F M o +=3 （2）0=R ()R L F M D +=310． mm x c 8.60= 120=c y ；0=c x mm y c 110= ；mm x c 2.51=mm y c 2.101=11．0=C x mm =C y 74.14 mm0=c x mm y c 112=第3章一、分析简答题1. 不一定要互相垂直，只要不平行即可。

FAy 1.5kN
y
0： FAy FB 0
FB 1.5kN
3-5 求图示各梁的支座反力。
q A
3m 3m 3m
B
A
5m
A
B
1m
M
3m 3m
B
3m
(a )
(b )
(c )
A
M1
2m 4m
M2
2m
B A
q
l
(e ) 题 3-5 图
q B A
(f)
l
B
(d )
解：以梁 AB 为研究对象。采用数学中一般平面直角坐标系。 设所有的垂直反力向上的画，水平反力指向右。反力偶逆时针画。 (a)
yC
A x
i
i
第三章 3-1 用两根绳子 AC 和 BC 悬挂一个重 G = 1kN 的物体。绳 AC 长 0.8 m，绳 BC 长 1.6 m，A、B 点在 同一水平线上，相距 2 m。求这两根绳子所受的拉力。
【解】以整体为研究对象
cos
0.82 22 1.62 0.6500 2 0.8 2 1.62 22 0.82 cos 0.9250 2 1.6 2
F4 100kN 。
解：1.计算每个力在 x 轴上的投影，并求和。
F F
x
F1 60
1 1 3 1
2 2
F2 80
1 1 1 1
2 2
F3 F4 50 100
2 1 22 2
2
x
12 32
12 12
12 22
-1.848
解【分析】求力系合力的题目的一般步骤如下： 选定一点为简化中心。建立坐标系（一般以简化中心为坐标原点） ； 计算所有力在 x 轴上投影并求和，即主知在 x 轴上的投影 Fx； 计算所有力在 y 轴上投影并求和，即主知在 y 轴上的投影 Fy； 根据公式： F '

力偶使物体转动效应一般通过力偶矩来衡量， 力偶矩的大小为Fd，方向由右手法则确定，平 面力偶矩也为代数量，用M（F，F′）来表示 ，即
M（F，F′）=±2S△ABC
力偶——大小相等的二反向平行力。 ⑴、作用效果：只引起物体的转动。 ⑵、力和力偶是静力学的二基本要素。
力偶特性一：力偶在任何坐标轴上的投影等于零。力偶对物体只 产生转动效应，不产生移动效应。
E
4×4=16m
G
5kN
F
H
52
解:取整体为研究对象画受力图。 去掉零杆BC和FG。
10kN
D
10kN
10kN
2×3= 6m
5kN
A FA
C B
E
4×4=16m
G
5kN
F
H
FH
53
MA(Fi) = 0 -10×(4+8+12)-5×16+16FH = 0
FH = 20 kN
FA = 20 kN
取节点A为研究对象画受力图。
受力分析步骤全攻略
1. 确定研究对象（题中给出）。一旦明确，即刻将其分离，画出它的结 构简图。研究对象总是从受力简单的构件开始，如二力杆。
2. 分析主动力。第一考虑重力，第二考虑题中给出的主动力如拉力等。 （题中会明确给出）
3. 分析被动力。观察研究对象与哪些物体接触，约束力作用于接触点， 其方向总是与该约束所能限制的运动方向相反。（简单的来说由于约 束的作用，杆件在X方向不能运动，则约束力存在X方向的分量；杆件 在Y方向不能运动，则约束力存在Y方向的分量）——根据被动力的特 性，X、 Y方向的分量正负和大小都需要更多已知条件来确定。
教学要求
前言
定义： 位于同一平面内的诸力其作用线既不汇交

XA
mA YA
2-15解：
M B
2-15---1
F
F F
X
0
2 2
XA 6 2
Y
1 2 4 3 0; X A 0 0; YA 6kN ()
2 2
0
2 2
YA 6 2
XA
46 2
2 2
q
A
M A 0
1 2
YA
4 3 1 3 4 10 m A 6 2
M YA qa F 3 Fa qa 2a 4
2-17解：
空载时配重与起重机自身重量平衡
M
A
0
P2 x P (3 1.5) 0 P2 x 4.5P
满载时配重与起重机自身重量、起重重量平衡
M
B
0
P2 ( x 3) 1.5 P 10 P 1 0 P2 x 3P2 1.5P 10P 1 4.5 P 3P 2 1.5 P 10P 1 0 P2 1.5 P 103P 4.5 P 1.5600 103250 4.5600 233.3kN
YA
YB
F
b)
Y
0
F YB YA 0 YA Fa2aM ()
q
A
M
F B
MA
0
a
2
q a YB
M F 3a Y B 2a 0
2a
XA
YA
YB
M 3aF qa a 2
()
F
Y
0
qa F YB YA 0
XA RA
A

建筑力学习题答案建筑力学习题答案是建筑工程学习中的重要组成部分，通过解答这些题目，可以帮助学生巩固对建筑力学原理的理解和应用。

在这篇文章中，我将为大家提供一些建筑力学习题的答案，并解释其中的原理和推导过程，希望对学习建筑力学的同学们有所帮助。

1. 一根悬臂梁上有一个集中力作用，求梁的弯矩分布。

答案：根据悬臂梁的受力分析，可以得到集中力作用点处的弯矩为F*l，其中F为集中力的大小，l为集中力到悬臂梁固定点的距离。

在集中力作用点以外的位置，弯矩为零。

2. 一个简支梁上均匀分布有一个载荷，求梁的弯矩分布。

答案：对于均匀分布载荷作用下的简支梁，弯矩分布是一个抛物线形状。

最大弯矩出现在梁的中点，为w*l^2/8，其中w为单位长度的载荷大小，l为梁的长度。

3. 一根悬臂梁上有一个均匀分布载荷，求梁的弯矩分布。

答案：对于均匀分布载荷作用下的悬臂梁，弯矩分布是一个三次函数形状。

最大弯矩出现在悬臂梁的固定端，为w*l^2/3，其中w为单位长度的载荷大小，l为悬臂梁的长度。

4. 一个简支梁上有一个集中力和一个集中力矩作用，求梁的弯矩分布。

答案：对于简支梁上的集中力和集中力矩作用，可以将它们分别看作两个集中力的叠加。

根据叠加原理，可以分别求出集中力和集中力矩作用下的弯矩分布，然后将两者相加得到最终的弯矩分布。

5. 一个悬臂梁上有一个集中力和一个集中力矩作用，求梁的弯矩分布。

答案：对于悬臂梁上的集中力和集中力矩作用，可以将它们分别看作两个集中力的叠加。

根据叠加原理，可以分别求出集中力和集中力矩作用下的弯矩分布，然后将两者相加得到最终的弯矩分布。

6. 一个简支梁上有一个均匀分布载荷和一个集中力作用，求梁的弯矩分布。

答案：对于简支梁上的均匀分布载荷和集中力作用，可以将它们分别求出弯矩分布，然后将两者相加得到最终的弯矩分布。

通过以上几个例题的解答，我们可以看到不同受力情况下梁的弯矩分布规律是不同的。

掌握这些规律可以帮助我们更好地理解建筑力学的基本原理，并能够应用于实际工程中。

2-8单元2-2、有一饱和的原状土样切满于容积为21.7cm 3的环刀内，称得总质量为72.49g ，经105℃烘干至恒重为61.28g ，已知环刀质量为32.54g ，土粒比重为2.74，试求该土样的湿密度、含水量、干密度及孔隙比（要求汇出土的三相比例示意图，按三相比例指标的定义求解）。

解：3/84.17.2154.3249.72cm g V m =-==ρ%3954.3228.6128.6149.72=--==S W m m ω 3/32.17.2154.3228.61cm g V m S d =-==ρ 069.149.1021.11===S V V V e 2-3、某原状土样的密度为1.85g/cm 3，含水量为34%，土粒相对密度为2.71，试求该土样的饱和密度、有效密度和有效重度（先推导公式然后求解）。

解：（1）VV m WV s sat ρρ⋅+=W S m m m +=Θ SW m m =ω 设1=S m ρω+=∴1VW S S S V m d ρ=Θ WS W S S S d d m V ρρ⋅=⋅=∴1()()()()()()3W S S WS SW W satcm /87g .1171.20.341171.285.1d 11d 11d 111d 11111=+⨯+-⨯=++-=+++⎪⎪⎭⎫ ⎝⎛-=+-++=+⎪⎪⎭⎫ ⎝⎛⋅-++=∴ρωρωρωρωρρωρρωρρρωρW S d 有（2）()3'/87.0187.1cm g VV V V V V V m V V m W sat W V Ssat WV W V W S S W S S =-=-=+-=-+-=-=ρρρρρρρρρ （3）3''/7.81087.0cm kN g =⨯=⋅=ργ 或3'3/7.8107.18/7.181087.1cmkN cm kN g W sat sat sat =-=-==⨯=⋅=γγγργ2-4、某砂土土样的密度为1.77g/cm 3，含水量9.8%，土粒相对密度为2.67，烘干后测定最小孔隙比为0.461，最大孔隙比为0.943，试求孔隙比e 和相对密实度Dr ，并评定该砂土的密实度。

建筑力学课后习题答案,建筑力学课后习题答案李前程《建筑力学》习题集一、单项选择题在下列每小题的四个备选答案中选出一个正确的答案，并将其字母标号填入题干的括号内。

1.三力平衡定理是指()A.共面不平行的三个力若平衡必汇交于一点B.共面三力若平衡，必汇交于一点C.三力汇交于一点，则这三个力必互相平衡D.三力若平衡，必汇交于一点2.光滑面对物体的约束反力，作用点在接触面上，其方向沿接触面的公法线，并且有()A.指向受力物体，为拉力B.指向受力物体，为压力C.背离物体，为压力D.背离物体，为拉力3.两根拉杆的材料、横截面积和受力均相同，而一杆的长度为另一杆长度的两倍。

试比较它们的轴力、横截面上的正应力、轴向正应变和轴向变形。

正确的是()A.两杆的轴力、正应力、正应变和轴向变形都相同B.两杆的轴力、正应力相同，而长杆的正应变和轴向变形较短杆的大C.两杆的轴力、正应力和正应变都相同，而长杆的轴向变形较短杆的大D.两杆的轴力相同，而长杆的正应力、正应变和轴向变形都较短杆的大4.圆轴扭转时，若已知轴的直径为d，所受扭矩为T，试问轴内的最大剪应力τma x和最大正应力σmax各为()A.τmax=16T/(πd)，σmax=0B.τmax=32T/(πd)，σmax=0C.τmax=16T/(πd)，σmax=32T/(πd)D.τmax=16T/(πd)，σmax=16T/(πd)5.梁受力如图示，则其最大弯曲正应力公式:σmax=Mymax/Iz中，ymax为()333333A.dB.(D-d)/2C.DD.D/26.工程中一般是以哪个指标来区分塑性材料和脆性材料的()A.弹性模量B.强度极限C.比例极限D.延伸率7.一悬臂梁及其所在坐标系如图所示。

其自由端的()A.挠度为正，转角为负C.挠度和转角都为正B.挠度为负，转角为正D.挠度和转角都为负8.梁的横截面是由一个圆形中央去除一个正方形而形成的，梁承受竖直方向上的载荷而产生平面弯曲。

第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。

通常把以发生弯曲变形为主的杆件称为梁。

本章主要讨论直梁的平面弯曲问题，内容包括：弯曲概念和静定梁的力学简图；弯曲内力及内力图；弯曲应力和强度计算；弯曲变形和刚度计算。

其中，梁的内力分析和画弯矩图是本章的重点。

第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时，杆轴由直线弯成曲线，这种在外力作用下其轴线变成了一条曲线。

这种形式的变形称为弯曲变形。

工程上通常把以弯曲变形为主的杆件称为梁。

图 6-1 弯曲变形是工程中最常见的一种基本变形。

例如房屋建筑中的楼面梁和阳台挑梁，受到楼面荷载和梁自重的作用，将发生弯曲变形，如图6-2所示。

一些杆件在荷载作用下不仅发生弯曲变形，还发生扭转等变形，当讨论其弯曲变形时，仍然把这些杆件看做梁。

图6-2工程实际中常见到的直梁，其横截面大多有一根纵向对称轴，如图6-3所示。

梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面，如图6-4所示。

图 6-3 图6-4若梁上的所有外力（包括力偶）作用在梁的纵向对称平面内，梁的轴线将在其纵向对称平面内弯成一条平面曲线，梁的这种弯曲称为平面弯曲，它是最常见、最基本的弯曲变形。

本章主要讨论直梁的平面弯曲变形。

从以上工程实例中可以得出，直梁平面弯曲的受力与变形特点是：外力作用于梁的纵向对称平面内，梁的轴线在此纵向对称面内弯成一条平面曲线。

二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度，需建立梁的力学简图。

梁的力学简图（力学模型）包括梁的简化、荷载的简化和支座的简化。

1、梁的简化由前述平面弯曲的概念可知，载荷作用在梁的纵向对称平面内，梁的轴线弯成一条平面曲线。

因此，无论梁的外形尺寸如何复杂，用梁的轴线来代替梁可以使问题得到简化。

例如，图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁，可分别用梁的轴线AB代替梁进行简化（图6-1b和图6-2b）。

发现规划环境影响报告书质量存在重大问题的，审查时应当提出对环境影响报告书进行修改并重新审查的意见。（6）对建设项目实施环境监测的建议。
⒋中年男人见到了儿子分）4（．文中画横线的句子使用了什么修辞手法？请简要分析其表达效果。21如果说这之前这位父亲路人的感觉是一棵被人踏在脚下奄奄一息的草，那么此时的他，则变成了一座可让人依靠的顶天立地的大山！．请用两个词语概括文中父亲的形象特点。文章结尾写到“这样的父亲，应该有这样出色的儿子”，请结合文意，谈谈你对这句话深刻含义的理解与感悟。22分）6（八、记叙文分）1分，每空4④敬重或感动（共）③中年男人叙述家庭遭遇（或“中年男人叙述家庭不幸”或“中年男人叙述妻子走失的事” ②惊讶．①厌恶20，形象地写出了生活的负担对父亲的重压，也写出了父亲的卑微和无助；把父亲比作“顶分）把父亲比作“奄奄一息的草”1（．运用了比喻的修辞手法。21）分。1，无具体分析，则只给分，若只答出“生动形象”3（，形象地写出了父亲的坚强和伟岸，父爱的深沉和厚重。天立地的大山”（注意：在两个方面都要答对一个分）1（）（或“自尊、坚毅、坚忍、乐观、有责任感、能担当、深沉”“坚强”；分）1（）（或“拘谨”“卑微”．形象特点：22）分。2词方可得要点：①父亲尽到了自己的责任，尽自己所能给儿子创造了良好的成长环境；②父亲自尊、坚强、昂扬的精神面貌对儿子产生了潜移默化的影响；③儿子的）（言之成理，答对两点给满分，其它答案酌情给分。分）4（出色是对伟大、厚重父爱的最好回报。益阳分）11（题。22-25（四）阅读下文，完成香椿张晓风香椿芽刚冒上来的时候，是暗红色，仿佛可以看见一股地液喷上来，把每片嫩叶都充了血。①每次回屏东娘家，我总要摘一大抱香椿芽回来，孩子们都不在家，老爸老妈坐对四棵前后院的香椿，当然是来不及吃的。② ?可是现在，大家都走了，爸妈倒是弄了前前后后记忆里妈妈不种什么树，七个孩子已经够排成一列树栽子了，她总是说?都发了人了，就发不了树啦！③满庭的花，满庭的树。我踮起脚来，摘那最高的尖芽。④为什么，椿树是传统文学里被看作一种象征父亲的树。对我而言，椿树是父亲，椿树也是母亲，而我是站在树下摘树芽的小孩。那样坦然的摘着，那样⑤心安理得的摘，仿佛做一棵香椿树就该给出这些嫩芽似的。不知年复一年我摘取，年复一年，那棵树给予。⑥我的手指已习惯于接触那柔软潮湿的初生叶子的感觉，那种攀摘令人惊讶浩叹，那不胜柔弱的嫩芽上竟仍把得出大地的脉动，所有的树都是大地单向而⑦流的血管，而香椿芽，是大地最细致的微血管。我把主干拉弯，那树忍着，我把支干扯低，那树忍着，我把树芽采下，那树默无一语。我撇下树回头走了，那树的伤痕上也自己努力结了疤，并且再长⑧新芽，以供我下次攀摘。我把树芽带回台北，放在冰箱里，不时取出几枝，切碎，和蛋，炒得喷香的放在餐桌上，我的丈夫和孩子争着嚷着炒得太少了。⑨我把香椿挟进嘴里，急急地品味那奇异的芳烈的气味，世界仿佛一刹时凝止下来，浮士德的魔鬼给予的种种尘世欢乐之后仍然迟迟说不出口的那句话，⑩我觉得我是能说的。??太完美了，让时间在这一瞬间停止吧！?不纯是为了那树芽的美味，而是为了那背后种种因缘，岛上最南端的小城，城里的老宅，老宅的故园，园中的树，象征父亲也象征母亲的树。?万物于人原来蚵以如此亲和的。吃，原来也可以像宗教一般庄严肃穆的。?版）2010，未来出版社（选自《意林》分）2（作者描写景物语言细致，请赏析下面句中加点的词。22.上来，把每片嫩叶都充了血。香椿芽刚冒上来的时候，是暗红色，仿佛可以看见一股地液喷．分）2（，结合文章内容，谈谈你对这句话的理解。第⑤自然段作者写到“对我而言，椿树是父亲，椿树也是母亲”23.分）4（第⑧自然段画波浪线句子运用了什么修辞方法，简要分析其表达效果。24.分）3（结合全文主旨，联系自己的切身体验，谈谈你阅读本文的感受或启示。25.分）11（（四）分）示例：一个“喷”字，有动感，与前面的“冒’字相照应，形象地写出了香椿芽生长速度极快的特点，同时也表达了作者对嫩香椿芽的喜爱之情。2（22. 2“椿树是父亲，椿树也是母亲“。（分）示例：香椿只是给予，从不索取。父母默默奉献，勇于担当，椿树的品格与父母是相同的，所以作者说：23.分）拟；排比的修辞手法，使作者的感情表2分）运用了拟人、排比的修辞手法（4（24.达更强烈。分）3（25.示例一：香椿的嫩芽被掐了又长，长了又掐，父母如同香椿一样，默默忍受，无私奉献，可怜天下父母心！父爱，母爱是世界上最纯洁、最崇高、最伟大的爱。示例二：父母为子女的成长默默担当，无私奉献，他们对子女的不断索取无怨无悔，我们要常怀感恩之心，敬畏之情，努力学习，长大后成为社会的有用之材，回报父母，回报社会。示例三：父母对子女的爱是博大无私的，而我们很多时候太不珍惜这种爱了，衣来伸手，饭来张口，把父母对儿女的奉献看做是应尽的义务，是理所当然的，思想上不上进，学习不努力，辜负了父母的一片好心。湖南株洲（三）一碗汤的温度叶倾城?但也许有的人生活在亚热带，连秋天都没见过呢。又或者，真正的寒潮会在明天才陡然到?每个人生命中，都会有一两次寒冬。⒈那时，我对自己说：达，把我冻僵。啊，我还没减肥成功，史上最胖的一尊冰雕。⒉最山穷水尽的时候，我找到了一份大圈子。微有阳光、全无暖意的下午，我扣紧羽绒服所有的扣子，穿过四环积雪未融的桥洞去搭公车，黄花鱼一样贴着边，经常有疾驰的三轮车、电动车与我擦身而过。应该有车水马龙，记忆里却死寂，许是我聋了，要么内心的哭喊太大声。⒊在车上，我迟钝地看着窗外，看到一块?周记米粉?的招牌，我下了车。，我连汤都喝尽，热流一点一滴，在全身弥漫开⒋是临街民居的底楼，要上几步台阶，一进门暖气扑面，满眼郁郁葱葱的绿叶植物。叫了份?招牌米粉?来，像一只手轻轻拂过我全身。不够给力，不是一把揽我入怀，但已经够让我有力气去搭长长的一程车。⒌就这样，每天车行此处，我就下来吃一碗米粉。有时是正饭点，一屋子人，更显得热闹。玻璃板下压着井字蓝格桌布，老板娘扬声向后厨报客人点的餐。我的米粉端上来，扑我一脸热气，是食物的舌吻。我突然间，意识到了饿，是知觉被唤醒。不用因此承担得不到的绝望。真正的无欲则刚。——?饿过劲?了。求而不得，于是索性不求⒍曾经的我，粉像一群滑梯上的小孩子，嗤溜嗤溜、排着队下肚。周身都发出满足的低吟。⒎但此刻，热汤在口腔里，米即使我还一无所有：爱人离开我，事业正低谷，我与世界爱恨交织。未来是紧闭着的嘴，我渴望它吐出祝福又怕会听到诅咒。但，能有一碗热汤粉吃，⒏就是幸福。，我还可以要牛腩。?没关系，即使他答?没鱼丸没粗面??老板，给我加一个蛋。⒐我把菜单看了又看，终于扬声：⒑握筷在手，我像《胡桃夹子》里被魔法变身的王子，一点点，从指尖开始，从木偶人化回血肉之躯。啊，吃饱了，多么好。我还不及成为熟客，公司就搬了家，我从此再没有去过那家店。回忆起那段日子，像《海洋》最后的一个镜头，被割去双翅的鲨鱼沉默地、沉默地坠进海底，一动不动，连血色都只有一点点，在海水里很快看不见了。。以及，冰冷世界里，一碗热汤粉。在我的冬天里，它是一《勇气》只有它，有声有色：绿植物，花桌布，老板娘温软的南方口音，常常放着一首歌：个名叫?春天?的岛屿。虽然，我不曾对它说感激，也没必要我是规规矩矩付了钱的。——活着，只需要阳光、空气、水和食物。只要不饿死，冬天就一定会过完。期）14年第2012（选自《中国新闻周刊》分）2（②．请在文中找出两个能反映作者心理变化的关键词：①17分）2（．有人认为第⑦段划波浪线句写得很好，你认为好在哪里？请简要分析。18分）2（页34第

一、钢质圆杆的直径d ＝10mm ，F ＝，弹性模量E ＝210GPa 。

求杆內最大应变和杆的总伸长。

答：1、计算各段轴力 (1)计算CD 段轴力a 、用1-1截面截开CD 段杆件，取右段分析，右段截面上內力用N 1代替，受力图如图（a ）。

b 、根据静力平衡条件计算N 1值 ∑F x ＝0 N 1－F ＝0 N 1＝F ＝ (2)计算BC 段轴力a 、用2-2截面截开BC 段杆件，取右段分析，右段截面上內力用N 2代替，受力图如图(b)。

b 、根据静力平衡条件计算N 2值 ∑F x ＝0 N 2＋2F －F ＝0 N 2＝－F ＝－ (3)计算AB 段轴力a 、用3-3截面截开AB 段杆件，取右段分析，右段截面上內力用N 3代替，受力图如图(c)。

b 、根据静力平衡条件计算N 3值 ∑F x ＝0 N 3＋2F －3F －F ＝0 N 3＝2F ＝2、计算杆內最大应变 应变=εEAFL L =∆ =CDε222331mm5N/m m 10210100.5EA N ⨯⨯⨯⨯=πN ＝×10-4（拉应变） =BCε222332mm5N/m m 10210100.5EA N ⨯⨯⨯⨯-=πN ＝－×10-4（压应变） =ABε222333mm5N/m m 10210100.10EA N ⨯⨯⨯⨯=πN ＝×10-4（拉应变） 3、计算杆的总伸长值CD BC AB L L L L ∆+∆+∆=∆ CD CD BC BC AB AB L L L ⨯+⨯+⨯εεε＝0.1m 1003.30.1m 1003.30.1m 1006.6444⨯⨯+⨯⨯-+⨯⨯---）（＝ m 1006.65-⨯＝--------------------------------------------------------------------------------------------------------------------------------------------------- 二、求图示等直杆的两端支座反力。

建筑力学课后答案1篇以下是网友分享的关于建筑力学课后答案的资料1篇,希望对您有所帮助，就爱阅读感谢您的支持。

第一篇吉林建筑大学土力学复习资料第一章作业相关说明：(1)公式证明时不允许用推导公式！(2)作业必须抄题，有附图的应将图画上，同时，不允许徒手画图。

(3)解题有必要的步骤，解题过程中公式一定要写全，推导公式无需证明，可以直接使用！［附加1・1］证明下列换算公式：(1)CdDdsSeDDDswDs(lQn)□w；(2)ODrw；(3)SrD IDelDeDwn［附加1・2］某干砂试样口=1.66g/cm3,ds=2.69,置于雨中，若砂样体积不变，饱和度增至40%时，此砂在雨中的含水量w为多少？［附加1・3］将土以不同含水量配制成试样，用标准的夯击能将土样击实，测得其密度，dswop(要求：绘制w〜Eld曲线时，必须采用方格纸) 1-2某地基土层，用体积为72cm3的环刀取样，测得环刀加湿土重170g,环刀重40g,烘干后土重122g,土粒相对密度为2.70,问该土样的w、e、sr、口、Eld、dsat和口口各为多少？并比较各种重度的大小。

1-3一土样重200g,己知含水率为16%,若要制备含水率为20%的土样，需加多少水？加水后土样重量为多少？1-4某土样孔隙体积等于土颗粒体积，试求孔隙比e；若土粒相对密度dsQ2.66,试求干密度口山若孔隙被水充满，试求密度□与含水率w。

1-5已知某土样土粒相对密度为2.72,孔隙比为0.95,饱和度为0.37。

若孔隙比保持不变，将土样的饱和度提高到0.9,试求每lm3土应加多少水？1-6从甲、乙两地粘性土中各取出土样进行稠度试验。

两土样液限、塑性都相同,wLQ40%,wPD25%o但甲地土的天然含水量wD45%,而乙地的wD20%o问两地的液性指数IL各为多少？处于何种状态？按IP分类时，该土的名称是什么？试说明哪一地区的土较适宜于用作天然地基？1-7某砂土土样的密度为l.77g/cm3,含水率为9.8%,土粒相对密度为2.67,测得最小孔隙比为0.461,最大孔隙比为0.943,试求孔隙比e和相对密度Dr,并确定该砂土的密实度。