用spss软件进行随机分组

利用SPSS的冠心病分组变量探索性分析摘要：随着人民生活水平提高，医疗条件改善，大医院收治的冠心病患者逐渐增多。

由于冠心病的预防工作做的不是很完善，所以导致冠心病患者人数不断增长；随着我国的医保条件逐渐改善，国内的医疗水平也在不断的提高，冠心病患者有机会享受昂贵的治疗方法；我国冠心病方面的医生技术水平有了很大的提升。

利用SPSS软件对数据进行分组变量分析冠心病具体患病率和治愈率的影响。

关键词：SPSS；冠心病；相关分析；影响因素冠心病是指冠状动脉粥样硬化性心脏病，因冠状动脉粥样硬化，使血管狭窄或阻塞和冠状动脉功能改变，导致心肌缺血缺氧和坏死而引起的心脏病。

冠心病可以表现为胸痛，心悸，胸闷，大多与日常生活习惯、情绪和活动有关。

通过利用SPSS统计软件对冠心病的临床症状表现与发病率的相关性和患病率的影响因素进行研究，并且提出一些建议，对疾病高发人群在日常生活中的注意饮食等问题。

从而使冠心病的发病率降低。

1.研究背景及目的1.1研究背景中国心血管病现患人数大约有2.9亿，其中冠心病1100万，国民心血管病危险因素普遍暴露，已经形成明显的流行趋势，导致了心血管病的发病人数持续增加。

根据《年中国卫生和计划生育统计年鉴》2015年中国城市居民冠心病死亡率为110.67/10万缺血性心脏病的患病率：2013年中国第5次卫生服务调查：城乡合计为10.2%。

年龄＞60岁人群缺血性心脏病患病率为27.8%。

在我国，冠心病发病率约为0.77%，尚未达到西方国家那么高的程度，但自上世纪90年代以来，呈显著上升趋势。

我国冠心病发病高峰尚未达到，未来10~20年内冠心病的患病率仍将持续上升。

目前冠心病严重威胁人类的健康，根据世界卫生组织的统计，目前冠心病仍然是全球最常见的死亡原因，其致死的人数超过了所有肿瘤死亡人数的总和，冠心病好发于35岁以上的人群，在发达国家，其每年的死亡人数，可以占到中老年总死亡人数的三分之一。

1.2研究目的随着我国逐步实现现代化，冠心病患者也越来越多。

（精编资料推荐）随机区组设计随机区组设计方差分析概述随机区组设计又称为配伍设计，该方法属于两因素方差分析（Two-WayANOVA），用于多个样本均数间的比较，比如动物按体重、窝别等性质配伍，然后随机地分配到各个处理组中，即保证每一个区组内的观察对象的特征尽可能相近。

同一受试对象在不同时间点上观察，或同一样品分成多份，每一份给予不同处理的比较也可用随机区组设计进行分析。

随机区组设计分组原则：在某些研究中，先将受试对象按可能影响试验结果的属性分组（非随机组），分组的原则是将属性相同或相近的受试对象分在同一组内，如将病人按年龄/性别/职业或病情分组，或者将动物按性别/体重分组，然后采取随机化的方法对每个组内的受试对象分配各种处理。

如此以来，可使得区组内的观察单位同质性好，使各比较组的可比性强，使组间均衡性好，处理因素的效应更容易检测处理。

随机区组设计方差分析用于分析两个或两个以上因素是否对不同水平下样本的均值产生显著的影响；检验多个因素取值水平的不同组合之间，因变量的均值是否存在显著性差异。

其既可以分析单个因素的作用（主效应），也可以分析因素之间的交互作用（交互效应），还可以进行协方差分析，以及各因素变量与协变量之间的交互作用。

若有两个因素A与B，因素A与B间不存在交互作用，那么可以对因素A和B各自进行独立分析，在后续分析中去除不显著的因素。

如果方差分析结果显示因素A和B间存在交互作用，则需对数据进行进一步分析，具体包括：在因素A的某个水平下，因素B对响应变量的作用在因素B的某个水平下，因素A对响应变量的作用在所有因素（A/B）的组合中，哪两组的差异最大SPSS实现随机区组设计方差分析示例：研究3种不同的避孕药A/B/C在体内的半衰期，考虑到窝别对结果的影响，采用随机区组设计方案。

将同一窝别的3只雌性大白鼠随机分配到A/B/C3组，测定该药在血液中的半衰期（小时），试分析3种药物的半衰期有无不同？1.示例分析：目的：确认3种药物的半衰期有无不同；不同窝别对半衰期有所影响，考虑该该问题，按照窝别进行配伍设计，在同一配伍内随机分配A/B/C三种药物。

SPSS详细教程：轻松实现随机分组我们常常把随机分组挂在嘴边，好像只要⼀提到随机化，整个研究就能提升⼀个level。

但是在实际的研究过程中，很多研究者并不知道怎么才能正确的实现随机分组。

所以，⼩咖决定⼿把⼿来教⼤家如何通过SPSS，轻松实现随机分组。

随机分组随机分组，就是将参加研究的受试对象，按照随机化的原则，分配到不同处理组的过程。

随机分组可以保证每⼀个受试者均有相同的机会被分配到试验组或对照组，使得⼀些可能影响试验结果的临床特征和⼲扰因素在组间分配均衡，具有较好的可⽐性。

结果不受⾮处理因素的⼲扰和影响，从⽽有效避免了各种⼈为的客观因素和/或主观因素对研究结果产⽣的偏倚，使结果更加真实可靠。

随机分组的基本思路尽管随机分组看上去⾮常简单，但是在临床试验的具体操作过程中，往往会被误解和误⽤。

例如有研究⼈员按照研究对象的⼊组顺序，把受试者交替纳⼊试验组和对照组，这种分组⽅法很容易被误认为是随机分组，但实际上当前⼀个研究对象的分组被确定时，也就决定了下⼀个研究对象的分组，因此⽆法保证研究对象有相同的机会进⼊不同的处理组。

那么⼀般⽤什么⽅法实现随机分组呢？随机分组可以采⽤抽签、掷硬币或掷骰⼦等⽅法，但更科学、更可靠的是使⽤随机数字来进⾏分组，其基本思路为：1. 对临床试验中纳⼊的每⼀研究对象产⽣⼀个对应的随机数字；2. 按照随机数字由⼩到⼤（或由⼤到⼩）的顺序进⾏排序；3. 根据事先设定的各个处理组样本量⼤⼩，按随机数字顺序选择相应的样本数量，分配到不同的处理组。

在临床试验中，研究对象往往是陆续⼊组的，研究者不可能要等到研究对象都收集⾜够的时候，再分组进⾏试验，所以⼀般在研究开始前，要事先按照研究对象的⼊组顺序，根据对应的随机数字将研究对象随机地分配⾄不同的处理组，并做好分组隐匿。

⼀旦研究对象符合⼊选条件纳⼊研究时，就可以根据事先确定好的分组⽅案，直接进⼊对应的分组开始试验。

随机分组SPSS操作⼀、研究实例假设某研究拟纳⼊330名研究对象，按照研究对象⼊组顺序进⾏编号，研究对象⼊组后被随机分配到A、B、C三组给予不同的治疗措施，其中A为安慰剂组，B为常规⽤药组，C为联合⽤药组，每组各110⼈。

SPSS软件在正交试验设计、结果分析中的应用SPSS软件在正交试验设计与结果分析中的应用一、引言正交试验设计是一种经典的统计方法，用于研究多个因素对于实验结果的影响。

该方法将实验因素进行有序的组合，既能减少试验次数，又能避免因素之间的相互影响。

而SPSS软件作为统计分析领域中的瑞士军刀，拥有强大的数据处理和分析功能，为研究者提供了便利的工具。

本文将探讨SPSS软件在正交试验设计与结果分析中的应用。

二、正交试验设计的基本原理正交试验设计遵循一定的规则和原则。

首先，需要明确要研究的因素，这些因素可以是实验操作，也可以是实验条件。

其次，确定各个因素的水平，水平的选择要充分考虑实验的目的和研究对象。

然后，在确定因素和水平的基础上，构建正交试验设计表，以便按照设计表中的规则进行试验。

最后，根据试验结果，进行数据分析和结果解释。

三、SPSS软件在正交试验设计中的应用1. 设计试验方案SPSS软件提供了一系列的数据输入工具和试验设计模块，可以帮助研究者轻松地构建正交试验设计。

通过SPSS软件，可以灵活地选择因素和水平，并生成正交试验设计表。

同时，SPSS软件还提供了随机分组和重复设计等功能，以满足实验设计的要求。

2. 数据输入与整理SPSS软件支持多种数据输入方式，可以通过导入Excel表格、文本文件等格式的数据，或者直接在软件中手动输入数据。

在正交试验设计中，往往涉及大量的数据输入，SPSS软件的数据输入功能可以帮助研究者快速、准确地输入数据。

同时，SPSS软件还提供了数据整理和清理功能，可以对异常值、缺失值等进行处理，使得数据更加可靠。

3. 数据分析与解释SPSS软件的数据分析功能非常强大，可以进行多元方差分析、协方差分析、回归分析、相关分析等多种统计分析方法。

在正交试验设计中，可以使用SPSS软件进行多因素方差分析，以确定各个因素对实验结果的影响。

同时，SPSS软件还提供了图表制作功能，可以直观地展示分析结果。

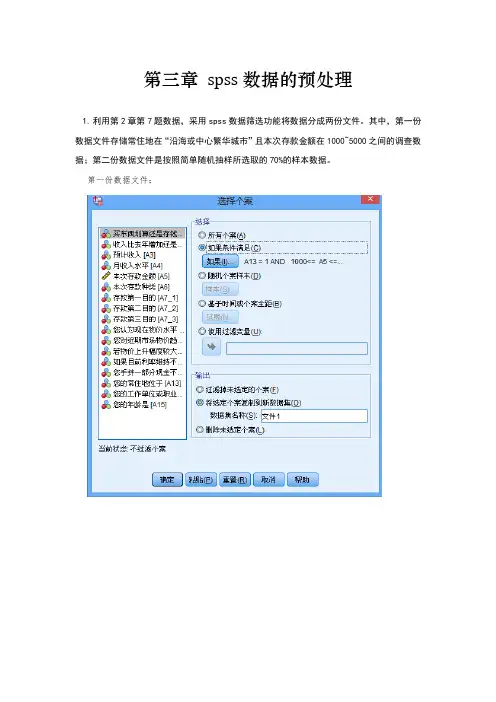
第三章spss数据的预处理1.利用第2章第7题数据，采用spss数据筛选功能将数据分成两份文件。

其中，第一份数据文件存储常住地在“沿海或中心繁华城市”且本次存款金额在1000~5000之间的调查数据；第二份数据文件是按照简单随机抽样所选取的70%的样本数据。

第一份数据文件：第二份数据文件：2.利用第2章第7题数据，将其按常住地（升序）、收入水平（升序）、存款金额（降序）进行多重排序。

3.利用第2章第9题的完整数据，对每个学生计算得优课程数和得良课程数，并按得优课程数的降序排序。

定义：得优分数段90-100得良分数段80-90计算得优课程数：从输出结果可知：60名学生中有四门成绩得优的学生有2个，属于品学兼优的少数人；两门成绩得优的学生有9个；一门成绩得优的学生有23个，没有成绩得优的学生有26个，累计占到百分之八十，说明该60名学生成绩普遍不是很理想。

计算得良课程数：从输出结果可知：60名学生中有四门成绩得良的学生有6个；三门成绩得良的学生有12个；两门成绩得良的学生有15个；一门成绩得良的学生有15个；没有成绩得良的学生有12个。

其中有70%的学生得良课程在两门及两门以下，成绩仍旧不乐观。

按得优课程数降序排序：4.利用第2章第9题的完整数据，计算每个学生课程的平均分以及标准差。

同时，计算男生和女生各科成绩的平均分。

每个学生课程平均分ave：每个学生课程标准差s：平均分ave与标准差s：男生与女生各科成绩平均分：第一步：按性别拆分文件第二步：分析→统计描述→描述第三步：结果输出5. 利用第2章第7题数据，大致浏览存款金额的数据分布状况，并选择恰当的组限和组距进行组距分组。

数据分组过程： K=1+2n 1n2821=9 组距=91-100001=11111 近似取12000数据分组结果：6.在第2章第7题的数据中，如果认为调查中“今年的收入比去年增加”且“预计未来一两年收入仍会增加”的人是对自己收入比较满意和乐观的人，请利用spss的计数和数据筛选功能找到这些人。

统计描述方法计量资料：采用SPSS 13.0进行数据分析，实验数据采用 X ±s表示，Shapiro-Wilk 对数据进行正态分布检验，非正态分布数据进行对数变换。

计量资料多组间差异用完全随机设计方差分析，根据Levene方差齐性检验，组间两两比较采用LSD 检验分析。

两组间计量资料差异比较采用t检验。

检验水准α=0.05。

计数资料：采用SPSS 13.0进行数据分析，应用卡方检验（χ2检验）分析（寄养家庭的自身素质、对犬的管教、培训犬接触的社会环境、人与犬的互动时间）四因素对（导盲犬培训成功率）的影响。

P<0.05为差异有统计学意义。

对于数据分析，我们的实验数据包括计量资料及计数资料两种。

其中，计量资料指连续的数据，通常有具体的数值，是用仪器、工具或其它定量方法对每个观察单位的某项标志进行测量，并把测量结果用数值大小表示出来的资料，一般带有度量衡或其它单位。

如检测小鼠体质量和肝质量，需要称重，通常以克为单位，测得许多大小不一的质量值；计数资料每个观察单位之间没有量的差别，但各组之间具有质的不同，不同性质的观察单位不能归入一组。

对这类资料通常是先计算百分比或率等相对数，需要时做百分比或率之间的比较，也可做两事物之间相关的相关分析。

我们常采用SPSS软件进行数据分析。

计量资料统计方法一、数据的整理在应用SPSS软件对数据进行分析之前，需将数据整理到Excel表格里，以p-ERK蛋白检测的数据为例（计量资料），如下图所示（附件1）：实验数据分为三组（Wt组(1.00)，P组(2.00)，T组(3.00)），所有数字均保留两位有效数字。

标明组别和数据字样，以利于后期统计分析。

二、正态分布检验保存并关闭Excel，打开SPSS软件，打开保存的数据。

在对数据进行统计之前先进行正态分布检验，正态分布检验包括小样本Shapiro-Wilk检验（2000以下）或大样本Kolmogorov-Smirnv检验（2000以上）。

10.11统计分析软件&SPSS建立数据目录10.11统计分析软件&SPSS建立数据 (1)10.25数据加工作图 (1)11. 08绘图解答&描述性分析： (3)2.描述性统计分析： (4)四格表卡方检验：（检验某个连续变量的分布是否与某种理论分布一致，如是否符合正态分布） (7)第七章非参数检验 (10)1.单样本的非参数检验 (11)（1）卡方检验 (11)（2）二项分布检验 (13)2.两独立样本的非参数检验 (14)3.多独立样本的非参数检验 (16)4.两相关样本的非参数检验 (16)5.多相关样本的非参数检验 (18)第五章均值检验与T检验 (21)1.Means过程（均值检验）（ (21)4. 单样本T检验 (22)5. 两独立样本T检验 (23)6.两配对样本T检验 (24)第六章方差分析 (26)单因素方差分析： (26)多因素方差分析： (30)10.25数据加工作图1.Excel中随机取值：=randbetween(55,99)2.SPSS中新建数据，一列40个，正态分布随机数：先在40那里随便输入一个数表示选择40个可用的，然后按一下操作步骤：3.排序：个案排秩4.数据选取：数据-选择个案-如果条件满足：计算新变量：5.频次分析：分析-统计描述-频率还原：个案-全部6.加权：还原7.画图：11. 08绘图解答&描述性分析：1.课后题：长条图2.描述性统计分析：（1）频数分析：（2）描述性分析：描述性统计分析没有图形功能，也不能生成频数表，但描述性分析可以将原始数据转换成标准化得分，并以变量形式存入数据文件中，以便后续分析时应用。

操作：分析—描述性分析：然后对结果进行筛选，去掉异常值，就得到标准化的数据：任何形态的数据经过Z标准化处理之后就会是正态分布的<—错误！标准化是等比例缩放的，不会改变数据的原始分布状态，（3）探索分析：（检验是否是正态分布：茎叶图、箱图）实例：操作：（4）交叉列联表（探索定类型的变量间的相关性）：【纯数值的变量用回归分析，名义变量用交叉分析】操作：实例：四格表卡方检验：（检验某个连续变量的分布是否与某种理论分布一致，如是否符合正态分布）例子：第1步建立数据文建：第2步：对数据进行预处理；（给数据加权）第3步进行卡方检验：第4步结果分析P＝0.011<0.05，则在5%显著性水平下拒绝原假设，差异有显著性意义，即药物加化疗与单用药物治疗癌症的疗效有显著性差异。

SPSS随机分组操作步骤SPSS（19.0）随机分组操作步骤1.输入原始数据纵向输入原始数据，包括原编号、分组依据的变量，变量列降序排列（Sort Descending）。

2.生成随机种子转换（Transform）→随机数字生成器（Random Number Generators）勾选“活动生成器初始化（Active Generator Initialization）”中的“设置起点（Set Starting Value）”，选中“固定值（Fixed Value）”，默认2,000,000，单击“确定（OK）”。

3.生成随机数字转换（Transform）→计算变量（Compute Variable）目标变量（Target Variable）：random函数组（Function Group）：随机数字（Random Number）函数和随机变量（Functions and Special Variables）：Rv.Uniform，双击选中数字表达式（Numberic Expression）：RV.UNIFORM（1,100）→单击“确定（OK）”。

4.输入分组后新编号假设分为a个组，每组n个样本，输入a个1，a个2，……a个n。

5.分组转换（Transform）→个案排秩（Rank Cases）变量（Variable(s)）：random排序标准（By）：新编号列将秩1指定给（Assign Rank 1 to ）“最大值”（Largest value）→单击“确定（OK）”。

“Rrandom”列升序排列（Sort Ascending）。

“Rrandom”列即分组后的组别，“新编号”列即分组后的编号。

利用SPSS产生随机数字的常用方法作者简介徐州医学院公共卫生学院流行病与卫生统计学教研室(221002)金英良黄水平赵华硕在医学研究中,科研工作者常常需要把研究对象进行随机分组,实现不同处理因素实验顺序的随机化或在总体中随机抽取部分样本作为研究。

以上问题均涉及到统计学中随机化的问题,其目的主要是减少偏性,提高均衡性,是统计学能够得出客观推断的前提。

实现随机化的主要方法有两种,即随机数字表和计算机的随机数发生器。

所谓的随机数发生器就是通过一定的算法,对事先选定的随机种子做复杂运算,用产生的结果来近似地模拟完全随机数,这种随机数被称作伪随机数〔1〕。

一些医学文献或书籍常常只是简单提及SPSS 产生随机数字的菜单操作命令,没有作为重要知识点进行讲解。

笔者主要介绍如何利用SPSS 13·0统计分析软件产生随机数字的常用方法。

利用随机数生成函数生成随机数字在SPSS统计软件中,利用随机数生成函数生成一列随机数字的方法是调用Transform菜单下的compute子菜单,如图1所示。

在Function group列表中列出了可以实现各种功能的函数,这里我们选择RandomNumbers,立刻会在其下面的Functions and SpecialVar-iables子对话框中会提供了一系列随机数生成函数列表。

不同函数表示各自所产生的随机数字符合特定的分布,如t分布、F分布和Poisson分布等函数,当我们选取相应函数时,其左侧对话框内会有相应的函数功能英文介绍说明。

这里我们以常用的正态分布函数为例进行讲解。

软件所生成的随机数个数与数据库中的记录数相同,这里我们事先建立NO变量,并输入从1到10作为要进行随机化的记录编号。

在ComputeVariable对话框下的TargetVariable框中输入随机数的变量名,这里我们定义为random,然后选取Functions and SpecialVariables子对话框下的Rv.Norma,l点击按钮,在Numeric Expression表达式框内会出现函数表达式两个问号分别代表我们要定义的正态分布均数和标准差,这里我们以输入均数=100,标准差=10为例,最后点击OK按钮提交,结果在SPSS13.0数据窗口中的random变量一列会产生一组随机数字,见图2。

例题和SPSS 电脑实验一、用SPSS 产生随机数字并进行完全随机设计分组【例题 1 】将符合研究的受试对象60 例随机分为两组，每组30 例.操作：1．建立SPSS数据文件：设一个变量(NO) ，输入受试对象的编号1～60. 2．设定随机种子(SETSEED) ：Transform → Random Number Generators ⋯→ Random Number Generators √ SetStarting Point⊙ Fixed ValueValue ：12345OK 此时，在结果窗口出现“ SET SEED=12345. ”，SET SEED 是设定种子，随机数取值在1～200 000 之间.3．产生随机数：Transform → Computer Variable ⋯→ Computer VariableTarget Variable( 目标变量名)：Random Function group: Random Numbers Functionsand Special :Rv.Uniform 点击向上箭头Nuneric Expression: Rv.Uniform(?,?) →Rv.Uniform(0,1) OK此时，数据窗口产生一列Random. 产生随机数字通常用Uniform(0,N) 函数产生，本例题用Uniform(0,1) 产生0～ 1 之间的随机数，系统默认随机数字的小数点位数为两位，当出现随机数字相同时，可以将随机数字的小数点位数增加到 4 位或以上，可见随机数字无重复. 4．对随机数编秩：Transform →Rank case ⋯→ Rank caseRandom → Variable(s) 框中此时，数据窗口又产生一列RRandom.5．对随机数秩次排列：按照随机数秩次从小到大进行升序排列，规定秩次1～30 归入第一组，31～60 归入第二组.Transform → Recode into DifferentVariables ⋯→ Recode into DifferentVariablesRRandom → Numeric Variable ->OutputOutput Variable,Name:group → Change⊙ Range: 上框输入1，下框输入30⊙ Value:1AddOld - New:1 thru 30 1⊙ Range: 上框输入31 ，下框输入60⊙ Value:2AddOld - New:31 thru 60 2ContinueOK此时数据窗口又产生一列分组变量group. 也可以单数归入group 1 ，双数归入group 2.6．随机安排处理因素：随机确定group 1 为治疗组，group 2 为对照组.例题 2 】将符合研究的受试对象90 例随机分为两组，每组30 例.SPSS实验过程与例题【1】基本相同.操作：1．建立SPSS数据文件：设一个变量（NO），输入受试对象的编号1～90.2 ．设定随机种子：543213．产生随机数4．对随机数编秩：5．对随机数秩次排列：按照随机数秩次从小到大进行升序排列，规定秩次60 归入第二组，61 ～90 归入第三组.6．随机安排处理因素二、用SPSS 产生随机数字并进行配对（或配伍）设计分组【例题3】将20 对受试对象（40 个受试对象）随机分入甲乙两个处理组. 操作：1～30 归入第一组，311．建立SPSS 数据文件：设 2 个变量：①NO，输入受试对象的编号20.2 ．设定随机种子：Transform → Random Number Generators ⋯1～40；②Block ：输入对子号 1 → Random NumberGenerators√ Set StartingPoint ⊙ FixedValueValue ：20120101OK此时，在结果窗口出现“ SET SEED=20120101. ”3 ．产生随机数：Transform → Computer Variable ⋯→ Computer VariableTarget Variable( 目标变量名)：RandomFunction group: Random NumbersFunctions and Special :Rv.Uniform点击向上箭头→ Nuneric Expression: Rv.Uniform(?,?) → Rv.Uniform(0,1)OK此时，数据窗口产生一列Random. 用Uniform（0,1）函数产生0～1 之间的随机数.4 ．对随机数编秩(按照Block 编秩)：Transform →Rank case ⋯→Random → Variable(s) 框中Rank caseBy:Block OK此时，数据窗口又产生一列 5 ．随机分组：随机确定RRandom 6．随机安排处理因素：随机确定“RRandom.列的“1”组，“ 2”组.1”为甲处理组，“ 2”为乙处理组.例题4】将40 只SD雄性大鼠按照体重为区组因素随机分入甲乙丙丁四个处理组（操作：1．建立SPSS 数据文件：设 2 个变量：① NO，输入大鼠的编号10 个配伍组）1～40；② Block ：输入对子号1 10.2．设定随机种子：Transform → Random Number Generators√ Set Starting Point → Random Number Generators⊙ Fixed ValueValue ：11223344OK 此时，在结果窗口出现“ SET SEED=11223344. ” .3．产生随机数：Transform → Computer Variable ⋯→ Computer Variable Target Variable( 目标变量名)：Random Function group: Random Numbers Functions and Special :Rv.Uniform点击向上箭头→ Nuneric Expression: Rv.Uniform(?,?) → Rv.Uniform(0,1) OK 此时，数据窗口产生一列Random. 用Uniform(0,1) 函数产生0～1 之间的随机数.4．对随机数编秩(按照Block 编秩)：Transform →Rank case ⋯→Rank caseRandom → Variable(s) 框中By:Block OK此时，数据窗口又产生一列RRandom.5．随机分组：随机确定RRandom 列的“ 1”组，“ 2”组，“ 3”组，“ 4”组. 6．随机安排处理因素：随机确定“ 1”为甲处理组，“ 2”为乙处理组，“ 3”为丙处理组，“ 4 为丁处理组.。