2014年选修数学模型大作业

一、以下两题任选一道完成三章第一节配件厂为装配线生产若干种产品，轮换产品时因更换设备要付生产准备费，产量大于需求时要付贮存费. 该厂生产能力非常大，即所需数量可在很短时间内产出.已知某产品日需求量100件，生产准备费5000元，贮存费每日每件1元. 试安排该产品的生产计划，即多少天生产一次（生产周期），每次产量多少，使总费用最小.1.（1）在第三章第一节存储模型的总费用中增加购买货物的费用，重新确定订货周期和订货量，证明在不允许缺货模型中结果与原来一样，而在允许缺货模型中最优订货周期和订货量都比原来减少。

（2）在第三章森林救火模型中，如果考虑消防队员的灭火速度λ与开始救火时的火势b有关，试建立一个合理的函数关系，然后重新求解。

2、观察鱼在水中的运动，发现它不是进行水平运动，而是突发性、锯齿形地向上运动，然后向下滑行。

可以认为这是在长期进化过程中鱼类选择的消耗能量最小的运动方式。

（1）设鱼总是以常速v运动，鱼在水中净重w ，向下滑行的阻力是w在运动方向的分力；向上游动时所需的力是w在运动方向与运动所受阻力之和，而游动的阻力是滑行阻力的k倍。

水平方向游动时的阻力也是滑行阻力的k倍。

写出这些力的表达式。

（2）证明当鱼要从A点到达处于同一水平线上的B点时（见右图），沿折线ACB运动消耗的能量与沿水平线AB运动消耗的能量之比（向下滑行不消耗能量）为(k*sinα+sinβ)/[k*sin(α+β)]。

（3）据实际观察，tanα≈0.2。

试对不同的值（1.5, 2, 3），根据消耗能量最小的准则估计最佳的β值。

二、以下两个题目任选一道：1、某银行经理计划用一笔资金进行证券投资业务，可供购进的证券及其相应信息如下表所示，且有如下规定和限制：（1）市政证券的收益可以免税，其它证券的收益需要按50%的税率纳税；（2）政府及代办机构的证券总共至少购进400万元；（3）所购证券的平均信用等级不超过1.4（信用等级越小，信用程度越高）；（1）若该经理有1000万资金，应如何投资？（2）在（1）的条件下，如果能够以2.75%的利率借到不超过100万元，该经理应该如何操作？（3）在1000万元资金情况下，若证券A的税前收益增加为4.5%，投资应否改变？若证券C的税前收益减少为4.8%，投资应否改变？注：为简化问题起见，题中的税前收益率和利率都与年限无关，即都为固定值。

中华女子学院成绩2014 — 2015学年第二学期期末考试（论文类）论文题目数学建模算法之蒙特卡罗算法课程代码 01课程名称数学建模学号 9姓名陈可心院系计算机系专业计算机科学与技术考试时间 2015年5月27日一、数学建模十大算法1、蒙特卡罗算法该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟可以来检验自己模型的正确性，是比赛时必用的方法。

接下来本文将着重介绍这一算法。

2、数据拟合、参数估计、插值等数据处理算法比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具。

3、线性规划、整数规划、多元规划、二次规划等规划类问题建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现。

这个也是我们数学建模选修课时主要介绍的问题，所以对这方面比较熟悉，也了解了Lindo、Lingo软件的基本用法。

4、图论算法这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，上学期数据结构课程以及离散数学课程中都有介绍。

它提供了对很多问题都很有效的一种简单而系统的建模方式。

5、动态规划、回溯搜索、分治算法、分支定界等计算机算法这些算法是算法设计中比较常用的方法，很多场合可以用到竞赛中6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用。

7、网格算法和穷举法网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具。

8、一些连续离散化方法很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。

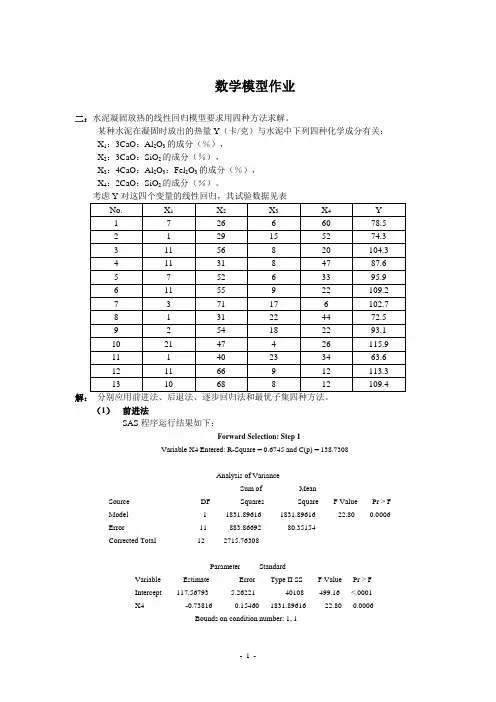
数学模型作业二：水泥凝固放热的线性回归模型要求用四种方法求解。

某种水泥在凝固时放出的热量Y（卡/克）与水泥中下列四种化学成分有关：X1：3CaO：Al2O3的成分（％），X2：3CaO：SiO2的成分（％），X3：4CaO：Al2O3：Fel2O3的成分（％），X4：2CaO：SiO2的成分（％）。

解：分别应用前进法、后退法、逐步回归法和最优子集四种方法。

（1）前进法SAS程序运行结果如下：Forward Selection: Step 1Variable X4 Entered: R-Square = 0.6745 and C(p) = 138.7308Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > FModel 1 1831.89616 1831.89616 22.80 0.0006Error 11 883.86692 80.35154Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 117.56793 5.26221 40108 499.16 <.0001X4 -0.73816 0.15460 1831.89616 22.80 0.0006Bounds on condition number: 1, 1Forward Selection: Step 2Variable X1 Entered: R-Square = 0.9725 and C(p) = 5.4959Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > F Model 2 2641.00096 1320.50048 176.63 <.0001 Error 10 74.76211 7.47621Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 103.09738 2.12398 17615 2356.10 <.0001X1 1.43996 0.13842 809.10480 108.22 <.0001X4 -0.61395 0.04864 1190.92464 159.30 <.0001Bounds on condition number: 1.0641, 4.2564Forward Selection: Step 3Variable X2 Entered: R-Square = 0.9823 and C(p) = 3.0182Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > F Model 3 2667.79035 889.26345 166.83 <.0001 Error 9 47.97273 5.33030Corrected Total 12 2715.76308Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 71.64831 14.14239 136.81003 25.67 0.0007X1 1.45194 0.11700 820.90740 154.01 <.0001X2 0.41611 0.18561 26.78938 5.03 0.0517X4 -0.23654 0.17329 9.93175 1.86 0.2054Bounds on condition number: 18.94, 116.36No other variable met the 0.5000 significance level for entry into the model.Summary of Forward SelectionVariable Number Partial ModelStep Entered Vars In R-Square R-Square C(p) F Value Pr > F1 X4 1 0.6745 0.6745 138.731 22.80 0.00062 X1 2 0.2979 0.9725 5.4959 108.22 <.00013 X2 3 0.0099 0.9823 3.0182 5.03 0.0517在前进法中，模型中变量从无到有依次选一变量进入模型，并根据该变量在模型中的Ⅱ型离差平和(SS2)计算F统计量及P值。

2014高考选做题汇编1 （辽宁）（本小题满分10分）选修4-1：几何证明选讲如图，EP 交圆于E 、C 两点，PD 切圆于D ，G 为CE 上一点且PG PD =，连接DG 并延长交圆于点A ，作弦AB 垂直EP ，垂足为F. （1）求证：AB 为圆的直径； （2）若AC=BD ，求证：AB=ED.解.（Ⅰ）因为PD =PG ,所以∠PDG =∠PGD .由于PD 为切线，故∠PDA =∠DBA ,又由于∠PGD =∠EGA ,故∠DBA =∠EGA ,所以∠DBA +∠BAD =∠EGA +∠BAD ,从而∠BDA =∠PFA .由于AF 垂直EP ，所以∠PFA =90°，于是∠BDA =90°，故AB 是直径. (Ⅱ)连接BC ，DC .由于AB 是直径，故∠BDA =∠ACB =90°， 在Rt △BDA 与Rt △ACB 中，AB =BA ,AC =BD ， 从而Rt △BDA ≌Rt △ACB ，于是∠DAB =∠CBA . 又因为∠DCB =∠DAB ,所以∠DCB =∠CBA ，故DC ∥AB . 由于,,AB EP DC EP DCE ⊥⊥∠所以为直角 于是ED 是直径，由（Ⅰ）得ED =AB .2（辽宁）（本小题满分10分）选修4-4：坐标系与参数方程将圆221x y +=上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C.（1）写出C 的参数方程；（2）设直线:220l x y +-=与C 的交点为12,P P ，以坐标原点为极点，x 轴正半轴为极坐标建立极坐标系，求过线段12PP 的中点且与l 垂直的直线的极坐标方程.解.（Ⅰ）设11(,)x y 为圆上的点，在已知变换下位C 上点（x ，y ），依题意，得112x x y y =⎧⎨=⎩由22111x y += 得22()12y x +=，即曲线C 的方程为2214y x +=.，故C 得参数方程为 cos 2sin x t y t ⎧⎨⎩＝＝ （t 为参数）.(Ⅱ)由2214220y x x y ⎧+=⎪⎨⎪+-=⎩解得：10x y =⎧⎨=⎩，或02x y =⎧⎨=⎩. 不妨设12(1,0),(0,2)P P ,则线段12PP 的中点坐标为1(,1)2,所求直线的斜率为12k =，于是所求直线方程为111()22y x -=-，化极坐标方程，并整理得2cos 4sin 3ρθρθ-=-，即34sin 2cos ρθθ=-.3（辽宁）（本小题满分10分）选修4-5：不等式选讲设函数()2|1|1f x x x =-+-，2()1681g x x x =-+，记()1f x ≤的解集为M ，()4g x ≤的解集为N. （1）求M ； （2）当x MN ∈时，证明：221()[()]4x f x x f x +≤. 解.（Ⅰ）33,[1,)()1,(,1)x x f x x x -∈+∞⎧=⎨-∈-∞⎩当1x ≥时，由()331f x x =-≤得43x ≤，故413x ≤≤； 当1x <时，由()11f x x =-≤得0x ≥，故01x ≤<；所以()1f x ≤的解集为4{|0}3M x x =≤≤.(Ⅱ)由2()16814g x x x =-+≤得2116()4,4x -≤解得1344x -≤≤，因此13{|}44N x x =-≤≤，故3{|0}4M N x x =≤≤.当x M N ∈时，()1f x x =-，于是22()[()]()[()]x f x x f x xf x x f x +⋅=+2111()(1)()424x f x x x x =⋅=-=--≤.4..（新课标二22）（本小题满分10）选修4—1：几何证明选讲 如图，P 是O 外一点，PA 是切线，A 为切点，割线PBC 与O 相交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交O 于点E.证明：（Ⅰ）BE=EC ； （Ⅱ）AD ⋅DE=22PB（1）EC.BE BE ∠CE ∠BE ∠αBE,∠βαβBE ∠∠DEB ∠PDA ∠∠∠∠∠.AE ∠CE ,∠EB ∠,,,2===+=+∴+===+=+====∠Δ=∴==，所以，即即则连接为等腰三角形。

数学模型选修钢管问题年级：专业：姓名：学号：日期：问题简介：现有15米长的钢管若干，生产某产品须4米、5米、7米长的钢管各100、150、120根。

（1）问如何截取才可使原材料最省，试建立模型。

（2）客户增加需求：6米钢管100根，问如何截取才可使原 材料最省，试建立模型（3）由于采用不同切割模式太多，会增加生产和管理成本，规定切割模式不能超过3种。

如何下料最节省？钢管下料问题1 模型准备：模型假设：为满足客户需要，按照哪些种合理模式，每种模式切割多少根原料钢管，最为节省？两种标准1. 原料钢管剩余总余量最小2. 所用原料钢管总根数最少 决策变量xi ~按第i 种模式切割的原料钢管根数(i =1,2,…7) 目标1（总余量） 模型构成：654311323x x x x x Z Min ++++=约束 满足需求整数约束： xi 为整数 模型求解：最优解： x2=120 x7=50 其余为0； 最优值：按模式2切割120根,按模式7切割50根，共170根，余料0米。

目标2（总根数） 模型构成：约束条件不变x i 为整数模型求解：最优解： x2=50 x6=35 x7=50 其余为0；最优值：135。

模型结果分析：按模式2切割50根，按模式6切割35根，按模式7切割50根，共135根，余料35米 与目标1的结果“共切割170根，余料0米” 相比 虽然余料多35米，但根数却少了35根当余料没有用处时，通常以总根数最少为目标 因此以模式2切割最合适。

模型假设，模型构成，模型求解，模型分析 钢管下料问题2增加一种需求：6米100根；切割模式不超过3种。

模型准备：现有4种需求：4米100根，5米150根，6米100根，7米120根，用枚举法确定合理切割模式，过于复杂。

对大规模问题，用模型的约束条件界定合理模式 模型构成： 决策变量xi ~按第i 种模式切割的原料钢管根数(i =1,2,3)r 1i , r 2i , r 3i , r 4i ~ 第i 种切割模式下，每根原料钢管生产4米、5米、6米和1002234321≥+++x x x x 150327543≥+++x x x x 1202652≥++x x x 76543212x x x x x x x Z Min ++++++=1002234321≥+++x x x x 150327543≥+++x x x x 1202652≥++x x x7米长的钢管的数量 目标函数（总根数） 约束条件 满足需求 模式合理：每根余料不超过3米整数约束： xi ,r 1i , r 2i , r 3i , r 4i (i =1,2,3)为整数 整数非线性规划模型增加约束，缩小可行域，便于求解需求：4米100根，5米150根，6米100根，7米120根 每根原料钢管长15米 原料钢管总根数下界： 特殊生产计划：对每根原料钢管模式1：切割成1根4米，1根5米和1根6米钢管，需100根； 模式2：切割成1根5米和1根7米钢管，需50根； 模式3：切割成2根7米钢管，需35根。

城市学院数学建模与实践期末测试论文格式要求●各小组自行组队，至多按三人一组合作完成论文。

●从5个小题中任选一题。

●论文用白色A4纸单面打印；上下左右各留出至少2.5厘米的页边距；从左侧装订。

●论文第一页为封面，具体内容为：我们选择的题号是（1题/2题/3题/4题/5题）：小组队员(打印并签名) ：1. 专业班级姓名联系电话签名2. 专业班级姓名联系电话签名3. 专业班级姓名联系电话签名●论文题目、摘要和关键词写在论文第二页上，从第三页开始是论文正文，不要目录。

●论文从第二页开始编写页码，页码必须位于每页页脚中部，用阿拉伯数字从“1”开始连续编号。

●论文题目用三号黑体字、一级标题用四号黑体字，并居中；二级、三级标题用小四号黑体字，左端对齐（不居中）。

论文中其他汉字一律采用小四号宋体字，行距用单倍行距。

打印文字内容时，应尽量避免彩色打印（必要的彩色图形、图表除外）。

●提请大家注意：摘要应该是一份简明扼要的详细摘要（包括关键词），在整篇论文评阅中占有重要权重，请认真书写（注意篇幅不能超过一页，且无需译成英文）。

评阅时将首先根据摘要和论文整体结构及概貌对论文进行级别划分。

●论文应该思路清晰，表达简洁（正文不少于1500字，附录不算）。

●在论文纸质版附录中，应给出各小组实际使用的软件名称、命令和编写的全部计算机源程序（若有的话）。

●引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。

正文引用处用方括号标示参考文献的编号，如[1][3]等；引用书籍还必须指出页码。

参考文献按正文中的引用次序列出，其中书籍的表述方式为：[编号] 作者，书名，出版地：出版社，出版年。

参考文献中期刊杂志论文的表述方式为：[编号] 作者，论文名，杂志名，卷期号：起止页码，出版年。

参考文献中网上资源的表述方式为：[编号] 作者，资源标题，网址，访问时间（年月日）。

●如果评阅小组在审阅论文时发现抄袭现象，将取消该组成绩。

A 最优行驶轨迹
设一艘轮船经一强水流区域。

水流方向是已知的位置函数
(,),V u u x y y h
==- (,)0,v v x y ==
式中x 和y 为直角坐标；
u 和v 分别是水流在x 和y 方向的速度分量；V 是轮船相对水的速度，为一常数；h 为恒值。

1. 试建立数学模型，讨论如何驾驶轮船，使得船以最短时间从起点（003.66, 1.86x y h h ==-）驾驶到（0,0f f x y h h ==）
； 2. 模拟出船行驶的相应轨迹。

B题：“大球时代”乒乓球直径与赛事观赏性2000年，国际乒乓球联合会（简称国际乒联）将国际乒乓球职业赛事中的官方用球直径由38mm增加至40mm。

其宗旨在于进一步增加球在空中运行中的空气阻力，减缓比赛中球运行的速度，从而达到进一步增加和丰富乒乓球职业运动员击球技术和技巧的目的，最终增加乒乓球赛事的整体观赏性。

然而自乒乓球“大球时代”到来迄今为止，关于用球直径的争议始终未有停止。

国内外各界教练和运动员褒贬不一。

值得注意的事，由于职业运动员身高，打球习惯，握拍习惯的不同，其对球直径变化的敏感度也颇有差异。

请通过建模分析当前的比赛用球直径是否较之“小球时代”提升了运动员的体验质量和观众的观赏质量？请通过建模进一步分析您认为的最佳乒乓球直径的长度？。

课后作业(十九) 函数y ＝A sin(ωx ＋φ)的图象及三角函数模型的应用一、选择题1．(2013·某某模拟)要得到函数y ＝sin(x －π6)的图象可将函数y ＝sin(x ＋π6)的图象上的所有点( )A ．向右平移π6个长度单位B ．向左平移π6个长度单位C ．向右平移π3个长度单位D ．向左平移π3个长度单位图3－4－72．函数f (x )＝A sin(2x ＋φ)(A ，φ∈R)的部分图象如图3－4－7所示，那么f (0)＝( )A ．－12B ．－1C ．－32D ．－ 33．(2013·某某模拟)要得到函数y ＝cos 2x 的图象，只需把函数y ＝sin x 的图象( ) A ．沿x 轴向左平移π2个单位，再把横坐标伸长为原来的2倍，纵坐标不变B ．沿x 轴向右平移π2个单位，再把横坐标伸长为原来的2倍，纵坐标不变C ．横坐标缩短为原来的12，纵坐标不变，再沿x 轴向右平移π4个单位D ．横坐标缩短为原来的12，纵坐标不变，再沿x 轴向左平移π4个单位图3－4－84．(2013·某某模拟)已知函数f (x )＝A cos(ωx ＋φ)(A ＞0，ω＞0，0＜φ＜π)为奇函数，该函数的部分图象如图3－4－8所示，△EFG 是边长为2的等边三角形，则f (1)的值为( )A ．－32B ．－62C. 3D ．－ 35．已知函数f (x )＝sin(ωx ＋π4)(x ∈R，ω＞0)的最小正周期为π，将y ＝f (x )的图象向左平移|φ|个单位长度，所得图象关于y 轴对称，则φ的一个值是( )A.π2B.3π8C.π4D.π8图3－4－96．已知函数f (x )＝A tan(ωx ＋φ)(ω＞0，|φ|＜π2)，y ＝f (x )的部分图象如图3－4－9，则f (π24)＝( )A ．2＋3B. 3 C.33D ．2－ 3二、填空题7．函数f (x )＝tan ωx (ω＞0)的图象的相邻两支截直线y ＝π4所得线段长为π4，则f (π4)＝________．8．(2013·荆州模拟)已知f (x )＝cos(2x ＋φ)，其中φ∈[0，2π)，若f (π6)＝f (π3)，且f (x )在区间(π6，π3)上有最小值，无最大值，则φ＝________．9．(2013·某某模拟)若将函数y ＝sin(ωx ＋5π6)(ω＞0)的图象向右平移π3个单位长度后，与函数y ＝sin(ωx ＋π4)的图象重合，则ω的最小值为________．10．已知函数f (x )＝2cos 2x ＋23sin x cos x －1. (1)求f (x )的周期和单调递增区间；(2)说明f (x )的图象可由y ＝sin x 的图象经过怎样变化得到．11．(2012·某某调研)将正弦函数f 1(x )＝sin x 与余弦函数f 2(x )＝cos x 线性组合成函数f (x )＝Af 1(x )＋Bf 2(x )(A ，B 是常数，x ∈R)，函数f (x )的图象称为(A ，B )曲线．(1)若(A ，B )曲线与(C ，D )曲线重合，求证：A ＝C ，B ＝D ；(2)已知点P 1(x 1，y 1)与点P 2(x 2，y 2)且x 1－x 2≠k π(k ∈Z)，求证：经过点P 1与点P 2的(A ，B )曲线有且仅有一条．12．已知函数f (x )＝3sin(ωx ＋φ)－cos(ωx ＋φ)(0＜φ＜π，ω＞0)为偶函数，且函数y ＝f (x )图象的两相邻对称轴间的距离为π2.(1)求f (π8)的值；(2)将函数y ＝f (x )的图象向右平移π6个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y ＝g (x )的图象，求g (x )的单调递减区间．解析及答案一、选择题1．【解析】 由y ＝sin[(x －π3)＋π6]＝sin(x －π6)知选C.2．【解析】 由图象知A ＝2，图象过点(π3，2)∴2sin(π3×2＋φ)＝2，∴2π3＋φ＝π2＋2k π，k ∈Z，∴φ＝－π6＋2k π，k ∈Z，∴φ＝－π6，∴f (0)＝2sin(－π6)＝－1.【答案】B3．【解析】 ∵y ＝cos 2x ＝sin(2x ＋π2)＝sin[2(x ＋π4)]，∴函数y ＝sin x 的图象横坐标缩短为原来的12，纵坐标不变，再沿x 轴向左平移π4个单位即可得到y ＝cos 2x 的图象．【答案】D4．【解析】 由△EFG 是边长为2的等边三角形知，A ＝3，周期T ＝4，∴ω＝π2， 又f (x )是奇函数且0＜φ＜π，∴φ＝π2，∴f (x )＝3cos(π2x ＋π2)，∴f (1)＝3cos π＝－ 3.【答案】D5．【解析】 ∵2πω＝π，∴ω＝2，则f (x )＝sin(2x ＋π4)．将它向左平移|φ|个单位长度，得g (x )＝sin[2(x ＋|φ|)＋π4]．∵g (x )的图象关于y 轴对称， ∴2(0＋|φ|)＋π4＝π2＋k π，k ∈Z，∴|φ|＝π8＋k π2，k ∈Z，∴φ的一个值为π8.【答案】D6．【解析】 由图形知，T ＝πω＝2(38π－π8)＝π2，∴ω＝2， 又x ＝π8是渐近线，且|φ|＜π2，∴2×π8＋φ＝k π＋π2，k ∈Z，∴φ＝π4，又f (0)＝1，从而可求A ＝1，∴f (x )＝tan(2x ＋π4)，因此f (π24)＝tan(π12＋π4)＝tan π3＝ 3.【答案】B二、填空题7．【解析】 依题意πω＝π4，∴ω＝4，f (x )＝tan 4x ，所以f (π4)＝tan π＝0.【答案】 08．【解析】 由题意知，当x ＝π4时，f (x )取最小值，∴2×π4＋φ＝π＋2k π，k ∈Z，∴φ＝π2＋2k π，k ∈Z，又0≤φ＜2π， ∴φ＝π2.【答案】π29．【解析】y ＝sin(ωx ＋5π6)＝sin[ω(x ＋5π6ω)]y ＝sin(ωx ＋π4)＝sin[ω(x ＋π4ω)]， 由题意知，当5π6ω－π4ω＝π3时，ω最小，解得ω＝74.【答案】74三、解答题10．【解】 (1)f (x )＝cos 2x ＋3sin 2x ＝2(32sin 2x ＋12cos 2x )＝2sin(2x ＋π6)， f (x )最小正周期为π，由2k π－π2≤2x ＋π6≤2k π＋π2(k ∈Z)，可得k π－π3≤x ≤k π＋π6(k ∈Z)，所以，函数f (x )的单调递增区间为[k π－π3，k π＋π6](k ∈Z)．(2)将y ＝sin x 的图象纵坐标不变，横坐标缩短为原来的12倍，将所得图象向左平移π12个单位，再将所得的图象横坐标不变，纵坐标伸长为原来的2倍得到f (x )的图象．11．【证明】 (1)∵A sin x ＋B cos x ＝C sin x ＋D cos x 对∀x ∈R 成立，取x ＝π2代入知A ＝C ，取x ＝0代入知B ＝D .(2)假设(A ，B )曲线经过点P 1(x 1，y 1)，P 2(x 2，y 2)，则 A sin x 1＋B cos x 1＝y 1，① A sin x 2＋B cos x 2＝y 2，②①×cos x 2－cos x 1×②得A sin(x 1－x 2)＝y 1cos x 2－y 2cos x 1， ∵x 1－x 2≠k π(k ∈Z)，∴sin(x 1－x 2)≠0， ∴A ＝y 1cos x 2－y 2cos x 1sin （x 1－x 2），同理B ＝y 2sin x 1－y 1sin x 2sin （x 1－x 2）.所以A ，B 由P 1，P 2坐标唯一确定，即经过点P 1与点P 2的(A ，B )曲线有且仅有一条． 12．【解】 (1)f (x )＝3sin(ωx ＋φ)－cos(ωx ＋φ) ＝2[32sin(ωx ＋φ)－12cos(ωx ＋φ)] ＝2sin(ωx ＋φ－π6)．∵y ＝2sin(ωx ＋φ－π6)是偶函数，∴φ－π6＝k π＋π2，k ∈Z.又0＜φ＜π， ∴φ－π6＝π2.∴f (x )＝2sin(ωx ＋π2)＝2cos ωx .由题意得2πω＝2·π2，所以ω＝2.故f (x )＝2cos 2x . 因此f (π8)＝2cos π4＝ 2.(2)将f (x )的图象向右平移π6个单位后，得到f (x －π6)的图象，再将所得图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到f (x 4－π6)的图象．所以g (x )＝f (x 4－π6)＝2cos[2(x 4－π6)]＝2cos(x 2－π3)．当2k π≤x 2－π3≤2k π＋π(k ∈Z)，即4k π＋2π3≤x ≤4k π＋8π3(k ∈Z)时，g (x )单调递减．因此g (x )的递减区间为[4k π＋2π3，4k π＋8π3](k ∈Z)．。

(1) 用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. （10个数字自己选择，方法要一般）(2)有一个45⨯矩阵,编程求出其绝对值最大值及其所处的位置. （用abs 函数求绝对值）(3)编程求201!n n =∑ （ 分别用for 和while 循环）(4)一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10次反弹有多高? (5)有一函数2(,)sin 2f x y x xy y =++,写一程序,输入自变量的值,输出函数值，并画出其图像，加上图例和注释. （区间自理） (6) 建立一个脚本M 文件将向量a,b 的值互换。

(7) 某商场对顾客所购买的商品实行打折销售，标准如下(商品价格用price 来表示)： price<200 没有折扣; 200≤price<500 3%折扣; 500≤price<1000 5%折扣; 1000≤price<2500 8%折扣; 2500≤price<5000 10%折扣;5000≤price 14%折扣;输入所售商品的价格，求其实际销售价格。

(用input 函数) (8) 已知y ，22221111123y n=++++,当n=100时，求y 的值。

(9)画出分段函数2221y 1 122 1 2x x x x x x x ⎧<⎪=-≤<⎨⎪-+≥⎩的图像，并求分段函数在任意几点的函数值。

(用hold on 函数)(10) 给定5阶方阵，求方阵的行列式、特征值、迹、上三角元素的和。

(11) 输入40个数字，按照从小到大的顺序排列输出。

(12) 把当前窗口分成四个区域，在每个区域中分别用不同的颜色和线形画sin ;tan y x y x==，x y e =和31y x x =++的图像。

（区间自理）(13) 对于,AXB YA B==，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，，求解X,Y ;(14) 如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，242679836B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求1122,*,.*,,,,T A B A B A B AB A B A A ---。

N 单元 选修4系列15．[2014·某某卷] (几何证明选讲选做题)如图1­3所示，在平行四边形ABCD 中，点E 在AB 上且EB ＝2AE ，AC 与DE 交于点F ，则△CDF 的面积△AEF 的面积＝________．图1­315．9 [解析] 本题考查相似三角形的性质定理，面积比等于相似比的平方． ∵EB ＝2AE ，∴AE ＝13AB ＝13CD .又∵四边形ABCD 是平行四边形，∴△AEF ∽△CDF ，∴△CDF 的面积△AEF 的面积＝⎝ ⎛⎭⎪⎫CD AE 2＝9.15．[2014·某某卷] (选修4­1：几何证明选讲)如图1­3，P 为⊙O 外一点，过P 点作⊙O 的两条切线，切点分别为A ，B ，过PA 的中点Q 作割线交⊙O 于C ，D 两点，若．15．4 [解析] 由切线长定理得QA 2＝QC ·QD ＝1×(1＋3)＝4，解得QA ＝2.故PB ＝PA ＝2QA ＝4.12．[2014·某某卷] 如图1­3所示，已知AB ，BC 是⊙O 的两条弦，AO ⊥BC ，AB ＝3，BC ＝22，则⊙O 的半径等于________．12.32[解析] 设圆的半径为r ，记AO 与BC 交于点D ，依题可知AD ＝1.由相交弦定理可得1×(2r －1)＝2×2，解得r ＝32.22．[2014·某某卷] 选修4­1：几何证明选讲如图1­7所示，EP 交圆于E ，C 两点，PD 切圆于D ，G 为CE 上—点且PG ＝PD ，连接DG 并延长交圆于点A ，作弦AB 垂直EP ，垂足为F .(1)求证：AB 为圆的直径；(2)若AC＝BD，求证：AB＝ED.22．证明：(1)因为PD＝PG，所以∠PDG＝∠PGD.由于PD为切线，故∠PDA＝∠DBA，又因为∠PGD＝∠EGA，所以∠DBA＝∠EGA，所以∠DBA＋∠BAD＝∠EGA＋∠BAD，从而∠BDA＝∠PFA.又AF⊥EP，所以∠PFA＝90°，所以∠BDA＝90°，故AB为圆的直径．(2)连接BC，DC.由于AB是直径，故∠BDA＝∠在Rt△BDA与Rt△ACB中，AB＝BA，AC＝BD，从而得Rt△BDA≌Rt△ACB，于是∠DAB＝∠CBA.又因为∠DCB＝∠DAB，所以∠DCB＝∠CBA，故DC∥AB.因为AB⊥EP，所以DC⊥EP，∠DCE为直角，所以ED为直径，又由(1)知AB为圆的直径，所以ED＝AB.22．[2014·新课标全国卷Ⅰ] 选修4­1：几何证明选讲如图1­6，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB＝CE.图1­6(1)证明：∠D＝∠E；(2)设AD不是⊙O的直径，AD的中点为M，且MB＝MC，证明：△ADE为等边三角形．22．证明：(1)由题设知A，B，C，D四点共圆，所以∠D＝∠CBE.由已知得∠CBE＝∠E，故∠D＝∠E.(2)设BC的中点为N，连接MN，则由MB＝MC知MN⊥BC，故O在直线MN上．又AD不是⊙O的直径，M为AD的中点，故OM⊥AD，即MN⊥AD，所以AD∥BC，故∠A＝∠CBE.又∠CBE＝∠E，故∠A＝∠E，由(1)知，∠D＝∠E，所以△ADE为等边三角形．22．[2014·新课标全国卷Ⅱ] 选修4­1：几何证明选讲如图1­4，P 是⊙O 外一点，PA 是切线，A 为切点，割线PBC 与⊙O 相交于点B ，C ，PC ＝2PA ，D 为PC 的中点，AD 的延长线交⊙O 于点E ，证明：(1)BE ＝EC ；(2)AD ·DE ＝2PB 2.22．证明：(1)连接AB ，AC .由题设知PA ＝PD ， 故∠PAD ＝∠PDA .因为∠PDA ＝∠DAC ＋∠DCA ， ∠PAD ＝∠BAD ＋∠PAB ， ∠DCA ＝∠PAB ，所以∠DAC ＝∠BAD ，从而BE ＝EC . 因此BE ＝EC .(2)由切割线定理得PA 2＝PB ·因为PA ＝PD ＝DC ，所以DC ＝2PB ，BD ＝PB . 由相交弦定理得AD ·DE ＝BD ·DC ，所以AD ·DE ＝2PB 2. 15．[2014·某某卷]图1­3B ．(几何证明选做题)如图1­3，△ABC 中，BC ＝6，以BC 为直径的半圆分别交AB ，AC 于点E ，F ，若AC ＝2AE ，则EF ＝________．15． B ．3 [解析] B ．由题意，可知∠AEF ＝∠ACB ，又∠A ＝∠A ，所以△AEF ∽ACB ，所以AE AC ＝EF BC.因为AC ＝2AE ，BC ＝6，所以EF ＝3.6．[2014·某某卷]图1­2如图1­2所示，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于点E，过点B的圆的切线与AD的延长线交于点F.在上述条件下，给出下列四个结论：①BD平分∠CBF；②FB2＝FD·FA；③AE·CE＝BE·DE；④AF·BD＝AB·BF.则所有正确结论的序号是( )A．①② B．③④C．①②③ D．①②④6．D [解析] 如图所示，∵∠1＝∠3，∠2＝∠4，且∠1＝∠2，∴∠4＝∠3，∴BD平分∠CBF，∴△ABF∽△BDF.∵ABBD＝AFBF，∴AB·BF＝AF·BD.∵AFBF＝BFDF，∴BF2＝AF·DF.故①②④正确．14．[2014·某某卷] 过圆外一点P作圆的切线PA(A为切点)，再作割线PBC依次交圆于B，C.若PA＝6，AC＝8，BC＝9，则AB＝________．14．4 [解析] 根据题意，作出图形如图所示，由切割线定理，得PA2＝PB·PC＝PB·(PB ＋BC)，即36＝PB·(PB＋9)∴PB＝3，∴PC＝12.由弦切角定理知∠PAB＝∠PCA，又∠APB＝∠CPA，∴△PAB∽△PCA，∴ABCA＝PBPA，即AB＝PB·CAPA＝3×86＝4.21．[2014·某某卷] (Ⅰ)选修4­2：矩阵与变换已知矩阵A的逆矩阵．(1)求矩阵A；(2)求矩阵A－1的特征值以及属于每个特征值的一个特征向量．21. (Ⅰ)解：(1)因为矩阵A 是矩阵A －1的逆矩阵，且||A－1＝2×2－1×1＝3≠0，所以A ＝13⎝ ⎛⎭⎪⎫2 －1－1 2＝.(2)矩阵A －1的特征多项式为f (λ)＝⎪⎪⎪⎪⎪⎪λ－2 －1－1 λ－2＝λ2－4λ＋3＝(λ－1)(λ－3)，令f (λ)＝0，得矩阵A －1的特征值为λ1＝1或λ2＝3，所以ξ1＝⎝ ⎛⎭⎪⎫1－1)是矩阵A －1的属于特征值λ1＝1的一个特征向量，ξ2＝⎝ ⎛⎭⎪⎫11)是矩阵A －1的属于特征值λ2＝3的一个特征向量．13．[2014·某某卷] 在以O 为极点的极坐标系中，圆ρ＝4sin θ和直线ρsin θ＝a 相交于A ，B 两点．若△AOB 是等边三角形，则a 的值为________．13．3 [解析] 将ρ＝4sin θ与ρsin θ＝a 转化为直角坐标方程分别为x 2＋(y －2)2＝4与y ＝a .联立⎩⎪⎨⎪⎧y ＝a ，x 2＋（y －2）2＝4，得x 2＝－a 2＋4a ，且0<a <4.∵△AOB 为等边三角形，∴a 2＝3(－a 2＋4a )，解得a ＝3或a ＝0(舍)．4．[2014·某某卷] 以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l 的参数方程是⎩⎪⎨⎪⎧x ＝t ＋1，y ＝t －3(t 为参数)，圆C 的极坐标方程是ρ＝4cos θ，则直线l 被圆C 截得的弦长为( )A.14 B ．214C. 2 D ．2 24．D [解析] 直线l 的普通方程为y ＝x －4，圆C 的直角坐标方程是(x －2)2＋y 2＝4，圆心(2，0)到直线l 的距离d ＝|2－0－4|2＝2，所以直线l 被圆C 截得的弦长为222－（2）2＝2 2.3．[2014·卷] 曲线⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( )A ．在直线y ＝2x 上B ．在直线y ＝－2x 上C ．在直线y ＝x －1上D ．在直线y ＝x ＋1上3．B [解析] 曲线方程消参化为(x ＋1)2＋(y －2)2＝1，其对称中心点为(－1，2)，验证知其在直线y ＝－2x 上．21． [2014·某某卷](Ⅱ)选修4­4：坐标系与参数方程已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a －2t ，y ＝－4t (t 为参数)，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ(θ为参数)．(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，某某数a 的取值X 围． 21. (Ⅱ)解：(1)直线l 的普通方程为2x －y －2a ＝0，圆C 的普通方程为x 2＋y 2＝16. (2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝≤4，解得－25≤a ≤2 5. 14．[2014·某某卷] (坐标系与参数方程选做题)在极坐标系中，曲线C 1和C 2的方程分别为ρsin 2θ＝cos θ和ρsin θ＝1.以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，则曲线C 1和C 2交点的直角坐标为________．14．(1，1) [解析] 本题主要考查将极坐标方程化为直角坐标方程的方法．将曲线C 1的方程ρsin2θ＝cos θ化为直角坐标方程为y 2＝x ，将曲线C 2的方程ρsin θ＝1化为直角坐标方程为y ＝1.由⎩⎪⎨⎪⎧y 2＝x ，y ＝1，解得⎩⎪⎨⎪⎧x ＝1，y ＝1.故曲线C 1和C 2交点的直角坐标为(1，1)．16．[2014·某某卷] (选修4­4：坐标系与参数方程)已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝t ，y ＝3t 3(t 为参数)．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ＝2，则C 1与C 2交点的直角坐标为________．16.()3，1 [解析] 由⎩⎪⎨⎪⎧x ＝t ，y ＝3t 3，消去t 得y ＝33x (x ≥0)，即曲线C 1的普通方程是y ＝33x (x ≥0)；由ρ＝2，得ρ2＝4，得x 2＋y 2＝4，即曲线C 2的直角坐标方程是x 2＋y 2＝4.联立⎩⎪⎨⎪⎧y ＝33x （x ≥0），x 2＋y 2＝4，解得⎩⎨⎧x ＝3，y ＝1.故曲线C 1与C 2的交点坐标为()3，1.11．[2014·某某卷] 在平面直角坐标系中，倾斜角为π4的直线l 与曲线C ：⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝1＋sin α(α为参数)交于A ，B 两点，且|AB |＝2.以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，则直线l 的极坐标方程是________．11．ρcos θ－ρsin θ＝1 [解析] 依题意可设直线l ：y ＝x ＋b ，曲线C ：⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝1＋sin α的普通方程为(x －2)2＋(y －1)2＝1.由|AB |＝2可知圆心(2，1)在直线l ：y ＝x ＋b 上，即l ：y ＝x －1，所以l 的极坐标方程是ρcos θ－ρsin θ－1＝0.11．[2014·某某卷] (2)(坐标系与参数方程选做题)若以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，则线段y ＝1－x (0≤x ≤1)的极坐标方程为( )A ．ρ＝1cos θ＋sin θ，0≤θ≤π2B ．ρ＝1cos θ＋sin θ，0≤θ≤π4C ．ρ＝cos θ＋sin θ，0≤θ≤π2D ．ρ＝cos θ＋sin θ，0≤θ≤π411．(2)A [解析] 依题意，方程y ＝1－x 的极坐标方程为ρ(cos θ＋sin θ)＝1，整理得ρ＝1cos θ＋sin θ.因为0≤x ≤1，所以 0≤y ≤1，结合图形可知，0≤θ≤π2.23．[2014·某某卷] 选修4­4：坐标系与参数方程 将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．23．解：(1)设(x 1，y 1)为圆上的点，在已知变换下变为C 上点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1，由x 21＋y 21＝1得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为⎩⎪⎨⎪⎧x ＝cos t ，y ＝2sin t (t 为参数)．(2)由⎩⎪⎨⎪⎧x 2＋y 24＝1，2x ＋y －2＝0，解得⎩⎪⎨⎪⎧x ＝1，y ＝0或⎩⎪⎨⎪⎧x ＝0，y ＝2.不妨设P 1(1，0)，P 2(0，2)，则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12，1，所求直线的斜率k ＝12，于是所求直线方程为y －1＝12⎝ ⎛⎭⎪⎫x －12，化为极坐标方程，并整理得2ρcos θ－4ρsin θ＝－3，即ρ＝34sin θ－2cos θ.23．[2014·新课标全国卷Ⅰ] 选修4­4：坐标系与参数方程已知曲线C ：x 24＋y 29＝1，直线l ：⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数)．(1)写出曲线C 的参数方程，直线l 的普通方程；(2)过曲线C 上任意一点P 作与l 夹角为30°的直线，交l 于点A ，求|PA |的最大值与最小值．23．解：(1)曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝3sin θ(θ为参数)，直线l 的普通方程为2x ＋y －6＝0.(2)曲线C 上任意一点P (2cos θ，3sin θ)到l 的距离d ＝55|4cos θ＋3sin θ－6|， 则|PA |＝d sin 30°＝255|5sin(θ＋α)－6|，其中α为锐角，且tan α＝43.当sin(θ＋α)＝－1时，|PA |取得最大值，最大值为2255. 当sin(θ＋α)＝1时，|PA |取得最小值，最小值为255.23．[2014·新课标全国卷Ⅱ] 选修4­4：坐标系与参数方程在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为ρ＝2cos θ，θ∈⎣⎢⎡⎦⎥⎤0，π2.(1)求C 的参数方程；(2)设点D 在C 上，C 在D 处的切线与直线l ：y ＝3x ＋2垂直，根据(1)中你得到的参数方程，确定D 的坐标．23．解：(1)C 的普通方程为(x －1)2＋y 2＝1(0≤y ≤1)． 可得C 的参数方程为 ⎩⎪⎨⎪⎧x ＝1＋cos t ，y ＝sin t ，(t 为参数，0≤t ≤π)． (2)设D (1＋cos t ，sin t )．由(1)知C 是以G (1，0)为圆心，1为半径的上半圆．因为C 在点D 处的切线与l 垂直，所以直线GD 与l 的斜率相同，tan t ＝3，t ＝π3.故D 的直角坐标为⎝ ⎛⎭⎪⎫1＋cos π3，sin π3，即⎝ ⎛⎭⎪⎫32，32. 15．[2014·某某卷] C ．(坐标系与参数方程选做题)在极坐标系中，点⎝⎛⎭⎪⎫2，π6到直线ρsin ⎝⎛⎭⎪⎫θ－π6＝1的距离是________．15．C ．1 [解析] C ．点⎝⎛⎭⎪⎫2，π6的极坐标可化为x ＝ρcos θ＝2cos π6＝3，y ＝ρsinθ＝2sin π6＝1，即点⎝⎛⎭⎪⎫2，π6在平面直角坐标系中的坐标为(3，1)．直线ρsin ⎝⎛⎭⎪⎫θ－π6＝ρsin θcos π6－ρcos θsin π6＝1，即该直线在直角坐标系中的方程为x －3y ＋2＝0，由点到直线的距离公式得所求距离为d ＝|3－3＋2|12＋（－3）2＝1.自选模块2．[2014·某某卷] (1)在极坐标系Ox 中，设集合A ＝{(ρ，θ)|0≤θ≤π4，0≤ρ≤cos θ}，求集合A 所表示区域的面积；(2)在直角坐标系xOy 中，直线l ：⎩⎪⎨⎪⎧x ＝－4＋t cos π4，y ＝t sin π4(t 为参数)，曲线C ：⎩⎪⎨⎪⎧x ＝a cos θ，y ＝2sin θ(θ为参数)，其中a ＞0.若曲线C 上所有点均在直线l 的右下方，求a 的取值X 围．解：(1)在ρ＝cos θ两边同乘ρ，得ρ2＝ρcos θ.化成直角坐标方程，得x 2＋y 2＝x ，即⎝ ⎛⎭⎪⎫x －122＋y 2＝14.所以集合A 所表示的区域为：由射线y ＝x (x ≥0)，y ＝0(x ≥0)，圆⎝ ⎛⎭⎪⎫x －122＋y 2＝14所围成的区域，如图所示的阴影部分，所求面积为π16＋18.(2)由题意知，直线l 因为曲线C 上所有点均在直线l 的右下方，故对θ∈R ，有a cos θ－2sin θ＋4＞0恒成立，即a 2＋4cos(θ＋φ)＞－4⎝ ⎛⎭⎪⎫其中tan φ＝2a 恒成立，所以a 2＋4＜4.又a ＞0，得0＜a ＜2 3. 15．[2014·某某卷] 已知直线l的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝3＋t (t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0(ρ≥0，0≤θ<2π)，则直线l 与曲线C 的公共点的极径ρ＝________．15. 5 [解析] 由题意，得直线l 的普通方程为x －y ＋1＝0，曲线C 的平面直角坐标方程为y 2＝4x ，联立直线l 与曲线C 的方程，解得⎩⎪⎨⎪⎧x ＝1，y ＝2，所以直线l 与曲线C 的公共点的极径ρ＝（1－0）2＋（2－0）2＝ 5.21．[2014·某某卷](Ⅲ)选修4­5：不等式选讲已知定义在R 上的函数f (x )＝|x ＋1|＋|x －2|的最小值为a . (1)求a 的值；(2)若p ，q ，r 是正实数，且满足p ＋q ＋r ＝a ，求证：p 2＋q 2＋r 2≥3. 21. (Ⅲ)解：(1)因为|x ＋1|＋|x －2|≥|(x ＋1)－(x －2)|＝3， 当且仅当－1≤x ≤2时，等号成立， 所以f (x )的最小值等于3，即a ＝3.(2)由(1)知p ＋q ＋r ＝3，又p ，q ，r 是正实数，所以(p 2＋q 2＋r 2)(12＋12＋12)≥(p ×1＋q ×1＋r ×1)2＝(p ＋q ＋r )2＝9，即p 2＋q 2＋r 2≥3.8．、[2014·某某卷] 设集合A ＝{(x 1，x 2，x 3，x 4，x 5)|x i ∈{－1，0，1}，i ＝1，2，3，4，5}，那么集合A 中满足条件“1≤|x 1|＋|x 2|＋|x 3|＋|x 4|＋|x 5|≤3”的元素个数为( )A ．60B ．90C ．120D ．1308．D [解析] 本题考查排列组合等知识，考查的是用排列组合思想去解决问题，主要根据X 围利用分类讨论思想求解．由“1≤|x 1|＋|x 2|＋|x 3|＋|x 4|＋|x 5|≤3”考虑x 1，x 2，x 3，x 4，x 5的可能取值，设集合M ＝{0}，N ＝{－1，1}．当x 1，x 2，x 3，x 4，x 5中有2个取值为0时，另外3个从N 中取，共有C 25×23种方法；当x 1，x 2，x 3，x 4，x 5中有3个取值为0时，另外2个从N 中取，共有C 35×22种方法；当x 1，x 2，x 3，x 4，x 5中有4个取值为0时，另外1个从N 中取，共有C 45×2种方法．故总共有C 25×23＋C 35×22＋C 45×2＝130种方法， 即满足题意的元素个数为130.9．[2014·某某卷] 不等式|x －1|＋|x ＋2|≥5的解集为________． 9．(－∞，－3]∪[2，＋∞) [解析] 本题考查绝对值不等式的解法．|x －1|＋|x ＋2|≥5的几何意义是数轴上的点到1与－2的距离之和大于等于5的实数，所以不等式的解为x ≤－3或x ≥2，即不等式的解集为(－∞，－3]∪[2，＋∞)．13．[2014·某某卷] 若关于x 的不等式|ax －2|＜3的解集为⎩⎨⎧⎭⎬⎫x －53＜x ＜13，则a ＝________．13．－3 [解析] 依题意可得－3＜ax －2＜3，即－1＜ax ＜5 ，而－53＜x ＜13，即－1＜－3x ＜5，所以a ＝－3.11．[2014·某某卷] (1)(不等式选做题)对任意x ，y ∈R ，|x －1|＋|x |＋|y －1|＋|y ＋1|的最小值为( )A ．1B ．2C ．3D ．411．(1)C [解析] 易知|x －1|＋|x |≥1，当且仅当0≤x ≤1时等号成立；|y －1|＋|y ＋1|≥2, 当且仅当－1≤y ≤1时等号成立．故|x －1|＋|x |＋|y －1|＋|y ＋1|≥3.24．[2014·某某卷] 选修4­5：不等式选讲设函数f (x )＝2|x －1|＋x －1，g (x )＝16x 2－8x ＋1.记f (x )≤1的解集为M ，g (x )≤4的解集为N .(1)求M ；(2)当x ∈M ∩N 时，证明：x 2f (x )＋x [f (x )]2≤14.24．解：(1)f (x )＝⎩⎪⎨⎪⎧3x －3，x ∈[1，＋∞），1－x ，x ∈（－∞，1）.当x ≥1时，由f (x )＝3x －3≤1得x ≤43，故1≤x ≤43；当x <1时，由f (x )＝1－x ≤1得x ≥0，故0≤x <1.所以f (x )≤1的解集M ＝⎩⎨⎧⎭⎬⎫x 0≤x ≤43.(2)由g (x )＝16x 2－8x ＋1≤4得16⎝ ⎛⎭⎪⎫x －142≤4，解得－14≤x ≤34，因此N ＝⎩⎨⎧⎭⎬⎫x －14≤x ≤34，故M ∩N ＝⎩⎨⎧⎭⎬⎫x 0≤x ≤34.当x ∈M ∩N 时，f (x )＝1－x ，于是x 2f (x )＋x ·[f (x )]2＝xf (x )[x ＋f (x )]＝xf (x )＝x (1－x )＝14－⎝ ⎛⎭⎪⎫x －122≤14.24．[2014·新课标全国卷Ⅰ] 选修4­5：不等式选讲若a >0，b >0，且1a ＋1b＝ab .(1)求a 3＋b 3的最小值．(2)是否存在a ，b ，使得2a ＋3b ＝6？并说明理由.24.解：(1)由ab ＝1a ＋1b≥2ab，得ab ≥2，当且仅当a ＝b ＝2时等号成立．故a 3＋b 3≥2a 3b 3≥4 2，当且仅当a ＝b ＝ 2时等号成立．所以a 3＋b 3的最小值为4 2.(2)由(1)知，2a ＋3b ≥26ab ≥4 3.由于43>6，从而不存在a ，b ，使2a ＋3b ＝6.24．[2014·新课标全国卷Ⅱ] 选修4­5：不等式选讲设函数f (x )＝⎪⎪⎪⎪⎪⎪x ＋1a ＋|x －a |(a ＞0)．(1)证明：f (x )≥2；(2)若f (3)＜5，求a 的取值X 围．24．解：(1)证明：由a >0，有f (x )＝⎪⎪⎪⎪⎪⎪x ＋1a ＋|x －a |≥⎪⎪⎪⎪⎪⎪x ＋1a－（x －a ）＝1a＋a ≥2，所以f (x )≥2.(2)f (3)＝⎪⎪⎪⎪⎪⎪3＋1a ＋|3－a |.当a >3时，f (3)＝a ＋1a，由f (3)<5得3<a <5＋212.当0<a ≤3时，f (3)＝6－a ＋1a ，由f (3)<5得1＋52<a ≤3.综上，a 的取值X 围是⎝⎛⎭⎪⎫1＋52，5＋212.15．[2014·某某卷] A ．(不等式选做题)设a ，b ，m ，n ∈R ，且a 2＋b 2＝5，ma ＋nb ＝5，则m 2＋n 2的最小值为________．15．A. 5 [解析] A ．由柯西不等式可知(a 2＋b 2)(m 2＋n 2)≥(ma ＋nb )2，代入数据，得m 2＋n 2≥5，当且仅当an ＝bm 时，等号成立，故m 2＋n 2的最小值为 5.自选模块1．[2014·某某卷] (1)解不等式2|x －2|－|x ＋1|＞3；(2)设正数a ，b ，c 满足abc ＝a ＋b ＋c ，求证：ab ＋4bc ＋9ac ≥36，并给出等号成立条件．解：(1)当x ≤－1时，2(2－x )＋(x ＋1)＞3，得x ＜2，此时x ≤－1； 当－1＜x ≤2时，2(2－x )－(x ＋1)＞3，得x ＜0，此时 －1<x <0；当x >2时，2(x －2)－(x ＋1)＞3，得x >8，此时x >8. 综上所述，原不等式的解集是(－∞，0)∪(8，＋∞)．(2)证明：由abc ＝a ＋b ＋c ，得1ab ＋1bc ＋1ca＝1.由柯西不等式，得(ab ＋4bc ＋9ac )⎝ ⎛⎭⎪⎫1ab ＋1bc ＋1ca ≥(1＋2＋3)2，所以ab ＋4bc ＋9ac ≥36，当且仅当a ＝2，b ＝3，c ＝1时，等号成立．16．[2014·某某卷] 若不等式|2x －1|＋|x ＋2|≥a 2＋12a ＋2对任意实数x 恒成立，则实数a 的取值X 围是________．16.⎣⎢⎡⎦⎥⎤－1，12 [解析] 令f (x )＝|2x －1|＋|x ＋2|，则①当x <－2时，f (x )＝－2x ＋1－x －2＝－3x －1>5；②当－2≤x ≤12时，f (x )＝－2x ＋1＋x ＋2＝－x ＋3，故52≤f (x )≤5；③当x >12时，f (x )＝2x －1＋x ＋2＝3x ＋1>52.综合①②③可知f (x )≥52，所以要使不等式恒成立，则需a 2＋12a ＋2≤52，解得－1≤a ≤12.1．[2014·某某模拟] 已知点P 所在曲线的极坐标方程为ρ＝2cos θ，点Q 所在曲线的参数方程为⎩⎪⎨⎪⎧x ＝1＋t ，y ＝4＋2t (t 为参数)，则|PQ |的最小值是( )A ．2 B.4 55＋1C ．1 D.4 55－11．D [解析] 易知点P 在圆x 2＋y 2－2x ＝0上，圆心为(1，0)，半径为1，点Q 在直线2x －y ＋2＝0上，故|PQ |的最小值是|2＋2|5－1＝4 55－1.4．[2014·株洲模拟] 在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎨⎧x ＝2cos α，y ＝3sin α(α为参数)．在极坐标系(与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴的正半轴为极轴)中，直线C 2的方程为ρ(cos θ－sin θ)＋1＝0，则曲线C 1与C 2的交点的个数为________．4．2 [解析] 由题意，曲线C 1的参数方程⎩⎨⎧x ＝2cos α，y ＝3sin α(α为参数)可化为一般方程x 24＋y 23＝1，直线C 2的极坐标方程ρ·(cos θ－sin θ)＋1＝0可化为普通方程x －y ＋1＝0.联立两个方程，消去y 可得x 24＋（x ＋1）23＝1，即7x 2＋8x －8＝0.因为Δ＝82＋4×7×8>0，所以直线与椭圆相交，且有两个交点．5．[2014·某某长郡中学月考] 在极坐标系中，圆C 1的方程为ρ＝4 2cos ⎝ ⎛⎭⎪⎫θ－π4，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，已知圆C 2的参数方程为⎩⎪⎨⎪⎧x ＝－1＋a cos θ，y ＝－1＋a sin θ(a ＞0，θ为参数)．若圆C 1与圆C 2外切，则实数a ＝____________． 5.2[解析] 依题意，ρ＝4 2cos θ－π4＝4cos θ＋4sin θ，化成普通方程为x 2＋y 2＝4x ＋4y ，即(x －2)2＋(y －2)2＝8，即该圆的圆心为C 1(2，2)，半径r 1＝2 2.将⎩⎪⎨⎪⎧x ＝－1＋a cos θ，y ＝－1＋a sin θ(a >0，θ为参数)化成普通方程为(x ＋1)2＋(y ＋1)2＝a 2，即圆心为C 2(－1，－1)，半径r 2＝a .由丙点间两圆外切可得|C 1C 2|＝3 2＝2 2＋a ，所以a ＝ 2.6．[2014·某某模拟] 已知曲线C 的极坐标方程为ρ＝4cos θ.若以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，则曲线C 的参数方程为________．6.⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数) [解析] 由曲线C 的极坐标方程为ρ＝4cos θ，可得其普通方程为x2＋y 2＝4x ，即(x －2)2＋y 2＝4，所以曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数)．7．[2014·某某雅礼中学月考] 已知极坐标系下曲线ρ＝4sin θ表示圆，则点A ⎝⎛⎭⎪⎫4，π6到圆心的距离为____________．7．2 3 [解析] 将曲线ρ＝4sin θ化成普通方程为x 2＋y 2＝4y ，则该圆的圆心为(0，2)，而点A ⎝ ⎛⎭⎪⎫4，π6的直角坐标为(2 3，2)，由两点间距离公式可得d ＝（2 3）2＋（2－2）2＝2 3.8．[2014·某某十三校联考] 以直角坐标系的原点为极点，x 轴的正半轴为极轴建立极坐标系．已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t ，y ＝t －a (t 为参数)，圆C 的极坐标方程为ρ＝2cos θ，若直线l 经过圆C 的圆心，则常数a 的值为________．8．1 [解析] 将直线l 的参数方程⎩⎪⎨⎪⎧x ＝t ，y ＝t －a(t 为参数)化为普通方程为y ＝x －a ，将圆C 的极坐标方程ρ＝2cos θ化为普通方程为x 2＋y 2＝2x ，则圆心为(1，0)，代入直线y ＝x－a 可得a ＝1.9．[2014·某某师大附中月考] 在极坐标系中，已知点A 的极坐标为(2，π)，直线l 的极坐标方程为ρsin θ＋π4＝2，则点A 到直线l 的距离是____________．9．2 2 [解析] 由题意，直线l 的极坐标方程为ρsin θcos π4＋cos θsin π4＝2，即ρsin θ＋ρcos θ＝2，则直线l 的直角坐标方程为x ＋y －2＝0.又点A 的直角坐标为(－2，0)，所以点A 到直线l 的距离d ＝|－2－2|2＝2 2.。

2014-2015学年第一学期期末考试课程试卷参考答案课名称: 数学建模方法 课程号: SAM12I001 考核方式: 考查一、设计划生产生产A 、B 、C 、D 、E 五种产品分别为 单位, 则可建立线性规划问题数学模型： ⎪⎪⎩⎪⎪⎨⎧≥≤++++≤+++≤+++++++=0,,,,2122222423102..2119132518max 54321543215431532154321x x x x x x x x x x x x x x x x x x t s x x x x x SMax=18*x1+25*x2+13*x3+19*x4+21*x5; X1+2*x2+x3+x5<10; X1+x3+3*x4+2*x5<24 ;X1+2*x2+2*x3+2*x4+2*x5<21 ;二、首先引进松弛变量 、 , 将线性规划问题化成标准型: ⎪⎩⎪⎨⎧≥=+++=+++++=0,,,,3054345536..500300400S max 5432153214321321x x x x x x x x x x x x x t s x x x得最优解: 。

去掉松弛变量, 得到原线性规划问题的最优解: 。

三（1）问题的最优解为: 。

即：最有生产方案为生产A 型号产品400单位、C 型号产品70单位、D 型号产品10单位, B 型号产品不生产。

可使利润达到最大, 最大利润为4450元。

（2）对偶线性规划问题为:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+++≥+++≥+++≥++++++=0,,,84551185264289644..300020002400480min 432143214321432143214321y y y y y y y y y y y y y y y y y y y y t s y y y y w对偶问题的最优解为:4450min ;75.0,5.0;0,5.24321=====w y y y y 。

2014高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）D题储药柜的设计储药柜的结构类似于书橱，通常由若干个横向隔板和竖向隔板将储药柜分割成若干个储药槽(如图1所示)。

为保证药品分拣的准确率，防止发药错误，一个储药槽内只能摆放同一种药品。

药品在储药槽中的排列方式如图2所示。

药品从后端放入，从前端取出。

一个实际储药柜中药品的摆放情况如图3所示。

为保证药品在储药槽内顺利出入，要求药盒与两侧竖向隔板之间、与上下两层横向隔板之间应留2mm的间隙，同时还要求药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转。

在忽略横向和竖向隔板厚度的情况下，建立数学模型，给出下面几个问题的解决方案。

1.药房内的盒装药品种类繁多，药盒尺寸规格差异较大，附件1中给出了一些药盒的规格。

请利用附件1的数据，给出竖向隔板间距类型最少的储药柜设计方案，包括类型的数量和每种类型所对应的药盒规格。

2. 药盒与两侧竖向隔板之间的间隙超出2mm的部分可视为宽度冗余。

增加竖向隔板的间距类型数量可以有效地减少宽度冗余，但会增加储药柜的加工成本，同时降低了储药槽的适应能力。

设计时希望总宽度冗余尽可能小，同时也希望间距的类型数量尽可能少。

仍利用附件1的数据，给出合理的竖向隔板间距类型的数量以及每种类型对应的药品编号。

3.考虑补药的便利性，储药柜的宽度不超过2.5m、高度不超过2m，传送装置占用的高度为0.5m，即储药柜的最大允许有效高度为1.5m。

药盒与两层横向隔板之间的间隙超出2mm的部分可视为高度冗余，平面冗余＝高度冗余×宽度冗余。

在问题2计算结果的基础上，确定储药柜横向隔板间距的类型数量，使得储药柜的总平面冗余量尽可能地小，且横向隔板间距的类型数量也尽可能地少。

4. 附件2给出了每一种药品编号对应的最大日需求量。

在储药槽的长度为1.5m、每天仅集中补药一次的情况下，请计算每一种药品需要的储药槽个数。

A 题：图书馆购书计划的制定现代化图书馆馆藏图书，主要目的不是为了收藏而是为了使用。

除了国家图书馆等特大型的图书馆以外，一般图书馆都有特定的服务群体，办馆宗旨就是要尽量好地为这些特定群体服务，提高馆藏资源的利用率、读者文献信息需求的满足率以及对图书馆服务功能的满意率。

图书馆每年用于购书的经费是有限的，如何合理分配使用，以便使有限的购书经费最大限度地发挥其特定的经济效益是图书馆工作的重要环节之一。

以学校图书馆为例，要实现办馆效益，必须做到入藏文献合乎本校教师、学生（有时也兼顾社会）的需求，使图书馆藏书结构（学科结构、文种结构、文献类型结构等）满足本校教学科研的要求，以求藏书体系与本校专业设置相适应。

所购图书要能够真实地反映读者的实际需要，使读者结构和藏书结构尽量吻合，以便减少读者借不到图书的现象，即降低读者被借的比率、增加满足率。

文献只有在流通中才能传播信息，产生效益。

文献资料得不到利用，购置文献资料所耗费的资金就体现不出其价值。

因此，图书馆在增加藏书规模的同时，要千方百计地把文献提供给读者，以增加图书的出借次数、出借时间以及在借图书的数量等，力求使有限的价值投入获得最大的办馆效益。

设某普通高校现有十个系：计算机科学与技术系，在校学生960 人，信息科学与工程系，在校学生900 人，信息与计算科学系，在校学生280 人，生物与制药工程系，在校学生1500 人，机电工程系，在校学生1440 人，建筑工程系，在校生960 人，外语系，在校学生720 人，法律系，在校学生460 人，新闻系，在校学生642 人，经济与管理系，在校学生2400 人。

此外，该校目前还有“药物分子设计及生物化工”和“土木建筑工程”2 个重点学科；“外国语言学及应用语言学”重点扶植学科以及“计算机科学与技术”、“市场营销”2 个重点专业。

该校图书馆每学年都要投入大量资金购置图书，图书覆盖全院各学科专业、具有较完整的中外文文献资源。

【优化探究】（教师用书）2014高考数学总复习 2-10函数的模型及其应用配套试题理新人教B版[命题报告·教师用书独具]考查知识点及角度题号及难度基础中档稍难一次、二次函数模型1、24、7、10分段函数模型35、11指数函数模型68、9121．(2013年某某模拟)某人在三个时间段内，分别乘摩托车、汽车和火车走了整个行程的三分之一，如果该人乘摩托车、汽车和火车的速度分别为v1，v2，v3，则该人整个行程的平均速度是( )A.v1＋v2＋v33B.1v1＋1v2＋1v33C.3v1v2v3D.31v1＋1v2＋1v3解析：设整个行程为3S，乘摩托车、汽车和火车的时间分别为t1，t2，t3，则t1＝Sv1，t2＝Sv2，t3＝Sv3，整个行程的平均速度为3St1＋t2＋t3＝3SSv1＋Sv2＋Sv3＝31v1＋1v2＋1v3，选D.答案：D2．(2013年某某调研)某公司租地建仓库，已知仓库每月占用费y1与仓库到车站的距离成反比，而每月车存货物的运费y2与仓库到车站的距离成正比．据测算，如果在距离车站10 km处建仓库，这两项费用y1，y2分别是2万元，8万元，那么要使这两项费用之和最小，则仓库应建在离车站( )A．5 km处 B．4 km处C．3 km处 D．2 km处解析：设仓库建在离车站x km 处，则y 1＝k 1x，y 2＝k 2x ，根据已知数据可得k 1＝20，k 2＝0.8，两项费用之和y ＝20x ＋0.8x ≥220x×0.8x ＝8，当且仅当x ＝5时，等号成立，故仓库应建在离车站5 km 处．答案：A3．(2013年某某模拟)如图，有一直角墙角，两边的长度足够长，在P 处有一棵树与两墙的距离分别是a m(0<a <12)、4 m ，不考虑树的粗细．现在用16 m 长的篱笆，借助墙角围成一个矩形的花圃ABCD .设此矩形花圃的面积为S m 2，S 的最大值为f (a )，若将这棵树围在花圃内，则函数u ＝f (a )的图象大致是( )解析：设CD ＝x m ，则AD ＝(16－x )m ，由题意可知⎩⎪⎨⎪⎧16－x >a ，x >4，解得4<x <16－a ，矩形花圃的面积S ＝x (16－x )，其最大值f (a )＝⎩⎪⎨⎪⎧64， 0<a <8，－a 2＋16a ，8≤a <12，故其图象为C.答案：C4．某工厂的大门是一抛物线型水泥建筑物，大门的地面宽度为8 m ，两侧距离地面3 m 高处各有一个壁灯，两壁灯之间的水平距离为6 m ，如图所示．则厂门的高约为(水泥建筑物厚度忽略不计，精确到0.1 m)( )A ．6.9 mB ．7.0 mC ．7.1 mD ．6.8 m解析：建立如图所示的坐标系，于是由题设条件知抛物线的方程为y ＝ax 2(a <0)，设点A 的坐标为(4，－h )，则C (3,3－h )，将这两点的坐标代入y ＝ax 2，可得⎩⎪⎨⎪⎧－h ＝a ·42，3－h ＝a ·32，解得⎩⎪⎨⎪⎧a ＝－37，h ＝487≈6.9，所以厂门的高约为6.9 m. 答案：A5．某学校制定奖励条例，对在教学中取得优异成绩的教职工实行奖励，其中有一个奖励项目是针对学生高考成绩的高低对任课教师进行奖励的．奖励公式为f (n )＝k (n )(n －10)，n >10(其中n 是任课教师所在班级学生参加高考该任课教师所任学科的平均成绩与该科省平均分之差，f (n )的单位为元)，而k (n )＝⎩⎪⎨⎪⎧0，n ≤10，100，10<n ≤15，200，15<n ≤20，300，20<n ≤25，400，n >25.现有甲、乙两位数学任课教师，甲所教的学生高考数学平均分超出省平均分18分，而乙所教的学生高考数学平均分超出省平均分21分．则乙所得奖励比甲所得奖励多( )A ．600元B ．900元C ．1 600元D ．1 700元 解析：∵k (18)＝200(元)，∴f (18)＝200×(18－10)＝1 600(元)． 又∵k (21)＝300(元)，∴f (21)＝300×(21－10)＝3 300(元)，∴f (21)－f (18)＝3 300－1 600＝1 700(元)．故选D. 答案：D 二、填空题6．由于电子技术的飞速发展，计算机的成本不断降低，若每隔5年计算机的价格降低13，则现在价格为8 100元的计算机经过15年的价格应降为________．解析：设经过3个5年，产品价格为y 元，则y ＝8 100×⎝ ⎛⎭⎪⎫1－133＝8 100×827＝2 400元．答案：2 400元7．一个工厂生产某种产品每年需要固定投资100万元，此外每生产1件该产品还需要增加投资1万元，年产量为x (x ∈N *)件．当x ≤20时，年销售总收入为(33x －x 2)万元；当x >20时，年销售总收入为260万元．记该工厂生产并销售这种产品所得的年利润为y 万元，则y (万元)与x (件)的函数关系式为______________，该工厂的年产量为________件时，所得年利润最大．(年利润＝年销售总收入－年总投资)解析：当0<x ≤20时y ＝(33x －x 2)－x －100＝－x 2＋32x －100. 当x >20时y ＝260－100－x ＝160－x .所以y ＝⎩⎪⎨⎪⎧－x 2＋32x －100，0<x ≤20，160－x ，x >20.(x ∈N *)．当0<x ≤20时y ＝－x 2＋32x －100＝－(x －16)2＋156，即x ＝16时y max ＝156，而当x >20时，160－x <140，故x ＝16时年利润最大．答案：y ＝⎩⎪⎨⎪⎧－x 2＋32x －100，0<x ≤20，160－x ， x >0，x ∈N * 168．(2013年某某模拟)将甲桶中的a 升水缓慢注入空桶乙中，t 分钟后甲桶中剩余的水量符合指数衰减曲线y ＝a ent ．假设过5分钟后甲桶和乙桶的水量相等，若再过m 分钟甲桶中的水只有a8升，则m ＝________. 解析：根据题意12＝e 5n ，令18a ＝a e nt ，即18＝e nt ，因为12＝e 5n，故18＝e 15n ，解得t ＝15，故m ＝15－5＝10.答案：109．(2013年某某模拟)鲁能泰山足球俱乐部准备为救助失学儿童在某某省体育中心体育场举行一场足球义赛，预计卖出门票2.4万X ，票价有3元、5元和8元三种，且票价3元和5元的X 数的积为0.6(万X)2.设x 是门票的总收入，经预算，扣除其他各项开支后，此次足球义赛的纯收入函数为y ＝lg 2x，则这三种门票分别为________万X 时为失学儿童募捐纯收入最大．解析：函数模型y ＝lg 2x已给定，因而只需要将条件信息提取出来，按实际情况代入，应用于函数即可解决问题．设3元、5元、8元门票的X 数分别为a 、b 、c ，则⎩⎪⎨⎪⎧a ＋b ＋c ＝2.4， ①ab ＝0.6， ②x ＝3a ＋5b ＋8c ， ③把①代入③得x ＝19.2－(5a ＋3b )≤19.2－215ab ＝13.2(万元)，当且仅当⎩⎪⎨⎪⎧5a ＝3b ，ab ＝0.6，时等号成立，解得a ＝0.6，b ＝1，c ＝0.8.由于y ＝lg 2x为增函数，即此时y 也恰有最大值．故三种门票分别为0.6、1、0.8万X 时为失学儿童募捐纯收入最大． 答案：0.6,1,0.8 三、解答题10．(2013年某某模拟)某租赁公司拥有汽车100辆，当每辆车的月租金为3 000元时，可全部租出，当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需要维护费150元，未租出的车辆每月需要维护费50元．(1)当每辆车的月租金定为3 600元时，能租出多少辆车？(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？ 解析：(1)租金增加了600元，所以未租出的车有12辆，一共租出了88辆． (2)设每辆车的月租金为x 元(x ≥3 000)，租赁公司的月收益为y 元，则y ＝x ⎝⎛⎭⎪⎫100－x －3 00050－x －3 00050×50－⎝⎛⎭⎪⎫100－x －3 00050×150＝－x 250＋162x －21 000＝－150(x －4 050)2＋307 050，当x ＝4 050时，y max ＝307 050.所以每辆车的月租金定为4 050元时，租赁公司的月收益最大为307 050元． 11．(2013年某某一中月考)某分公司经销某品牌产品，每件产品成本3元，且每件产品需向总公司交a 元(3≤a ≤5)的管理费，预计当每件产品的售价为x 元(9≤x ≤11)时，一年的销售量为(12－x )2万件．(1)求分公司一年的利润L (万元)与每件产品的售价x (元)的函数关系式；(2)当每件产品的售价为多少元时，分公司一年的利润L 最大？并求出L 的最大值Q (a )． 解析：(1)根据题意可知，L (x )＝(x －3－a )(12－x )2，x ∈[9，11]．(2)由(1)知，L ′(x )＝(12－x )(18＋2a －3x )，令L ′(x )＝0，解得x ＝6＋2a 3或x ＝12(舍去)，∵3≤a ≤5，∴8≤6＋2a 3≤283.①当8≤6＋2a 3<9，即3≤a <92时，L max ＝L (9)＝9(6－a )，②当9≤6＋2a 3≤283，即92≤a ≤5时，L max ＝L ⎝ ⎛⎭⎪⎫6＋2a 3＝4(3－a 3)3.∴Q (a )＝⎩⎪⎨⎪⎧96－a ，3≤a <92，4⎝ ⎛⎭⎪⎫3－a 33，92≤a ≤5.∴若3≤a <92，则每件产品的售价为9元时，L 最大，最大值为9(6－a )万元；若92≤a ≤5，则每件产品的售价为⎝ ⎛⎭⎪⎫6＋2a 3元时，L 最大，最大值为4⎝ ⎛⎭⎪⎫3－a 33万元．12．(能力提升)某医药研究所开发的一种新药，如果成年人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y (微克)与时间t (小时)之间近似满足如图所示的曲线．(1)写出第一次服药后y 与t 之间的函数关系式y ＝f (t )；(2)据进一步测定：每毫升血液中含药量不少于0.25微克时，治疗有效．求服药一次后治疗有效的时间是多长？解析：(1)设y ＝⎩⎪⎨⎪⎧kt ， 0≤t ≤1，⎝ ⎛⎭⎪⎫12t －a， t ≥1，当t ＝1时，由y ＝4得k ＝4，由⎝ ⎛⎭⎪⎫121－a＝4得a ＝3.则y ＝⎩⎪⎨⎪⎧4t ，0≤t ≤1，⎝ ⎛⎭⎪⎫12t －3，t >1.(2)由y ≥0.25得⎩⎪⎨⎪⎧0≤t ≤1，4t ≥0.25或⎩⎪⎨⎪⎧t ≥1，⎝ ⎛⎭⎪⎫12t －3≥0.25，解得116≤t ≤5.因此服药一次后治疗有效的时间是5－116＝7916(小时)．[因材施教·学生备选练习](2012年高考某某卷)某企业接到生产3 000台某产品的A ，B ，C 三种部件的订单，每台产品需要这三种部件的数量分别为2,2,1(单位：件)．已知每个工人每天可生产A 部件6件，或B 部件3件，或C 部件2件．该企业计划安排200名工人分成三组分别生产这三种部件，生产B 部件的人数与生产A 部件的人数成正比，比例系数为k (k 为正整数)．(1)设生产A 部件的人数为x ，分别写出完成A ，B ，C 三种部件生产需要的时间； (2)假设这三种部件的生产同时开工，试确定正整数k 的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案．解析：(1)设完成A ，B ，C 三种部件的生产任务需要的时间(单位：天)分别为T 1(x )，T 2(x )，T 3(x )，由题设有T 1(x )＝2×3 0006x ＝1 000x ，T 2(x )＝2 000kx ，T 3(x )＝ 1 500200－1＋kx，其中x ，kx,200－(1＋k )x 均为1到200之间的正整数．(2)完成订单任务的时间为f (x )＝max{T 1(x )，T 2(x )，T 3(x )}，其定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0<x <2001＋k ，x ∈N*，易知，T 1(x )，T 2(x )为减函数，T 3(x )为增函数，注意到T 2(x )＝2k T 1(x )，于是①当k ＝2时，T 1(x )＝T 2(x )，此时f (x )＝max{T 1(x )，T 3(x )}＝max ⎩⎨⎧⎭⎬⎫1 000x，1 500200－3x . 由函数T 1(x )，T 3(x )的单调性知，当1 000x ＝ 1 500200－3x 时f (x )取得最小值，解得x ＝4009.由于44<4009<45，而f (44)＝T 1(44)＝25011，f (45)＝T 3(45)＝30013，f (44)<f (45)．故当x ＝44时完成订单任务的时间最短，且最短时间为f (44)＝25011. ②当k >2时，T 1(x )>T 2(x )，由于k 为正整数， 故k ≥3，此时 1 500200－1＋kx ≥1 500200－1＋3x ＝37550－x. 记T (x )＝37550－x ，φ(x )＝max{T 1(x )，T (x )}，易知T (x )是增函数，则f (x )＝max{T 1(x )，T 3(x )}≥max{T 1(x )，T (x )}＝φ(x )＝max⎩⎨⎧⎭⎬⎫1 000x，37550－x . 由函数T 1(x )，T (x )的单调性知， 当1 000x ＝37550－x时φ(x )取最小值，解得x ＝40011.由于36<40011<37，而φ(36)＝T 1(36)＝2509>25011，φ(37)＝T (37)＝37513>25011.此时完成订单任务的最短时间大于25011.③当k <2时，T 1(x )<T 2(x )， 由于k 为正整数，故k ＝1，此时f (x )＝max{T 2(x )，T 3(x )}＝max ⎩⎨⎧⎭⎬⎫2 000x，750100－x . 由函数T 2(x )，T 3(x )的单调性知，当2 000x ＝750100－x 时f (x )取最小值，解得x ＝80011，类似(1)的讨论，此时完成订单任务的最短时间为2509，大于25011.综上所述，当k ＝2时，完成订单任务的时间最短，此时，生产A ，B ，C 三种部件的人数分别为44,88,68.。