2014-2015(1)期末考试试卷(A)(线性代数)

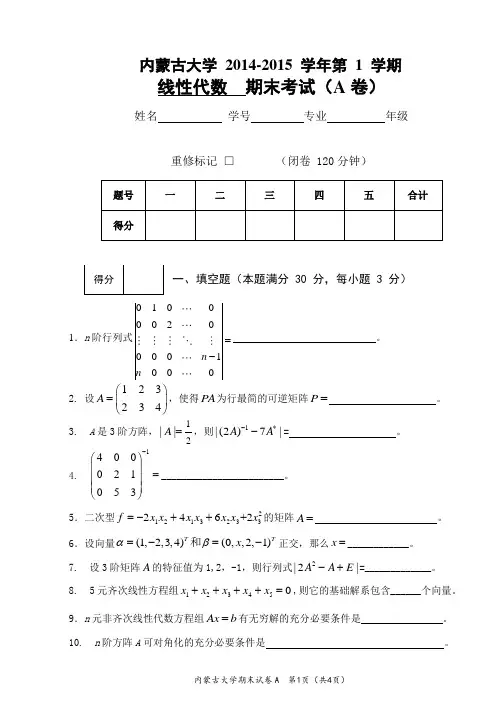
内蒙古大学 2014-2015 学年第 1 学期线性代数 期末考试（A 卷）姓名 学号 专业 年级重修标记 □ （闭卷 120分钟）一、填空题（本题满分 30 分，每小题 3 分）1．n 阶行列式0100002000100n n =- 。

2. 设123234A ⎛⎫= ⎪⎝⎭，使得PA 为行最简的可逆矩阵P = 。

3. A 是3阶方阵，12||A =，则1|(2)7|A A -*-= 。

4. 1400021053-⎛⎫ ⎪= ⎪⎪⎝⎭________________________。

5．二次型21213233246+2f x x x x x x x =-++的矩阵A = 。

6．设向量(1,2,3,4)(0,,2,1)T Tx αβ=-=-和正交，那么x =____________。

7. 设3阶矩阵A 的特征值为1,2，-1，则行列式2|2|A A E -+=_____________。

8. 5元齐次线性方程组123450x x x x x ++++=,则它的基础解系包含______个向量。

9．n 元非齐次线性代数方程组Ax b =有无穷解的充分必要条件是 。

10. n 阶方阵A 可对角化的充分必要条件是 。

二、计算下列各题（本题满分20分，每小题10 分）(1) 设3112513421111233D---=---，求D的代数余子式的和11213141A A A A+++(2) 求非齐次线性方程组12341234123421363251054x x x xx x x xx x x x++-=⎧⎪+--=⎨⎪++-=⎩的通解，并求所对应的齐次线性方程组的基础解系。

三、计算题（本题满分20分，每小题 10 分）(1) 求解矩阵方程AX B =,其中21311122,2013225A B --⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭。

(2) 求向量组1234(2,1,4,3),(1,1,6,6),(1,1,2,7),(2,4,4,9)T T T Tαααα==--=-=的秩和一个最大无关组，并把不属于最大无关组的列向量用最大无关组线性表示。

2014-2015-1线性代数参考答案及评分标准一（每小题3分，共15分）1、32 2 、3 3 、1 4、2 5、0二（每小题3分，共15分）1 B2 B3 C4 A5 D三（5分）0321103221036666=D ……………………………………………………（2分） 40000400121011116---=…………………………………………… （2分）96-=……………………………………………………………（1分）四（10分）1-=A ，A 可逆…………………………………………………（1分） 121)(---=-=A A E A A B ……………………………………………………（4分）()⎪⎪⎪⎭⎫ ⎝⎛---→100100110010211001,E A⎪⎪⎪⎭⎫ ⎝⎛---=-1001102111A ……………………………………………………………（4分） ⎪⎪⎪⎭⎫ ⎝⎛=000000120B …………………………………………………………………（1分） 五（15分）()211111211112-=-----λλλλλλλ………………………………………………（5分） 0≠λ且2≠λ时，有唯一解…………………………………………………（2分）2=λ时()⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛-----=100051103111111111133111,b A3),(2)(=<=b A R A R ，方程组无解…………………………………………（3分）0=λ时，()⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛=000000001111111111111111,b A3),(1)(<==b A R A R 方程组有无穷多解，1321+--=x x x 取2312,c x c x ==得方程组通解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=00110101121321c c x x x x ………………………（5分）六（12分）()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=0000010000712100230102301085235703273812,,,,54321a a a a a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-→00000100000121002301……………………………………（4分） 向量组秩为3，……………………………………………………………（2分） 一个最大无关组为：521,,a a a ……………………………………………（2分） 21323a a a +=………………………………………………………………（2分） 2152a a a -=…………………………………………………………………（2分） 七（10分）证明：设存在数1k ，2k ，3k ，使0332211=++βββk k k ………………（2分） 将1β，2β，3β带入并整理得0)32()()2(33212321131=+-+-+-++αααk k k k k k k k …………………（2分）由1α，2α，3α线性无关知⎪⎩⎪⎨⎧=+-=-+-=+03200232132131k k k k k k k k ， 因0312111201=---，故齐次线性方程组有非零解，…………………（4分）从而存在1k ，2k ，3k 不全为零，使0332211=++βββk k k ，从而1β，2β，3β是线性相关的。

方式二：
向量组1,2 ,3 线性相关，知 R(2 ,3,1) R(1,2,3) 3 -----------1 分 向量组2 ,3,4 线性无关，知 R(2 ,3,4 )=3.
由整体无关则部分无关，知2 ,3 也线性无关。---------------------2 分
而 R(2 ,3,1) R(2 ,3) 2 ，综上知
--------------6 分
A卷3
A卷4
1 1
1 2 1, 3 2 为特征值
1 1
当 1 1解方程组 (A E)x 0 ，得正交的的特征向量为 p1 1 , p2 1
0
2
1
当
3
2
解方程组 ( A
2E)x
0
得
p3
1
为对应特征向量
1
故所求正交矩阵 P 为
1
1
1
2
P(
p1
,
p2
,
p3
) 1
p1 p2 p3 2
…
…
31
11
… …
4 31 23 若 1,4 是最大无关组，则3 2 1 2 4 ，2 2 1 2 4
…
4. k=-2.
装
订
线
… … … …
A卷1
四、（本题 15 分）
（1）a=-8,b≠1,无解；--------------6 分
（2）a≠-8,唯一解；--------------8 分
,3
线性表示。-----------------6
分
第二部分还可以用反证法：假设即4 能由1,2 ,3 线性表示，由于1 能由2 ,3 线性表示，
且表示法唯一，故4 能由2 ,3 线性表示，------------5 分

装 订 线 内 不 要 答 题自觉遵 守 考 试 规 则，诚 信 考 试，绝 不作 弊)(A 2)(2121211ββααα-+++k k )(B 2)(2121211ββααα++-+k k )(C 2)(2121211ββββα-+++k k )(D 2)(2121211ββββα++-+k k4．设矩阵21407003A a -⎛⎫ ⎪= ⎪ ⎪⎝⎭与10002000b ⎛⎫⎪Λ= ⎪ ⎪⎝⎭相似，则a ，b 满足 （ C ）)(A 1,3a b =-= )(B 1,3a b ==- )(C 1,3a b == )(D 1,3a b =-=- 5．若二次型2221231231223(,,)22f x x x x x x x x tx x =++++正定，则t 的取值范围是（ C ） （A）0t << （B ）22t -<< （C）t << （D）22t -<<三、(本题10分)设2XA X B =+，其中311010003A ⎛⎫⎪= ⎪ ⎪⎝⎭，101321B -⎛⎫= ⎪-⎝⎭，求X .解 由2XA X B =+得1(2)X B A I -=-110100(2)010*********A I I ⎛⎫ ⎪-=- ⎪ ⎪⎝⎭100110010010001001⎛⎫⎪→- ⎪ ⎪⎝⎭1110101111(2)010*********X B A I -⎛⎫---⎛⎫⎛⎫⎪=-=-= ⎪ ⎪ ⎪--⎝⎭⎝⎭⎪⎝⎭四、(本题10分) 求向量组()11,1,1,1T α=--，()20,1,0,1Tα=-，()33,2,1,4T α=--，()44,5,2,7Tα=--的秩和它的一个极大线性无关组，并用该极大线性无关组表示其余向量. 解103410341034101112501110111010210120022001100111147011300220000⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪-- ⎪ ⎪ ⎪ ⎪→→→⎪ ⎪ ⎪⎪--- ⎪ ⎪ ⎪⎪---------⎝⎭⎝⎭⎝⎭⎝⎭初等行变换初等行变换初等行变换所以1234(,,,r αααα)=3，向量组123,,ααα是一个极大线性无关组，41232αααα=++五、(本题10分)求通过点(2,0,1)P -且又通过直线12213x y z +-==-的平面方程. 解 已知直线过点(1,0,2)M -，方向向量{2,1,3}s =-， 所求平面的法向量{3,15,3}n MP s ⨯=---，取{1,5,1}n = 所求平面方程为(1)5(0)(2)0x y z ++-+-=，即510x y z ++-=六、(本题12分) λ取何值时，线性方程组123123123322x x x x x x x x x λλλλ++=-⎧⎪++=-⎨⎪++=-⎩有唯一解，无解或有无穷多解？当方程组有无穷多解时求其通解.解 2112112112011011301133A λλλλλλλλλλ--⎛⎫⎛⎫ ⎪ ⎪=-→-- ⎪⎪⎪ ⎪----⎝⎭⎝⎭初等行变换112011000(1)(2)3(1)λλλλλλ-⎛⎫⎪→-- ⎪ ⎪--+-⎝⎭初等行变换 (1) 当2λ≠-且1λ≠时, 原方程组有唯一解. (2) 当2λ=-时，原方程组无解.(3) 当1λ=时, 原方程组有无穷多解， 111200000000A -⎛⎫⎪→ ⎪ ⎪⎝⎭通解为12(2,0,0)(1,1,0)(1,0,1)TTTx k k =-+-+-，12,k k 为任意常数.七、(本题12分)求一个正交变换x Qy =，将二次型22212312323(,,)2334f x x x x x x x x =+++化成标准形，并指出123(,,)4f x x x =表示的曲面名称. 解 二次型的矩阵 200032023A ⎛⎫⎪= ⎪ ⎪⎝⎭，232(2)(1)(5)0023I A λλλλλλλ--=--=---=--得特征值为11λ=，232,5λλ== 对11λ=，由1()0I A x λ-=得()10,1,1Tξ=-，单位化得)10,1,1Te =- 对22λ=，由2()0I A x λ-=得()21,0,0Tξ=，单位化得()21,0,0Te =， 对35λ=，由3()0I A x λ-=得()30,1,1Tξ=，单位化得)30,1,1Te =取01000Q ⎛⎫ ⎪=，由x Qy =得222123123(,,)25f x x x y y y =++ 曲面123(,,)4f x x x =表示椭球面.八、（本题6分）设n 阶实对称矩阵A 的特征值为12,,,n λλλ，α是A 的对应于特征值1λ的单位特征向量，矩阵1TB A λαα=-，证明：B 的特征值为20,,,n λλ. 证明 因为A 为n 阶实对称矩阵，且有特征值12,,,n λλλ所以存在正交矩阵12(,,,)n P p p p =，使得12(,,,)T n P AP diag λλλ=因为α是A 对应于特征值1λ的单位特征向量，取1p α=，且(,)0,2,3,,i p i n α==1110TB A ααλαααλαλα=-=-=，所以0是B 的特征值 10,2,3,,T i i i i i i i Bp Ap p p p i n λααλλ=-=-==，所以,2,3,,i i n λ=也是B 的特征值综上，B 的特征值为20,,,n λλ.。

2014-2015 第一学期期终试题 （考试时间： 2015.1.13）
一、单项选择（请将正确选项填写在后面的括号中，每小题 3 分，共 15 分）
1．
设矩阵 A
1 0 3 0
0 2 0 4
2 0 4 0
1003 ，则行列式 2 A 的值为
（A） 320
（B） 320
（C） 40
（D） 40
【
】
（A） 必可由 , , 线性表示 （B） 必可由 , , 线性表示
（C） 必可由 , , 线性表示 （D） 必不可由 , , 线性表示
4．
设矩阵 A
1 x
3
1 4
3
1 y
5
有
3
个线性无关的特征向量，
2
是二重特征值，
则 x 和 y 依次为
【
】
（A） 2, 2 （B） 2, 2 （C） 3, 1 （D） 1, 3
四、（12 分） 取何值时，线性方程组
(22x1()5x12) xx22
2x3 4x3
1 2
2x1 4x2 (5 )x3 1
有唯一解、无解、无穷多解？并在有无穷多解时，求其结构解.
五、（12 分）设有直线 L
:
3xxyy3z
与点
1
M
(1,0,1)
.
（1）求 L 的对称式方程； （2）求点 M 到直线 L 的距离.
【
】
2．
0 0 1
0 1 0
1 0 0
1896
a d g
b e h
c f i
0 0 1
0 1 0
1 0 0
2015
=
【
】
（A）

线性代数a期末考试题及答案一、选择题（每题5分，共20分）1. 以下哪个矩阵是可逆的？A. 零矩阵B. 单位矩阵C. 对角矩阵D. 奇异矩阵答案：B2. 矩阵的秩是指：A. 矩阵的行数B. 矩阵的列数C. 矩阵中非零行的最大数目D. 矩阵中非零列的最大数目答案：C3. 如果一个矩阵A的行列式为0，则：A. A是可逆的B. A是不可逆的C. A是正定的D. A是负定的答案：B4. 以下哪个选项不是线性方程组解的性质？A. 唯一性B. 存在性C. 零解D. 非零解答案：D二、填空题（每题5分，共20分）1. 矩阵的________是矩阵中所有元素的和。

答案：迹2. 如果一个向量组线性无关，则该向量组的________等于向量的个数。

答案：秩3. 对于一个n阶方阵A，如果存在一个非零向量x使得Ax=0，则称x为矩阵A的________。

答案：零空间4. 一个矩阵的________是指矩阵中所有行向量或列向量的最大线性无关组的个数。

答案：秩三、解答题（每题10分，共60分）1. 已知矩阵A=\[\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\]，求A的行列式。

答案：\[ \text{det}(A) = 1*4 - 2*3 = 4 - 6 = -2 \]2. 设A=\[\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\]，B=\[\begin{pmatrix} 2 & 0 \\ 1 & 3 \end{pmatrix}\]，求AB。

答案：\[ AB = \begin{pmatrix} 1*2 + 2*1 & 1*0 + 2*3 \\ 3*2 +4*1 & 3*0 + 4*3 \end{pmatrix} = \begin{pmatrix} 4 & 6 \\ 10 & 12 \end{pmatrix} \]3. 已知矩阵A=\[\begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix}\]，求A的特征值。

e2

1
1
0
1 2

1 1

,
e3

2
1 6

1 1

2 0 2
(3)取 P (e1 e2 e3 )
1

6
2 2
3 3
1 ，正交变换 x Py ， 1
第 6页（A 卷，共 7页）
第 1页（A 卷，共 7页）
6. 已知 n 阶方阵 A 满足 A2 A 2E O ,则【 】.
A. A E 与 A 2E 均可逆
B. A 与 E A 均可逆
C. A 可逆， E A 不可逆
D. A 不可逆， E A 可逆
7. 下列说法错误的是【 】. A. 实对称矩阵的特征值均为实数 B. 实反对称矩阵的特征值为零或虚数 C. 实正交矩阵的特征值的模为 1 D. 若 A 与 B 相似，则 A 与 B 合同
0 1
1 0
0 1



0 0
1 0
0 1
0 1
1 0
01
1 0 2

A

(B

2E )1


0
1
0

.
1 0 1
第 4页（A 卷，共 7页）
6. AT A* AT A A* A AT A | A | E
| A |2 ( | A |)3 | A | 0 or | A | 1 .
10．曲线 ez y2 关于 Oz 轴旋转而成的旋转曲面方程为【 】.
二、计算题与证明题（共 8 小题，每小题 5 分，共 40 分）

线性代数期末考试试题及答案一、选择题（每题5分，共30分）1. 若矩阵A的秩为r(A)，则下列结论正确的是（）A. r(A) ≤ n，其中n是矩阵A的列数B. r(A) ≤ m，其中m是矩阵A的行数C. r(A) ≤ min(m, n)D. r(A) = max(m, n)答案：C2. 下列矩阵中，哪一个不是对称矩阵？（）A. \(\begin{pmatrix} 1 & 2 \\ 2 & 3 \end{pmatrix}\)B. \(\begin{pmatrix} 1 & -1 \\ -1 & 2 \end{pmatrix}\)C. \(\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 4 \\ 3 & 4 &5 \end{pmatrix}\)D. \(\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 &9 \end{pmatrix}\)答案：D3. 若向量组α1, α2, α3线性无关，则向量组（）A. α1 + α2, α2 +α3, α3 + α1 线性无关B. α1 - α2, α2 - α3, α3 - α1 线性无关C. α1 + 2α2, 2α2 + 3α3, 3α3 + α1 线性无关D. α1 + α2 + α3, 2α2 + 3α3, 3α3 + α1 线性无关答案：B4. 设矩阵A是n阶可逆矩阵，则下列结论正确的是（）A. A的伴随矩阵A也是可逆矩阵B. A的逆矩阵A-1也是可逆矩阵C. A的转置矩阵AT也是可逆矩阵D. A的n次幂An也是可逆矩阵答案：D5. 若行列式D = |A|的值为0，则下列结论正确的是（）A. 方程组Ax = b有唯一解B. 方程组Ax = b无解C. 方程组Ax = 0有非零解D. 方程组Ax = b有无穷多解答案：C6. 若矩阵A是正交矩阵，则下列结论正确的是（）A. A的行列式值为1B. A的行列式值为-1C. A的转置矩阵AT等于A的逆矩阵A-1D. A的平方等于单位矩阵E答案：CD二、填空题（每题5分，共30分）7. 若矩阵A的行列式值为3，则矩阵A的伴随矩阵A的行列式值为________。

线性代数期末考试试题及答案第一节：选择题1. 下列哪个向量不是矩阵A的特征向量？A. [2, 1, 0]B. [0, 1, 0]C. [1, 1, 1]D. [0, 0, 0]答案：D2. 线性变换T：R^n -> R^m 可逆的充分必要条件是？A. T是一个单射B. T是一个满射C. T是一个双射D. T是一个线性变换答案：C3. 设线性空间V的维数为n，下列哪个陈述是正确的？A. V中的任意n个线性无关的向量都可以作为V的基B. V中的任意n - 1个非零向量都可以扩充为V的基C. V中的任意n个非零向量都可以扩充为V的基D. V中的任意n - 1个非零向量都可以作为V的基答案：A4. 设A和B是n阶方阵，并且AB = 0，则下列哪个陈述是正确的？A. A = 0 或 B = 0B. A = 0 且 B = 0C. A ≠ 0 且 B = 0D. A = 0 且B ≠ 0答案：C第二节：计算题1. 计算矩阵乘法A = [1, 2; 3, 4]B = [5, 6; 7, 8]答案：AB = [19, 22; 43, 50]2. 计算矩阵的逆A = [1, 2; 3, 4]答案：A^(-1) = [-2, 1/2; 3/2, -1/2]3. 计算向量的内积u = [1, 2, 3]v = [4, 5, 6]答案：u ∙ v = 32第三节：证明题证明：对于任意向量x和y，成立下列关系式：(x + y) ∙ (x - y) = x ∙ x - y ∙ y证明：设x = [x1, x2, ..., xn]，y = [y1, y2, ..., yn]。

左边：(x + y) ∙ (x - y) = [x1 + y1, x2 + y2, ..., xn + yn] ∙ [x1 - y1, x2 - y2, ..., xn - yn]= (x1 + y1)(x1 - y1) + (x2 + y2)(x2 - y2) + ... + (xn + yn)(xn - yn)= x1^2 - y1^2 + x2^2 - y2^2 + ... + xn^2 - yn^2= (x1^2 + x2^2 + ... + xn^2) - (y1^2 + y2^2 + ... + yn^2)= x ∙ x - y ∙ y右边，由向量的内积定义可得：x ∙ x - y ∙ y = x1^2 + x2^2 + ... + xn^2 - (y1^2 + y2^2 + ... + yn^2)综上，左边等于右边，证毕。

5．5．已知3阶方阵A 的特征值分别为1，－2，3则|A|＝（ ） A ． 2 B ．6 C ．-6D ． 06.若方程组 02020kx z x ky z kx y z +=⎧⎪++=⎨⎪-+=⎩有非零解，则k =( D )A. -2B. -1C. 0D. 2二、填空题（本大题共6小题，每小题3分，共18分）1．设A ＝［1，2，4］，B ＝［－2，－1，1］，则AB T ＝ 0 .2．设矩阵A ＝⎪⎭⎫ ⎝⎛--4321，则矩阵A 的伴随矩阵A *＝ ⎪⎪⎭⎫⎝⎛1324 3．设向量α＝（－1，2，－2，4），则其单位向量的是______________. 4. 设方阵A 满足A 3-2A+E=0，则21(A 2E)-- = -A . 5．已知向量)2,1,1(-=α与向量),2,2(x -=β正交，则=x -2.6.设线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡211111111321x x x a a a 有无穷多个解，则a = 1 . 三、计算题（1,2,3,4每小题8分；5，6每题12分。

共56分）1.求行列式11213513241211111----。

解：11213513241211111----=1122051504111111----- (2)=145008130032101111--- ……4=342002030032101111---- (6)=14203410032101111---=-142 (8)2.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=432122102101a a A 且R(A)<3，求R(A)及数a 。

解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=432122102101a a A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-→a a a 4622202102101 ……2 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→a a a 6622002102101 (4)由于R(A)<3，所以066022=-=-a a ,, (6)故21==)(,A R a (8)3.设向量组)7,3,1,2(1=α )0,1,0.1(2-=α，)7,1,1,4(3=α)3,0.1,3(4---=α)3,1,3,4(5--=α求其一个最大无关组，并将其他向量用此最大无关组线性表示。

C. a= b或a + 2b ≠ 0 ；
D. a ≠ b且a + 2b ≠ 0 .
三、计算题：（每题 10 分，5 题共 63 分）
1234 4567 11.(10 分)设 D = 1 2 1 2 ，设 Aij 为元素 aij 的代数余子式。 3362
(1)(4 分) 计算 A12 + 4 A22 + A32 + 3A42 ；
x1
−
x2
−
k 2 x3
=−k
一解和有无穷多解，并在有无穷多解时，求它的通解。
16.(11 分)设二次型 f = ax12 + x22 + 2x32 − 2x1x3 + 2x2 x3 对应的矩阵秩为 2，试确定参数 a 的
值，并用正交变换将此二次型化为标准形(需写出正交变换及标准形)。
四、证明题：（每题 6 分，2 题共 12 分）
121
1 1 −1
0
12. 解：设
J
=
1
0
，则
A=
J +I
2 0
0
= 因为 J 2 = 0 0 , J 3 0 2 0 0
所以
An =(J + I )n =I n + Cn1I n−1J + Cn2I n−2 J 2
1
=I
+
nJ
+
n(n −1) 2
J2
= n n(n −1)
1 2n
1
1
1
1 −1
14.(12 分)= 求向量组 α1 (1= , 2,3, 4)T ,α2 (1= ,3, 4, 2)T ,α3 (1= , 0,1, a)T ,α3 (3, 7,10,10)T

线性代数期末考试试题及答案线性代数期末考试试题及答案线性代数是一门重要的数学课程，广泛应用于各个领域，如物理学、工程学、计算机科学等。

期末考试是对学生对于线性代数知识的综合考察，下面将给出一些线性代数期末考试试题及答案，供大家参考。

一、选择题（每题2分，共20分）1. 设A是一个3×3矩阵，若A的行列式值为0，则A的秩为：A. 0B. 1C. 2D. 3答案：C2. 设A是一个3×3矩阵，若A的特征值为1，2，3，则A的特征向量个数为：A. 0B. 1C. 2D. 3答案：D3. 设A是一个3×3矩阵，若A的秩为2，则A的零空间的维数为：A. 0B. 1C. 2D. 3答案：B4. 设A是一个3×3矩阵，若A的行向量组线性无关，则A的列向量组是否线性无关？A. 是B. 否答案：A5. 设A是一个3×3矩阵，若A的行向量组线性相关，则A的列向量组是否线性相关？A. 是B. 否答案：A6. 设A是一个3×3矩阵，若A的秩为2，则A的行空间的维数为：A. 0B. 1C. 2D. 3答案：C7. 设A是一个2×2矩阵，若A的特征值为1，2，则A的特征向量个数为：A. 0B. 1C. 2答案：C8. 设A是一个2×2矩阵，若A的特征值为1，1，则A的特征向量个数为：A. 0B. 1C. 2答案：B9. 设A是一个2×2矩阵，若A的秩为1，则A的零空间的维数为：A. 0B. 1C. 2答案：B10. 设A是一个2×2矩阵，若A的秩为2，则A的行空间的维数为：A. 0B. 1C. 2答案：C二、填空题（每题3分，共30分）1. 设A是一个3×3矩阵，若A的行向量组线性无关，则A的秩为____。

答案：32. 设A是一个3×3矩阵，若A的列向量组线性无关，则A的秩为____。

答案：33. 设A是一个3×3矩阵，若A的行向量组线性相关，则A的秩为____。

D ．12.n ααα⋅⋅⋅中任一部分线性无关。

5．下列条件中不是n 阶方阵A 可逆的充要条件的是（ ）。

A ．0A ≠；B ．()R A n =；C ．A 是正定矩阵；D ．A 等价于n 阶单位矩阵。

二、填空题（每小题3分，共15分）6．123212233031332x x x x x x x x x ------=+-的根的个数为 个。

7．20102009100110100001012010010101001-⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪-= ⎪ ⎪⎪ ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭。

8．010100002A x ⎛⎫ ⎪=- ⎪ ⎪⎝⎭，当 时，矩阵A 为正交矩阵。

9．设A 为5阶方阵，且()3R A =，则()*R A = 。

10．设三阶方阵A 的特征值为1、2、2，则14A E --= 。

三、计算题（每小题10分，共50分）11．计算行列式ab ac ae bd cd de bfcf ef ---。

得分 得分12．已知111022003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，求()1*A -、()*1A -、1A -。

13．问,a b 各取何值时，线性方程组1231231232021324x x x x x ax x x x b ++=⎧⎪++=⎨⎪++=⎩有唯一解？无解？有无穷多解？有无穷多解时求其通解。

得分 得分14．设向量组()131T a α=，()223T b α=，()3121T α=，()4231T α=的秩为2，求,a b 。

15. 设n 维向量(),0,0,T a a α=⋅⋅⋅，0a <，且T A E αα=-⋅,11T A E a αα-=+⋅,求a 。

得分得分学院：专业：班级：四、解答题（10分）16．设3阶对称矩阵A的特征值为6、3、3，与6对应的特征向量为()1111TP=,,，求矩阵A。

得分五、证明题（每小题5分，共10分） 17．设A 、B 为两个n 阶方阵，且A 的n 个特征值互异，若A 的特征向量恒为B 的特征向量，证明AB BA =。

广州大学2014-2015 学年第一学期考试卷课程：《线性代数H 》考试形式：闭卷考试一、填空题(每空3分，本大题满分18分)1•设A , B 都为3阶方阵,且| A 」|=5, |3B|=54,则| AB ■'戶——2.若对三阶阵A 先交换第一，三行,然后第二行乘2后再加到第三行，则相当于在A的 ___ 边乘三阶阵3•若阵A 为3阶方阵,且秩R(A) =1，则R(AA *)二—一4•设向量组「1 =(1,1,a), :- 2 (1,a,1), ：1 (a,1,1)所生成的向量空间为 2维的,则 a =_./an a 12 a 13an a 12a 135.已知A =3 3 3 ,其特征值为1,-2,3, B = a 21a 22a 23 ,则B 的行列式&31a32a 33 >l a31a 32a33 J中元素的代数余子式A 21 A 22 A 23二—.二、选择题(每小题3分，本大题满分15分) 1•若AB 为n 阶单位阵，则必有( ).(A ) BA 也n 阶为单位阵；(B ) BA 可能无意义；(C ) R(BA) = n ； (D )以上都不对.「％ ■ x 2 ■ ■ 2x 3 二 02•齐次线性方程组X 1“-X2+x 3=0的系数矩阵记为A 。

若存在三阶阵B H O,X"! +x 2 +&3 =0 使得AB = O ，则().(A) % 二-2，且 |B| = 0 ; (B )箱二—2，且 |B|=0 ;(C ) ■ =1，且 |B|=0 ; (D ) ■ =1，且 |B|=0.3•对含n 个未知数,n 1个方程的线性方程组Ax 二b ,行列式|（A,b ）卜0是它有解 的（ ）（A ）充分条件； （B ）必要条件； （C ）充要条件； （D ）非充分非必要条件列向量组线性相关的为（）.（A ） 1, 2 , 3 ；（B ）1, 2 ,4 ； （C ）5•设｛〉1,〉2,〉3｝分别为同维无关向量组，而｛〉1「2,〉3「1 * 为相关向量组，则有 （） 成立•（A ） ｛〉1,〉2, • ：｝为相关向量组；（B ） ｛〉2「3「1」｝为无关向量组； （C ） R （｛： 1,： 2,： 3, J ） =R （｛： 1,： 2,： 3｝） 1 ；（D ） R （｛： 1, ： 2,： 3, J ） =R （｛： 1,： 2,： 3｝） -1三、（本题满分12分）'0 3 3'设A= 11 0，且A 满足矩阵方程AX=A + 2X ,求X .-1 2 3 丿广1<c 3 yJT 1 ,其中 l C4丿G ,C 2,C 3,C 4为任意常数，则下 1, 3, 4； (D)广&2丿四、（本题满分82 1 -5 1计算行列式 1 -3 0 -60 2 -1 21 4 -7 6五、（本题满分6分）（1设AP =PB ,其中p =d10,求A .六、（本题满分10分）X i -X2 5x3 -X4 = 0求齐次线性方程组 X i X2 -2X3 • 3X4 =0的所有解.3为一x2 8X3 x4 = 0八、（本题满分9分）设A 为2阶方阵，且存在正整数1（1-2）,使得A 1 = 0,证明:1） A 的秩乞 1 . 2） A 2 =0. 九、（本题满分12分）‘12 2、求矩阵A = 2 12的特征值和特征向量<2 2 b一1 -2 -1 0 2设人=（口1,口2,口3,。

安徽师范大学 2014-2015 学年 第一学期化学与材料科学学院 化学(非师范)、应用化学、材料化学、化学工程与工艺专业2014级《线性代数（化材学院）》课程期末考试试卷（(A 卷) 120分钟 闭卷）一、单选题（5小题，每小题4分，共20分）1、设A , B 均为n 阶方阵，且A (B -E )=O ，则⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ( )(A) A =O 或B =E (B)0=A 或0=-E B (C) 0=A 或1=B (D)A =BA2、用A =⎪⎪⎪⎭⎫ ⎝⎛872113112左乘矩阵⎪⎪⎪⎭⎫ ⎝⎛010100001，结果相当于进行对A 实施⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅( )(A) r 1↔r 2 (B) r 2↔r 3 (C) c 1↔c 2 (D) c 2↔c 33、设向量⎪⎪⎪⎭⎫ ⎝⎛=0021α, ⎪⎪⎪⎭⎫⎝⎛-=3002α，下列向量中哪个是α1, α2的线性组合⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ( )(A)⎪⎪⎪⎭⎫ ⎝⎛-403 (B)⎪⎪⎪⎭⎫ ⎝⎛010 (C)⎪⎪⎪⎭⎫ ⎝⎛011 (D)⎪⎪⎪⎭⎫⎝⎛-1104、已知向量组α1, α2, …, αs 的秩为4，则下列论断中正确的是⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ( )(A) 如果α1, α2, …, αs 的一个部分组所含的向量个数不超过4，则这个部分组一定线性无关 (B) α1, α2, α3, α4是α1, α2, …, αs 的一个最大无关组(C) 如果α1, α2, …, αs 的一个部分组是线性无关的，则这个部分所含的向量个数一定不超过4(D) 如果α1, α2, …, αs 的一个部分组是线性相关的，则这个部分所含的向量个数一定大于45、若n 阶方阵A 相似于某个对角阵Λ，则⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ( )(A) R (A )=n(B) A 有不同的特征值(C) A 是实对称矩阵 (D) A 有n 个线性无关的特征向量二、填空题（5小题，每小题4分，共20分）1、设A 是可逆矩阵，且∣A ∣=3，则∣A -1∣=__________；∣AA T ∣=__________.2、矩阵A =⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000500021201011的秩为__________. 3、设线性方程组⎪⎩⎪⎨⎧=-+=+-+=+-+λ222 553 43 243243214321x x x x x x x x x x x ，则该方程组有解的充分必要条件是 λ = __________.4、设向量组α1, α2, α3线性无关，而p α1-α2, s α2-α3, t α3-α1线性相关，则p , s , t 应该满足关系式 __________.5、矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=1111111111111111A 的非零特征值为__________.第 3 页 共 8 页 第 4 页 共 8 页三、计算题（5小题，每小题7分，共35分）1、设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=111111111A ，矩阵B 满足A *B =A -1+2B ，其中A *是A 的伴随矩阵. 求矩阵B .2、已知⎪⎪⎪⎭⎫⎝⎛=204020101A ，解矩阵方程2AX +3E =2A 2+X .3、已知向量组α1=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-21146, α2=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-43201, α3=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--2216941, α4=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-31017. 求向量组的秩.4、已知⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2312α, ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=1221β. 求α, β, [α, β], βα+5、设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=53342111x Α，且A 的特征值为λ1=6，λ2=λ3=2，求x 的值.四、证明题（2小题，每小题8分，共16分）1、设A 为m ⨯n 矩阵，B 为n ⨯m 矩阵，且m >n ，证明：⎪AB ⎪=0.2、证明：n 维列向量α1, α2, …, αn 线性无关的充分必要条件是0212221212111≠nT n T n T n nT T T nT T T ααααααααααααααααααΛΛΛΛΛΛΛ第 7 页 共 8 页 第 8 页 共 8 页五、综合题（1小题，每小题9分，共9分）已知⎪⎪⎪⎭⎫ ⎝⎛----=142252001A .(1) A 是否能相似对角化. 若能，求可逆阵P 和对角阵Λ，使得P -1AP =Λ；若不能，说明理由. (2) 求A n (n ∈N +)。

广东财经大年夜学试题参考答案及评分标准
2014-2015学年第一学期
课程名称线性代数〔A卷〕课程代码101044共4页…………………………………………………………………………………………………
一、填空题〔每题3分，共30分〕
1.正;
2.;
3.5;
4.；
5.;
6.;
7.;
8.-1/3;
9.-4；10.36.
二、单项选择题〔每题3分，共15分〕1.A2.D3.C4.C5.B
三、打算题〔每题10分，共40分〕
1.解：原式=〔3分〕
=(6分)
=(8分)
=-92(10分)
2.解：作方程组的增广矩阵，并对它施以初等行变卦
那么(3分)
即原方程组与方程组同解，其中为自由变量
取，得方程组的一个解〔6分〕
取自由变量分不为，即得导出组基础解系：
(9分)
因此全体解为：，其中为任意常数。

(10分)
3.解：方法一：〔2分〕
，，
，，
，，〔8分〕
那么〔10分〕
方法二：初等变卦
4.解：对矩阵施以初等行变卦
=(4分)
因此矩阵秩为3
因此为一组极大年夜线性有关组(8分)
(10分)
四、运用题〔10分〕
解：由=
得：，〔2分〕
将代入得
其基础解系：，；运用施密特正交化方法，将正交化
令，〔5分〕
时，得：
，其基础解系：〔7分〕
将单位化有：
，，〔9分〕
令正交矩阵,那么有〔10分〕五、证明题〔5分〕
证明：(1分)
那么：
(4分)
(5分)。

课程模拟考核参考答案及评分标准考试课程：线性代数 学年学期：2014-2015-1 试卷类型：A 考试时间：120分钟适用专业：13级机械设计制造及其自动化师范职教师资本科、13级生物工程非师范本科层次：本科一、选择题(每小题2分，共20分）1. 设0333231232221131211≠=a a a a a a a a a D , ij A 是D 的元素ij a 的代数余子式, 若∑=313i ij i A a ≠0, 则 ( C ) .(A) 1=j (B) 2=j (C) 3=j (D) 1=j 或3=j2. 在函数xxx x x f ----=231112)(中，3x 的系数是( B ) . (A) 1 (B) 2 (C) 3 (D) 4 3. =⎥⎦⎤⎢⎣⎡++++c b b a z y y x ( C ) . (A)⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡00b y c a z x (B)⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡c b z y a x (C)⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡c b z y b a y x (D)⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡b c y z b a y x 4. 设A,B,C 均为n 阶方阵，且|A|≠0, 则必有( B ) .(A) AB=CA ⇒ B=C; (B) AB=AC ⇒ B=C; (C) BC=0 ⇒ C=0; (D) AB=C ⇒ B=E. 5. 向量组α1, α2, … αn 线性无关的充要条件是( D ) . (A) α1, α2, … αn 均不为零向量(B) α1, α2, … αn 中任意两个向量的对应分量不成比例 (C) α1, α2, … αn 中有一个部分向量线性无关(D) α1, α2, … αn 中任意一个向量都不能由其余1-n 个向量线性表示 6. 矩阵A 经行初等行变换化为阶梯形矩阵后( C ) .(A) 秩变大 (B) 秩变小 (C) 秩不变 (D) 化为单位方阵 7. 设A 是2阶可逆矩阵, λ为实数, 如果 |λA|=4|A|, 则 ( A ) . (A) λ=±2; (B) λ=±1; (C) λ=±3; (D) λ=4.8. 设n 元齐次线性方程组Ax=0的系数矩阵A 的秩为r ，则Ax=0有非零解的充分必要条件是( B ) . (A) r=n; (B) r<n; (C) r≥n ; (D) r>n.9. 设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡43503362a ，且矩阵A 的秩R(A)=2, 则a=( B ) . (A) 9; (B) 18; (C) 0; (D) 任何数.10. 若方程组⎪⎩⎪⎨⎧=-=+=++02003131321x x ax x x x ax 仅有零解, 则a ≠ ( A ) .(A) 21-; (B) 21; (C) 41; (D) 41-.二、判断题 (每小题2分，共20分)1. n 阶行列式中, 若0元素多于n 2-n 个, 则行列式的值为0. （ √ ）2. n 阶方阵A 可逆的充分必要条件是|A|=0. （ × ）3. 设A,B 都是n 阶方阵, 若AB=0, 则B=0. （ × ）4. 333333222222111111d c c b b a d c c b b a d c c b b a +++++++++333222111c b a c b a c b a =333222111d c b d c b d c b +. （ × ） 5. 设A 与B 为n 阶方阵，则|AB|=|A||B|. （ √ ） 6. 设A,B 都是m ×n 矩阵, 则A+B=B+A. （ √ ） 7. 两个n 阶可逆矩阵之和一定是可逆矩阵. （ × ）8. 元素a ij 的代数余子式A ij 与不仅与a ij 所在有行、列有关, 而且与a ij 的值有关. （ × ）9.010100001111010001100111001111100010111100010001d c b a d c b a+++=. （ √ ） 10. 如果A 与B 可交换, 且A 可逆, 则1-A 与B 可交换. （ √ ）三、填空题(每小题2分，共20分) 1. 排列36715284的逆序数为 13 .2. 若010100≠---abb a，则a,b 满足的条件是 a≠0 或b≠0 .3. 行列式=cb fe da 0002101030 -3abc . 4. 设|A|=2, 且A 为三阶方阵，则|3A|= 54 . .5. 设行列式96330221a中，余子式321=M ，则=a 5/2 . 6. 设()()TT2,3,1,1,1,221-=-=αα, 若()T5,,13λα=可由21,αα线性表示，则=λ -8 .7. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101010101,10010101B x A , 且A=B, 则x= 1 . 8. 设⎥⎦⎤⎢⎣⎡=101a A ，则=nA ⎥⎦⎤⎢⎣⎡101na .9. 设)0(,≠-⎥⎦⎤⎢⎣⎡=cb ad d c b a A , 则A -1= ⎥⎦⎤⎢⎣⎡---a c b d bc ad 1 . 10. 行列式=-000010020100nn !)1(2)1(n n n -- .四、计算题 (每小题5分共30分)1.计算行列式20031001541121---- 解：原式=4121-0231- (2分) = 6∙6= 36. (3分)2. 解方程 013011132=x x解：按第一列展开, x 2-2x-3=0, (2分) 解为 x= -1, 3. (3分) 3. 计算 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡-103110021212321 解：原式=⎥⎦⎤⎢⎣⎡---1341410 (5分)4. k 为何值时，行列式k2002k 0001k 10011≠0. 解：原行列式=(k-1)(k 2-4), (2分) 故 k ≠1且k ≠±2. (3分) 5. 解线性方程组 ⎪⎪⎩⎪⎪⎨⎧=+-+=+-=+-=-+-0x 3x 2x x 0x 8x 14x 40x 4x 7x 20x x 5x x 43214324324321.解：经过初等行变换，原方程的矩阵化为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0000000022/71012/301, (2分) 故其解为 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=--=2413212211cx c x c 2c 27x c c 23x . (3分)6. k 为何值时，方程组 ⎪⎩⎪⎨⎧=+-=-+=-+0z y x 20z ky x 0z y kx 仅有0解.解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---1121111k k −−−−→−+⨯-...,)3()2(2R⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----3210111102k k k k (2分) −−−−−→−+⨯-...,)1()3(3/)1(k R ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----32101103/)2(02k k k k , k 2+k-2≠0即 k≠1, -2. (3分) 五、证明题(每小题5分共10分)1. 设A 可逆, 试证明 (A*)-1 = (A -1)* .证明：∵AA*=|A|E, (2分) ∴(A*)-1 = A/|A|=(A -1)-1/|A| = (A -1)*/(|A -1|·|A|) = (A -1)*. (3分) 2. 证明向量组α1=(1,2,0,1), α2=(1,3,0,−1), α3=(−1,−1,1,0),线性无关。