(完整版)第一单元大数的认识知识点归纳
- 格式:doc
- 大小:25.01 KB
- 文档页数:3

人教版四年级数学上册知识点整理(完整版)第一单元大数的认识一、数的认识(一)数的产生:古时候,人们在生产劳动中,逐渐有了计数的需要(结绳计数,刻道计数)。
(二)计数单位1、一(个)、十、百、千、万、十万、百万、千万、亿都是计数单位。
2、十进制计数法:每相邻两个计数单位之间的进率都是十,也就是“满十进一”的计数方法。
(三)数位顺序表1、数位(1)概念:在用数字表示数的时候,这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位;(2)数位上的数字表示相应数位上计数单位的个数。
2、数级(1)概念:按照我国的计数习惯,从右边起,每四个数位是一级,依次是个级、万级、亿级…(2)个级:个位、十位、百位、千位属于“个级”(表示几个一)。
(3)万级:万位、十万位、百万位、千万位属于“万级”(表示几个万)。
(4)亿级:亿位、十亿位、百亿位、千亿位属于“亿级”(表示几个亿)。
3、数位顺序表:把数位按照从低位到高位、从右向左的顺序排列起来,可制成数位顺序表。
(四)自然数1、概念:表示物体个数的1,2,3,4,5,6,7,8,9…都是自然数;一个也没有,用0表示,0也是自然数。
2、范围:最小的自然数是0,没有最大的自然数,所有的自然数都是整数。
二、亿以内数的读法和写法(含有两个数级)(一)读数的本质就是读出每个计数单位的个数,整万、整亿数可以按照个级的数的读法来读,读完后要在后面加上一个“万”字或“亿”字。
(二)读法:(1)先读万级、再读个级;(2)万级的数要按照个级的数的读法来读,再在后面加上一个“万”字。
(3)每级末尾不管有几个0,都不读;其他数位上有一个0或连续几个0,都只读一个0(三)写法(1)先写万级,再写个级;(2)哪个数位上一个计数单位也没有,就在哪个数位上写“0”;三、数的大小比较(1)位数不同时,位数多的那个数大。
(2)位数相同时,从最高位比起,最高位上的数大的那个数就大,如果最高位上的数相同,就依次比较下一个数位上的数,直到比较出大小。

千里之行,始于足下。
四年级上册第一单元《大数的认识》知识点总结《大数的认识》是四年级上册的第一单元,主要介绍了大数的概念和认识。
下面是对该单元的知识点总结。
1. 大数的概念大数是指有很多位的数,它由单位、十位、百位、千位等组成。
大数的位数增加时,数字的值也会增大。
2. 大数的读法大数的读法可以根据数字的位数从左到右依次读出每一位上的数字,并在每个单位之间加上适当的单位词。
3. 大数的写法大数的写法可以直接把每位数字写在相应的位上,并在需要的地方加上逗号分隔。
4. 大数与身边的事物关联大数可以与我们日常生活中的事物建立关联,以便更好地理解大数的概念。
例如:人口数量、汽车数量、钱数等等。
5. 大数的比较比较大数的大小时,可以逐位进行比较。
从左到右比较每一位上的数字,当某一位的数字不相等时,就能确定大小关系。
6. 大数的加法和减法第1页/共2页锲而不舍,金石可镂。
大数的加法和减法与小数的运算类似,按位相加或相减,并注意进位和借位。
在运算中,要对齐各位数字,并注意处理末位和进位。
7. 大数的估算对于非常大的数,可以通过估算的方式来快速计算。
例如,可以将一个大数近似为最接近它的一个较小的数,然后进行计算。
8. 多位数的乘法多位数的乘法可以通过分解法和竖式乘法来计算。
分解法就是将一个大数拆分成多个小数的乘法,并将结果相加。
竖式乘法则是逐位相乘,并注意进位。
9. 大数的单位换算大数的单位换算可以通过移动小数点的位置来实现。
向左移动一位,数值变大10倍;向右移动一位,数值变小10倍。
10. 大数的应用大数的应用非常广泛,主要用于计算、统计和表示数量等方面。
在日常生活中,我们经常会遇到需要处理大数的情况。
这些是《大数的认识》这一单元的主要知识点总结。
通过学习和掌握这些知识,我们可以更好地理解和运用大数,提高数学能力并应用到实际生活中。

千里之行,始于足下。
四年级上册第一单元《大数的认识》知识点总
结
《大数的认识》是四年级上册数学教材的第一单元,主要涉及大数的认识
和读写大数的技巧。
以下是该单元的知识点总结:
1. 大数的认识:
- 大数是指整数中比较大的数。
- 大数可以用数字和单位(十、百、千、万、亿)来表示。
2. 十进制与数位:
- 十进制是一种数的表示方法,它由0-9这10个数字组成。
- 数字按照位的大小排列,每一位代表一个权值,从右到左依次为个位、十位、百位、千位等。
3. 大数的读法:
- 读大数时,先读每一位的数字,再读对应的单位。
4. 大数的写法:
- 大数从左到右,每四位分成一组,每组之间用顿号“,”隔开。
- 每组内按照千分位、百分位、十分位、个位的顺序分别写出数字和单位。
5. 大数的比较:
- 大数比较时,先比较最高位的数字大小,如果相同再比较次高位,依次类推。
- 当两个大数的对应位数都相同,但有一个大数已经没有更高位了,则较短的大数更小。
第1页/共2页
锲而不舍,金石可镂。
以上是《大数的认识》这一单元的主要知识点总结,通过学习这些知识,学生可以掌握大数的概念、认识大数的读写方法,以及比较大数的技巧。

人教版四年级数学上册第一单元大数的认识知识点一、十的读法和读数法则在大数中,我们首先要学习的是“十”的读法和读数法则。
理解“十”的概念对于认识大数至关重要。
1. 十的读法:我们读“十”时,可以读作“十”,也可以读作“一十”。
2. 读数法则:- 十后面没有个位数时,用“十”表示。
例如:20读作“二十”,30读作“三十”。
- 十后面有个位数时,十位数读作“十”,个位数读作普通数字。
例如:23读作“二十三”,39读作“三十九”。
二、百的认识和读数法则在大数中,百是一个重要的概念,它比十更大。
理解百的概念和读数法则,有助于我们更好地认识和运用大数。
1. 百的概念:百是十十,即十个十是一百。
2. 读数法则:- 百后面没有十位和个位数时,用“百”表示。
例如:100读作“一百”,200读作“二百”。
- 百后面只有十位数时,读作“一百多几十”。
例如:130读作“一百三十”,180读作“一百八十”。
- 百后面只有个位数时,读作“一百零几”。
例如:103读作“一百零三”,109读作“一百零九”。
- 百后面既有十位数又有个位数时,读作“一百几十几”。
例如:126读作“一百二十六”,189读作“一百八十九”。
三、千的认识和读数法则千是大数中比百更大的一个概念。
理解千的概念和读数法则,是学习和应用大数的关键。
1. 千的概念:千是百百,即一百个一百是一千。
2. 读数法则:- 千位后面没有百位、十位和个位数时,用“千”表示。
例如:1000读作“一千”,2000读作“二千”。
- 千位后面只有百位时,读作“一千多几百”。
例如:1300读作“一千三百”,1800读作“一千八百”。
- 千位后面只有十位和个位数时,读作“一千零几十几”。
例如:1024读作“一千零二十四”,1079读作“一千零七十九”。
- 千位后面既有百位又有十位和个位数时,读作“一千几百几十几”。
例如:1234读作“一千二百三十四”,1890读作“一千八百九十”。
四、万和亿的认识和读数法则在大数中,万和亿是更大的概念,理解万和亿的概念和读数法则,能够帮助我们更准确地表达和理解大数。

第一单元大数的认识知识点归纳第一单元大数的认识是数学中的一个重要概念。
在该单元中,我们将学习到如何识别、读写和比较大数,并且了解到大数的意义和应用。
1.大数的认识大数是指位数较多的数。
在日常生活和工作中,我们经常会遇到大数,例如表示人口、财富、天文现象等。
大数往往具有很多位数,可能包括整数位数和小数位数,但当位数较多时,我们通常会采用科学记数法来表示。
2.科学记数法科学记数法是一种用科学计数法表示大数或小数的方式。
科学计数法的表示形式为:a×10^n,其中a是一个介于1到10之间的数,n是一个整数。
通过科学记数法,我们可以更方便地阅读和书写大数。
3.大数的读写当我们遇到大数时,我们需要学会正确地读写它们。
大数的读写可以分为整数部分和小数部分的读写。
整数部分的读写是根据位数依次读取各个数位,小数部分的读写则使用小数点后面的数字。
4.大数的比较比较大数的大小是数学中常见的操作之一、当我们需要比较两个大数的大小时,可以逐位进行比较,从高位到低位依次比较每一位的大小。
根据每一位数的大小关系,我们可以确定两个大数的大小关系。
5.大数的加减乘除对于大数的加减乘除运算,我们可以采用类似的方法进行计算。
对于加法和减法,我们可以逐位相加或相减,注意进位和借位的处理。
对于乘法和除法,我们可以采用竖式计算的方法,逐位进行乘法或除法运算。
6.大数的意义和应用大数在很多领域都有着重要的应用,例如科学研究、工程计算、经济统计等。
大数可以帮助我们更好地理解和描述一些复杂的现象,例如宇宙的演化、地球的变化、人口的增长等。
在日常生活中,大数也经常出现在金融、统计和经济方面的数据中,例如国内生产总值、企业利润、股票指数等。
总结:大数是数学中的一个重要概念,通过学习大数的认识,我们可以更好地理解和应用大数。
科学记数法可以方便地表示大数或小数,大数的读写和比较可以帮助我们准确地理解和描述大数。
对于大数的加减乘除运算,我们可以采用逐位运算的方法进行计算。

人教版数学四年级上册第一单元《大数的认识》知识点归纳一、大数的认识1. 大数的意义:在日常生活中,我们经常遇到很大的数,例如用来表示人口、货币、距离等。
这些数被称为大数。
2. 大数的组成:大数由数字0-9组成,其中最高位的数字不能为0。
二、大数的读法和写法1. 大数的读法:读大数时,通常按照千位、百位、十位和个位的顺序来读数,中间可以使用“零”进行分隔。
例如:7894读作“七千八百九十四”,5050读作“五千零五十”。
2. 大数的写法:大数采用阿拉伯数字的形式进行书写。
例如:7894用7894表示,5050用5050表示。
三、大数的比较1. 大数的大小比较原则:比较两个大数的大小时,先比较最高位的数字,如果相同,则比较次高位的数字,以此类推,直到找到不相同的数字为止。
例如:在比较7894和5050的大小时,先比较千位数,由于7大于5,所以7894大于5050。
2. 大数的比较运算:除了比较大小外,大数还可以进行相等、不等、大于和小于的比较运算。
四、大数的加法和减法1. 大数的加法:大数的加法和小数的加法类似,按照个位数、十位数、百位数、千位数的顺序从右往左进行计算。
如果相加的两个位数之和大于等于10,则需要进位。
例如:7894 + 5050的计算过程为:4 + 0 = 4(个位数)9 + 5 = 14,需要进位1(十位数)8 + 5 + 1 = 14,需要进位1(百位数)7 + 0 + 1 = 8(千位数)所以,7894 + 5050 = 12944。
2. 大数的减法:大数的减法也类似于小数的减法,按照个位数、十位数、百位数、千位数的顺序从右往左进行计算。
如果被减数的某一位小于减数的对应位,则需要向前一位借位。
例如:7894 - 5050的计算过程为:4 - 0 = 4(个位数)9 - 5 = 4(十位数)8 - 5 = 3(百位数)因为7小于5,所以需要向前一位借位10 - 5 - 1 = 4(千位数)所以,7894 - 5050 = 2844。

第一单元大数的认识知识点归纳1、计数单位:一(个)、十、百、千、万……亿等等,都是计数单位。
相邻两个计数单位之间的进率是十。
10个一万是十万,10个十万是一百万,10个百万是一千万,10个千万是一亿。
2、数位:个位、十位、百位、……亿位等等,都是数位。
数位名称就是在相应的计数单位后添一个“位”字,如万 万位。
3、数级:个级、万级、亿级……都是数级,一个数级包括四个数位。
4、数位顺序表:含有数级、数位和相应的计数单位的表格叫做数位顺序表,如下。
数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位数级…亿级万级个级计数单位…千亿百亿十亿亿千万百万十万万千百十个注意:按照我国的计数习惯,从右边起,每四个数位是一级5、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367是一个5位数,其中的1在万位上,表示“1个万”,2在千位上,表示“2个千”,3在百位上,表示“3个百”,6在十位上,表示“6个十”,7在个位上,表示“7个一”。
某个数级上的数字表示几个这个数级的计数单位。
如:36472845中的3647在万级上,表示“3647个万”6、大数的读法:①从高位数读起,一级一级往下读。
含有三级的数要先读亿级,再读万级,最后读个级;②亿级的数要按照个级的数的读法来读,再在后面加一个“亿”或者“万”字。
③每级末尾不管有几个零都不读,其他数位有一个“零”或连续几个“零”,都只读一个“零”。
读数注意事项:“2”读作“二”;如果是大数的最高位是十位、十万位、十亿位……且最高位上的数字是“1”时,这个“1”不读,如125046读作“十二万五千零四十六”7、大数的写法:①从高级写起,一级一级往下写。
先写亿级,再写万级,最后写个级。
②当哪一位上一个计数单位也没有,就在哪一位上写0写数注意事项:一定要注意“四位一级”,保证每级有四个数位,不够的要用0补足。
8、读写数检验方法:读数和写数可以互相检验,即读数后再写出来和原数比对,而写数后可以自己读出。
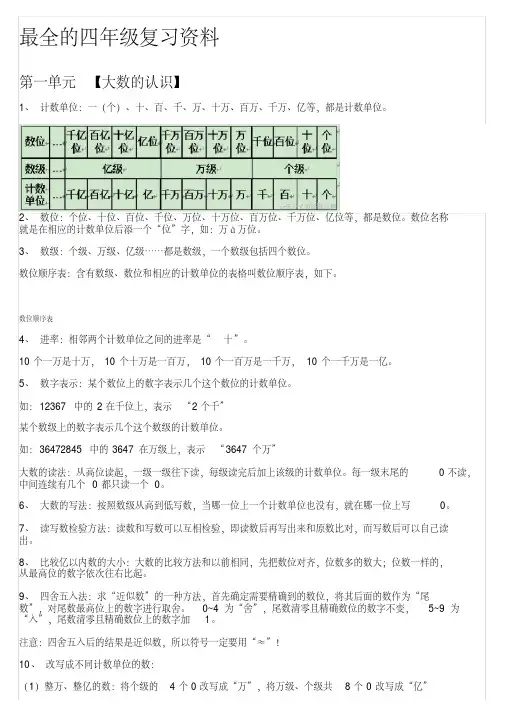
最全的四年级复习资料第一单元【大数的认识】1、计数单位:一(个)、十、百、千、万、十万、百万、千万、亿等,都是计数单位。
2、数位:个位、十位、百位、千位、万位、十万位、百万位、千万位、亿位等,都是数位。
数位名称就是在相应的计数单位后添一个“位”字,如:万à万位。
3、数级:个级、万级、亿级……都是数级,一个数级包括四个数位。
数位顺序表:含有数级、数位和相应的计数单位的表格叫数位顺序表,如下。
数位顺序表4、进率:相邻两个计数单位之间的进率是“十”。
10个一万是十万,10个十万是一百万,10个一百万是一千万,10个一千万是一亿。
5、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367 中的2在千位上,表示“2个千”某个数级上的数字表示几个这个数级的计数单位。
如:36472845中的3647在万级上,表示“3647个万”大数的读法:从高位读起,一级一级往下读,每级读完后加上该级的计数单位。
每一级末尾的0不读,中间连续有几个0都只读一个0。
6、大数的写法:按照数级从高到低写数,当哪一位上一个计数单位也没有,就在哪一位上写0。
7、读写数检验方法:读数和写数可以互相检验,即读数后再写出来和原数比对,而写数后可以自己读出。
8、比较亿以内数的大小:大数的比较方法和以前相同,先把数位对齐,位数多的数大;位数一样的,从最高位的数字依次往右比起。
9、四舍五入法:求“近似数”的一种方法,首先确定需要精确到的数位,将其后面的数作为“尾数”,对尾数最高位上的数字进行取舍。
0~4为“舍”,尾数清零且精确数位的数字不变,5~9为“入”,尾数清零且精确数位上的数字加1。
注意:四舍五入后的结果是近似数,所以符号一定要用“≈”!10、改写成不同计数单位的数:(1)整万、整亿的数:将个级的4个0改写成“万”,将万级、个级共8个0改写成“亿”注意:整万、整亿的数的改写属于准确数,要用“=”连接!(2)非整万的数改写成以“万”为单位的数:将万位以后的数作为尾数,对尾数的最高位(千位)四舍五入,再改写成以“万”为单位的数(3)非整亿的数改写成以“亿”为单位的数:将亿位以后的数作为尾数,对尾数的最高位(千万位)四舍五入,再改写成以“亿”为单位的数11、十进制:每相邻两个计数单位之间的进率之间都是十的计数方法叫做十进制计数法。

四年级数学上册知识点归纳(完整版) 小学四年级上册数学知识点归纳第一单元:大数的认识1.数的组成:十个一千是一万;十个一万是十万;十个十万是一百万;十个一百万是一千万;十个一千万是一亿;十个一亿是十亿;十个十亿是一百亿;十个百亿是一千亿。
2.数级:数级是为方便记读阿拉伯数的一种识读方法。
在位值制(数位顺序)的基础上,以三位或四位分级的原则,把数读、写出来。
通常在阿拉伯数的书写上,以逗号或者空格作为各个数级的标识,从右向左把数分开。
3.数级分类:1)四位分级法:即以四位数为一个数级的分级方法。
我国读数的惯,就是按这种方法读的。
如:万(数字后面4个)、亿(数字后面8个)、兆(数字后面12个,这是中法计数)……。
这些级分别叫做个级,万级,亿级……。
2)三位分级法:即以三位数为一个数级的分级方法。
这是西方的分级方法,也是国际通行的分级方法。
如:千,数字后面3个、百万,数字后面6个、十亿,数字后面9个……。
4.数位:在用数字表示数的时候,这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位。
5.数位顺序表:1.十进制计数法:每相邻两个计数单位之间的进率都是十的计数方法叫做十进制计数法(即满十进一)。
6.含有两级的数的读法:1)先读万级,再读个级;2)万级的数,要按照个级的数的读法来读,再在后面加上一个“万”字;3)每级末尾不管有几个,都不读,其他数位上有一个或连续几个,都只读一个。
7.含有两级的数的写法:1)先写万级,再写个级;2)哪个数位上一个单位也没有,就在那个数位上写0.8.亿以上的数的读法:1)先分级,再从最高级读起;2)读完“亿级”或“万级”的数要加“亿”字或“万”字;3)每级末尾的零都不读,其他数位上有一个或连续几个,都只读一个0.9.亿以上的数的写法:1)先看这个数有几级,再从最高级写起;2)哪个数位上一个单位也没有,就在那个数位上写0.10.两个数比较大小:1)首先看位数,位数多的那个数就大;2)位数相同的两个数,从最高位比起,最高位上的数大的那个数就大,如果最高位上的数相同,就比较下一个数位上的数。

完整版)四年级上册数学知识点归纳一.大数的认识1.含有两级的数的读法先读万级,再读个级;万级的数,要按照个级的数的读法来读,再在后面加上一个“万”字;每级末尾不管有几个都不读,其他数位上有一个或连续几个都只读一个0.2.含有两级的数的写法先写万级,再写个级;哪个数位上一个单位也没有,就在那个数位上写0.3.比较两个数的大小的方法先看数位,数位多的数就大;位数相同的两个数。
从最高位比起,最高位上的数大的那个数就大,如果高位上的数相同,就比较下个数位上的数。
4.十进制计数法数级:亿级、万级、个级数位计数单位:个(一)、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿每相邻两个计数单位间的进率都是十的计数方法叫十进制计数法。
5.亿以上数的读法先分级,再从最高位读起;亿级或万级的数要按照个级的数的读法来读,再在后面加上“亿”字或“万”字;每级末尾不管有几个都不读,其他数位上有一个或连续几个都只读一个0.6.亿以上数的写法先看这个数有几级,再从最高级写起;哪个数位上一个单位也没有,就在那个数位上写0.7.计算工具的认识和使用常用的计算工具有算盘和计算器,算盘的1颗上珠表示5,1颗下珠表示1.二.公顷和平方千米1.1公顷有多大边长是100米的正方形的面积是1公顷。
1公顷=平方米。
2.1平方千米有多大计量较大的土地面积常用“平方千米”(k㎡)作单位,边长是1千米的正方形的面积是1平方千米。
1平方千米=xxxxxxx平方米=100公顷。
三.角的度量1.线段、直线和射线的特征及表示方法线段:有两个端点,可以量出长度。
直线:没有端点,可以向两端无限延伸,是无限长的。
1.直线和射线的定义直线是由无数个点无限延伸而成的图形。
射线只有一个端点,可以向一端无限延伸。
2.角的定义及表示符号当从一个点引出两条射线时,它们所形成的图形叫做角。
这个点叫做角的顶点,这两条射线叫做角的边。
角通常用符号“∠”表示。
3.用量角器量角的步骤要用量角器量角,需要将量角器的中心与角的顶点重合,刻度线与角的一条边重合。
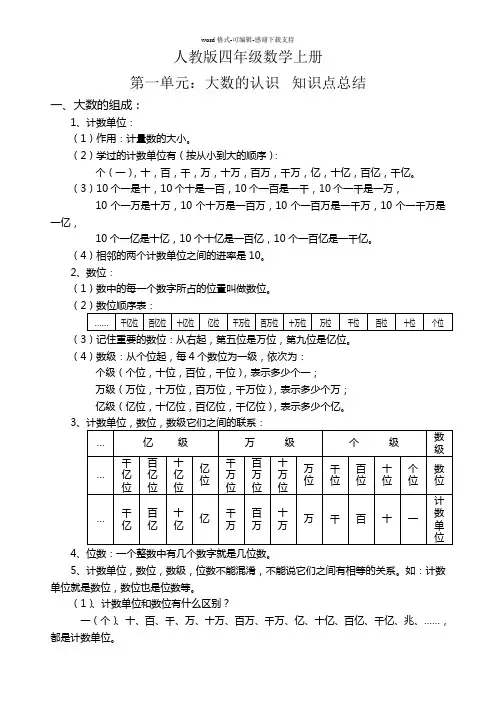
人教版四年级数学上册第一单元:大数的认识知识点总结一、大数的组成:1、计数单位:(1)作用:计量数的大小。
(2)学过的计数单位有(按从小到大的顺序):个(一),十,百,千,万,十万,百万,千万,亿,十亿,百亿,千亿。
(3)10个一是十,10个十是一百,10个一百是一千,10个一千是一万,10个一万是十万,10个十万是一百万,10个一百万是一千万,10个一千万是一亿,10个一亿是十亿,10个十亿是一百亿,10个一百亿是一千亿。
(4)相邻的两个计数单位之间的进率是10。
2、数位:(1)数中的每一个数字所占的位置叫做数位。
((3)记住重要的数位:从右起,第五位是万位,第九位是亿位。
(4)数级:从个位起,每4个数位为一级,依次为:个级(个位,十位,百位,千位),表示多少个一;万级(万位,十万位,百万位,千万位),表示多少个万;亿级(亿位,十亿位,百亿位,千亿位),表示多少个亿。
34、位数:一个整数中有几个数字就是几位数。
5、计数单位,数位,数级,位数不能混淆,不能说它们之间有相等的关系。
如:计数单位就是数位,数位也是位数等。
(1)、计数单位和数位有什么区别?一(个)、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿、兆、……,都是计数单位。
数位是指写数时,把数字并列排成横列,一个数字占有一个位置,这些位置,都叫做数位。
从右端算起,第一位是“个位”,第二位是“十位”,第三位是“百位”,第四位是“千位”,第五位是“万位”,等等。
这就说明计数单位和数位的概念是不同的。
但是,它们之间的关系又是非常密切的。
这是因为“个位”上的计数单位是“一(个),“十位”上的计数单位是“十”,“百位”上的计数单位是“百”,“千位”上的计数单位是“千”,“万位”上的计数单位是“万”,等等。
例如:8475,“8”在千位上,它表示8个千,“4”在百位上,它表示4个百,“7”在十位上,它表示7个十,“5”在个位上,它表示5个一。
(2)区分“数位”与“位数”。
第一单元大数的认识一、认识数位顺序表1、数级:按照我国的计数习惯,从右边起,每四个数位是一级。
个级、万级、亿级……都是数级,一个数级包括四个数位。
2、数位:这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位。
个级的数位有:个位、十位、百位、千位。
万级的数位有:万位、十万位、百万位、千万位。
亿级的数位有:亿位、十亿位、百亿位、千亿位。
3、计数单位:一(个)、个、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿等都是计数单位。
个级的计数单位有:个、十、百、千。
万级的计数单位有:万、十万、百万、千万。
亿级的计数单位有:亿、十亿、百亿、千亿。
4、十进制计数法:每相邻两个计数单位之间的进率都是10,这样的计数方法叫十进制计数法。
5、10个一万是十万;10个十万是一百万;10个一百万是一千万;10个一千万是一亿;10个一亿是十亿;10个十亿是一百亿;10个一百亿是一千亿;100个一万是一百万;100个十万是一千万;100个一百万是一亿;100个一千万是十亿;100个一亿是一百亿;100个十亿是一千亿。
6、从右边数起,第5位是万位;第9位是亿位。
7、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367 中的2在千位上,表示“2个千”。
某个数级上的数字表示几个这个数级的计数单位。
如:36472845中的3647在万级上,表示“3647个万”。
如:308¦4000¦0860是由3个百亿、8个亿、4个千万、8个百、6个十组成;也可以说是由308个亿、4000个万、860个一组成。
二、读数的方法(写汉字)1、亿以内数的读法(含有两级的数的读法)(1)读数之前,先分级。
从个位起,每四个数位是一级。
例如:(2496¦0000)(2)先读万级,再读个级。
(3)万级的数,要按照个级的数的读法来读,再在后面加上一个“万”字。
(4)每级末尾不管有几个0,都不读;其他数位上有一个0或连续几个0,都只读一个0。
一.大数的认识1.大数的读法1)方法总结:①分级:从个位起,按照四个数位一级的方法从右向左对大数进行分级,一直分到不能再分为止②读数:先读高级,再读低级。
万级和亿级的数,先按照个级的数的读法去读,读完后在后面加“万”或“亿”字③关于0的处理:每级末尾的0不读,开头的0与中间的0,不管有多少个,都只读一个0.④第二级与第三级的数,若0在开头,则0与后面的数字分开读;若0在中间或末尾,则作为整体一口气读出来。
2)示例讲解200800573075步骤一:分级:2008、0057、0370亿级万级个级步骤二:读数:先读亿级,再读万级,最后读个级,即:二千零八亿零五十七万零三百七十亿级2008的两个0在中间,要读,由于两个是连在一起,只要读一个零。
万级0057两个0在开头,00与57分开来读,两个重复的零,只需读一个零即可,57读成五十七个级0370第一个0在前面,要读;第二个0在末尾,不用读。
2.大数的写法1)方法总结:①从高级写起,一级级往下写,除了最高数级可能没有四位数外,其它数级都有四个数位,注意写满。
②哪个数位上一个单位也没有,就在哪个数位上写零2)示例讲解五十三亿零八万零四百零六步骤一:先写亿级:53步骤二:再写万级:8,8是一位数,处在万位上,这个数级必须有四位数,除了万位有数之外,其它三个数位没说,必须在8的前面先写三个零.步骤三:最后写个级:406是三位数,这个数级必须有四位数,千位没有单位,所以在406的前面先写一个零。
3.数的大小比较1)方法总结①先数数位②若数位不同,则数位多的数较大;若数位相同,则从最高数位比起,最高位大的数较大;若最高数位相同,则依次向下一数位比起,一直到比出来为止。
2)示例讲解:例一:比较45798 和 102496的大小45798是五位数,102496是六位数,所以45798小于102496例二:比较45798与45801的大小两个数都是五位数,先从最高位“万位”比起,它们的“万位”都是4,比不出大小,接着比千位,它们的千位都是5,还是比不出来,再接着比百位,它们的百位前一个是7,后一个是8,则后一个数较大。
第一单元大数的认识知识点归纳1、计数单位:一(个)、十、百、千、万……亿等等,都是计数单位。
相邻两个计数单位之间的进率是十。
2、数位:个位、十位、百位、……亿位等等,都是数位。
数位名称就是在相应的计数单位后添一个“位”字,如万万位。
3、数级:个级、万级、亿级……都是数级,一个数级包括四个数位。
4、数位顺序表:含有数级、数位和相应的计数单位的表格叫做数位顺序表,如下。
数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位数级…亿级万级个级计数单位…千亿百亿十亿亿千万百万十万万千百十个5、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367 中的2在千位上,表示“2个千”某个数级上的数字表示几个这个数级的计数单位。
如:中的3647在万级上,表示“3647个万”6、大数的读法:①从高位数读起,一级一级往下读。
②万级的数要按照个级的数的读法来读,再在后面加一个万字。
③每级末尾不管有几个零都不读,其他数位有一个“零”或连续几个“零”,都只读一个“零”。
读数注意事项:“2”读作“二”;如果是大数的最高位是十位、十万位、十亿位……且最高位上的数字是“1”时,这个“1”不读,如125046读作“十二万五千零四十六”7、大数的写法:①从高级写起,一级一级往下写。
②当哪一位上一个计数单位也没有,就在哪一位上写0 。
写数注意事项:一定要注意“四位一级”,保证每级有四个数位,不够的要用0补足。
8、读写数检验方法:读数和写数可以互相检验,即读数后再写出来和原数比对,而写数后可以自己读出。
9、写出所组成的数:对照数位顺序表把每个部分的数字分别写入,再用0补足。
如:10、大数的比较:①位数多的这个数就比较大。
②当这两个数位数相同的时候,我们就应该从左起的第一位比起,也就是从最高位开始比,哪个数最高位上的数大,这个数就大。
③如果碰到最高位上的数相同的时候,就再比下一位,以此类推,直到我们比较出相同的数位上的那个数,哪个数大的时候,我们就可以断定这个数比较大。
四年级人教版上册数学知识点归纳第一单元大数的认识1.大数的读法(1)从高位读起,先读亿级,再读万级,最后读个级。
(2)读亿级和万级时,按个级的读法来读,读完亿级后加上一个“亿”字,读完万级后加上一个“万”字。
(3)每级末尾不管有几个0,都不读,其他数位上有一个0或连续几个0,都读一个零。
2.大数的写法(1)从高位起,先写亿级,再写万级,最后写个级。
(2)哪个数位上一个单位也没有,就在那个数位上写0。
3.数位顺序表:数级……亿级万级个级数位……千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位计数单位……千亿百亿十亿亿千万百万十万万千百十个4.大数的改写(1)如果是整万的数,直接去掉末尾的4个0,在后面加上“万”字;如果是整亿的数,直接去掉末尾的8个0,在后面加上“亿”字。
都用“=”连接。
(2)如果不是整万的数,就从数的末尾起向左数出4位后,根据“四舍五入”法改写成整万的数;如果不是整亿的数,就从数的末尾起向左数出8位后,根据“四舍五入”法改写成整亿的数。
都用“≈”连接。
5.大数的大小的比较(1)先看位数,位数多的数大。
(2)位数相同时,比较最高位,最高位大的数就大。
(3)最高位相同时,再比较下一位,依次找下去。
6.表示物体个数的0,1,2,3,4,5,6,7,8,9,10,11……的数叫做自然数。
0也是自然数。
最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
7.每相邻的两个计数单位之间的进率都是十。
这种计数方法叫做十进制计数法。
第二单元公顷与平方千米我们学过的面积单位有平方厘米、平方分米、平方米、公顷、平方千米。
1.边长是100米的正方形的面积是1公顷。
“鸟巢”的占地面积约20公顷1公顷=10000平方米公顷用字母hm 表示。
2.边长是1000米的正方形的面积是1平方千米。
1平方千米=1000000平方米=100公顷平方千米用字母km²表示。
第三单元角的度量1.线段、直线、射线(1)经过一点可以画无数条线段、直线和射线。
(人教版)小学数学四年级上册【知识点】第一单元大数的认识一.亿以内数的认识1.数位:在用数字表示数的时候,这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位。
数级:按照我国的计数习惯,每四个数位是一级。
个位、十位、百位、千位是个级;万位、十万位、百万位、千万位是万级;亿位、十亿位、百亿位、千亿位是亿级。
2.亿以内数的读法:(1)先读万级,再读个级;(2)万级的数都要按照个级的数的读法来读,再在后面加上一个“万”字;(3)每级末尾不管有几个0,都不读,其他数位有一个0或连续几个0,都只读一个“零”。
例:780¦6009 读作:七百八十万¦六千零九3.亿以内数的写法:(1)先写万级,再写个级;(2)哪个数位上一个单位也没有,就在那个数位上写0。
例:三百零二万¦六千写作:302¦60004.亿以内数的大小比较:位数不同时,位数多的数大;位数相同时,从最高位比起,最高位的数大的那个数就大,如果最高位上的数相同,就比较下一个数位上的数,直到比较出大小为止。
例:50¦6012>5¦0601 50¦6012<50¦60225.整万的数改写成用“万”作单位的数:去掉末尾的4个0,再加上一个“万”字;例:32¦0000=32万(目的是为了读写方便)6.不是整万的数改写成“万”作单位的近似数:要将“千位”上的数四舍五人,然后再加上“万”字。
例:5¦3850≈5¦0000=5万5¦7220≈6¦0000=6万7.四舍五入法:求一个数的近似数,要先看省略的尾数部分的最高位是小于5,还是等于或大于5;如果小于5就把它和后面的尾数全部舍去,改写成0;如果等于或大于5就先向前一位进1,再把它和后面的尾数全部舍去,改写成0。
这种求近似数的方法叫做四舍五入法。
8.数的产生:数是应人们生产生活的需要而产生的。
四年级上册数学第一单元大数的认识知识点一、大数的概念在数学中,我们常常会遇到大量的数字,这些数字往往非常庞大,例如:5000、10000、100000等等。
为了方便处理这些大数,我们引入了大数的概念。
大数指的是有很多位数的数,它的位数比较多,因此我们需要学习一些方法来认识和处理大数。
二、数字的位数和读法1. 位数:一个数字有几位,就有几个数字位。
例如:10有1个数字位,100有2个数字位,1000有3个数字位,以此类推。
2. 读法:读出一个数字时要按照从左到右的顺序读,每三位为一组,从右往左每组之间要用“万”、“亿”等单位隔开。
例如:123456789读作“一亿二千三百四十五万六千七百八十九”。
三、大数的比较当我们遇到两个大数需要比较大小时,可以通过以下方法进行比较:1. 首先比较最高位,最高位数字较大的数大;2. 如果最高位相同,再比较次高位,次高位数字较大的数大;3. 以此类推,直到比较出两个数的大小。
四、大数的加法对于大数的加法,我们要从低位逐位相加,逢十进一。
具体步骤如下:1. 从个位数开始相加,将两个数对应位数的数字相加得到个位数;2. 如果相加的结果大于等于10,则十位数进一;3. 逐位相加,直到所有位数相加完毕。
五、大数的减法对于大数的减法,我们要从低位逐位相减。
具体步骤如下:1. 从个位数开始相减,将被减数对应位数的数字减去减数对应位数的数字,得到个位数;2. 如果被减数的某一位减去减数的相应位时,需要向高位借位,则向高位借位;3. 逐位相减,直到所有位数相减完毕。
六、大数的乘法对于大数的乘法,我们要采用竖式的方法进行计算。
具体步骤如下:1. 将一个大数(被乘数)竖着写在上面,乘数写在下面;2. 从乘数的个位数开始,一位一位与被乘数的每一位相乘;3. 每一位相乘完毕后,将结果相加,得到最后的乘积。
七、大数的除法对于大数的除法,我们要采用长除法的方法进行计算。
具体步骤如下:1. 将被除数写在长除法的左边,除数写在长除法的左边;2. 从被除数的左边第一位开始,将这一位与除数相除得商;3. 将商写在长除法的上方,并将除数与商相乘后写在被除数下方;4. 重复上述步骤,直到所有位数都相除完毕。
第一单元大数的认识知识点归纳
1、计数单位:
一(个)、十、百、千、万……亿等等,都是计数单位。
相邻两个计数单位之间的进率是十。
2、数位:个位、十位、百位、……亿位等等,都是数位。
数位名称就是在相应的计数单位后添一个“位”字,如万万位。
3、数级:个级、万级、亿级……都是数级,一个数级包括四个数位。
4、数位顺序表:含有数级、数位和相应的计数单位的表格叫做数位顺序表,
如下。
数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位数级…亿级万级个级计数单位…千亿百亿十亿亿千万百万十万万千百十个5、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367 中的2在千位上,表示“2个千”
某个数级上的数字表示几个这个数级的计数单位。
如:36472845中的3647在万级上,表示“3647个万”
6、大数的读法:①从高位数读起,一级一级往下读。
②万级的数要按照个级的数的读法来读,再在后面加一个万字。
③每级末尾不管有几个零都不读,其他数位有一个“零”或连续几个“零”,都只读一个“零”。
读数注意事项:“2”读作“二”;如果是大数的最高位是十位、十万
位、十亿位……且最高位上的数字是“1”时,这个“1”不读,如125046读作“十二万五千零四十六”
7、大数的写法:①从高级写起,一级一级往下写。
②当哪一位上一个计数单位也没有,就在哪一位上写0 。
写数注意事项:一定要注意“四位一级”,保证每级有四个数位,不够的要用0补足。
8、读写数检验方法:读数和写数可以互相检验,即读数后再写出来和原数比对,而写数后可以自己读出。
9、写出所组成的数:对照数位顺序表把每个部分的数字分别写入,再用0补足。
如:10、大数的比较:①位数多的这个数就比较大。
②当这两个数位数相同的时候,我们就应该从左起的第一位比起,也就是从最高位开始比,哪个数最高位上的数大,这个数就大。
③如果碰到最高位上的数相同的时候,就再比下一位,以此类推,直到我们比较出相同的数位上的那个数,哪个数大的时候,我们就可以断定这个数比较大。
11、四舍五入法:求“近似数”的一种方法,首先确定需要精确到的数位,将其后面的数作为“尾数”,对尾数最高位上的数字进行取舍。
0~4为“舍”,尾数清零且精确数位的数字不变,5~9为“入”,尾数清零且精确数位上的数字加1。
如,12,5933 (精确到万位)≈13,0000 12,5933 (精确到千位)≈12,6000 12,5933 (精确到百位)≈12,5900 12,5933 (精确到十位)≈12,5930
注意:四舍五入后的结果是近似数,所以符号一定要用“≈”!
12、改写成不同计数单位的数:(1)整万数:将个级的4个0改写成“万”,整亿数:将万级、个级共8个0改写成“亿”如,15,0000 = 15万24,0000,0000 = 24,0000万= 24亿370,0000 = 370万注意:整万、整亿的数的改写属于准确数,要用“=”连接!(2)非整万的数改写成以“万”为单位的数:将万位以后的数作为尾数,对尾数的最高位(千位)四舍五入,再改写成以“万”为单位的数如14,7283 ,因为千位上的数字是7,属于“入”的情况,所以14,7283 ≈15,0000 = 15万或者直接写成14,7283 ≈15万(3)非整亿的数改写成以“亿”为单位的数:将亿位以后的数作为尾数,对尾数的最高位(千万位)四舍五入,再改写成以“亿”为单位的数如56,0384,9182 ,因为千万位上的数字是0,属于“舍”的情况,所以56,0384,9182 ≈56,0000,0000 = 56 亿或者直接写成56,0384,9182≈56亿
13、按要求组数:(1)组成最大、最小的数:“用2、4、5、6、0、9组成最大的六位数和最小的六位数”最大的数:把给定的数字按照从大到小的顺序排列即可,得965420 最小的数:把给定的数字按照从小到大的顺序排列即可,若最高位上的数字是0,将第一个非0数字提前作为最高位,得024569 –》204569。