自然对流与强制对流及计算实例
- 格式:docx
- 大小:125.08 KB
- 文档页数:9

对流传热系数的计算公式
对流传热系数是热传导中的一种传热方式,常用于热交换器、冷却塔、加热器等传热设备的设计与计算中。
对于流体在壁面上的流动,其对流传热系数与流速、温度、粘度等变量密切相关。
在实际应用中,针对不同的流体与流动状态,可采用不同的计算公式。
下面列举几种常用的对流传热系数计算公式:
1. 自然对流传热系数公式:
h = 1.13 * (gβΔT)^1/4
其中,h为对流传热系数,g为重力加速度,β为热膨胀系数,ΔT为壁面温度与流体温度的差值。
2. 强制对流传热系数公式:
Nu = CRe^mPr^n
其中,Nu为努塞尔数,Re为雷诺数,Pr为普朗特数,C、m、n 为经验系数。
3. 线性对流传热系数公式:
h = kΔT
其中,k为比例常数,ΔT为温度差值。
需要注意的是,以上公式仅适用于理想条件下的流动状态,而实际应用中因存在多种不确定因素,其计算结果仅供参考,具体设计与计算仍需进行实际测试与验证。
- 1 -。

各种对流换热过程的特征及其计算公式对流换热是指热量通过传导和传导的方式从一个物体转移到另一个物体的过程。
在许多工程和自然现象中,对流换热都起着重要的作用。
下面是各种对流换热过程的特征及其计算公式。
1.强制对流换热:强制对流换热是指通过对流传热介质(如气体或液体)的外力驱动,使热量从一个物体转移到另一个物体的过程。
其特征包括:-较高的传热速率:由于外力使传热介质保持流动状态,因此强制对流传热速率较高。
-计算公式:Q=h*A*(Ts-T∞)其中,Q是传热速率,h是对流换热系数,A是传热面积,Ts是表面温度,T∞是流体温度。
2.自然对流换热:自然对流换热是指在没有外力驱动的情况下,通过自然气流或自然对流传热介质(如气体或液体)进行热量传输的过程。
其特征包括:-由温度差引起的自然循环:由于温度差异造成的密度差异,导致气体或液体在物体表面形成循环,从而传热。
-计算公式:Q=α*A*ΔT其中,Q是传热速率,α是自然对流换热系数,A是传热面积,ΔT 是温度差。
3.相变换热:相变换热是指物体在相变过程中吸收或释放的热量。
其特征包括:-温度保持不变:当物体处于相变过程中时,温度保持不变,热量主要用于相变过程。
-计算公式:Q=m*L其中,Q是传热速率,m是物体的质量,L是单位质量的相变潜热。
4.辐射换热:辐射换热是指通过电磁辐射传播热量的过程。
其特征包括:-不需要传热介质:辐射传热不需要传热介质,可以在真空中传递热量。
-计算公式:Q=ε*σ*A*(Th^4-Tc^4)其中,Q是传热速率,ε是辐射率,σ是斯特藩-玻尔兹曼常数,A 是物体表面积,Th和Tc分别是辐射物体和周围环境的温度。
总结:不同的对流换热过程具有不同的特征和计算公式。
在实际应用中,根据具体的情况选择适当的计算公式可以帮助我们准确计算和分析热量的传递过程。
要注意,实际的对流换热过程可能是多种换热方式的复合,需要综合考虑不同的换热方式。

自然对流及强制对流及计算实例自然对流和强制对流是流体传热过程中两种常见的方式。
本文将分别介绍自然对流和强制对流的概念及原理,并给出两个计算实例。
一、自然对流自然对流是指在一定温度差的作用下,由于密度差异而产生的流动。
当热源加热后,周围的流体受热膨胀,密度减小,上升;而冷却的流体密度增大,下降。
这种密度差异引起的流动即为自然对流。
自然对流的计算通常基于格拉希霍夫数(Grashof number),其计算公式为:Gr=g×β×(Ts−T∞)×L^3/ν^2其中,g为重力加速度,β为热膨胀系数,Ts为表面温度,T∞为远场流体温度,L为特征长度,ν为流体的运动黏度。
计算实例:假设有一个热源表面温度Ts=100°C,周围流体的温度为T∞=20°C,表面积为A=2m^2,特征长度L=1m,流体的运动黏度为ν=0.01m^2/s,重力加速度g=9.8m/s^2,热膨胀系数β=0.001K^-1、求解此情况下的格拉希霍夫数。
解:Gr=g×β×(Ts−T∞)×L^3/ν^2=9.8×0.001×(100-20)×1^3/0.01^2=7840根据格拉希霍夫数的大小,可以判断自然对流的状况。
当Gr<10^8时,自然对流的影响较小;当10^8<Gr<10^10时,自然对流的影响较大;当Gr>10^10时,自然对流的影响非常显著。
二、强制对流强制对流是通过外部力驱动流体运动,使传热加剧的一种方式。
常见的外部力包括压差、气流、涡流等。
强制对流通常具有较高的传热效率和传热速度。
强制对流的计算通常基于雷诺数(Reynolds number),其计算公式为:Re=ρ×V×L/μ其中,ρ为流体密度,V为流体速度,L为特征长度,μ为流体的黏度。
计算实例:假设有一段液体流经一个直径为0.1m的水管,流速为1m/s,液体密度为1000kg/m^3,液体黏度为0.01kg/ms。


自然对流传热强制对流传热机理
自然对流传热是指在液体或气体中由于温度差异而产生的自发流动,而强制对流传热是通过外部力量驱动使流体产生流动。
自然对流传热机理:
当液体或气体中存在温度差异时,由于热胀冷缩效应,密度较高的冷流体下沉,密度较低的热流体上升,从而形成自然对流。
这种流动会在液体或气体中形成对流传热。
自然对流传热的速率取决于温差、流体性质、流体的运动性能和流体与外部物体之间的传热面积。
强制对流传热机理:
强制对流传热是通过外部力量驱动使流体产生流动,这种流动可以通过搅拌器、风扇、泵等方式实现。
外部力量的作用下,流体会形成流动,从而增加了传热的速率。
强制对流传热的速率可以通过控制外部力量来调节。
总而言之,自然对流传热是通过温度差异所产生的自发流动,而强制对流传热是通过外部力量驱动使流体产生流动。
两种机制在传热过程中起着重要的作用,具体的传热速率取决于流体的性质和运动性能以及与外部物体的接触面积。

自然对流与强制对流及计算实例热设计就是电子设备开发中必不可少得环节。
本连载从热设计得基础——传热着手,介绍基本得热设计方法。
前面介绍得热传导具有消除个体内温差得效果。
上篇绍得热对流,则具有降低平均温度得效果。
下面就通过具体得计算来分别说明自然对流与强制对流得情况。
首先,自然对流得传热系数可以表述为公式(2)。
热流量=自然对流传热系数×物体表面积×(表面温度-流体温度) (2)很多文献中都记载了计算传热系数得公式,可以把流体得特性值带入公式中进行计算,可以适用于所有流体。
但每次计算得时候,都必须代入五个特性值。
因此,公式(3)事先代入了空气得特性值,简化了公式。
自然对流传热系数h=2 、51C(⊿T/L)0、25(W/m2K) (3)2、51就是代入空气得特性值后求得得系数。
如果就是向水中散热,2、51需要换成水得特性值。
公式(3)出现了C、L、⊿T三个参数。
C与L从表1中选择。
例如,发热板竖立与横躺时,周围空气得流动各不相同。
对流传热系数也会随之改变,系数C就负责吸收这一差异。
代表长度L与C就是成对定义得。
计算代表长度得公式因物体形状而异,因此,在计算得时候,需要从表1中选择相似得形状。
需要注意得就是,表示大小得L位于分母。
这就表示物体越小,对流传热系数越大。
⊿T就是指公式(2)中得(表面温度-流体温度)。
温差变大后,传热系数也会变大。
物体与空气之间得温差越大,紧邻物体那部分空气得升温越大。
因此,风速加快后,传热系数也会变大。
公式(3)叫做“半理论半实验公式”。
第二篇中介绍得热传导公式能够通过求解微分方程得方式求出,但自然对流与气流有关,没有完全适用得理论公式。
能建立理论公式得,只有产生得气流较简单得平板垂直放置得情况。
因为在这种情况下,理论上得温度边界线得厚度可以计算出来。
但就是,如果发热板水平放置,气流就会变得复杂,计算得难度也会增加。
这种情况下,就要根据原始得理论公式,通过实验求出系数。


自然对流与强制对流及计算实例自然对流是指通过密度差异引起的流体运动。
当热量在流体中引起密度变化时,会产生浮力,使得流体发生运动,形成自然对流。
自然对流的特点是流动速度较慢,主要发生在静止的流体中。
强制对流是指通过外部力量引起的流体运动。
外部力可以包括压力差、离心力、涡流等。
强制对流的特点是流动速度较快,主要发生在外界施加力的情况下。
下面将通过两个计算实例来分别说明自然对流和强制对流的特点。
自然对流计算实例:假设有一个加热器,它发出的热量通过空气引起自然对流。
现在我们希望计算空气温度沿着加热器表面的变化情况。
首先,我们需要根据加热器表面的温度分布和空气的物理特性来确定空气的密度变化。
假设加热器表面的温度为T1,空气的初始温度为T0,空气的密度为ρ0,空气的热膨胀系数为β。
根据自然对流的特点,我们可以假设空气在垂直方向上的速度为v(z),其中z表示高度。
根据连续性方程,流体的质量守恒原理可以得到:ρ(z)v(z)A = const.其中A表示加热器截面的面积。
根据浮力和牛顿第二定律的平衡条件,可以得到:F(z) - mg = const.其中F(z)表示在高度z上空气受到的浮力,m表示空气的质量,g表示重力加速度。
根据马格努斯公式,可以得到:F(z)=ρ(z)Vg其中V表示加热器截面的体积。
综合以上方程,可以得到:ρ(z)v(z)A=ρ0V即:v(z)=(ρ0V)/(Aρ(z))根据热力学第一定律,可以得到:v(z) = sqrt(2gβ(T1 - T0)/ρ0)根据上述方程,我们可以计算空气在各个高度上的速度分布,从而得到空气温度沿着加热器表面的变化情况。
强制对流计算实例:假设有一根直径为D的管道,长度为L,两端分别接有一个压力差为ΔP的气缸。
现在我们希望计算气体在管道中的流速。
首先,我们需要根据气体的物理特性和流体动力学原理来确定气体的流动情况。
假设气体的密度为ρ,黏度为μ,管道的内壁粗糙度为ε。

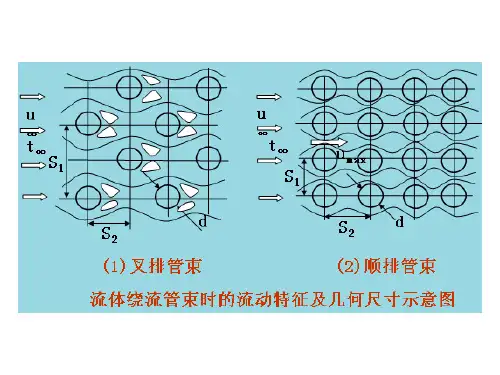
对流换热系数的确定核心提示:1.自然对流时的对流换热系数炉墙、炉顶和架空炉底与车间空气间的对流换热均属自然对流换热。
2.强制对流时的对流换热系数(1)气流沿1.自然对流时的对流换热系数炉墙、炉顶和架空炉底与车间空气间的对流换热均属自然对流换热。
2.强制对流时的对流换热系数(1)气流沿平面强制流动时气流沿平面流动时,烧结炉其对流换热系数可按表1-1的近似公式计算。
表1-1对流换热系数计算vo=C4.65(m/s) x;o>4.65(m/s)光滑表面a=5.58+4.25z'o a^V.Slvg78轧制表面a-=5.81+4.25vo a=7.53vin.粗糙表面o=6.16+4.49vo a=T.94vi78气流沿长形工件强制流动时当加热长形工件时,循环空气对工件表面的对流换热系数可用下述近似公式计算气流在通道内层流流动时气流呈层流流动时,对流换热系数主要决定于炉气的热导率,而与炉气的流速无关。
绝对黑体的概念当物体受热后一部分热能转变为辐射能并以电磁波的形式向外放射,其波长从lfmi到若干m。
各种不同波长的射线具有不同性质,可见光和红外线能被物体吸收转化为热能,称它们为热射线。
各种物体由于原子结构和表面状态的不同,其辐射和吸收热射线的能力有明显差别。
当能量为Q的一束热射线投射到物体表面时,也和可见光一样,一部分能量Qa将被吸收,一部分能量Qr被反射,还有一部分能量Qu透射过物体(如图1-5)。
按能量守恒定律则有图1-5辐射能的吸收、反射和透过如果A=l,则R=D=0,即辐射能全部被吸收,这种物体称绝对黑体,简称黑体。
如果R=l,则A=D=0,即辐射能全部被反射,这种物体称绝对白体,简称白体。
如果D= 1,则A=K=0,即辐射能全部被透过,这种物体称绝对透过体,简称透过体。
自然界中,黑体、白体和透过体是不存在的,它们都是假定的理想物体。
对于一种实际物体来说数值,不仅取决于物体的特性,还与表面状态、温度以及投射射线的波长等有关。

对流和辐射计算公式流和辐射计算公式是在热力学和辐射传热学中广泛应用的公式,用于计算热量和热能的传递。
一、流计算公式1.线热流密度(q)计算公式:线热流密度是单位时间内通过单位长度的传热量,通常以瓦特/米表示。
q=λ*ΔT/Δx其中,q表示线热流密度,λ表示热导率,ΔT表示温度差,Δx表示传热距离。
这个公式适用于常导热系数情况下的传热。
2.对流热传导公式(q):对流热传导是通过流体(气体或液体)传递热量的过程,可以通过以下公式计算:q=h*A*ΔT其中,q表示热量传递速率,h表示对流传热系数,A表示传热面积,ΔT表示温差。
3.对流传热系数(h)计算:对流传热系数是对流热传导中的一个参数,它表示单位面积传递的热量。
对于强制对流和自然对流,其计算公式分别为:对于强制对流:h=Nu*λ/L对于自然对流:h=Nu*λ/Lf其中,h表示传热系数,Nu表示努塞尔数,λ表示热导率,L表示流动方向的特征长度,Lf表示特征长度。
4.热传导效应(Bi):热传导效应是描述对流与热传导相对重要性的参数,可以用如下公式计算:Bi=h*L/λ其中,Bi表示热传导效应,h表示对流传热系数,L表示特征长度,λ表示热导率。
当Bi<0.1时,热传导可以忽略不计;当Bi>0.1时,热传导效应非常重要。
1.斯特藩-玻尔兹曼定律:根据斯特藩-玻尔兹曼定律,一个黑体单位时间内发射的辐射功率(P)与其绝对温度(T)的四次方成正比,可以用以下公式表示:P=σ*ε*A*T^4其中,P表示辐射功率,σ为斯特藩-玻尔兹曼常数(5.67*10^-8W/(m^2·K^4)),ε表示发射率,A表示表面积,T表示绝对温度。
2.斯特藩-玻尔兹曼定律(应用于非黑体):对于非黑体,通过引入一个修正因子,斯特藩-玻尔兹曼定律可以表示为:P=σ*ε*A*T^4*F其中,P表示辐射功率,σ为斯特藩-玻尔兹曼常数,ε表示发射率,A表示表面积,T表示绝对温度,F表示修正因子。
自然对流强制对流传热流化床系数的比较
答案:
自然对流传热系数与强制对流时的对流传热系数相比,自然对流传热系数要小得多。
自然对流和强制对流是两种不同的对流换热方式,它们的传热系数受到流体流动的原因和条件的影响。
自然对流是由于温差引起的密度差异导致的流体运动,而强制对流则是通过外部力量(如泵或风扇)驱动的流体运动。
这两种流动形态决定了它们各自的传热效率。
自然对流的传热系数相对较低,因为它依赖于流体内部的自然温差引起的密度差异,这种流动通常较为缓慢,不利于高效的热量传递。
例如,空气自然对流换热系数大约在5到25 W/(m²·℃)之间。
强制对流则通过外部力量驱动流体流动,可以显著提高流速和湍流程度,从而增强传热效果。
强制对流的流速较高,因此其对流换热系数也较高,有利于提高传热效率。
流化床作为一种特殊的传热方式,其传热系数与自然对流和强制对流相比,可能会有所不同,具体取决于流化床的操作条件和流体特性。
但一般来说,强制对流的传热效率要高于自然对流,而流化床的传热效率可能会介于两者之间,具体取决于流化床的设计和操作参数。
综上所述,虽然具体数值会因条件而异,但总体上可以认为自然对流的传热系数与强制对流的传热系数相比要小得多。
这表明在设计和优化传热系统时,通过适当的方式(如使用泵或风扇)促进流体流动,可以提高传热效率。
自然对流与强制对流及计算实例集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#自然对流与强制对流及计算实例热设计是电子设备开发中必不可少的环节。
本连载从热设计的基础——传热着手,介绍基本的热设计方法。
前面介绍的热传导具有消除个体内温差的效果。
上篇绍的热对流,则具有降低平均温度的效果。
下面就通过具体的计算来分别说明自然对流与强制对流的情况。
首先,自然对流的传热系数可以表述为公式(2)。
热流量=自然对流传热系数×物体表面积×(表面温度-流体温度) (2)很多文献中都记载了计算传热系数的公式,可以把流体的特性值带入公式中进行计算,可以适用于所有流体。
但每次计算的时候,都必须代入五个特性值。
因此,公式(3)事先代入了空气的特性值,简化了公式。
自然对流传热系数h=2 .51C(⊿T/L)(W/m2K) (3)是代入空气的特性值后求得的系数。
如果是向水中散热,需要换成水的特性值。
公式(3)出现了C、L、⊿T三个参数。
C和L从表1中选择。
例如,发热板竖立和横躺时,周围空气的流动各不相同。
对流传热系数也会随之改变,系数C就负责吸收这一差异。
代表长度L与C是成对定义的。
计算代表长度的公式因物体形状而异,因此,在计算的时候,需要从表1中选择相似的形状。
需要注意的是,表示大小的L位于分母。
这就表示物体越小,对流传热系数越大。
⊿T是指公式(2)中的(表面温度-流体温度)。
温差变大后,传热系数也会变大。
物体与空气之间的温差越大,紧邻物体那部分空气的升温越大。
因此,风速加快后,传热系数也会变大。
公式(3)叫做“半理论半实验公式”。
第二篇中介绍的热传导公式能够通过求解微分方程的方式求出,但自然对流与气流有关,没有完全适用的理论公式。
能建立理论公式的,只有产生的气流较简单的平板垂直放置的情况。
因为在这种情况下,理论上的温度边界线的厚度可以计算出来。
但是,如果发热板水平放置,气流就会变得复杂,计算的难度也会增加。
天然对流与强迫对流及盘算实例热设计是电子装备开辟中必不成少的环节.本连载从热设计的基本——传热着手,介绍根本的热设计办法.前面介绍的热传导具有清除个别内温差的后果.上篇绍的热对流,则具有下降平均温度的后果.下面就经由过程具体的盘算来分离解释天然对流与强迫对流的情形.起首,天然对流的传热系数可以表述为公式(2).热流量=天然对传播热系数×物体概况积×(概况温度-流体温度) (2)许多文献中都记录了盘算传热系数的公式,可以把流体的特征值带入公式中进行盘算,可以实用于所有流体.但每次盘算的时刻,都必须代入五个特征值.是以,公式(3)事先代入了空气的特征值,简化了公式.天然对传播热系数h=2 .51C(⊿T/L)0.25(W/m2K) (3)2.51是代入空气的特征值后求得的系数.假如是向水中散热,2.51须要换成水的特征值.公式(3)消失了C.L.⊿T三个参数.C和L从表1中选择.例如,发烧板竖立和横躺时,四周空气的流淌各不雷同.对传播热系数也会随之改变,系数C就负责接收这一差别.代表长度L与C是成对界说的.盘算代表长度的公式因物体外形而异,是以,在盘算的时刻,须要从表1中选择类似的外形.须要留意的是,暗示大小的L位于分母.这就暗示物体越小,对传播热系数越大.⊿T是指公式(2)中的(概况温度-流体温度).温差变大后,传热系数也会变大.物体与空气之间的温差越大,紧邻物体那部分空气的升温越大.是以,风速加快后,传热系数也会变大.公式(3)叫做“半理论半试验公式”.第二篇中介绍的热传导公式可以或许经由过程求解微分方程的方法求出,但天然对流与气流有关,没有完整实用的理论公式.能树立理论公式的,只有产生的气流较简略的平板垂直放置的情形.因为在这种情形下,理论上的温度鸿沟线的厚度可以盘算出来.但是,假如发烧板程度放置,气流就会变得庞杂,盘算的难度也会增长.这种情形下,就要依据原始的理论公式,经由过程试验求出系数.也就是说,在公式(3)中,理论盘算得出的数值0.25可以直接套用,C的值则要经由过程试验求出.天然对传播热系数无法大幅改变图4:天然对传播热系数无法大幅改变物体沿流淌偏向的尺寸越小,单位面积的散热量越大.天然对流的传热系数随斜率和面的曲率变更,但变更的幅度不大.而强迫空冷可以经由过程进步风速和湍流化,大幅改变传热系数.外形和设置装备摆设对于天然对流的传热系数会产生多大的影响(图4)?举例来说,平面的传热系数h等于2.51×0.56×((Ts-Ta)/H)0.25,而圆筒面的传热系数h等于2.51×0.55×((Ts-T<a)/H)0.25.平面为0.56,圆筒面为0.55,不同只有2%阁下,由此可见,平面与圆筒面的传热系数不同不大.这就意味着当发烧板竖直时,下概况的传热才能会越来越差,而上概况的传热才能根本不变.产生竖直后,下概况只受到沿竖直面的向量成分的浮力.也就是说,下概况的浮力变弱.假设垂直时的传热系数为hv,竖直时的传热系数为hθ,物体沿垂直偏向竖直角度θ,此时,下概况的传热系数大致为:hθ=hv.(cosθ)0.25 (4)(θ在0~60度阁下的规模内时公式成立)假如竖直45度,传热系数将缩小8%阁下.由此可知,即使竖直发烧板,传热系数也没有太大变更.但一旦接近程度,传热系数就会急剧下降.经由过程上面的介绍,大家应当已经明确,进步天然对传播热系数其实难度颇大.但物体越小,对传播热系数越大.比方说,我们可以采取把散热器翅片朋分成几个部分的办法.在翅片截断的地方,热鸿沟层将重置,起到阻拦鸿沟层变厚的感化,借此可以进步对传播热系数.但如许做会削减翅片的概况积,总的散热才能依旧变更不大.强迫对传播热系数的简略单纯盘算公式接下来看看强迫对流的传热系数.装配电扇的强迫对流的公式如下. 热流量=强迫对传播热系数×物体概况积×(概况温度-流体温度) (5)强迫对传播热系数的盘算也有许多种公式(图5).图5:强迫对流热传导的简略单纯盘算公式强迫对流时,盘算热流量应用与强迫对流对应的传热系数.依据流体的流淌是在层流区域照样在湍流区域,盘算应用的传热系数均不合.强迫对流时,一旦进步风速,状况也会在途中随之改变.比方说,即等于在没有风的房间里,喷鼻烟的烟雾也是一开端径直向上,在途中四处飘散.径直向上的地方是层流,飘散的地方是湍流.在层流区,喷鼻烟烟雾中颗粒物是单向流淌.而在湍流区,颗粒物会到处乱飞,跟着时光的推移,烟雾的外形将产生改变.湍流长短定常流,流向会随时光改变.印刷电路板周边的空气也一样,最初为层流,半途改变成湍流.从散热的角度来看,湍流更有利于散热.因为在湍流中,热空气与冷空气将互相混杂,冷空气会得到接近壁面的机遇,加倍轻易传热.也就是说,湍流化可以或许下降温度.尤其是对于低流速和水冷式,湍流化十分有用.但湍流化也会导致流体阻力增大,这回增长电扇和水泵的负荷.强迫形成湍流化的肇端点时,可以采取在流体的通道中设置崛起物(湍流促进器)的方法.在强迫空冷的散热器中,可以看到这种设置崛起的例子(注4).(注4)天然对流也消失湍流,但在电子产品的热设计中,可以以为根本不消失天然湍流化.但温度达到500~600℃的高温后,因为浮力加强,所以也会消失湍流化.遏制流淌的力与促进流淌的力,二者的均衡决议着湍流的肇端点.遏制流淌的力是粘性力,在壁面邻近的感化较强,而促进流淌的力则是惯性力或浮力.粘性力强,则流淌受到遏制.因为气流之间会互相束缚.例如,在细缝和接近壁面的地方,粘性力较强.同样,翅片与翅片之间的距离越窄,粘性力越强,也就很难产生湍流化.而惯性力由速度产生,只要进步速度,惯性力就会随之增大. 仍以喷鼻烟的烟雾为例,在烟雾开端流淌时,热源上部的空气迟缓上升,产生流淌的区域也十分狭小.但跟着流淌的进行,四周的静止流体也被带动,流淌的区域不竭扩展.是以,粘性力会下降.而在浮力的加快感化下,空气的流速不竭加快.因而产生了湍流化.依据层流和湍流的不合,强迫对流的传热系数公式消失相当大的不同.起首是层流的公式.层流平均传热系数hm=3.86√(V/L) (6)个中参加了空气的特征值,3.86与天然对流公式(3)中的2.51寄义雷同.湍流相干公式是试验性公式,系数和指数都有变更.湍流平均传热系数hm=6×(V/L0.25)0.8 (7)要想简略进行断定的话,无妨把两个系数都盘算出来,选择传热系数大的一方.下面,让我们应用上面介绍的常识,定量研讨对流的散热才能. 【演习1】平板的放置方法与散热才能假设有一块长200mm.宽100mm(疏忽厚度),温度保持在40℃的平板(图6),平板的温度平均,并且没有热辐射,下列放置方法的散热才能有多大不同?图6:【演习1】平板的放置方法与散热才能思虑纵长200mm×横宽100mm(疏忽厚度)的平板的升温保持在40K(℃)时,图中3种模式的散热才能.假设平板的温度平均,且没有热辐射.(a)垂直放置(以100mm的短边为高)(b)垂直放置(以200mm的长边为高)(c)程度放置须请求的数值是热流量,相当于散热量,这就必须起首求出传热系数,须要应用公式(3).(a)和(b)是垂直放置,C值应用平板垂直放置时的数值.因为升温固定在40K(℃),所以⊿T为40(注5).至此,所稀有值已经完好,可以盘算出传热系数.(注5)温度必须要多次盘算,比较麻烦.假如不知道温度,就求不出传热系数,是以,最初先假设温度为30℃,盘算出h.把成果代入公式进行盘算,得到的温度一般不等于30℃,此时要应用得出的数值从新盘算.经由重复盘算,逐渐逼近精确数值.(a)以100mm的短边为高的垂直平板传热系数 h概况积S=0.1×0.2×2=0.04m2散热量W=0.04×6.29×40=10.1W(b)以200mm的长边为高的垂直平板传热系数 h=概况积S=0.1×0.2×2=0.04m2散热量W=0.04×5.29×40=8.5W由上述盘算可知,(b)的散热量比(a)低15%阁下.但盘算的前提是平板的温度完整平均,也就是导热系数无穷大,假如是印刷电路板,散热量上的不同还会更大.倘使导热才能差,平板上侧与下侧之间将会消失温差.纵向放置的话,上侧与下侧的温差会更大,最高温度将消失相当大的不同.程度放置时,平板上侧与下侧的传热系数不合,盘算比较庞杂.上侧的C值为0.52,下侧为0.26,刚好是上侧的一半.是以,下侧的散热量也是上侧的一半.这种情形须要分离盘算上侧和下侧的散热量,然后相加.(c)程度放置平板代表长度 L=(0.1×0.2×2)/(0.1+0.2)=0.133m上概况对传播热系数 h=5.43 W/m2K上概况概况积S=0.1×0.2=0.02m2上概况散热量W=0.02×5.43×40=4.34W下概况对传播热系数 h=2.72 W/m2K下概况概况积S=0.1×0.2=0.02m2下概况散热量W=0.02×2.72×40=2.17W总散热量 W=4.34+2.17=6.51W这采取的是热盘算中经常应用的盘算每个面的发烧量,然后相加的办法.【演习2】大空间产生热对流,小空间产生热传导接下来看一下在200mm×200mm×20mm的平整机壳中装配180mm×180mm×1mm的电路板(发烧功率5W)的情形(图7). 图7:【演习2】空间大为热对流,空间小为热传导思虑在尺寸为200mm×200mm×20mm的机壳内装配180mm×180mm×1mm的印刷电路板(发烧功率为5W)时,图中3种情形下的散热才能.假设没有热辐射.大家可以将其算作是加热器.关于电路板的装配地位,下面哪种是精确的?别的,这里假设热辐射可以疏忽.(a)电路板设置在上部(距离机壳顶面1mm)时温度最低(b)电路板设置在中部(距离机壳顶面7.5mm)时温度最低(c)电路板设置鄙人部(距离机壳顶面15mm)时温度最低这个标题中有一点要留意,那就是空间狭小.空气无法流淌时,产生的是热传导,空间够大时产生的是热对流.划分的界线值随状况和发烧量而变,大致为几毫米.假如小于该界线值,空气将无法流淌,大于该界线值空气就可以流淌.定性地来说,只要距离足够,空气就能轮回,从而带走热能,使部件释放的热传到机壳顶面并发散出去,由此起到降温的感化.上面提到,当距离很小时产生的是热传导.热传导的热阻等于空气层的厚度/(传热面积×空气的导热系数),是以(a)的情形下, 热阻(1mm)=0.001/(0.18×0.18×0.03)=1.03K/W;(b)的情形下,热阻(7.5㎜)=0.0075/(0.18×0.18×0.03)=7.7K/W,比(a)的热阻大许多.而在(c)的情形下,距离达到15mm,可以以为能充分产生对流.此时,对流的热阻增长到两个(电路板概况→空气,空气→机壳顶面).按照传热系数为10W/m2K盘算,电路板到空气的对流热阻=1/(电路板概况积×天然对传播热系数(程度))空气到机壳的对流热阻=1/(机壳概况积×天然对传播热系数(程度))热阻(15mm)=1/(0.18×0.18×10)+1/(0.2×0.2×10)由此可知,(a)的情形下热阻最小.温度最低.估量(b)的温度最高,原因是根本没有产生流淌.传热系数单靠手工盘算很可贵到精确成果,是以,笔者试着应用热流体解析模仿进行周详盘算,得到了这三种情形下电路板的温度.成果为,当情形温度为35℃时,(a)距离1mm时,电路板温度为56℃(b)距离7.5mm时,电路板温度为72.5℃(c)距离15mm时,电路板温度为59.6℃这就意味着必须要防止温度最高的(b)的情形.5~7mm阁下的距离难以产生对流,进行热传导时消失空气层过厚的问题,很难散热,是最好要避开的距离.装配部件的时刻很轻易产生这么大的裂缝,在这种情形下,无妨直接让电路板与机壳接触,经由过程热传导散热.。
什么是自然对流传热强制对流传热机理自然对流和强制对流是传热中常用的两种机制。
对于物体的传热过程而言,了解这两种机制对于提高传热效率非常重要。
首先,我们来了解一下自然对流传热。
自然对流传热是指在没有外力驱动的情况下,由于温度差异引起的流体运动。
举一个简单的例子,我们烧开一锅水,水底部受热,热量导致水底部的温度升高,使得水在底部膨胀,密度减小。
这样,热水就会上浮,而凉水则会下沉。
这种自然的流动,将有助于传热,将热量从底部传递到其他部位。
自然对流传热在许多领域都有应用,例如地球大气层的对流循环就是自然对流的典型示例。
而强制对流传热则是在外力的驱动下,例如风,液流等,由于流体的强制运动传导热量。
以汽车的散热风扇为例,风扇通过强制流动的气流,将汽车发动机散发的热量迅速带走。
同样的原理也适用于液流,例如水在工业冷却设备中的运用,液体通过管道强制流动,以带走热量,从而冷却设备。
自然对流和强制对流在传热中的机理略有不同。
自然对流主要依靠温度差异产生的密度差来驱动流动,而强制对流则依靠外力推动流体运动。
此外,在传热效率上也存在差异。
自然对流传热受限于流体自身产生的流动,热量传递效率相对较低。
而强制对流传热通过外力的驱动,可以达到更高的传热效率,从而更快、更有效地将热量从热源传递到周围环境。
在实际应用中,我们需要根据不同的情况选择合适的传热机制。
对于自然对流传热,因为其效率较低,通常适用于传热量较小,或者不需要特别快速传热的情况下。
例如,太阳能集热器利用太阳辐射产生的热量,热量会经由集热器内的流体自然对流传递出去。
而对于强制对流传热,由于其更高的传热效率,通常适用于传热量较大,或者需要迅速传热的情况下。
综上所述,自然对流传热和强制对流传热是传热过程中两种常见的机制。
了解这两种机制的原理和适用范围,对于在实际应用中选择合适的传热方式具有重要意义。
无论是优化热能利用效率,还是设计高效的传热设备,都离不开对这两种机制的深入理解和充分应用。
自然对流与强制对流及计算实例热设计是电子设备开发中必不可少的环节。
本连载从热设计的基础——传热着手,介绍基本的热设计方法。
前面介绍的热传导具有消除个体内温差的效果。
上篇绍的热对流,则具有降低平均温度的效果。
下面就通过具体的计算来分别说明自然对流与强制对流的情况。
首先,自然对流的传热系数可以表述为公式(2)。
热流量=自然对流传热系数×物体表面积×(表面温度-流体温度) (2)很多文献中都记载了计算传热系数的公式,可以把流体的特性值带入公式中进行计算,可以适用于所有流体。
但每次计算的时候,都必须代入五个特性值。
因此,公式(3)事先代入了空气的特性值,简化了公式。
自然对流传热系数h=2 .51C(⊿T/L)0.25(W/m2K) (3)2.51是代入空气的特性值后求得的系数。
如果是向水中散热,2.51需要换成水的特性值。
公式(3)出现了C、L、⊿T三个参数。
C和L从表1中选择。
例如,发热板竖立和横躺时,周围空气的流动各不相同。
对流传热系数也会随之改变,系数C 就负责吸收这一差异。
代表长度L与C是成对定义的。
计算代表长度的公式因物体形状而异,因此,在计算的时候,需要从表1中选择相似的形状。
需要注意的是,表示大小的L位于分母。
这就表示物体越小,对流传热系数越大。
⊿T是指公式(2)中的(表面温度-流体温度)。
温差变大后,传热系数也会变大。
物体与空气之间的温差越大,紧邻物体那部分空气的升温越大。
因此,风速加快后,传热系数也会变大。
公式(3)叫做“半理论半实验公式”。
第二篇中介绍的热传导公式能够通过求解微分方程的方式求出,但自然对流与气流有关,没有完全适用的理论公式。
能建立理论公式的,只有产生的气流较简单的平板垂直放置的情况。
因为在这种情况下,理论上的温度边界线的厚度可以计算出来。
但是,如果发热板水平放置,气流就会变得复杂,计算的难度也会增加。
这种情况下,就要根据原始的理论公式,通过实验求出系数。
自然对流与强制对流及计算实例热设计是电子设备开发中必不可少的环节。
本连载从热设计的基础——传热着手,介绍基本的热设计方法。
前面介绍的热传导具有消除个体内温差的效果。
上篇绍的热对流,则具有降低平均温度的效果。
下面就通过具体的计算来分别说明自然对流与强制对流的情况。
首先,自然对流的传热系数可以表述为公式(2)。
热流量=自然对流传热系数×物体表面积×(表面温度-流体温度) (2)很多文献中都记载了计算传热系数的公式,可以把流体的特性值带入公式中进行计算,可以适用于所有流体。
但每次计算的时候,都必须代入五个特性值。
因此,公式(3)事先代入了空气的特性值,简化了公式。
自然对流传热系数h=2 .51C(⊿T/L)(W/m2K) (3)是代入空气的特性值后求得的系数。
如果是向水中散热,需要换成水的特性值。
公式(3)出现了C、L、⊿T三个参数。
C和L从表1中选择。
例如,发热板竖立和横躺时,周围空气的流动各不相同。
对流传热系数也会随之改变,系数C 就负责吸收这一差异。
代表长度L与C是成对定义的。
计算代表长度的公式因物体形状而异,因此,在计算的时候,需要从表1中选择相似的形状。
需要注意的是,表示大小的L位于分母。
这就表示物体越小,对流传热系数越大。
⊿T是指公式(2)中的(表面温度-流体温度)。
温差变大后,传热系数也会变大。
物体与空气之间的温差越大,紧邻物体那部分空气的升温越大。
因此,风速加快后,传热系数也会变大。
公式(3)叫做“半理论半实验公式”。
第二篇中介绍的热传导公式能够通过求解微分方程的方式求出,但自然对流与气流有关,没有完全适用的理论公式。
能建立理论公式的,只有产生的气流较简单的平板垂直放置的情况。
因为在这种情况下,理论上的温度边界线的厚度可以计算出来。
但是,如果发热板水平放置,气流就会变得复杂,计算的难度也会增加。
这种情况下,就要根据原始的理论公式,通过实验求出系数。
也就是说,在公式(3)中,理论计算得出的数值可以直接套用,C的值则要通过实验求出。
自然对流传热系数无法大幅改变?图4:自然对流传热系数无法大幅改变物体沿流动方向的尺寸越小,单位面积的散热量越大。
自然对流的传热系数随斜率和面的曲率变化,但变化的幅度不大。
而强制空冷可以通过提高风速和湍流化,大幅改变传热系数。
形状和配置对于自然对流的传热系数会产生多大的影响(图4)?举例来说,平面的传热系数h等于××((Ts-Ta)/H),而圆筒面的传热系数h等于××((Ts-T<a)/H)。
平面为,圆筒面为,差别只有2%左右,由此可见,平面与圆筒面的传热系数差别不大。
这就意味着当发热板倾斜时,下表面的传热能力会越来越差,而上表面的传热能力基本不变。
发生倾斜后,下表面只受到沿倾斜面的向量成分的浮力。
也就是说,下表面的浮力变弱。
假设垂直时的传热系数为hv,倾斜时的传热系数为hθ,物体沿垂直方向倾斜角度θ,此时,下表面的传热系数大致为:hθ=hv.(cosθ) (4)(θ在0~60度左右的范围内时公式成立)如果倾斜45度,传热系数将缩小8%左右。
由此可知,即使倾斜发热板,传热系数也没有太大变化。
但一旦接近水平,传热系数就会急剧降低。
通过上面的介绍,大家应该已经明白,提高自然对流传热系数其实难度颇大。
但物体越小,对流传热系数越大。
比方说,我们可以采用把翅片分割成几个部分的方法。
在翅片截断的地方,热边界层将重置,起到阻止边界层变厚的作用,借此可以提高对流传热系数。
但这样做会减少翅片的表面积,总的散热能力依然变化不大。
强制对流传热系数的简易计算公式接下来看看强制对流的传热系数。
安装的强制对流的公式如下。
热流量=强制对流传热系数×物体表面积×(表面温度-流体温度) (5)强制对流传热系数的计算也有很多种公式(图5)。
图5:强制对流热传导的简易计算公式强制对流时,计算热流量使用与强制对流对应的传热系数。
根据流体的流动是在层流区域还是在湍流区域,计算使用的传热系数均不同。
强制对流时,一旦提高风速,状态也会在途中随之改变。
比方说,即便是在没有风的房间里,香烟的烟雾也是一开始径直向上,在途中四处飘散。
径直向上的地方是层流,飘散的地方是湍流。
在层流区,香烟烟雾中颗粒物是单向流动。
而在湍流区,颗粒物会到处乱飞,随着时间的推移,烟雾的形状将发生改变。
湍流是非定常流,流向会随时间改变。
印刷电路板周边的空气也一样,最初为层流,中途转变为湍流。
从散热的角度来看,湍流更有利于散热。
因为在湍流中,热空气与冷空气将相互混合,冷空气会得到靠近壁面的机会,更加容易传热。
也就是说,湍流化能够降低温度。
尤其是对于低流速和水冷式,湍流化十分有效。
但湍流化也会导致流体阻力增大,这回增加风扇和水泵的负荷。
强制形成湍流化的起始点时,可以采用在流体的通道中设置突起物(湍流促进器)的方式。
在强制空冷的散热器中,可以看到这种设置突起的例子(注4)。
(注4)自然对流也存在湍流,但在电子产品的热设计中,可以认为基本不存在自然湍流化。
但温度达到500~600℃的高温后,因为浮力增强,所以也会出现湍流化。
遏制流动的力与促进流动的力,二者的平衡决定着湍流的起始点。
遏制流动的力是粘性力,在壁面附近的作用较强,而促进流动的力则是惯性力或浮力。
粘性力强,则流动受到遏制。
因为气流之间会相互约束。
例如,在细缝和靠近壁面的地方,粘性力较强。
同样,翅片与翅片之间的距离越窄,粘性力越强,也就很难发生湍流化。
而惯性力由速度产生,只要提高速度,惯性力就会随之增大。
仍以香烟的烟雾为例,在烟雾开始流动时,热源上部的空气缓慢上升,发生流动的区域也十分狭窄。
但随着流动的进行,周围的静止流体也被带动,流动的区域不断扩大。
因此,粘性力会降低。
而在浮力的加速作用下,空气的流速不断加快。
因而产生了湍流化。
根据层流和湍流的不同,强制对流的传热系数公式存在相当大的差别。
首先是层流的公式。
层流平均传热系数hm=√(V/L) (6)其中加入了空气的特性值,与自然对流公式(3)中的含义相同。
湍流相关公式是实验性公式,系数和指数都有变化。
湍流平均传热系数hm=6×(V/) (7)要想简单进行判断的话,不妨把两个系数都计算出来,选择传热系数大的一方。
下面,让我们使用上面介绍的知识,定量研究对流的散热能力。
【练习1】平板的放置方式与散热能力假设有一块长200mm、宽100mm(忽略厚度),温度保持在40℃的平板(图6),平板的温度均匀,而且没有热辐射,下列放置方式的散热能力有多大差别?图6:【练习1】平板的放置方式与散热能力思考纵长200mm×横宽100mm(无视厚度)的平板的升温保持在40K(℃)时,图中3种模式的散热能力。
假设平板的温度均匀,且没有热辐射。
(a)垂直放置(以100mm的短边为高)(b)垂直放置(以200mm的长边为高)(c)水平放置需要求的数值是热流量,相当于散热量,这就必须首先求出传热系数,需要使用公式(3)。
(a)和(b)是垂直放置,C值使用平板垂直放置时的数值。
因为升温固定在40K(℃),所以⊿T为40(注5)。
至此,所有数值已经齐备,可以计算出传热系数。
(注5)温度必须要多次计算,比较麻烦。
如果不知道温度,就求不出传热系数,因此,最初先假设温度为30℃,计算出h。
把结果代入公式进行计算,得到的温度一般不等于30℃,此时要使用得出的数值重新计算。
经过反复计算,逐渐逼近正确数值。
(a)以100mm的短边为高的垂直平板传热系数 h=××(40/)=m2K表面积S=××2=散热量W=××40=(b)以200mm的长边为高的垂直平板传热系数 h=××(40/)=m2K表面积S=××2=散热量W=××40=由上述计算可知,(b)的散热量比(a)低15%左右。
但计算的条件是平板的温度完全均匀,也就是导热系数无限大,如果是印刷电路板,散热量上的差别还会更大。
倘若导热能力差,平板上侧与下侧之间将会出现温差。
纵向放置的话,上侧与下侧的温差会更大,最高温度将出现相当大的差别。
水平放置时,平板上侧与下侧的传热系数不同,计算比较复杂。
上侧的C值为,下侧为,刚好是上侧的一半。
因此,下侧的散热量也是上侧的一半。
这种情况需要分别计算上侧和下侧的散热量,然后相加。
(c)水平放置平板代表长度 L=(××2)/(+)=上表面对流传热系数 h=××(40/)= W/m2K上表面表面积S=×=上表面散热量W=××40=下表面对流传热系数 h=××(40/)= W/m2K下表面表面积S=×=下表面散热量W=××40=总散热量 W=+=这采用的是热计算中经常使用的计算每个面的发热量,然后相加的方法。
【练习2】大空间发生热对流,小空间发生热传导接下来看一下在200mm×200mm×20mm的平整机壳中安装180mm×180mm×1mm的电路板(发热功率5W)的情况(图7)。
图7:【练习2】空间大为热对流,空间小为热传导思考在尺寸为200mm×200mm×20mm的机壳内安装180mm×180mm×1mm的印刷电路板(发热功率为5W)时,图中3种情况下的散热能力。
假设没有热辐射。
大家可以将其看成是加热器。
关于电路板的安装位置,下面哪种是正确的?另外,这里假设热辐射可以忽略。
(a)电路板设置在上部(距离机壳顶面1mm)时温度最低(b)电路板设置在中部(距离机壳顶面)时温度最低(c)电路板设置在下部(距离机壳顶面15mm)时温度最低这个题目中有一点要注意,那就是空间狭窄、空气无法流动时,发生的是热传导,空间够大时发生的是热对流。
划分的界限值随状态和发热量而变,大致为几毫米。
如果小于该界限值,空气将无法流动,大于该界限值空气就可以流动。
定性地来说,只要距离足够,空气就能循环,从而带走热能,使部件释放的热传到机壳顶面并发散出去,由此起到降温的作用。
上面提到,当距离很小时发生的是热传导。
热传导的热阻等于空气层的厚度/(传热面积×空气的导热系数),因此(a)的情况下,热阻(1mm)=(××)=W;(b)的情况下,热阻(㎜)=(××)=W,比(a)的热阻大很多。
而在(c)的情况下,距离达到15mm,可以认为能充分产生对流。
此时,对流的热阻增加到两个(电路板表面→空气,空气→机壳顶面)。
按照传热系数为10W/m2K计算,电路板到空气的对流热阻=1/(电路板表面积×自然对流传热系数(水平))空气到机壳的对流热阻=1/(机壳表面积×自然对流传热系数(水平))热阻(15mm)=1/(××10)+1/(××10)=W由此可知,(a)的情况下热阻最小、温度最低。