数值模拟步骤演示教学

数值模拟1、CFD方法简介利用CFD方法,采用流体力学分析软件Fluent对三相分离器的流场进行了研究与分析,为实验研究提供理论支持。

CFD就是英文Computational Fluid Dynamics(计算流体动力学) 的缩写,就是一门用数值计算方法求解流动主控方程以发现各种流动现象规律的学科]。

用CFD 技术进行数值求解的基本思想就是: 把原来在空间与时间坐标中连续的物理量的场, 用一系列有限个离散点上的值的集合来代替, 通过一定的原则来建立离散点上变量值之间关系的代数方程, 求解代数方程以获得所求解变量的近似值。

其主要用途就是对流态进行数值仿真模拟计算,因此,CFD技术的用途十分广泛,可用于传质、传热、动量传递及燃烧等方面的研究。

流体机械的研究中多用CFD方法对分离器进行仿真模拟,其基本应用步骤如下:1) 利用Gimbit进行前处理a、根据分离的形状、结构及尺寸建立几何模型;b、对所建立的几何模型进行网格划分;2) 利用Fluent进行求解a、确定计算模型及材料属性;b、对研究模型设置边界条件;c、对前期设置进行初始化,选择监视器,进行迭代计算;3)利用Fluent进行后续处理,实现计算结果可视化及动画处理。

上述迭代求解后的结果就是离散后的各网格节点上的数值,这样的结果不直观。

因此需要将求解结果的速度场、温度场或浓度场等用计算机表示出来,这也就是CFD 技术应用的必要组成部分。

利用CFD方法进行仿真模拟可以对分离器的结构设计及参数选择作出指导,保证设计的准确度,也可以为分离器样机的试验提供理论参考。

由于CFD仿真模拟的广泛使用及其重要性,国内外很多学者,如Mark D Turrell、M、Narasimha、师奇威等都对其进行了研究,尤其就是A、F、 Nowakowski及Daniel J、SUASNABAR等人]对CFD技术在旋流器模拟方面的应用做了详细的介绍,这些工作对CFD技术的发展起到了积极的促进作用。

物理实验技术中的数值模拟方法与技巧在物理实验中，数值模拟是一种非常重要的工具，它可以帮助实验人员更好地理解实验现象、验证理论模型以及优化实验方案。

本文将介绍物理实验技术中常用的数值模拟方法与技巧，希望能够对物理实验研究者有所启发和帮助。

一、数值模拟方法的选择在进行物理实验的数值模拟时，选择合适的数值模拟方法是至关重要的。

常用的数值模拟方法包括有限元法、有限差分法、蒙特卡洛方法等。

对于不同的实验问题，需要根据具体情况选择适合的数值模拟方法。

以有限元法为例，它适用于解决复杂几何形状和边界条件下的物理问题。

在实验人员进行物体的结构研究时，有限元法可以帮助求解物体的应力、变形等参数。

因为几何形状和边界条件的复杂性，解析方法往往难以直接求解，而有限元法则可以通过将整个问题划分为很多个小单元，从而近似求解。

而在研究物体的流动行为时，有限差分法则是一种常用的数值模拟方法。

通过将空间离散化，时间离散化，将连续的偏微分方程转化为离散的差分方程，可以模拟物体的流动行为。

在实验人员研究小尺度流动、多相流、湍流等问题时，有限差分法可以提供一种较为便捷的数值模拟方法。

二、数值模拟技巧的应用在进行物理实验的数值模拟时，除了选择合适的数值模拟方法外，还需要掌握一些数值模拟技巧，从而提高数值模拟的准确性和效率。

首先，合理地选择网格大小是数值模拟中的重要技巧之一。

网格大小的选择直接影响到模拟结果的准确性和计算效率。

若网格过于粗糙，会导致模拟结果的偏离；若网格过于细致，会增加计算量。

因此，实验人员需要在准确性和计算效率之间进行权衡，选择适当的网格大小。

其次，合理地选择边界条件也是数值模拟中的关键技巧。

边界条件是模拟问题中的重要约束条件，对模拟结果有着重要影响。

实验人员需要根据物理实验的具体设置，将实验问题转化为数值模拟问题，并选择适当的边界条件进行模拟。

合理的边界条件可以更好地反映实验现象，提高数值模拟的准确性。

最后，灵活地利用数值模拟软件也是一项重要技巧。

数值模拟流程说明
1.画出界面command，text以及标明文字
2.画出铸件轮廓
3.画出网格线，将整个铸件铸型按纵向分为四个部分，铸件
上面，铸件上半部与铸型，铸件下半部与铸型，铸件下面，用循环语句定义出点的位置，然后用，，B画出每个网格，通过每个方格的位置涂色
4.定义二维数组表示每个网格横纵坐标，依然将网格分为四
个部分，以二维数组形式表示出来，分为铸件上方，铸件上半部与铸型，铸件下半部区域与铸型，铸型下面，以此赋入初始温度
5.找出铸件的左上点，中部左上点，左下，右下，右上点，
中部右上点，赋入变化规律
6.找出左边，右边，上边，中上边，下边位置，赋入变化规
律
7.找出铸件内部范围，赋入变化规律，特殊要注意左右边界
上各有一点，虽在边界范围内不过其受热为铸件内部点
8.找出与靠近铸件铸型边界各范围，赋入变化规律
9.找出两个边界角，中铸件中部，铸件紧贴的铸型点，赋入
变化规律
10.找出铸型与空气接触的上下左右边界，赋入变化规律
11.找出铸型与空气接触四角点，赋入变化规律，再将整个铸
型分成四部分，依次选出范围，赋入变化规律
12.找出特殊铸型六点，赋入变化规律
13.画出（20,14）（20,20）两点的温度变化曲线
14.将数据导入text文件中
15.复制到excel中，画出曲线图。

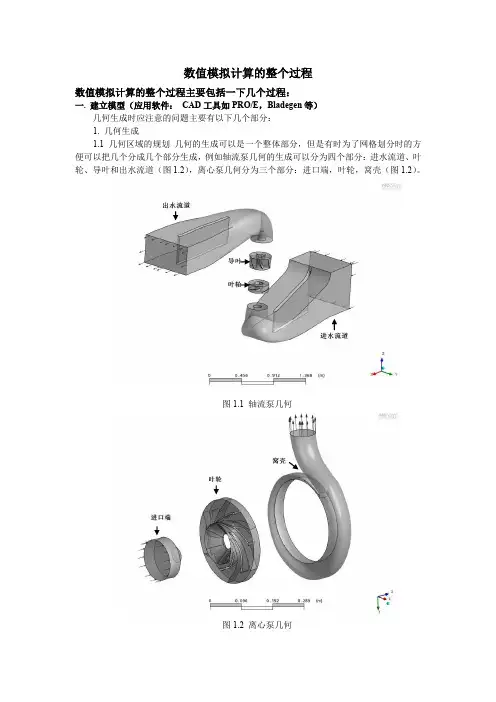
数值模拟计算的整个过程数值模拟计算的整个过程主要包括一下几个过程：一.建立模型（应用软件：CAD工具如PRO/E，Bladegen等）几何生成时应注意的问题主要有以下几个部分：1. 几何生成1.1 几何区域的规划几何的生成可以是一个整体部分，但是有时为了网格划分时的方便可以把几个分成几个部分生成，例如轴流泵几何的生成可以分为四个部分：进水流道、叶轮、导叶和出水流道（图1.2），离心泵几何分为三个部分：进口端，叶轮，窝壳（图1.2）。

图1.1 轴流泵几何图1.2 离心泵几何1.2几何生成的方法1.2.1泵的叶轮和导叶部分可以根据各自的木模图使用BLADEGEN较为方便的生成1.2.2而其他部分则可以通过Pro E等三维CAD工具生成，其中离心泵窝壳由窝壳木模图先将各断面绘制成型，再利用扫掠的方法成型。

1.3.几何输出1.3.1从PRO/E中导出文件时可以选择保存成igs格式，也可以保存成stp格式，在导出时按其默认格式保存，即igs格式的保存成面的形式，stp格式的保存成体和壳的形式。

1.3.2. 进出水流道部分（轴流泵），进口端（离心泵）要做适当的延伸。

1.3.3 从PRO/E中导出之前可以可以改单位，或者明确几何生成时所用单位，以便导入。

1.3.4各部分的特征位置的坐标要明确，如几何中心，原点，以便各部分导入后的合并。

二.网格划分（软件: ANSYS ICEM ）网格划分主要有以下几部分：2.1. 几何检查及修复通过检查几何命令检查几何并将错误的部分根据实际情况修复（以轴流泵出水流道为例，见图2.1）图2.1（a）轴流泵出水流道几何检查图2.1（b）修复后的轴流泵出水流道几何2.2 设置part图2.2设置part2.3. 建立物质点（生成四面体网格时必须）图2.3建立物质点2.4. 设置网格大小，生成网格2.4.1六面体网格的生成。

分块六面体网格生成主要是分块的思想，一般不外乎O型，C型，H型，J型。

（全）Fluent数值模拟步骤Fluent数值模拟的主要步骤使用Gambit划分网格的工作：首先建立几何模型，再进行网格划分，最后定义边界条件。

Gambit中采用的单位是mm，Fluent默认的长度是m。

Fluent数值模拟的主要步骤：（1）根据具体问题选择2D或3D求解器进行数值模拟；（2）导入网格(File-Read-Case)，然后选择由Gambit导出的msh文件。

（3）检查网格(Grid-Check)，如果网格最小体积为负值，就要重新进行网格划分。

（4）选择计算模型(Define-Models-Solver)。

（6）（5）确定流体的物理性质(Define-Materials)。

（6）定义操作环境(Define-Operating Conditions)。

（7）指定边界条件(Define-Boundary Conditions )。

（8）求解方法的设置及其控制（Solve-Control-Solution）。

（9）流场初始化（Solve-Initialize）。

（10）打开残插图（Solve-Monitors-Residual）可动态显示残差，然后保存当前的Case和Data文件（File-Writer-Case&Data）。

（11）迭代求解（Solve-Iterate）。

（12）检查结果。

（13）保存结果（File-Writer-Case&Data），后处理等。

在运行Fluent软件包时，会经常遇到以下形式的文件：.jou文件：日志文档，可以编辑运行。

.dbs文件：Gambit工作文件，若想修改网格，可以打开这个文件进行再编辑。

.msh文件：Gambit输出的网格文件。

.cas文件：是.msh文件经过Fluent处理后得到的文件。

.dat文件：Fluent计算数据结果的数据文件。

三维定常速度场的计算实例操作步骤对于三维管道的速度场的数值模拟，首先利用Gambit画出计算区域，并且对边界条件进行相应的指定，然后导出Mesh文件。

流体力学数值模拟软件的使用流程1. 简介流体力学数值模拟软件是一种用于模拟流体力学现象的工具。

通过数值计算和模拟，该软件可以预测和分析各种流体在不同条件下的行为。

本文将介绍使用流体力学数值模拟软件的详细流程。

2. 安装软件在开始使用流体力学数值模拟软件之前，首先需要确保软件已经安装在您的计算机上。

根据您使用的操作系统，选择正确的安装文件并按照提示完成安装过程。

3. 准备模拟对象在进行流体力学数值模拟之前，需要准备好模拟对象的几何模型。

可以使用CAD软件创建模型，或者导入现有的模型文件。

确保模型的几何尺寸和细节符合实际需求。

4. 设置模拟参数在进行流体力学数值模拟之前，需要设置模拟的参数。

这些参数包括但不限于流体的性质、边界条件、初始条件等。

根据实际需求和模拟对象的特点，合理设置这些参数以获得准确的模拟结果。

•流体性质：设置流体的密度、粘度等性质参数。

•边界条件：设置流体的进口和出口边界条件。

•初始条件：设置流体的初始状态。

5. 网格划分在进行流体力学数值模拟之前，需要将模拟对象划分成有限个小单元，即网格。

网格的划分精度将直接影响模拟结果的准确性和计算的效率。

•划分大小：根据模拟对象的几何尺寸和复杂程度，合理划分网格的大小。

•划分密度：根据模拟对象内部流动特点，划分网格的密度。

6. 模拟计算在完成网格划分后，即可进行流体力学数值模拟的计算。

•求解方程：根据模拟对象的性质和参数设置，利用流体力学的基本方程进行求解。

•迭代计算：利用迭代算法，将模拟结果逐步逼近真实结果。

•模拟结果：最终得到模拟结果，包括流体的速度、压力、温度等信息。

7. 结果分析在获得模拟结果后，可以对结果进行进一步分析和处理。

根据实际需求，可以选择不同的处理方法和工具。

•可视化结果：使用可视化工具将模拟结果以图形或动画的方式展示出来。

•结果比对：将模拟结果与实际观测结果进行比对，判断模拟结果的准确性。

•结果导出：将模拟结果导出为文档或数据文件，方便后续参考和使用。

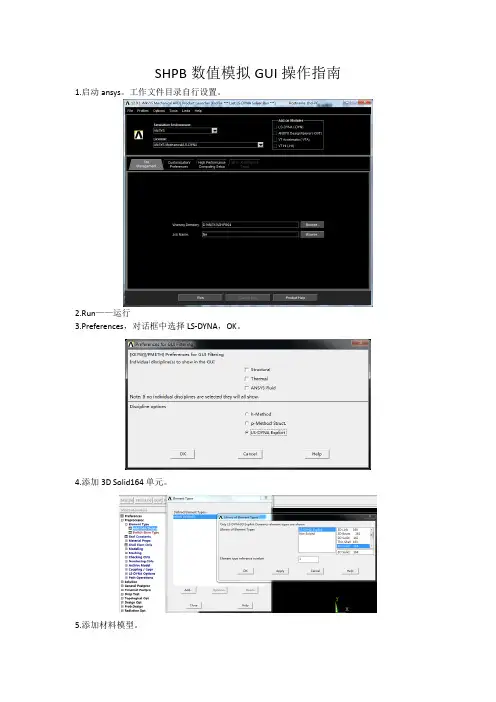
SHPB数值模拟GUI操作指南1.启动ansys。

工作文件目录自行设置。

2.Run——运行3.Preferences，对话框中选择LS-DYNA，OK。

4.添加3D Solid164单元。

5.添加材料模型。

Preprocesser>Material Props>Material Models，弹出Define Material Model Behavoir对话框，在对话框中选择LS-DYNA>Linear>Elastic>Isotropic，在弹出的对话框中分别输入密度、弹性模量和泊松比。

定义第二种材料模型：在Define Material Model Behavoir对话框中单击Material>New Model…在弹出的对话框中填2，OK关闭对话框。

定义材料2，同材料1，弹性。

LS-DYNA>Linear>Elastic>Isotropic定义材料3，在Define Material Model Behavoir对话框中单击Material>New Model…在弹出的对话框中填3，点击LS-DYNA>Equation of State>Gruneisen>Johnson-Cook，弹出对话框，设置密度为7.9，随后点击OK关闭对话框。

其他参数在后面的K文件中添加。

6.建模。

Preprocesser>Modeling>Creat>Volumes>Sylinder>By Dimensions，弹出Creat Cylinder by Dimensions对话框。

依次建立子弹、入射杆、试样、和透射杆模型。

本文设置子弹、压杆和试样直径均为30mm，弹长20cm，入射杆长100cm，试样长2cm，透射杆长80cm。

文中所使用的单位系统是cm-g-μs(长度/重量/时间)。

因系统为对称结构，建立1/4模型。