绳子末端速度的分解问题

人教版2020年高考物理考点---点对点专题强化-----运动的合成与分解知识点：1．合运动和分运动的关系2.运动的合成与分解的运算法则运动的合成与分解是指描述运动的各物理量即位移、速度、加速度的合成与分解，由于它们均是矢量，故合成与分解都遵循平行四边形定则． 3．合运动性质的判断⎩⎪⎨⎪⎧加速度⎩⎪⎨⎪⎧恒定：匀变速运动变化：非匀变速运动加速度方向与速度方向⎩⎪⎨⎪⎧共线：直线运动不共线：曲线运动4．两个直线运动的合运动性质的判断5.运动分解的两类金典案例： 一、小船渡河问题1．小船渡河问题的分析思路2．小船渡河的两类问题、三种情景当船头方向垂直于河岸时，渡河时间最短，最短时间如果角垂直于河岸，渡河位移最短，等于河宽如果向最短，等于二、绳(杆)端速度分解模型：(1)模型特点：绳(杆)拉物体或物体拉绳(杆)，以及两物体通过绳(杆)相连，物体运动方向与绳(杆)不在一条直线上，求解运动过程中它们的速度关系，都属于该模型． (2)模型分析①合运动→绳拉物体的实际运动速度v②分运动→⎩⎪⎨⎪⎧其一：沿绳（或杆）的分速度v 1其二：与绳（或杆）垂直的分速度v 2(3)解题原则：根据沿绳(杆)方向的分速度大小相等求解．常见实例如下：(注：A 沿斜 面下滑)(4)解题思路对点训练：典例1：（运动的合成与分解）质量为2 kg的质点在xOy平面上做曲线运动，在x方向的速度图象和y方向的位移图象如图所示，下列说法正确的是()A．质点的初速度为5 m/s B．质点所受的合外力为3 N，做匀加速曲线运动C．2 s末质点速度大小为6 m/s D．2 s内质点的位移大小约为12 m【答案】ABD典例1解码：由x方向的速度图象可知，在x方向的加速度为1.5 m/s2，受力F x＝3 N，由y方向的位移图象可知在y方向做匀速直线运动，速度为v y＝4 m/s，受力F y＝0.因此质点的初速度为5 m/s，A选项正确；受到的合外力为3 N，显然，质点初速度方向与合外力方向不在同一条直线上，B选项正确；2 s末质点速度应该为v＝62＋42m/s＝213 m/s，C选项错误；2 s内x方向上位移大小x＝v x t＋12at2＝9 m，y方向上位移大小y＝8 m，合位移大小l＝x2＋y2＝145 m≈12 m，D选项正确．典例2：（小船渡河问题）小船在200 m宽的河中横渡，水流速度为2 m/s，船在静水中的速度为4 m/s.(1)若小船的船头始终正对对岸，它将在何时、何处到达对岸？(2)要使小船到达正对岸，应如何航行？历时多长？(3)小船渡河的最短时间为多长？(4)若水流速度是5 m/s ，船在静水中的速度是3 m/s ，则怎样渡河才能使船漂向下游的距离最短？最短距离是多少？ 【答案】见解析 典例2解码:(1)小船参与了两个分运动，即船随水漂流的运动和船在静水中的运动．因为分运动之间具有独立性和等时性，故小船渡河的时间等于垂直于河岸方向的分运动的时间， 即t ＝d v 船＝2004s ＝50 s小船沿水流方向的位移s 水＝v 水t ＝2×50 m ＝100 m 即船将在正对岸下游100 m 处靠岸．(2)要使小船到达正对岸，合速度v 应垂直于河岸，如图甲所示，则cos θ＝v 水v 船＝24＝12，故θ＝60°即船的航向与上游河岸成60°，渡河时间t ＝d v ＝2004sin 60° s ＝10033s.(3)考虑一般情况，设船头与上游河岸成任意角θ，如图乙所示．船渡河的时间取决于垂直于河岸方向的分速度v ⊥＝v 船sin θ，故小船渡河的时间为t ＝dv 船sin θ.当θ＝90°，即船头与河岸垂直时，渡河时间最短，最短时间为t min ＝50 s.(4)因为v 船＝3 m/s<v 水＝5 m/s ，所以船不可能垂直河岸横渡，不论航向如何，总被水流冲向下游．如图丙所示，设船头(v 船)与上游河岸成θ角，合速度v 与下游河岸成α角，可以看出：α角越大，船漂向下游的距离x ′越短．以v 水的矢尖为圆心，以v 船的大小为半径画圆，当合速度v 与圆相切时，α角最大．则cos θ＝v 船v 水＝35，故船头与上游河岸的夹角θ＝53°又x ′d ＝v v 船＝v 2水－v 2船v 船，代入数据解得x ′≈267 m. 典例3：（绳端速度分解模型）如图所示，做匀速直线运动的小车A 通过一根绕过定滑轮的长绳吊起一重物B ，设重物和小车速度的大小分别为v B 、v A ，则( )A ．v A ＞vB B ．v A ＜v BC ．绳的拉力等于B 的重力D ．绳的拉力大于B 的重力 【答案】 AD 典例3解码：小车A 向左运动的过程中，小车的速度是合速度，可分解为沿绳方向与垂直于绳方向的速度，如图所示，由图可知v B ＝v A cos θ，则v B ＜v A ，小车向左运动的过程中θ角减小，v B 增大，B 向上做加速运动，故绳的拉力大于B 的重力．故选项A 、D 正确．典例4：（轻杆末端速度分解模型）如图所示，一根长直轻杆AB 在墙角沿竖直墙与水平地面滑动．当AB 杆和墙的夹角为θ时，杆的A 端沿墙下滑的速度大小为v 1，B 端沿地面滑动的速度大小为v 2，则v 1、v 2的关系是( )A ．v 1＝v 2B ．v 1＝v 2cos θC ．v 1＝v 2tan θD ．v 1＝v 2sin θ【答案】C 典例4解码：将A 、B 两点的速度分解为沿AB 方向与垂直于AB 方向的分速度，沿AB 方向的速度分别为v 1∥和v 2∥，由于AB 不可伸长，两点沿AB 方向的速度分量应相同，则有v 1∥＝v 1cos θ，v 2∥＝v 2sin θ，由v 1∥＝v 2∥，得v 1＝v 2tan θ，选项C 正确．针对训练：1.如图，图甲所示，在杂技表演中，猴子沿竖直杆向上运动，其v-t 图象如图乙所示．人顶杆沿水平地面运动的s-t 图象如图丙所示．若以地面为参考系，下列说法中正确的是（ ）A ．猴子的运动轨迹为直线B ．猴子在2s 内做匀变速曲线运动C ．t =0时猴子的速度大小为8m/sD ．t =2s 时猴子的加速度为4m/s 2 【答案】BD【解析】竖直方向为初速度s m v x /8=、加速度2/4s m a -=的匀减速直线运动，水平方向为速度s m v x /4-=的匀速直线运动，初速度大小为，方向与合外力方向不在同一条直线上，故做匀变速曲线运动，故选项B 正确，选项A 错误；t=2s 时，2/4s m a y -=0=x a ，则合加速度为2/4s m a -=，选项C 错误，选项D 正确。

绳(杆)端速度分解模型一、基础知识 1、模型特点沿绳(或杆)方向的速度分量大小相等． 2、思路与方法合运动→绳拉物体的实际运动速度v分运动→⎩⎪⎨⎪⎧其一：沿绳(或杆)的速度v 1其二：与绳(或杆)垂直的分速度v 2方法：v 1与v 2的合成遵循平行四边形定则． 3、解决此类问题时应把握以下两点： (1)确定合速度，它应是小船的实际速度；(2)小船的运动引起了两个效果：一是绳子的收缩，二是绳绕滑轮的转 动．应根据实际效果进行运动的分解． 二、练习1、如图所示，轻绳通过定滑轮拉动物体，使其在水平面上运动．若拉绳的速度为v 0，当绳与水平方向夹角为θ时，物体的速度v 为________．若此时绳上的拉力大小为F ，物体的质量为m ，忽略地面的摩擦力，那么，此时物体的加速度为________． 答案v 0cos θ F cos θm解析 物体的运动(即绳的末端的运动)可看做两个分运动的合成： (1)沿绳的方向被牵引，绳长缩短，缩短的速度等于v 0；(2)垂直于 绳以定滑轮为圆心的摆动，它不改变绳长．即速度v 分解为沿绳方向和垂直绳方向的分速度，如图所示，v cos θ＝v 0，v ＝v 0cos θ.拉力F 产生竖直向上拉物体和水平向右拉物体的效果，其水平分量为F cos θ，加速度a ＝F cos θm.2、如图所示，一人站在岸上，利用绳和定滑轮拉船靠岸，在某一时刻绳的速度为v ，绳AO 段与水平面的夹角为θ，OB 段与水平面的夹角为α.不计摩擦和轮的质量，则此时小船的速度多大？解析 小船的运动引起了绳子的收缩以及绳子绕定滑轮转动的效果， 所以将小船的运动分解到绳子收缩的方向和垂直于绳子的方向，分解如图所示，则由图可知 v A ＝v cos θ. 答案v cos θ3、如图所示，在水平地面上做匀速直线运动的小车，通过定滑轮用绳子吊起一个物体，若小车和被吊的物体在同一 时刻的速度分别为v 1和v 2，绳子对物体的拉力为F T ，物体所 受重力为G ，则下列说法正确的是( )A ．物体做匀速运动，且v 1＝v 2B ．物体做加速运动，且v 2>v 1C ．物体做加速运动，且F T >GD ．物体做匀速运动，且F T ＝G答案 C解析 把v 1分解如图所示，v 2＝v 1cos α，α变小，v 2变大，物体做加速 运动，超重，F T >G ，选项C 正确．4、人用绳子通过定滑轮拉物体A ，A 穿在光滑的竖直杆上，当以速度v 0匀速地拉绳使物体A 到达如图所示位置时，绳与竖直杆的夹角为θ，则物体A 实际运动的速度是( )A ．v 0sin θ B.v 0sin θ C ．v 0cos θD.v 0cos θ答案 D解析 由运动的合成与分解可知，物体A 参与两个分运动：一个是沿着与它相连接的绳子的运动，另一个是垂直于绳子斜向上的运动． 而物体A 实际运动轨迹是沿着竖直杆向上的，这一轨迹所对应的运动就是物体A 的合运动，它们之间的关系如图所示．由几何关系可得v ＝v 0cos θ，所以D项正确．5、如图，人沿平直的河岸以速度v 行走，且通过不可伸长的绳拖船，船沿绳的方向行进，此过程中绳始终与水面平行．当绳与河岸的夹角为α时，船的速率为()A．v sin α B.vsin αC．v cos α D.vcos α答案 C解析如图所示，把人的速度沿绳和垂直绳的方向分解，由几何知识有v船＝v cos α，所以C正确，A、B、D错误．6、A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体A以v1的速度向右匀速运动，当绳被拉成与水平面夹角分别为α、β时，如图所示．物体B的运动速度v B 为(绳始终有拉力) ()A．v1sin α/sin βB．v1cos α/sin βC．v1sin α/cos βD．v1cos α/cos β答案 D解析A、B两物体的速度分解如图．由图可知：v绳A＝v1cos αv绳B＝v B cos β由于v绳A＝v绳B所以v B＝v1cos α/cos β，故D对．。

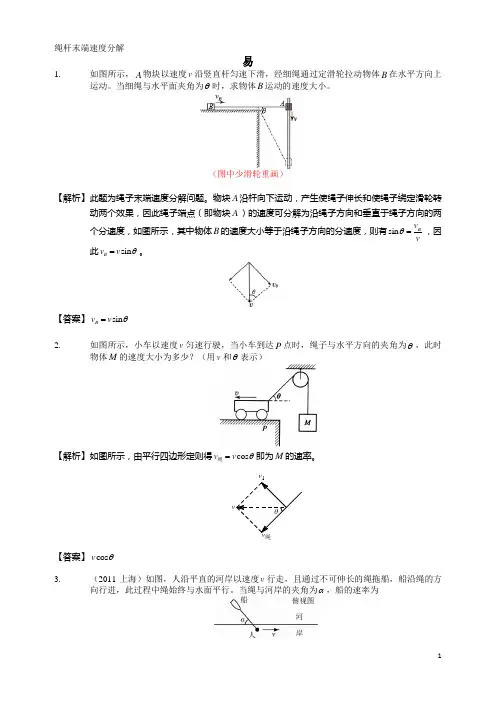
绳杆末端速度分解易1.如图所示，A 物块以速度v 沿竖直杆匀速下滑，经细绳通过定滑轮拉动物体B 在水平方向上运动。

当细绳与水平面夹角为θ时，求物体B 运动的速度大小。

（图中少滑轮重画）【解析】 此题为绳子末端速度分解问题。

物块A 沿杆向下运动，产生使绳子伸长和使绳子绕定滑轮转动两个效果，因此绳子端点（即物块A ）的速度可分解为沿绳子方向和垂直于绳子方向的两个分速度，如图所示，其中物体B 的速度大小等于沿绳子方向的分速度，则有sin B vvθ=，因此sin B v v θ=。

【答案】 sin B v v θ=2.如图所示，小车以速度v 匀速行驶，当小车到达P 点时，绳子与水平方向的夹角为θ，此时物体M 的速度大小为多少？（用v 和θ表示）【解析】 如图所示，由平行四边形定则得cos v v θ=绳即为M 的速率。

【答案】 cos v θ 3. （2011上海）如图，人沿平直的河岸以速度v 行走，且通过不可伸长的绳拖船，船沿绳的方向行进，此过程中绳始终与水面平行。

当绳与河岸的夹角为α，船的速率为v 绳A ．sin v αB ．sin vα C ．cos v αD ．cos v α【答案】 C中4.在水平面上有A 、B 两物体，通过一根跨过滑轮的不可伸长的轻绳相连接，现A 物体以A v 的速度向右匀速运动，当绳被拉成与水平面夹角分别为α、β时（如图所示），B 物体的运动速度B v 为（绳始终有拉力）A ．sin /sin A v αβB ．cos /sin A v αβC ．sin /cos A v αβD ．cos /cos A v αβ【解析】 将A 和B 的速度分别分解为沿着绳的速度1A v 、1B v 和垂直于绳的速度2A v 、2B v ，则1cos A A v v α=，1cos B B v v β=，因为轻绳不可伸长，所以沿着绳方向速度大小相等，即11A B v v =，有cos /cos B A v v αβ=。

专题姓名：一、小船渡河问题小船渡河问题一般有渡河时间最短和渡河位移最短两类问题： (1)渡河时间最短问题若要渡河时间最短，由于水流速度始终沿河道方向，不能提供指向河对岸的分速度．因此只要使船头垂直于河岸航行即可．由图 3 可知，此时 t d ，此时船渡河的位移d短位移方向满足 tan θ＝v船.v 水(2)渡河位移最短问题 (v 水<v 船 )d最短的位移为河宽 d ，此时渡河所用时间 t ＝v 船 sin θ ，船头与 上游河岸夹角 θ满足 v 船 cos θ ＝v 水 ，如图 4 所示．【例 1】 小船在 200 m 宽的河中横渡，水流速度是 2 m/s ，小船在静水中的航速是 4 m/s.求：(1)要使小船渡河耗时最少，应如何航行？ (2)要使小船航程最短，应如何航行？延伸思考 当船在静水中的航行速度 v 1 大于水流速度 v 2 时，船航行的最短航程为河宽． 若水流速度 v 2 大于船在静水中的航行速度 v 1，则怎样才能使船的航程最短？最短航程是什么？二、 “绳联物体 ” 的速度分解问题“绳联物体”指物拉绳 (杆)或绳 (杆 )拉物问题 (下面为了方便， 统一说“绳” )．解题原则是：把物体的实际速度分解为垂直于绳和平行于绳的两个分量，根据沿绳方向的分速度大小与绳上各点的速率相同求解．1．合速度方向：物体实际运动方向2．分速度方向：(1)沿绳方向：使绳伸 (缩)(2)垂直于绳方向：使绳转动3．速度投影定理：不可伸长的绳，若各点速度不同，各点速度沿绳方向的投影相同．【例 2】如图 5 所示，汽车甲以速度 v1拉汽车乙前进，乙的速度为 v2，甲、乙都在水平面上运动，拉汽车乙的绳子与水平方向夹角为α，求 v1∶ v2.练习题1．关于运动的合成与分解，以下说法正确的是() A．合运动的速度大小等于分运动的速度大小之和B．物体的两个分运动若是直线运动，则它的合运动一定是直线运动C．合运动和分运动具有等时性D．若合运动是曲线运动，则其分运动中至少有一个是曲线运动2. 一物体在光滑的水平桌面上运动，在相互垂直的x 方向和 y 方向上的分运动速度随时间变化的规律如图 6 所示．关于物体的运动，下列说法正确的是()A ．物体做曲线运动B．物体做直线运动C．物体运动的初速度大小为50 m/sD．物体运动的初速度大小为10 m/sv0，绳某时刻与水平方3. 如图 7 所示，某人用绳通过定滑轮拉小船，设人匀速拉绳的速度为向夹角为α，则船的运动性质及此时刻小船水平速度v x为 ( )v0v x＝cosB．船做变加速运动， v x＝v0cos αv0C．船做匀速直线运动， v x＝cosαD．船做匀速直线运动， v x＝ v0cos α4. 如图11 所示，物体滑轮与轴之间的摩擦则 ( ) A 和 B 的质量均为 m，且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、)在用水平变力 F 拉物体 B 沿水平方向向右做匀速直线运动的过程中，A ．物体 A 也做匀速直线运动B．绳子拉力始终等于物体 A 所受重力C．绳子对 A 物体的拉力逐渐增大D．绳子对 A 物体的拉力逐渐减小5．如图 12 所示，重物 M 沿竖直杆下滑，并通过绳带动小车沿斜面升高．问：当滑轮右侧的绳与竖直方向成θ角，且重物下滑的速率为v 时，小车的速度为()A ．vsin θB．v/cos θC．vcos θD．v/sin θ6.(2014 南·京模拟 )小船在静水中速度为 4 m/s，它在宽为 200 m ，流速为 3 m/s 的河中渡河，船头始终垂直河岸，如图13 所示．则渡河需要的时间为()A ．40 s B．50 sC．66.7 s D． 90 s7．下列图中实线为河岸，河水的流动方向如图中v 的箭头所示，虚线为小船从河岸M 驶向对岸 N 的实际航线．则其中可能正确的是( )8．某小船在静水中的速度大小保持不变，该小船要渡过一条河，渡河时小船船头垂直指向河岸．若船行至河中间时，水流速度突然增大，则()A ．小船渡河时间不变B．小船航行方向不变C．小船航行速度不变D．小船到达对岸地点不变9．如图14 所示，一条小船位于200 m 宽的河中央 A 点处，从这里向下游100 3 m 处有一危险的急流区，当时水流速度为 4 m/s，为使小船避开危险区沿直线到达对岸，小船在静水中的速度至少为( )4 3 8 3A. 3 m/sB. 3 m/sC．2 m/s D． 4 m/s10．小船在 200 m 宽的河中横渡，水流速度为 3 m/s，船在静水中的航速是 5 m/s，求：(1)当小船的船头始终正对对岸行驶时，它将在何时、何处到达对岸？(2)要使小船到达河的正对岸，应如何行驶？多长时间能到达对岸？(sin 37°＝ 0.6)11．已知某船在静水中的速率为v1＝4 m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为 d＝ 100 m，河水的流动速度为 v2＝ 3 m/s，方向与河岸平行．试分析：(1)欲使船以最短时间渡过河去，船的航向怎样？最短时间是多少？到达对岸的位置怎样？船发生的位移是多大？(2)欲使船渡河过程中的航行距离最短，船的航向又应怎样？渡河所用时间是多少？。

教课资料范本2020年高考物理 100考点最新模拟试题千题精练专题绳端速度分解问题含分析编辑： __________________时间： __________________专题 4．2绳端速度分解一．选择题1.（20xx安徽江淮十校联考）如下图，重物 M沿竖直杆下滑，并经过一根不行伸长的细绳带动小车沿水平面向右运动。

若当滑轮右边的绳与竖直方向成β 角，且重物下滑的速率为 v时，滑轮左边的绳与水平方向成α角，则小车的速度为（）A． v sin B． v sin C． vcos D． v cossin cos sin cos【参照答案】 .D【名师分析】设小车的速度为v车，沿细绳方向的分速度为v3=v车 cosα，重物 M速度沿细绳方向的分速度 v1 =vcosβ。

因为细绳不行伸长，小车和重物沿细绳方向的速度相等，即v车cosα= v cosv cosβ，解得 v车=，选项D正确，cos2（20xx洛阳联考）如下图，长为L的轻直棒一端可绕固定轴O转动，另一端固定一质量为 m 的小球，小球搁在水平起落台上，起落平台以速度v匀速上涨，以下说法正确的选项是()A．小球做匀速圆周运动B．当棒与竖直方向的夹角为α时，小球的速度为C．棒的角速度渐渐增大v Lcos αD．当棒与竖直方向的夹角为α时，棒的角速度为【参照答案】 Dv Lsinα【名师分析】棒与平台接触点( 即小球 ) 的运动可视为竖直向上的匀速运动和沿平台向左的运动的合成．小球的实质运动即合运动方向是垂直于棒指向左上方，如下图．设棒的角速度为ω，则合速度 v实＝ωL，沿竖直向上方向上的速度重量等于v，即ωLsinv vα＝v，所以ω＝Lsinα，小球速度为 v实＝ω L＝sinα，由此可知棒 ( 小球 ) 的角速度随棒与竖直方向的夹角α的增大而减小，小球做角速度愈来愈小的变速圆周运动．选项ABC错误D 正确。

3.（20xx湖南师大附中月考）如下图， A、B两球分别套在两圆滑的水平直杆上，两球经过一轻绳绕过必定滑轮相连，此刻A球以速度 v向左匀速挪动，某时辰连结两球的轻绳与水平方向的夹角分别为α、β，以下说法正确的选项是 ( )cos αA．此时 B球的速度为cosβvsinαB．此时 B球的速度为sinβvC．在β增大到 90°的过程中， B球做匀速运动D．在β增大到 90°的过程中， B球做加快运动【参照答案】 .AD【名师分析】因为两球沿绳方向的速度大小相等，所以vcos α＝ v B cos β，解得 v B＝ vcos αcosβ，A项正确， B项错误；在β增大到 90°的过程中，α在减小，所以 B球的速度在增大，4．如下图，一辆货车利用越过圆滑定滑轮的轻质缆绳提高一箱货物，已知货箱的质量为m 0，货物的质量为 m ，货车以速度 v 向左做匀速直线运动，在将货物提高到图示的地点时，以下说法正确的选项是( )A ．货箱向上运动的速度大于 vB ．缆绳中的拉力 F T 等于(m 0＋ m) gC ．货箱向上运动的速度等于 vcos θD ．货物对货箱底部的压力等于 mg【参照答案】C【名师分析】将货车的速度进行正交分解，如下图。

运动的合成与分解——“关联”速度问题●问题概述：绳、杆等有长度的物体,在运动过程中,其两端点的速度通常是不一样的,但两端点的速度是有联系的,称之为“关联”速度。

关联速度的关系——沿杆(或绳)方向的速度分量大小相等。

●关键点：1.绳子末端运动速度的分解,应按运动的实际效果进行。

2.速度投影定理:不可伸长的杆(或绳),尽管各点速度不同,但各点速度沿绳方向的投影相同。

●例题：如图所示,人用绳子通过定滑轮拉物体A,当人以速度v0匀速前进时,物体A将做( )A.匀速运动B.加速运动B.C.匀加速运动 D.减速运动解题探究:①物体A的运动有两个运动效果,分别是什么?②将该物体的速度沿哪两个方向分解?●规律总结求解绳(杆)拉物体运动的合成与分解问题的思路和方法:①先明确合运动的方向：物体的实际运动方向②然后弄清运动的实际效果：沿绳或者杆的伸缩效果；使绳子或者杆转动的效果。

③再确定两个分运动的方向：沿着绳子（杆）、垂直于绳子（杆）●常见的模型●巩固练习1、如图所示，人以水平速度v跨过定滑轮匀速拉动绳子，当拉小车的绳子与水平地面的夹角为β时，小车沿水平地面运动的速度为( )A．V B.vcosβC.vsinβD．v cosβ2、如图所示，纤绳以恒定速率v1沿水平方向通过定滑轮牵引小船靠向岸边，设小船速度为v2，则小船靠岸过程的运动情况是( )A．加速靠岸，v2＞v1 B．加速靠岸，v2＜v1C．减速靠岸，v2＞v1 D．匀速靠岸，v2＜v13、两根光滑的杆互相垂直地固定在一起,上面分别穿有一个小球,小球a、b间用一细直棒相连,如图所示。

当细直棒与竖直杆夹角为θ时,两小球实际速度大小之比为( )A.sinθB.cosθC.tanθD.cotθ4、如图所示，物体A以速度v沿杆匀速下滑，A用细绳通过定滑轮拉物体B，当绳与水平夹角为θ时，B的速度为（）A．v cosθ B．v sinθC．v/cosθ D．v/sinθ5、（不定项）如图所示，在水平地面上做匀速直线运动的小车，通过定滑轮用绳子吊起一个物体，若小车和被吊的物体在同一时刻速度分别为1v 和2v ，绳子对物体的拉力为T ，物体所受重力为G ，则下面说法正确的是( )A ．物体做匀速运动，且v 1=v 2B ．B ．物体做加速运动，且v 1>v 2C ．物体做加速运动，且T>GD ．物体做匀速运动，且T ＝G6、如图所示，套在竖直细杆上的环A 由跨过定滑轮的不可伸长的轻绳与重物B 相连。

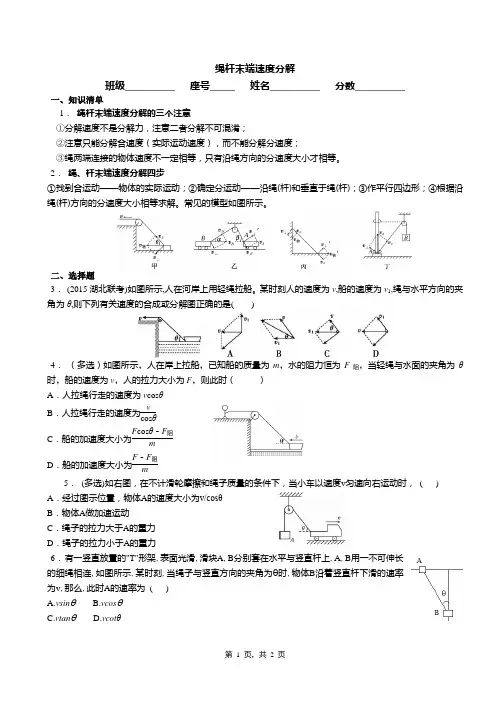
绳杆末端速度分解班级__________ 座号_____ 姓名__________ 分数__________一、知识清单1．绳杆末端速度分解的三个注意①分解速度不是分解力，注意二者分解不可混淆；②注意只能分解合速度（实际运动速度），而不能分解分速度；③绳两端连接的物体速度不一定相等，只有沿绳方向的分速度大小才相等。

2．绳、杆末端速度分解四步①找到合运动——物体的实际运动；②确定分运动——沿绳(杆)和垂直于绳(杆)；③作平行四边形；④根据沿绳(杆)方向的分速度大小相等求解。

常见的模型如图所示。

二、选择题3．(2015湖北联考)如图所示,人在河岸上用轻绳拉船。

某时刻人的速度为v,船的速度为v1,绳与水平方向的夹角为θ,则下列有关速度的合成或分解图正确的是()5．(多选)如右图，在不计滑轮摩擦和绳子质量的条件下，当小车以速度v匀速向右运动时，( )A．经过图示位置，物体A的速度大小为v/cosθB．物体A做加速运动C．绳子的拉力大于A的重力D．绳子的拉力小于A的重力6．有一竖直放置的"T"形架,表面光滑,滑块A,B分别套在水平与竖直杆上,A,B用一不可伸长的细绳相连,如图所示,某时刻,当绳子与竖直方向的夹角为θ时,物体B沿着竖直杆下滑的速率为v,那么,此时A的速率为( )A.vsinθB.vcosθC.vtanθD.vcotθ7． 如图所示，套在竖直细杆上的环A 由跨过定滑轮的不可伸长的轻绳与重物B 相连．由于B 的质量较大，故在释放B 后，A 将沿杆上升，当A 环上升至与定滑轮的连线水平时，其上升速度v 1≠0，若这时B 的速度为v2，则（ ）A ．v 2＝0B ．v 2＞v 1C ．v 2≠0D ．v 2＝v 18． （2011上海）如图，人沿平直的河岸以速度v 行走，且通过不可伸长的绳拖船，船沿绳的方向行进，此过程中绳始终与水面平行。

当绳与河岸的夹角为α，船的速率为（ ）(A)sin v α (B)sin vα (C)cos v α (D)cos v α9． 如图8所示，一铁球用细线悬挂于天花板上，静止垂在桌子的边缘，悬线穿过一光盘的中间孔，手推光盘在桌面上平移，光盘带动悬线紧贴着桌子的边缘以水平速度v 匀速运动，当光盘由A 位置运动到图中虚线所示的B 位置时，悬线与竖直方向的夹角为θ，此时铁球( )A ．竖直方向速度大小为v cos θB ．竖直方向速度大小为v sin θC ．竖直方向速度大小为v tan θD ．相对于地面速度大小为v。