复变函数第六章共形映射习题

p269第六章习题(一) [ 7, 8, 9, 10, 11, 12, 13, 14 ]7. 从⎰C e i z /√z dz 出发，其中C 是如图所示之周线(√z 沿正实轴取正值)，证明：⎰(0, +∞) cos x /√x dx = ⎰(0, +∞) sin x /√x dx = √(π/2)．【解】| ⎰C (R ) e i z /√z dz | ≤ ⎰C (R ) | e i z |/R 1/2 ds= ⎰[0, π/2] | e i ρ (cos θ + i sin θ )|/R 1/2 · R d θ = ⎰[0, π/2] | e - R sin θ | R 1/2 d θ≤ R 1/2 ⎰[0, π/2] e - R sin θ d θ．由sin θ ≥ 2θ/π (θ∈[0, π/2] )，故R 1/2⎰[0, π/2] e - R sin θ d θ≤ R 1/2 ⎰[0, π/2] e - (2R / π)θ d θ = (π/(2R 1/2))(1 – e - R ) ≤ π/(2R 1/2)．所以，| ⎰C (R ) e i z /√z dz | → 0 (as R →+∞)．而由| ⎰C (r ) e i z /√z dz | ≤ (π/(2r 1/2))(1 – e - r )知| ⎰C (r ) e i z /√z dz | → 0 (as r → 0+ )．当r → 0+，R →+∞时，⎰[r , R ] e i z /√z dz = ⎰[r , R ] e i x /√x dx = ⎰[r , R ] (cos x + i sin x )/√x dx→ ⎰(0, +∞) cos x /√x dx + i ⎰(0, +∞) sin x /√x dx ．⎰[r i , R i ] e i z /√z dz = ⎰[r , R ] e i (i y )/√(i y ) i dy = ⎰[r , R ] e - y e i π/4/√y dy ．= (1 + i )/√2 · ⎰[r , R ] e - y /√y dy = 2(1 + i )/√2 · ⎰[√r , √R ] e - u ^2 du→ (1 + i )√2 · ⎰(0, +∞) e - u ^2 du = (1 + i )√2 · √π/2 = (1 + i )√(π/2)．由Cauchy 积分定理，⎰C e i z /√z dz = 0，故其极限也为0，所以，⎰(0, +∞) cos x /√x dx + i ⎰(0, +∞) sin x /√x dx = (1 + i )√(π/2)，即⎰(0, +∞) cos x /√x dx = ⎰(0, +∞) sin x /√x dx = √(π/2)．8. 从⎰C √z ln z /(1 + z )2 dz 出发，其中C 是如图所示之周线，证明：⎰(0, +∞) √x ln x /(1 + x )2 dx = π，⎰(0, +∞) √x /(1 + x )2 dx = π/2．【解】在割去原点及正实轴的z 平面上，√z ，ln z 都能分出单值解析分支，√z 取在正实轴的上岸取正值的那个分支，ln z 取在正实轴的上岸取实数值的那个分支．记f (z ) = √z ln z /(1 + z )2 dz ．f (z )的有限奇点只有- 1，且- 1是f (z )的2阶极点．Res[√z ln z /(1 + z )2; - 1] = lim z → - 1 ((1 + z )2 · f (z ))’= lim z → - 1 (√z ln z )’ = lim z → - 1 (((1/2) ln z + 1 )√z /z )= ((1/2) ln (- 1) + 1 )√(- 1)/(- 1)= - ((1/2) πi + 1 )i = (1/2) π - i ．当r < 1 < R 时，⎰C √z ln z /(1 + z )2 dz= ⎰C (r ) + ⎰C (R ) + ⎰L (1) + ⎰L (2) = 2πi Res[√z ln z /(1 + z )2; -1] = 2π + π2 i ．⎰L (1) √z ln z /(1 + z )2 dz = ⎰(r , R ) √x ln x /(1 + x )2 dx→ ⎰(0, +∞) √x ln x /(1 + x )2 dx (当r → 0+，R →+∞时)⎰L (2) √z ln z /(1 + z )2 dz = ⎰(R , r ) (-√x )(ln x + 2πi )/(1 + x )2 dx= ⎰(r , R ) (√x ln x )/(1 + x )2 dx + 2πi ⎰(r , R )√x /(1 + x )2 dx→ ⎰(0, +∞) √x ln x /(1 + x )2 dx + 2πi ⎰(0, +∞) √x /(1 + x )2 dx (当r → 0+，R →+∞时)． 因为z · √z ln z /(1 + z )2 → 0 (当| z |→ +∞时)，故⎰C(R) √z ln z/(1 + z)2dz→ 0 (当R → +∞时)．因为z ·√z ln z/(1 + z)2 → 0 (当| z |→ 0时)，故⎰C(r) √z ln z/(1 + z)2dz→ 0 (当r → 0时)．所以，⎰L(1)+ ⎰L(2)→π/2 -i (当r→ 0+，R→+∞时)．故2⎰(0, +∞)√x ln x/(1 + x)2dx + 2πi⎰(0, +∞) √x /(1 + x)2dx = 2π + π2i．所以，⎰(0, +∞)√x ln x/(1 + x)2dx = π，⎰(0, +∞)√x /(1 + x)2dx = π/2．9. 证明：I = ⎰(0, 1) 1/((1 + x2)(1 -x2)1/2) dx = π/23/2．在割线的上岸(1 -z2)1/2取正值的那一支．因i和-i都是f(z)的一阶极点，故Res[ f(z); i] = 1/(2z (1 -z2)1/2)|z = i= -i/23/2．Res[ f(z); i] = 1/(2z (1 -z2)1/2)|z = –i= -i/23/2．若x在上岸，则f(x) = 1/((1 + x2)(1 -x2)1/2)；若x在下岸，则f(x) = e-i π/((1 + x2)(1 -x2)1/2)；⎰L(1) f(z) dz = ⎰[– 1 + r, 1 –r] f(x) dx．⎰L(2) f(z) dz = ⎰[– 1 + r, 1 –r] f(x) dx．因为lim z→–1 (1 + z) f(z) = 0，lim z→ 1 (1 -z) f(z) = 0，故⎰S(r) f(z) dz→ 0，⎰T(r) f(z) dz→ 0 (as r → 0)．因为lim z→∞z f(z) = 0，故⎰C(R) f(z) dz→ 0 (as R → +∞)．故⎰L(1) f(z) dz + ⎰L(2) f(z) dz→ (2πi)(Res[ f(z); i] + Res[ f(z); -i]) (as r→ 0+，R→+∞)．所以2⎰(– 1, 1) f(x) dx = (2πi)(Res[ f(z); i] + Res[ f(z); -i]) = (2πi)(-i/23/2) = 2π/23/2．故⎰(– 1, 1) f(x) dx = π/23/2．10. 证明方程e z-λ= z ( λ> 1 )在单位圆| z | < 1内恰有一个根，且为实根．【解】在单位圆周C : | z | = 1上，设z = x + i y，则z-λ= (x -λ) + i y，故| e z-λ| = | e (x -λ) + i y | = | e x -λ| < 1 = | z |，由Rouché定理，N(z - e z-λ, C) = N(z, C) = 1．故z - e z-λ = 0在单位圆内恰有一个根．设f(x) = x - e x-λ，x∈ ．因f(- 1) = (- 1)- e-1 -λ < 0，f(1) = 1- e 1 -λ > 0，故x - e x-λ = 0在区间(- 1, 1)内有根．所以方程e z-λ= z ( λ> 1 )在单位圆| z | < 1内的唯一根为实根．[原题是错题．例如c = 1/2，λ= 2，则∀z∈ ，当| z | < 1时，| c z-λ| = | exp((z-λ) Ln c)| = | exp(( z– 2)(ln| 1/2| + 2kπi)) | = e (2 –z)ln2 > 1 > | z |．]11. 证明方程e z- eλz n= 0 ( λ> 1 )在单位圆| z | < 1内有n个根．【解】在单位圆周C : | z | = 1上，| e z| = e Re(z)≤ e | z |≤ e < eλ= | eλz n |，由Rouché定理，N(eλz n- e z, C) = N(eλz n, C) = N(z n, C) = n．12. 若f(z)在周线C内部除有一个一阶极点外解析，且连续到C，在C上| f(z) | = 1，证明f(z) = a ( | a | > 1 )在C内部恰好有一个根．【解】考虑圆K = { z∈ | | z–a | < | a |}．因为| (a-f(z)) -a | = | f(z) | = 1 < | a |，故a-f(z)∈K．因ln(a-f(z))的每个分支，以及他们的导数(ln(a-f(z))’都在K内解析；故i ∆C arg (a-f(z) ) = ⎰C(ln(a-f(z))’dz = 0．由辐角原理，N(a -f(z), C) -P(a -f(z), C) = (2π)–1∆C arg (a-f(z) ) = 0．而a -f(z)在周线C内部除有一个一阶极点外解析，故P(a -f(z), C) = 1．因此N(a -f(z), C) = 1，故f(z) = a ( | a | > 1 )在C内部恰好有一个根．13. 若f(z)在周线C的内部亚纯且连续到C，试证：(1) 若z∈C时，| f(z) | < 1，则方程f(z) = 1在C的内部的根的个数，等于f(z)在C 的内部的极点个数．(2) 若z∈C时，| f(z) | > 1，则方程f(z) = 1在C的内部的根的个数，等于f(z)在C 的内部的零点个数．【解】(1) 类似第12题，设K = { z∈ | | z– 1 | < 1}．因| (1 -f(z)) – 1 | = | f(z) | < 1，故(1 -f(z))∈K．因i ∆C arg (a-f(z) ) = ⎰C(ln(1 -f(z))’dz = 0．故由辐角原理，N(1-f(z), C) -P(1-f(z), C) = (2π)–1∆C arg (a-f(z) ) = 0．而P(1-f(z), C) = P( f(z), C)，所以，N(1-f(z), C) = P( f(z), C)．(2) 因z∈C时，| f(z) | > 1，故在C上，恒有f(z) ≠ 0，即f(z)在C上无零点．设g(z) = 1/f(z) ( 若z是f(z)极点则规定g(z) = 0，若z是f(z)的零点不定义g(z))．那么，g(z)在C的内部亚纯且连续到C，并且当z∈C时，| g(z) | < 1．由(1)的结论，在C的内部，方程g(z) = 1的根的个数等于g(z)的极点的个数．再注意到方程g(z) = 1和方程f(z) = 1在C的内部的根的个数相同，并且，因为在C的内部，z是f(z)的零点⇔z是g(z)的极点，故g(z)的极点个数等于f(z)的零点个数；所以，方程f(z) = 1在C的内部的根的个数，等于f(z)在C的内部的零点个数．14. 设ϕ(z)在C : | z | = 1内部解析，且连续到C．在C上，| ϕ(z) | < 1．试证：在C的内部只有一个点z0，使ϕ(z0) = z0．【解】设f(z) = z，则f(z)在C内部解析且连续到C，在C上，| f(z) | = 1 > | ϕ(z) |．由Rouché定理，N( f(z) -ϕ(z), C) = N( f(z), C) = 1．即方程ϕ(z) = z在C的内部只有一个根．p273第六章习题(二) [ 2, 3, 4, 5 ]2. 计算积分(1/(2πi))⎰C 1/(ζ(ζ- z)) dζ，其中C为单位圆周| ζ| = 1，z∉C．【解】设f(ζ) = 1/(ζ(ζ- z))．当| z | > 1时，f(ζ)在C内部的唯一奇点0是1阶极点，故(1/(2πi))⎰C f(ζ) dζ = Res[f(ζ), 0] = - 1/z．当0 < | z | < 1时，f(ζ)在C内部的两个奇点0, z都是1阶极点，故(1/(2πi))⎰C f(ζ) dζ = Res[f(ζ), 0] + Res[f(ζ), z] = (- 1/z) + (1/z) = 0．当| z | = 0时，f(ζ)在C内部的唯一奇点0是2阶极点，故(1/(2πi))⎰C f(ζ) dζ = Res[f(ζ), 0] = 0．3. 设f(z)在| z | < 1内解析，在| z | ≤ 1上连续，试证：(1 - | z |2) f(z) = (1/(2πi))⎰C : | ζ| = 1f(ζ) ((1-z*ζ)/(ζ- z)) dζ，其中z属于C的内部．【解】设g(ζ) = f(ζ) ((1-z*ζ)/(ζ- z))．若f(z) = 0，则z是g(ζ)的解析点，因此g(ζ)在| ζ | < 1内解析，在| ζ | ≤ 1上连续，故⎰C : | ζ| = 1g(ζ) dζ = 0，因此等式成立．若f(z) ≠ 0，则z是g(ζ)的一阶极点，故(1/(2πi))⎰C : | ζ| = 1f(ζ) ((1-z*ζ)/(ζ- z)) dζ = Res[f(ζ) ((1-z*ζ)/(ζ- z)), z]= f(z) (1-z*z ) = (1 - | z |2) f(z)．4. 试证：(z n/n! )2 = (1/(2πi))⎰C : | ζ| = 1 (z n e zζ)/(n! ζ n + 1 ) dζ，这里C是围绕原点的一条周线．【解】只需要证明，当z≠ 0时，z n/n! = (1/(2πi))⎰C : | ζ| = 1 e zζ/ζ n + 1dζ．由高阶导数公式，(n!/(2πi))⎰C : | ζ| = 1 e zζ/ζ n + 1dζ = (e zζ)(n)|ζ= 0= (z n e zζ)|ζ= 0= z n．或(1/(2πi))⎰C : | ζ| = 1 e zζ/ζ n + 1dζ = Res[e zζ/ζ n + 1, 0] = ((e zζ)(n)|ζ= 0)/n!= z n/n!．5. 试证(含∞的区域的留数定理)：设D是 ∞内含有∞的区域，其边界C是由有限条互不包含且互不相交的周线C1, C2, ..., C m组成，又设函数f(z)在D内除去有限个孤立奇点z1, z2, ..., z n及∞外解析，且连续到边界C，则⎰-C f(z) dz = 2πi ( ∑1≤k≤n Res[f(z), z k] + Res[f(z), ∞] )．【解】∀j : 1 ≤j ≤m，因∞不在C j上，故C j ⊆ 中，因此C j是有界集．故可取充分大的R > 0，使得周线C1, C2, ..., C m及在 中的孤立奇点z1, z2, ..., z n 都在圆K = { z∈ | | z | < R }内．由留数定理，⎰∂K f(z) dz + ⎰-C f(z) dz = 2πi∑1≤k≤n Res[f(z), z k]；而Res[f(z), ∞] = - (1/(2πi))⎰∂K f(z) dz，所以，⎰-C f(z) dz = 2πi ( ∑1≤k≤n Res[f(z), z k] + Res[f(z), ∞] )．∀∃∅-⨯±≠≥·◦≤≡⊕⊗≅αβχδεφγηιϕκλμνοπθρστυϖωξψζ∞•︒ℵℜ℘∇∏∑⎰⊥∠ √§ψ∈∉⊆⊂⊃⊇⊄⊄∠⇒♣♦♥♠§ #↔→←↑↓⌝∨∧⋃⋂⇔⇒⇐∆∑ΓΦΛΩ∂∀m∈ +，★z∈ ∞α1, α2, ...αn lim n→∞，+n→∞∀ε > 0，∑u n，∑n≥ 1u n，m∈ ，∀ε > 0，∃δ> 0，【解】z⎰[0, 2π]l 2 dx，f(x) = (-∞, +∞)[-π, π]∑1 ≤k≤n u n，[0, 2π]。

习题六解答A 类1．求23z w =在z=i 处的伸缩率和旋转角，问23z w =将经过点z=i 且平行于实轴正向的曲线的切线方向映射成w 平面上哪一个方向？并作图。

解 由题()z z w 63'2='=，从而()()2i 6arg i 'arg π==w ，()6|i 6|i '==w ，当i =z 时，()332-==i w ，即i =z ，3-=w ，且旋转2π。

2．求映射z w i =下，下列图形映射成什么图形？ （1）以i 1=z ，12-=z ，13=z 为顶点的三角形。

（2）闭圆域：1|1|≤-z 。

解（1）在z w i =下，i 1=z ，12-=z ，13=z ，被映成11-=w ，i 2-=w ，i 3=w ，即将三角形映成三角形。

（2）在z w i =下，01=z ，i 12+=z ，23=z ，被映成01=w ，i 12+-=w ，i 23=w ，由保圆性知11≤-z 被映成1i ≤-z 。

3．证明映射z z w 1+=把圆周)0(>=c z 映射成椭圆：θcos )1(c c u +=，θsin )1(c c v -=。

证 设)sin i (cos θθ+=r z ，v u w i +=，则)sin i (cos 1)sin i (cos 1θθθθ+++=+=r r z z w=θθθθθθθθsin )1i(cos )1()sin (cos sin i cos sin i cos 22r r r r r r r -++=+-++w=i zw=i z又cz =，即c r =，所以θθsin )1i(cos )1(c c c c w -++=从而θcos )1(c c u +=，θsin )1(c c v -=。

4．证明在映射ze w i =下，互相正交的直线族1Re c z =与2Im c z =依次映射成互相正交的直线族1tan c u v =与圆族2222c e v u -=+证设y x z i +=，v u w i +=，x c z ==1Re ，y c z ==2Im ，所以)sin i (cos i x x e e w yz +==-，即1cos 2c eu c -=，1sin 2c ev c-=，1tan tan c u x u v ==是一族直线，22222c y e e v u --==+是一族圆，显然，过原点的直线与以圆点为心的圆是正交的。

第一章 复数与复变函数一、选择题 1．当iiz -+=11时，5075100z z z ++的值等于（ ） （A ）i （B ）i - （C ）1 （D ）1- 2．设复数z 满足3)2(π=+z arc ，65)2(π=-z arc ，那么=z （ ） （A ）i 31+- （B ）i +-3 （C ）i 2321+-（D ）i 2123+- 3．复数)2(tan πθπθ<<-=i z 的三角表示式是（ ） （A ）)]2sin()2[cos(sec θπθπθ+++i （B ）)]23sin()23[cos(sec θπθπθ+++i （C ）)]23sin()23[cos(sec θπθπθ+++-i （D ）)]2sin()2[cos(sec θπθπθ+++-i 4．若z 为非零复数，则22z z -与z z 2的关系是（ ） （A ）z z z z 222≥- （B ）z z z z 222=- （C ）z z z z 222≤- （D ）不能比较大小５．设y x ,为实数，yi x z yi x z +-=++=11,1121且有1221=+z z ，则动点),(y x 的轨迹是（ ）（A ）圆 （B ）椭圆 （C ）双曲线 （D ）抛物线 ６．一个向量顺时针旋转3π，向右平移３个单位，再向下平移１个单位后对应的复数为i 31-，则原向量对应的复数是（ ）（A ）2 （B ）i 31+（C ）i -3 （D ）i +3７．使得22z z =成立的复数z 是（ ）（A ）不存在的 （B ）唯一的 （C ）纯虚数 （D ）实数 ８．设z 为复数，则方程i z z +=+2的解是（ ） （A ）i +-43 （B ）i +43 （C ）i -43 （D ）i --43 ９．满足不等式2≤+-iz iz 的所有点z 构成的集合是（ ） （A ）有界区域 （B ）无界区域 （C ）有界闭区域 （D ）无界闭区域 10．方程232=-+i z 所代表的曲线是（ ）（A ）中心为i 32-，半径为2的圆周 （B ）中心为i 32+-，半径为２的圆周 （C ）中心为i 32+-，半径为2的圆周 （D ）中心为i 32-，半径为２的圆周 11．下列方程所表示的曲线中，不是圆周的为（ ） （A ）221=+-z z （B ）433=--+z z （C ）)1(11<=--a azaz （D ）)0(0>=-+++c c a a z a z a z z12．设,5,32,1)(21i z i z z z f -=+=-=，则=-)(21z z f （ ） （A ）i 44--（B ）i 44+（C ）i 44-（D ）i 44+-13．00)Im()Im(lim0z z z z x x --→（ ）（A ）等于i （B ）等于i -（C ）等于0（D ）不存在14．函数),(),()(y x iv y x u z f +=在点000iy x z +=处连续的充要条件是（ ） （A ）),(y x u 在),(00y x 处连续（B ）),(y x v 在),(00y x 处连续（C ）),(y x u 和),(y x v 在),(00y x 处连续（D ）),(),(y x v y x u +在),(00y x 处连续15．设C z ∈且1=z ，则函数zz z z f 1)(2+-=的最小值为（ ）（A ）3- （B ）2- （C ）1- （D ）1二、填空题1．设)2)(3()3)(2)(1(i i i i i z ++--+=，则=z2．设)2)(32(i i z +--=，则=z arg 3．设43)arg(,5π=-=i z z ，则=z 4．复数22)3sin 3(cos )5sin 5(cos θθθθi i -+的指数表示式为 5．以方程i z 1576-=的根的对应点为顶点的多边形的面积为６．不等式522<++-z z 所表示的区域是曲线的内部 ７．方程1)1(212=----zi iz 所表示曲线的直角坐标方程为８．方程i z i z +-=-+221所表示的曲线是连续点和的线段的垂直平分线 ９．对于映射zi =ω，圆周1)1(22=-+y x 的像曲线为 10．=+++→)21(lim 421z z iz三、若复数z 满足03)21()21(=+++-+z i z i z z ，试求2+z 的取值范围． 四、设0≥a ，在复数集C 中解方程a z z =+22. 五、设复数i z ±≠，试证21z z+是实数的充要条件为1=z 或0)(=z IM . 六、对于映射)1(21zz +=ω，求出圆周4=z 的像. 七、试证１.)0(0221≠≥z z z 的充要条件为2121z z z z +=+； ２.)),,2,1,,,0(021n j k j k z z z j =≠≠≥的充要条件为 n n z z z z z z +++=+++ 2121.八、若0)(lim 0≠=→A z f x x ，则存在0>δ，使得当δ<-<00z z 时有A z f 21)(>. 九、设iy x z +=，试证y x z y x +≤≤+2.十、设iy x z +=，试讨论下列函数的连续性：1.⎪⎩⎪⎨⎧=≠+=0,00,2)(22z z yx xyz f2.⎪⎩⎪⎨⎧=≠+=0,00,)(223z z y x y x z f .第二章解析函数一、选择题：1．函数23)(z z f =在点0=z 处是( )（A ）解析的 （B ）可导的（C ）不可导的 （D ）既不解析也不可导 2．函数)(z f 在点z 可导是)(z f 在点z 解析的( )（A ）充分不必要条件 （B ）必要不充分条件（C ）充分必要条件 （D ）既非充分条件也非必要条件 3．下列命题中，正确的是( )（A ）设y x ,为实数，则1)cos(≤+iy x（B ）若0z 是函数)(z f 的奇点，则)(z f 在点0z 不可导（C ）若v u ,在区域D 内满足柯西-黎曼方程，则iv u z f +=)(在D 内解析 （D ）若)(z f 在区域D 内解析，则)(z if 在D 内也解析 4．下列函数中，为解析函数的是( )（A ）xyi y x 222--（B ）xyi x +2（C ）)2()1(222x x y i y x +-+-（D ）33iy x +5．函数)Im()(2z z z f =在=z 处的导数( )（A ）等于0 （B ）等于1 （C ）等于1-（D ）不存在6．若函数)(2)(2222x axy y i y xy x z f -++-+=在复平面内处处解析，那么实常数=a ( )（A ）0（B ）1（C ）2（D ）2-7．如果)(z f '在单位圆1<z 内处处为零，且1)0(-=f ，那么在1<z 内≡)(z f ( )（A ）0（B ）1（C ）1-（D ）任意常数8．设函数)(z f 在区域D 内有定义，则下列命题中，正确的是（A ）若)(z f 在D 内是一常数，则)(z f 在D 内是一常数 （B ）若))(Re(z f 在D 内是一常数，则)(z f 在D 内是一常数 （C ）若)(z f 与)(z f 在D 内解析，则)(z f 在D 内是一常数 （D ）若)(arg z f 在D 内是一常数，则)(z f 在D 内是一常数 9．设22)(iy x z f +=，则=+')1(i f ( ) （A ）2（B ）i 2（C ）i +1（D ）i 22+ 10．i i 的主值为( )（A ）0（B ）1（C ）2πe （D ）2π-e11．z e 在复平面上( )（A ）无可导点（B ）有可导点，但不解析（C ）有可导点，且在可导点集上解析（D ）处处解析 12．设z z f sin )(=，则下列命题中，不正确的是( ) （A ）)(z f 在复平面上处处解析（B ）)(z f 以π2为周期（C ）2)(iziz e e z f --=（D ）)(z f 是无界的13．设α为任意实数，则α1( ) （A ）无定义（B ）等于1（C ）是复数，其实部等于1（D ）是复数，其模等于1 14．下列数中，为实数的是( )（A ）3)1(i -（B ）i cos （C ）i ln （D ）i e 23π-15．设α是复数，则( )（A ）αz 在复平面上处处解析（B ）αz 的模为αz（C ）αz 一般是多值函数（D ）αz 的辐角为z 的辐角的α倍 二、填空题1．设i f f +='=1)0(,1)0(，则=-→zz f z 1)(lim2．设iv u z f +=)(在区域D 内是解析的，如果v u +是实常数，那么)(z f 在D 内是 3．导函数xv i x u z f ∂∂+∂∂=')(在区域D 内解析的充要条件为 4．设2233)(y ix y x z f ++=，则=+-')2323(i f5．若解析函数iv u z f +=)(的实部22y x u -=，那么=)(z f6．函数)Re()Im()(z z z z f -=仅在点=z 处可导 7．设z i z z f )1(51)(5+-=，则方程0)(='z f 的所有根为 8．复数i i 的模为 9．=-)}43Im{ln(i10．方程01=--z e 的全部解为 三、设),(),()(y x iv y x u z f +=为iyx z +=的解析函数，若记)2,2()2,2(),(iz z z z iv i z z z z u z z w -++-+=，则0=∂∂z w．四、试证下列函数在z 平面上解析，并分别求出其导数 1．;sinh sin cosh cos )(y x i y x z f -=2．);sin cos ()sin cos ()(y ix y y ie y y y x e z f xx++-=五、设023=+-ze zw w ，求22,dz wd dz dw . 六、设⎪⎩⎪⎨⎧=≠++=0,00,)()(422z z y x iy x xy z f 试证)(z f 在原点满足柯西-黎曼方程，但却不可导.七、已知22y x v u -=-，试确定解析函数iv u z f +=)(. 八、设s 和n 为平面向量，将s按逆时针方向旋转2π即得n .如果iv u z f +=)(为解析函数，则有s v n u n v s u ∂∂-=∂∂∂∂=∂∂,（s ∂∂与n∂∂分别表示沿s ,n 的方向导数）. 九、若函数)(z f 在上半平面内解析，试证函数)(z f 在下半平面内解析. 十、解方程i z i z 4cos sin =+.第三章复变函数的积分一、选择题：1．设c 为从原点沿x y =2至i +1的弧段，则=+⎰cdz iy x )(2( )（A ）i 6561- （B ）i 6561+- （C ）i 6561-- （D ）i 6561+ 2．设c 为不经过点1与1-的正向简单闭曲线，则dz z z zc⎰+-2)1)(1(为( ) （A ）2i π（B ）2iπ-（C ）0 （D ）(A)(B)(C)都有可能3．设1:1=z c 为负向，3:2=z c 正向，则=⎰+=dz z zc c c 212sin ( ) （A ） i π2- （B ）0 （C ）i π2 （D ）i π4 4．设c 为正向圆周2=z ，则=-⎰dz z zc 2)1(cos ( ) （A ）1sin -（B ）1sin （C ）1sin 2i π-（D ）1sin 2i π5．设c 为正向圆周21=z ，则=--⎰dz z z z c23)1(21cos( ) （A ）)1sin 1cos 3(2-i π（B ）0（C ）1cos 6i π（D ）1sin 2i π-6．设ξξξξd ze zf ⎰=-=4)(，其中4≠z ，则='）i f π(( )（A ）i π2-（B ）1-（C ）i π2（D ）17．设)(z f 在单连通域B 内处处解析且不为零，c 为B 内任何一条简单闭曲线，则积分dz z f z f z f z f c⎰+'+'')()()(2)( ( )（A ）于i π2（B ）等于i π2-（C ）等于0（D ）不能确定 8．设c 是从0到i 21π+的直线段，则积分=⎰c z dz ze （ ）（A ）21e π-(B) 21e π--(C)i e 21π+(D) i e 21π- 9．设c 为正向圆周0222=-+x y x ，则=-⎰dz z z c1)4sin(2π( )（A ）i π22（B ）i π2（C ）0（D ）i π22- 10．设c 为正向圆周i a i z ≠=-,1，则=-⎰cdz i a zz 2)(cos ( ) （A ）ie π2（B ）eiπ2（C ）0（D ）i i cos 11．设)(z f 在区域D 内解析，c 为D 内任一条正向简单闭曲线，它的内部全属于D ．如果)(z f 在c 上的值为2，那么对c 内任一点0z ,)(0z f ( )（A ）等于0 （B ）等于1 （C ）等于2 （D ）不能确定 12．下列命题中，不正确的是( ) （A ）积分⎰=--ra z dz az 1的值与半径)0(>r r 的大小无关 （B ）2)(22≤+⎰cdz iy x,其中c 为连接i -到i 的线段（C ）若在区域D 内有)()(z g z f ='，则在D 内)(z g '存在且解析（D ）若)(z f 在10<<z 内解析，且沿任何圆周)10(:<<=r r z c 的积分等于零，则)(z f 在0=z 处解析13．设c 为任意实常数，那么由调和函数22y x u -=确定的解析函数iv u z f +=)(是( )(A)c iz +2（B ）ic iz +2 （C ）c z +2（D ）ic z +2 14．下列命题中，正确的是( )（A ）设21,v v 在区域D 内均为u 的共轭调和函数，则必有21v v = （B ）解析函数的实部是虚部的共轭调和函数 （C ）若iv u z f +=)(在区域D 内解析，则xu∂∂为D 内的调和函数 （D ）以调和函数为实部与虚部的函数是解析函数15．设),(y x v 在区域D 内为),(y x u 的共轭调和函数，则下列函数中为D 内解析函数的是( )（A ）),(),(y x iu y x v +（B ）),(),(y x iu y x v - （C ）),(),(y x iv y x u -（D ）xv i x u ∂∂-∂∂ 二、填空题1．设c 为沿原点0=z 到点i z +=1的直线段，则=⎰cdz z 22．设c 为正向圆周14=-z ，则=-+-⎰c dz z z z 22)4(233．设⎰=-=2)2sin()(ξξξξπd zz f ,其中2≠z ，则=')3(f 4．设c 为正向圆周3=z ，则5．设c 为负向圆周4=z ，则=-⎰c zdz i z e 5)(π =+⎰cdz zzz6．解析函数在圆心处的值等于它在圆周上的7．设)(z f 在单连通域B 内连续，且对于B 内任何一条简单闭曲线c 都有0)(=⎰cdz z f ，那么)(z f 在B 内8．调和函数xy y x =),(ϕ的共轭调和函数为9．若函数23),(axy x y x u +=为某一解析函数的虚部，则常数=a10．设),(y x u 的共轭调和函数为),(y x v ，那么),(y x v 的共轭调和函数为 三、计算积分 1.⎰=+-Rz dz z z z)2)(1(62,其中1,0≠>R R 且2≠R ; 2.⎰=++22422z z z dz． 四、设)(z f 在单连通域B 内解析，且满足)(1)(1B x z f ∈<-.试证１．在B 内处处有0)(≠z f ； ２．对于B 内任意一条闭曲线c ，都有0)()(=''⎰cdz z f z f 五、设)(z f 在圆域R a z <-内解析，若)0()()(max R r r M z f ra z <<==-，则),2,1()(!)()( =≤n rr M n a fnn . 六、求积分⎰=1z zdz z e ，从而证明πθθπθ=⎰0cos )cos(sin d e . 七、设)(z f 在复平面上处处解析且有界，对于任意给定的两个复数b a ,，试求极限⎰=+∞→--R z R dz b z a z z f ))(()(lim并由此推证)()(b f a f =（刘维尔Liouville 定理）.八、设)(z f 在)1(><R R z 内解析，且2)0(,1)0(='=f f ，试计算积分⎰=+122)()1(z dz zz f z 并由此得出⎰πθθθ202)(2cos d e f i 之值.九、设iv u z f +=)(是z 的解析函数，证明222222222))(1()(4))(1ln())(1ln(z f z f y z f x z f +'=∂+∂+∂+∂.十、若)(22y x u u +=，试求解析函数iv u z f +=)(.第四章级数一、选择题：1．设),2,1(4)1( =++-=n n nia n n ，则n n a ∞→lim ( ) （A ）等于0 （B ）等于1 （C ）等于i （D ）不存在 2．下列级数中，条件收敛的级数为( )（A ）∑∞=+1)231(n ni （B ）∑∞=+1!)43(n nn i （C ） ∑∞=1n n n i （D ）∑∞=++-11)1(n n n i3．下列级数中，绝对收敛的级数为( )（B ） ∑∞=+1)1(1n n in（B ）∑∞=+-1]2)1([n n n i n (C)∑∞=2ln n n n i （D ）∑∞=-12)1(n nnn i 4．若幂级数∑∞=0n n nz c在i z 21+=处收敛，那么该级数在2=z 处的敛散性为( )（A ）绝对收敛（B ）条件收敛 （C ）发散（D ）不能确定 5．设幂级数∑∑∞=-∞=01,n n n n nn znc z c 和∑∞=++011n n n z n c 的收敛半径分别为321,,R R R ，则321,,R R R 之间的关系是( )（A ）321R R R << （B ）321R R R >>（C ）321R R R <=（D ）321R R R == 6．设10<<q ，则幂级数∑∞=02n n n z q 的收敛半径=R ( )（A ）q （B ）q1（C ）0 （D ）∞+ 7．幂级数∑∞=1)2(2sinn n z n n π的收敛半径=R ( ) （A ） 1（B ）2（C ）2（D ）∞+8．幂级数∑∞=++-011)1(n n n z n 在1<z 内的和函数为 （A ）)1ln(z +（B ）)1ln(z - （D ）z +11ln(D) z-11ln 9．设函数z e z cos 的泰勒展开式为∑∞=0n nn z c ，那么幂级数∑∞=0n n n z c 的收敛半径=R ( )（A ）∞+（B ）1（C ）2π（D ）π 10．级数+++++22111z z z z的收敛域是( ) （A ）1<z （B ）10<<z （C ）+∞<<z 1（D ）不存在的 11．函数21z 在1-=z 处的泰勒展开式为( )（A ）)11()1()1(11<++-∑∞=-z z n n n n（B ）)11()1()1(111<++-∑∞=--z z n n n n（C ）)11()1(11<++-∑∞=-z z n n n （D ）)11()1(11<++∑∞=-z z n n n12．函数z sin ，在2π=z 处的泰勒展开式为( )（A ）)2()2()!12()1(012+∞<--+-∑∞=+ππz z n n n n（B ）)2()2()!2()1(02+∞<---∑∞=ππz z n n n n（C ）)2()2()!12()1(0121+∞<--+-∑∞=++ππz z n n n n（D ）)2()2()!2()1(021+∞<---∑∞=+ππz z n n n n13．设)(z f 在圆环域201:R z z R H <-<内的洛朗展开式为∑∞-∞=-n n nz z c)(0，c 为H 内绕0z 的任一条正向简单闭曲线，那么=-⎰c dz z z z f 20)()(( )(A)12-ic π （B ）12ic π （C ）22ic π（D ）)(20z f i 'π14．若⎩⎨⎧--==-+= ,2,1,4,2,1,0,)1(3n n c nn n n ，则双边幂级数∑∞-∞=n nn z c 的收敛域为( ) （A ）3141<<z （B ）43<<z （C ）+∞<<z 41（D ）+∞<<z 3115．设函数)4)(1(1)(++=z z z z f 在以原点为中心的圆环内的洛朗展开式有m 个，那么=m ( )（A ）1（B ）2 （C ）3（D ）4 二、填空题 1．若幂级数∑∞=+0)(n n ni z c在i z =处发散，那么该级数在2=z 处的收敛性为．2．设幂级数∑∞=0n nnz c与∑∞=0)][Re(n n n z c 的收敛半径分别为1R 和2R ，那么1R 与2R 之间的关系是． 3．幂级数∑∞=+012)2(n n nz i 的收敛半径=R4．设)(z f 在区域D 内解析，0z 为内的一点，d 为0z 到D 的边界上各点的最短距离，那么当d z z <-0时，∑∞=-=00)()(n n n z z c z f 成立，其中=n c ．5．函数z arctan 在0=z 处的泰勒展开式为 ． 6．设幂级数∑∞=0n nnz c的收敛半径为R ，那么幂级数∑∞=-0)12(n n n n z c 的收敛半径为．7．双边幂级数∑∑∞=∞=--+--112)21()1()2(1)1(n n n nnz z 的收敛域为． 8．函数zze e 1+在+∞<<z 0内洛朗展开式为．9．设函数z cot 在原点的去心邻域R z <<0内的洛朗展开式为∑∞-∞=n n nz c，那么该洛朗级数收敛域的外半径=R ． 10．函数)(1i z z -在+∞<-<i z 1内的洛朗展开式为．三、若函数211z z --在0=z 处的泰勒展开式为∑∞=0n n n z a ，则称{}n a 为菲波那契(Fibonacci)数列，试确定n a 满足的递推关系式，并明确给出n a 的表达式． 四、试证明 1．);(11+∞<≤-≤-z ez ee zzz2．);1()1(1)3(<-≤-≤-z ze e z e z五、设函数)(z f 在圆域R z <内解析，∑==nk kk n z k f S 0)(!)0(试证 1．)()(21)(111R r z d z z f iz S n rn n n <<--=+=++⎰ξξξξξπξ.2．)()()(2)((11R r z d z f iz z S z f rn n n <<-=-⎰=++ξξξξπξ）。

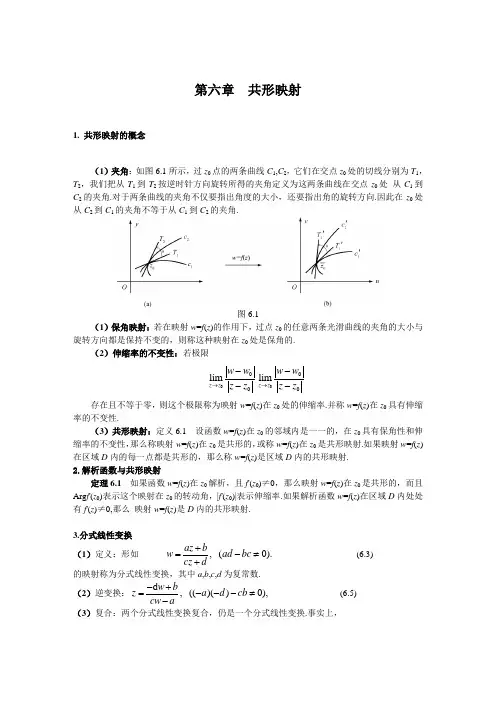
第六章 共形映射1. 共形映射的概念（1）夹角：如图6.1所示，过z 0点的两条曲线C 1,C 2，它们在交点z 0处的切线分别为T 1，T 2，我们把从T 1到T 2按逆时针方向旋转所得的夹角定义为这两条曲线在交点z 0处 从C 1到C 2的夹角.对于两条曲线的夹角不仅要指出角度的大小，还要指出角的旋转方向.因此在z 0处从C 2到C 1的夹角不等于从C 1到C 2的夹角.图6.1（1）保角映射：若在映射w =f (z )的作用下，过点z 0的任意两条光滑曲线的夹角的大小与旋转方向都是保持不变的，则称这种映射在z 0处是保角的.（2）伸缩率的不变性：若极限00limz z w w z z →--000limz z w w z z →--存在且不等于零，则这个极限称为映射w =f (z )在z 0处的伸缩率.并称w =f (z )在z 0具有伸缩率的不变性.（3）共形映射：定义6.1 设函数w =f (z )在z 0的邻域内是一一的，在z 0具有保角性和伸缩率的不变性，那么称映射w =f (z )在z 0是共形的，或称w =f (z )在z 0是共形映射.如果映射w =f (z )在区域D 内的每一点都是共形的，那么称w =f (z )是区域D 内的共形映射. 2.解析函数与共形映射定理6.1 如果函数w =f (z )在z 0解析，且f '(z 0)≠0，那么映射w =f (z )在z 0是共形的，而且Arg f '(z 0)表示这个映射在z 0的转动角，|f '(z 0)|表示伸缩率.如果解析函数w =f (z )在区域D 内处处有f '(z )≠0,那么 映射w =f (z )是D 内的共形映射.3.分式线性变换（1）定义：形如 , (0).az bw ad bc cz d+=-≠+ (6.3) 的映射称为分式线性变换，其中a ,b ,c ,d 为复常数. （2）逆变换：d , (()()0),w bz a d cb cw a-+=---≠- (6.5)（3）复合：两个分式线性变换复合，仍是一个分式线性变换.事实上，(0),(0).z w z αξβαβαδγβξαδβγγξδγδ''++''''=-≠=-≠''++把后式代入前式得az b w cz d+=+ 其中()()0.ad bc αδγβαδβγ''''-=--≠（4）分解：根据这个事实，我们可以把一个一般形式的分式线性变换分解成一些简单映射的复合.不妨设c ≠0，于是.()az b a bc adw cz d c c cz d +-==+++令,a bc adA B c c-==则上式变为 .Bw A cz d=++ 它由下列三个变换复合而成;1;,z cz d z z w A Bz '=+''='''=+ (6.5) 其中(6.5)中的第一和第三式为整线性变换. 4.分式线性变换性质1° 共形性定理6.2 分式线性变换在扩充复平面上是一一对应的，且是共形的. 2°保圆性定理6.3 分式线性变换将扩充z 平面上的圆映射成扩充w 平面上的圆，即具有保圆性. 在扩充复平面上把直线看成是半径为无穷大的圆周.推论6.1 在分式线性变换下，圆C 映射成圆C '.如果在C 内任取一点z 0，而点z 0的象在C '的内部，那么C 的内部就是映射到C '的内部；如果z 0的象在C '的外部，那么C 的内部就映射成C '的外部.3° 保对称性先引进对称点的概念.定义6.2 设C 为以z 0点为中心，R 为半径的圆周.如果点z ,z *在从z 0出发的射线上，且满足|z -z 0|·|z *-z 0|=R 2, (6.6)则称z ,z *关于圆周C 是对称的.如果C 是直线，则当以z 和z *为端点的线段被C 平分时，称z ,z *关于直线C 为对称的.我们规定： 无穷远点关于圆周的对称点是圆心.定理6.4 设点z ,z *是关于圆周C 的一对对称点，那么在分式线性变换下，它们的象点w 及w *也是关于C 的像曲线C '的一对对称点.5. 确定分式线性变换的条件定理6.5 在z 平面上任意给定三个不同点z 1,z 2,z 3，在w 平面上也任意给定三个不同点w 1,w 2,w 3，那么就存在分式线性变换，将z k 依次映射成w k (k =1,2,3)，且这种变换是唯一的.推论6.2 z 1,z 2,z 3所在的圆C 的象C ′是w 1,w 2,w 3所在的圆.且如果C 依z 1→z 2→z 3 的绕向与C ′依w 1→w 2→w 3的绕向相同时，则C 的内部就映射成C ′的内部（相反时，C 的内部就映射成C ′的外部）图6.8例6.1 求将上半平面映射为单位圆，且将上半平面的定点z 0映射为圆心w =0的分式线性变换.所求映射的一般形式为00, Im 0.i z z w e z z z θ-=>- (6.8) 例6.2 求将单位圆|z |<1映射为单位圆|w |<1的分式线性变换. 所求映射的一般形式为00 (1)1i z z w e z z zθ-=<-. 6. 几个初等函数所构成的映射（1） 幂函数：w =zn(n ≥2)作用： 1° 圆|z |=r 映射成|w |=r n ，即在以原点为中心的圆有保圆性.2°射线0θθ=映射成射线0n ϕθ=，特别地，正实轴θ=0映成正实轴ϕ=0； 3°将角形域02π0()nθθ<<<映射成角形域00n ϕθ<<.(a) 公式图6.10（2）指数函数：w =e z作用： 1° 平面上的直线x =常数，被映射成w 平面上的圆周ρ=常数；而y =常数，被映射成射线ϕ=常数.2° 把水平带形域0Im (2π)z a a <<≤映射成角形域0arg w a <<.（如图6.12(a)） 3° 带形域0Im 2πz <<映射成沿正实轴剪开的w 平面：0arg 2πw <<(如图6.12(b)).3.求2w z =在z =i 处的伸缩率和旋转角，问：2w z =将经过点z =i 且平行于实轴正向的曲线的切线方向映成w 平面 上哪一个方向？并作图.例6.5 求将|z |<1,Im z >0映为|w |>1的一个共形映射.。

第六章共形映射（The Conformal mapping）第一讲授课题目：§6.1共形映射的概念；§6.2共形映射的基本问题教学内容：导数的几何意义、共形映射的概念、解析函数的保域性与边界对应原理、共形映射的存在唯一性.学时安排：2学时.教学目标：1、理解导数的几何意义；2、弄清共形映射的概念；3、掌握解析函数的保域性与边界对应原理、共形映射的存在唯一性；教学重点：解析函数的保域性与边界对应原理；教学难点：解析函数的保域性与边界对应原理；教学方式：多媒体与板书相结合.P习题六：1-3作业布置：164板书设计：一、导数的几何意义；二、共形映射的概念；三、解析函数的保域性与边界对应原理；四、共形映射的存在唯一性参考资料：1、《复变函数》，西交大高等数学教研室，高等教育出版社；2、《复变函数与积分变换学习辅导与习题全解》，高等教育出版；3、《复变函数论》，（钟玉泉编，高等教育出版社，第二版）2005年5月4、《复变函数与积分变换》苏变萍陈东立编，高等教育出版社，2008年4月课后记事：1、基本掌握共形映射的概念；2、不能灵活运用解析函数的保域性与边界对应原理；教学过程：§6.1共形映射的概念(The conception of conformal mapping)一、导数的几何意义（Geometric meaning of derivative ）1、解析变换的保域性（Transform domain of security analysis ）解析函数所确定的映射是共形映射.它是复变函数论中最重要的概念之一，与物理中的概念有密切的联系，而且对物理学中许多领域有重要的应用.如应用共形映射成功地解决了流体力学与空气动力学、弹性力学、磁场、电场与热场理论以及其他方面的许多实际问题.我们主要研究单叶解析函数的映射性质.注1：单叶函数是一个单射的解析函数.例 1 函数α+=z w 及z w α=是z 平面上的单叶解析函数它们把z 平面映射成w 平面，其中α是复常数，并且对于第二个映射0≠α.例 2 z e w =在每个带形,2Im π+<<a z a 内单叶解析，并且把这个带形区域映射成w 平面上除去从原点出发的一条射线而得的区域，，其中a 是任意实常数.引理（Lemma ）：设函数)(z f 在0z z =解析，并且)(00z f w =.设...)3,2,1(0)(,0)(...)('')('0)(0)1(00=≠====-p z f z f z f z f p p ，那么0)(w z f -在0z 有p 阶零点，并且对充分小的正数ρ，存在着一个正数μ，使得当μ<-<||00w w 时，w z f -)(在ρ<-<||00z z 内有p 个一阶零点.证明：由已知条件可知0)(w z f -在0z 有p 阶零点.由于)(z f 不恒等于零，作以0z 为心的开圆盘ρ<-|:|0z z D ，其边界为C ，使得)(z f 在C D D ⋃=上解析，并且使得0)(w z f -及)(z f '除去0z z =外在D 上无其它零点.有0|)(|min 0>=-∈μw z f Cz 取w ，使μ<-<||00w w .由儒歇定理，比较w z f -)(及0)(w z f -在内D 的零点的个数.由于),())(()(00w w w z f w z f -+-=-而当C z ∈时,0|||)(|00>->≥-w w w z f μ可见w z f -)(及0)(w z f -在D 内的零点个数同为p （每个n 阶零点作n 个零点）.因为0w w ≠，所以0z z ≠，而0]')([0≠-≠z z w z f . 所以w z f -)(在D 内的每个零点都是一阶的.由此引理可证明下面定理定理(Theorem)6.1、设函数)(z f 在区域D 内单叶解析，则D z ∈∀，有 .0)('≠z f注2：这个定理的逆定理不成立，例如z e w =的导数在z 平面上任意一点不为零，而z e w =在整个z 平面上不是单叶的.定理(Theorem)6.2设函数)(z f w =在0z z =解析，并且0)('0≠z f ，那么)(z f 在0z 的一个邻域内单叶解析.定理(Theorem)6.3设函数)(z f w =在区域D 内解析，并且不恒等于常数，则)(1D f D =是一个区域.注3：如果)(z f w =在区域D 内单叶解析，根据定理6.3，它把区域D 双射成区域)(D f .于是)(z f 有一个在)(D f 内确定的反函数)(w z ϕ=.定理(Theorem)6.4设函数)(z f 在区域D 内单叶解析，则)(z f w =在)(D f 内存在单叶解析的反函数)(w z ϕ=，且 .)('1)('z f w =ϕ 证明：考虑以下思路：)(0D f w ∈∀，有D z ∈∀0,1)()(000000z z w w w w z z w w w w --=--=--ϕϕ 因为当0w w →时，)()(00z z w z ϕϕ=→=，所以,)('1)()(lim 1lim 1)()(lim 0000000000z f z z z f z f z z w w w w w w z z z z w w =⎪⎪⎭⎫ ⎝--=⎪⎪⎭⎫ ⎝⎛--=--→→→ϕϕ即可给出定理的证明.2、导数的几何意义(Geometric meaning of derivative)设函数)(z f w =是区域D 内的单叶解析函数.)(,000z f w D z =∈.则有0)('0≠z f .过0z 作一条简单光滑曲线C ： ),()()()(b t a t iy t x t z z ≤≤+==]),[()(000b a t z t z ∈=.)(')(')('t iy t x t z dtdz +== 则)(0t z '存在，且0)(0≠'t z作过曲线C 上点)(00t z z =及)(11t z z =的割线，割线的方向向量为0101t t z z --，当1t 趋近于0t 时，向量0101t t z z --与实轴的夹角0101arg t t z z --存在极限，即为曲线C 在0z z =的切线的位置.已知,0)('lim 0010101≠=--→t z t t z z t t 所以，有),('arg arg lim 0010101t z t t z z t t =--→ 这就是曲线C 在)(00t z z =处切线与实轴的夹角，在这里幅角是连续变动的，并且极限式两边幅角的数值是相应地适当选取的. 函数)(z f w =把简单光滑曲线C 映射成一条简单曲线Γ： ),())((1t t t t z f w o ≤≤=由于())('))(('000t z t z f t w ='，可见Γ也是一条光滑曲线；它在0w 的切线与实轴的夹角是()),('arg ))(('arg )('))(('arg arg 00000t z t z f t z t z f t w +==' 因此，Γ在0w 处切线与实轴的夹角及C 在0z 处切线与实轴的夹角相差)('arg 0t z .注4：这里的)('arg 0t z 与曲线C 的形状及在0z 处切线的方无关.另外在D 内过0z 另有一条简单光滑曲线)(:11t z z C =，函数)(z f w =把它映射成一条简单光滑曲线))((:11t z f w =Γ.和上面一样，1C 与1Γ在0z 及0w 处切线与实轴的夹角分别是)('arg 01t z 及),('arg ))(('arg )('))(('arg 01010101t z t z f t z t z f +=所以，在0w 处曲线Γ到曲线1Γ的夹角恰好等于在0z 处曲线C 到曲线1C 的夹角：),('arg )('arg )('))(('arg )('))(('arg 001000101t z t z t z t z f t z t z f -=-因此，用单叶解析函数作映射时，曲线间的夹角的大小及方向保持不变，我们称这个性质为单叶解析函数所作映射的保角性.下面再说明它的模的几何意义.因为,|||)()(|lim |)('|0000z z z f z f z f z z --=→ 由于|)('|0z f 是比值|||)()(|00z z z f z f --的极限，它可以近似地表示这种比值.在)(z f w =所作映射下，||0z z -及|)()(|0z f z f -分别表示z 平面上向量0z z -及w 平面上向量)()(0z f z f -的长度，这里向量0z z -及)()(0z f z f -的起点分别取在0z 及)(0z f .当较小||0z z -时，|)()(|0z f z f -近似地表示通过映射后，|)()(|0z f z f -对||0z z -的伸缩倍数，而且这一倍数与向量0z z -的方向无关.我们把|)('|0z f 称为在点0z 的伸缩率.从几何直观上来看.设)(z f w =是在区域D 内解析的函数，0)(',),(,00000≠∈=∈z f D z z f w D z ，那么)(z f w =把z 平面上半径充分小的圆ρ=-||0z z 近似地映射成w 平面上圆),0(|)('|||00+∞<<=-ρρz f w w因此，解析函数在导数不为零的地方具有旋转角不变性和伸缩率不变性.二、共形映射的概念(The concept of conformal mapping) 定义(Definition)6.1对于区域D 内的映射)(z f w =，如果它在区域D 内任意一点具有保角性和伸缩率不变性，则称映射)(z f w =是第一类保角映射；如果它在区域D 内任意一点保持曲线的交角的大小不变，则称映射)(z f w =是第二类保角映射.定理(Theorem)6.5如)(z f w =在区域D 内解析，且0)(≠'z f 则)(z f w =所构成的映射是第一类保角映射. 定义(Definition)6.2设)(z f w =是区域D 内的第一类保角映射，如果当21z z ≠时，有()21)(z f z f ≠，，则称)(z f 为共形映射.例1z e w =在复平面上解析，且0)(≠='z z e e ，因此z e 在任何区域内都构成第一类保角映射，但它在复平面上不是共形映射，而在区域π4Im 0<<z 内，z e w =构成共形映射.§6.2共形映射的基本问题(The basic problem of conformal mapping)一、共形映射的基本问题(The basic problem of conformalmapping)对于共形映射，我们主要研究下列两个方面的问题.问题一 对于给定的区域D 和定义在D 上的解析函数()z f =ω，求像集()D f G =，并讨论()z f 是否将D 共形的映射为G .问题二 给定两个区域D 和G ，求一解析函数()z f =ω，使得()z f 将D 共形的映射为G .对于问题二，我们只需考虑能把D 变为单位圆内部即可.这是因为若存在函数()z f =ξ把D 变为1<ξ，而函数()ωξg =把G 变为1<ξ，则()()z f g 1-=ω把D 映射为G （下图）.二、 解析函数的保域性与边界对应原理(Analytic functions of protection domain and the boundary correspondence principle )对于问题一，有下面两个定理.定理(Theorem)6.6（保域性定理） 设函数()z f 在区域D 内解析，且不恒为常数，则像集合()D f G =是区域.定理(Theorem)6.7 （边界对应原理）设区域D 的边界为简单闭曲线C ，函数()z f =ω在C D D Y =上解析，且将C 双方单值的映射成简单闭曲线Γ.当z 沿C 正向绕行时，相应的ω的绕行方向定为Γ的正向，并令G 是以Γ为边界的区域，则()z f =ω将D 共形的映射为G .注1：定理6.6说明了解析函数把区域变为区域， 注2：定理6.7为像区域的确定给出了一个一般性的方法. 注3：是Γ的方向.（如下图），区域D 在曲线C 的内部，在C 上沿逆时针方向取三个点321,,z z z ，函数()z f =ω将C 于321,,z z z 分别映射为Γ和321,,ωωω.若321,,ωωω也按逆时针方向排列，则像区域G 在Γ的内部.例1 设区域⎭⎬⎫⎩⎨⎧<<<<=10,2arg 0:z z z D π，求区域D 在映射3z =ω下的像区域G .解：（如下图），设区域D 的边界为321C C C ++，其中1C 的方程为θi e z =（θ从0到2π），相应的像曲线1Γ的方程为 ϕθωi i e e ==3（ϕ从0到23π）； 2C 的方程为iy z =（y 从1到0），相应的像曲线2Γ的方程为()iv y i =-=3ω （v 从-1到0）3C 的方程为x z =（x 从0到1），相应的像区线3Γ的方程为u x ==3ω（u 从0到1）.因此像区域为()b⎭⎬⎫⎩⎨⎧<<<<=23arg 0,10:πωωωG .三、 共形映射的存在唯一性(Conformal mapping of the existence and uniqueness)1、问题二函数的存在性：当区域D 是下面两种情况之一时，将不存在解析函数，使之保形地映射为单位圆内部.第一，区域是扩充复平面；第二，区域是扩充复平面除去一点（不妨设为∞点，如果是有限点z ，只需做一映射01z z -=ξ即可）.无论哪一种情况，如果存在函数)(z f =ω将它们共形映射为1<ω，则)(z f 在整个复平面上解析，且1)(<z f .根据刘维尔定理（见§3.4）)(z f 必恒为常数.这显然不是我们所要求的映射.2、问题二函数的唯一性： 一般说来是不唯一的，例如，对任意给定的常数0θ，映射0θωi ze =均把单位圆内部映射为单位圆内部.那么，到底在什么情况下，共形映射函数存在且唯一呢？黎曼（Riemann ）在1851年给出了下面的定理，它是共形映射的基本定理.定理(Theorem)6.8（黎曼存在唯一性定理） 设D 与G 是任意给定的两个单连域，它们的边界至少包含两点，则一定存在解析函数)(z f =ω 把D 保形的映射为G .如果在D 和G 内在再分别任意指定一点0z 和0ω，并任給一实数)(00πθπθ≤<-，要求函数)(z f =ω满足00)(ω=z f 且00)(arg θ='z f 则映射)(z f =ω是唯一的.注4：黎曼存在唯一性定理肯定了满足给定条件的函数的存在唯一性，但没有给出具体的求解方法.2 1§6.3 分式线性映射分式线性函数及其分解、分式线性映射的保圆性、保行性、保对称点性、唯一决定分式线性映射的条件、两个典型区域间的映射.1、理解分式线性函数所构成的映射2、掌握分式线性映射的性质3、切实掌握两个典型区域间的映射分式线性映射的保圆性、保行性解析函数的保域性与边界对应原理分式线性映射的保对称点性、唯一决定分式线性映射的条件讲授法多媒体与板书相结合P习题六：4-9164一、分式线性函数及其分解二、分式线性映射的保圆性三、分式线性映射的保行性四、分式线性映射的保对称点性五、两个典型区域间的映射[1]《复变函数》，西交大高等数学教研室，高等教育出版社.[2]《复变函数与积分变换学习辅导与习题全解》，高等教育出版社.[3]《复变函数论》，（钟玉泉编，高等教育出版社，第二版）2005.[4]《复变函数与积分变换》,苏变萍陈东立编，高等教育出版社，2008. 基本掌握分式线性函数所构成的映射第二讲授课题目：§6.3 分式线性映射；教学内容：分式线性函数及其分解、分式线性映射的保圆性、保行性、保对称点性、唯一决定分式线性映射的条件、两个典型区域间的映射.学时安排：2学时.教学目标：1、理解分式线性函数所构成的映射；2、掌握分式线性映射的性质；3、切实掌握两个典型区域间的映射；教学重点：分式线性映射的保圆性、保行性；教学难点：分式线性映射的保对称点性、唯一决定分式线性映射的条件；教学方式：多媒体与板书相结合.P习题六：4-9作业布置：164板书设计：一、分式线性函数及其分解；二、分式线性映射的保圆性；三、分式线性映射的保行性；四、分式线性映射的保对称点性；五、两个典型区域间的映射参考资料：1、《复变函数》，西交大高等数学教研室，高等教育出版社；2、《复变函数与积分变换学习辅导与习题全解》，高等教育出版；3、《复变函数论》，（钟玉泉编，高等教育出版社，第二版）2005年5月；4、《复变函数与积分变换》苏变萍陈东立编，高等教育出版社，2008年4月；课后记事：基本掌握分式线性函数所构成的映射；教学过程：§6.2 分式线性映射（The fraction linearity mapping ）形如：dz c baz w ++=的函数，称为分式线性函数.其中d c b a ,,,是复常数，而且0≠-bc ad .在0=γ时，我们也称它为整式线性函数. 一、 分式线性函数及其分解(Fractional linear function and its decomposition) 一般分式线性函数总可以分解为下列四种简单函数复合： （1）α+=z w （α为一个复数）； （2）z e w i θ=（θ为一个实数）； （3）rz w =（0>r ）； （4）、zw 1=. 例2 将分式线性函数iz zw +=2分解为四种简单函数复合 解：⎪⎭⎫ ⎝⎛++=+-+=+=-i z e i z ii z z w i 1222222π，其复合过程为w z z z z z z z ez z iz i −−→−−→−−−→−−→−−→−++-242321143221π1、平移、旋转与相似映射 (1) 平移映射：α+=z w令iy x z +=，21ib b b +=，iv u w +=，则有1b x u +=，2b y v +=，它将曲线C 沿b 的方向平移到曲线γ(2)旋转映射：z e w i θ=令0θi e z =，则有)(0θθ+=i e w ，它将曲线C 绕原点旋转到曲线γ. (3 ) 相似映射：rz w =令θρi e z =，则有θρi e r w =，它将曲线C 放大（或缩小）到曲线γ 2、反演映射：zw 1=令θi re z =，则有)(1θ-=i e r w 即zw 1=，zw arg arg -=由zw 1=可知，当1<z 时，1>w ；当1>z 时，1<w 因此反演映射zw 1=的特点是将单位圆内部（或外部）的任一点映射到将单位圆外部（或内，部）且辐角反号.反演映射zw 1=可以分两步进行，第一步，将z 映射为z w 11=:zw 11=,且 z w arg arg 1=再将1w 映射为w 满足: 1w w=,且11arg arg w w -=定义 6.3设某圆的半径为B A R ,,为两点在从圆心出发地射线上，且2R B o A o =⋅,则称B A 与是关于圆周对称的.即设已给圆)0(|:|0+∞<<=-R R z z C ，如果两个有限点1z 及2z 在过0z 的同一射线上，并且20201||||R z z z z =--，那么我们说1z 及2z 是关于圆C 的对称点.因此，zw 1=可由单位圆对称映射与实轴对称映射复合而成. 二、分式线性映射的保行性(Fractional linear maps preserving feasibility)规定：在扩充复平面上，任一直线看成半径是无穷大的圆. 定理(Theorem)6.8 在扩充复平面上，分式线性函数把圆映射成圆.证明：由于分式线性函数所确定的映射是平移、旋转、相似映射及zw 1=型的函数所确定的映射复合而得，但前三个映射显然把圆映射成圆，所以只用证明映射z w 1=也把圆映射为圆即可. 由此可得如下定理定理(Theorem)6.9分式线性函数在扩充复平面上是共形映射.三、分式线性映射的保圆性(Fractional linear maps preserving circle of)定理(Theorem)6.10扩充 z 平面上任何圆，可以用一个分式线性函数映射成扩充 w 平面上任何圆. 证明：由映射zw 1=把圆映射为圆可证明此定理. 注1：圆C 上的点是它本身关于圆C 的对称点；注2：规定0z 及∞是关于圆C 的对称点；注3 :利用此定理也可以解释关于直线的对称点.例1 求实轴在映射iz i w +=2下的像曲线. 解：在实轴上取三点∞=1z ，02=z ，13=z ，则对应的三个像点为01=w ，22=w ，i w +=13，所以像曲线为11=-w ，上半平面被映射到圆的内部，而下半平面被映射到圆的外部.四、分式线性映射的保对称点性(Fractional linear maps of symmetric point of)引理:不同两点1z 及2z 是关于圆C 的对称点的必要与充分条件是通过1z 及2z 的任何圆与圆C 直交.定理(Theorem)6.11设点1z 及2z 关于圆C 的对称，则在分式线性映射下，它们的像点1w 及2w 关于圆C 的像曲线Γ对称.证明：设Γ'是过1w 及2w 的任意一个圆，则其原像C '是过1z 及2z 的圆.由1z 及2z 是关于圆C 对称，有C '与C 正交，由保角性Γ'与Γ正交，即过1w 与2w 的任意圆Γ'与Γ正交，因此1w 及2w 关于圆C 的像曲线Γ对称.五、唯一决定分式线性映射的条件(The only decision the conditions of fractional linear maps)定理(Theorem)6.12 在z 平面上任意三个不同的点321,,z z z 以及扩充 w 平面上任意三个不同的点321,,w w w ，存在唯一的分式线性函数，把321,,z z z 分别映射成321,,w w w .证明：在z 平面上，考虑已给各点都是有限点的情形.设所求分式线性函数（也称为分式线性变换）是d cz b az w ++=那么，由dcz b az w d cz b az w d cz b az w ++=++=++=222222111,, 得))(())(())((1111d cz d cz d cz b az d cz b az w w ++++-++=-))(())((11d cz d cz bc ad z z +++-= 同理，有：))(())((131313d cz d cz bc ad z z w w +++-=-，))(())((232323d cz d cz bc ad z z w w +++-=-，))(())((222d cz d cz bc ad z z w w +++-=-， 因此，有231321231321::z z z z z z z z w w w w w w w w ----=----， 将上式整理后可以解出形如dcz b az w ++=的分式线性函数.显然得这样的分式线性函数是唯一的. 由此，我们可以解出分式线性函数.由此也显然得这样的分式线性函数也是唯一的.推论1：如果k z ，或k w 中有一个为∞，则只需要将对应点公式中含有∞的项换为1.推论2：设)(z f w =是一分式线性映射，且)(11z f w =及)(22z f w =，则它可表示成2121z z z z k w w w w --=-- （k 为复常数） 特别：当01=w ，∞=2w 时，有 21z z z z k w --= （k 为复常数） 六、 两个典型区域间的映射(Mapping between the twotypical regions)例1 求一分式线性映射把上半平面0Im >z 保形映射成单位圆盘内部1<w .解：所求映射一方面把0Im >z 内某一点0z 映射成0=w ，另一方面把0Im =z 映射成1=w .由于线性映射把关于实轴0Im =z 的对称点映射成为关于圆1=w 的对称点，所求映射不仅把0z 映射成0=w ，而且把0z 映射成∞=w .因此这种映射形如：0z z z z k w --= （k 为待定的复常数） 当z 是实数时，有,1||00=--z z z z 对应1=w ，所以,1||=k 于是θi e k =，其中θ是一个实常数.因此所求的映射一般为：,00z z z z e w i --=θ 由于z 是实数时，1=w ，因此它把直线0Im =z 映射成圆1=w ，从而把上半平面0Im >z 映射成1<w ，取i z -0，0=θ，得所求映射为：iz i z w +-= 例2 求一分式线性映射把单位圆内部1<z 保形映射成单位圆盘内部1<w .解：在|z |<1内任取一点0z ，映射成00=w ，并且把1=z 映射成1=w .由于0z 与01z 关于圆1=z 对称，所以这种映射把01z 映射成∞=w .因此这种映射形如：01001/1z z z z k z z z z k w --=--= （01z k k -=为待定的复常数） 当|z|=1时，有),(1000z z z z z z z z z -=-=- 于是,1|||1|||||1001==--=k z z z z k w 因此θi e k =1，其中θ是一个实常数.所求的映射为：,100z z z z e w i --=θ2 1§6.4几个初等函数构成的共形映射幂函数、指数函数、综合举例1、掌握幂函数构成的共形映射2、掌握指数函数构成的共形映射函数构成的共形映射指数函数构成的共形映射讲授法多媒体与板书相结合P习题六：4-9164一、幂函数构成的共形映射二、指数函数构成的共形映射三、综合举例[1]《复变函数》，西交大高等数学教研室，高等教育出版社.[2]《复变函数与积分变换学习辅导与习题全解》，高等教育出版社.[3]《复变函数论》，（钟玉泉编，高等教育出版社，第二版）2005.[4]《复变函数与积分变换》,苏变萍陈东立编，高等教育出版社，2008. 基本掌握幂函数构成的共形映射，指数函数构成的共形映射掌握不好第三讲授课题目：§6.4几个初等函数构成的共形映射；教学内容：幂函数、指数函数、综合举例学时安排：2学时.教学目标：1、掌握幂函数构成的共形映射；2、掌握指数函数构成的共形映射；教学重点：函数构成的共形映射；教学难点：指数函数构成的共形映射；教学方式：多媒体与板书相结合.P习题六：4-9作业布置：164板书设计：一、幂函数构成的共形映射；二、指数函数构成的共形映射；三、综合举例；参考资料：1、《复变函数》，西交大高等数学教研室，高等教育出版社；2、《复变函数与积分变换学习辅导与习题全解》，高等教育出版；3、《复变函数论》，（钟玉泉编，高等教育出版社，第二版）2005年5月；4、《复变函数与积分变换》苏变萍陈东立编，高等教育出版社，2008年4月；课后记事：基本掌握幂函数构成的共形映射，指数函数构成的共形映射掌握不好；§6.4几个初等函数构成的共形映射(Conformal mapping composed of several elementary functions)一、 幂函数(Power function)()整数2≥=n z w n容易得到：函数n z w =将角形域)2(000nπθθθ≤<<共形映射为角形域00θϕn <<（如下图）.因此通俗地讲，幂函数的特点是扩大角形域.相应地，根式函数n z w =作为幂函数的逆映射，则是将角形域)2(000nπθθθ≤<<共形映射为角形域00θϕ<<.同样，我们也通常说，根式函数的特点是缩小角形域.注意：如果是扇形域（即模有限），则模要相应的扩大或缩小，这一点往往容易忽略.例1 区域{}0Re ,0Im ,1:>><=z z z z D 求一共形映射，将D 变为上半平面.解: 如下图，首先由21z z =将D 变为上半单位圆域.接着由分式线形映射11211z z z -+=将其变为第一象限，最后由映射22z =ω将其变为上半平面.因此所求映射为22211⎪⎪⎭⎫ ⎝⎛-+=z z ω. 二、指数函数(Exponential function)z e w =容易得到 ：函数z e w =将带形域()π2Im 0≤<<h h z 共形映射为角形域h w <<arg 0（图6.20）.因此可以简单的说，指数函数的特点是将带形域变成角形域.相应的，对数函数z w ln =作为指数函数的逆映射，则是将角形域()π2arg 0≤<<h h w 变成带形域h z <<Im 0.例2 求一共形映射，将带形域⎭⎬⎫⎩⎨⎧<<=ππz z D Im 2:映射为上半平面.解: 如下图，首先由平移映射i z z 21π-=将带形域D 变为带形域2Im 01π<<z ，再由相似映射122z z =变为带形域2Im 02π<<z ，最后由指数函数2z e w =变为上半平面.因此所求的映射为⎪⎭⎫⎝⎛-=i z ew 22π.三、综合举例（Comprehensive example ）例3 设区域{}0Im ,1:><=z z z D ，求一个共形映射，将区域D 保形映射成上半平面.解： 作一分式线性映射11'-+=z z w 把-1及+1分别映射成w '平面上的0及∞两点，于是把1=z 及0Im =z 映射成w '平面上在原点互相直交的两条直线.z 平面上的实轴映射成w '平面上的实轴； 0=z 映射成1-='w ，半圆的直径AC 映射成w '平面上的负半实轴；平面-z O)1(-B )(i D -)0(A C平面-'w C)1(-D )1(B )0(A C平面-w圆1=z 映射成w '平面上的虚轴；又由于i z =映射成i i i w -=-+=11'半圆ADC 映射成w '平面上的下半虚轴.由在保形映射下区域及其边界之间的对应关系，已给半圆盘映射到w '平面上的的区域：第三象限23'arg ππ<<w . 作映射2'w w =当w '在第三象限中变化时，w arg 在π2及π3之间变化.因此w '平面上的第三象限就映射成w 平面上的上半平面. 因此，所求共形映射为：22)11('-+==z z w w . 例4 求一个共形映射，把z 平面上的带形π<<z Im 0保形映射成w 平面上的单位圆1<w .解：由于指数函数z e w ='把w 平面上的已给带形保形映射成w '平面上的上半平面. 取w '平面上关于实轴的对称点-i 及i ，那么函数iw iw w +-='', 把的w '平面上的上半平面保形映射成w 平面上的单位圆1<w . 因此，所求共形映射为：ie i e w z z +-=Oi-i平面-'w 平面-z。

105第6章 保角映射6.1 分式线性映射导数的几何意义是保角映射的理论基础.6-1 映射2w z =在i z =-处的伸缩率k 与旋转角α是（ ）.（A ）π1,2k α==（B ）π2,2k α==- （C ）π1,2k α==- （D ）π2,2k α==解 i i π||2,Arg ()|.2z z k w f z α=-=-''====- 选（B ）.平移变换加伸缩反射得相似图形，相似比即||w '.6-2 在映射1w z=下，将|1|1z -<映射为（ ）.（A ）右半平面0u > （B ）下半平面0v < （C ）半平面12u > （D ）12v <- 解1 221i i x y w u v z x y -===++ 2222,xyu v x y x y -==++ 而 2|1|1z -<，即222x y x +<，故 221.2x u x y=>+ 选（C ）. 解2 1w z =是分式线性变换，具有保圆性.而|1|1z -=，将0z =变到,2w z =∞=变到1,1i 2w z ==+变到1i 2w +=，故1w z =将圆变为直线12u =，而圆心1z =变到112w =>，故1w z=将|1|1z -<变为半平面12u >. （C ）. 6-3 映射1w z=将Im()1z >的区域映射为（ ）.（A ）Im()1w < （B ）Re()1w < （C ）圆2211()22u v ++< （D ）2211()22u v ++>解 由1w z =的保圆性，知1w z=将1y =映射为直线或圆，由z =∞映射为0,1i z =+，映射为1i,1i 2w z -==-+映为1i2--知，将Im()1z =映射为w 平面上的圆： 2211()22u v ++=图6-1而2i z =映射为11i 2i 2=-.故1w z=将Im()1z >映射为圆内. 选（C ）1066-4 求将圆||2z <映射到右半平面，且(0)1,arg (0)π/2w w '==的分式线性映射.解 令ax b w z b +=+，则2()ab b w z b -'=+.由πarg (0)2w '=，可令 21(0)i ab b a w b b--'===，得1i a b =+，于是 (1i )b z bw z b++=+.由于圆||2z =应映射为虚轴，故又令(2)i w =得22i 2i i b b b ++=+，解得2(1i)2i 1+ib --== 于是 22i2iw z -+=+（这时圆上点2i z =-映射为∞点，故满足所求）. 6-5 求把上半平面Im()0z >映射成单位圆||1w <的分式线性映射，且满足条件（1）()0,(1)1w i w =-=； （2）1(0)1,().2w w i ==解 （1）令z iw cz d-=+ 1i(1)1w c d---==-+，即1i c d --=-+ 令z =∞时，i w =-，得i c =，1d =-，于是得到一个满足要求的映射ii 1z w z -=- （2）由(0)1w =，可令az bw z b+=+ 更令()1w ∞=-，得1a =-，更由1(i)2w =得2(i )i b b -+=+故3i b =-，从而3i3iz w z --=- 要求||1z =时||1w =，故取212z w z λ-=-时，||1,λλ=也可写作i e θ只要定θ即可. 6-6 求将上半平面映射为单位圆||1w <的分式线性变换.解 设az b w cz d +=+，将I m ()0z >映射为||1w <，则它将bz a =-映为圆心0w =.而将b z a-=-映为∞，记,b b a aαα-=-=-，而有dc α-=，故变换为.a z w c z αα-=- 由于0z =变到||1w =上一点，即||1a c =，记i e acθ=， 则 i e z w z θαα-=-（其中Im()0α>）. θ是待定实数.1076-7 求把上半平面Im()0z >映射成单位圆||1w <的分式线性映射，并满足条件：（1）(i)0;(1)1f f =-=； （2）(i)0,arg (i)0f f '==； （3）(1)1,(i)f f ==解 （1）设i i e i z w z θ-=+，于是i 1i e 11i θ--=-+即i πe i()2θθ= 所求映射为 i i+iz w z -=. （2）设映射为i ie +iz w z θ-= i 22i()e (+i)w z z θ'=故πi()21π(i)e ,22w θθ-'=-=所求映射为 ii iz w z -=+ （3）设i e z w z θαα-=- 由(1)1w =得i i e (1)1(i )(i )θθαααα-=--=-令x iy α=+，上两式相比得)(1)()(1)i αααα--=-- （1）取共轭(i )(1)()(1)i αααα--=-- 上两式两边相乘得225|(1)i ||(1)i |x y x y -+-=-++解得 2231x y y +=- （2） 将（1）式乘开，比较实部与虚部可得1)(1)1)x y -= （3）及221)()1)1)x y x y +=+ （4） 将（2）代入（4），消去22x y +后解得：2,3y x ==， 于是i 21i3e θ==5=12i)3=108 所求映射i )3w =.6-8 求将单位圆||1z <映射为单位圆||1w <的分式线性映射.解 设所求的分式线性变换把||1z <内的点α映射为0w =，那么，它将1α即与α关于||1z =的对称点映射为∞，故所求的映射为1/1z z w z z ααλλααα--==-+-+ 设1z =对应于||1w =上某点，则有11||||1αλαλαα-==-，故i e θλα= 即 i e (||1,1z w zθααθα-=<-是实数） 这时 i 21()e(1)w z z θααα-'=-i 1()e 1w θααα'=-故θ是z α=点变换时的旋转角 同样，将z 平面上||1z <映射为w 平面上||1w >的分式线性变换是 i e (||1,1z w zθααθα-=>-是实数） 6-9 求将右半平面Re()0z >映射为单位圆||1w <的分式线性映射.解1 设z bw z dλ+=+，它将z b =-映为0w =点，而将z d =-映为w =∞点.记a b =-，则Re()0α>，由对称性，()d α-=-.因此，z w z αλα-=+，且|(0)|||||1w αλλα-===，故i e θλ=得i e (Re()0,z w z θααθα-=>+是实数）. 解2 由6-13题，先作旋转i z ζ=，将右半平面旋转为上半平面，于是将Im()0ζ>变为||1w <的映射是（见6-13题）i e (Im()0)w θζββζβ-=>- 故 i i i i e e i i z z w z z θθββββ-+==-+ 记 i βα=-，则i (i )ββα=-=而Re()0α>i e z w z θαα-=+与解1的结果同. 利用0w =与w =∞两点是关于两个同心圆皆对称的点而有保对称性.从而知12,z z 皆是实数，及对二圆都有对称性，从而解出1z 和2z . 6-10 求一分式线性映射，把由||9z >与|8|16z -<所确定的区域映射为w 平面上的同心圆环：||1w <与||w r > (01).r <<解 本题关键在设12()0,()w z w z ==∞，由于0、∞关于两个同心圆||1w =与||w r =皆对称；故1z 与2z 应同时与|3|9z -=及|8|16z -=皆对称.从而知12,z z 应在此二圆圆心的联线上，109即1z 与2z 皆是实数，且有221212(3)(3)9,(8)(8)16z z z z --=--=即 212123()99z z z z -+=- 2212128()168z z z z -+=- 得121224,0z z z z +=-=，取120,24z z ==-.则 24zw z λ=+ 由于0z =在|3|9z -<内部，故此映射将|3|9z -=映为||w r =，而将|8|16z -=映为||1w =即 i i 2816e ,e 24zz w z ϕθ=+=+ 取1224,0z z =-=，则24z w zλ+= 这时，由124z =-在|8|16z ->内，而0w =在||w r <内，故此映射将|8|16z -=映为||w r =而将|3|9z -=映为||1w =，即令i 39e z ϕ=+便应有i i 279e |||| 1.3+9e w ϕϕλ+==故i 11||,e 33θλλ==所求映射为i 24e 3z w zθ+=. 6.2 几个初等函数所构成的映射按要求一步一步变，注意每一步的要求.6-11 试将由||1z <及|1|1z -<所确定的区域保角地映射为上半平面. 解 如图6.2，我们采取如下步骤作映射.图6.2(1)作分式线性映射，使12映射于原点，而12映射为w =∞点.110 即1ζ=（2）令321ζζ=，则映射成不含2ζ的负实半轴的全平面，22π4π.ϕ≤<（3）令1/232ζζ=，则映射为下半平面.（4）令3w ζ=-，则映射为上半平面，故此映射为3/2w =-6-12 试将由Im()1,||2z z ><所确定的区域保角地映射为上半平面. 解 如图6.3，分以下步骤： （1）将弓形域映射为角形域1ζ=（2）321ζζ=映射为下半平面. （3）2w ζ=-，即为所求也就是3w =-图6.36-13 求把单位圆外部||1z >，且沿虚轴1y >有割痕的域映射为上半平面的一个保角映射.解 分以下步骤：（1）作分式线性映射，将单位圆外部映射为半平面，并使割痕转到实轴，即1i+iz z ζ-=（2）平方且反射，使割痕到22i (1,0),i z z ζ-⎛⎫-=- ⎪+⎝⎭（3）平移后开方得122(1)w ζ=+111即 1/22i 1i z w z ⎡⎤-⎛⎫=-⎢⎥⎪+⎝⎭⎢⎥⎣⎦为所求映射.6-14 将图6.4z 平面中阴影部分所示区域，即由Re()1,||1z z >->所确定区域映射为上半平面.解 分以下步骤：（1）作分式线性映射111z z ζ-=+，则所给域映射为10Re()1ζ<<； （2）旋转伸长，即令21πi ζζ=，得条形域20Im()πζ<<；（3）作指数映射i e w ϕ=即得上半平面.即映射为1i π1ez z w -+=图6.46-15 将如图6.5所示的z 平面区域，即由||2,|1|1z z <->所确定的区域，映射为上半平面.解 （1）作分式线性变换：12zz ζ=-，将|1|1z -=映射为1Re()0ζ=，而将||2z =映射为11Re()2ζ.由此，将已知域映射为带状域.（2）旋转伸缩：212πi ζζ=.映射为20Im()πζ<<（3）取指数函数的映射2e w ζ=便是本题所求，即2πi2ez z w -=.112图6.56-16 将沿虚轴有割痕从0z =至2i z =的上半平面，保角地映射为上半平面.解 （1）将上半平面映射为全平面后并平移，使割痕位于实轴的10ζ=至14ζ=处.214z ζ=+.（2）开方使割痕好似被展平在实轴的(2,2)-上：121w ζ=.即 21/2(4)w z =+.（见图6.7）图6.66-17 图6.7所示的z 平面上单位圆||1z <中有割痕：沿实轴从0z =至1z =的区域，试将其保角地映射为半平面.解（1）开方将圆映射为半圆，割痕仍在x 轴上：121z ζ=； （2）作分式线性映射，将半圆映射为1/4平面：12111ζζζ+=-+； （3）平方22w ζ=即2.w =113图6.76-18 将图6.8所示，由πRe()0,0Im()2z z ><<确定的z 平面上的区域，保角映射为上半平面.解 （1）将其旋转伸缩于第4象限：12z ζ=-（2）取指数函数：12e ζζ=将1ζ中的区域映射为半圆域：222||e 1,Arg 0x ζπζ-=<<< （3）作分式线性映射：23211ζζζ-=+ 将半圆映射为1/4平面.（4）令23w ζ=即为所求的映射，即22e 1e .e 1z z --⎛⎫-= ⎪+⎝⎭图6.86-19 求把实轴上有割痕：112x ≤<的单位圆||1z <映射为||1w <的一个映射.解 （1）令112112z z ζ-=-，使割痕在10Re()1ζ≤<上；114 （2）作2ζ= （3）再作23211ζζζ+=-，将半圆映射为3()ζ的I 象限部分； （4）作243ζζ=，便将此映射为上半平面； （5）最后将上半平面映为单位圆：（见图6.9）44i i w ζζ-=+经归纳223422224322i i [(1)/(1)]i i i [(1)/(1)]i w ζζζζζζζζ--+--===+++-+==图6.96-20 求把半带形域ππRe(),Im()022z z -<<>，映为上半平面Im()0w >的映射()w f z =，使π()1,(0)0.2f f ±=±=解 （1）作旋转与平移：1πi i 2z ζ=+，使之映为1ζ平面的半带形域：110Im()π,Re()0.ζζ<<<（2）作指数映射：12e ζζ=，将之映为2ζ平面上的半圆域：22||1,Im()0;ζζ<>（3）作分式线性映射：23211ζζζ+=-，将半圆域映为3ζ平面第1象限； （4）243ζζ=，将之映为4ζ的上半平面，只是未满足π()12f ±=±及(0)0f =的条件；（5）由上半平面映为上半平面，且∞映为1,0-点映为1及1-映为0.即得：4411w ζζ+=-（见图6.10）归纳222223222232211111121111wζζζζζζζζ⎛⎫++ ⎪-++⎝⎭===--⎛⎫+- ⎪-⎝⎭1111ππ(i i)i i22211e e e e e222ez zζζζζ-++-+++=-=-=-i ie esin2z zz-+==，为所求的映射.图6.10115。

习题六1. 求映射1w z=下，下列曲线的像. (1) 22x y ax += (0a ≠，为实数) 解：222211i=+i i x y w u v z x y x y x y ===-+++ 221x x u x y ax a===+, 所以1w z =将22x y ax +=映成直线1u a=. (2) .y kx =(k 为实数) 解： 22221i x y w z x y x y ==-++ 故1w z=将y kx =映成直线v ku =-. 2. 下列区域在指定的映射下映成什么？（1）Im()0,(1i)z w z >=+；解： (1i)(i )()i(+)w x y x y x y =+⋅+=-+所以Im()Re()w w >.故(1i)w z =+⋅将Im()0,z >映成Im()Re()w w >.(2) Re(z )>0. 0<Im(z )<1, i w z=. 解：设z =x +i y , x >0, 0<y <1.Re(w )>0. Im(w )>0. 若w =u +i v , 则因为0<y <1,则22221101,()22u u v u v <<-+>+ 故i w z=将Re(z )>0, 0<Im(z )<1.映为 Re(w )>0,Im(w )>0, 1212w > (以（12,0）为圆心、12为半径的圆) 3. 求w =z 2在z =i 处的伸缩率和旋转角，问w =z 2将经过点z =i 且平行于实轴正向的曲线的切线方向映成w 平面上哪一个方向？并作图.解：因为w '=2z ,所以w '(i)=2i , |w '|=2, 旋转角arg w '=π2. 于是, 经过点i 且平行实轴正向的向量映成w 平面上过点-1，且方向垂直向上的向量.如图所示.→4. 一个解析函数，所构成的映射在什么条件下具有伸缩率和旋转角的不变性？映射w =z 2在z 平面上每一点都具有这个性质吗？答：一个解析函数所构成的映射在导数不为零的条件下具有伸缩率和旋转不变性映射w =z 2在z =0处导数为零，所以在z =0处不具备这个性质.5. 求将区域0<x <1变为本身的整体线性质变换w z αβ=⋅+的一般形式.6. 试求所有使点1±不动的分式线性变换. 解：设所求分式线性变换为az bw cz d +=+(ad -bc ≠0)由11-→-.得 因为(1)a z c dw cz d ++-=+, 即(1)(1)1a z c z w cz d ++++=+,由11→代入上式，得22a ca d c d +=⇒=+. 因此11(1)(1)dcd cd c w z z cz d z +++=+=+⋅++ 令dq c =，得其中a 为复数.反之也成立，故所求分式线性映射为1111w z a w z ++=⋅--， a 为复数.7. 若分式线性映射，az bw cz d +=+将圆周|z |=1映射成直线则其余数应满足什么条件？ 解：若az bw cz d +=+将圆周|z |=1映成直线，则dz c =-映成w =∞. 而dz c =-落在单位圆周|z |=1,所以1dc -=,|c |=|d |.故系数应满足ad -bc ≠0,且|c |=|d |.8. 试确定映射，11z w z -=+作用下，下列集合的像.(1) Re()0z =; (2) |z |=2; (3) Im(z )>0.解：(1) Re(z )=0是虚轴，即z =i y 代入得. 写成参数方程为2211y u y -+=+， 221y v y =+, y -∞<<+∞.消去y 得，像曲线方程为单位圆,即u 2+v 2=1.(2) |z |=2.是一圆围，令i 2e ,02πz θθ=≤≤.代入得i i 2e 12e 1w θθ-=+化为参数方程.消去θ得，像曲线方程为一阿波罗斯圆.即(3) 当Im(z )>0时，即11Im()011w w z w w ++=-⇒<--, 令w =u +i v 得221(1)i 2Im()Im()01(1)i (1)w u v v w u v u v +++-==<--+-+. 即v >0,故Im(z )>0的像为Im(w )>0.9. 求出一个将右半平面Re(z )>0映射成单位圆|w |<1的分式线性变换.解：设映射将右半平面z 0映射成w =0，则z 0关于轴对称点0z 的像为w =∞， 所以所求分式线性变换形式为00z z w k z z -=⋅-其中k 为常数. 又因为00z z w k z z -=⋅-,而虚轴上的点z 对应|w |=1,不妨设z =0，则 故000e (Re()0)i z z w z z z θ-=⋅>-.10. 映射e 1i z w zϕαα-=⋅-⋅将||1z <映射成||1w <,实数ϕ的几何意义显什么？ 解：因为 从而2i i 2221||1()e e (1||)1||w ϕϕαααα-'=⋅=⋅-- 所以i 2arg ()arge arg (1||)w ϕααϕ'=-⋅-=故ϕ表示i e 1z w zθαα-=⋅-在单位圆内α处的旋转角arg ()w α'. 11. 求将上半平面Im(z )>0,映射成|w |<1单位圆的分式线性变换w =f (z )，并满足条件(1) f (i)=0, arg (i)f '=0; (2) f (1)=1, f. 解：将上半平面Im(z )>0, 映为单位圆|w |<1的一般分式线性映射为w =k z z αα-⋅-(Im(α)>0). (1) 由f (i)=0得α=i ，又由arg (i)0f '=,即i 22i ()e (i)f z z θ'=⋅+, πi()21(i)e 02f θ-'==，得π2θ=，所以 i i iz w z -=⋅+. (2) 由f (1)=1,得k =11αα--；由f,得kα联立解得w =12. 求将|z |<1映射成|w |<1的分式线性变换w =f (z)，并满足条件：(1) f (12)=0, f (-1)=1.(2) f (12)=0, 12πarg ()2f '=, (3) f (a )=a , arg ()f a ϕ'=.解：将单位圆|z |<1映成单位圆|w |<1的分式线性映射，为 i e 1z w zθαα-=-⋅ , |α|<1. (1) 由f (12)=0，知12α=.又由f (-1)=1，知 1i i i 2121e e (1)1e 1π1θθθθ--⋅=-=⇒=-⇒=+. 故12221112z z z w z --=-⋅=--. (2) 由f (12)=0，知12α=，又i 254e (2)z w z θ-'=⋅- i 11224π()e arg ()32f f θθ''=⇒==， 于是 π21i 2221e ()i 12z z z w z --==⋅--. (3) 先求=()z ξϕ，使z =a 0ξ→=，arg ()a ϕθ'=,且|z |<1映成|ξ|<1.则可知 i =()=e 1z a z a zθξϕ-⋅-⋅ 再求w =g (ξ)，使ξ=0→w =a , arg (0)0g '=,且|ξ|<1映成|w |<1.先求其反函数=()w ξψ,它使|w|<1映为|ξ|<1,w =a 映为ξ=0，且arg ()arg(1/(0))0w g ψ''==,则 =()=1w a w a wξψ--⋅. 因此，所求w 由等式给出.i =e 11w a z a a w a zθ--⋅-⋅-⋅. 13. 求将顶点在0，1，i 的三角形式的内部映射为顶点依次为0，2，1+i 的三角形的内部的分式线性映射. 解：直接用交比不变性公式即可求得02w w --∶1i 01i 2+-+-=02z z --∶i 0i 1-- 2w w -.1i 21i +-+=1z z -.i 1i-4z (i 1)(1i)w z -=--+. 14. 求出将圆环域2<|z |<5映射为圆环域4<|w |<10且使f (5)=-4的分式线性映射.解：因为z=5,-5,-2,2映为w=-4,4,10,-10,由交比不变性，有2525-+∶2525---+=104104-+--∶104104+- 故w =f (z )应为55z z -+∶2525---+=44w w +-∶104105+- 即 44w w +-=55z z --+20w z⇒=-. 讨论求得映射是否合乎要求，由于w =f (z )将|z |=2映为|w |=10，且将z =5映为w =-4.所以|z |>2映为|w |<10.又w =f (z )将|z |=5映为|w |=4，将z =2映为w =-10，所以将|z |<5映为|w |>4，由此确认，此函数合乎要求.15.映射2w z =将z 平面上的曲线221124x y ⎛⎫-+= ⎪⎝⎭映射到w 平面上的什么曲线？ 解：略.16. 映射w =e z 将下列区域映为什么图形.(1) 直线网Re(z )=C 1,Im(z )=C 2;(2) 带形区域Im(),02πz αβαβ<<≤<≤;(3) 半带形区域 Re()0,0Im(),02πz z αα><<≤≤.解：（1） 令z =x +i y , Re(z )=C 1,z =C 1+i y 1i =e e C y w ⇒⋅, Im(z )=C 2,则z =x +i C 22i =e e C x w ⇒⋅故=e z w 将直线Re(z )映成圆周1e C ρ=；直线Im(z )=C 2映为射线2C ϕ=.（2） 令z =x +i y ，y αβ<<,则i i =e e e e ,z x y x y w y αβ+==⋅<<故=e z w 将带形区域Im()z αβ<<映为arg()w αβ<<的张角为βα-的角形区域.（3） 令z =x +i y ，x >0，0<y < α, 02πα≤≤.则故=e zw 将半带形区域Re(z )>0,0<Im(z )<α, 02πα≤≤映为 |w |>1, 0arg w α<<(02πα≤≤).17. 求将单位圆的外部|z |>1保形映射为全平面除去线段-1<Re(w )<1,Im(w )=0的映射. 解：先用映射11w z=将|z |>1映为|w 1|<1,再用分式线性映射. 1211i 1w w w +=-⋅-将|w 1|<1映为上半平面Im(w 2)>0, 然后用幂函数232w w =映为有割痕为正实轴的全平面，最后用分式线性映射3311w w w -=+将区域映为有割痕[-1,1]的全平面. 故221121132222132111111i 1111111()11211i 1111z z z z w w w w w z w w z w w ⎛⎫⎛⎫++--⋅- ⎪ ⎪----⎝⎭⎝⎭=====+++⎛⎫⎛⎫++-⋅++ ⎪ ⎪--⎝⎭⎝⎭. 18. 求出将割去负实轴Re()0z -∞<≤,Im(z )=0的带形区域ππI m ()22z -<<映射为半带形区域πIm()πw -<<,Re(w )>0的映射.解：用1e z w =将区域映为有割痕(0,1)的右半平面Re(w 1)>0；再用1211ln 1w w w +=-将半平面映为有割痕(-∞,-1]的单位圆外域；又用3w =将区域映为去上半单位圆内部的上半平面；再用43ln w w =将区域映为半带形0<Im(w 4)<π,Re(w 4)>0；最后用42i πw w =-映为所求区域，故e 1ln e 1z z w +=-. 19. 求将Im(z )<1去掉单位圆|z |<1保形映射为上半平面Im(w )>0的映射.解：略.20. 映射cos w z =将半带形区域0<Re(z )<π,Im(z )>0保形映射为∞平面上的什么区域.解：因为 1cos ()2iz iz w z e e -==+ 可以分解为 w 1=i z ，12e ww =，32211()2w w w =+ 由于cos w z =在所给区域单叶解析，所以（1） w 1=i z 将半带域旋转π2，映为0<Im(w 1)<π,Re(w 1)<0. （2） 12e w w =将区域映为单位圆的上半圆内部|w 2|<1,Im(w 2)>0.（3） 2211()2w w w =+将区域映为下半平面Im(w )<0.。

第 1 页 共 10 页《复变函数》习题及答案一、 判断题1、若函数f (z )在z 0解析，则f (z )在z 0的某个邻域内可导。

（ ）2、如果z 0是f (z )的本性奇点，则)(lim 0z f z z →一定不存在。

（ ）3、若函数),(),()(y x iv y x u z f +=在D 内连续，则u (x,y )与v (x,y )都在D 内连续。

( )4、cos z 与sin z 在复平面内有界。

（ ）5、若z 0是)(z f 的m 阶零点，则z 0是1/)(z f 的m 阶极点。

（ ）6、若f (z )在z 0处满足柯西-黎曼条件，则f (z )在z 0解析。

（ ）7、若)(lim 0z f z z →存在且有限，则z 0是函数的可去奇点。

（ ）8、若f (z )在单连通区域D 内解析，则对D 内任一简单闭曲线C 都有0)(=⎰Cdz z f 。

（ ）9、若函数f (z )是单连通区域D 内的解析函数，则它在D 内有任意阶导数。

（ ）10、若函数f (z )在区域D 内的解析，且在D 内某个圆内恒为常数，则在区域D 内恒等于常数。

（ ）11、若函数f (z )在z 0解析，则f (z )在z 0连续。

（ ） 12、有界整函数必为常数。

（ ） 13、若}{n z 收敛，则} {Re n z 与} {Im n z 都收敛。

( )14、若f (z )在区域D 内解析，且0)('≡z f ，则C z f ≡)(（常数）。

（ ） 15、若函数f (z )在z 0处解析，则它在该点的某个邻域内可以展开为幂级数。

（ ） 16、若f (z )在z 0解析，则f (z )在z 0处满足柯西-黎曼条件。

（ ） 17、若函数f (z )在z 0可导，则f (z )在z 0解析。

（ ） 18、若f (z )在区域D 内解析，则|f (z )|也在D 内解析。

（ ）19、若幂级数的收敛半径大于零，则其和函数必在收敛圆内解析。

第六章 共形映射一、选择题：1．若函数z z w 22+=构成的映射将z 平面上区域G 缩小，那么该区域G 是 ( )（A ）21<z （B ）211<+z （C ）21>z （D ）211>+z 2．映射iz iz w +-=3在i z 20=处的旋转角为( ) （A ）0 （B ）2π （C ）π （D ）2π-3．映射2iz ew =在点i z =0处的伸缩率为( )（A ）1 （B ）2 (C)1-e （D ）e4．在映射ieiz w 4π+=下，区域0)Im(<z 的像为( )(A)22)Re(>w （B ）22)Re(->w （C ）22)Im(>z （D ）22)Im(->w 5．下列命题中，正确的是( )（A ）n z w =在复平面上处处保角（此处n 为自然数） （B ）映射z z w 43+=在0=z 处的伸缩率为零（C ） 若)(1z f w =与)(2z f w =是同时把单位圆1<z 映射到上半平面0)Im(>w 的分式线性变换，那么)()(21z f z f =（D ）函数z w =构成的映射属于第二类保角映射 6．i +1关于圆周4)1()2(22=-+-y x 的对称点是( )（A ）i +6 （B ）i +4 （C ）i +-2 （D ）i7．函数iz iz w +-=33将角形域3arg 0π<<z 映射为 ( )(A)1<w （B ）1>w （C ） 0)Im(>w （D ）0)Im(<w 8．将点1,,1-=i z 分别映射为点0,1,-∞=w 的分式线性变换为（ ）（A ） 11-+=z z w （B ）zz w -+=11（C ）z z e w i-+=112π(D) 112-+=z z e w i π9．分式线性变换zz w --=212把圆周1=z 映射为( ) （A ） 1=w (B) 2=w （B ） 11=-w (D) 21=-w10．分式线性变换zz w -+=11将区域:1<z 且0)Im(>z 映射为( ) （A ）ππ<<-w arg 2（B ） 0arg 2<<-w π（C ）ππ<<w arg 2（D ）2arg 0π<<w11．设,,,,d c b a 为实数且0<-bc ad ，那么分式线性变换dcz baz w ++=把上半平面映射为w 平面的( )（A ）单位圆内部 （B ）单位圆外部 （C ）上半平面 （D ）下半平面12．把上半平面0)Im(>z 映射成圆域2<w 且满足1)(,0)(='=i w i w 的分式线性变换)(z w 为( )（A ）z i z i i+-2 （B ）i z i z i +-2 （C ）z i z i +-2 （D ）iz iz +-2 13．把单位圆1<z 映射成单位圆1<w 且满足0)0(,0)2(>'=w iw 的分式线性变换)(z w 为( )(A)iz i z --22 （B ）iz z i --22 （C ）iz i z +-22 （D ）izzi +-22 14．把带形域2)Im(0π<<z 映射成上半平面0)Im(>w 的一个映射可写为( )（A ）z e w 2= （B ）z e w 2= （C ）z ie w = （D ）ize w =15．函数ie ie w z z +---=11将带形域π<<)Im(0z 映射为( )（A ）0)Re(>w （B ）0)Re(>w （C ）1<w （D ）1>w 二、填空题1．若函数)(z f 在点0z 解析且0)(0≠'z f ，那么映射)(z f w =在0z 处具有 ． 2．将点2,,2-=i z 分别映射为点1,,1i w -=的分式线性变换为 ．3．把单位圆1<z 映射为圆域11<-w 且满足0)0(,1)0(>'=w w 的分式线性变换=)(z w 4．将单位圆1<z 映射为圆域R w <的分式线性变换的一般形式为 ．5．把上半平面0)Im(>z 映射成单位圆1)(<z w 且满足31)21(,0)1(=+=+i w i w 的分式线性变换的)(z w = ．6．把角形域4arg 0π<<z 映射成圆域4<w 的一个映射可写为 ．7．映射z e w =将带形域43)Im(0π<<z 映射为 ． 8．映射3z w =将扇形域：3arg 0π<<z 且2<z 映射为 ．9．映射z w ln =将上半z 平面映射为 ． 10．映射)1(21zz w +=将上半单位圆：2<z 且0)Im(>z 映射为 ． 三、设2222211111)(,)(d z c b z a z w d z c b z a z w ++=++=是两个分式线性变换，如果记⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-δγβα11111d c b a ,⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛d c b a d c b a d c b a 22221111 试证1．)(1z w 的逆变换为δγβα++=-z z z w )(11；2．)(1z w 与)(2z w 的复合变换为dcz baz z w w ++=)]([21．四、设1z 与2z 是关于圆周R a z =-Γ:的一对对称点，试证明圆周Γ可以写成如下形式λ=--21z z z z 其中Ra z a z R-=-=12λ．五、求分式线性变换)(z w ，使1=z 映射为1=w ，且使i z +=1,1映射为∞=,1w ． 六、求把扩充复平面上具有割痕：0)Im(=z 且0)Re(≤<∞-z 的带形域ππ<<-)Im(z 映射成带形域ππ<<-)Im(w 的一个映射．七、设0>>a b ，试求区域a a z D >-:且b b z <-到上半平面0)Im(>w 的一个映射)(z w ．八、求把具有割痕：0)Im(=w 且1)Re(21<≤z 的单位圆1<z 映射成上半平面的一个映射．九、求一分式线性变换，它把偏心圆域⎭⎬⎫⎩⎨⎧<->2511:z z z 且映射为同心圆环域R w <<1，并求R 的值．十、利用儒可夫斯基函数，求把椭圆1452222=+y x 的外部映射成单位圆外部1>w 的一个映射．第六章 共形映射一、1．（B ） 2．（D ） 3．（B ） 4．（A ） ５．（D ）６．（C ） ７．（A ） ８．（C ） ９．（A ） 10．（D ） 11．（D ） 12．（B ） 13．（C ） 14．（B ） 15．（C ） 二、1．保角性与伸缩率的不变性 2． 236--=iz iz w 3．z +14．az a z w i --=θ1Re（θ为实数，1<a ） 5．iz iz +---11 6．λ-λ-=ϕ444z z ew i （ϕ为实数，0)Im(>λ） 7．角形域43arg 0π<<w8．扇形域π<<w arg 0且8<w 9．带形域π<<)Im(0w 10．下半平面0)Im(<w 五、)1(1)1(i z z i w ++-+-=. 六、)1ln(-=ze w .七、⎭⎬⎫⎩⎨⎧--π=z a z a b i b w 2exp . 八、221212121⎪⎪⎪⎪⎪⎭⎫⎝⎛-----+=z z z z w . 九、θ++=i e z z w 414（θ为实数），2=R . 十、)9(912-+=z z w .答案。