蝴蝶理论

蝴蝶定理的公式蝴蝶定理是混沌理论中的一个重要概念，它描述了一个微小的初始条件的变化可能会在某些系统中引起巨大的结果。

这个定理的公式化形式是Δx=Δy*e^λt，其中Δx表示初始条件的微小变化，Δy 表示结果的变化，λ表示系统中的一个参数，t表示时间。

蝴蝶定理最早由美国气象学家爱德华·洛伦兹在1963年提出。

他在研究大气运动时发现，微小的初始条件的变化可能会导致天气预测的巨大误差。

他将这个现象形象地比喻为在巴西一只蝴蝶拍动了翅膀，可能引起美国得克萨斯州的一场龙卷风。

蝴蝶定理揭示了非线性动力系统中的混沌现象。

在这样的系统中，微小的初始条件的变化会通过系统的非线性特性被放大，最终导致结果的巨大变化。

这种敏感依赖于初始条件的特性被称为“初始条件敏感性”。

蝴蝶定理的公式化形式Δx=Δy*e^λt中的参数λ被称为“李雅普诺夫指数”，它描述了系统中的敏感性和不可预测性。

如果λ大于0，系统就是混沌的，即微小的变化会导致结果的巨大差异；如果λ等于0，系统是稳定的，即微小的变化不会引起结果的显著变化；如果λ小于0，系统是收敛的，即微小的变化会逐渐趋于稳定状态。

蝴蝶定理的应用非常广泛。

在天气预测中，由于气象系统的复杂性和初始条件的微小变化，所以长期天气预测往往会出现较大的误差。

在经济学中，由于经济系统的复杂性和初始条件的微小变化，所以经济预测也往往会出现较大的误差。

在生态学中，蝴蝶定理也被用来研究生态系统的稳定性和可持续性。

蝴蝶定理的发现对科学和人类社会产生了深远的影响。

它揭示了世界的不确定性和复杂性，挑战了人类对于预测和控制的能力。

蝴蝶定理的公式化形式也成为了混沌理论的基石，为研究非线性系统和复杂系统提供了重要的工具和方法。

蝴蝶定理是混沌理论中的一个重要概念，它描述了微小的初始条件的变化可能会在某些系统中引起巨大的结果。

它的公式化形式Δx=Δy*e^λt揭示了初始条件敏感性和不可预测性，对于天气预测、经济预测和生态系统的研究具有重要的意义。

蝴蝶定理的公式蝴蝶定理，也称为混沌理论中的敏感依赖条件，指的是一个微小的初始条件的改变可能会引起系统状态的巨大变化。

这个理论最早由美国气象学家洛伦兹提出，他通过对气象模型的研究发现，即使是微小的测量误差，也会导致天气预报的巨大误差。

蝴蝶定理的公式可以用以下方式表示：在一个动力系统中，假设x和y是系统状态的两个变量，f是系统的动力学函数。

那么，根据蝴蝶定理，如果初始状态（x0，y0）有一个微小的变化（δx，δy），那么随着时间的推移，这个微小的变化将会被放大为（δx'，δy'），其中δx' = f(x0+δx, y0+δy) - f(x0, y0) ，δy' = f(x0, y0+δy) - f(x0, y0)。

蝴蝶定理的含义是，即使是微小的初始条件的改变，也会导致系统的演化轨迹发生巨大的变化。

这是由于非线性动力系统的特性所决定的，即系统的演化是不可预测的。

在这样的系统中，微小的初始条件的差异会被放大，最终导致系统的行为完全不同。

蝴蝶定理的一个著名的例子就是“蝴蝶效应”。

据说在巴西的一个地方，一只蝴蝶在某个时间点扇动了它的翅膀，最终导致了一个月后美国得克萨斯州的一场龙卷风。

虽然这个故事可能有些夸张，但它很好地说明了蝴蝶定理的概念。

蝴蝶定理的发现对于科学研究和实际应用有着重要的影响。

它揭示了复杂系统的不确定性，使我们认识到，即使是微小的变化也可能会产生巨大的影响。

这对于天气预报、气候模拟、金融市场预测等领域都具有重要意义。

除了在科学领域有着重要的应用外，蝴蝶定理也给我们的生活带来了一些启示。

它提醒我们要注意微小的变化，因为它们可能会在未来产生意想不到的结果。

我们应该对自己的行为和决策负责，因为它们可能会对我们的生活产生深远的影响。

蝴蝶定理还告诉我们，我们生活的世界是非线性的，复杂的，很难完全预测。

我们不能简单地根据过去的经验和规律来预测未来的发展。

相反，我们需要保持警惕，随时准备应对不确定性和变化。

蝴蝶理论蝴蝶理论最早出现在1935年一个叫H.M.GARTLEY（加特利）所著《股市利润》里面。

之后在1999年SCOCTT.M.CARNEY出版的《和谐交易》一书中做出了详细的讨论。

分析界对该理论有很高的评价，号称是波浪理论，周期理论之后又一经典理论。

美中不足的是其操作要求较高，必须形态以及行情精度达到相应的标准。

认识蝴蝶理论经典的蝴蝶理论有六种形态，包括：1，CRAB螃蟹；2，BUTTERFLY 蝴蝶；3，BAT蝙蝠；4，GARTLY加特利；5，THREE DRIVES三角；6，AB=CD菱形（又称经典螃蟹）。

每种形态包括二种划分----BULLISH(看涨信号)，BEARISH（看跌信号）1，AB=CD菱形（又称经典螃蟹）这一形态是蝴蝶形态里面的核心部分，即简单，又最重要，所以被称为经典螃蟹。

该形态的运用往往可以忽略X点的存在直接将形态看做是AB=CD形态上图的四个数字是一一对应的，也就是(0.786/1.27),(0.618/1.618)这样的对应关系。

1.ab 必须等于cd的长度, 公差0.152.时间上ab和cd的形成差不多一样3.a必须是最高或最低点4.角的形态必须明显的对称5.c必须在ab的0.618到0.718 之间，这是书中的介绍，但好多实例说明，c在0.382-0.786上都可以的。

6.d必须在ab的1.27到1.618 之间，这也是书中的介绍，但事实上，d可以去到1.27-2.24这个范围上的。

7.在好的市场，也就是强势市场，d的目标是1.618，最大可以去到2.618。

2, GARTLY加特利形态加特利形态是所有蝴蝶形态中最经典的形态，俗称“222”形态加特利形态里面包含了经典螃蟹形态（AB=CD）对比经典螃蟹形态，加特利形态多出了XA这一线。

3, BUTTERFLY 蝴蝶这一形态的目标位是最多的，也是相当重要的，它基本包括所有的形态。

其演变形态可以成为加特利形态。

（区别在于D点和X点的位置关系。

蝴蝶模型定理蝴蝶模型定理，又被称为“蝴蝶效应”，是一种深奥的物理理论，揭示了微小的初始条件对于整个系统的影响可能是巨大而不可预测的。

这一理论源自于混沌理论，强调了复杂系统中微小变化可能引起巨大效应的重要性。

蝴蝶模型定理的提出，使我们认识到了自然界中的复杂性和不确定性，引起了人们对于系统性思维和长期影响的深刻思考。

蝴蝶模型定理最初由美国气象学家洛伦兹提出，他在研究大气环流系统时发现，微小的初值误差可能会导致系统的完全不同的演化轨迹。

洛伦兹曾经提出了一个著名的例子：假设在亚马逊雨林的某个角落有只蝴蝶煽动了它的翅膀，可能会引起一场飓风在美国德克萨斯州的产生。

这一例子生动地说明了微小的变化可能在长时间尺度上引起系统的巨大差异。

蝴蝶模型定理的核心思想是“敏感依赖于初值”，即系统在初始条件上的微小变化可能会在演化过程中放大，并最终导致系统的完全不同状态。

这种“灵敏依赖”使得我们无法精确地预测某些系统的未来发展，因为微小的误差可能会在演化过程中放大，产生巨大的影响。

蝴蝶模型定理不仅适用于气象系统，还可以用来解释金融市场、生态系统、人类行为等复杂系统中的现象。

在金融市场中，一家公司的微小变化可能会引起整个市场的震荡；在生态系统中，一种物种的灭绝可能导致整个生态系统的崩溃；在人类行为中，一个人的微小决定可能会影响整个社会的发展方向。

蝴蝶模型定理的普适性使得人们更加重视初值条件的准确性和系统的复杂性，避免犯下严重的错误和后果。

在现代社会中，蝴蝶模型定理的启示意义更加重要。

我们生活在一个复杂而不确定的世界中，各种因素相互作用，系统性思维和长期影响的认识变得尤为重要。

我们需要更加注重细节和初值条件的准确性，避免因为一时的疏忽而导致不可挽回的后果。

同时，我们也需要认识到系统的复杂性和不确定性，不要轻易对系统的发展做出过于简单的预测和判断。

总的来说，蝴蝶模型定理揭示了自然界中微小变化可能引起巨大效应的现象，引起了人们对系统性思维和长期影响的深刻思考。

蝴蝶理论蝴蝶理论 2009-05-19 12:46 阅读401 评论0字号：大中小早在1935年有个叫h.m.gartley的人出了一本书，叫《股市利润》(“profits in the stock market”)，这是一本关于形态技术分析的书，其最为精华的部分在第222页讨论了一个最佳时间与价格的形态，这个形态是非常的强大和有效，后来这个形态被命名为gartley222，这是以人的名字做为形态的名称。

现在网上一般流行一本电子书名为：价值连城的精确短线交易技术—gartley“222”。

这就是根据《股市利润》里面的内容整理的。

之后scott m.carney在1999年出版了一本叫《和谐的交易》("the harmonic trader")的书，这还是一本形态分析和交易的书，carney在书的第3部分在讨论了gartley222后介绍和详细讨论了蝴蝶形态（butterfly ),蝴蝶形态分为牛市蝴蝶形态和熊市蝴蝶形态，蝴蝶形态的基础就是gartley2 22，丰富了gartley形态的内涵和内容。

到现在为止，scott m.carney，已经出版了三本关于蝴蝶形态的书籍了，我只看过《和谐交易》这本，其中两本想必会更精彩，另两本书名好似为《harmonic trading of the financial markets: volume two》，《harmonic trading of the financial markets:volume one》。

蝴蝶理论的基础与大众所知的波浪理论有着同样的理论基础：黄金分割率，也就是斐波纳奇数例。

larry pesavento 所写的《fibonacci ratios with pattern recognition》是一本关于黄金分割率介绍和应用的书。

在后面我会给出黄金回调位与目标位的关系。

蝴蝶理论与大众所熟悉的波浪理论有着同样的理论基础：黄金分割率，也就是斐波纳奇数。

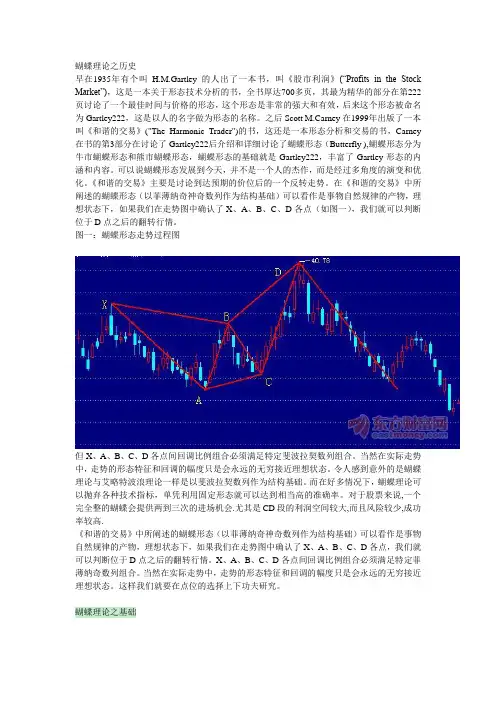
蝴蝶理论之历史早在1935年有个叫H.M.Gartley的人出了一本书，叫《股市利润》(“Profits in the Stock Market”)，这是一本关于形态技术分析的书，全书厚达700多页，其最为精华的部分在第222页讨论了一个最佳时间与价格的形态，这个形态是非常的强大和有效，后来这个形态被命名为Gartley222，这是以人的名字做为形态的名称。

之后Scott M.Carney在1999年出版了一本叫《和谐的交易》("The Harmonic Trader")的书，这还是一本形态分析和交易的书，Carney 在书的第3部分在讨论了Gartley222后介绍和详细讨论了蝴蝶形态（Butterfly ),蝴蝶形态分为牛市蝴蝶形态和熊市蝴蝶形态，蝴蝶形态的基础就是Gartley222，丰富了Gartley形态的内涵和内容。

可以说蝴蝶形态发展到今天，并不是一个人的杰作，而是经过多角度的演变和优化。

《和谐的交易》主要是讨论到达预期的价位后的一个反转走势。

在《和谐的交易》中所阐述的蝴蝶形态（以菲薄纳奇神奇数列作为结构基础）可以看作是事物自然规律的产物，理想状态下，如果我们在走势图中确认了X、A、B、C、D各点（如图一），我们就可以判断位于D点之后的翻转行情。

图一：蝴蝶形态走势过程图但X、A、B、C、D各点间回调比例组合必须满足特定斐波拉契数列组合。

当然在实际走势中，走势的形态特征和回调的幅度只是会永远的无穷接近理想状态。

令人感到意外的是蝴蝶理论与艾略特波浪理论一样是以斐波拉契数列作为结构基础。

而在好多情况下，蝴蝶理论可以抛弃各种技术指标，单凭利用固定形态就可以达到相当高的准确率。

对于股票来说,一个完全整的蝴蝶会提供两到三次的进场机会.尤其是CD段的利润空间较大,而且风险较少,成功率较高.《和谐的交易》中所阐述的蝴蝶形态（以菲薄纳奇神奇数列作为结构基础）可以看作是事物自然规律的产物，理想状态下，如果我们在走势图中确认了X、A、B、C、D各点，我们就可以判断位于D点之后的翻转行情。

毕业论文蝴蝶定理摘要：毕业论文探讨了蝴蝶定理，这是一个数学上的理论，它强调了复杂系统的非线性和敏感性依赖于初始条件的变化。

在这篇文章中，我们介绍了蝴蝶定理的基本概念和一些例子，其中包括介绍了混沌现象，迭代函数和概率混沌系统等。

关键词：蝴蝶定理；混沌现象；迭代函数；概率混沌系统1. 引言蝴蝶定理是一个非常著名的理论，它通常被用来解释复杂系统中的随机性。

该理论最初由美国气象学家爱德华·洛伦兹在20世纪60年代提出，他试图通过模型来预测天气变化的趋势。

他发现即使是微小的变化都会导致不同的结果，这一现象被称为“敏感依赖于初始条件”，也就是蝴蝶定理。

2. 蝴蝶定理的概念蝴蝶定理描述的是一个简单的转化过程：蝴蝶轻轻地扇动了它的翅膀，这个微小的行为最终会导致一个复杂的系统，如一个飓风的形成。

这就是蝴蝶效应，指的是一个系统的最终状态和最初状态非常不同，即便是微小的变化也会导致完全不同的结果。

蝴蝶定理通常与混沌状态相关联。

混沌现象通常被描述为系统对于初始条件的敏感依赖，也就是微小的变化会导致系统在未来的行为有很大的不同。

混沌现象也被描述为一种无序状态，既不是完全随机也不是完全预测。

在混沌系统中，过程看似随机但是是受着规律的影响。

3. 蝴蝶定理的例子蝴蝶定理可以在很多不同的系统中观察到。

例如，气象学中的天气预测是典型的例子。

天气系统是一个非常复杂的系统，受到很多不同的因素的影响，例如温度，压力和湿度等。

即便是微小的变化，例如温度变化，也会导致最终的结果迥然不同。

另一个例子是电路系统中的混沌现象。

电路是由许多元器件构成的复杂系统。

即便是微小的变化，例如电容的值的变化，也会导致系统在未来的行为有很大的不同。

4. 蝴蝶定理的应用蝴蝶定理具有广泛的应用，尤其是在模拟和预测复杂系统方面。

例如，许多人试图预测股市的趋势。

通过使用蝴蝶定理，可以考虑到不同的因素，如利率和政治事件，这些可以导致股市的变化而且难以被预测。

蝴蝶定理也被用来解释生物系统的现象，例如进化和遗传。

蝴蝶定理的推导过程一、引言蝴蝶定理，又称为混沌理论中的蝴蝶效应，是指一个微小的初始差异可能会在某个非线性系统中产生巨大的影响。

它最早由美国气象学家爱德华·洛伦兹在1963年提出，是混沌理论中最为知名的概念之一。

二、混沌系统和蝴蝶定理混沌系统是指那些具有灵敏依赖于初始条件的非线性动力学系统。

在这类系统中，即使是微小的初始差异也可能会导致长时间的不可预测性行为。

这些行为通常表现为“混沌现象”，包括周期轨道、奇异吸引子、分形等。

洛伦兹通过研究大气运动方程，发现了一个有趣的现象：即使微小的初始扰动也可以导致天气预报结果出现极大误差。

他将这种现象命名为“蝴蝶效应”，并提出了“如果一只蝴蝶在巴西拍动了翅膀，在德克萨斯就可能引起一场龙卷风”的说法。

三、三维对流方程和洛伦兹模型洛伦兹模型是指由三个非线性偏微分方程组成的系统，用于描述流体力学中的对流现象。

这些方程可以表示为：dx/dt = σ(y-x)dy/dt = x(ρ-z)-ydz/dt = xy-βz其中，x、y、z分别表示流体中某一点的速度、温度和密度；σ、ρ、β是常数。

四、蝴蝶定理的推导在洛伦兹模型中，我们可以通过改变初始条件来观察结果的变化。

例如，我们可以将x的初始值从1.0000改为1.0001，然后运行模型并比较结果。

我们可以发现，在运行一段时间后，两个结果之间存在了很大的差异。

这是因为微小的初始扰动在非线性系统中被放大了很多倍。

我们可以通过数学公式来证明这个结论。

假设我们有两个非常接近的初始条件x0和x0+δx，在t时间后它们分别演化成了x(t)和x(t)+δx(t)。

则有：∣∣δx(t)∣∣≤Ceλt∣∣δx(0)∣∣其中，C和λ是常数。

这个公式表明，随着时间的增加，微小扰动会被指数级放大。

这就是蝴蝶定理的本质。

五、结论蝴蝶定理揭示了非线性系统中微小扰动的重要性，它告诉我们即使微小的初始差异也可能会导致长时间的不可预测性行为。

这个定理在气象学、流体力学、经济学等领域都有广泛的应用，对于理解复杂系统和预测未来趋势具有重要意义。

蝴蝶定理的妙用及变式推广
蝴蝶定理源于混沌理论，是一种描述微小变化能够导致巨大影响的现象。

在实践中，蝴蝶定理被应用于许多领域，如气象、金融、交通、生态等。

1.气象预测。

蝴蝶定理在气象学中的应用是最为著名的。

由于天气是一个非常复杂的系统，微小变化可能会引起巨大影响，因此气象预测非常困难。

通过使用蝴蝶定理，科学家们能够预测天气的趋势和可能的变化，从而提高气象预测的准确性。

2.金融分析。

蝴蝶定理在金融分析中也有应用。

金融市场同样是一个非常复杂的系统，最小的变化都可能引起巨大的波动。

理解蝴蝶定理可以帮助投资者预测金融市场的变化趋势，从而更好地制定投资计划。

3.交通。

蝴蝶定理在交通领域的应用主要表现在交通拥堵方面。

微小的交通变化可能会影响整个城市的流量，并导致交通拥堵。

通过了解蝴蝶定理，交通规划者可以更好地解决交通问题，从而提高城市的交通效率。

4.生态学。

蝴蝶定理也可以被用来研究生态系统中的变化。

生态系统是一个复杂的系统，其中一个物种数量的微小变化可能会影响整个系统的平衡。

理解蝴蝶定理可以帮助科学家们更好地了解生态系统的变化趋势，从而更好地保护生态环境。

变式推广：
除了上述领域，蝴蝶定理还被用来研究一些其他的问题。

例如，蝴蝶定理可以被用来研究人口增长、化学反应、艺术创作等问题。

蝴蝶定理的应用不仅仅局限于科学领域，它也可以被用来探讨哲学、文化等领域的问题。