1997-1998学年度天津市初二数学竞赛决赛试题

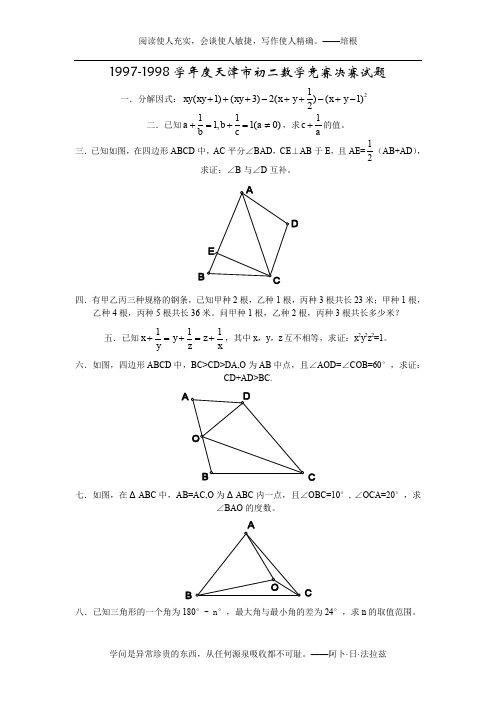
1997-1998学年度天津市初二数学竞赛决赛试题一．分解因式：21(1)(3)2()(1)2xy xy xy x y x y +++-++-+- 二．已知111,1(0)a b a b c +=+=≠，求1c a+的值。

三．已知如图，在四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于E ，且AE=12（AB+AD ），求证：∠B 与∠D 互补。

BD四．有甲乙丙三种规格的钢条，已知甲种2根，乙种1根，丙种3根共长23米；甲种1根，乙种4根，丙种5根共长36米。

问甲种1根，乙种2根，丙种3根共长多少米？五．已知111x y z y z x+=+=+，其中x ，y ，z 互不相等，求证：x 2y 2z 2=1。

六．如图，四边形ABCD 中，BC>CD>DA,O 为AB 中点，且∠AOD=∠COB=60°，求证：CD+AD>BC.AC七．如图，在ΔABC 中，AB=AC,O 为ΔABC 内一点，且∠OBC=10°, ∠OCA=20°，求∠BAO 的度数。

B C八．已知三角形的一个角为180°- n °，最大角与最小角的差为24°，求n 的取值范围。

九．对任给的93个互异的正整数a1,a2,…,a93，试证其中一定存在四个正整数a m,a n,a p,a q，使(a m-a n)(a p-a q)为1998的倍数。

十．将4×4方格纸的每一格中放一个数，使得每一行，每一列,每一对角线的四个数之和都等于1998，求这张4×4方格纸上的四角所放的四个数之和是多少？。

1998年全国初中数学联赛试题(含答案)1998年全国数学联赛试卷一、选择题：（每小题6分，共30分） 1、已知a 、b 、c 都是实数，并且c b a >>，那么下列式子中正确的是（ ）（Ａ）bc ab >（Ｂ）c b b a +>+（Ｃ）c b b a ->-（Ｄ）cb c a > 2、如果方程()0012>=++p px x的两根之差是1，那么p的值为（ ）（Ａ）2（Ｂ）4（Ｃ）3（Ｄ）53、在△ABC 中，已知BD 和CE 分别是两边上的中线，并且BD ⊥CE ，BD=4，CE=6，那么△ABC 的面积等于（ ）（Ａ）12（Ｂ）14（Ｃ）16（Ｄ）184、已知0≠abc ，并且p ba c a cbc b a =+=+=+，那么直线ppx y +=一定通过第（ ）象限（Ａ）一、二（Ｂ）二、三（Ｃ）三、四（Ｄ）一、四5、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1，2，3，那么适合这个不等式组的整数a 、b 的有序数对（a 、b ）共有（ ）（Ａ）17个（Ｂ）64个（Ｃ）72个（Ｄ）81个 二、填空题：（每小题6分，共30分）6、在矩形ABCD 中，已知两邻边AD=12，AB=5，P 是AD 边上任意一点，PE ⊥BD ，PF ⊥AC ，E 、F 分别是垂足，那么PE+PF=___________。

7、已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点，O 为坐标原点，那么△OAB 的面积等于___________。

8、已知圆环内直径为a cm ，外直径为b cm ，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为___________cm 。

9、已知方程()015132832222=+-+--a a x a ax a （其中a 是非负整数），至少有一个整数根，那么a =___________。

八年级数学竞赛决赛试题各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢一、（本题25分）如图1，是一个活动衣架，固定位置后，呈现给大家的是两个菱形，连结其中一个菱形四条边的中点，可得到一个矩形.联想学过的四边形知识，试探究：（1）一个任意四边形的各边中点连线组成的四边形（中点四边形）是什么图形？（2）如果原四边形是特殊四边形（矩形、菱形或正方形），那么中点四边形是什么图形？（3）如果中点四边形是特殊四边形（矩形、菱形或正方形），那么原四边形又是什么图形？二、（本题25分）众所周知，菠萝味道鲜美，很受大家喜爱.某超市为方便顾客，把菠萝去皮后出售，但由于定价不合理而无人问津.现根据如下统计数据重新定价，你认为如何划定去皮菠萝的价格，人们才会觉得合理？菠萝ABcDE去皮前去皮后三、（本题25分）南水北调工程引人注目：根据工程规划，2008年黄河之水可调入北京，xxxx年南水北调中线工程全线建成后长江之水也可调入北京.南水北调进京后，通过与北京当地水联合调度，供水范围达到5876平方公里，覆盖北京平原地区的90%.南水北调中线工程河北段第一个建设项目--滤沱河倒吸工程于xxxx年12月30日上午正式开工.现有若干只装有工程物资的箱子需运到施工地，其总重量为10吨，且每只箱子的重量不超过1吨，为了保证把这些箱子一次运到施工地，问至少需要多少辆载重3吨的汽车？四、（本题30分）学完四边形后，类比三角形全等的条件，张老师给同学们总结了特殊四边形全等的条件：边长相等的两个正方形全等；相邻两边对应相等的两个矩形全等；边长和一内角对应相等的两个菱形全等.接着，他让大家交流讨论任意四边形全等的条件：如图2，两个任意四边形和.问：当满足什么条件时，就能保证它们全等？小明：“我认为只要且就能保证它们全等.”小强：“我认为只要且就能保证它们全等.”假设你作为第三人加入他们两人的讨论，你是如何看待他们的观点的？你还有其他判定两个任意四边形全等的方法吗？请自拟题目，写一篇200~400字的数学作文，阐述你的观点.五、（本题45分）从下列题目中任选其一，联系相关知识及现实生活，写一篇数学作文，字数控制在800字以内.．只言片语话三角形；2．勾股定理知多少；3．谈谈生活中的对称美；4．感悟函数学习；5．函数•方程•不等式；6．一则数学日记；7．“忽如一夜春风来，千树万树梨花开”，xxxx年9月，新课程在全国38个国家级实验区进行实验开始，新课程走进校园，走进了师生的生活，莘莘学子们切身感受到新课程带来的理念、目标、学法等各方面的变化，试结合“学用杯”数学知识应用竞赛，自拟题目，谈谈你的感受.各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢。

----------------------------精品word 文档 值得下载 值得拥有---------------------------------------------- 199年全国初中数学联赛试题解答第 一 试一、选择题1．（C ）2．（C ）)35(2)23(4-<<-x ， 3.727.1<<x3．（A ）∵ 222)()()(a c c b b a -+-+-2)(27c b a ++-=≤27.4．（D ）因为上述任意三个边长都不能构成同一个三角形的三条边长，所以至少要有7个点.5．（A ）延长BA ，CD 交于点H ，∵ ︒=∠30B ，︒=∠60C ，∴ ︒=∠90BHC ，在BHC Rt ∆中，M ,N ,H 三点共线，∴ 27=HM ，21=HN ， ∴ 21=AN ， 故 1=AD ，4)(21=+=BC AD EF . 6．（B ）如图，延长BP 交AA 1于'1A ，过P 作11//'B A PP 交AA 1于'P ，过'A 作11//'B A D A 交BB 1于D .∵ B A ∠=∠，∴ P A AP '=.∴ '''A P AP =.∵ 11'PP AA AP -= =17-16=1，∴ 212'=⨯=AA .∴ 5)217(20'11=--=-=A A BB BD .由勾股定理 13512'222211=+=+=BD B A B A . 即 13=+PB AP .二、填空题1．327.由 a 23531=++， ∴36=a ， 32733643432=⨯⨯==∆a S .----------------------------精品word 文档 值得下载 值得拥有---------------------------------------------- 2．13. ∵ 9)3(322--=-=a a a b ， 又 0)0(=f ，3211)5(=f ，∴ 916-≤b ≤9105， b 可取到的整数值为-1，0，1，…，11共有13个.3．521-≤S ≤314 ∵ 753=+b a , ①S b a =-32. ②①×3+②×5,得 S a 52119+=，①×2-②×3,得 S b 31419-=.由 21+5S ≥0得 S ≥521-, 14-3S ≥0得 S ≤314. 故 512-≤S ≤314. ③ 反之，若S 满足③，易知有满足①，②的a ,b 存在，所以512-≤S ≤314. 4．63.不妨设x 为奇数，y 为偶数，因为22y x +的个位数字是7，因此2x ,2y 的个位数字必是1,6;x ,y 的个位数字必是1,4或1,6或9,4或9,6.又)4(mod 11997≡，则x ,y 除以4的余数必为1,0.由19972<x 知45<x ，因此x 可能值为1,9;21,29;41.经检验，仅当29=x 时，有34=y ，使1997342922=+，29+34=63.第 二 试一、证明：∵ CPF EFP EPG ∠=∠=∠，∴ EPG APG DPB ∠+︒=∠=∠45CPF ∠+︒=45CPF BPF ∠+∠= BPC ∠=.∵ PC =PD ,PB 公用，故 PDB ∆≌PCB ∆，∴ BC =BD .又∵ ︒=∠=∠45CBP PBD ，故 ︒=∠90CBD ，∴ DB BC ⊥.二、由方程 04)(332=+++ab x b a x----------------------------精品word 文档 值得下载 值得拥有---------------------------------------------- 得 )(b a +-=+βα,ab 3=αβ， ① 从条件)1)(1()1()1(++=+++βαββαα，得 13)(2=-+αββα. ②将①代入②，有 14)(2=-+ab b a ， ③即 1)(2=-b a ，∵b a >，故 1=-b a . ④由判别式Δ≥0得：2)(3b a +≥16ab . ⑤将③代入⑤，有2)(b a +≤4. ⑥：由⑤,⑥可知，满足条件的(a ,b )只能是(1,0)或(0,-1).三、n 的最大可能值是9.先证c b a ++能被3整除.事实上，)2(352b a b a b a c b a +=+++=++，∴ c b a ++是3的倍数.设a ,b 被3除后的余数分别为a r 和b r ，则0≠a r ,0≠b r .若b a r r ≠，则1=a r ,2=b r 或者,2=a r 1=b r ，此时，b a 52+必是3的倍数，即c 为合数，矛盾.故b a r r =，则1==b a r r 或者2==b a r r ，此时b a 2+必为3的倍数，从而c b a ++是9的倍数. 再证9是最大的.∵ 4755112=⨯+⨯中，6347511=++，而 6175132=⨯+⨯中，8161713=++.9)81,63(=.因此，9是最大可能的值.。

97-98学年度第二学期初二期末数学试卷一、填空（每格2分，共38分）１、坐标平面上的点与________是一一对应的。

２、函数中自变量x的取值范围是________________。

３、若x轴上一点Ｐ与点Ａ(1,－3)的距离等于5，则Ｐ的坐标为________________。

４、当m______时，方程无实数解。

５、已知函数,,当m______时，y＝f(x)是反比例函数；当m______时，y＝f(x)是正比例函数，且图象在二、四象限。

６、函数y＝x2-2x-1的对称轴方程是________，顶点坐标是_________。

７、方程的解是________。

８、抛物线与y轴交点关于原点对称的点的坐标是___________。

９、已知线段a＝3，b＝2，c＝4，则a,b,c第4比例项d＝______。

１０、若两个相似多边形对应对角线的比为2:3，则这两个多边形的周长的比为________，面积的比为__________。

１１、已知线段ＡＢ＝a，若Ｃ把ＡＢ分成黄金分割（ＡＣ>ＢＣ），则ＡＣ＝_________１２、若梯形的上底为3cm，下底为7cn，则梯形中位线被一条对角线分成两部分长是________________。

１３、若梯形ＡＢＣＤ中，ＤＣ∥ＡＢ，ＡＣ交ＢＤ于点Ｏ，且ＡＢ＝12ＣＤ＝4，ＢＤ＝15，则ＢＯ＝_______。

１４、已知：ＡＢ是Ｒt△ＡＢＣ的斜边，ＣＤ⊥ＡＢ于Ｄ，ＡＤ＝9，ＣＤ＝6，则ＢＤ＝_______。

１５、已知平行四边形ＡＢＣＤ中，点Ｅ在ＡＢ上且ＡＥ:ＥＢ＝1:2，ＤＥ交ＡＣ于Ｆ，则ＡＦ:ＦＣ＝__________，ＳΔDFC:Ｓ四边形BCFE＝__________二、选择题（每题2分，共12分）１６、下列语句正确的是Ａ、顺次连结正方形四边中点所得的四边形是正方形Ｂ、顺次连结矩形四边中点所得的四边形是矩形Ｃ、顺次连结菱形四边中点所得的四边形是菱形Ｄ、顺次连结梯形四边中点所得的四边形是梯形１７、下列各组图形相似的是Ａ、两个面积相等的矩形Ｂ、两个等腰梯形Ｃ、两个含30°内角的菱形Ｄ、两条邻边对应成比例的平行四边形１８、如图，ＡＣ⊥ＢＣ，ＣＤ⊥ＡＢ于Ｄ，下列结论中错误的是Ａ、ＢＣ*ＡＤ＝ＡＣ*ＢＤＢ、ＣＤ2＝ＡＤ*ＢＤＣ、ＡＣ2＝ＡＤ*ＢＤＤ、ＡＣ :ＢＣ＝ＡＤ:ＢＤ１９、一次函数y＝m(x－m)(m<0)的图象经过Ａ、第一、二、四象限Ｂ、第一、二、三象限Ｃ、第一、三、四象限Ｄ、第二、三、四象限２０、函数y＝K(x＋1)与y＝K/x（k≠0）的图象大致是¡¡¡¡¡¡¡¡２１、二次函数y＝x2的图象向左平移2个单位，再向上平移3个单位，得到y＝x2-2x+1，那么Ａ、p＝6，q＝4 Ｂ、p＝4，q＝6Ｃ、p＝6，q＝－6 Ｄ、p＝－6，q＝6答案：一、1、有序实数对2、-1≤x≤2且x≠03、（5，0）或（-3，0）4、5、=16、x=1；（1，-2）7、x=98、9、10、2∶3；4∶911、12、1.5cm和3.5cm13、11.2514、415、1∶3；9∶11二、16-21 ACADCD。

第27讲三角形中的不等关系几何不等式之所以特别吸引人，是由于人们很容易地掌握它们的陈述，同时它们又是创造性的数学思想和现代数学精神的一个极好的入门。

——N.D.扎卡里诺夫知识方法扫描1．三角形中边的不等关系：两边之和大于第三边；两边之差小于第三边；在直角三角形中，斜边大于直角边。

2．三角形中角的不等关系：三角形的一个外角大于它的任何一个不相邻的内角。

3．同一个三角形中的边角不等关系：大角对大边，小角对小边；大边对大角，大角对大边4．两个三角形中的边角不等关系：有两条边相等的两个三角形中，若夹角不相等，则其夹角大的所对的第三边也大；反之，若第三边不等，则第三边大的所对的角也大。

5．运用几何变换（平移，旋转，对称）的方法来改变几何元素的相对位置关系，是处理几何不等式问题的常用方法。

6．用代数方法来比较两个几何量的大小，体现了数形结合的思想，也是一种常用的方法。

经典例题解析例1（第一届“祖冲之杯”数学邀请赛试题）设凸四边形ABCD的对角线相交于O，且AC⊥BD，已知OA>OC,OB>OD,求证：BC+AD>AB+CD.B D证明在OA上截取OC‟=OC，在OB上截取OD‟=0D，连结AD‟,BC‟,C‟D‟. 显然有△AOD≌△AOD‟, △COB≌△COB‟, △COD≌△C‟OD‟..于是有AD=AD‟,BC=BC‟，CD=C‟D‟.所以BC+AD= BC‟+ AD‟=BP+PC…+AP+PD‟ >AB+C…D‟=AB+CD。

例2（1997-1998学年度天津市初中数学竞赛试题）如图，四边形ABCD中，BC>CD>DA,O为AB中点，且∠AOD=∠COB=60°，求证：CD+AD>BC.AC证明如图,在OC上截取OE=OD连接DE,BE, 因∠EOD=180°-∠AOD-∠COB =60°，故△DOE为等边三角形.又OA=OB，∠AOD=∠COB，OD=OE，于是△ADO≌△BEO, 故AD=BE.又在△DEC中，∠CED>∠OED, ∴CD>CE.∴AD+CD>BE+CE>BC.例3（1982年湖北省初中数学竞赛试题）在等腰三角形ABC的一腰AB上取一点D，在另一腰A彻底延长线上取CE=BD，连BD，则DE>BC。

1998年全国初中数学竞赛试卷一、选择题：（每小题6分，共30分）1、已知a 、b 、c 都是实数，并且c b a ，那么下列式子中正确的是（ ） A 、bc ab B 、c b b a ++ C 、c b b a -- D 、cb c a2、如果方程()0012 p px x =++的两根之差是1，那么p 的值为（ ） A 、2 B 、4 C 、3 D 、53、在ABC ∆中，已知BD 和CE 分别是两边上的中线，并且CE BD ⊥，4=BD ，6=CE ，那么ABC ∆的面积等于（ ）A 、12B 、14C 、16D 、18 4、已知0≠abc ，并且pba c ac b cb a =+=+=+，那么直线p px y +=一定通过第（ ）象限A 、一、二B 、二、三C 、三、四D 、一、四 5、如果不等式组⎩⎨⎧-≥-0809 b x a x 的整数解仅为1，2，3，那么适合这个不等式组的整数a 、b 的有序数对（a 、b ）共有（ ）A 、17个B 、64个C 、72个D 、81个 二、填空题：（每小题6分，共30分）6、在矩形ABCD 中，已知两邻边12=AD ，5=AB ，P 是AD 边上任意一点，BD PE ⊥，ACPF ⊥，E 、F 分别是垂足，那么=+PF PE ___________.27、已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点，O 为坐标原点，那么OAB ∆的面积等于___________.8、已知圆环内直径为acm ，外直径为bcm ，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为cm__________.9、已知方程()015132832222=+-+--a a x a a x a （其中a 是非负整数），至少有一个整数根，那么_______=a .10、B 船在A 船的西偏北450处，两船相距210，若A 船向西航行，B 船同时向南航行，且B 船的速度为A 船速度的2倍，那么A 、B 两船的最近距离是km __________.三、解答题：（每小题20分，共60分）11、如图，在等腰ABC ∆中，1=AB ，︒=∠90A ，点E 为腰AC 中点，点F 在底边BC 上，且BE FE ⊥，求CEF ∆的面积。

A B C P 2O P 31第3讲 等腰三角形和等边三角形几何学是在不准确的图形上进行正确推理的艺术。

——波利亚 知识方法扫描有两条边相等的三角形叫做等腰三角形，等腰三角形是一种轴对称图形，它的底角相等，它的底边上的高和中线，顶角的平分线重合。

三边相等的三角形叫等边三角形，等边三角形三个内角都是60º。

在出现等腰三角形的题目中，常用的辅助线作出等腰三角形底边上的高（对称轴）。

这样可以得到一对全等的直角三角形。

根据题目的条件与结论，选取合适的对称轴往往是解题的突破口。

此外，在有一个角是60º的情况下，构造等边三角形也是常用的方法。

经典例题解析例1．（2003年重庆市初中数学竞赛决赛试题）在等边三角形ABC 所在平面内确定一点P,使PAB ∆、PAC ∆、PBC ∆都是等腰三角形。

则满足条件的点P 共有（ ） （A ）1个 （B ）4个 （C ）7个 （D ）10个解 除了等边三角形ABC 的中心外，我们考察BC 垂直平分线上的点：P 1是A 点上方的点，A P 1等于等边三角形ABC 的边长；P 1是BC 下方的点，A P 2等于等边三角形ABC 的边长；P 3也是BC 下方的点，三角形P 3BC 是等边三角形。

在AB ，AC 的垂直平分线上也各有3个点，一共是3+3+3+1=10个点。

选D 。

例2．（2003年全国初中数学联赛试题）如图，AA ′，BB ′分别是∠EAB ，∠DBC 的平分线，若AA ′＝BB ′＝AB ，则∠BAC 的度数为________。

解 设∠BAC 的度数为x 。

因AB ＝BB ′，所以∠B ′BD ＝2x ，∠CBD ＝4x 。

又AB ＝AA ′，故∠AA ′B ＝∠ABA ′＝∠CBD ＝4x 。

因∠A ′AB ＝21（180°－x ）， 所以21（180°－x ）＋4x ＋4x ＝180°。

解之得 x ＝12°。

初二数学竞赛试题及答案一〔说明：本卷可使用计算器，考试时间120 分钟，总分值120 分〕一、选择题〔每题 5 分，共 30 分〕1、使a b a b 成立的条件是〔〕A 、 ab＞ 0B、 ab＞ 1C、 ab≤ 0 D 、 ab≤ 12、某商品的标价比本钱价高p%，当该商品降价出售时，为了不亏损本钱，售价的折扣〔即降价的百分数〕不得超过 d%，那么 d 可用 p 表示为〔〕A 、pp B 、 p C、 100 p D、 100 p100100 p100 p3、有一种足球由32 块黑白相间的牛皮缝制而成，黑皮为正五边形，白皮为正六边形，且边长都相等，那么白皮的块数是〔〕A 、 22B 、 20C、 18 D 、 164、某个班的全体学生进行短跑、跳高、铅球三个工程的测试，有5 名学生在这三个工程的测试中都没有到达优秀，其余学生到达优秀的工程、人数如下表：短跳铅短跑、跳高、跑高球跳高铅球铅球、短跑短跑、跳高、铅球1718156652那么这个班的学生总数是〔〕A 、 35B 、 37C、 40 D 、 485、甲、乙、丙三个学生分别在 A 、B 、C 三所大学学习数学、物理、化学中的一个专业，假设：①甲不在 A 校学习；②乙不在 B 校学习；③在 B 校学习的学数学；④在 A 校学习的不学化学；⑤乙不学物理，那么〔〕A 、甲在B 校学习，丙在 A 校学习B、甲在 B 校学习，丙在C 校学习C、甲在 C 校学习，丙在 B 校学习 D 、甲在 C 校学习，丙在 A 校学习6、： a、b 是正数，且 a+b=2，那么a21b2 4 的最小值是〔〕A 、13B 、5C、25 D 、7二、填空题〔每题 5 分，共30 分〕7、2x=a, 3x=t,那么24x=(用含 a,t 的代数式表示 )8、△ ABC 中， AB=AC=5 ， BC=6 ，点 F 在 BC 上，那么点 F 到另外两边的距离和是21999( x 2) 3( x 1) 211 的值为9、x5x0 ，那么代数式x2C 10、如图，正方形ABCD 的面积为 256，D点 F 在 AD 上，点 E 在 AB 的延长线上，F 直角△ CEF 的面积为200，那么 BE ＝.11、把 7 本不同的书分给甲、乙两人，A BE 甲至少要分到 2 本，乙至少要分到 1 本，两人的本数不能只相差1，那么不同的分法共有种 .12、如果用两个 1，两个2，两个3，两个 4，要求排成具有以下特征的数列：一对 1 之间正好有一个数字，一对2之间正好有两个数字，一对3之间正好有三个数字，一对 4 之间正好有四个数字，请写出一个正确答案.三、解答〔每小15 分，共 60 分〕13、某商店有 A 种本出售，每本零售0.30 元，一打〔 12 本〕售价 3.00 元， 10 打以上的，每打可以按2.70 元付款 .（1〕初二〔 1〕班共 57 人，每人需要 1 本 A 种本，班集体去，最少需要付多少元？（2〕初三年共 227 人，每人需要 1 本 A 种本，年集体去，最少需付多少元？14、察式子1×2× 3× 4＋ 1=5 22× 3×4× 5＋ 1＝112B3× 4×5× 6＋ 1＝192⋯⋯〔1〕猜测 20000× 20001× 20002× 20003+1＝〔〕2〔2〕写出一个具有普遍性的，并出明. 15、如：四形ABCD 中， AD ＝ DC，∠ ABC ＝ 30°，∠ADC ＝ 60° .探索以 AB 、 BC、 BD ，能否成直角三角形，并明理由 .AC16、四位数abcd是一个完全平方数，且D ab 2cd 1，求个四位数.[参答 ]1、C2、C3、 B4、C5、 A6、A7、a3 t8、9、 200410、 1211、 4912、 41312432 或 2342131413、〔1〕可买 5 打或 4 打 9 本，前者需付款× 5＝，后者只需付款× 4＋× 9＝ 14.7 元 .故该班集体去买时，最少需付14.7 元.〔2〕227＝ 12×18＋11，可买 19 打或 18 打加 11 本，前者需付款×19＝；后者需付款 2.70 ×18＋×11＝51.9 元，比前者还要多付 0.6 元.故该年级集体去买，最少需付 51.3 元.14、〔1〕 400060001〔2〕对于一切自然数n，有 n〔n+1〕 (n+2)(n+3)+1＝(n2+3n+1)2.证略故20000×20001×20002× 20003＋1＝〔 200002＋3×20000＋1〕2.＝400060001215、明：以BC 作等△ BCE ， AE 、 AC.因∠ ABC ＝ 30°，∠ CBE ＝ 60°，所以∠ ABE ＝90°，所以 AB 2＋ BE2＝AE 2①， AD ＝ DC ，∠ ADC ＝ 60°，所以△ ADC 是等三角形.因在△ DCB 和△ ACE 中， DC＝ AC ，∠DCB ＝∠ DCA ＋∠ ACB ＝∠ ECB ＋∠ ACB ＝∠ ACE ，而BC ＝CE，所以△ DCB ≌△ ACE ，所以 BD ＝ AE，而 BC ＝BE ，由①式，得BD 2＝AB 2＋ BC 2BA ECD16、设abcd m 2，那么32≤m≤99.又设 cd x ，那么 ab 2x 1.于是100〔2x＋1〕＋x＝m2，201x= m2－100即67×3x＝〔 m+10〕 (m－10).由于 67 是质数，故 m＋10 与 m－ 10 中至少有一个是67 的倍数 .〔1〕假设 m＋10＝67k〔k 是正整数〕，因为 32≤m≤99，则m+10=67,即 m＝57.检验知 572＝3249，不合题意，舍去 .〔2〕假设 m－10＝67k〔k 是正整数〕，那么 m－10＝67， m＝77.所以， abcd 77 25929.。