Cantor集的性质及其应用

Cantor集的性质及应用
李翠香;石凌;刘丽霞
【期刊名称】《大学数学》
【年(卷),期】2011(027)002
【摘要】Cantor集是实函数论中一类重要的集合.本文从定义、性质及应用三方面研究了Cantor集.目的是帮助初学者对Cantor集有一个较全面的认识.
【总页数】3页(P156-158)
【作者】李翠香;石凌;刘丽霞
【作者单位】河北师范大学,数学与信息科学学院,河北,石家庄,050016;河北师范大学,数学与信息科学学院,河北,石家庄,050016;河北师范大学,数学与信息科学学院,河北,石家庄,050016
【正文语种】中文
【中图分类】O174.1
【相关文献】
1.齐次Cantor集的网测度性质及应用 [J], 丰德军;饶辉;吴军
2.Cantor集性质的应用 [J], 董大校
3.Cantor集的性质及应用 [J], 刘小洋;江南
4.关于2n+1分Cantor集构造的一个基本性质及其应用 [J], 胡晓梅
5.Cantor集与Cantor函数性质探究 [J], 栾佳璇
因版权原因，仅展示原文概要，查看原文内容请购买。

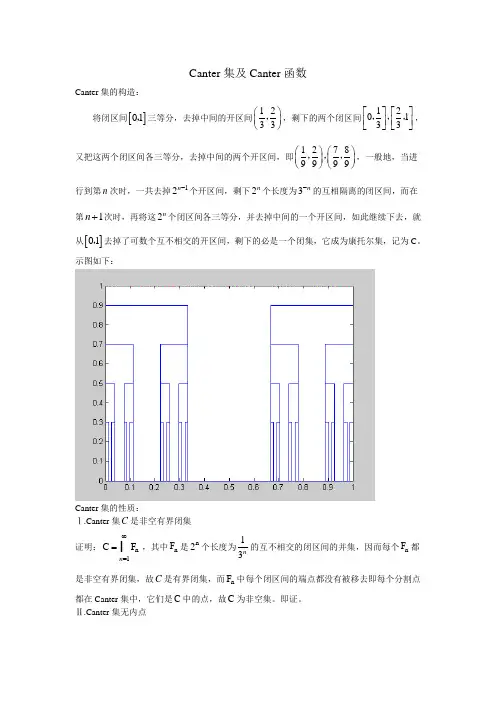
Canter 集及Canter 函数Canter 集的构造：将闭区间[]01，三等分，去掉中间的开区间1233⎛⎫⎪⎝⎭，，剩下的两个闭区间120133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦，，，，又把这两个闭区间各三等分，去掉中间的两个开区间，即12789999⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，，，，一般地，当进行到第n 次时，一共去掉12n -个开区间，剩下2n个长度为3n-的互相隔离的闭区间，而在第1n +次时，再将这2n个闭区间各三等分，并去掉中间的一个开区间，如此继续下去，就从[]01，去掉了可数个互不相交的开区间，剩下的必是一个闭集，它成为康托尔集，记为C 。

示图如下：Canter 集的性质：Ⅰ.Canter 集C 是非空有界闭集 证明：n 1C F n ∞==，其中n F 是n 2个长度为13n 的互不相交的闭区间的并集，因而每个n F 都是非空有界闭集，故C 是有界闭集，而n F 中每个闭区间的端点都没有被移去即每个分割点都在Canter 集中，它们是C 中的点，故C 为非空集。

即证。

Ⅱ.Canter 集无内点证明：令[]G=01\C ，,容易看出[]G 01=，，从而C =∅。

，那么Canter 就没有内点。

Ⅲ.canter 集中所有的点都是聚点，故是完备集证明：即证'C=C ，令x C ∈，则对,n n x F ∀∈，即对每个,n x 属于长度为13n 的某个区间中。

0n δ∀>∃，，满足13n δ<，使得n F 中包含x 的区间含于()x x δδ-+，，此时闭区间的两个端点是C 的点，且总有一个不是x ，这说明x 是C 的极限点，故'C C ⊃，故又因为C 是有界闭集，'C C ⊂，那么即证'C=C 。

Ⅳ.canter 集是疏朗集证明：任取开区间()αβ，，若()αβ，不含C 中的点，则不必讨论，显然证明Canter 是疏朗集。

若()αβ，中含有C 中的点x ，令{}m i n ,x x δαβ=--，则0δ>，故只需证明0n 充分大，便有13n δ<，既然x 是永远去不掉的点，x 也应该属于玩掉0n 之后余下的某一个闭区间中，设这个区间为[]00αβ，，则[]()00αβαβ⊂，，，再将[]00αβ，三等分是，所挖去的中间的开区间，设它为()''I ,αβ=，则()()'',αβαβ⊂，，且()'',C αβ⋂=∅，所以C 是疏朗集。

Cantor三分集在数学⽅⾯，Cantor三分集是由德国数学家康托(G.Cantor)于1883年引⼊的（但在1875年就由Henry John Stephen Smith发现了），它是⼀个取⾃简单直线段上的点集，它有若⼲⾮凡⽽⼜深刻的性质。

通过对它的思考，康托和其他助⼿奠定了现代⼀般拓扑学基础。

虽然康托⾃⼰⽤抽象的⽅法定义了这个集合，但⼀般⽽⾔，现代最流⾏的构造是康托三分集，它是通过将⼀条线段的中间部分去掉⽽获得的。

康托⾃⼰只是顺便提及了三重构造，作为⽆处稠密的完备集的⼀般例⼦。

三分集的构造 康托三分集是由重复删除直线段中间的三分之⼀开区间⽽创造出来的。

先从区间[0，1]中间删除开区间(1/3, 2/3)，留下两边线段：[0, 1/3] ∪ [2/3, 1]。

下⼀步，删除留下的线段的各⾃的三分之⼀中间段，剩下四条直线段：[0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1]。

⽆限重复这⼀过程，则第n个集合是合是：康托三分集包含区间[0, 1]内在每⼀步没被删除的所有的点。

计算表明康托集不包括任何⾮零的长度。

事实上，令⼈惊讶的是，它可能在所有中间被扣掉的部分之和就等于它的最初的长度。

然⽽，仔细观察这个过程却有很重要的东西被剩下，因为重复地消除只是中间的1/3开集（这个集合不包含它的端点）。

从最初的[0，1]线段中除去(1/3, 2/3)，⽽两个端点1/3和 2/3被留下。

随后的操作，不移动这些端点，因为被移除的部分总是在剩余部分的内部。

所以康托集是⾮空的，⽽事实上，它包括⽆限多个点。

Cantor三分集的Lebesgue测度为0，通俗点说长度为零。

康托三分集具有1）⾃相似性；2）精细结构；3）⽆穷操作或迭代过程；4）传统⼏何学陷⼊危机。

⽤传统的⼏何学术语难以描述，它既不满⾜某些简单条件如点的轨迹，也不是任何简单⽅程的解集。

其局部也同样难于描述。

因为每⼀点附近都有⼤量被各种不同间隔分开的其它点存在。

Cantor集、连续延拓定理Cantor集对[0,1]区间三等分, 去掉中间⼀个开区间, 然后对留下的两个闭区间继续三等分,去掉中间的开区间, 不断做下去, 最后留下来的点集称为Cantor 三分集, 记为C.它的性质(1) 分割点⼀定在Cantor集中,(2) C的"长度"为0，去掉的区间长度和$$\sum{\infty}_{n=1}\frac{1}{3n}\cdot 2^{n-1}=\frac{\frac{1}{3}}{1-\frac{2}{3}}=1.$$(3) C没有内点证明：对任意x∈C, x必被含于在第n次时留下的2n个长为1/3n的互不相交的某个闭区间I(n)i中,∀ε>0,1/3n<ε,I(n)i⊂B(x,ε),但由Cantor集的做法，要继续三等分去掉中间的⼀个开区间, 从⽽B(x,ε)内⾄少有⼀点不属于C, 所以x不可能是C的内点.(4) C中的点都是聚点, 从⽽没有孤⽴点.数的进制⼗进制⼩数：相应于对[0,1]⼗等分⼆进制⼩数：相应于对[0,1]⼆等分说明：对应于[0,1]⼗等分的端点有两种表⽰，如0.2000000..., 0.1999999...(⼗进制⼩数)(5) C的基数为ℵ,(利⽤三进制证明)证明思路：把[0,1]区间中的点都写成三进制⼩数, 则Cantor集的做法中去掉的点为⼩数位出现1的数的全体, 从⽽Cantor集为⼩数位只是0，2的点的全体，做对应X∈P→x=∞∑k=1a k3k(ak=0,2).说明：三等分的端点有必要特殊考虑, 因为它有两种表⽰,0.100000...=0.022222..., 0.200000...=0.122222...对x∈C, 令A={k|a k=0},则A⊂N+.对应关系x→A构成了C到P(N+)的⼀⼀映射.第⼀章集合与点集第六节点集间的距离定义1.16 设E⊂R n, f是定义在E上的实值函数, x0∈E, 若∀ε>0,∃δ>0,使得x∈E∩B(x0,δ)时候，|f(x)−f(x0)|<ε.称为f在x0点处连续.注：若f在E上连续, ⽽E0⊂E, 则f在E0连续.定理1.22 若E1,E2是闭集, f定义于E1∪E2上, 且分别在E1,E2上连续, 则f相对于E1∪E2也⼀定连续.证明：若x∈E1∪E2. 不妨设它为聚点, 因为E1,E2为闭集, 则E1∪E2内任⼀以x0为极限的点列{y k}只能有两种情况:其⼀, 从某⼀项起, 全部y k属于E1或E2(相应x0∈E1或x0∈E2.)容易证明.其⼆, {y k}由两个分别属于E1,E2的⽆穷⼦列组成, 此时, x0∈E1∪E2, 因为lim因此\lim\limits_{k\to\infty} f(y_k)=f(x_0).定理1.23 设f是\mathbb{R}^n中有界闭集E上的连续函数, 则(1) f在E上有界(2) f在E上取得最⼤值和最⼩值(3) f在E上⼀致连续定理1.24 设E\subset\mathbb{R}^n, f_1,f_2,\cdots是E上的连续函数列, 且k\to\infty时, \{f_k\}在E上⼀致收敛到函数f, 则f在E上连续.例20 对于任意的x_0\in\mathbb{R}^n, E\subset\mathbb{R}^n, 定义x_0到E的距离为d(x_0,E)=\inf\{d(x_0,y)|y\in E\}.证明：(1)若E是闭集, 则存在y_0\in E, 使得d(x_0,y_0)=d(x_0,E).对于任意点集A, B, 定义A, B之间的距离为d(A,B)=\inf\{d(x,y)|x\in A,y\in B\}.证明：(2)若A和B都是闭集, 其中⾄少有⼀个有界, 则存在x_0\in A, y_0\in B, 使得d(x_0,y_0)=d(A,B).集合的简单写法：{x\in E|f(x)>a}:=E(f>a).定理1.25 若函数f在E上连续, 则对任意的实数a, 存在开集G_a\subset\mathbb{R}^n, 使得E(f>a)=G_a\cap E.也存在开集H_a\subset\mathbb{R}^n, 使得E(f<a)=H_a\cap E.证明：对任意x\in E(f>a), 由于f在E上的点x连续, 必存在\delta=\delta(x,a)>0,使得y\in E\cap B(x,\delta)时, f(y)>a.因此若令G_a=\bigcup_{x\in E(f>a)} B(x,\delta), 则G_a是开集, 并且E(f>a)=G_a\cap E.同理可证, H_a.推论1 若函数f在E上连续, 则对任意的实数a, 存在闭集F_a\subset\mathbb{R}^n, 使得E(f\geq a)=F_a\cap E.也存在开集K_a\subset\mathbb{R}^n, 使得E(f\leq a)=K_a\cap E.推论2 若f在开集E连续, 则对于任意实数a, E(f>a)和E(f<a)是开集, 若函数f在闭集E上连续, 则对于任意实数a, E(f\geq a), E(f\leq a)是闭集.定理1.26 若f是\mathbb{R}^n的函数, 则对于任意实数a, E(f>a), E(f<a)总是开集, 则f在\mathbb{R}^n上连续. (开集与开集的交是开集，闭集与闭集的交为闭集）连续延拓定理引理：若F_1,F_2是\mathbb{R}^n中的两个不交的⾮空闭集, 则有连续函数f(x), 使得(1) 0\leq f(x)\leq 1(x\in\mathbb{R}^n);(2) F_1=\{x: f(x)=1\}, F_2=\{x: f(x)=0\}.证明：构造函数f(x)=\frac{d(x,F_2)}{d(x,F_1)+d(x,F_2)}, x\in\mathbb{R}^n.定理1.27 连续延拓定理：若F是\mathbb{R}^n中的闭集, f(x)是F上的连续函数, 且|f(x)|\leq M(x\in F),则存在\mathbb{R}^n上的连续函数g(x)满⾜|g(x)|\leq M, g(x)=f(x), x\in F.证明：把F分成三个点集：A=\{x\in F:M/3\leq f(x)\leq M\},B=\{x\in F:-M\leq f(x)\leq -M/3\},C=\{x\in F:其他\}.并作函数g_1(x)=\frac{M}{3}\cdot\frac{d(x,B)-d(x,A)}{d(x,B)+d(x,A)},x\in\mathbb{R}^n.Loading [MathJax]/jax/element/mml/optable/BasicLatin.js。

康托尔集的性质及应用1 Cantor集的概念及性质1.1 Cantor集的概念我们先来回忆一下康托尔集的作法。

12将闭区间三等分，去掉中间的开区间，剩下两个闭区间[0,1](,)3312。

又把这两个闭区间各三等分，去掉中间的两个开区间，即[0,],[,1]33 1278n,1n。

一般地，当进行到第n次时，一共去掉个开区间，剩下个22(,),(,)9999n,n长度是的相互隔离的闭区间，而在第n+1次时，再将这2个闭区间各三等分，3并去掉中间的一个开区间，如此继续下去，就从去掉了可数个互不相交(而[0,1]且没有公共端点)的开区间。

剩下的集合称为康托尔集，记为P。

Cantor集是一个完全集,为具有连续基数的点集和不可数的零测度集,其性质在对许多问题的讨论中都起着很大的作用,也常是构造反例的基础,其特殊的构造过程和算术结构使它有许多奇特的性质.1.2 集合的性质Cantor集具有如下性质:非空有界闭集;具有连续基数,其基数为c;完备集,亦即为无孤立点的闭集,被挖去的开集G没有相邻接的构成区间;疏朗集;可测集且异常的公式结尾函数Lebesgue可积且积分值为零;P上的任何函数均是可测函数,零测度集上的任何函数均是可测函数。

下面我们从康托尔集合的做法中讨论一下它的性质，仅供读者学习实变函数论之参考。

2 Cantor集性质的应用2. 1 研究集合的有关性质为了推广区间长度的概念,对一般点集建立一种能反映集合的“容量”与长度概念相当的度量,这种度量既要发展长度的概念,又必须保留长度概念的某些最基本的性质,也就是集合的“测度”,测度理论是建立新型积分理论的基础.,定理1 对任何非负数,,,可作[,]ab的一个完备疏朗集E,0,,,llba,,使。

mE,,证明按下面的步骤完成E的构造:,,lG[,]ab第1步:在的中心处挖去的长度为的开区间,该开区间记为; 13l,,1第2步:在余下的两个闭区间中分别挖去其中心处的长度为,的开区33 G间,这些开区间的并记为; 2………l,,1n,1n,12第n步:在余下的个闭区间中,分别挖去其中心处的长度为的开,()33n,1G2区间,记这个互不相交的开区间之并为。

晋中学院XX学院本科毕业论文（设计）题目cantor集合的构造及推广院系XX学院_____________专业XXXXXX ___________姓名XXX __________________学号XXXXXXX ___________________ 学习年限20XX 年XX 月至201XX 年XX月指导教师XXX 职称讲师申请学位学士学位Can tor集的构造及其推广学生姓名:X X （XX级XX班）指导教师:XXX摘要：Can tor集是实变函数课程中一个重要的例子，它的非同寻常和神奇，不但表现在它的构造的特殊性，而且在于它有许多奇特的性质.本文首先从一维空间Can tor集的构造出发，讨论了它的性质，并给出了其一些简单的应用.同时，阐述了Cantor函数的定义；其次，从不同方面、不同角度探讨了一维空间中推广的Cantor集的构造，另外，还给出了一类疏朗完备集在区间a,b】中的构造方法；最后，简单论述了二维空间的类Can tor集的构造.关键词：Cantor集；性质；应用；疏朗集；推广Construction and Generalization of Cantor setStudent: X XXInstructor: X XXAbstract: The Can tor set is an importa nt example in the course of real variable fun ctio n , it unusual and mysterious, not only in its structure is special, moreover lies in its unique properties. This paper first from one dime nsional Can tor sets ou, discussed its properties and gives some simple applicati ons. At the same time, elaborated the Can tor fun ctio n is defi ned； Sec on dly, from differe nt aspects, differe nt an gles of the on e-dime nsional space of gen eralized Can tor set con struct ion, in additi on , a con structi on method of nondense set in closed in terval a, b 1 is give n in this paper；Fin ally , discusses the two-dime nsional space of class Can tor sets simply.Key words: Can tor se；properties； applicati on；nondense sejt gen eralizati on目录引言 (1)1 .集合论的产生背景与历史意义 (1)2. 一维空间中的Can tor集 (2)2. 2 Can tor 集的构造 (2)2. 2 Can tor集的重要性质 (2)2. 3 Can tor集的应用 (5)3. ...................................................................................................................... Ca ntor 函数的定义及性质 .. (8)4. 一维空间中推广的Cantor集 (10)4. 1 一维空间中推广的Can tor集的构造 (10)4. 2 P n{,b的重要性质 (11)5. 二维空间的类Cantor集 (12)参考文献 (14)引言集合论是19世纪末20世纪初德国伟大的数学家康托尔创立的，是现代数学中的基础理论，同时也被誉为“数学大厦的基石”.它的概念和方法已经渗透到分析、代数及拓扑学等众多数学分支以及物理学等一些学科中，并为这些学科提供了理论基础，推动了它们的发展.Cantor集也是实变函数中的一类重要的集合，其特殊的构造过程和算术结构，使它拥有许多奇特的性质，康托尔三分集就是Can tor集合中最常见的构造.本文阐述了Cantor集在一维空间中的构造、性质、应用以及Cantor函数的定义，叙述了一维空间中推广的Can tor集的构造及其重要性质，最后简单的说明了二维空间的类Cantor集.1. 集合论的产生背景与历史意义集合论在19世纪诞生的基本原因，来自数学分析基础的批判运动.数学分析的发展必然涉及到无穷过程，无穷小和无穷大这些无穷概念.在18世纪，由于无穷概念没有精确的定义，使微积分理论不仅遇到严重的逻辑困难，而且还使无穷概念在数学中信誉扫地.19世纪上半叶，柯西给出了极限概念的精确描述•在这基础上建立起连续、导数、微分、积分以及无穷级数的理论.正是这19世纪发展起来的极限理论相当完美的解决了微积分理论所遇到的逻辑困难.但是，柯西并没有彻底完成微积分的严密化.柯西思想有一定的模糊性，甚至产生逻辑矛盾.19世纪后期的数学家们发现使柯西产生逻辑矛盾的问题的原因在奠定微积分基础的极限概念上•严格地说柯西的极限概念并没有真正地摆脱几何直观，确实地建立在纯粹严密的算术的基础上.于是，许多受分析基础危机影响的数学家致力于分析的严格化•在这一过程中，都涉及到对微积分的基本研究对象一连续函数的描述.在数与连续性的定义中，有涉及关于无限的理论.因此，无限集合在数学上的存在问题又被提出来了•这自然也就导致寻求无限集合的理论基础的工作•总之，为寻求微积分彻底严密的算术化倾向，成了集合论产生的一个重要原因•如果没有集合论的观点，很难对现代数学获得一个深刻的理解.所以康托尔对集合论的创立，不仅对数学基础的研究有重要的意义，而且对现代数学的发展、哲学、逻辑学的学习也有深远的的影响.因此康托尔成为世纪之交的最伟大的数学家之一.2. 一维空间中Cantor集2.1 Cantor集的构造Cantor 集的构造主要是指Cantor 三分集的构造.将直线上的基本空间〔0,11用分点1和2三等分，去掉中间的开区间，记为3 3-把剩下两个闭区间Y ，予分别再三等分，然后各去掉中间的开区间,又分别把这些闭区间三等分，并各去掉中间的开区间，记为小6自，如此方法进行下去，第n 次时，去掉的开区间（称为第n 级区间，每个区间的长度为*， 计有2n 」个）:记G o I k ， k =1,2,3，…P'n = 1,2/这是开集，所以P o - b,1 L G °是闭级，称P o 为 n ,kCan tor 集.2.2 Can tor 集的重要性质1. P 0是非空闭集•这是显然的，在P o 的构造中G o 是任意个开集的并，所以G o 仍是 开集，P o 是G o 的补集，所以P o 是闭集•同时被去掉的开区间的端点及 0，1都不会被除 去而留在P o 内，所以P o 是非空的•所以P o 是非空闭集.明P o 中无孤立点，若不然，假设P o 有一个孤立点X o ，易知端点0与1是P o 的聚点，故X o = o 或1.在o,1中存在构成区间=o ,X o 与X °「o ，其中均无P o 的点，即- o ,X o G o 且 X o , ：o G o ，但X o^G o . 〉o ,X o ， X o , ：o 将分别包含在的两个构成区间 :,X o 与 Xo/中，也即X o 为G o 的某个构成区间的公共端点，而据 G o 的构造可知，这是不可能 的.所以,P o 是无孤立点的非空闭集• P o 是完备集3. R 没有内点且为疏朗集.事实上，在P o 的作法中讲过，“去掉”过程进行到第n 次 记为『二,9'1鳥9,9 .余下4个闭区间Q 宁，訂，昇I 23 =炸，'3- 39,|?，'「爭笋「=扌易，自昴，…，「I = 3n -2 3n 3n -1 亍」 2. R 是完备集.由性质1可知, P o 是一个非空闭集.欲证明P o 是完备集，只须证为止时，剩下2n个长度是3』的互相隔离的闭区间，因此任何一点P o必含在这2n个闭区间的某一个里面.从而在x o的任一邻域U x°,3』内至少有一点不属于P o，但3』＞o n—:],故x o不可能是P o的内点.R既然是没有内点的闭集，那么在直线上任一开区间I内必至少含有开集P o的一点，从而I内必至少有一子开区间，其中不含P o的点.凡是一个点集E （不限于R1中），如果具有性质：空间任一邻域内至少包含某点的一个邻域，其中不含E的点，则称E为疏朗集合，或无处稠密集合（E是疏朗集合的特征是E没有内点）.因此P o是一个疏朗集合•4. F o有连续基数.先用三进位有限小数来表示P o的余区间的端点•则有Ii O= (0.1,0.2 ), lQ=(0.01,0.02 ), 0=(0.21,0.22 ), I『)=( 0.001,0.002 ),123二0.021,0.022 , 133二0.201,0.202 , 143二0.221,0.222 .可以看出第n级余区间I k n k =1,2^l,2nJ形如0.—2川:」,0；" 2—2，其中-1,〉2,川.〉n_1都是0或2.因此，P o的余区间中的点有形式0〉1〉2…….即0,1 G中的数展成三进制小数时，其中至少有一位是 1.我们考察形如十III的小数，其中每个系数:n都是0或者2,这种小数全体记为A.由于A 0,11而0,1L G o中的数展开成三进制小数中0jl-G o：n至少有一位是1，所以中没有A的数，因而有A P o.令B是〔0,11的二进制小数表示全体（也采用二进制有理小数的有限位小数表示）.作■n1 -n n n3n nJ 2n 2其中^=0或2,这个映射是一一映射，但B 的基数是X ,所以A 的基数也是X .由A Po 得 P o —X ，又 P o ，所以 P o .5. F 0是不可列集.若不然，假设P o 是可列的，将P o 中点编号成点列X !,X 2/ ,X k/ ， 也就是说，P o 中任一点必在上述点列中出现.显然，o,l 与-,1中应有一个不含有X !，1 3」［3」用I l 表示这个闭区间.将I l 三等分后所得的左与右两个闭区间中，应有一个不含X 2，用丨2 表示它.然后用I 3表示三等分12时不含X 3的左或右的那个闭区间，如此等等.这样，根 据归纳法，得到一个闭区间列M “kN .由所述取法知，h 二 12二 二 I k 二，X k Tk ，k N ;同时，易见I k 的长为2 > o^ ：：.于是根据数学分析中区间套定理，存在点 I k ，3k ・N .可是•是I k 等的端点集的聚点，从而是闭集 P o 的聚点，故：P o .由于上面已指 出X k 「T k ， k N ，故.X k ， k N .这是一个矛盾.故P o 不可列.6. P o 的测度为零.为了证明P o 的测度为零，只需证明被挖去的区间* ! k =1,2j||,2nJ 的长度之和为1.事实上，第n 级区间I k n 的长度是冷，但第n 级区 3 间共有2n4个，所以被挖去的区间1的总长度为牛=1 .则 nm 3所以P o 是一个测度为零的不可列集7. R 上的任何函数均是可测函数.零测度集上的任何子集都是可测的.8. P o 上的任何函数勒贝格可积.零测度集上的任何函数勒贝格可积，且积分值为2.3 Cantor 集的应用O0 :X 二、 n =1 mR 二 m b,11 - G 二 m b,1 丨-mG 二 1 -m U I ,n,k 3n 二 o.例1试作一闭集F 0,1 1,使F 中不含任何开区间，且^F =-.4解仿照Can tor 集的作法步骤完成F 的构造：第一步：在0,1 ]的中央去掉长为-的开区间G i 二4们的并是却唱却；第n 步：在余下的2nd 个闭区间中，分别去掉其中央处长为 1 -的开区间，记这2心13丿 4个互不相交的开区间之并为G n .令G 为开集，且F = 0,11 —G 与Can tor 集具有类似的性质；从而F 为可测集，且例2在0,1上定义f x :在Cantor 集P 。