第三章多项式插值方法习题

第三章多项式插值方法教学目的及要求：要求掌握基本的定理及各种插值方法。

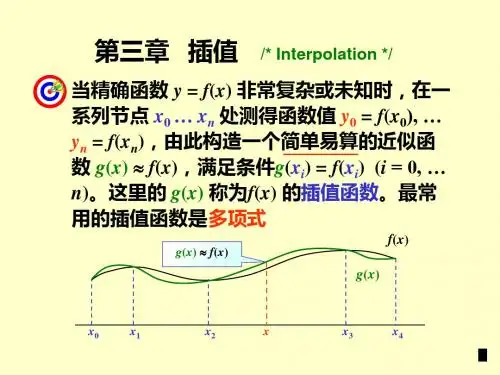
插值方法是数学分析中很古老的一个分支.它有悠久的历史.等距结点内插公式是由我国隋朝数学家刘焯(公元544—610年)首先提出的;而不等距结点内插公式是由唐朝数学家张遂(公元683—727年) 提出的.这比西欧学者相应结果早一千年.插值方法在数值分析的许多分支(例如, 数值积分, 数值微分, 微分方程数值解,曲线曲面拟合,函数值近似计算,等等)均有应用.下面仅以近似计算函数值为例来说明设已知某个函数关系()x f y =的列表函数值nn y y y yx x x x110而()n i x x i ,1,0=≠问应该如何估值().x f y =对于函数关系()x f y =,我们所知道仅仅上述的表列值,它们常常是间接求得的.例如是由实验(观测)得来的,或者是从级数或微分方程求得的.我们可以使用插值方法估计y. 插值方法的目的是寻求简单的连续函数()x ϕ,使它在n+1个点n x x x ,,,10 处取给定值()()),,1,0(n i x f y x i i i ===ϕ,而在别处希望它也能近似地代表函数()x f .因为()x ϕ已是有解析表达式的简单函数,所以它在x x =处的值可以按表达式精确地计算出来.这样我们就可以将()x ϕ看成().x f y =的近似值了给定点n x x x ,,,10 为插值结点.称函数()x ϕ为函数()x f 的关于n x x x ,,,10 的插值函数.称()x f y =为被插函数.严格的说,插值方法一词只用于x 落在给定点n x x x ,,,10 之间的情形,所以也称它为内插法.如果x 落在给定点n x x x ,,,10 之外,并且仍以插值函数()x ϕ在x 处近似地代替().x f ,则一般称这种近似计算函数的方法为外插法.本章我只研究多项式插值，亦即()x ϕ是x 的多项式的情形.这不仅仅因为多项式是最简单的函数，而且因为在许多场合，函数()x f 容易用多项式近似地表示出来.此外,用多项式作插值函数可满意地解决一系列有应用价值的重要问题.特别是数值积分与数值微分的问题.本章讲不涉及三角插值法.其实,只要理解了代数多项式插值方法的实质读者就不难自行导出关于三角多项式插值方法的一系列相应与代数多项式插值方法的理论结果§1. Lagrange 插值公式设()x f y =是实变量x 得单值函数，且已知()x f 在给定的n+1个互异点n x x x ,,,10 处的值n y y y ,,,10 ,即().,,0,n i x f y i i ==插值的基本问题是,寻求多项式()x p ,使得 ()()1.1.,0,n i y x p i i ==设()x p 是一个m 次多项式()0,2210≠++++=m m m a x a x a x a a x p则插值问题是，如何确定()x p 中的系数m a a a ,,,10 ,使得(1.1)式得以满足.所以该问题等价于求解下述的线性方程组:()2.1,,,22101121211000202010⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++n m n m n n mm mm y x a x a x a a y x a x a x a a y x a x a x a a上述的线性方程组的系数矩阵为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=m n m m nnx x x x x x x x x A102211200111 它是一个(n+1)×（m+1）矩阵.当m>n 时，A 的列数大于行数.不难证明矩阵A 的秩数为n+1.因为A 的前n+1列所组成的行列式为(称为Vandermonde 行列式)()mnmm n n n n x x x x x x x x x d e f x x x W10221120010111,.,-我们有()()()3.1,.,10∏>--=ij i j n n x x x x x W为证(1.3),考虑n 次多项式()nnnn n n n n n xx xx x x x x x x x x x x x W2121112110200101111,.,----= 显然110,,,-n x x x 均为它的零点,且它的n x 系数恰为()10.,-n x x W 即 ()()()()101010.,,.,-----=n n n x x x x x x W x x x W 从而有下述递推关系式()()()()101010.,,.,-----=n n n n n n x x W x x x x x x x W运用它即可证明(1.3)式根据(1.3),并注意到诸n x x x ,,,10 互异，从而线性方程组(1.2)的系数矩阵的秩数为n+1 .它表明(1.2)的解是不唯一的，即插值问题(1.1)的解不唯一。

[整理]多项式多点求值快速插值0.多点求值描述：给定n阶多项式f(x)，求其m个点值f(a_1),\dots,f(a_m)。

乍⼀看这个东西似乎是不太可做的，我们先考虑如何缩⼩问题规模也就是多项式阶数。

根据因式定理我们知道⼀个被(x-a)整除的多项式在a处的点值为0，考虑通过这种⽅式转化问题。

接下来就⽐较妙，我们将点值分成左右两半，然后设g_0(x)=\prod\limits_{i=1}^{\lfloor n/2\rfloor}(x-a_i)，右半边同理设为g_1(x)。

然后我们发现显然这个东西带⼊属于沓那⼀边后都会得到0，那么⼀个简单的想法就是直接把f对沓取模，我们以左边为例。

设f(x)=q(x)g_0(x)+r(x)，沓带⼊左边的点值会得到r(x)，⽽r(x)的次数⼀定⾄少减半，所以我们成功缩⼩了问题规模。

每⼀步的g_0和g_1可以预先分治处理出来。

由于⾃带⼤常数，所以为了卡过板⼦题采取了⼩范围暴⼒的⽅法，代码可能会很难看：（略去了多项式板⼦，可以去⾥看）int n,m,F[N],a[N],b[N],*G[N],siz[N];void Build(int k,int l,int r){//类似线段树建树从下往上合并if(r-l<=50){siz[k]=r-l+1,G[k]=new int[siz[k]+1],G[k][0]=1;for(int i=l;i<=r;i++){for(int j=i-l+1;~j;j--)G[k][j+1]=G[k][j];G[k][0]=0;for(int j=0;j<=i-l+1;j++){(G[k][j]+=p-(LL)G[k][j+1]*a[i]%p)%=p;}}return;}Build(ls,l,nmid),Build(rs,nmid+1,r);siz[k]=siz[ls]+siz[rs],G[k]=new int[siz[k]+1];Mul(G[ls],G[rs],G[k],siz[ls],siz[rs]);}int Q[N];void Solve(int k,int l,int r,int *f){if(r-l<=500){//卡常，经测试⼤概500左右暴⼒最快for(int i=l;i<=r;i++){int res=0;for(int j=siz[k]-1;~j;j--){res=((LL)res*a[i]%p+f[j])%p;}b[i]=res;}return;}int R[siz[k]+2<<1];Divide(f,G[ls],siz[k]-1,siz[ls],Q,R);Solve(ls,l,nmid,R);Divide(f,G[rs],siz[k]-1,siz[rs],Q,R);Solve(rs,nmid+1,r,R);}void Print(int x){if(x>9)Print(x/10);putchar(x%10+48);}int main(){Read(n),Read(m);for(int i=0;i<=n;i++)Read(F[i]);for(int i=1;i<=m;i++)Read(a[i]);Build(1,1,m);if(n>=m)Divide(F,G[1],n,m,Q,F);int st=clock();Solve(1,1,m,F);for(int i=1;i<=m;i++)Print(b[i]),putchar('\n');cerr<<(dv)(clock()-st)/CLOCKS_PER_SEC<<endl;KafuuChino HotoKokoa}转置原理的做法会在之后的某个时间补上1.快速插值描述：给定n个点值(x_1,y_1),\dots,(x_n,y_n)，插值出n-1次多项式f(x)。

第三章 参数多项式的插值与逼近2009年8月29日10时35分 1本章内容•几何不变性与参数变换•参数多项式插值与逼近的基本概念•参数多项式插值曲线与逼近曲线•张量积曲面•参数双三次曲面片2009年8月29日10时35分 22009年8月29日10时35分 3第一节 几何不变性和参数变换 • 一、几何不变性：1、定义：指曲线曲面不依赖于坐标系的 选择，或者说在旋转与平移变化下不变 的性质。

2、曲线曲面的基表示： 0 n i i i P a j = = å r r 其中： 为矢量系数，修改它可以改变曲线曲面的形状i a r i j 为单参数（表示曲线时）或双参数（表示曲面时） 的基函数，决定曲线曲面的几何性质2009年8月29日10时35分 43、基表示的分类：（1）规范基表示：即满足Cauchy 条件 也称权性。

这种表示下，曲线 （面）上的点是矢量系数的一个重心组 合，重心坐标是基函数。

其中 一、几何不变性：0 1n i i j = º å 我们常见的线性插值就是一种规范基表示。

（2）部分规范基表示：即满足 0 1,0 ki i k n j = º£< å 如： 01 () p u a a u =+ r r r 0 1j =一、几何不变性：（3）非规范基表示：除规范基表示和部分规范基表示以外的其它基表示。

4、基表示与几何不变性的关系：曲线曲面的规范基表示具有仿射不变性， 其余两种只具有几何不变性。

5、几何不变性的意义： （1）方便局部坐标与整体坐标之间的转换；（2）便于平移和旋转变换；（3）节省了计算量。

2009年8月29日10时35分 5• 1、概述• 曲线的参数域总是有界的。

• 曲线的参数可能有某种几何意义，也可能没有。

• 曲线的参数化：即确定曲线上的点与参数域中的参数值之间的一种对应关系。

• 这种对应关系可以是一一对应的，也可以不是一一对应的，后者称为奇点（Singularpoint），如曲线的自交点。

习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值，试通过一个二次插值函解：0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 （1） 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则（2）采用Newton插值多项式2()y N x =≈ 根据题意作差商表：224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==，试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。

注意到：若1n +个节点()0,1,...,i x i n =互异，则对任意次数n ≤的多项式()f x ，它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。

可见，当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身，故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地，当0k =时，有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式，并验证插值多项式的唯一性。

埃尔米特插值多项式练习题埃尔米特插值多项式练习题埃尔米特插值多项式是一种用于逼近函数的方法，它不仅可以通过给定的函数值来逼近函数的值，还可以通过给定的导数值来逼近函数的导数值。

在数值计算和插值问题中，埃尔米特插值多项式是一种非常有用的工具。

假设我们有一个函数f(x)，我们想要通过给定的函数值和导数值来逼近这个函数。

埃尔米特插值多项式可以通过以下步骤来求解：1. 首先，我们需要确定插值点。

插值点是我们已知的函数值和导数值的点。

通常，我们选择一组等距的插值点，以便于计算。

2. 接下来，我们需要构建拉格朗日插值多项式。

拉格朗日插值多项式是通过给定的函数值来逼近函数的值的多项式。

它可以通过以下公式来计算：L(x) = Σ [ f(xi) * Li(x) ] (i=0 to n)其中，Li(x)是拉格朗日基函数，它可以通过以下公式来计算：Li(x) = Π [ (x - xj) / (xi - xj) ] (j=0 to n, j ≠ i)这样，我们就可以得到拉格朗日插值多项式L(x)。

3. 接下来，我们需要构建埃尔米特插值多项式。

埃尔米特插值多项式是通过给定的函数值和导数值来逼近函数的多项式。

它可以通过以下公式来计算：H(x) = Σ [ f(xi) * Hi(x) + f'(xi) * Hi'(x) ] (i=0 to n)其中，Hi(x)是埃尔米特基函数，它可以通过以下公式来计算：Hi(x) = [ 1 - 2 * (x - xi) * Li'(xi) ] * (Li(x))^2Hi'(x)是埃尔米特基函数的导数，它可以通过以下公式来计算：Hi'(x) = (x - xi) * (Li(x))^2这样，我们就可以得到埃尔米特插值多项式H(x)。

通过以上步骤，我们可以得到一个逼近函数f(x)的埃尔米特插值多项式H(x)。

这个多项式可以在给定的插值点上非常精确地逼近函数的值和导数值。

数字信号处理刘顺兰第三章完整版习题解答一、题目解答1. 题目利用时域抽样、频域抽样、零填充、插值法等，实现信号的变换。

1.1 时域抽样时域抽样是指将一个连续时间信号在时间轴上的等间隔位置上进行采样，可以得到一个离散时间信号。

时域抽样的原理是，将时间轴上的信号按照一定的时间间隔进行采样，每个采样点的振幅值就是该点对应的连续时间信号的振幅值。

时域抽样可以通过以下步骤进行实现：1.假设连续时间信号为x(t)，采样频率为Fs（采样频率是指每秒采样的次数），采样间隔为Ts（采样间隔是指相邻两个采样点之间的时间间隔）。

2.根据采样频率和采样间隔，计算出采样点数N：N =Fs * T，其中T为采样时长。

为Ts。

4.在每段的中点位置进行采样，得到N个采样点。

5.将N个采样点按照时域顺序排列，即可得到离散时间信号。

1.2 频域抽样频域抽样是指将一个连续频谱信号在频率轴上的等间隔位置上进行采样，可以得到一个离散频谱信号。

频域抽样的原理是，将频率轴上的信号按照一定的频率间隔进行采样，每个采样频率点上的能量值就是该频率点对应的连续频谱信号的能量值。

频域抽样可以通过以下步骤进行实现：1.假设连续频谱信号为X(f)，采样频率为Fs（采样频率是指每秒采样的次数），采样间隔为Δf（采样间隔是指相邻两个采样频率点之间的频率间隔）。

2.根据采样频率和采样间隔，计算出采样点数N：N =Fs / Δf，其中Δf为采样频率点之间的频率间隔。

为Δf。

4.在每段的中点位置进行采样，得到N个采样频率点。

5.将N个采样频率点按照频域顺序排列，即可得到离散频谱信号。

1.3 零填充零填充是指在信号的末尾添加一些零值样本，使得信号的长度变长。

零填充的原理是，通过增加信号的长度，可以在时域和频域上提高信号的分辨率，从而更精确地观察信号的特征。

零填充可以通过以下步骤进行实现：1.假设原始信号为x(n)，长度为N。

2.计算需要填充的长度L，L > 0。

一、填空题：1． 满足()a a f x x =，()b b f x x =，()c c f x x =的拉格朗日插值余项为 。

答：()()()()()3!a b c f R x x x x x x x ξ'''=---2．已知函数()f x 的函数值()()()()()0,2,3,5,6f f f f f ，以及均差如下 ()()()()()00,0,24,0,2,35,0,2,3,51,0,2,3,5,60f f f f f ===== 那么由这些数据构造的牛顿插值多项式的最高次幂的系数是 答： 1二、选择题1. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足（ ） A ．()00l x ＝0，()110l x = B ． ()00l x ＝0，()111l x = C ．()00l x ＝1，()110l x = D ． ()00l x ＝1，()111l x = 答：D2．. 已知等距节点的插值型求积公式()()352kkk f x dx A f x =≈∑⎰，那么3kk A==∑（ ）A ．1 B. 2 C. 3 D. 4 答：C3．过点(x 0,y 0), (x 1,y 1)，…，(x 5,y 5)的插值多项式P(x)是( )次的多项式。

(A). 6 (B).5 (C).4 (D).3． 答：B 三、证明题1. 设 f (x) = (x-1) (x-2) .证明对任意的x 有： f [1, 2, x)]= 1证明:f [1, 2] = [f (1) – f (2)]/ (1 – 2) = [0 – 0]/ (-1) = 0, 对任意的x 有F[2, x] = [f (2) – f (x)]/ (2 – x) = [0 – (x-1) (x-2)]/ (2 – x) = (x-1),所以 f [1, 2, x] = [f (1, 2) - f (2, x)]/ (1 – x) = [0 - (x-1)]/ (1 – x) = 12.设在上具有二阶连续导数，且，求证：解：由，则在的线性插值多项式为：，于是由，可得：3． 试利用差分性质证明：证明：记：可以证明：， 又： 故：. 四、计算题： 1.．已知数值表试用二次插值计算()0.57681f 的近似值，计算过程保留五位小数。

《计算方法教程(第二版)》习题答案第一章 习题答案1、浮点数系),,,(U L t F β共有 1)1()1(21++---L U t ββ 个数。

3、a ．4097b ．62211101110.0,211101000.0⨯⨯c ．6211111101.0⨯4、设实数R x ∈，则按β进制可表达为：,1,,,3,2,011)11221(+=<≤<≤⨯++++++±=t t j jd d lt t d t t d dd x βββββββ按四舍五入的原则，当它进入浮点数系),,,(U L t F β时，若β211<+t d ，则 l tt d dd x fl ββββ⨯++±=)221()(若 β211≥+t d ，则 l tt d d d x fl ββββ⨯+++±=)1221()(对第一种情况：t l lt l t t d x fl x -++=⨯≤⨯+=-βββββ21)21(1)()(11对第二种情况：t l ltl t t d x fl x -++=⨯≤⨯--=-ββββββ21)21(1)(11 就是说总有： tl x fl x -≤-β21)( 另一方面，浮点数要求 β<≤11d ， 故有l x ββ1≥，将此两者相除，便得t x x fl x -≤-121)(β 5、a ． 5960.1 b ． 5962.1 后一种准确6、最后一个计算式：00025509.0原因：避免相近数相减，避免大数相乘，减少运算次数7、a ．]!3)2(!2)2(2[2132 +++=x x x yb ．)21)(1(22x x x y ++=c ．)11(222-++=x x x yd ． +-+-=!2)2(!6)2(!4)2(!2)2(2642x x x x ye ．222qp p q y ++=8、01786.098.5521==x x9、 m )10(m f - 1 233406.0- 3 20757.0- 5 8.07 710计算宜采用：])!42151()!32141()!22131[()(2432+⨯-+⨯-+⨯--=x x x f第二章 习题答案1、a ．T x )2,1,3(= b ．T x )1,2,1,2(--= c ．无法解2、a ．与 b ．同上， c ．T T x )2188.1,3125.0,2188.1,5312.0()39,10,39,17(321---≈---=7、a ．⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛---14112111473123247212122123211231321213122 b ． ⎪⎪⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛----333211212110211221213231532223522121⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎪⎭⎫⎝⎛-=111211212130213221219、T x )3415.46,3659.85,1220.95,1220.95,3659.85,3415.46(1= T x )8293.26,3171.7,4390.2,4390.2,3171.7,8293.26(2= 10、T LDL 分解：)015.0,579.3,9.1,10(diag D =⎪⎪⎪⎪⎪⎭⎫⎝⎛=16030.07895.05.018947.07.019.01L Cholesky 分解⎪⎪⎪⎪⎪⎭⎫⎝⎛=1225.01408.10833.15811.18918.12333.12136.23784.18460.21623.3G 解：)1,1,2,2(--=x 12、16,12,1612111===∞A A A611,4083.1,61122212===∞A A A2)(940)()(12111===∞A Cond A Cond A Cond524)(748)()(22221===∞A C o n d A C o n d A C o n d⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=--180.0000180.0000- 30.0000 180.0000- 192.0000 36.0000- 30.0000 36.0000- 9.0000,0.0139 0.1111- 0.0694- 0.1111- 0.0556 0.1111- 0.0694- 0.1111- 0.0139 1211A A1151.372,1666.0212211==--A A15、 1A ：对应 Seidel Gauss - 迭代收敛，Jacobi 迭代不收敛； 2A ：对应 Seidel Gauss - 迭代收敛，Jacobi 迭代不收敛； 3A ：对应 Seidel Gauss - 迭代收敛，Jacobi 迭代收敛；第三章 习题答案1、Lagrange 插值多项式：)80.466.5)(20.366.5)(70.266.5)(00.166.5()80.4)(20.3)(70.2)(00.1(7.51)66.580.4)(20.380.4)(70.280.4)(00.180.4()66.5)(20.3)(70.2)(00.1(3.38)66.520.3)(80.420.3)(70.220.3)(00.120.3()66.5)(80.4)(70.2)(00.1(0.22)66.570.2)(80.470.2)(20.370.2)(00.170.2()66.5)(80.4)(20.3)(00.1(8.17)66.500.1)(80.400.1)(20.300.1)(70.200.1()66.5)(80.4)(20.3)(70.2(2.14)(4--------⨯+--------⨯+--------⨯+--------⨯+--------⨯=x x x x x x x x x x x x x x x x x x x x x L Newton 插值多项式：)80.4)(20.3)(70.2)(00.1(21444779.0)20.3)(70.2)(00.1(527480131.0)70.2)(00.1(855614973.2)00.1(117647059.22.14)(4----+------+-+=x x x x x x x x x x x N2、设)(x y y =，其反函数是以y 为自变量的函数)(y x x =，对)(y x 作插值多项式：)1744.0)(1081.0)(4016.0)(7001.0(01253.0)1081.0)(4016.0)(7001.0(01531.0)4016.0)(7001.0(009640.0)7001.0(3350.01000.0)(----+---+--+--=y y y y y y y y y y y N 3376.0)0(=N 是0)(=x y 在]4.0,3.0[中的近似根。