沪科版九年级数学下册 视图与投影知识点梳理

新知讲解
投影线集中于一点
投影线互相平行， 且斜着照射投影面
投影线垂直 于投影面
中心投影
斜投影
正投影
平行投影
投影
新课讲解 1. 如图，把一根直的细铁丝 (记为线段AB) 放在三个不同位置.
(1) 铁丝平行于投影面；
(2)铁丝倾斜于投影面；
(3) 铁丝垂直于投影面 (铁丝不一定要与投影面有交点).
三种情形下铁丝
新课 讲授
图①与图②③的投影 线有什么区别？
图②③的投影线与投影面的 位置关系又有什么区别？
图①
图②
图③
观察与思考 下图是三角形纸板在光线照射下形成投影
新课 讲授
图（1）中的投影线集中于一点，
图①与图②③的投影
形成中心投影；
线有什么区别？
图（2）图（3）中，投影线互相平行，
形成平行投影；
图①
图②
图③
平行投影与中心投影的区别与联系
平行投影 中心投影
光线
平行的 投射线
从一点 出发的 投射线
区别
物体与投影面 平行时的投影
联系
全等
放大(位 似变换)
都是物体在 光线的照射 下，在某个 平面内形成 的影子。(即 都是投影)
如图所示① ② ③ ④是木杆一天中四个不同时刻在地面
练
习：
上的影子，将它们按时间先后顺序排列正确的一项是
几何体的正投影
A′ D′
B′ C′
AD
BC
P
F′ A′ D′
G′
E
FA D
H
G B
C
B′ C′ P
视图： 几何体在一个平面上的正投影叫做这个几何体的视图

投影特性
积聚成一个 点 直线段,实长
直线段,缩短垂直积聚成一 条线段 Nhomakorabea面
平行
平面,实形
倾斜
平面,缩小
直线和平面的投影特性:
1、积聚性：当直线段或平面与投影面垂 直时，其投影就积聚成一点或一线段。
2、真实性：当直线或平面与投影面平行 时,其投影反映实长或实形。
3、类似性：当直线或平面与投影面倾斜时， 投影就缩短或缩小。
三、视图
1、视图的概念： 一个物体向投影面投影所得到的图形，
称为视图。
现代人每天生活在纷繁、复杂的社会当中，紧张、高速的节奏让人难得有休闲和放松的时光。人们在奋斗事业的搏斗中深感身心的疲惫。然而，如果你细心观察，你会发现作 为现代人，其实人们每天都在尽可能的放松自己，调整生活节奏，追求充实快乐的人生。看似纷繁的社会里，人们的生活方式其实也不复杂。大家在忙忙碌碌中体味着平凡的 人生乐趣。由此我悟出一个道理，那就是----生活简单就是幸福。生活简单就是幸福。一首优美的音乐、一支喜爱的歌曲，会让你心境开朗。你可以静静地欣赏你喜爱的音乐， 可以在流荡的旋律中回忆些什么，或者什么都不去想；你可以一个人在房间里大声的放着摇滚，也可以在网上用耳麦与远方的朋友静静地共享；你还可以一边放送着音乐，一 边做着家务....生活简单就是幸福。一杯清茶，或一杯咖啡，放在你的桌边，你的心情格外的怡然。你可以浏览当天的报纸，了解最新的国内外动态，哪怕是街头趣闻；或者捧 一本自己喜欢的杂志、小说，从字里行间获得那种特别的轻松和愉悦....生活简单就是幸福。经过精心的烹制，一桌可心的菜肴就在你的面前，你招呼家人快来品尝，再备上最 喜欢的美酒，这是多么难得的享受！生活简单就是幸福。春暖花开的季节，或是清风送爽的金秋，你和家人一起，或是朋友结伴，走出户外，来一次假日的郊游，享受大自然 带给你的美丽、芬芳。吸一口新鲜的空气，忘却都市的喧嚣，身心仿佛受到一番洗涤，这是一种什么样的轻松感受！生活简单就是幸福。你参加朋友们的一次聚会，那久违的 感觉带给你温馨和激动，在觥酬交错之间你享受与回味真挚的友情。朋友，是那样的弥足珍贵....生活简单就是幸福。周末的夜晚，一家老小围坐在电视机旁，尽享团圆的欢乐 现代人越来越会生活，越来越会用各种不同的方式来放松自己。垂钓、上网、打牌、玩球、唱卡拉OK、下棋.....不一而足。人们根据自己的兴趣爱好寻找放松身心的最佳方式， 在相对固定的社交圈子里怡然的生活，而且不断的扩大交往的圈子，结交新的朋友有时，你会为新添置的一套漂亮时装而快乐无比；有时，你会为孩子的一次小考成绩优异而 倍感欣慰；有时，你会为刚参加的一项比赛拿了名次而喜不自胜；有时，你会为完成了上司交给的一个任务而信心大增生活简单就是幸福！生活简单就是幸福，不意味着我们 放弃了对目标的追逐，是在忙碌中的停歇，是身心的恢复和调整，是下一步冲刺的前奏，是以饱满的精力和旺盛的热情去投入新的“战斗”的一个“驿站”；生活简单就是幸 福，不意味着我们放弃了对生活的热爱，是于点点滴滴中去积累人生，在平平淡淡中寻求充实和快乐。放下沉重的负累，敞开明丽的心扉，去过好你的每一天。生活简单就是 幸福！我的心徜徉于春风又绿的江南岸，纯粹，清透，雀跃，欣喜。原来，真正的愉悦感莫过于触摸到一颗不染的初心。人到中年，初心依然，纯真依然，情怀依然，幸甚至 哉。生而为人，芳华刹那，真的不必太多要求，一盏茶，一本书，一颗笃静的心，三两心灵知己，兴趣爱好一二，足矣。亦舒说：“什么叫做理想生活？不用吃得太好穿得太 好住得太好，但必需自由自在，不感到任何压力，不做工作的奴隶，不受名利的支配，有志同道合的伴侣，活泼可爱的孩子，丰衣足食，已经算是理想。”时间如此猝不及防， 生命如此仓促，忠于自己的内心才是真正的勇敢，以不张扬的姿态，将自己活成一道独一无二的风景，才是最大的成功。试问，你有多久没有靠在门槛上看月亮了，你有多久 没有在家门口的那棵大树下乘凉了，你有多久没有因为一个人一件事而心生感动了，你又有多久没有审视自己的内心了？与命运的较量中，我们被迫前行，却忘记了来时的方

A.圆柱 B.正方体 C.棱柱 D.圆 锥
2.某长方体的主视图和左视图如图所示 （单位：cm）,则其俯视图的面积是多少？
解 俯视图的长等于主视图的宽，为3cm 俯视图的宽等于左视图的宽，为2cm
则 其俯视图的面积为:3×2=6cm2
课后作业
1.从教材习题中选取. 2.完成练习册本课时的习题.
25.2 三视图
第1课时 三视图
沪科版 九年级下册
新课导入
如果已知一个几何体在水平面上的视 图是圆，你能断定这个几何体是球吗？
圆柱和球在水平面上的视图都是圆.
新课推进
要想清楚地刻画一个几何体的形 状与大小，通常需要画出它在三个互 相垂直的投影面上的正投影.面叫做侧面.
主视图要放在左上方，它的正下方是俯视 图，它的正右方是左视图.
主
左
视
视
图
高高
图
长
宽
长 宽
高平齐
长对正
宽相等
俯视图
主视图与俯视图的长对正，主视图与左视 图的高平齐，左视图与俯视图的宽相等.
练习
1. 将图中的几何体与其对应的三视图用线连起来.
画三视图
例1 画出图中几何体的三视图.
画三视图的方法： 第一步，确定主视图的位置，画出主视图； 第二步，在主视图正下方画出俯视图，注意 与主视图长对正； 第三步，在主视图正右方画出左视图，注意 与主视图高平齐，与俯视图宽相等.
三视图
自几何体的前方向后投
V W
射，在正面投影面V上得到
的视图称为主视图；
H
自几何体的上方向下投
V W
射，在水平面投影面H上得
到的视图称为俯视图；
H
自几何体的左侧向右投

感悟新知
知4－讲
2. 由三视图想象几何体形状的常用途径 (1)根据主视图、俯视图和左视图想象几何体的正面、上 面和左面的形状以及几何体的“长、宽、高 ”； (2)根据实线和虚线想象几何体看得见和看不见的轮廓 线；
感悟新知
知4－讲
(3)熟记一些简单几何体的三视图会对复杂几何体的想象有 帮助 ；
(4)利用由三视图画几何体与由几何体画三视图的互逆过程， 反复练习，不断总结方法 .
感悟新知
知2－讲
3. 画三视图的规定 画三视图时，看得见的部分的轮廓线 画成实线，因被其他部分遮挡而看不见的部分的轮廓线画 成虚线 .
感悟新知
知2－练
例2 一种机器上有一个零件叫燕尾槽(如图 25.2－4)，请 画出它的三视图 .
感悟新知
解：这个燕尾槽的三视图如图 25.2－5 所示 .
知2－练
感悟新知
3. 常见几何体的三视图
知4－讲
感悟新知
知4－练
例5 [ 中考·湖北 ] 如图 25.2－12 是一个立体图形的三
视图，该立体图形是( )
A. 长方体 B. 正方体
C. 三棱柱 D. 圆柱
感悟新知
解题秘方：根据三视图直接判断即可． 解：根据三视图可知，该立体图形是长方体 . 答案：A
知4－练
感悟新知
要点解读
知4－讲
几何体、三视图和展开图之间的关系：
1. 几何体的三视图和展开图都是平面图形，几何体、
三视图和展开图中，三者知其一，就能确定另外两种图
形，即三者之间可以互相转化 .
2. 对于稍复杂的视图，可先将其分解成几个简单的
图形，再综合分析 .
感悟新知
知4－讲
3. 一个摆好的几何体的视图是唯一的，但从视图反 过来考虑几何体时，有多种可能性，如正方体的主视图 是正方形，但主视图是正方形的几何体可能是直棱柱、 长方体、圆柱等 .

投影与视图知识点总结在我们的日常生活和学习中，投影与视图是一个重要的数学概念，它不仅在数学领域有着广泛的应用，在工程、建筑、设计等实际领域也发挥着关键作用。

接下来，让我们一起深入了解投影与视图的相关知识点。

一、投影投影是光线（投射线）通过物体，向选定的面（投影面）投射，并在该面上得到图形的方法。

1、中心投影由同一点（点光源）发出的光线形成的投影叫做中心投影。

比如，夜晚路灯下的人影就是中心投影的例子。

其特点是：等长的物体平行于地面放置时，在灯光下，离点光源越近的物体的影子越短，离点光源越远的物体的影子越长。

2、平行投影由平行光线（太阳光线）形成的投影称为平行投影。

平行投影又分为正投影和斜投影。

正投影是指投射线垂直于投影面的平行投影。

在平行投影中，同一时刻，不同物体的物高和影长成比例。

二、视图视图是将物体按正投影向投影面投射所得到的图形。

1、三视图三视图包括主视图、俯视图和左视图。

主视图：从物体的前面向后面投射所得的视图。

俯视图：从物体的上面向下面投射所得的视图。

左视图：从物体的左面向右面投射所得的视图。

三视图的位置关系：主视图在上方，俯视图在主视图的正下方，左视图在主视图的正右方。

三视图的大小关系：长对正、高平齐、宽相等。

即主视图与俯视图的长相等，主视图与左视图的高相等，俯视图与左视图的宽相等。

2、常见几何体的三视图（1）正方体：三视图都是正方形。

（2）长方体：主视图、左视图是长方形，俯视图是长方形。

（3）圆柱：主视图、左视图是长方形，俯视图是圆。

（4）圆锥：主视图、左视图是三角形，俯视图是圆及圆心。

（5）球：三视图都是圆。

三、根据视图还原几何体根据三视图还原几何体时，要先分别根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状，然后综合起来考虑整体形状。

四、投影与视图的应用1、在建筑设计中，设计师需要通过绘制三视图来准确表达建筑物的形状和尺寸，以便施工人员能够按照设计进行施工。

2、在机械制造中，工程师需要根据零件的三视图来制造零件，确保零件的精度和质量。

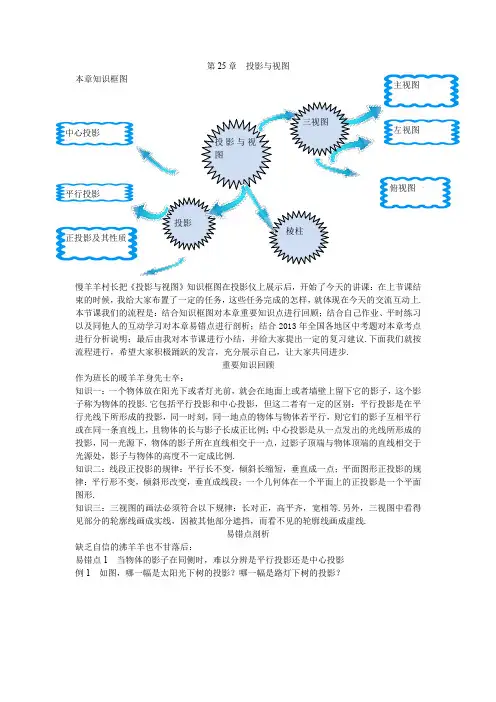
第25章 投影与视图本章知识框图慢羊羊村长把《投影与视图》知识框图在投影仪上展示后，开始了今天的讲课：在上节课结束的时候，我给大家布置了一定的任务，这些任务完成的怎样，就体现在今天的交流互动上.本节课我们的流程是：结合知识框图对本章重要知识点进行回顾；结合自己作业、平时练习以及同他人的互动学习对本章易错点进行剖析；结合2013年全国各地区中考题对本章考点进行分析说明；最后由我对本节课进行小结，并给大家提出一定的复习建议.下面我们就按流程进行，希望大家积极踊跃的发言，充分展示自己，让大家共同进步.重要知识回顾作为班长的暖羊羊身先士卒：知识一：一个物体放在阳光下或者灯光前，就会在地面上或者墙壁上留下它的影子，这个影子称为物体的投影.它包括平行投影和中心投影，但这二者有一定的区别：平行投影是在平行光线下所形成的投影，同一时刻，同一地点的物体与物体若平行，则它们的影子互相平行或在同一条直线上，且物体的长与影子长成正比例；中心投影是从一点发出的光线所形成的投影，同一光源下，物体的影子所在直线相交于一点，过影子顶端与物体顶端的直线相交于光源处，影子与物体的高度不一定成比例.知识二：线段正投影的规律：平行长不变，倾斜长缩短，垂直成一点；平面图形正投影的规律：平行形不变，倾斜形改变，垂直成线段；一个几何体在一个平面上的正投影是一个平面图形.知识三：三视图的画法必须符合以下规律：长对正，高平齐，宽相等.另外，三视图中看得见部分的轮廓线画成实线，因被其他部分遮挡，而看不见的轮廓线画成虚线.易错点剖析缺乏自信的沸羊羊也不甘落后：易错点1 当物体的影子在同侧时，难以分辨是平行投影还是中心投影例1 如图，哪一幅是太阳光下树的投影？哪一幅是路灯下树的投影？投影平行投影 中心投影正投影及其性质主视图 左视图 俯视图【错解】图（1）中的投影是太阳光下树的投影，图（2）中的投影是路灯下树的投影.【剖析】分辨是平行投影还是中心投影，关键是把握平行投影与中心投影的图形特征.分别过两棵树的顶端和影子的顶端作直线，若两直线平行，则树影是在太阳光下形成的；若两直线相交，则树影是在路灯下形成的.【正解】图（1）中的投影是路灯下树的投影，图（2）中的投影是太阳光下树的投影.易错点2 考虑问题不全面，平面图形的投影判断错误例2 小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影可能是（）A．①③④B．②③C．③④D．②③④【错解】B【剖析】根据矩形不同的放置位置，可以得到不同的投影，竖直放置时，投影为②；水平放置且阳光垂直照射时，投影为③；当水平或倾斜放置，且阳光斜射时，投影为④. 我们在解决投影时，要注意物体所放的位置以及投射线的照射情形，这样才不会出错或漏掉一些情况.【正解】D易错点3 凭生活经验，感觉“长者影长，短者影短”例3 如图，有一棵大树和一棵小树，在大树的左边还有一盏比大树高的路灯，灯杆、大树、小树的底部在一条直线上，无论是在阳光还是在这盏路灯的照射下，大树的影子长，还是小树的影子长？【错解】无论是在阳光还是在这盏路灯的照射下，均是大树的影子长.【剖析】解答本题常出现的错误是凭主观判断，认为大树高，影子必然长；有的虽然判断正确，但是不能正确地画出图形予以说明. 解答的思路是依据平行投影和中心投影的特性画图，但是，已知图中未画出路灯的具体位置，解答时务必注意到这一点. 【正解】如图1，在阳光下，设BE是大树AB的影长，DF是小树CD的影长.因为△ABE ∽△CDF，所以两树影长与树高成比例.因为大树高，所以大树的影子长.在灯光下，两树影子的长短与路灯的位置有关.如果路灯在如图2所示的点P1处，两树影子长相等；如果路灯在点P1右面的适当位置（如图3所示的点P2处），那么大树的影长较短；如果路灯在点P1的左面，那么大树的影长较长.易错点4 不能正确画出物体的三视图例4 画出如图所示物体的三视图.【错解】如图所示【剖析】画立体图形的视图时，无论哪种视图都要求正对物体，因此两侧的平面在视图上变成线，因此主视图正确，而左视图错误，俯视图中将棱和顶点都漏画了，画三视图时，要把能看得见的边缘、棱、顶点都体现出来，看不到的轮廓线要画虚线.【正解】如图所示.易错点5 不能正确理解视图与几何体之间的关系例5 由相同的小正方体搭成的几何体的三视图如图所示，则搭成这个几何体的小正方体的个数是（）A．4 B．5 C．6 D．11【错解】D【剖析】已知由小正方体搭成的几何体中的三视图，判断该几何体小正方体的个数时，应该通过“长对正，高平齐，宽相等”来想象几何体的形状，易知该几何体由5个小正方体构成，其形状如图所示.千万不要误以为是图中正方形个数的叠加而误选D.【正解】B.考点分析聪明机智的喜羊羊把大家的智慧集中分类总结：考点一平行投影例1 （2013•达州）下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序正确的是（）A．（3）（1）（4）（2）B．（3）（2）（1）（4）C．（3）（4）（1）（2）D．（2）（4）（1）（3）分析：太阳由东升起的过程中，物体的影子投向西侧，且由长到短；太阳偏西，物体的影子也转投向东侧，且由短到长.西为（3），西北为（4），东北为（1），东为（2），所以将它们按时间先后顺序排列为（3）（4）（1）（2）．解：C.评注：因为一天之中，太阳东升西落，所以早晨物体的影子朝西，傍晚物体的影子朝东，但因为我国地处北半球，即使是夏天的正午，也由于太阳直射点的关系，物体的影子略微向北微移.故一天之中影子方向的变化顺序为：正西→北偏西→正北→北偏东→正东；一天之中影子的长度的变化规律为：长→短→长.考点二中心投影例2 （2013•太仓市二模）如图，S为一个点光源，照射在底面半径和高都为2m的圆锥体上，在地面上形成的影子为EB，且∠SBA=30°．（以下计算结果都保留根号）（1）求影子EB的长；（2）若∠SAC=60°，求光源S离开地面的高度．分析：（1）根据已知得出CH=HE=2m，进而得出HB的长，即可得出BE的长；（2）作CD ⊥SA于点D，首先求出CD的长进而得出∠DSC=45°，利用锐角三角函数关系得出SC的，评注：此题主要考查了解直角三角形的应用以及中心投影的知识，熟练应用锐角三角函数关系是解题关键．考点三三视图例3 （2013•梧州）如图，由四个正方体组成的图形，观察这个图形，不能得到的平面图形是（）A．B．C．D．分析：分别找出这个图形的主视图、俯视图、左视图，然后结合选项选出正确答案即可．该图形的主视图为：，俯视图为：，左视图为：，A、该图形为原图形的主视图，本选项正确；B、该图形为原图形的俯视图，本选项正确；C、该图形为原图形的左视图，本选项正确；D、观察原图形，不能得到此平面图形，故本选项错误.故选D．解：D.评注：本题考查了简单组合体的三视图，要求同学们掌握主视图是从物体的正面看得到的视图，俯视图是从物体的上面看得到的视图，左视图是从物体的左面看得到的视图．考点四由三视图判断几何体的形状例4 （2013•遵义）一个几何体的三视图如图所示，则这个几何体是（）A．B．C．D．分析：观察几何体的主视图和左视图，可知该几何体是柱体，而俯视图又是三角形，所以这个几何体为三棱柱，故选D.解：D.评注：本题考查了由三视图判断几何体的知识，主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形．结合图形，使用排除法来解答．考点五根据三视图计算几何体的侧面积或体积例5 （2013•宁夏）如图是某几何体的三视图，其侧面积（）A．6 B．4πC．6πD．12π分析：根据三视图判断，该几何体为圆柱，其高为3cm，底面直径为2cm，所以这个几何体的侧面积为πdh=2π×3=6π．故选C．解：C.评注：本题考查了由三视图判断几何体及圆柱侧面积的计算，解题的关键是首先判断出该几何体，然后利用其侧面积公式计算即可．考点六根据视图判断组成几何体的小正方形的个数例6 （2013•益阳）一个物体由多个完全相同的小正方体组成，它的三视图如图所示，那么组成这个物体的小正方体的个数为（）A．2个B．3个C．5个D．10个分析：本题是由组合几何体的主视图、左视图、俯视图来确定该几何体中小正方体的个数.结合主视图来看俯视图可以得到俯视图从左到右小正方体的个数依次为2，1，2，而这也正符合左视图的要求，所以组成这个物体的小正方体的个数为2+1+2=5个.解：C.评注：考查学生对三视图的掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．复习建议慢羊羊村长的忠告：1．重视本章内容与实际的联系，不要刻意追求对抽象概念的理解，多选择实例，借助实物模型，直观地、感性地认识，了解这些空间位置关系并把这种认识迁移到类似情形中. 2．注重立体图形与平面图形的相互转化问题，即“由物画图”（从长、宽、高三个维度画一个几何体的三视图）和“由图想物”（依据主视图、左视图和俯视图想象出对应的几何体）.。

用排除法选 D.
答案：D
感悟新知
知1－练
特别提醒
投影是生活中一种常见的现象，没有特殊说明时，本
章中的投影问题均指在平面上形成的投影 .
感悟新知
知识点 2 平行投影
1. 平行投影的定义
知2－讲
由平行的光线所形成的投影叫做平行投
影. 例如，太阳光可以看成平行光线，太阳光照射物体所
形成的影子属于平行投影 .
由一点(点光源)发出的光线所形成的投
影叫做中心投影 . 如物体在灯泡发出的光照射下形成的影
子就是中心投影 .
特别提醒： 中心投影的光源是点光源，它的光线相交于一
点，常见的点光源有手电筒、路灯、台灯等 .
感悟新知
知3－讲
示图
中心投影示意图如图 25.1 － 5 所示 .
感悟新知
知3－讲
2. 中心投影的性质
影线和投影面相同的情况下，不同形状的物体的投影一
般不同 .
感悟新知
知1－练
例1
下列现象不属于投影的是(
A. 皮影
B. 树影
C. 手影
D. 素描画
)
感悟新知
知1－练
解题秘方：紧扣“投影的定义”中的三个条件进
行识别 .
解：皮影、树影和手影都符合“用光线照射物体在某个
平面上得到的影子”，因此选项 A， B， C 都属于投影 .
洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面
的桌面后，在地面上形成如图 25.1 － 6 所示的圆环形阴
影．已知桌面直径为 1.2 m，桌面离地面 1 m，若灯泡离地
面 3 m，则地面圆环形阴影的面积是(
A. 0.324π m2
B. 0.288π m2

俯俯俯俯视视视视图图图图
小结
通过这节课学习你有什么收获？
作业 必做:课本85页B组2 选做:85页C组2 预习题:
第27.1 思考：什么是必然事件、不可能事件和随机事件
其余底各面面叫 ，相邻侧侧面面的交线叫做
，当侧侧棱棱垂
直于底面时，棱柱称为
例:如何画三棱柱和四棱柱的三视图
几何体
三种视图
主视图
长对正 高平齐 宽相等
俯视图
左视图
几何体
三种视图
主视图 俯视图
左视图
4.常见几何体的三视图
例1：如下图所示，是由一些小正方体搭成的几何 理
左视图
A．5
正视图
B．8
俯视图
C．7
D．6
5.如图，水平放置的下列几何体，主视图不是长方形的是 （B）
A Ａ．
BＢ．
CＣ．
DＤ．
6.观察下列几何体，主视图、左视图和俯视图都是矩形的 是（ B ）
A
B
C
D
A
B
C
D
7. 如图是一个几何体的三 视图，已知正视图和 左视图都是边长为 2的等边三角形，则这个 几 何体的全面积为
（A）2 ( B )3
(C)2 3
(D)(1 2 3)
8.长方体的主视图与俯视图如图所示，则这个长方体 的体积是（ ） A．52 B．32 C．24 D．9
3 4
2 4
9.补全下列物体的三种视图：
⑴
图左 视
⑵ 图左 视
10.如下图几何体，请画出这个物体的三种视图。
主主视主主视图视视图图图
左左左左视视视视图图图图
自学提纲
1.完成课本82页“主要知识回顾”

初三数学：投影与视图知识点归纳一、知识要点1、投影(1)投影:用光线照射物体，在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection)，照射光线叫做投影线，投影所在的平面叫做投影面。

(2)平行投影:有时光线是一组互相平行的射线，例如太阳光或探照灯光的一束光中的光线。

由平行光线形成的投影是平行投影(parallel projection).(3)中心投影:由同一点(点光源发出的光线)形成的投影叫做中心投影(center projection)。

(4)正投影:投影线垂直于投影面产生的投影叫做正投影。

注:物体正投影的形状、大小与它相对于投影面的位置有关。

2、三视图(1)三视图:是指观测者从三个不同位置观察同一个空间几何体而画出的图形。

将人的视线规定为平行投影线，然后正对着物体看过去，将所见物体的轮廓用正投影法绘制出来该图形称为视图。

一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图--能反映物体的前面形状，从物体的上面向下面投射所得的视图称俯视图--能反映物体的上面形状，从物体的左面向右面投射所得的视图称左视图--能反映物体的左面形三视图就是主视图、俯视图、左视图的总称。

(2)特点:一个视图只能反映物体的一个方位的形状，不能完整反映物体的结构形状。

三视图是从三个不同方向对同一个物体进行投射的结果，另外还有如剖面图、半剖面图等做为辅助，基本能完整的表达物体的结构。

一个视图只能反映物体的一个方位的形状，不能完整反映物体的结构形状。

三视图是从加速度学习网我的学习也要加速三个不同方向对同一个物体进行投射的结果，另外还有如剖面图、半剖面图等做为辅助，基本能完整的表达物体的结构。

二、经验之谈:多读两遍吧!有兴趣的同学可以多画图观察。

何体
的一般步骤
第26讲┃投影与视图
经典示例
例3 [2014·安徽模拟] 图26－11是由四个相同的小立方体
组成的立体图形的主视图和左视图，那么这个立体图形不可能 是 ．．． ( C )
图26 －11
第26讲┃投影与视图
图26－12
第26讲┃投影与视图
[解析 ] 由主视图可知，右侧小正方形是一层，所以不可能是 C 选项，左视图与四个立体图都吻合．故选 C.
图26－2
A．逐渐变短 B．逐渐变长 C．先变短后变长 D．先变长后变短
第26讲┃投影与视图
3．在一次数学活动课上，李老师带领学生去测教学楼的高度， 在阳光下，测得身高1.65米的黄丽同学BC的影长AB为 1.1米，与此同 时，测得教学楼DE的影长DF为12.1米． (1) 请你在图中画出此时教学楼DE在阳光下的投影DF ； (2) 请你根据已测得的数据，求出教学楼DE的高度(精确到0.1 米)．
图26－17
第26讲┃投影与视图
1．图 26－18是常用的一种圆顶螺杆，它的俯视图正确的是 ( B )
图26 －18
第26讲┃投影与视图
图26－19
第26讲┃投影与视图
2．图 26－20是一个正方体的表面展开图，则原正方体中与 “建”字所在的面相对的面上标的字是 ( D )
图26 －20
A．美 B．丽
核心练习
7．[ 2014·淮南模拟] 一个几何体的三视图如图26－ 14所示，则 这个几何体的形状是( A )
图26 －14
第26讲┃投影与视图
图26－15
第26讲┃投影与视图
8．[ 2014·永州] 若某几何体的三视图如图 26－16所示，则这个 几何体是( C )

长方形；
②正方体的一侧面与投影面平行，则该正方体有 4 个面的正投影是线段；
③圆锥的轴截面与投影面平行，则圆锥在投影面上的正投影是等腰三角
形．
A．3 个 B．2 个 C．1 个 D．0 个
自主学习
基础夯实
整合运用
思维拓展
第 14 页
九年级 数学 下册 沪科版
10．某图形的正投影是一条线段，则该图形可能是
自主学习
基础夯实
整合运用
思维拓展
第 16 页
九年级 数学 下册 沪科版
12．如图，长方体的一个底面 ABCD 在投影面 P 上，M，N 分别是侧棱 BF， CG 的中点，矩形 EFGH 与矩形 EMNH 的投影都是矩形 ABCD.设它们的面积 分别是 S1，S2，S，则 S1，S2，S 的关系是_S_2＞S1＝_S_(用“＞”“＝”或 “＜”连起来)．
九年级 数学 下册 沪科版
2．一个物体的正投影是圆，则这个物体不可能是 A．圆锥 B．正方体 C．圆柱 D．球
(B )
自主学习
基础夯实
整合运用
思维拓展
第6页
九年级 数学 下册 沪科版
3．下列投影中，正投影是__③④⑤__(只填序号)．
自主学习
基础夯实
整合运用
思维拓展
第7页
九年级 数学 下册 沪科版
【名师支招】求物体正投影的面积，先确定其正投影的形状，再根据题 意，求出相应线段长，从而得出答案．
自主学习
基础夯实
整合运用
思维拓展
第4页
九年级 数学 下册 沪科版
知识点 1：正投影的判断及作图
1．把一个正三棱柱如图摆放，光线由上向下照射此正三棱柱时的正投影

投影1．投影的概念一般地，用光线照射物体，在某个平面上得到的影子叫做投影．这时的照射光线叫做投射线，投影所在的平面叫做投影面．物体形成投影需要具备两个条件：一是有光线，二是有投影面． 【例1】老师利用幻灯投影仪将一个平行四边形投放在黑板左侧的墙面上，请说出其中的投影、投射线、投影面．分析：根据投影的概念来确定．解：墙面上的平行四边形是投影，投影仪发出的光线是投射线，投影面是墙面．2．平行投影由平行的光线所形成的投影是平行投影．太阳光可以看成平行光，所以在阳光下大树的影子，阳光照到窗户上在屋里所形成的窗户的影子都是平行投影． 太阳光与影子是日常生活中的常见现象，太阳光是沿直线传播的，若物体不透光，便被反射或吸收了，这样地面上或墙上没有被遮住的地方有太阳光，而被遮住的部分是黑暗的，知识要点 内容详解在同一时刻，平行投影的物高与影长的关系(1)如图①所示，等高的物体垂直于地面放置时，同一时刻，它们在太阳光下的影子一样长；(2)如图②所示，等长的物体平行于地面放置时，同一时刻，它们在太阳光下的影子一样长，并且都等于物体本身的长度；(3)如图③所示，不等高的物体垂直于地面放置时，同一时刻，它们在太阳光下的物高与影长的比相等，其理论依据是相似三角形对应边成比例．不同时刻，阳光下物体影子的方向和长度变化(北半球)方向变化：正西→正北→正东；长度变化：长→短→长 平行投影的特征投影线平行 平行投影的应用 (1)根据阳光下物体影子的大小、位置的变化判断时刻的不同； (2)已知一物体及其在阳光下的影子，可作出同一时刻另一物体在阳光下的影子；(3)根据物高与影长的关系求物高或影长平行投影是物体投影的一种，是在平行光线的照射下产生的．利用平行投影的知识解决阳光下物体影子的问题时，首先要看是否在同一时刻，在不同时刻，同一物体的平行投影方向与大小一般不同，在相同时刻，不同物体的物高与影长成比例，物体与影子上的对应点的连线是平行的就说明是平行投影．【例2】下面是一天中四个不同时刻两个建筑物的影子，将它们按时间的先后顺序进行排列为_________.解析：太阳在东方，刚升起不久，光线与地平面的夹角小，物体的影子应当长，且方向由东向西，所以C为早晨的影子；随着时间推移，到了上午影子渐短，影子方向北偏西，所以D是上午某时刻的影子；到了中午，物体的影子最短；而到了下午，物体的影子又逐渐变长，且方向为北偏东，所以A为下午某一时刻的影子；到了接近晚上时，太阳在西方，光线与地平面的夹角小，物体的影子长，且方向由西向东，所以B是接近晚上时的物体的影子．所以按时间的顺序进行排列为CDAB．答案：CDAB3．中心投影由同一点(点光源)发出的光线形成的投影叫做中心投影，那个点叫做投影中心．在中心投影的情况下，点光源、物体边缘的点以及它在影子上的对应点在同一条直线上．由于点光源的光线是发散的，所以灯光下物体的影长与物体的高度不一定成比例．(1)等高的物体垂直地面放置时，中心投影如下图：(2)等长的物体平行于地面放置时，中心投影如下图．在中心投影的情况下，还有这样一个重要结论：点光源、物体边缘的点以及它在影子上的对应点在同一条直线上，根据其中两个点，就可以确定第三个点的位置．【例3】如图所示，快下降到地面的某伞兵在灯光下的影子为AB．试确定灯源P的位置，并画出竖立在地面上木桩的影子EF.(保留作图痕迹，不要求写作法)分析：先连接伞兵的伞顶和脚与对应的影子的直线，两直线的交点即为点P，过点P作过木桩顶端的直线与地面的交点即为F.解：如图．4．正投影(1)正投影的概念在平行投影中，如果投射线垂直．．于投影面，那么这种投影叫做正投影．(如图所示)(2)正投影(投射线与投射面垂直的平行投影)的性质线段的正投影(分三种情况)①当线段AB平行于投影面P时，它的正投影是线段A1B1，这时AB＝A1B1；②当线段AB倾斜于投影面P时，它的正投影是线段A2B2，这时A2B2＜AB；③当线段AB垂直于投影面P时，它的正投影是一个点A3(B3)．如图．一般地，线段正投影有如下规律：平行长不变，倾斜长缩短，垂直成一点．平面图形的正投影(分三种情况)①当平面图形平行于投影面Q时，它的正投影与这个平面图形的形状、大小完全相同，即正投影与这个平面图形全等；②当平面图形倾斜于投影面Q时，平面图形的正投影的形状、大小发生变化，即会缩小，但不一定相似；③当平面图形垂直于投影面Q时，它的正投影是直线或直线的一部分．如图．一般地，平面图形正投影有如下规律：平行形不变，倾斜形改变，垂直成线段．正投影能如实地反映物体的形状和大小，画图也很方便，所以生产上的图样主要是用这种方法绘制．【例4－1】在一个晴朗的上午，皮皮拿着一块正方形木板在阳光下做投影实验，正方形木板在地面上形成的投影不可能是( )．解析：因是正方形在阳光下投影，正方形的对边互相平行，正方形的对边的影子应该平行且相等，所以A是不可能．答案：A(3)一般地，一个几何体在一个平面上的正投影是一个平面图形．几何体在一个平面上的正投影叫做这个几何体的视图．(4)作物体的正投影作物体的正投影，观察和思考的过程是这样的：把要作投影的物体放在投影面和观察者的中间，按观察者——物体——投影面的顺序摆好，由观察者的眼睛假想发出一束平行的投影线，这些投影线经过物体轮廓线上的顶点后，名称内容作空间点在投影面上的正投影过空间点作投影面的垂线，垂线与投影面的交点就是空间点在投影面上的正投影作直线在投影面上的正投影分别作出直线上两点在投影面上的正投影，然后过两投影点作直线即可行于投影面P且垂直于投影面Q，画出这个物体在两个投影面上的正投影．分析：此例考查的是物体在不同投影面上正投影的作图，特别要注意投影线的方向和物体在两个投影面上投影的基本图形．解：画出的正投影如图所示．正方体、金属丝在投影面P上的正投影是正方形A1B1C1D1，及折线A1E1F1C1；在投影面Q上的正投影为A2B2C2D2及A2B2C2.5．平行投影与中心投影的关系(1)联系①中心投影、平行投影都是研究物体的投影中的一种，只不过平行投影是在平行光线下所形成的投影．通常的平行光线有太阳光线，而中心投影是从一点发出的光线所形成的投影．②在平行投影中，同一时刻改变物体的方向和位置，其投影也跟着发生变化，不同物体和它们的影子之间存在着相似关系．在中心投影中，同一灯光下，改变物体的位置和方向，其投影也跟着发生变化，固定物体的位置和方向，改变灯光的位置，物体投影的方向和位置也要发生变化．(2)区别①太阳光线是平行的，因此在同一时刻下，太阳光下的影子长度都与物体高度成比例；灯光是发散的，灯光下的影子长度与物体高度不一定成比例．②同一时刻，太阳光下影子的方向总是在同一方向，而灯光下的影子可能在同一方向，也可能在不同方向．(3)如何判断物体的投影是在太阳光下还是在灯光下形成的：①太阳光线是平行光线，灯光光线是从一点发出的，如图所示．因此在判断是太阳光线还是灯光光线时，只要看光线呈什么形状就可得出结论．②如果已知影子，则先找两对物体与影子的对应点，然后连接它们找交点，由两条光线可大致判断它们是否平行，若平行则为太阳光线，若光线相交即为灯光光线．【例5－1】如图，小亮同学在晚上由路灯A 走向路灯B ，当他走到点P 时，发现他的身影顶部正好接触路灯B 的底部，这时他离路灯A 25米，离路灯B 5米，如果小亮的身高为1.6米，那么路灯高度为( )．A ．6.4米B ．8米C ．9.6米D ．11.2米解析：路灯A 可以看作点光源，根据点光源所形成的影子的特征可知路灯A 的顶端、小亮的头顶和路灯B 的底端位于一条直线上，设路灯的高度为x 米，根据三角形相似，得x 1.6＝305，解得x ＝9.6.故选C ． 答案：C【例5－2】(1)如图(1)是同一时刻的两棵树及其影子，请你在图中画出形成树影的光线，并判断它是太阳光线还是灯光的光线？若是灯光的光线，请确定光源的位置．(2)请判断如图(2)所示的两棵树的影子是在太阳光下形成的，还是灯光下形成的？并画出同一时刻旗杆的影子(用线段表示)．分析：本题是由树及其影子寻找光线，具体方法是过树的顶端及其影子的顶端作两条直线作为光线，若两条直线平行，则是太阳光线；若两条直线相交，则是灯光光线，其交点就是光源的位置．解：(1)图(1)是灯光的光线．原因是过一棵树的顶端及其影子的顶端作一条直线，再过另一棵树的顶端及其影子的顶端作一条直线，两直线相交，其交点就是光源的位置．(2)图(2)是太阳光的光线．原因是过一棵树的顶端及其影子的顶端作一条直线，再过另一棵树的顶端及其影子的顶端作一条直线，两直线平行．然后再过旗杆的顶端作一条与已知光线平行的直线，交地面于一点，连接这点与旗杆底端的线段就是旗杆的影子．6．中心投影的计算与太阳光相比，灯光对我们来说是近距离的，我们可以把灯光光线看成是四射的，而且同一物体对于同一光源在不同的地点影长也不相同．物体中心投影的大小是随着投影中心距离物体的远近变化而变化的．根据中心投影的性质结合相似三角形的知识，可以进行如求影长、物体的高度等的计算．【例6】如图，路灯(P 点)距地面8米，身高1.6米的小明从距路灯的底部(O 点)20米的A 点，沿AO 所在的直线行走14米到B 点时，身影的长度是变长了还是变短了？并求变长或变短了多少米．分析：观察图形可知，△MAC ∽△MOP ，△NBD ∽△NOP ，由相似三角形的性质分别求出影长MA ，NB ，比较即可．解：∵∠MAC ＝∠MOP ＝90°，∠AMC ＝∠OMP ，∴△MAC ∽△MOP . ∴MA MO ＝AC OP ，即MA 20＋MA ＝1.68.解得MA ＝5. 同理，由△NBD ∽△NOP ，可求得NB ＝1.5.∴MA －NB ＝5－1.5＝3.5.答：小明的身影变短了3.5米．7．投影的创新应用灵活地利用平行投影和中心投影的性质，结合具体问题构造出相似三角形，把具体问题转化为相似三角形的问题，可以解决生活中看似与投影无关的实际问题．在一次数学活动课上，李老师带领学生去测教学楼的高度．在阳光下，测得身高 1.65米的黄丽同学BC 的影长BA 为1.1米，与此同时，测得教学楼DE 的影长DF 为12.1米．请你根据已测得的数据，求出教学楼DE 的高度(精确到0.1米)．本题根据太阳光线是平行光线，得到△ABC∽△FDE，利用比例线段进行求解．∴BCAB＝DEFD，即1.651.1＝DE12.1，解得DE＝18.15≈18.2.答：教学楼DE的高度约为18.2米．【例7】检查视力时，规定人与视力表之间的距离应为5 m，现因房间两墙之间的距离为3 m，因此借助平面镜来解决房间小的问题，若使镜子呈现出完整的视力表，由平面镜成像原理作出了光路图如下图所示，其中视力表AB的上、下边沿A，B发出的光线经平面镜MM′的上下沿反射入眼睛C处，若视力表的全长为0.8 m，请计算出镜子至少为多少米？分析：根据平面镜成像原理，作出视力表AB关于平面镜MM′所成的像，由检查视力表的要求可知C到A′B′的距离CE应等于5 m，A′B′长为0.8 m.由中心投影的特征可知△CMM′≌△CA′B′，因此可利用相似三角形的性质求解．解：如上图，过点C作CD⊥MM′于点D，并延长交AB的像A′B′于点E.∵AB∥MM′∥A′B′，CE⊥A′B′，∴△CMM′∽△CA′B′，∴MM′A′B′＝CDCE.∵CD＝5－3＝2，CE＝5，A′B′＝0.8，∴MM′0.8＝25.∴MM′＝0.32(m)．答：镜子长至少应为0.32 m.。

例：长方体的主视图与俯视图如图所示， 则这个长方体的体积是 36 .
3. 常 见 几 何 体 的 三
视图常见几何体的 三视图பைடு நூலகம்知识点二 ：投影
4.平行投影
由平行光线形成的投影．
5.中心投影
由同一点(点光源)发出的光线形成的投影．
在平行投影中求影长，一般把实际问题 抽象到相似三角形中，利用相似三角形 的相似比，列出方程，通过解方程求出 的影长． 例：小明和他的同学在太阳下行走，小 明身高 1.4 米，他的影长为 1.75 米，他 同学的身高为 1.6 米， 则此时他的同学的 影长为 2 米．
第 25 讲
一、 知识清单梳理 知识点一：三视图 内 容 主视图：从正面看到的图形. 俯视图：从上面看到的图形. 左视图：从左面看到的图形.
视图与投影
关键点拨
1.三视图 2. 三 视 图 的 对 应 关
系
(1)长对正：主视图与俯视图的长相等，且相互对正； (2)高平齐：主视图与左视图的高相等，且相互平齐； (3)宽相等：俯视图与左视图的宽相等，且相互平行． 正方体：正方体的三视图都是正方形. 圆柱：圆柱的三视图有两个是矩形，另一个是圆. 圆锥：圆锥的三视图中有两个是三角形，另一个是圆. 球的三视图都是圆.

九下数学【投影与视图】知识点汇总，尖子生也未必全会为了同学们更好的掌握知识，王老师专门整理了初中所有科目的知识点，帮同学们把各个科目里最精华的部分归纳起来，并且是准备了一些真题，让大家在复习后可以刷题巩固。

今天和大家分享的是九下数学【投影与视图】知识点汇总，有需要的同学可以做起来了。

初三数学语文英语初三年级语文、数学、英语学习考试资料分享，名师课程免费学习，初中生和家长都在关注！公众号投影与视图A）三视图·主视图——从正面看到的图左视图——从左面看到的图俯视图——从上面看到的图·画物体的三视图时,要符合如下原则:大小：长对正,高平齐,宽相等.·虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.B）投影·物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影现象.·太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影。

·在同一时刻,物体高度与影子长度成比例.·物体的三视图实际上就是该物体在某一平行光线(垂直于投影面的平行光线)下的平行投影.·探照灯,手电筒,路灯,和台灯的光线可以看成是从一点出发的光线,像这样的光线所形成的投影称为中心投影·皮影和手影都是在灯光照射下形成的影子.它们是中心投影。

C）视点、视线、盲区的定义以及在生活中的应用。

. 眼睛所在的位置称为视点，. 由视点发出的光线称为视线，. 眼睛看不到的地方称为盲区一、重点清单1. 明确常见几何体的展开图，通过几何体的展开与折叠，体会平面图形与立体图形之间的关系。

2. 三视图是中考必考热点，一般考查由物体确定视图，由视图确定物体较少见，抓住三视图从三个方向观看这个特点，发挥空间想象力，便可做出准确判断。

二、提分策略1. 图形的展开与折叠。

常见几何体的展开与折叠：①棱柱的平面展开图是由两个相同的多边形和一些长方形组成，按棱柱表面不同的棱剪开，可能得到不同组合方式的平面展开图，特别关注正方体的表面展开图；②圆柱的平面展开图是由两个相同的圆形和一个长方形连成的；③圆锥的平面展开图是由一个圆形和一个扇形组成的。

第25章 投影与视图
25.2 三视图
知识点 三视图
“横看成岭侧成峰,远近高低各不同.”这是宋代大文豪苏轼写 下的千古流传的名句.从数学的角度看,苏轼从不同角度看到了庐山 多姿多彩的风貌,写下了他心中的庐山的美.
知识点 三视图的画法
在工程设计过程中,常常需要把三维形体用二维平面图形表达在 纸面上,要达到这个目的,我们可以靠投影法来实现.投影法就是用正 投影的方法在平面上画出机械零件的三种视图.
学科素养课件
新课标沪科版·数学 九年级下投影
北京故宫里的日晷闻名世界,是我国光辉灿烂文化的瑰宝, 它是我国古代利用日影测定时刻的仪器,它是由“晷面”与 “晷针”组成的,当太阳光照在日晷中轴上产生投影时,晷针的 影子就会投向晷面,随着时间的推移,晷针的影子在晷面上慢慢 移动,聪明的古人以此来显示时刻.
知识点 投影与平行投影
太阳光线可以看成是平行线,同一时刻两棵树所形成的影 子和它们自身的高度成正比例.
知识点 中心投影
手影不需要复杂设备,只要有灯光,就可以通过手势的变化, 做出兔子、狗、猫等小动物的影子,简单又好玩.
知识点 中心投影
中心投影和平行投影的联系和区别:
光线
区别
物体与投影面平行 时的投影
联系
平行投影 平行的投影线
全等
都是物体在光线的照射
中心投影
从一点发出的投 影线
放大(位似变换)
下,在某个平面内形成的 影子(即都是投影)
知识点 正投影与视图
光线由上往下照射一个长方体茶叶盒(如图所示),它的 上、下底面的正投影是边长为6 cm的正方形.
知识点 正投影与视图
正投影的前提条件是投影线垂直于投影面.
知识点 由三视图确定几何体的形状

问题探究
当小棒与太阳光线平行时，它们的影子形成一个点. 当小棒与投影面平行时，它们的影子的大小和形状与原物全等
问题探究
（2）思考固定投影面，改变三角形纸片的摆放位置和方向，它 的影子分别发生了什么变化？
当三角形纸片与太阳光线平行时，它们的影子形成一条线. 当三角形纸片与投影面平行时，它们的影子的大小和形状与原 三角形全等.画出下面 几何体的三视图：
主视图 左视图
俯视图
※做一做
右图是底面
为等腰直角三角
形的三棱柱的俯
视图，尝试画出 1 它们的主视图和
左视图。
主视图
左视图
2
主视图
左视图
※做一做
右图是底
面为等腰梯形
四棱柱的俯视
图，尝试画出
它们的主视图
1
和左视图。
主视图
2
主视图
左视图 左视图
※随堂练习
投影定义：物体在光线的照射下，在某个平面内（如在地 面或墙壁上）形成的影子，这就是投影.这时，光线叫做投射线， 影子（也叫投影）所在的平面叫做投影面．
问题探究
探究一
观察下列图片,你认为太阳光线有什么特征？
太阳离我们非常遥远，太阳光线可以看成平行光线，像 这样的由平行的投射线（如太阳光线）所形成的投影叫做平 行投影。
第28章 投影与视图
创设情景
活动一：教师展示丰富的关于阳光与影子的实例.日晷是我 国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成， 当太阳光照在日晷上时，晷针的影子就会投向晷面，随着时间 的推移，晷针的影子在晷面上慢慢移动，聪明的古人以此来显 示时刻．
创设情景
活动二： 影子随处可见，请问你能举出生活中关于物体 在光线的照射下形成影子的实例吗？