下载文档原格式
计算机图形学基础课后答案1. 什么是计算机图形学？计算机图形学是研究如何使用计算机表示、生成、操作和渲染图像的科学和技术领域。
它涵盖了很多方面，包括图像的数学表示、3D建模与渲染、光线追踪、图像处理、动画等。
计算机图形学通常用于创建和处理图像、动画和视觉效果。
2. 计算机图形学的应用领域有哪些？计算机图形学的应用领域非常广泛，包括但不限于以下几个方面：1.游戏开发：计算机图形学在游戏开发中起着非常重要的作用，可以实现逼真的游戏场景和角色设计。
2.电影和电视广告制作：计算机图形学在电影和电视广告中被广泛应用，可以实现令人惊叹的特效和视觉效果。
3.虚拟现实和增强现实：计算机图形学可以用于创建虚拟现实和增强现实的场景和效果，使用户可以沉浸在虚拟环境中。
4.医学图像处理：计算机图形学在医学图像处理中可以用于大脑扫描、X光片分析等，帮助医生进行诊断。
5.工程设计：计算机图形学可以用于工程设计中的建模和渲染，例如建筑设计、汽车设计等。
6.数据可视化：计算机图形学可以用于将数据以图形的方式展示，帮助人们理解和分析复杂的信息。
3. 什么是光栅化？光栅化是计算机图形学中将连续的几何形状转换为离散数据的过程。
在光栅化过程中，3D对象被映射到2D屏幕上的像素阵列中，以便显示和渲染。
在光栅化过程中，首先将3D对象的几何形状进行投影，以确定如何在2D屏幕上呈现。
然后，使用扫描线算法或边界填充算法等方法，将几何形状转换为像素阵列，并确定像素的颜色和亮度。
光栅化是计算机图形学中的关键步骤，它可以使计算机能够实时处理和显示图形，并在屏幕上呈现各种特效和细节。
4. 什么是图形渲染管线？图形渲染管线是计算机图形学中的一个核心概念，它描述了图形生成和渲染的过程。
图形渲染管线通常包括几个关键阶段，每个阶段都负责图形处理的一个特定方面。
典型的图形渲染管线包括以下阶段：1.顶点输入：将3D对象的顶点数据作为输入，其中包括顶点的位置、法线、颜色等信息。
计算机图形学基础教程孔令德课后答案【篇一：大学计算机图形学课程设】息科学与工程学院课程设计任务书题目：小组成员：巴春华、焦国栋成员学号：专业班级：计算机科学与技术、2009级本2班课程：计算机图形学指导教师：燕孝飞职称：讲师完成时间： 2011年12 月----2011年 12 月枣庄学院信息科学与工程学院制2011年12 月20日课程设计任务书及成绩评定12【篇二：计算机动画】第一篇《计算机图形学》小结《计算机图形学》第一章：从计算机的辅助设计，艺术，和虚拟现实技术等方面介绍了计算机图形学的应用领域；接下了解了有关计算机图形学的概念和发展情况和图新显示器的发展和阴极射线管光栅扫描显示等的工作原理；最后介绍了图形学的最新技术。
第二章：介绍了面向对象程序设计，visual c++下的编程，主要基于mfc的编程，更重要的是绘制图形的方法。
第三章：图形的扫描与转换：主要分两部分，一是：直线，圆，和椭圆的扫描和转换中的一些重要而经典的算法。
二是：反走样技术，尤其，直线距离加权反走样的算法。
第四章：主要介绍了多边形填充，有多边形的的概述到有效边表填充，边缘填充，最后区域填充的原理和算法第五章：二维变换和裁剪：主要介绍了裁剪的方法：cohen sutherland算法是最著名的算法，除此之外还有重点分割裁剪算法，梁友栋——barsky算法。
第二篇计算机动画2.1计算机动画的概念：计算机动画是指采用图形与图像的处理技术，借助于编程或动画制作软件生成一系列的景物画面，其中当前帧是前一帧的部分修改。
计算机动画是采用连续播放静止图像的方法产生下图1-1几幅图片就是用计算机动画（a）（b）（c）（d）图2-1 计算机动画示例2.2 计算机动画的发展：计算机动画的发展大致分为三阶段：第一阶段：初出茅庐阶段：20世纪60年代初。
第一部计算机动画片诞生，之后大约20年，二维动画是计算机动画研究的重心，同时，二维动画也被应用于教学演示和辅助传统的动画片制作。
第一章1、试述计算机图形学研究的基本内容？答：见课本P5-6页的1.1.4节。
2、计算机图形学、图形处理与模式识别本质区别是什么？请各举一例说明。
答：计算机图形学是研究根据给定的描述，用计算机生成相应的图形、图像，且所生成的图形、图像可以显示屏幕上、硬拷贝输出或作为数据集存在计算机中的学科。
计算机图形学研究的是从数据描述到图形生成的过程。
例如计算机动画制作。
图形处理是利用计算机对原来存在物体的映像进行分析处理，然后再现图像。
例如工业中的射线探伤。
模式识别是指计算机对图形信息进行识别和分析描述，是从图形（图像）到描述的表达过程。
例如邮件分捡设备扫描信件上手写的邮政编码，并将编码用图像复原成数字。
3、计算机图形学与CAD、CAM技术关系如何？答：见课本P4-5页的1.1.3节。
4、举3个例子说明计算机图形学的应用。
答：①事务管理中的交互绘图应用图形学最多的领域之一是绘制事务管理中的各种图形。
通过从简明的形式呈现出数据的模型和趋势以增加对复杂现象的理解，并促使决策的制定。
②地理信息系统地理信息系统是建立在地理图形基础上的信息管理系统。
利用计算机图形生成技术可以绘制地理的、地质的以及其它自然现象的高精度勘探、测量图形。
③计算机动画用图形学的方法产生动画片，其形象逼真、生动，轻而易举地解决了人工绘图时难以解决的问题，大大提高了工作效率。
5、计算机绘图有哪些特点？答：见课本P8页的1.3.1节。
6、计算机生成图形的方法有哪些？答：计算机生成图形的方法有两种：矢量法和描点法。
①矢量法：在显示屏上先给定一系列坐标点，然后控制电子束在屏幕上按一定的顺序扫描，逐个“点亮”临近两点间的短矢量，从而得到一条近似的曲线。
尽管显示器产生的只是一些短直线的线段，但当直线段很短时，连成的曲线看起来还是光滑的。
②描点法：把显示屏幕分成有限个可发亮的离散点，每个离散点叫做一个像素，屏幕上由像素点组成的阵列称为光栅，曲线的绘制过程就是将该曲线在光栅上经过的那些像素点串接起来，使它们发亮，所显示的每一曲线都是由一定大小的像素点组成的。
《计算机图形学》习题与解答第一章概述1. 试描述你所熟悉的计算机图形系统的硬软件环境。
计算机图形系统是计算机硬件、图形输入输出设备、计算机系统软件和图形软件的集合。
例如：计算机硬件采用PC、操作系统采用windows2000，图形输入设备有键盘、鼠标、光笔、触摸屏等，图形输出设备有CRT、LCD等，安装3D MAX图形软件。
2. 计算机图形系统与一般的计算机系统最主要的差别是什么？3. 图形硬件设备主要包括哪些？请按类别举出典型的物理设备?图形输入设备：鼠标、光笔、触摸屏和坐标数字化仪，以及图形扫描仪等。
图形显示设备：CRT、液晶显示器（LCD）等。
图形绘制设备：打印机、绘图仪等。
图形处理器：GPU（图形处理单元）、图形加速卡等等。
4. 为什么要制定图形软件标准？可分为哪两类？为了提高计算机图形软件、计算机图形的应用软件以及相关软件的编程人员在不同计算机和图形设备之间的可移植性。
图形软件标准通常是指图形系统及其相关应用系统中各界面之间进行数据传送和通信的接口标准，另外还有供图形应用程序调用的子程序功能及其格式标准。
5. 请列举出当前已成为国际标准的几种图形软件标准，并简述其主要功能。
（1）CGI(Computer Graphics Interface)，它所提供的主要功能集包括控制功能集、独立于设备的图形对象输出功能集、图段功能集、输入和应答功能集以及产生、修改、检索和显示以像素数据形式存储的光栅功能集。
（2）GKS(Graphcis Kernel System)，提供了应用程序和图形输入输出设备之间的接口，包括一系列交互和非交互式图形设备的全部图形处理功能。
主要功能如下：控制功能、输入输出功能、变换功能、图段功能、询问功能等。
6. 试列举计算机图形学的三个应用实例。
（1）CAD/CAM（2）VISC（3）VR.第二章光栅图形学1. 在图形设备上如何输出一个点？为输出一条任意斜率的直线，一般受到哪些因素影响？若图形设备是光栅图形显示器，光栅图形显示器可以看作是一个像素的矩阵，光栅图形显示器上的点是像素点的集合。
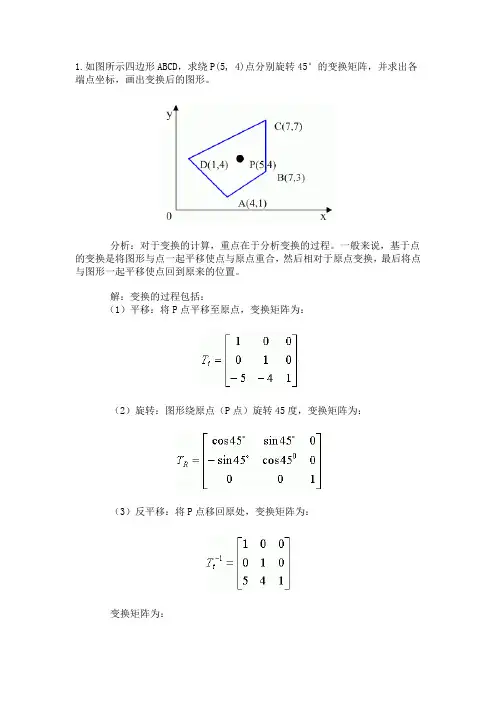
1.如图所示四边形ABCD，求绕P(5, 4)点分别旋转45°的变换矩阵，并求出各端点坐标，画出变换后的图形。
分析：对于变换的计算，重点在于分析变换的过程。
一般来说，基于点的变换是将图形与点一起平移使点与原点重合，然后相对于原点变换，最后将点与图形一起平移使点回到原来的位置。
解：变换的过程包括：
（1）平移：将P点平移至原点，变换矩阵为：
（2）旋转：图形绕原点（P点）旋转45度，变换矩阵为：
（3）反平移：将P点移回原处，变换矩阵为：
变换矩阵为：
变换过程为：
7.2 假定一空间直线AB的两端点坐标为A(0, 0, 0)和B(2, 2, 2),试写出绕AB旋转30o的三维复合变换矩阵。
分析：三维空间中绕任意轴旋转是较为复杂的过程。
在经过平移使轴通过原点之后，通常需要经过两次旋转才能使轴与某个坐标轴重合：第一次将轴与某个坐标轴构造成一个面，并将这个面绕这个坐标轴旋转到某个坐标平面内，然后在该坐标平面中通过旋转使轴与该平面中的任意一个坐标轴重合；在绕轴旋转之后需要反旋转使轴回到原来的方向，最后反平移使轴回到原始的位置。
这里需要注意旋转角度的正负以及角度值的确定。
解：变换步骤如下
(1) 将ABB'绕x轴逆时针旋转α角，则AB旋转到xoz平面上。
(2)将OB绕y轴顺时针旋转β角，则OB旋转到z轴上。
(3)此时AB轴与z轴重合，绕AB轴的旋转转换为绕z轴的旋转。
(4)最后，求TRx，TRy的逆变换，回到AB原来的位置。
最后的变换矩阵是这5个矩阵相乘的形式：。
1.列举计算机图形学的主要研究内容。
计算机中图形的表示方法、图形的计算、图形的处理和图形的显示。
图形硬件、图形标准、图形交互技术、光栅图形生成算法、曲线曲面造型、实体造型、真实感图形计算与显示算法，以及科学计算可视化、计算机动画、自然景物仿真、虚拟现实等。
2.常用的图形输出设备是什么？显示器（CRT、LCD、等离子）、打印机、绘图仪等。
2.常用的图形输入设备是什么？键盘、鼠标、跟踪球、空间球、数据手套、光笔、触摸屏、扫描仪等。
3.列出3种图形软件工具。
AutoCAD、SolidWorks、UG、ProEngineer、CorelDraw、Photoshop、PaintShop、Visio、3DMAX、MAYA、Alias、Softimage等。
错误：CAD4.写出|k|>1的直线Bresenham画线算法。
dddd设直线方程为：y=kx+b，即x=(y-b)/k，有x i+1=x i+(y i+1-y i)/k=x i+1/k，其中k=dy/dx。
因为直线的起始点在象素中心，所以误差项d的初值d0=0。
y下标每增加1，d的值相应递增1/k，即d＝d＋1/k。
一旦d≥1，就把它减去1，这样保证d 在0、1之间。
●当d≥0.5时，最接近于当前象素的右上方象素(x i+1,y i+1)，x方向加1，d减去1；●而当d<0.5时，更接近于上方象素(x i,y i+1)。
为方便计算，令e=d－0.5，e的初值为－0.5，增量为1/k。
●当e≥0时，取当前象素(x i,y i)的右上方象素(x i+1,y i+1)，e减小1；●而当e<0时，更接近于上方象素(x i,y i+1)。
void Bresenhamline (int x0,int y0,int x1, int y1,int color){ int x, y, dx, dy;float k, e;dx = x1－x0, dy = y1－y0, k=dy/dx;e=－0.5, x=x0, y=y0;for (i=0; i≤dy; i++){ drawpixel (x, y, color);y=y+1，e=e+1/k;if (e≥0){ x++, e=e－1;}}}4.写出|k|>1的直线中点画线算法。
1.列举计算机图形学的主要研究内容。
计算机中图形的表示方法、图形的计算、图形的处理和图形的显示。
图形硬件、图形标准、图形交互技术、光栅图形生成算法、曲线曲面造型、实体造型、真实感图形计算与显示算法，以及科学计算可视化、计算机动画、自然景物仿真、虚拟现实等。
2.常用的图形输出设备是什么？
显示器（CRT、LCD、等离子）、打印机、绘图仪等。
2.常用的图形输入设备是什么？
键盘、鼠标、跟踪球、空间球、数据手套、光笔、触摸屏、扫描仪等。
3.列出3种图形软件工具。
AutoCAD、SolidWorks、UG、ProEngineer、CorelDraw、Photoshop、PaintShop、Visio、3DMAX、MAY A、Alias、Softimage等。
错误：CAD
4.写出|k|>1的直线Bresenham画线算法。
d
d
d
d
设直线方程为：y=kx+b，即x=(y-b)/k，有x i+1=x i+(y i+1-y i)/k = x i+1/k，其中k=dy/dx。
因为直线的起始点在象素中心，所以误差项d的初值d0=0。
y下标每增加1，d的值相应递增1/k，即d＝d＋1/k。
一旦d≥1，就把它减去1，这样保证d在0、1之间。
●当d≥0.5时，最接近于当前象素的右上方象素(x i+1,y i+1)，x方向加1，d减
去1；
●而当d<0.5时，更接近于上方象素(x i,y i+1)。
为方便计算，令e=d－0.5，e的初值为－0.5，增量为1/k。
●当e≥0时，取当前象素(x i,y i)的右上方象素(x i+1,y i+1)，e减小1；
●而当e<0时，更接近于上方象素(x i,y i+1)。
void Bresenhamline (int x0,int y0,int x1, int y1,int color)
{ int x, y, dx, dy;
float k, e;
dx = x1－x0, dy = y1－y0, k=dy/dx;
e=－0.5, x=x0, y=y0;
for (i=0; i≤dy; i++)
{ drawpixel (x, y, color);
y=y+1，e=e+1/k;
if (e≥0)
{ x++, e=e－1;}
}
}
4.写出|k|>1的直线中点画线算法。
构造判别式：d=F(M)=F(x p+0.5,y p+1)=a(x p+0.5)+b(y p+1)+c
●当d<0，M在Q点左侧，取右上方P2为下一个象素；
●当d>0，M在Q点右侧，取上方P1为下一个象素；
●当d=0，选P1或P2均可，约定取P1为下一个象素；
增量计算：
●若d≥0，取正上方象素P1 (x p, y p+1)，要判下一个象素位置，应计算
d1= F(M1)=F(x p+0.5, y p+2)=a(x p+0.5)+b(y p+2)+c=d+b
增量为b。
●若d<0，取右上方象素P2 (x p+1, y p+1)。
要判断再下一象素，则要计算
d2= F(M2)=F(x p+1.5, y p+2)=a(x p+1.5)+b(y p+2)+c=d+a+b
增量为a＋b。
●d的初值d0=F(x0+0.5, y0+1)=F(x0, y0)+0.5a+b =0.5a+b
用2d代替d的算法：
void Midpoint Line (int x0,int y0,int x1, int y1,int color)
{ int a, b, d1, d2, d, x, y;
a=y0-y1, b=x1-x0, d=a+2*b;
d1=2*b, d2=2*(a+b);
x=x0, y=y0;
drawpixel(x, y, color);
while (y<y1)
{ if (d<0) {x++, y++, d+=d2; }
else {y++, d+=d1;}
drawpixel (x, y, color);
} /* while */
} /* mid PointLine */
5.写出下图中多边形的边表（新边表）。
5.写出下图中多边形的边表（新边表）。
6. 写出以原点为球心，半径为2的球体的旋转生成算法。
算法一：以点为基本图元 for(j=0;j<72;j++)
{
绕Y 轴逆时针旋转5度，⎥⎥⎥
⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎣
⎡-=1000036cos 036sin
0010
036sin
036cos π
π
π
πy R ；
//画出半圆
画点(0,2,0)； for(i=0;i<36;i++)
{
将当前点绕Z 轴逆时针旋转5度，⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎣
⎡-=100001000036cos 36sin
0036
sin
36cos π
π
π
πz R ；
画变换后的点⎥⎥⎥⎥
⎦
⎤⎢⎢⎢⎢⎣⎡⋅⋅=⎥⎥⎥⎥
⎦
⎤
⎢⎢⎢⎢⎣⎡'''10201z
y R R z y x ；}}
算法二：以圆弧为基本图元 for(j=0;j<72;j++)
{ 绕Y 轴逆时针旋转5度，⎥⎥⎥
⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎣⎡-=1000
036cos 036sin
0010
036sin
036cos π
π
π
πy R ；
画半圆；}。
