MatLab在有限元刚度矩阵推导中的应用

Matlab在线性立体有限元分析中的应用摘要：Matlab具有强大的运算功能，本文以线性四面体元为例，详细介绍MATLAB在刚度矩阵推导，静力结构等有限元分析中的具体应用，编写了刚度矩阵，引用边界条件以及后处理各步骤的程序，该方法可以进一步推广到其他单元甚至更复杂的结构分析中。

关键词：Matlab 有限元刚度矩阵0 引言Matlab是美国MathWork公司开发的用于数值计算，算法研究，建模仿真，实时实现的理想集成环境，因其完整的专业体系和强大的运算功能已广泛应用于工业、电子、信号处理、控制、建筑、教学等各个领域。

有限元是近代数值计算最有效方法之一．有限元法的基础是单元划分以及刚度矩阵的推导，目前，有限元分析已有一个相对固定的模式，而烦琐、复杂的矩阵运算、微分、积分是分析过程中的主要内容．通常，这种矩阵运算是由手工来完成的，工作量大，而且极易出错．利用MatLab丰富的符号运算功能，构建有限单元模型，完成刚度矩阵推导及后处理过程中的运算，不但速度快，而且准确性高。

利用Matlab编写函数M文件并在运算过程中调用，能够依据具体问题对模型进行分析运算，并能在类似问题中得到推广应用。

1 线性四面体有限元分析中的基本方程线性四面体（立体）元（liner tetrahedral(solid)element）是既有局部坐标又有总体坐标的三维有限元，用线性函数描述。

线性四面体元的系数有弹性模量E 和泊松比ν，每个线性四面体与元有四个节点并且每个节点有三个自由度，如图1所示。

这四个节点的总体坐标用111x （,y ,z ）、222x （,y ,z ）、333x （,y ,z ）、444x （,y ,z ）表示。

单元刚度矩阵给定如下：[][][][]T k V B D B = （1.1）式中V 是单元的体积，由下式给出：11122233344411611x y z x y z V x y z x y z =（1.2）图1 线性四面体（立体）元 矩阵[]B 由下式（1.3）确定：[]312431243124331122443311224431122000000000000000000000000000000000x x x x y y y y z z z z y x y x y x y x z y z y z y z y zxzxN N N N N N N N N N N N B N N N N N N N N N N N N N N N N N N N N N ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂3440zxzx N N N ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦在方程（1.3）中，形函数由下式给出：111111()6N x y z V αβγδ=+++222221()6N x y z V αβγδ=+++333331()6N x y z Vαβγδ=+++444441()6N x y z Vαβγδ=+++ （1.4）在方程（1.1）中，矩阵[]D 由下式（1.5）确定：[]10001000100012000002(1)(12)120000021200002E D νννννννννννννν-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥=⎢⎥+-⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦2 建立的Matlab 函数TetrahedronElementV olume(x1,y1,z1,x2,y2,z2,x3,y3,z3,x4,y4,z4),该函数根据给出的第一个节点坐标111(,,)x y z ，第二个节点坐标222(,,)x y z ，第三个节点坐标333(,,)x y z 和第四个节点坐标444(,,)x y z 返回单元的体积。

function y = SpringElementForces(k,u)
%SpringElementForces This function returns the element nodal force
%
vector given the element stiffness matrix k
%
and the element nodal displacement vector u.
2019/11/28
§2-1 弹簧元
u1=U(1:2); f1=SpringElementForces(k1,u1);
f1 = -15.0000 15.0000
u2=U(2:3); f2=SpringElementForces(k2,u2);
f2 = -15.0000 15.0000
12
§3-1 弹簧元
%
modulus of elasticity E, cross-sectional
%
area A, and length L. The size of the
%
element stiffness matrix is 2 x 2.
y = [E*A/L -E*A/L ; -E*A/L E*A/L];
2019/11/28
3.1 单元刚度矩阵的形成
function y = SpringElementStiffness(k)
%SpringElementStiffness This function returns the element stiffness %matrix for a spring with stiffness k. %The size of the element stiffness matrix is 2 x 2.

一、概述有限元方法是工程学和科学领域中常用的数值分析工具，用于求解复杂的结构力学问题。

在有限元分析中，刚度矩阵是一个重要的概念，它描述了结构的刚度性质，并可以用于求解结构的位移、应力和应变分布。

MATLAB是一款功能强大的数学软件，它提供了丰富的工具和函数，可以用于编程求解有限元刚度矩阵。

本文将介绍如何使用MATLAB编程求解有限元刚度矩阵，并给出详细的步骤和代码示例。

二、有限元刚度矩阵的理论基础有限元分析的基本思想是将一个复杂的结构分解成许多小的单元，每个单元都可以用简单的数学方程描述。

在有限元分析中，每个单元都有一个刚度矩阵，它描述了单元的刚度性质。

结构的总刚度矩阵可以通过合并所有单元的刚度矩阵得到。

总刚度矩阵可以用于求解结构的位移、应力和应变分布，是有限元分析的核心之一。

三、MATLAB编程求解有限元刚度矩阵的步骤在MATLAB中，可以通过以下步骤编程求解有限元刚度矩阵：1. 定义结构的几何形状和材料性质，确定结构的边界条件和加载条件。

2. 将结构分解成有限元单元，根据单元的几何形状和材料性质建立单元的刚度矩阵。

3. 合并所有单元的刚度矩阵，得到结构的总刚度矩阵。

4. 根据边界条件和加载条件，求解结构的位移。

5. 根据结构的总刚度矩阵和位移，计算结构的应力和应变分布。

四、MATLAB编程求解有限元刚度矩阵的代码示例以下是一个简单的MATLAB代码示例，用于求解一维弹簧元的刚度矩阵：```MATLAB定义弹簧元的长度和弹性模量L = 1;E = 1;计算弹簧元的刚度矩阵k = E * A / L;K = [k, -k; -k, k];```以上代码示例中，我们首先定义了弹簧元的长度L和弹性模量E，然后通过公式计算了弹簧元的刚度矩阵K。

这是一个简单的一维情况，实际工程中可能涉及到更复杂的二维、三维情况，但基本的求解步骤是相似的。

五、总结MATLAB是一个强大的数学软件，可以用于编程求解有限元刚度矩阵。

工程构件受力和刚度计算的MATLAB分析法工程构件受力和刚度计算是结构设计和分析中非常重要的一部分，它涉及到对构件受力和刚度进行计算的理论基础和方法。

而MATLAB作为一种广泛应用于科学计算和工程领域的软件工具，其强大的数学和算法功能使得其成为进行工程构件受力和刚度计算的理想选择。

在进行工程构件的受力和刚度计算时，首先需要建立合适的受力与形变模型。

其次，需要根据受到的外力和形变条件，建立构件的力平衡方程和形变方程。

最后，利用MATLAB的数值计算功能，对这些方程进行求解，以获得构件的受力和刚度。

在进行受力计算时，常用的方法包括静力方法、动力方法和有限元方法等。

其中，静力方法基于构件的受力平衡条件，通过求解受力方程组得到构件的受力分布。

动力方法则基于构件的振动特性，利用动力学方程求解得到构件的受力状态。

而有限元方法则是将结构离散为有限数量的单元，通过求解单元的刚度矩阵和载荷矩阵得到整个结构的受力情况。

在进行刚度计算时，常用的方法包括弹性刚度法和刚度矩阵法等。

其中，弹性刚度法是基于构件材料的弹性行为，通过求解弹性力学方程得到构件的刚度。

刚度矩阵法则是将结构离散为有限数量的节点，通过求解节点的刚度矩阵和载荷矩阵得到整个结构的刚度。

利用MATLAB进行工程构件受力和刚度计算时，用户可以编写自定义的函数和脚本来实现对受力和刚度方程的求解。

MATLAB提供了丰富的数学函数和工具箱，包括线性方程组的求解、特征值和特征向量的计算、矩阵运算等功能，这些功能可以大大简化受力和刚度计算的过程。

用户可以使用MATLAB的函数库来进行构件的受力和刚度计算，也可以根据实际需要进行函数的编写和修改。

总之，MATLAB分析法在工程构件受力和刚度计算中具有广泛的应用前景。

它通过提供强大的数学和算法功能，简化了受力和刚度计算的过程，并且可以根据实际需要进行函数的编写和修改。

工程师和科研人员可以利用MATLAB进行受力和刚度计算，以实现对工程构件的准确设计和分析。

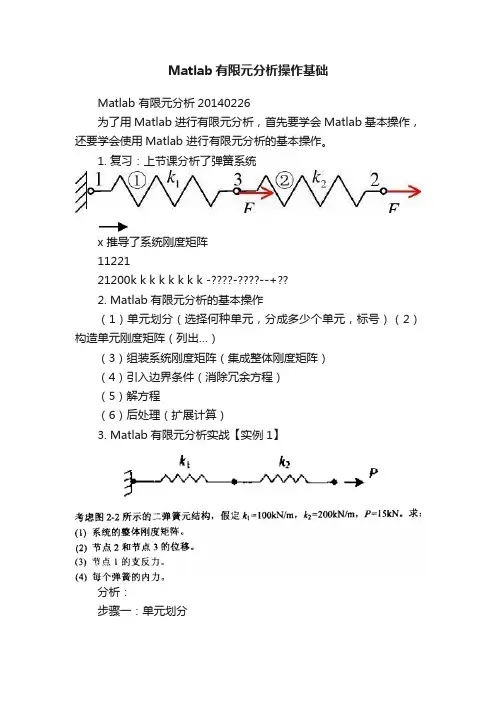
Matlab有限元分析操作基础Matlab 有限元分析20140226为了用Matlab 进行有限元分析，首先要学会Matlab 基本操作，还要学会使用Matlab 进行有限元分析的基本操作。

1. 复习：上节课分析了弹簧系统x 推导了系统刚度矩阵1122121200k k k k k k k k ----+??2. Matlab有限元分析的基本操作（1）单元划分（选择何种单元，分成多少个单元，标号）（2）构造单元刚度矩阵（列出…）（3）组装系统刚度矩阵（集成整体刚度矩阵）（4）引入边界条件（消除冗余方程）（5）解方程（6）后处理（扩展计算）3. Matlab有限元分析实战【实例1】分析：步骤一：单元划分步骤二：构造单元刚度矩阵>>k1=SpringElementStiffness(100) >>…?步骤三：构造系统刚度矩阵a) 分析SpringAssemble库函数function y = SpringAssemble(K,k,i,j)% This function assembles the element stiffness% matrix k of the spring with nodes i and j into the % global stiffness matrix K.% function returns the global stiffness matrix K% after the element stiffness matrix k is assembled. K(i,i) = K(i,i) + k(1,1);K(i,j) = K(i,j) + k(1,2);K(j,i) = K(j,i) + k(2,1);K(j,j) = K(j,j) + k(2,2);y = K;b) K是多大矩阵？今天的系统刚度矩阵是什么？因为11221212k kk kk k k k----+所以10001000200200 100200300----c) K=SpringAssemble(K,k1,1,2) function y = SpringAssemble(K,k,i,j) K(i,i) = K(i,i) + k(1,1);K(i,j) = K(i,j) + k(1,2);K(j,i) = K(j,i) + k(2,1);K(j,j) = K(j,j) + k(2,2); 1100100100100k -??=??-??10010001001000000K -??=-??K=SpringAssemble(K,k2,2,3) 1200200200200k -??10010001003002000200200K -??=---??1001000100010010030020002002000200200100200300----≠----步骤四：引入边界条件，消除冗余方程>>k=K(2:3,2:3)%构造不含冗余的方程>>f=[0;15]%构造外力列阵步骤五：解方程引例：已知1212u 31u u u +=??-=?，求 12u u 和解：类似求解KU=F ，输入下列Matlab 命令：>> K=[1 1;1,-1]>> F=[3;1]>> U=inv(K)*F>> U=K \F（继续弹簧系统求解）>>u=k \f %使用高斯消去法求解>>U=[0 ; u]%构造原方程组>>F=K*U %求出所有外力，含多余计算步骤六：后处理、扩展计算>>u1=[0;U(2)]%构造单元位移>>f1=SpringElementForces(k1,u1)%求单元1内力>>u2=[U(2) ; U(3)]%构造单元2位移>>f2=SpringElementForces(k2,u2)%求单元2内力4. 总结clck1=SpringElementStiffness(100)%创建单元刚度矩阵 1 k2=SpringElementStiffness(200)%创建单元刚度矩阵 2 K=zeros(3,3)%创建空白整体刚度矩阵K=SpringAssemble(K,k1,1,2)%按节点装入单元矩阵 1 K=SpringAssemble(K,k2,2,3)%按节点装入单元矩阵2 k=K(2:3,2:3)%构造不含冗余的方程f=[0;15]%构造外力列阵u=k\f%使用高斯消去法求解U=[0 ; u]%构造系统节点位移列阵F=K*U%求出所有外力，含多余计算u1=[0;U(2)]%构造单元位移f1=SpringElementForces(k1,u1)%求单元1内力u2=[U(2) ; U(3)]%构造单元2位移f2=SpringElementForces(k2,u2)%求单元2内力5. 练习1 Danyi 132 dan 34 3dan 35 4dan 35 dan5 54 dan6 42。

第三章MATLAB有限元分析与应用有限元分析（Finite Element Analysis, FEA）是一种工程计算方法，用于解决结构力学和流体力学等问题。

它将一个复杂的结构分割成多个简单的离散单元，通过建立数学模型和求解方程组，得到结构的力学、热力学和流体力学等性能参数。

MATLAB是一种功能强大的数学计算软件，具有直观的用户界面和丰富的工具箱，可以方便地进行有限元分析。

本章将介绍在MATLAB中进行有限元分析的基本步骤和方法，以及一些常见的应用例子。

首先，进行有限元分析需要将结构进行离散化。

常用的离散化方法有节点法和单元法。

节点法是将结构的几何形状划分为小的节点，并在节点上进行计算。

单元法是将结构划分为多个小的单元，并在每个单元内进行计算。

在MATLAB中，可以通过创建节点和单元的矩阵来描述结构和单元的关系。

例如，创建一个2D结构形式的节点矩阵：nodes = [0 0; 1 0; 0 1; 1 1];然后，通过创建描述节点连接关系的矩阵，来定义结构的单元：elements = [1 2 3; 2 4 3];这里的每一行代表一个单元，数字表示节点的编号。

接下来，需要定义材料的力学参数和边界条件。

材料的力学参数包括弹性模量、泊松比等。

边界条件包括支座约束和加载条件。

在MATLAB中，可以通过定义力学参数和边界条件的向量来描述。

例如，定义弹性模量和泊松比的向量：E=[200e9200e9];%弹性模量nu = [0.3 0.3]; % 泊松比定义支座约束的向量（1表示固定，0表示自由）：constraints = [1 1; 0 0; 0 1; 0 1];定义加载条件的向量（包括点力和面力）：最后，通过求解方程组得到结构的应力和位移等结果。

在MATLAB中，可以利用有限元分析工具箱中的函数进行计算。

例如，可以使用“assem”函数将节点和单元的信息组装成方程组，并使用“solveq”函数求解方程组。

题目：使用MATLAB编程实现有限元切线刚度矩阵计算一、引言有限元法是一种用于求解复杂工程问题的数值分析方法，它将连续介质划分为许多小的单元，通过对每个单元进行离散化处理，再用数学方法对这些单元进行组装，最终得到整个结构的解。

在有限元方法中，刚度矩阵是求解结构问题的关键步骤之一，而有限元切线刚度矩阵的计算则是其中的重要内容之一。

本文将介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。

二、有限元切线刚度矩阵的基本概念1. 切线刚度矩阵在有限元方法中，切线刚度矩阵是描述结构对外部载荷作用下的应变-应力关系的重要矩阵。

它描述了结构在外部载荷下的变形行为，是求解结构变形和应力的重要工具。

2. 切线刚度矩阵的计算切线刚度矩阵的计算是通过对单元的局部坐标系进行刚度矩阵的求解，并进行坐标变换得到全局坐标系下的切线刚度矩阵。

在实际计算中，需要考虑单元的几何形状、材料性质等因素，以及在单元上施加的外部载荷。

三、MATLAB编程实现有限元切线刚度矩阵的基本步骤1. 单元刚度矩阵的计算我们需要编写MATLAB函数来实现对单元刚度矩阵的计算。

这个函数需要考虑单元的几何形状、材料性质等因素，以及在单元上施加的外部载荷。

通常情况下，我们可以利用数值积分的方法来进行刚度矩阵的计算。

2. 坐标变换矩阵的计算在得到单元刚度矩阵之后，我们需要计算坐标变换矩阵，将单元刚度矩阵从局部坐标系变换到全局坐标系。

这也需要编写一个MATLAB函数来实现坐标变换矩阵的计算。

3. 矩阵组装我们需要将所有单元的切线刚度矩阵组装成整体刚度矩阵。

这通常需要考虑到单元之间的连接关系，以及边界条件等因素。

在MATLAB中，我们可以利用矩阵的组合和相加等运算来实现整体刚度矩阵的计算。

四、编程实例这里我们以一个简单的弹簧-弹簧系统为例，介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。

我们需要定义系统的几何形状、材料性质等参数，然后编写MATLAB函数来进行刚度矩阵的计算，坐标变换矩阵的计算，以及矩阵的组装，最终得到整体刚度矩阵，并求解系统的变形和应力。

PlaneFrameElementStiffness：
PlaneFrameAssemble：
PlaneFrameElementForces：
PlaneFrameElementAxialDiagram：
PlaneFrameElementShearDiagram PlaneFrameElementMomentDiagram PlaneFrameInclinedSupport——（T） ............
2、可视化及强大的图形功能。
（1）绘图 （2）界面编制
3、含有多种学科的工具箱[ToolBox]以及 程序代码的公开性。
4、程序可移植性好。
二、有限元方法的步骤：
一、离散化域 二、形成单元刚度矩阵 三、集成整体刚度矩阵 四、引入边界条件 五、求解方程 六、后处理
2020/11/11

8
简例： ——平面刚架元
实例：如图所示刚架, 已知各杆EI及A均相同, 且 A=2*10-2m2, I=5*10-5m4,E=210GPa.
PlaneFrameElementStiffness：
PlaneFrameAssemble：
整体刚度矩阵：
引入边界条件：
KUF
后处理：
四、结论和展望
Simple,Powerful and free
结束语
谢谢大家聆听！！！
39
MATLAB在有限元分析方法 中的应用PPT
一、“MATLAB”
1、前置处理 2、求解器 3、后置处理
Simple,Powerful and free
有限元软件的基本模块： 1、前置处理 2、求解器 3、后置处理
C、C++、Fortran等/MATLAB

利用MATLAB进行桁架结构内力及位移disp('----本程序用于计算桁架结构内力及位移----');disp('以下为本程序所用计算基本数据：');disp('[L]——结构杆件长度列阵(包括定位向量,即节点编号)');disp('[A]——结构杆件面积列阵');disp('[I]——结构杆件截面惯性矩列阵');disp('[E]——结构杆件材料弹性模量列阵');disp('[a]——结构杆件单元单元坐标系与整体坐标系夹角列阵，以逆时针为正');disp('[K]——结构整体刚度矩阵');disp('[B]——结构杆件单元刚度矩阵');disp('[T]——结构杆件单元刚度矩阵转换矩阵');disp(' n——杆件单元数目');disp('---程序初始化，输入基本数据---');n=input('\n请输入杆件单元个数n=');A=zeros(1,n);s=input('\n请输入杆件单元截面面积s=');A=A+s;I=zeros(1,n);i=input('\n请输入杆件单元截面惯性矩i=');I=I+i;E=zeros(1,n);e=input('\n请输入杆件单元材料弹性模量e=');E=E+e;a=zeros(1,n);j=input('\n请输入杆件单元单元坐标系与整体坐标系夹角j=');a=a+j;L=zeros(n,3);L=input('\n请输入杆件长度和节点编号L=');T=zeros(6,6);B=zeros(6,6);K=zeros(3*n,3*n);disp('---生成整体刚度矩阵---');for i=1:ndisp('---生成单元坐标系下的单元刚度矩阵---');B(1,1)=E(i)*A(i)/L(i,1);B(2,2)=12*E(i)*I(i)/L(i,1)^3;B(3,2)=-6*E(i)*I(i)/L(i,1)^2;B(3,3)=E(i)*I(i)/L(i,1);B(4,1)=-E(i)*A(i)/L(i,1);B(5,2)=-12*E(i)*I(i)/L(i,1)^3;B(5,3)=6*E(i)*I(i)/L(i,1)^2;B(6,2)=-6*E(i)*I(i)/L(i,1)^2;B(6,3)=E(i)*I(i)/L(i,1);B(6,5)=6*E(i)*I(i)/L(i,1)^2;B(6,6)=4*E(i)*I(i)/L(i,1);B=B+B';disp('---生成单元刚度矩阵转换矩阵---');T(1,1)=cos(a(i));T(1,2)=-sin(a(i));T(2,1)=sin(a(i));T(2,2)=cos(a(i));T(3,3)=1;T([4,6],[4,6])=T([1,3],[1,3]);disp('---生成整体坐标系下的单元刚度矩阵---');B=T'*B*T;disp('---由单元刚度矩阵组装整体刚度矩阵---');K([L(i,2),L(i,2)+2],[L(i,2),L(i,2)+2])=B([1,3],[1,3]);K([L(i,2),L(i,2)+2],[L(i,3),L(i,3)+2])=B([1,3],[4,6]);K([L(i,3),L(i,3)+2],[L(i,2),L(i,2)+2])=B([4,6],[1,3]);K([L(i,3),L(i,3)+2],[L(i,3),L(i,3)+2])=B([4,6],[4,6]);end以上是利用MATLAB编写的有单元刚度矩阵生成整体刚度矩阵的小程序.。

基于MATLAB的有限元结构分析王剑(重庆交通大学土木建筑学院,重庆400074)摘要: MATLAB 是当今国际科学界最具影响力和活力的软件。

文章介绍了MATLAB 语言的特点，详细介绍了用MATLAB语言编写结构内力的有限元方法，并通过实例对平面钢架结构进行了内力分析。

关键词：MATLAB 有限元结构0引言MATLAB是Mathworks公司推出的，集算法开发、数值运算、符号运算以及图形处理等强大功能于一体的高级技术计算语言和交互式环境。

MATLAB意为矩阵实验室，它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言的编辑模式，代表了当今国际科学计算软件的先进水平。

有限元法的基本思想是将物体（即连续求解域）离散成有限个且按一定方式相互连接在一起的单元组合，来模拟和逼近原来的物体，从而将一个连续的无限自由度问题简化为离散的有限自由度问题求解的数值分析法。

有限元法还有一个特点是，它的理论采用矩阵形式表达。

这并不利于一般的计算机语言编制计算机程序，因为传统的计算机语言处理的对象是标量，使用矩阵形式的有限元理论时，必须把矩阵形式的公式转换成标量表示的公式。

而如果采用MATLAB，这个特点就变成了有限元法的优点，运算更便捷。

1运用MATLAB编写有限元程序的操作步骤1.1建立有限元模型建立有限元模型就是为求解有限元模型做铺垫。

需要对节点、单元以及材料的定义。

同时对约束条件、集中力、分布力进行定义。

然后在M函数文件中以矩阵或向量的形式输入单元号、节点数、材料的性质、约束条件、集中力、分布力。

1.2求解有限元模型用MATLAB写出每个单元的单元刚度矩阵。

按照刚度集成法，把各个单元的刚度矩阵分别放到整体刚度矩阵中的相应位置上，然后根据边界条件进行修正得到整体刚度矩阵。

优化设计
在满足一定约束条件下，寻找使某个或多个设 计指标达到最优的设计方案的过程。
目标函数
用于衡量设计方案优劣的数学表达式，通常是 最小化或最大化的某个性能指标。
约束条件
限制设计方案选择的条件，包括设计变量的上下界、设计变量的关系等。
基于Matlab的有限元优化设计方法
MATLAB优化工具箱
提供了一系列用于求解各种优化问题的函数和算法，包括线性规划、非线性规划、混合 整数规划等。
有限元模型
由一组离散化的元素组成，每个 元素代表系统的一部分，并具有 特定的属性和行为。
节点
元素之间的连接点，用于传递力 和位移。
有限元分析的基本步骤
前处理
01
建立有限元模型，包括定义元素类型、几何形状、材料属性、
边界条件和载荷等。
Байду номын сангаас求解
02
应用数学方程求解有限元模型的节点位移和应力分布。
后处理
03
对于一些复杂模型，如具有非线性、大变形、多 材料等特性，建模难度大，需要发展更高级的建 模方法和技术。
数据安全与隐私保护
在进行有限元分析时，需要处理大量的数据，如 何保证数据的安全和隐私保护是一个重要的问题 。需要采取有效的数据加密和保护措施来确保数 据的安全性和隐私性。
未来发展方向与展望
跨学科融合
结果后处理
显示结果
使用Matlab的图形功能，如`plot`、`mesh`等，绘制 结果的可视化图像。
分析结果
对结果进行详细的分析，如查看位移分布、应力分布 等。
结果优化
根据分析结果，对模型进行优化设计，以提高性能或 降低成本。
03
有限元分析实例
Chapter

维普资讯
第 ６卷 第 １ 期
２００６ 年 ３月
南通纺 织职 业技 术学 院学报 （ 合版 ） 综
Ｊｕｒａ ｆＮａ ｏ ｇＴ ｘｉ ｏ ａｉｎ ｌＴｅ ｈ ｏｏ ｙＣｏｌｇ ｏ ｎ ｌｏ ｎｔｎ ｅ ｔｅ Ｖ ｃ ｔ ａ ｃ ｎ ｌｇ ｌｅ ｅ ｌ ｏ
用 ＭＡ Ｌ Ｂ程序 运 算的 一些技 巧． ＴＡ
【 关键词】 Ａ Ｌ Ｂ 有限元； 矩阵运算 Ｍ ＴＡ ； ［ 中图分类号］ Ｂ １ 【 Ｔ １５ 文献标识码】 【 Ａ 文章编号】１７－ １ １２０ ） １ ０ １— ３ ６ １６９ （０ ６０ － ０ ３ ０
０ 引 言
ＭＡ Ｌ Ｂ（ Ｔｉ Ｌ Ｂ ｒｔｒ， 阵 实验 室 ） 集数 值运算 、 号运 算及 图形处 理 等功 能于 一 体 的交 互 Ｔ Ａ ＭＡ ｒ Ａ ｏａ ｙ矩 ｘ ｏ 是 符 式 科学 计算 语 言 ， 称科 学 计算软 件环境 ．作 为强 大 的科学 计 算平 台 ， 几 乎能 满 足所 有 的 计算需 求 ．同 或 它 时 ， 这种 交互 的 高效 的矩 阵 计算 环境 下 ， 在 问题 和解 答 的表达 形 式几 乎和 它 们 的数学 表 达式 完 全一 样 ， 因
收 稿 日期 ： ０ ６ ０ 一 ４ ２ ０ — ｌ０
图 １ 节 点 应 力 与 位 移 示 意 图
作 者 简 介 ：庞 晓琛 （９ １ ）江 阴 职 业 技 术 学 院 机 电 系讲 师 １７ 一 ，
维普资讯
南通 纺织 职 业技 术 学 院学 报 （ 合版 ） 综
因此matlab可以使这些原本复杂的程序在保持相当精度的基础上得到简化极大地提高了编程的效率质量和可靠性并且程序可读性强调试简单易于维护若将其引入到有限元编程领域必定会大大加快有限元软件的开发应用笔者采用matlab编写了弹性力学问题中平面应力问题的三节点三角形单元的程序该程序通过读入问题的单元划分材料载荷和边界条件等信息形成总刚度和总载荷矩阵最后求解出单元应力

有限元刚架结构matlab程序clcclearformat compactformat shortGjd=input('请输⼊节点数：');dy=input('请输⼊单元数：');E=input('请输⼊杨⽒模量E：');I=input('请输⼊惯性矩I：');L=input('请输⼊单元长度L：');A=input('请输⼊单元截⾯积：');FAI=input('请输⼊单元相对旋转⾓度：');%输⼊对应关系时，⼩节点放前⾯[单元节点1 节点2]dy_jd=input('请输⼊单元与节点对应关系：');%输⼊⼒与扭矩约束[值作⽤节点作⽤类型]（转矩为3 x⽅向为1 y⽅向为2）lys=input('⼒与转矩约束矩阵：');%输⼊结构约束[作⽤节点作⽤类型]（转⾓为3 x⽅向为1 y⽅向为2）wys=input('结构约束矩阵：');%原始数据% L=1;% E=3*10^10;% P=1000;% A=0.05;% dy=2;jd=3;LL=[L 2*L];I=20*A;% dy_jd=[1 1 2;2 2 3];% FAI=[pi/2 0];% q=P/L;M=P*L/10;% lys=[44/125*P 1 1;-12*P*L/125 1 3;81/125*P 2 1;-P 2 2;-67/750*P*L 2 3;-P 3 2;P*L/3 3 3]; % wys=[1 1;1 2;1 3;3 1;3 2;3 3];%对⼒约束与位移约束式⼦分别进⾏编号处理wys(:,3)=(wys(:,1)-1)*3+wys(:,2);lys(:,4)=(lys(:,2)-1)*3+lys(:,3);%对⼒约束与位移约束式⼦进⾏排序lys=sortrows(lys,4);wys=sortrows(wys,3);%单元刚度矩阵syms fai e a i l realk=[e*a/l 0 0 -e*a/l 0 0;0 12*e*i/l^3 6*e*i/l^2 0 -12*e*i/l^3 6*e*i/l^2;0 6*e*i/l^2 4*e*i/l 0 -6*e*i/l^2 2*e*i/l;-e*a/l 0 0 e*a/l 0 0;0 -12*e*i/l^3 -6*e*i/l^2 0 12*e*i/l^3 -6*e*i/l^2;0 6*e*i/l^2 2*e*i/l 0 -6*e*i/l^2 4*e*i/l];t=[ cos(fai), sin(fai), 0;-sin(fai), cos(fai), 0;0, 0, 1];%坐标变换矩阵T=blkdiag(t,t);%总体坐标系下的单元刚度矩阵K=T'*k*T;%带⼊每个单元的数，⽣成单元刚度矩阵kk，其每⼀页对应相应页数的单元的刚度矩阵for j=1:dy; e=E;i=I;l=LL(j);a=A;fai=FAI(j);kk(:,:,j)=eval(K);end%⽣成总体刚度矩阵KK%采⽤元胞数组的⽅式对各项进⾏保存%⽣成空元胞数组，元胞数组的⾏列⼤⼩与节点数相同for j=1:jd;for jj=1:jd;ling1{j,jj}=zeros(3);endendling2=ling1;%将对单元刚度矩阵部分分成4分加⼊元胞数组中for j=1:dy;kk1=kk(1:3,1:3,j);kk2=kk(1:3,4:6,j);kk3=kk(4:6,1:3,j);kk4=kk(4:6,4:6,j);ling2{dy_jd(j,2),dy_jd(j,2)}=kk1+ling2{dy_jd(j,2),dy_jd(j,2)}; ling2{dy_jd(j,2),dy_jd(j,3)}=kk2+ling2{dy_jd(j,2),dy_jd(j,3)}; ling2{dy_jd(j,3),dy_jd(j,2)}=kk3+ling2{dy_jd(j,3),dy_jd(j,2)}; ling2{dy_jd(j,3),dy_jd(j,3)}=kk4+ling2{dy_jd(j,3),dy_jd(j,3)}; end %将元胞数组进⾏拼接，形成总体刚度矩阵for j=1:jd;ling3(:,:,j)=cat(2,ling2{j,:});endKK=ling3(:,:,1);for j=2:jd;KK=[KK;ling3(:,:,j)];end%消去有已知位移的⾏与列b=KK;b(:,wys(:,3))=[];b(wys(:,3),:)=[];kjiejuzhen=inv(b);%提取对应外⼒lyss=lys;for j=1:size(wys,1);for jj=1:size(lys,1);if lyss(jj,4)==wys(j,3);lyss(jj,:)=0;endif jj==size(lyss,1);breakendendendlyss(all(lyss==0,2),:)=[];%求解weiyijie=[作⽤值作⽤节点作⽤类型（转⾓为3 x⽅向为1 y⽅向为2）序列] weiyijie=kjiejuzhen*lyss(:,1);weiyijie(:,1)=weiyijie;weiyijie(:,2)=lyss(:,2);weiyijie(:,3)=lyss(:,3);weiyijie(:,4)=lyss(:,4);%计算不计作⽤在约束⽅向上时的⽀反⼒lysjiee=[作⽤值作⽤节点作⽤类型（转⾓为3 x⽅向为1 y⽅向为2）序列] lysjie(:,1)=KK(wys(:,3),lyss(:,4))*weiyijie(:,1);lysjie(:,2:4)=wys(:,1:3);%将作⽤在约束⽅向上时的⽀反⼒加在上⾯的求解结果上for j=1:size(lysjie,1)for jj=1:size(lys,1);if lysjie(j,4)==lys(jj,4);lysjie(j,1)=lysjie(j,1)-lys(jj,1);endendend%答案weiyijielysjie。

matlab桁架结构有限元计算摘要：一、引言二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号2.组装刚度矩阵3.求解器求解4.后处理三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析2.基于MATLAB 的三维桁架有限元分析3.五杆桁架有限元分析四、用MATLAB 编写程序求解桁架结构内力问题1.静定结构绘制简图2.计算结构力学3.机动分析五、结论正文：一、引言在工程领域中，桁架结构由于其优越的力学性能和简单的结构形式，被广泛应用于桥梁、塔架等大型建筑结构中。

为了确保桁架结构的安全性和稳定性，对其进行有限元分析是非常必要的。

MATLAB 作为一种强大的数学软件，可以方便地进行桁架结构的有限元计算。

本文将介绍如何使用MATLAB 进行桁架结构有限元计算。

二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号在进行有限元分析之前，首先需要对桁架结构进行离散化处理，将连续的桁架杆件划分为有限个小杆件。

同时，为了方便后续计算，需要对各个杆件和节点进行编号。

2.组装刚度矩阵根据桁架结构的几何参数和材料性能，可以计算出各个杆件的刚度矩阵。

将这些刚度矩阵组装成一个总的刚度矩阵，用于描述整个桁架结构的刚度特性。

3.求解器求解利用MATLAB 的求解器，可以对桁架结构进行有限元求解。

求解器会根据刚度矩阵和施加的边界条件，计算出节点的位移和单元的应力。

4.后处理在求解完成后，需要对计算结果进行后处理。

这包括对计算结果的保存、可视化以及结果的验证等。

三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析例如，可以针对一个空间桁架结构，使用MATLAB 进行有限元分析。

假设该桁架结构由铝制成的垂直和水平部分和钢制成的对角桁架构件组成。

结构承受荷载P，需要计算节点位移、单元应力以及支反力。

2.基于MATLAB 的三维桁架有限元分析还可以利用MATLAB 进行三维桁架有限元分析。

MATLAB有限元分析与应用有限元分析是一种基于数值方法的结构分析技术，广泛应用于工程领域中各种结构的设计与优化。

MATLAB作为一种强大的计算软件，提供了丰富的数值计算、数据可视化和编程功能，成为了进行有限元分析与应用的首选工具之一MATLAB的有限元分析工具箱（FEA）提供了一系列函数和工具，用于构建、求解和分析有限元模型。

用户可以根据实际问题构建有限元模型，包括定义几何形状、材料属性、边界条件和加载情况等。

利用有限元分析工具箱提供的函数，用户可以生成刚度矩阵和负载向量，并求解有限元方程组，得到结构的位移、应力和应变等信息。

此外，MATLAB还提供了可视化工具，可以将计算结果以图形的形式展示出来，方便用户进行结果的分析和评估。

1.结构力学：有限元分析可用于评估结构的强度和刚度，进行结构的静力和动力响应分析。

例如，在设计建筑物和桥梁时，可以通过有限元分析评估结构的变形、应力和疲劳寿命，确保结构的安全性和稳定性。

2.流体力学：有限元分析可用于求解流体介质中的运动方程和温度分布，分析流体流动的特性。

例如，在航空航天领域中，可以使用有限元分析来计算飞机机翼的气动性能，并优化机翼的设计。

3.电磁场：有限元分析可用于求解电磁场的分布和场强，以及电磁场对物体的影响。

例如，在电力系统中，可以使用有限元分析来评估导线和电力设备的电磁场分布，预测设备的电磁辐射水平，以及优化电磁屏蔽设计。

4.热传导：有限元分析可用于求解热传导方程，分析物体的温度分布和热流量分布。

例如，在热管理领域中，可以使用有限元分析来优化散热器的设计，提高散热效率。

5.多物理场耦合：有限元分析可用于求解多个物理场的耦合问题，分析各个物理场之间的相互影响。

例如，在电动汽车的电池设计中，可以使用有限元分析来研究电池的温升、电动力学响应和热耦合效应。

总之，MATLAB的有限元分析与应用广泛应用于工程领域中各种结构的设计与优化。

它提供了方便的数值计算、数据可视化和编程功能，可用于求解各种结构的力学、热力学、电磁学等问题。

Ｍ ｔａ 是美国 Ｍ ｔ ｒ 公司开发的用于数值 ａ． １ｈ ａ Ｗｏ ｈ ｋ 的集成环境 ， 因其完整的专业体系和强 大的运算功 能， 已广泛应用于工业 、 电子、 信号处理 、 控制 、 医疗、 建筑、 教学等各个领域 …． Ｍｔｈ ａ ． 本意是矩 阵实验 室（ ａｉ Ｌｂｒ ｏ ） １ ａ Ｍ ｔｘ ａｏ ｔ ｙ ， ｒ ａｒ
有限元是近代数值计算最有效方 法之一． 有限
推导已有一个相对固定的模式 ， 而烦琐 、 复杂的矩阵 运算 、 微分、 积分是刚度矩阵推导中的主要 内容． 通 常， 这种矩阵运算是 由手工来完成的， 工作量大 ， 而 且极易出错． 利用 Ｍ ｒｑ ａ． １ｈ丰富 的符号运算功能 ， 完
计算、 概念设计 、 算法研究、 建模仿真 、 实时实现理想 元法的基础是单元刚度矩阵的推导 ， 目前 ， 刚度矩阵
维普资讯
第２ ６卷 第 ２期 生
重
庆
交 通
学
院
学
报
ｖ １２ ０ ６
．
Ｎｏ． ２
Ｊ Ｕ Ｎ ＬＯ Ｈ Ｎ ） ＧＪＡ Ｔ Ｎ Ｎ Ｒ ＩＹ Ｏ Ｒ Ａ ＦＣ Ｏ Ｉ ＩＯ Ｏ ＧＵ ⅣＥ ＳＴ Ｎ ＿
Ａ ｒБайду номын сангаас０ ７ Ｄ．２０
Ｚ ＨＯＵ Ｓ ｕ ． ｉ ｇ ．，Ｃ ｈ ｉ ｎ － ＨＥＮ Ｓ ａ — ｎ ｘ ｈ ｎｌ ｉ
（ ．Ｃ ｏ ｇｉｇＵ ｉｅ ｉ ， ｈｎｑｎ ００ ５ Ｃ ｉａ １ ｈｎ ｑ ｎｖｒｔ Ｃ ｏ ｇｉｇ ０４ ， ｈｎ ； ｎ ｓｙ ４ ２ ｃｏｌ ｆ ｉｌ ｎ ｉｅｒ ｇ＆ Ａ ｃｉ ｃ ｒ，ｈ ｎｑｎ ｉ ｔ ｇＵ ｉ ｒｉ ，ｈｎ ｑｎ ０ ７ ， ｈｎ ） ．Ｓｈｏ ｖ ｇ ｅｉ ｏ Ｃ ｉＥ ｎ ｎ ｒｈ ｅｔ ｅ Ｃ ｏｇ ｉ Ｊ ｏｏ ｎ ｅｓｙ Ｃ ｏｇｉｇ ０ ０ ４ Ｃ ｉａ ｔ ｕ ｇ ａ ｎ ｖ ｔ ４

matlab有限元刚度矩阵编程有限元方法是一种常用的工程分析方法，用于解决结构的力学问题。

该方法将结构离散为有限数量的小单元，然后利用这些小单元的力学行为来近似整个结构的力学行为。

其中，有限元刚度矩阵是有限元方法中的重要概念之一。

有限元刚度矩阵描述了结构单元的刚度特性，并将其与结构整体刚度相联系。

通过求解刚度矩阵，可以得到结构的位移响应，并进一步计算出应力、应变等力学量。

因此，求解有限元刚度矩阵是有限元方法中的关键步骤。

在MATLAB中，可以使用矩阵运算和数值计算工具箱来编程实现有限元刚度矩阵的求解。

具体步骤如下：1. 网格划分：首先，将结构离散为有限数量的小单元。

这些小单元可以是三角形、四边形或其他形状，根据结构的特点和要求进行选择。

MATLAB提供了一些网格生成函数，如"meshgrid"和"trimesh"，可以帮助我们生成所需的网格。

2. 单元刚度矩阵计算：对于每个小单元，需要计算其刚度矩阵。

刚度矩阵的计算基于单元的几何形状和材料特性。

对于简单的结构单元，可以使用解析方法来计算刚度矩阵。

对于复杂的结构单元，可以使用数值方法，如数值积分或有限差分法，来近似计算刚度矩阵。

在MATLAB中，可以使用矩阵运算和数值计算函数来实现刚度矩阵的计算。

3. 组装刚度矩阵：将所有小单元的刚度矩阵组装成整个结构的刚度矩阵。

这涉及到将小单元的刚度矩阵按照其在整个结构中的位置进行组装。

在MATLAB中，可以使用矩阵运算和索引操作来实现刚度矩阵的组装。

4. 边界条件处理：在求解结构的位移响应时，需要考虑边界条件。

边界条件包括约束和加载。

约束是指结构的某些部分固定不动或具有特定的位移。

加载是指施加在结构上的外力或外力密度。

通过将边界条件转化为相应的约束方程和加载方程，可以将其应用于刚度矩阵求解过程。

在MATLAB中，可以使用约束和加载向量来表示边界条件，并使用矩阵运算来处理边界条件。