大学物理第10章热力学

大学物理热力学基础热力学是物理学的一个分支，它研究热现象中的物理规律，包括物质的热性质、热运动和热转化。

在大学物理课程中，热力学基础是物理学、化学、材料科学、工程学等学科的基础课程之一。

热力学基础主要涉及以下几个方面的内容：1、热力学第一定律热力学第一定律，也称为能量守恒定律，是指在一个封闭系统中，能量不能被创造或消除，只能从一种形式转化为另一种形式。

这个定律说明，能量在传递和转化过程中是守恒的，不会发生质的损失。

2、热力学第二定律热力学第二定律是指热量只能从高温物体传递到低温物体，而不能反过来。

这个定律说明，热量传递的方向是单向的，不可逆的。

这个定律对于理解能源转换和利用具有重要意义。

3、热力学第三定律热力学第三定律是指绝对零度下，物质的熵（表示物质混乱度的量）为零。

这个定律说明，在绝对零度下，所有物质的分子和原子都处于静止状态，没有热运动，因此熵为零。

这个定律对于理解物质在低温下的性质和行为具有重要意义。

4、理想气体状态方程理想气体状态方程是指一定质量的气体在恒温条件下，其压力、体积和密度之间的关系。

这个方程对于理解气体在平衡状态下的性质和行为具有重要意义。

5、热容和焓热容和焓是描述物质在加热和冷却过程中性质变化的物理量。

热容表示物质吸收或释放热量的能力，焓表示物质在恒温条件下加热或冷却时所吸收或释放的热量。

这两个物理量对于理解和分析热现象具有重要意义。

大学物理热力学基础是物理学的重要分支之一，它为我们提供了理解和分析热现象的基本理论工具。

通过学习热力学基础，我们可以更好地理解能源转换和利用的原理，为未来的学习和职业生涯打下坚实的基础。

在无机化学的领域中，化学热力学基础是理解物质性质、反应过程和能量转换的重要工具。

本篇文章将探讨化学热力学的基础概念、热力学第一定律、热力学第二定律以及热力学第三定律。

一、化学热力学的基础概念化学热力学是研究化学反应和相变过程中能量转换的科学。

它主要涉及物质的能量、压力、温度和体积等物理量之间的关系。

习题10-1. 如图所示，AB 、DC 是绝热过程，CEA 是等温过程，BED 是任意过程，组成一个循环。

若图中EDCE 所包围的面积为J 70，EABE 所包围的面积为J 30，CEA 过程中系统放热J 100，求BED 过程中系统吸热为多少？解：由题意可知在整个循环过程中内能不变，图中EDCE 所包围的面积为J 70，则意味着这个过程对外作功为70J ，也就是放热为70J ；EABE 所包围的面积为J 30，则意味着这个过程外界对它作功为30J ，也就是吸热为70J ，所以整个循环中放热是70-30=40J 。

而在这个循环中，AB 、DC 是绝热过程，没有热量的交换，所以如果CEA 过程中系统放热J 100，则BED 过程中系统吸热为100+40=140J 。

10-2. 如图所示，已知图中画不同斜线的两部分的面积分别为1S 和2S .（1）如果气体的膨胀过程为a ─1─b ，则气体对外做功多少？（2）如果气体进行a ─2─b ─1─a 的循环过程，则它对外做功又为多少？解：根据作功的定义，在P —V 图形中曲线围成的面积就是气体在这一过程所作的功。

则：（1）如果气体的膨胀过程为a ─1─b ，则气体对外做功为S 1+S 2 。

（2）如果气体进行a ─2─b ─1─a 的循环过程，则它对外做功为：－S 1 。

10-3. 一系统由如图所示的a 状态沿acb 到达b 状态，有334J 热量传入系统，系统做功J 126。

（1）经adb 过程，系统做功J 42，问有多少热量传入系统?（2）当系统由b 状态沿曲线ba 返回状态a 时，外界对系统做功为J 84，试问系统是吸热还是放热？热量传递了多少?解：由acb 过程可求出b 态和a 态的内能之差Q=ΔE+A ，ΔE=Q -A=334-126=208 Jadb 过程，系统作功A=42 J ， Q=ΔE+A=208+42=250J 系统吸收热量ba 过程，外界对系统作功A=-84 J ， Q=ΔE ＋A=-208-84=-292 J 系统放热10-4.温度为25o C 、压强为1atm 的1mol 刚性双原子分子理想气体，经等温过程体积膨胀至原来的3倍。

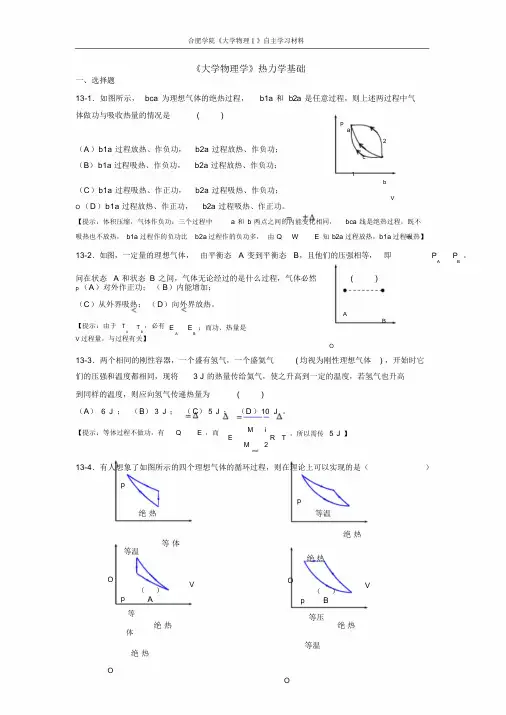
合肥学院《大学物理Ⅰ》自主学习材料《大学物理学》热力学基础一、选择题13-1．如图所示，bca 为理想气体的绝热过程，b1a 和b2a 是任意过程，则上述两过程中气体做功与吸收热量的情况是( )pa2（A）b1a 过程放热、作负功，b2a 过程放热、作负功；c（B）b1a 过程吸热、作负功，b2a 过程放热、作负功；1b（C）b1a 过程吸热、作正功，b2a 过程吸热、作负功；VO （D）b1a 过程放热、作正功，b2a 过程吸热、作正功。

【提示：体积压缩，气体作负功；三个过程中 a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b1a 过程作的负功比b2a 过程作的负功多，由Q W E 知b2a 过程放热，b1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态 A 变到平衡态B，且他们的压强相等，即P P 。

A B问在状态 A 和状态 B 之间，气体无论经过的是什么过程，气体必然( )p （A）对外作正功；（B）内能增加；（C）从外界吸热；（D）向外界放热。

AB【提示：由于T T ，必有A B E E ；而功、热量是A BV 过程量，与过程有关】O13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气( 均视为刚性理想气体) ，开始时它们的压强和温度都相同，现将 3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为( )（A） 6 J ；（B）3 J ；（C）5 J ；（D）10 J 。

【提示：等体过程不做功，有Q E ，而M iE R TM 2mol，所以需传 5 J 】13-4．有人想象了如图所示的四个理想气体的循环过程，则在理论上可以实现的是（）pp绝热等温绝热等体等温绝热Op 等（）AV Op（）B等压V 绝热绝热体等温绝热OOVV （）C（）D【提示：(A) 绝热线应该比等温线陡，（B）和（C）两条绝热线不能相交】热力学基础-1合肥学院《大学物理Ⅰ》自主学习材料13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J，则对外做功（）（A）2000 J ；（B）1000 J ；（C）4000 J ；（D）500 J 。

第十章 热力学【例题精选】例10-1两个完全相同的气缸内盛有同种气体，设其初始状态相同，今使它们分别作绝热压缩至相同的体积，其中气缸1内的压缩过程是非准静态过程，而气缸2内的压缩过程则是准静态过程．比较这两种情况的温度变化：(A) 气缸1和2内气体的温度变化相同． (B) 气缸1内的气体温度变化较大．(C) 气缸1内的气体的温度变化较小． (D) 两气缸内的气体的温度无变化． [ B ]例10-2 某理想气体状态变化时，内能随体积的变化关系如图中AB 直线所示．A →B 表示的过程是(A) 等压过程．(B) 等体过程．(C) 等温过程．(D) 绝热过程． [ A ] 例10-3用公式T C E V ∆=∆ν(式中V C 为定体摩尔热容量，视为常量，ν 为气体摩尔数)计算理想气体内能增量时，此式(A) 只适用于准静态的等体过程． (B) 只适用于一切等体过程．(C) 只适用于一切准静态过程． (D) 适用于一切始末态为平衡态的过程．[ D ]例10-4 如图，bca 为理想气体绝热过程，b 1a 和b 2a 是任意过程，则上述两过程中气体作功与吸收热量的情况是: (A) b 1a 过程放热，作负功；b 2a 过程放热，作负功．(B) b 1a 过程吸热，作负功；b 2a 过程放热，作负功．(C) b 1a 过程吸热，作正功；b 2a 过程吸热，作负功．(D) b 1a 过程放热，作正功；b 2a 过程吸热，作正功． [ B ]例10-5 、一定量理想气体，从A 状态 (2p 1，V 1)经历如图所示的直线过程变到B 状态(2p 1，V 2)，则AB 过程中系统作功W ＝ ；内能改变∆E = ． 1123V p 0 例10-6 一定量理想气体，从同一状态开始使其体积由V 1膨胀到2V 1，分别经历以下三种过程：(1) 等压过程；(2) 等温过程；(3)绝热过程．其中： 过程气体对外作功最多； 过程气体内能增加最多．等压 等压例10-7 比热容比γ＝的理想气体进行如图所示的循环．已知状态A 的温度为300 K ．求：(1) 状态B 、C 的温度； (2) 每一过程中气体所吸收的净热量．(普适气体常量R ＝ 11K mol J --⋅⋅)Vp p 2p 3)解：由图得 p A ＝400 Pa ， p B ＝p C ＝100 Pa ， V A ＝V B ＝2 m 3，V C ＝6 m 3．(1) C →A 为等体过程，据方程p A /T A = p C /T C 得 T C = T A p C / p A =75 KB →C 为等压过程，据方程V B /T B =V C T C 得 T B = T C V B / V C =225 K(2) 根据理想气体状态方程求出气体的物质的量(即摩尔数)ν 为ν = p A V A /RT A =0.321 mol由γ＝知该气体为双原子分子气体，R C V 25=，R C P 27= B →C 等压过程吸热 1400)(272-=-=B C T T R Q ν J ． C →A 等体过程吸热1500)(253=-=C A T T R Q ν J ． 循环过程ΔE =0，整个循环过程净吸热 600))((21=--==C B C A V V p p W Q J ． ∴ A →B 过程净吸热： Q 1=Q －Q 2－Q 3=500 J 例10-8 如图所示，体积为30L 的圆柱形容器内，有一能上下自由滑动的活塞（活塞的质量和厚度可忽略），容器内盛有1摩尔、温度为127℃的单原子分子理想气体．若容器外大气压强为1标准大气压，气温为27℃，求当容器内气体与周围达到平衡时需向外放热多少？（普适气体常量 R = J ·mol -1·K -1）解：开始时气体体积与温度分别为 V 1 =30×10－3 m 3，T 1＝127＋273＝400 K∴气体的压强为 p 1=RT 1/V 1 =×105 Pa 大气压p 0=×105 Pa ， p 1>p 0可见，气体的降温过程分为两个阶段：第一阶段等体降温，直至气体压强p 2 = p 0，此时温度为T 2，放热Q 1；第二阶段等压降温，直至温度T 3= T 0=27＋273 =300 K ，放热Q 2(1) )(23)(21211T T R T T C Q V -=-= K∴ Q 1= 428 J(2) )(25)(32322T T R T T C Q p -=-==1365 J ∴ 总计放热 Q = Q 1 + Q 2 = ×103 J例10-9 一热机从温度为 727℃的高温热源吸热，向温度为 527℃的低温热源放热．若热机在最大效率下工作，且每一循环吸热2000 J ，则此热机效率为 ；热机每一循环作功 J ．20% 400例10-10 两个卡诺热机的循环曲线如图所示，一个工作在温度为T 1与T 3的两个热源之间，另一个工作在温度为T 2 与T 3的 两个热源之间，已知这两个循环曲线所包围的面积相等．则：(A) 两个热机的效率一定相等．(B) 两个热机从高温热源所吸收的热量一定相等．(C) 两个热机向低温热源所放出的热量一定相等．(D) 两个热机吸收的热量与放出的热量（绝对值）的差值一定相等． [ D ] 活塞T 1 T 2 T 3 T 3 Vp O例10-11 温度分别为 327℃和27℃的高温热源和低温热源之间工作的热机，理论上的最大效率为(A) 25％ (B) 50％ (C) 75％ (D) ％ [ B ]例10-12 热力学第二定律表明：(A) 不可能从单一热源吸收热量使之全部变为有用的功．(B) 在一个可逆过程中，工作物质净吸热等于对外作的功．(C) 摩擦生热的过程是不可逆的．(D) 热量不可能从温度低的物体传到温度高的物体． [ C ]例10-13 “理想气体和单一热源接触作等温膨胀时，吸收的热量全部用来对外作功．”对此说法，有如下几种评论，哪种是正确的？(A) 不违反热力学第一定律，但违反热力学第二定律．(B) 不违反热力学第二定律，但违反热力学第一定律．(C) 不违反热力学第一定律，也不违反热力学第二定律．(D) 违反热力学第一定律，也违反热力学第二定律． [ C ]例10-14 一绝热容器被隔板分成两半，一半是真空，另一半是理想气体．若把隔板抽出，气体将进行自由膨胀，达到平衡后(A) 温度不变，熵增加． (B) 温度升高，熵增加．(C) 温度降低，熵增加． (D) 温度不变，熵不变． [ A ]【练习题】10-1 质量为0.02 kg 的氦气(视为理想气体)，温度由17℃升为27℃．若在升温过程中，(1) 体积保持不变；(2) 压强保持不变；(3) 不与外界交换热量；试分别求出气体内能的改变、吸收的热量、外界对气体所作的功．(普适气体常量R = 11K mol J --⋅)解：氦气为单原子分子理想气体，3=i(1) 等体过程，V ＝常量，W =0据 Q ＝∆E +W 可知 )(12T T C M M E Q V mol-=∆=＝623 J(2) 定压过程，p = 常量， )(12T T C M M Q p mol-==×103 J ∆E 与(1) 相同． W = Q - ∆E ＝417 J(3) Q =0，∆E 与(1) 同 W = -∆E=-623 J (负号表示外界作功)10-2 温度为25℃、压强为1 atm 的1 mol 刚性双原子分子理想气体，经等温过程体积膨胀至原来的3倍．(1) 计算这个过程中气体对外所作的功．(2) 假若气体经绝热过程体积膨胀为原来的3倍，那么气体对外作的功又是多少？ (普适气体常量R ＝ 1--⋅⋅K mol J 1，ln 3=解：(1) 等温过程气体对外作功为 ⎰⎰===000333ln d d V V V V RT V VRT V p W =×298× J = ×103 J (2) 绝热过程气体对外作功为 V V V p V p W V V V V d d 00003003⎰⎰-==γγRT V p 1311131001--=--=--γγγγ＝×103 J 10-3 ν 摩尔的某种理想气体，状态按p a V /=的规律变化(式中a 为正常量)，当气体体积从V 1膨胀到V 2时，气体所作的功W ＝ ；气体温度的变化T 1─T 2= ．).V /1V /1(a 212- ).V 1V 1(R a 212-ν (SI) 10-4 一定量的刚性双原子分子理想气体，开始时处于压强为 p 0 = ×105 Pa ，体积为V 0 =4×10-3 m 3，温度为T 0 = 300 K 的初态，后经等压膨胀过程温度上升到T 1 = 450 K ，再经绝热过程温度降回到T 2 = 300 K ，求气体在整个过程中对外作的功．解：等压过程末态的体积 1001T T V V = 等压过程气体对外作功 )1()(01000101-=-=T T V p V V p W =200 J 根据热力学第一定律，绝热过程气体对外作的功为 W 2 =－△E =－νC V (T 2－T 1) 这里 000RT V p =ν，R C V 25=，则500)(25120002==--=T T T V p W J 气体在整个过程中对外作的功为 W = W 1+W 2 =700 J ．10-5 一定量的单原子分子理想气体，从A 态出发经等压过程膨胀到(m 3) p 1×4×B 态，又经绝热过程膨胀到C 态，如图所示．试求这全过程中气体对外所作的功，内能的增量以及吸收的热量．解：由图可看出 p A V A = p C V C 从状态方程 pV =νRT 可知T A =T C ，因此全过程A →B →C 的∆E =0．B →C 过程是绝热过程，有Q BC = 0．A →B 过程是等压过程，有 )(25)( A A B B A B p AB V p V p T T C Q -=-=ν＝×105 J ． 故全过程A →B →C 的 Q = Q BC +Q AB =×105 J ． 根据热一律Q =W +∆E ，得全过程A →B →C 的 W = Q －∆E ＝×105 J ．10-6 一定量的某种理想气体，开始时处于压强、体积、温度分别为p 0=×106 Pa ，V 0=×10－3m 3，T 0=300K的初态，后经过一等体过程，温度升高到T 1=450K ，再经过一等温过程，压强降到p =p 0的末态．已知该理想气体的等压摩尔热容与等体摩尔热容之比C p /C V =5/3．求：(1) 该理想气体的等压摩尔热容C p 和等体摩尔热容C V ．(2) 气体从始态变到末态的全过程中从外界吸收的热量． (普适气体常量R = J·mol －1·K －1) 解：(1) 由 35=V p C C 和 R C C V p =- 可解得 R C p 25= 和 R C V 23= (2) 该理想气体的摩尔数 ==000RT V p ν 4 mol 在全过程中气体内能的改变量为 △E =ν C V (T 1－T 2)=×103 J 全过程中气体对外作的功为 011lnp p RT W ν= 式中p 1 ∕p 0=T 1 ∕T 0 则 30111006.6ln ⨯==T T RT W ν J ． 全过程中气体从外界吸的热量为 Q = △E +W =×104 J ． 10-7 一定量的单原子分子理想气体，从初态A 出发，沿图示直线过程变到另一状态B ，又经过等容、等压两过程回到状态A ． (1) 求A →B ，B →C ，C →A 各过程中系统对外所作的功W ，内能的增量∆E 以及 所吸收的热量Q ．（2）整个循环过程中系统对外所作的总功以及从外界吸收的总热量(过程吸热的代数和)． 解：(1) A →B ： ))((211A B A B V V p p W -+==200 J ． ΔE 1=ν C V (T B －T A )=3(p B V B －p A V A ) /2=750 J Q =W 1+ΔE 1＝950 J ．B →C ： W 2 =0 ΔE 2 =ν C V (T C －T B )=3( p C V C －p B V B ) /2 =－600 J ． Q 2 =W 2+ΔE 2＝－600 J ．C →A ： W 3 = p A (V A －V C )=－100 J ． 150)(23)(3-=-=-=∆C C A A C A V V p V p T T C E ν J ． Q 3 =W 3+ΔE 3＝－250 J(2) W = W 1 +W 2 +W 3=100 J ． Q = Q 1 +Q 2 +Q 3 =100 J1231 2 O V (10-3 m 3) 5 A B C10-8 一卡诺热机(可逆的)，低温热源的温度为27℃，热机效率为40％，其高温热源温度为 K ．今欲将该热机效率提高到50％，若低温热源保持不变，则高温热源的温度应增加 K ．500 10010-9 有一卡诺热机，用290 g 空气为工作物质，工作在27℃的高温热源与 -73℃的低温热源之间，此热机的效率η＝ ．若在等温膨胀的过程中气缸体积增大到倍，则此热机每一循环所作的功为 ．(空气的摩尔质量为29×10-3 kg/mol ，普适气体常量R ＝ 11K mol J --⋅⋅)％ ×103 J10-10 1mol 单原子分子理想气体的循环过程如T －V 图所示，其中c 点的温度为T c =600 K ．试求：(1) ab 、bc 、c a 各过程系统吸收的热量；(2) 经一循环系统所作的净功；(3) 循环的效率． (循环效率η=W /Q 1，W 为循环过程系统对外作的净功，Q 1为循环过程系统从外界吸收的热量ln2=解：(单原子分子的自由度i =3．从图可知，ab 是等压过程， V a /T a = V b /T b ，T a =T c =600 K T b = (V b /V a )T a =300 K(1) )()12()(c b c b p ab T T R iT T C Q -+=-= =－×103 J (放热))(2)(b c b c V bc T T R i T T C Q -=-= =×103 J (吸热) Q ca =RT c ln(V a /V c ) =×103 J (吸热)(2) W =( Q bc +Q ca )－|Q ab |=×103 J(3) Q 1=Q bc +Q ca ， η=W / Q 1=%10-11 1 mol 单原子分子的理想气体，经历如图所示的可逆循环，联结ac 两点的曲线Ⅲ的方程为2020/V V p p =, a 点的温度为T 0 试以T 0 , 普适气体常量R 表示Ⅰ、Ⅱ、Ⅲ过程中气体吸收的热量。

大学物理热力学第二定律知识点总结热力学第二定律是大学物理热学部分的重要内容，它揭示了热现象过程中的方向性和不可逆性。

理解和掌握热力学第二定律对于深入研究热学以及相关领域具有重要意义。

以下是对热力学第二定律相关知识点的详细总结。

一、热力学第二定律的表述1、克劳修斯表述热量不能自发地从低温物体传向高温物体。

这意味着热传递的过程具有方向性，如果没有外界的干预，热量只会从高温物体流向低温物体，而不会反向流动。

2、开尔文表述不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响。

也就是说，第二类永动机是不可能制成的。

第二类永动机是指一种能够从单一热源吸热，并将其全部转化为功，而不产生其他变化的热机。

二、热力学第二定律的微观解释从微观角度来看，热力学第二定律反映了大量分子热运动的无序性。

在一个孤立系统中，分子的热运动总是从有序趋向无序，这是一个自发的过程。

比如，将不同温度的气体混合在一起，它们会自发地达到温度均匀分布的状态，而不会自动地分离成原来的不同温度区域。

这是因为分子的无规则运动使得它们更容易趋向无序的分布。

三、熵熵是描述系统无序程度的热力学概念。

熵的增加表示系统的无序程度增加。

对于一个绝热过程，系统的熵永不减少。

如果是可逆绝热过程，熵不变；如果是不可逆绝热过程，熵增加。

熵的计算公式为：＄dS ＝＼frac{dQ}｛T}＄，其中＄dQ$ 是微元过程中的吸热量，＄T$ 是热力学温度。

四、卡诺循环与卡诺定理1、卡诺循环卡诺循环由两个等温过程和两个绝热过程组成，是一种理想的热机循环。

通过卡诺循环，可以计算出热机的效率。

卡诺热机的效率为：＄＼eta ＝ 1 ＼frac{T_2}｛T_1}＄，其中＄T_1$ 是高温热源的温度，＄T_2$ 是低温热源的温度。

2、卡诺定理（1）在相同的高温热源和低温热源之间工作的一切可逆热机，其效率都相等，与工作物质无关。

（2）在相同的高温热源和低温热源之间工作的一切不可逆热机，其效率都小于可逆热机的效率。