基于WEBENCH的巴特沃斯低通滤波器的设计

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展，各种科技产品在人类社会中随处可见，极大的丰富了人们的日常生活。

物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。

就目前而言，在几乎所有的电子产品中，各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用，例如可穿戴设备的语音信号输入系统中，运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除，来提高系统的音质和语音识别精准度等。

本论文通过对各种低通滤波器的通频带、增益和截止频率的分析，采用通频带最大扁平度技术（巴特沃斯技术）来设计实现四阶高性能低通滤波器，通过Multisum仿真软件，验证了设计的正确性。

在这基础上，本文还对如何提高该滤波器的响应速度进行了研究，提出了一种有效的提高响应速度的方案，并通过仿真软件得以验证。

这在低通滤波器的理论以及实际工程应用中，都具有非常重要的意义。

关键词：有源低通滤波器，巴特沃斯，运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS：active low-pass filter，butterworth，amplifier1绪论1.1 引言在近现代的科技发展中，滤波器作为一种必不可少的组成成分，在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展，各种科技产品在人类社会中随处可见，极大的丰富了人们的日常生活。

物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。

就目前而言，在几乎所有的电子产品中，各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用，例如可穿戴设备的语音信号输入系统中，运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除，来提高系统的音质和语音识别精准度等。

本论文通过对各种低通滤波器的通频带、增益和截止频率的分析，采用通频带最大扁平度技术（巴特沃斯技术）来设计实现四阶高性能低通滤波器，通过Multisum仿真软件，验证了设计的正确性。

在这基础上，本文还对如何提高该滤波器的响应速度进行了研究，提出了一种有效的提高响应速度的方案，并通过仿真软件得以验证。

这在低通滤波器的理论以及实际工程应用中，都具有非常重要的意义。

关键词：有源低通滤波器，巴特沃斯，运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS：active low-pass filter，butterworth，amplifier1绪论1.1 引言在近现代的科技发展中，滤波器作为一种必不可少的组成成分，在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。

巴特沃斯数字低通滤波器课程设计目录1.题目.......................................................................................... .22.要求 (2)3.设计原理 (2)3.1 数字滤波器基本概念 (2)3.2 数字滤波器工作原理 (2)3.3 巴特沃斯滤波器设计原理 (3)3.4脉冲响应不法 (5)3.5实验所用MATLAB函数说明 (7)4.设计思路 (9)5、实验内容 (9)5.1实验程序 (9)5.2实验结果分析 (13)6.设计总结 (13)7.参考文献 (14)一、题目：巴特沃斯数字低通滤波器二、要求：利用脉冲响应不变法设计巴特沃斯数字低通滤波器，通带截止频率100HZ,阻带截止频率120Hz,采样频率1000HZ，通带最大衰减为0.5HZ，阻带最小衰减为10HZ，画出幅频、相频相应曲线。

并假设一个信号x(t)=sin(2*pi*f1*t)+sin(2*pi*f2*t),其中f1=50HZ,f2=200HZ。

用此信号验证滤波器设计的正确性。

三、设计原理1、数字滤波器的基本概念所谓数字滤波器，是指输入、输出均为数字信号，通过数值运算处理改变输入信号所含频率成分的相对比例，或者滤波器除某些频率成分的数字器件或程序，因此，数字滤波的概念和模拟滤波相同，只是的形式和实现滤波方法不同。

正因为数字滤波通过数值运算实现滤波，所以数字滤波处理精度高、稳定、体积小、质量轻、灵活、不存在阻抗匹配问题，可以实验模拟滤波器无法实现的特殊滤波功能。

如果要处理的是模拟信号，可通过A\DC和D\AC,在信号形式上进行匹配转换，同样可以使用数字滤波器对模拟信号进行滤波。

2、数字滤波器的工作原理数字滤波器是一个离散时间系统，输入x(n)是一个时间序列，输出y(n)也是一个时间序列。

如数字滤波器的系统函数为H(Z),其脉冲响应为h(n),则在时间域内存在下列关系y(n)=x(n) h(n)在Z域内，输入输出存在下列关系Y(Z)=H(Z)X(Z)式中，X(Z),Y(Z)分别为输入x(n)和输出y(n)的Z 变换。

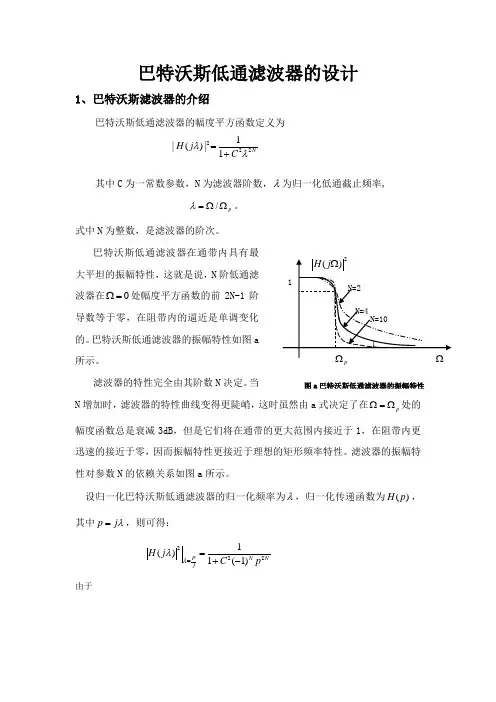
巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数，N 为滤波器阶数，λ为归一化低通截止频率,/p λ=ΩΩ。

式中N 为整数，是滤波器的阶次。

巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性，这就是说，N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零，在阻带内的逼近是单调变化的。

巴特沃斯低通滤波器的振幅特性如图a 所示。

滤波器的特性完全由其阶数N 决定。

当N 增加时，滤波器的特性曲线变得更陡峭，这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ，但是它们将在通带的更大范围内接近于1，在阻带内更迅速的接近于零，因而振幅特性更接近于理想的矩形频率特性。

滤波器的振幅特性对参数N 的依赖关系如图a 所示。

设归一化巴特沃斯低通滤波器的归一化频率为λ，归一化传递函数为()H p ，其中p j λ=，则可得：2221()1(1)N NpjH j C pλλ==+- 由于p图a 巴特沃斯低通滤波器的振幅特性221()()()1()a a jsNcH s H s A s j Ω=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。

2、常用设计巴特沃斯低通滤波器指标p λ：通带截止频率； p α：通带衰减，单位：dB ；s λ：阻带起始频率；s α：阻带衰减，单位：dB 。

说明：（1）衰减在这里以分贝（dB ）为单位；即222110lg10lg 1()NC H j αλλ⎡⎤==+⎣⎦（2）当3dB α=时p C Ω=Ω为通常意义上的截止频率。

（3）在滤波器设计中常选用归一化的频率/C λ=ΩΩ，即1,p sp s ppλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下：（1）计算归一化频率1p p pλΩ==Ω，ss pλΩ=Ω。

（2） 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ；注意当3p dB α=时 C=1。

电路基础课程设计巴特沃斯低通滤波器设计目标:通带边界频率ωc=4396rad/s (f c=700Hz);通带最大衰减αmax=3dB;阻带边界频率ωs=26376rad/s(f s=4200Hz); 阻带最小衰减αmin=30dB;1.设计步骤⑴设计电压转移函数①将给定的电压衰减技术指标进行频率归一化选取归一化角频率ωr=ωc，这样通带边界频率Ωc=ωc/ ωr=1,阻带边界频率Ωs=ωs/ ωr=ωs/ωc。

②根据归一化的技术指标求出电压转移函数巴特沃斯低通滤波器的阶数n=Log(100.1αmin−1) 2Log(Ωs)带入数据求得n=1.93 取整得n=2由a k=2sin(2k−1)π2n，b k=1和H(s)=U out(s)U in(s)=∏A ks2+a k s+b kn2k=1可得到电压转移函数H(s)=U out(s)U in(s)=1s2+√2s+1将转移函数进行反归一化，即另s=sωc 得到实际转移函数H(s)=U out(s)U in(s)=1s243962+√2s4396+1⑵转移函数的实现选取下图作为实现转移函数的具体电路：列节点方程求解转移函数节点1 U1(1R1+1R2+s∗C1)−1R1U in−1R2−s∗C1∗U2=0节点2 (1R2+s∗C2)U2−1R2U1=0又有U out=U3解得H(s)=U outU in=11+(R2+R2)s∗C2+C1C2R1R2s2对比解得的电压转移函数和推得的电压转移函数里各项的系数并且令R1= R2,C1=1μF,可以得到C1=11000000F=1μFR1=250000√21099Ω=321.705ΩR2=250000√21099Ω==321.705ΩC2=12000000F=0.5μF因实验室没有0.5μF的电容因此取C2=0.47μF2.计算机仿真⑴软件环境：Multisim 10⑵电路图：⑶仿真结果：①700Hz下的波形图②4200Hz下的波形图③波特图◎700Hz下衰减2.673dB◎4200Hz下衰减30.491dB3．实验室实际操作因实验室没有0.5μF的电容和321.705Ω的电阻，因此取C2=0.47μFR1=R2=330Ω实际连电路时，选取集成电路块的第1、2、3引脚分别作为放大器的输出端、负端和正端，第4和11引脚作为供电端，C2一端连接电压源的接地线。

巴特沃斯低通滤波器的设计巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数，N 为滤波器阶数，λ为归一化低通截止频率,/p λ=ΩΩ。

式中N 为整数，是滤波器的阶次。

巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性，这就是说，N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零，在阻带内的逼近是单调变化的。

巴特沃斯低通滤波器的振幅特性如图a 所示。

滤波器的特性完全由其阶数N 决定。

当N 增加时，滤波器的特性曲线变得更陡峭，这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ，但是它们将在通带的更大范围内接近于1，在阻带内更迅速的接近于零，因而振幅特性更接近于理想的矩形频率特性。

滤波器的振幅特性对参数N 的依赖关系如图a 所示。

设归一化巴特沃斯低通滤波器的归一化频率为λ，归一化传递函数为()H p ，其中p j λ=，则可得：2221()1(1)N Np jH j C pλλ==+-p 图a 巴特沃斯低通滤波器的振幅特性由于221()()()1()a a jsNcH s H s AsjΩ=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。

2、常用设计巴特沃斯低通滤波器指标pλ：通带截止频率；pα：通带衰减，单位：dB；sλ：阻带起始频率；sα：阻带衰减，单位：dB。

说明：（1）衰减在这里以分贝（dB）为单位；即222110lg10lg1()NCH jαλλ⎡⎤==+⎣⎦（2）当3dBα=时p CΩ=Ω为通常意义上的截止频率。

（3）在滤波器设计中常选用归一化的频率/Cλ=ΩΩ，即1,p sp sp pλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下：（1）计算归一化频率1p p pλΩ==Ω，ss pλΩ=Ω。

（2） 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ；注意当3p dB α=时 C=1。

基于巴特沃斯的数字滤波器设计付嘉琦(陕西理工学院物理与电信工程学院通信专业1102班，陕西汉中 723000)指导教师：陈莉[摘要]本文分析了国内外数字滤波技术的应用现状与发展趋势，介绍了数字滤波器的基本结构，并深入分析了该滤波器系统设计的功能特点、实现原理以及技术关键，阐述了使用Matlab进行滤波器设计及仿真的具体方法，而且设计了以Matlab为基础的基于巴特沃斯型的低通、带通、带阻、高通数字滤波器。

调试结果表明，本系统功能已达到设计的各项要求。

[关键词]Matlab;巴特沃斯；数字滤波器；Digital Filter Design with ButterworthFu Jiaqi(Grade11,Class 2,Major of Communication Engineering，School of Physics and telecommunication Engineering of Shaanxi University of Technology, Hanzhong 723001,China)Tutor: Chen Li[Abstract] This paper analyzes the situation of application and development of digital filter technology home and abroad. It introduces the basic structure of a digital filter and deeply analyzes the design features and principles of the filter system and the key technical in the design. Then it describs the use of Matlab in design and simulation of the digital filte design. And design based on Matlab with butterworth lowpass, bandpass, band stop, highpass digital filter .The result enunciation of debug, various functions of this system are already all request of this design.[Keywords] Matlab; Butterworth；Digital Filter;目录1.数字滤波器的简介 (1)1.1 数字滤波器的研究背景 (1)1.2 数字滤波器的研究意义 (1)1.3 数字滤波器的应用现状 (1)1.4 数字滤波器的发展趋势 (3)2.系统的总体设计 (4)2.1数字滤波器的实现方法分析 (4)2.2数字滤波器的基本结构 (4)2.2.1IIR滤波器的基本结构 (4)2.2.2 FIR滤波器的基本结构 (6)2.2.3 IIR数字滤波器的设计方法 (7)2.2.4 FIR数字滤波器的设计方法 (8)2.2.5 IIR滤波器与FIR滤波器的分析比较 (9)2.3数字滤波器的设计原理 (10)2.4本章小节 (11)3. 数字滤波器的算法设计 (12)3.1由模拟滤波器设计IIR数字滤波器 (12)3.2巴特沃斯滤波器 (12)3.3 MATLAB概述 (13)3.4用MA TLAB设计数字滤波器 (14)4.滤波器仿真过程 (15)4.1设定系统的仿真对象 (15)4.2系统对象滤波器设计方法 (15)4.3 MA TLAB程序仿真及结果分析 (15)4.3.1 低通数字滤波器仿真设计 (15)4.3.2 带通数字滤波器仿真设计 (16)4.3.3 带阻数字滤波器仿真设计 (17)4.3.4 高通数字滤波器仿真设计 (18)4.3.5数字滤波器整体仿真结果 (18)5.总结及体会 (21)致谢 (22)参考文献 (23)1.数字滤波器的简介1.1数字滤波器的研究背景当今，数字信号处理(DSP：Digtal Signal Processing)技术正飞速发展，它不但自成一门学科，更是以不同形式影响和渗透到其他学科：它与国民经济息息相关，与国防建设紧密相连；它影响或改变着我们的生产、生活方式，因此受到人们普遍的关注。

巴特沃斯低通滤波器一、设计要求（1）设计一巴特沃斯数字低通滤波器，在0.3π通带频率范围内，通带幅度波动小于1dB ，在0.5π~πrad 阻带频率范围内，阻带衰减大于12dB 。

二．设计过程巴特沃斯双线性变换法（1）数字指数:p w =0.3π，s w =0.5π，（2）求p Ω，s Ω利用频率预畸变公式得：p Ω=2T tan 2p w =2T tan 320π=1.019⨯1Ts Ω=2T tan 2s w =2T tan 4π=2T (3)确定滤波器阶数sp λ=s p ΩΩ=211.019TT ⨯=1.963 sp k≈0.132 N=—lg lg sp sp k λ=—lg 0.132lg1.963≈3.0023 N=4 (4)确定系统函数G(p)= 43212.613 3.4142 2.61311p p p p ++++ c Ω=p Ω()10.12101p a N --=1.019⨯1T⨯()10.1124101-⨯⨯-=1.2065T P=11211c s z s T z ---=Ω+=1c Ω⨯2T ⨯1111z z ---+=11211.20651z z ---+ H(z)=G(p)=12341234146434.1675441.3465432.542711.06234 1.69864z z z z z z z z--------++++-+-+三．软件仿真（1）将分子分母带入Matlab 验证b=[1 4 6 4 1];a=[34.16754 -41.34654 32.5427 -11.06234 1.69864];[H,w]=freqz(b,a,1000);plot(w,20*log10(abs(H)/max(H)),'-');grid;xlabel('frequency');ylabel('magnitude');-250-200-150-100frequency m a g n i t u d e图（a ）频率——幅度衰减图0.3π≈0.940.9250.930.9350.940.9450.950.955frequency m a g n i t u d e图(b)0.5π≈1.57frequency m a g n i t u d e图(c)（2）用Matlab 直接仿真出低通滤波器wp=2*tan(0.3*pi/2)*1000;ws=2*tan(0.5*pi/2)*1000;ap=1;as=12;[n,wn]=buttord(wp,ws,ap,as,'s');[b,a]=butter(n,wn,'s');[bn,an]=bilinear(b,a,1000);[H,w]=freqz(bn,an);plot(w,abs(H),'-');grid;xlabel('frequency');ylabel('magnitude');legend('双线性变化法');figure(2);plot(w,20*log10(abs(H)/max(H)),'-');grid;00.51 1.522.533.5frequency m a g n i t u d e0.3π≈0.94图(d)0.5π≈1.57图（e）四．分析将计算得出的低通滤波器系统函数H（z）的分子分母各项系数用Matlab验证，得图（a）幅频关系图。

电子技术课程设计----巴特沃斯数字低通滤波器的设计专业年级：姓名：学号：指导教师：日期：巴特沃斯数字低通滤波器的设计一、选题依据滤波器是能够过滤波动信号的电路, 它可以从具有各种不同频率成分的信号中, 取出具有特定频率成分的信号。

滤波器在信号处理、数据采集和传输、干扰抑制方面应用非常广泛, 其性能优劣直接影响整个系统的性能, 所以滤波器的设计在很多领域必不可少, 而且至关重要。

由于理想滤波器的特性难以实现, 在设计滤波器时关键是选择一个合适的逼近函数, 使其频率特性满足所需滤波器的所有要求。

目前比较成熟的逼近函数有巴特沃斯、切比雪夫、椭圆函数和贝塞尔滤等。

但是无论用哪种逼近函数设计滤波器都要经过繁琐的计算, 而且通过综合设计确定实现这个传递函数的电路及其元器件的方法也很复杂。

本文介绍了一种利用归一化表经过简单的计算就可以快速设计滤波器的方法。

模拟滤波器可以分为有源滤波和无源滤波两大类, 其中有源滤波器是由R、C 元件和OP 放大器构成。

与无源滤波器相比, 它具有易集成、易标准化、易制造、输出电阻低且不受负载影响, 体积小等优点。

因此得到了更加广泛的应用。

目前可实现的滤波器中巴特沃斯滤波器具有通带内响应平坦, 衰减特性和相位特性好, 对构成滤波器的器件的要求不甚严格, 易于得到符合设计值的特性, 适应性强, 在不知道使用哪种函数合适的情况下, 可以选择巴特沃斯型滤波器, 本文设计的就是巴特沃斯低通滤波器。

滤波器从广义上来说对特定的频点或频点以外的频率进行有效滤波的电路，这种电路保留输入信号中的有用信息，滤除不需要的信息，从而达到信号的检测、提取、识别等不同的目的。

如果处理的信号是时域离散信号，那么相应的处理系统就称为数字滤波器，由于在实际工作中被处理的信号都是幅度量化的数字信号，因此，数字滤波器实际上是用有限精度的算法实现一个线性时不变的时域离散系统。

目前，数字滤波器的应用越来越广泛，它已深入到很多领域，如图象处理、医学生物信息处理、地质信号处理和模式识别处理等。

巴特沃斯数字低通滤波器的设计与研究2013年11月11日一、matlab上的相关函数[N,wc]=buttord(wp, ws, αp, αs)用于计算巴特沃斯数字滤波器的阶数N和3dB截止频率wc。

调用参数wp，ws分别为数字滤波器的通带、阻带截止频率的归一化值，要求：0≤wp ≤1，0≤ws≤1。

1表示数字频率pi。

αp，αs分别为通带最大衰减和组带最小衰减（dB）。

[b，a]=butter(N, wc, ’ftype’)计算N阶巴特沃斯数字滤波器系统函数分子、分母多项式的系数向量b、a。

调用参数N和wc分别为巴特沃斯数字滤波器的阶数和3dB截止频率的归一化值（关于pi归一化），一般是调用buttord（1）格式计算N和wc。

系数b、a是按照z^-1的升幂排列。

二、巴特沃斯数字低通滤波器的设计及分解成SOS形式设计巴特沃斯数字低通滤波器，其中采样频率为1000Hz，巴特沃斯滤波器参数为n=4，wc=0.1π。

得到的数字滤波器传递函数为将SOS结合为gn对比发现gn与gz无差别。

三、巴特沃斯滤波器参数选择的影响研究巴特沃斯滤波器设计函数butter有两个关键的参数N和wc，下面研究参数选择对以下几个方面的影响：①滤波器曲线形状；②传递函数gz中az的系数大小；③传递函数gz拆分成的SOS的系数大小。

说明：max(abs(az))和min(abs(az))，分别指az中的系数最大、最小值。

Maxnum，minnum，分别指各SOS中统计出的系数最大、最小值。

（1）N的选择曲线图可见，随着n的增加，az系数的最大最小值数量级差异快速增大，而通过SOS分解后这种差异变化缓慢很多。

N的变化影响着曲线的斜度。

（2）wc的选择保持n=8，改变wc，结果如下：曲线图系数变化上有着与前面探讨n有同样的结论。

Wc的变化相当于曲线沿着f轴平移。

四、巴特沃斯滤波器SOS方式设计1.N=8，fs=2000HzDiscrete-time transfer function. Discrete-time transfer function.0.7π0.8πDiscrete-time transfer function. Discrete-time transfer function.2.N=6，fs=2000HzDiscrete-time transfer function.Discrete-time transfer function.0.7π0.8πDiscrete-time transfer function.Discrete-time transfer function.3. N=4，fs=2000HzDiscrete-time transfer function.Discrete-time transfer function.4. N=2，fs=2000HzDiscrete-time transfer function. Discrete-time transfer function.以下为wc=0.1π~0.4π的数据。