信号与系统习题

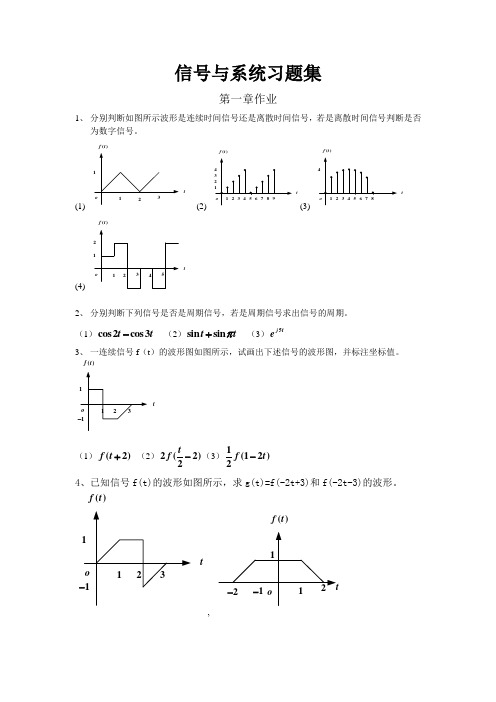
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号，若是离散时间信号判断是否为数字信号。

(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号，若是周期信号求出信号的周期。

（1）cos 2cos 3t t - （2）sin sin t t π+ （3）5j te3、 一连续信号f （t ）的波形图如图所示，试画出下述信号的波形图，并标注坐标值。

t()f t（1）(2)f t + （2）2(2)2t f -（3）1(12)2f t- 4、已知信号f(t)的波形如图所示，求g(t)=f(-2t+3)和f(-2t-3)的波形。

t()f t,()f t5、写出如图所示的各波形的函数式。

（1）t()f t（2）t()f t-6、画出下列各时间函数的波形。

（1）[](1)(2)t u t u t ---，（2）[](1)(2)(2)t u t u t u t ---+- （3）[](3)()(2)t u t u t --- 7、求下列函数值。

（1）2()()td r te u t dt-⎡⎤=⎣⎦，（2）3()()t r t e t δ-= （3）()cos ()4r t t t dt πδ∞-∞=-⎰，（4）2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。

()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的，时不变的，因果的？ （1）()(2)r t e t =- （2）()(3)r t e t = （3）()()(1)r t e t u t =- （4）()()r t te t =第二章作业1、已知系统的电路图如图所示，写出电压()o v t 的微分方程。

()e tR +-()o v t2、已知系统的微分方程和起始状态如下，求齐次解。

第一章绪论1、选择题1.1、f （5-2t ）是如下运算的结果 CA 、 f （-2t ）右移5B 、 f （-2t ）左移5C 、 f （-2t ）右移25 D 、 f （-2t ）左移251.2、f （t 0-a t ）是如下运算的结果 C 。

A 、f （-a t ）右移t 0；B 、f （-a t ）左移t 0 ；C 、f （-a t ）右移a t 0；D 、f （-a t ）左移at0 1.3、已知 系统的激励e(t)与响应r(t)的关系为：)()()(t u t e t r = 则该系统为 B 。

A 、线性时不变系统；B 、线性时变系统；C 、非线性时不变系统；D 、非线性时变系统 1.4、已知 系统的激励e(t)与响应r(t)的关系为：)()(2t e t r = 则该系统为 C 。

A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.5、已知 系统的激励e(t)与响应r(t)的关系为：)1()(t e t r -= 则该系统为 B 。

A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e(t)与响应r(t)的关系为：)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。

A 、π2 B 、π C 、2π D 、π21.8、信号)30cos()10cos(2)(t t t f -=的周期为： B 。

A 、15π B 、5π C 、π D 、10π1.9、dt t t )2(2cos 33+⎰-δπ等于 B 。

A.0 B.-1 C.2 D.-21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是： BA. )(t x -表示将此磁带倒转播放产生的信号B. )2(t x 表示将此磁带放音速度降低一半播放C. )(0t t x -表示将此磁带延迟0t 时间播放D. )(2t x 表示将磁带的音量放大一倍播放 1.11.=⋅)]([cos t u t dtdA A ．)()(sin t t u t δ+⋅- B. t sin - C. )(t δ D.t cos1.12．信号t t t x o 2cos 4)304cos(3)(++=的周期为 B 。

信号与系统考试题及答案（一）1． 系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3． 当信号是脉冲信号f(t)时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。

4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。

7． 若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 。

9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t-=21，信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

信号与系统专题练习题一、选择题1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。

A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。

A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。

A t>3 B t=0 C t<9 D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C 。

A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 BA. )()2(t t δδ= B 。

)(21)2(t t δδ= C. )(2)2(t t δδ= D 。

)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。

已知 系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。

⎰∞-=t d ττττδ2sin )( A 。

A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。

A 0 B —1 C 2 D —211．线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置；B 激励信号的形式;C 系统起始状态；D 以上均不对。

12．若系统的起始状态为0，在x （t)的激励下，所得的响应为 D . A 强迫响应;B 稳态响应；C 暂态响应;D 零状态响应。

练习题一、 单项选择题（共35题）1.下列信号中为周期信号的是【 B 】(A) t t t f πsin 2cos )(+= (B) t t t f 3cos 2sin )(+=(C) t t t f πsin 2cos 3)(+=(D))(cos )(t t t f επ=2. 积分dt t t e t ∫∞∞−−+)]()(['2δδ等于【 D 】(A) -1 (B)1 (C) 2 (D) 3 3. 卷积积分)()(t t t εε∗等于【 C 】(A) )(2t t ε (B) )(t t ε (C) )(212t t ε (D) )(2t t ε4. 卷积和)]1()([)(−−∗k k k δδε等于【 A 】(A) )(k δ (B) )1(−k δ (C) )2(−k δ (D) )(k ε5. 信号)()(2t e t f t ε−=的频谱函数)(ωj F 等于【 B 】(A)ωj 1 (B) ωj +21 (C) ωj −21 (D) ωj +−21 6. 系统的幅频特性|H (j ω)|和相频特性如图(a)(b)所示，则下列信号通过该系统时，不产生失真的是【 B 】(A) f (t ) = cos(t ) + cos(8t ) (B) f (t ) = sin(2t ) + sin(4t ) (C) f (t ) = sin(2t ) sin(4t ) (D) f (t ) = cos 2(4t )7. 象函数ses F −+=11)(的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t δ (B) )1(−t δ (C) )1()(−+t t δδ (D) )1()(−−t t δδ8.函数)]()[sin()(22t t dt d t f επ=的拉普拉斯变换=)(s F 【 C 】(A) 222π+s s (B) 22ππ+s (C) 222ππ+s s (D) 22ππ+s s 9. 序列)1(2)(2)(−−+=−k k k f k k εε的双边Z 变换=)(z F 【 B 】 (A)221,)2)(12(3<<−−z z z z (B) 221,)2)(12(3<<−−−z z z z(C)21,)2)(12(3>−−−z z z z (D) 2,)2)(12(3<−−−z z z z10. 象函数)2)(1()(2−+=z z z z F 其收敛域为2>z ，则其原序列=)(k f 【 A 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(3231[k k ε+(C) )(])2(32)1(31[k k k ε−+− (D) )1(])2(32)1(31[−−+−k k k ε11. 积分dt t t )(4sin(91δπ∫−−等于【 B 】(A)22(B) 22− (C) 2 (D) 2− 12. 卷积积分)()(t t εε∗等于【 C 】(A) )(2t ε (B) )(t ε (C) )(t t ε (D) 1 13. 卷积和)1()1(−∗−k k δε等于【 A 】(A) )2(−k ε (B) )(k ε (C) )1(−k δ (D) )2(−k δ 14. 信号t t f 2cos )(=的频谱函数)(ωj F 等于【 D 】(A) )1()1(++−ωδωδ (B) )]1()1([++−ωδωδπ (C))2()2(++−ωδωδ (D) )]2()2([++−ωδωδπ15. 已知)()(ωj F t f ↔，则函数)()2(t f t −的频谱函数为【 C 】(A))(2)(ωωωj F d j dF − (B) )(2)(ωωωj F d j dF +(C) )(2)(ωωωj F d j dF j− (D) )(2)(ωωωj F d j dF j + 16. 信号)1()()(−−=t t t f εε的拉普拉斯变换等于【 D 】(A))1(se − (B))1(1s e s − (C) )1(se −− (D) )1(1s e s−− 17. 象函数)1(1)(2s e s s F −+=的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t ε (B) )2(−t ε (C))2()(−+t t εε (D))2()(−−t t εε18. 序列)()1()(k k k f ε+=的双边Z 变换=)(z F 【 A 】(A) 1,)1(22>−z z z (B) 1,)1(22>+z z z(C) 1,)1(22<−z z z (D) 1,)1(22<+z z z 19. 象函数)2)(1()(2−+=z z z z F 其收敛域为1<z ，则其原序列=)(k f 【 D 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(32)1(31[k k k ε−−−(C))1(])2(32)1(31[−−+−k k k ε (D) )1(])2(32)1(31[−−−−−k k k ε20.)]([)1(t e dtdt t δ−−等于【 A 】 (A) )()('t t δδ+ (B) )()('t t δδ−(C) )(2)('t t δδ+ (D) )(2)('t t δδ−21.积分dt t t )1()4sin(03−−∫−δπ等于【 B 】(A) 1 (B) 0 (C)2 (D)322.)]([2t e dtdt ε−等于【 C 】(A) )()(2t et tεδ−− (B) )()(2t et tεδ−+ (C) )(2)(2t et tεδ−− (D) )(2)(2t et tεδ−+23. 积分dt t t ∫∞∞−−)('2)2(δ等于【 D 】 (A) 1 (B)2 (C) 3 (D) 424. 积分dt t t t ∫∞∞−)()2sin(δ等于【 B 】 (A) 1 (B)2 (C) 3 (D) 425. 卷积积分)]2()([)(−−∗t t t εεε等于【 D 】(A) )2()(−−t t t t εε (B) )2()(−+t t t t εε (C) )2()2()(−−+t t t t εε (D) )2()2()(−−−t t t t εε 26. 卷积积分)(')(t t δε∗等于【 C 】(A) )(2t δ (B) )(2t δ− (C) )(t δ (D) )(t δ− 27. 卷积积分)1()1(+∗−t t εε等于【 A 】(A) )(t t ε (B) )()1(t t ε− (C) )()2(t t ε− (D) )()1(t t ε+ 28. 卷积和)2()1(−∗−k k δδ等于【 D 】(A) )2(−k δ (B) )(k δ (C) )1(−k δ (D) )3(−k δ29. 已知卷积和)()1()()(k k k k εεε+=∗，则)4()3(−∗−k k εε等于【 B】(A) )6()6(−−k k ε (B) )7()6(−−k k ε (C) )6()7(−−k k ε (D) )7()7(−−k k ε 30.)]()2[cos(t t dtdε 的拉普拉斯变换等于【 C 】 (A)442+s (B) 442+−s(C)422+ss (D) 422+−ss31. 信号)()(t t t f ε=的拉普拉斯变换等于【 D 】(A)22s− (B)22s (C)21s− (D)21s32. 序列)(3)(2)(k k k f εδ+=的双边Z 变换=)(z F 【 A 】(A) 1,132>−+z z z (B) 1,132>−−z z z(C) 1,132>−+−z z z (D) 1,132>−−−z z z33. 序列)()(k k k f ε=的双边Z 变换=)(z F 【 A 】(A)1,)1(2>−z z z (B) 1,)1(2>+z z z(C) 1,)1(22>−z z z (D) 1,)1(22>+z z z 34. 象函数)3)(2(1)(−−=z z z F 其收敛域为3>z ，则其原序列=)(k f 【 C 】(A) )()32()(61k k k k εδ−− (B) )()32()(61k k k k εδ−+(C) )()32()(6111k k k k εδ−−−− (D) )()32()(6111k k k k εδ−−−+35. 序列)(])1(1[21)(k k f k ε−+=的双边Z 变换=)(z F 【 C 】(A)1,12>−z z z (B)1,12>+z z z(C) 1,122>−z z z (D) 1,122>+z z z二．填空题（共23题）：1. 已知信号)(t f 的波形如图所示，画出信号)2(t f −的波形为 )2(t f −O t2. 周期信号623sin(41)324cos(211)(ππππ−+−−=t t t f 的基波角频率=Ω s rad /.12π3. 信号11)(+=jt t f 的傅里叶变换等于 . 4. 频谱函数)3cos(2)(ωω=j F 的傅里叶逆变换=)(t f .)3()3(−++t t δδ5.信号)1()]1(sin[)()sin()(−−−=t t t t t f επεπ的拉普拉斯变换=)(s F . 22)1(ππ+−−s e s 6. 已知信号)(t f 的波形如图所示，画出信号)42(−t f的波形为 )42(−t fO t7. 序列)5.0cos()43sin()(k k k f ππ+=的周期为 . 88. 信号t tt f sin )(=的傅里叶变换等于 . )(2ωπg9.信号)1()()1(−=−−t et f t ε的拉普拉斯变换=)(s F .1+−s e s10.已知信号)(t f 的波形如图所示，则)(t f 的傅里叶变换等于 . )(2)(2ωωπδSa −11.若信号)(t f 的频谱函数为)(ωj F ，则)(b at f −的频谱函数为 ， 其中a 为非零常数。

信号与系统练习题——第1-3章信号与系统练习题（第1-3章）一、选择题1、下列信号的分类方法不正确的是（A ）A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中，哪个不是周期序列? （D ）A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的？（C ）。

A 、()3cos 2sin f t t t π=+；B 、()cos()()f t t t πε=；C 、()sin()76f k k ππ=+； D 、1()cos()53f k k π=+。

4、周期信号()sin6cos9f t t t =+的周期为（D ）A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为（C ）。

A 、πB 、2πC 、无周期D 、13π 6、以下序列中，周期为5的是（D ） A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是（D ）A 、两个周期信号()x t ，()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ，()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ，()y t 的周期分别为2和π，则信号()()x t y t +是周期信号D 、两个周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号8、下列说法不正确的是（A ）A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果（C ）A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为（A ）称为对信号()f t 的平移。

1．系统的激励是，响应为，若满足，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？）2．求积分的值为 5 。

3．当信号是脉冲信号时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。

4．若信号的最高频率是2kHz ，则的乃奎斯特抽样频率为 8kHz 。

5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6．系统阶跃响应的上升时间和系统的 截止频率 成反比。

7．若信号的，求该信号的。

8．为使LTI 连续系统是稳定的，其系统函数的极点必须在S 平面的 左半平面 。

9．已知信号的频谱函数是，则其时间信号为。

10．若信号的，则其初始值 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足 （ √ ）2.满足绝对可积条件的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ）得分)t (e )t (r dt)t (de )t (r =dt )t ()t (212-+⎰∞∞-δf(t)f(t)t)f(23s F(s)=(s+4)(s+2)=)j (F ωj 3(j +4)(j +2)ωωω)s (H ））00(()j (F ωωδωωδω--+=f(t)01sin()t j ωπf(t)211)s (s )s (F +-==+)(f 0)()(t t -=δδ∞<⎰∞∞-dt t f )(3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分，6题15分，共60分）1.信号，信号，试求。

.试题一一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 。

A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 。

A.因果时不变B.因果时变C.非因果时不变D.非因果时变 3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ，该系统是 。

A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。

A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇 5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 。

A. t t 22sinB. tt π2sin C. t t 44sin D.t t π4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 。

A. ∑∞-∞=-k k )52(52πωδπ B. ∑∞-∞=-k k )52(25πωδπC. ∑∞-∞=-k k )10(10πωδπD. ∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为 。

A.)}(Re{ωj e X j B. )}(Re{ωj e XC. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。

A. 500B. 1000C. 0.05D. 0.001 9、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x e t g t =，其傅立叶变换)(ωj G 收敛，则x(t)是 。

A. 左边B. 右边C. 双边D. 不确定10、一系统函数1}Re{1)(->+=s s e s H s，，该系统是 。

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦：e e sh 2x xx --=双曲余弦：e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =，C 为常数（下同）d()d d u v u v ±=±，u 、v 为t 的函数（下同） d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式（1）等比数列123,,,,N a a a a 的通项为11n n a a q -=，q 为公比，前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑（2）等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-，d 为公差，前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰， 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰，1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭，B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰，0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑，0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑，0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤，附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤，B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1（a）确定信号、连续时间信号、非周期信号、能量信号、非因果信号。

1,某系统7,4码)()(01201230123456c c c m m m m c c c c c c c ==c 其三位校验位与信息位的关系为：1求对应的生成矩阵和校验矩阵； 2计算该码的最小距离；3列出可纠差错图案和对应的伴随式；4若接收码字R =1110011,求发码;解：1 1000110010001100101110001101G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦101110011100100111001H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦2 d min =3 34. RH T=001 接收出错E =0000001 R+E=C = 1110010 发码2.已知(),X Y 的联合概率(),p x y 为： 求()H X ,()H Y ,(),H X Y ,();I X Y 解:(0)2/3p x == (1)1/3p x ==()()(1/3,2/3)H X H Y H === bit/symbol (),(1/3,1/3,1/3)H X Y H == bit/symbol ();()()(,)I X Y H X H Y H X Y =+-= bit/symbol3.一阶齐次马尔可夫信源消息集},,{321a a a X ∈,状态集},,{321S S S S∈,且令3,2,1,==i a S i i ,条件转移概率为01X Y011/31/301/3[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=03121313121141)/(i j S a P ,1画出该马氏链的状态转移图；2计算信源的极限熵; 解：12⎪⎪⎩⎪⎪⎨⎧=++=+=++=++1321323112123312311411332231141w w w w w w w w w w w w w w →⎪⎩⎪⎨⎧===3.03.04.0321w w wHX|S 1 =H 1/4,1/4,1/2=比特/符号HX|S 2=H 1/3,1/3,1/3=比特/符号HX|S 3=H 2/3,1/3= 比特/符号()3|0.4 1.50.3 1.5850.30.918 1.3511Hw H X S i ii ==⨯+⨯+⨯=∑∞=比特/符号 4.若有一信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2.08.021x x P X ,每秒钟发出个信源符号;将此信源的输出符号送入某一个二元信道中进行传输 假设信道是无噪无损的,容量为1bit/二元符号, 而信道每秒钟只传递2个二元符号;（1） 试问信源不通过编码即x 10,x 21在信道中传输 （2） 能否直接与信道连接（3） 若通过适当编码能否在此信道中进行无失真传输 （4） 试构造一种哈夫曼编码两个符号一起编码, （5） 使该信源可以在此信道中无失真传输;解：1不能,此时信源符号通过0,1在信道中传输,二元符号/s>2二元符号/s 2从信息率进行比较, (0.8,0.2)H = < 12可以进行无失真传输 3410.640.16*20.2*3i i i Kp K ===++=∑ 二元符号/2个信源符号此时 2=二元符号/s < 2二元符号/s 5.两个BSC 信道的级联如右图所示：1写出信道转移矩阵； 2求这个信道的信道容量; 解： 16.设随机变量,{21=x x X }1,0{21=Y的联合概率空间为 x 1x 1x 1x 2x 2x 1x 2x 20.64011100101 0.64定义一个新的随机变量Y X Z ⨯=普通乘积（1） 计算熵HX,HY,HZ,HXZ,HYZ,以及HXYZ ；（2） 计算条件熵 HX|Y,HY|X,HX|Z,HZ|X,HY|Z,HZ|Y,HX|YZ,HY|XZ 以及HZ|XY ； （3） 计算平均互信息量IX ；Y,IX ：Z,IY ：Z,IX ；Y|Z,IY ；Z|X 以及IX ：,Z|Y; 解：1 2 37.设二元对称信道的输入概率分布分别为]4/14/3[][=X P ,转移矩阵为[]⎥⎦⎤⎢⎣⎡=3/23/13/13/2|XY P ,（１） 求信道的输入熵,输出熵,平均互信息量； （２） 求信道容量和最佳输入分布； （３） 求信道剩余度; 解：1信道的输入熵4log 4/1)3/4(log 4/3)(22+=X H ；2最佳输入分布为]2/12/1[][=X P ,此时信道的容量为)3/1,3/2(1H C -=3信道的剩余度：);(Y X I C -8.[][]25.025.05.0=X P ,试确定最佳译码规则和极大似然译码规则,并计算出相应的平均差错率;解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8/124/112/112/18/124/112/16/14/1][XY P 最佳译码规则：⎪⎩⎪⎨⎧===331211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/6-1/8=11/24；极大似然规则：⎪⎩⎪⎨⎧===332211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/8-1/8=1/2;9.设有一批电阻,按阻值分70%是2k Ω,30%是5k Ω；按功耗分64%是1/8W,36%是1/4W;现已知2k Ω电阻中80%是1/8W,假如得知5k Ω电阻的功耗为1/4W,问获得多少信息量; 解：根据题意有⎥⎦⎤⎢⎣⎡===3.07.05221k r k r R ,⎥⎦⎤⎢⎣⎡===36.064.04/128/11w w W ,8.0)1/1(=r w p 由15/4)2/1()2/1()2()1/1()1()1(=⇒+=r w p r w p r p r w p r p w p 所以15/11)2/1(1)2/2(=-=r w p r w p得知5k Ω电阻的功耗为1/4W,获得的自信息量为=-))2/2((r w p lb10.已知6符号离散信源的出现概率为⎥⎥⎦⎤⎢⎢⎣⎡321321161814121654321a a a a a a ,试计算它的熵、Huffman 编码和费诺编码的码字、平均码长及编码效率; 解：该离散信源的熵为323213232116161881441221)()(61lb lb lb lb lb lb p lb p x H i i i +++++=-=∑== bit/符号11.在图片传输中,每帧约有2106个像素,为了能很好地重现图像,每像素能分256个亮度电平,并假设亮度电平等概分布;试计算每分钟传送两帧图片所需信道的带宽信噪功率比为30dB; 解：每个像素点对应的熵8256log log 22===n H bit/点 2帧图片的信息量bit H N I 7610*2.38*10*2*2**2===单位时间需要的信道容量s bit t I C t /10*3.56010*2.357===由香农信道容量公式Hz SNR C W SNR W C t t 4252210*35.5)10001(log 10*3.5)1(log )1(log ≈+=+=⇒+=12.求右图所示的信道的容量及达到信道容量时的输入分布; 解：由右图可知,该信道的转移概率矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=102/12/101P 可以看到,当该信道的输入分布取⎥⎦⎤⎢⎣⎡=2/102/1)(321a a a X P 时,⎥⎦⎤⎢⎣⎡=2/12/1)(21b bY P 此时2);(2)()/(log)/();(311211lb Y a X I lb b p a b p a bp Y a X I j j jj =====∑=同理可得， 而0);(2==Y a X I ,此分布满足⎩⎨⎧==≠=0);(02);(i i i i p Y x I p lb Y x I ;因此这个信道的容量为X Y b 1b 2a 1a 2a 3C=lb2=1bit/符号,而达到信道容量的输入分布可取⎥⎦⎤⎢⎣⎡=2/102/1)(321a a aX P ; D max =∑==414,3,2,1min i ijij dp ,由于ij i d p 和具有对称性,每个和式结果都为1/2,因此 Dmax= 1/2,13.设离散信源⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡p p p p U U U U u p U 21)1(21)1(2121)(4321其中21≤p 和接收变量V={v1,v2,v3,v4},失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=05.05.015.0015.05.0105.015.05.00D ,求D min,D max 、RD min 、RD max 、达到D min 和D max 时的编码器转移概率矩阵P; 解：由于失真矩阵每行每列都只有一个最小值“0”,所以可以达到D min =0,此时对应的信道转移概率矩阵应使得信源的每个输出经过信道转移后失真为0,即选择⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P ; RD min = R0= HU = 1-plog p –1-plog1-p = 1+Hp;对应的转移概率矩阵可取任意1列为全1,如⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P ,此时 RD max= R1/2= 0;14.设有一个二进制一阶马尔可夫信源,其信源符号为X ∈0,1,条件概率为p 0/0= p 1/0= p1/1= p 0/1=画出状态图并求出各符号稳态概率;15分15.设输入符号与输出符号为X ＝Y ∈{0,1,2,3},且输入符号等概率分布;设失真函数为汉明失真;求D max 和D min 及RD max 和RD min 20分解：()()()()012314p x p x p x p x ====失真矩阵的每一行都有0,因此D min =016.设随机变量}1,0{},{21==x x X和}1,0{},{21==y y Y 的联合概率空间为定义一个新的随机变量Y X Z ⨯=普通乘积计算熵HX,HY,HZ,HXZ,HYZ,以及HXYZ ；计算条件熵 HX|Y,HY|X,HX|Z,HZ|X,HY|Z,HZ|Y,HX|YZ,HY|XZ 以及HZ|XY ； 计算平均互信息量IX ；Y,IX ：Z,IY ：Z,IX ；Y|Z,IY ；Z|X 以及IX ：,Z|Y; 解：12))3/4(log 4/34log 4/1(2/1))3/4(log 4/34log 4/1(2/1)|(2222+++=Y XH3 )|()();(Y X H X H Y X I -=)|()();(Z X H X H Z X I -=分别为]4/14/3[][=XP ,转移17.设二元对称信道的输入概率分布矩阵为[]⎥⎦⎤⎢⎣⎡=3/23/13/13/2|XY P , 求信道的输入熵,输出熵,平均互信息量；求信道容量和最佳输入分布； 求信道剩余度; 解：1信道的输入熵4log 4/1)3/4(log 4/3)(22+=X H ；2最佳输入分布为]2/12/1[][=X P ,此时信道的容量为)3/1,3/2(1H C -=3信道的剩余度：);(Y X I C-设有ＤＭＣ,其转移矩阵为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2/16/13/13/12/16/16/13/12/1|X Y P ,若信道输入概率为[][]25.025.05.0=X P ,试确定最佳译码规则和极大似然译码规则,并计算出相应的平均差错率;解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8/124/112/112/18/124/112/16/14/1][XY P 最佳译码规则：⎪⎩⎪⎨⎧===331211)()()(a b F a b F a b F ,平均差错率为1-1/4-1/6-1/8=11/24；极大似然规则：⎪⎩⎪⎨⎧===332211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/8-1/8=1/2;一、概念简答题1.什么是平均自信息量与平均互信息,比较一下这两个概念的异同2.简述最大离散熵定理;对于一个有m 个符号的离散信源,其最大熵是多少3.解释信息传输率、信道容量、最佳输入分布的概念,说明平均互信息与信源的概率分布、信道的传递概率间分别是什么关系4.对于一个一般的通信系统,试给出其系统模型框图,并结合此图,解释数据处理定理;5.写出香农公式,并说明其物理意义;当信道带宽为5000Hz,信噪比为30dB 时求信道容量;6.解释无失真变长信源编码定理;7.解释有噪信道编码定理;8.什么是保真度准则 对二元信源,其失真矩阵,求a>0时率失真函数的和9.简述离散信源和连续信源的最大熵定理;10.解释等长信源编码定理和无失真变长信源编码定理,说明对于等长码和变长码,最佳码的每符号平均码长最小为多少编码效率最高可达多少11.解释最小错误概率译码准则,最大似然译码准则和最小距离译码准则,说明三者的关系; 12.设某二元码字C={111000,001011,010110,101110}, ①假设码字等概率分布,计算此码的编码效率②采用最小距离译码准则,当接收序列为110110时,应译成什么码字13.一平稳二元信源,它在任意时间,不论以前发出过什么符号,都按发出符号,求和平均符号熵14.分别说明信源的概率分布和信道转移概率对平均互信息的影响,说明平均互信息与信道容量的关系;15.二元无记忆信源,有求：1某一信源序列由100个二元符号组成,其中有m个“1”,求其自信息量2求100个符号构成的信源序列的熵;16.求以下三个信道的信道容量：,,17.已知一3,1,3卷积码编码器,输入输出关系为：试给出其编码原理框图;18. 简述信源的符号之间的依赖与信源冗余度的关系;19. 简述香农第一编码定理的物理意义20. 什么是最小码距, 以及它和检错纠错能力之间的关系;21. 简述信息的特征22. 简单介绍哈夫曼编码的步骤一、概念简答题每题5分,共40分1.答：平均自信息为表示信源的平均不确定度,也表示平均每个信源消息所提供的信息量;平均互信息表示从Y获得的关于每个X的平均信息量,也表示发X前后Y的平均不确定性减少的量,还表示通信前后整个系统不确定性减少的量;2.答：最大离散熵定理为：离散无记忆信源,等概率分布时熵最大;最大熵值为;3.答：信息传输率R指信道中平均每个符号所能传送的信息量;信道容量是一个信道所能达到的最大信息传输率;信息传输率达到信道容量时所对应的输入概率分布称为最佳输入概率分布;平均互信息是信源概率分布的∩型凸函数,是信道传递概率的U型凸函数;4.答：通信系统模型如下：数据处理定理为：串联信道的输入输出X、Y、Z组成一个马尔可夫链,且有,;说明经数据处理后,一般只会增加信息的损失;5.答：香农公式为,它是高斯加性白噪声信道在单位时间内的信道容量,其值取决于信噪比和带宽;由得,则6.答：只要,当N足够长时,一定存在一种无失真编码;7.答：当R＜C时,只要码长足够长,一定能找到一种编码方法和译码规则,使译码错误概率无穷小;8.答：1保真度准则为：平均失真度不大于允许的失真度;2因为失真矩阵中每行都有一个0,所以有,而;9.答：离散无记忆信源,等概率分布时熵最大;连续信源,峰值功率受限时,均匀分布的熵最大;平均功率受限时,高斯分布的熵最大;均值受限时,指数分布的熵最大;10.答：等长信源编码定理：对于任意,只要,则当L足够长时必可使译码差错;变长信源编码定理：只要,一定存在一种无失真编码;等长码和变长码的最小平均码长均为,编码效率最高可达100%;11.答：最小错误概率译码准则下,将接收序列译为后验概率最大时所对应的码字;最大似然译码准则下,将接收序列译为信道传递概率最大时所对应的码字;最小距离译码准则下,将接收序列译为与其距离最小的码字;三者关系为：输入为等概率分布时,最大似然译码准则等效于最小错误概率译码准则;在二元对称无记忆信道中,最小距离译码准则等效于最大似然译码准则;12.答：12令接收序列为,则有,,,,故接收序列应译为010110;13.答：14.答：平均互信息相对于信源概率分布为上凸函数,相对于信道传递概率分布为下凹函数;平均互信息的最大值为信道容量;15.答：1216.答：P1为一一对应确定信道,因此有;P2为具有归并性能的信道,因此有;P3为具有发散性能的信道,因此有;17.答：18.当信源的符号之间有依赖时,信源输出消息的不确定性减弱;而信源冗余度正是反映信源符号依赖关系的强弱,冗余度越大,依赖关系就越大;19.答：无失真信源编码,编码后尽可能等概率分布, 使每个码元平均信息量最大;从而使信道信息传输率R达到信道容量C, 实现信源与信道理想的统计匹配;20.某一码书C中, 任意两个码字之间汉明距离的最小值称为该码的最小码距Dmin.当已知某线性分组码的最小汉明距离为Dmin,那么这组码最多能检测出e =Dmin-1个码元错误,最多能纠正t =Dmin-1 /2个码元错误;21.答：信息的基本概念在于它的不确定性,任何已确定的事物都不含信息;接收者在收到信息之前,对它的内容是不知道的,所以信息是新知识、新内容;信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;信息可以产生,也可以消失,同时信息可以被携带、贮存及处理;信息是可以量度的,信息量有多少的差别;22.①将信源消息符号按其出现的概率大小依次排列px1≥px2≥…≥px n②取两个概率最小的符号分别配以0和1,并将这两个概率相加作为一个新符号的概率,与未分配码元的符号重新排队;③对重排后的两个概率最小符号重复步骤2的过程;④继续上述过程,直到最后两个符号配以0和1为止;⑤从最后一级开始,向前返回得到各个信源符号所对应的码元序列,即相应的码字;二、综合题每题10分,共60分1.黑白气象传真图的消息只有黑色和白色两种,求：1 黑色出现的概率为,白色出现的概率为;给出这个只有两个符号的信源X的数学模型;假设图上黑白消息出现前后没有关联,求熵；2 假设黑白消息出现前后有关联,其依赖关系为：,,,,求其熵；3分别求上述两种信源的冗余度,比较它们的大小并说明其物理意义;2.二元对称信道如图; ；1若,,求和； 2求该信道的信道容量和最佳输入分布;3.信源空间为,试分别构造二元和三元霍夫曼码,计算其平均码长和编码效率;4.设有一离散信道,其信道传递矩阵为,并设,试分别按最小错误概率准则与最大似然译码准则确定译码规则,并计算相应的平均错误概率;5.已知一8,5线性分组码的生成矩阵为;求：1输入为全00011和10100时该码的码字；2最小码距;6.设某一信号的信息传输率为s,在带宽为4kHz的高斯信道中传输,噪声功率谱NO=5×10－6mw/Hz;试求：1无差错传输需要的最小输入功率是多少2此时输入信号的最大连续熵是多少写出对应的输入概率密度函数的形式;7.二元平稳马氏链,已知P0/0=,P1/1=,求：1求该马氏信源的符号熵;2每三个符号合成一个来编二进制Huffman码,试建立新信源的模型,给出编码结果;3求每符号对应的平均码长和编码效率;8.设有一离散信道,其信道矩阵为,求：1最佳概率分布2当,时,求平均互信息 信道疑义度3输入为等概率分布时,试写出一译码规则,使平均译码错误率最小,并求此设线性分组码的生成矩阵为,求：1此n,k 码的n= k=,写出此n,k 码的所有码字;2求其对应的一致校验矩阵H;3确定最小码距,问此码能纠几位错列出其能纠错的所有错误图样和对应的伴随式;4若接收码字为000110,用伴随式法求译码结果;设一线性分组码具有一致监督矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110101100110111000H 1求此分组码n=,k=共有多少码字2求此分组码的生成矩阵G; 3写出此分组码的所有码字;4若接收到码字101001,求出伴随式并给出翻译结果;10.二元对称信道的信道矩阵为,信道传输速度为1500二元符号/秒,设信源为等概率分布,信源消息序列共有13000个二元符号,问：1试计算能否在10秒内将信源消息序列无失真传送完2若信源概率分布为,求无失真传送以上信源消息序列至少需要多长时间11.已知7,4循环码的生成多项式,求：1求该码的编码效率2求其对应的一致校验多项式3写出该码的生成矩阵,校验矩阵;4若消息码式为,求其码字;12.证明：平均互信息量同信息熵之间满足IX;Y=HX+HY-HXY13. 居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高米以上的,而女孩中身高米以上的占总数的一半;假如我们得知“身高米以上的某女孩是大学生”的消息,问获得多少信息量14. 有两个二元随机变量X 和Y ,它们的联合概率为Y Xx 1=0 x 2=1 y 1=0 1/8 3/8 y 2=13/81/8定义另一随机变量Z = XY 一般乘积,试计算HZ=15. 求以下二个信道的信道容量：, ,16. 已知一个高斯信道,输入信噪比比率为3;频带为3kHz,求最大可能传 送的信息率;若信噪比提高到15,理论上传送同样的信息率所需的频带为 多少17. 设信源为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡4/34/121x x P X X ,试求1信源的熵、信息含量效率以及冗余度；2求二次扩展信源的概率空间和熵;18. 什么是损失熵、噪声熵什么是无损信道和确定信道如输入输出为s r ⨯,则它们的分别信道容量为多少19. 信源编码的和信道编码的目的是什么20. 什么是香农容量公式为保证足够大的信道容量,可采用哪两种方法21. 什么是限失真信源编码二、综合题1.答：1信源模型为2由得则3119.02log )(121=-=X H γ 1分447.02log )(122=-=∞X H γ 1分12γγ>;说明：当信源的符号之间有依赖时,信源输出消息的不确定性减弱;而信源冗余度正是反映信源符号依赖关系的强弱,冗余度越大,依赖关系就越大;2分2.答：12,最佳输入概率分布为等概率分布;3.答：1二元码的码字依序为：10,11,010,011,1010,1011,1000,1001;平均码长,编码效率2三元码的码字依序为：1,00,02,20,21,22,010,011;平均码长,编码效率4.答：1最小似然译码准则下,有,2最大错误概率准则下,有,26.答：1无错传输时,有即则2在时,最大熵7.答：1由得极限概率：则符号熵为2新信源共8个序列,各序列的概率为信源模型为一种编码结果依信源模型中的序列次序为0,11,1001,1010,1011,10000,100010,10001138.答：1是准对称信道,因此其最佳输入概率分布为;2当,时,有则3此时可用最大似然译码准则,译码规则为且有答：1n=6,k=3,由C=mG可得所有码字为：000000,001011,010110,011101,100101,101110,110011,1110002此码是系统码,由G知,,则3由H可知,其任意2列线性无关,而有3列线性相关,故有,能纠一位错;错误图样E 伴随式100000 101010000 110001000 011000100 100000010 010000001 0014由知E＝010000,则解：1n=6,k=3,共有8个码字;3分2设码字()12345CCCCCCC=由TTHC0=得⎪⎩⎪⎨⎧=⊕⊕⊕=⊕⊕=⊕⊕1353412CCCCCCCCCC3分令监督位为()12CCC,则有⎪⎩⎪⎨⎧⊕=⊕=⊕=34451352CCCCCCCCC3分生成矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1111111112分3所有码字为000000,001101,010011,011110,100110,101011,110101,111000;4分4由TT HRS=得()101=S,2分该码字在第5位发生错误,101001纠正为101011,即译码为1010011分10.答：1信道容量为信源序列信息量为而10秒内信道能传递的信息量为故不能无失真地传送完;2此时信源序列信息量为信息传输率为则11.答：123,而412. 证明：()()()()()()()()()()Y X H X H y x p y x p x p y x p x p y x p y x p Y X I X X Y j i j i Y i j i XYi j i j i -=⎥⎦⎤⎢⎣⎡---==∑∑∑∑∑∑log log log; 2分同理 ()()()X Y H Y H Y X I-=; 1分则 ()()()Y X I Y H X Y H;-=因为 ()()()X Y H X H XY H+= 1分故()()()()Y X I Y H X H XY H;-+=即()()()()XY H Y H X H Y X I-+=; 1分13. 解：设A 表示“大学生”这一事件,B 表示“身高以上”这一事件,则 PA= pB= pB|A= 2分 故 pA|B=pAB/pB=pApB|A/pB== 2分 IA|B== 1分14. 解：Z = XY 的概率分布如下： 15. 答：P 1为一一对应确定信道,因此有; P2为具有归并性能的信道,因此有;16. 答:1 最大可能传送的信息率是Ct = w log 1+ Px/Pn = 3×1000 × log 1+ 3 = 6×1000比特/秒2 17. 解：12二次扩展信源的概率空间为：18. 答：将HX|Y 称为信道},,{|Y P X X Y 的疑义度或损失熵,损失熵为零的信道就是无损信道,信道容量为logr;将HY|X 称为信道},,{|Y P X X Y 的噪声熵,噪声熵为零的信道就是确定信道,信道容量为logs;19. 答：信源编码的作用：1符号变换：使信源的输出符号与信道的输入符号相匹配；2冗余度压缩：是编码之后的新信源概率均匀化,信息含量效率等于或接近于100%; 信道编码的作用：降低平均差错率; 20.答：香农信道容量公式：)1(log )(02BN P B P C SS +=,B 为白噪声的频带限制,0N 为常数,输入Xt 的平均功率受限于S P ;由此,为保证足够大的信道容量,可采用1用频带换信噪比；2用信噪比换频带;21. 答：有失真信源编码的中心任务：在允许的失真范围内把编码的信息率压缩到最小;。

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

10通信 信号与系统习题及答案1、无失真传输系统，其幅频特性为 ，相频特性为 。

2、某连续LTI 系统的单位冲激响应为h(t)，则该系统稳定的充要条件是 。

3、某连续LTI 系统的单位冲激响应为h(t)，则该系统因果的充要条件是 。

4、信号Sa(500t)的频谱密度函数为 ，频带宽度为 Hz(只计正频率)。

5、信号)(cos )(0t t w t f ε=的拉普拉斯变换表达式是 。

6、描述线性时不变连续系统的输入输出方程是 。

7、单边拉普拉斯变换F(s)=1+s 的原函数f(t)= 。

8、 描述线性时不变连续系统的输入输出方程是 。

已知离散信号 请问：该信号是否是周期信号 ，若是，则周期应为多少 。

9、已知,0)(≥t f )()1()(*)(t e t t f t f t ε--='，则)(jw F = ，)(t f = 。

1、下列各表达式中正确的是（ ）（A ）)()2(t t δδ= （B ）)(21)2(t t δδ=（C ）)(2)2(t t δδ= （D ）)2(21)(2t t δδ= 2、设：f(t)↔F(jω) 则f 1(t)=f(at+b)，a>0，的频谱F 1(jω)为( )(A) F 1(jω)=aF(j a ω)e -j bw (B) F 1(jω)=a 1F(j aω)e -j bw (C) F 1(jω)= a 1F(j a ω)ω-a b j e (D) F 1(jω)=aF(j aω)ω-a b j e 3、如图所示周期信号)(t f ，设其傅立叶系数为n C ，则0C = 。

A. 10B. 5C. 20D. 154、若矩形脉冲信号的脉宽加宽，则它的频带宽度（ ）(A) 不变 (B) 变窄 (C) 变宽 (D) 与脉冲宽度无关238cos()(πk k f =t f 1 (t)121-10tf 2 (t)121-10f(t)t0115、 无失真传输的条件是( )(A) 幅频特性等于常数 (B) 相位特性是通过原点的直线(C) 幅频特性等于常数，相位特性是通过原点的直线(D) 幅频特性是通过原点的直线，相位特性等于常数6、信号)()1()(2t u e t t f t --=的拉氏变换为（ ）(A) 2)2(1+s (B) 2)2(+s s (C) 22)2(+s s (D) 2)2(1++s s7、积分式⎰-+++4422)]dt -(t 2(t))[23(δδt t 的积分结果是（ ）（A) 14 （B) 24 （C ）26 （D ）288、若连续时间系统是因果稳定的，则其系统函数的极点 。

第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图（）(A) (B) (C) (D)2 ．函数式的值为（）（ A ）0 （ B ） 1 （ C ） 2 （ D ）3 ．已知x(3-2) 的波形如图1 所示，则x （t ）的波形应为图（）图1 （A）（B）（C）（D）4.已知信号x[n]波形如图2,信号的波形如图（）图2 （A）（B）(C) (D)5 ．卷积积分等于（）（A）（B）-2 （C）（D）-2 （E）-26 ．卷积和x[n] u[n-2] 等于（）（ A ）（ B ）（ C ）（ D ）（ E ）7 ．计算卷积的结果为（）（ A ）（ B ）（ C ）（ D ）8 ．已知信号x(t) 的波形如图3 所示，则信号的波形如图（）图3 （A）(B)(C) (D) 题九图9 ．已知信号x （t ）如图所示，其表达式为（）(A) (B)(C) (D)10 ．已知x（t)为原始信号，y(t)为变换后的信号,y(t) 的表达式为（）（ A ）（ B ）（ C ）（ D ）11 ．下列函数中（）是周期信号（ A ）（ B ）（ C ）（ D ）（ E ）12 ．函数的基波周期为（）。

（ A ）8 （ B ）12 （ C ）16 （ D ）2413 ．某系统输入—输出关系可表示为，则该系统是（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定14 ．某系统输入—输出关系可表示为，则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定15．某系统输入—输出关系可表示为,则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定16.某系统输入—输出关系可表示为，则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定17 ．某系统输入—输出关系可表示为，则系统为（）系统（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（）稳定18 ．下列系统中，（）是可逆系统（A）y[n]=nx[n] （B）y[n]=x[n]x[n-1] （C）y(t)=x(t-4) （D）y(t)=cos[x(t)] （ E ）y[n]=19 ．如图系统的冲激响应为（）（ A ）（ B ）（ C ）（ D ）20 ．某系统的输入x （t ）与输出y （t ）之间有如下关系，则该系统为（）（A）线性时变系统（B）线性非时变系统（C）非线性时变系统（D）非线性非时变系统21 ．一个LTI 系统在零状态条件下激励与响应的波形如图，则对激励的响应的波形（）(A) (B) (C) (D)22. 线形非时变系统的自然（固有）响应就是系统的（）（ A ）零输入响应（ B ）原有的储能作用引起的响应（ C ）零状态响应（ D ）完全的响应中去掉受迫（强制）响应分量后剩余各项之和23 ．零输入响应是（）（ A ）全部自由响应（ B ）部分零状态响应（ C ）部分自由响应（ D ）全响应与强迫响应之差24 ．下列叙述或等式正确的是（）(A) (B)(C)若,则(D)x(t) 和h(t) 是奇函数，则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的，则也是周期的(B) 若是周期的，则也是周期的(C) 若是周期的，则也是周期的(D) 若是周期的，则也是周期的26 ．有限长序列经过一个单位序列响应为的离散系统，则零状态响应为（）(A) (B)(C) (D)第二章习题1. 某LTI 连续时间系统具有一定的起始状态，已知激励为x （t ）时全响应，t 0 ，起始状态不变，激励为时，全响应y （t ）＝7e ＋2e ，t 0 ，则系统的零输入响应为（）（ A ）（ B ）（ C ）（ D ）2 ．微分方程的解是连续时间系统的（）(A) 零输入响应(B) 零状态响应(C) 自由响应(D) 瞬态响应（E）全响应3 ．单位阶跃响应是（）(A) 零状态响应(B) 瞬态响应(C) 稳态响应(D) 自由响应(E) 强迫响应4 ．已知系统如图所示，其中h (t) 为积分器，为单位延时器，h (t) 为倒相器，则总系统的冲激响应h (t) 为（）（ A ）（ B ）（ C ）（ D ）5 ．如图所示电路以为响应，其冲激响应h (t) 为（）(A) (B)(C) (D)6. 某LTI 系统如图所示，该系统的微分方程为（）(A ) (B)(C) (D)7 ．已知系统的微分方程, 则求系统单位冲激响应的边界条件h(0 ) 等于（）(A) －1 (B) 0 (C) 2 (D) ＋18 ．已知系统的微分方程则系统的单位冲激响应为（）(A) (B) (C) (D)9 ．已知描述系统的微分方程和初始状态0 值如下；y (0 ) ＝2 ，, , ，则初始条件0 值为（）(A) (B)(C) (D)10 ．已知描述系统的微分方程和初始状态0 值如y(t) ＋6 y (t) ＋8 y (t) ＝x (t) ＋2x (t) ，y (0 ) ＝1 ，y (0 ) ＝2 ，x (t) ＝（t ）则初始条件0 值为（）。

信号与系统 习题1一、填空题1.离散信号()2()k f k k ε=,则该信号的单边Z 变换为 ① .2.信号()f t 的傅里叶变换为()F j ω,则(23)f t -的傅里叶变换为 ① 。

3.已知周期信号()cos(230)sin(4+60)f t t t =++，则其周期为 ① s ，基波频率为 ② rad/s 。

4、已知)(1t f 和)(2t f 的波形如下图所示，设)()()(21t f t f t f *=，则=-)1(f ① ，=)0(f ② 。

5、单边拉氏变换())4(22+=s s s F ，其反变换()=t f ① 。

6、一离散系统的传输算子为23)(22+++=E E EE E H ,则系统对应的差分方程为 ① ，单位脉冲响应为 ② 。

二、单项选择题1. 下列说法不正确的是______。

A. 每个物理系统的数学模型都不相同。

B. 同一物理系统在不同的条件下，可以得到不同形式的数学模型。

C. 不同的物理系统经过抽象和近似，有可能得到形式上完全相同的数学模型。

D 。

对于较复杂的系统，同一系统模型可有多种不同的数学表现形式。

2. 周期信号f （t ）的傅立叶级数中所含有的频率分量是______.A 。

余弦项的奇次谐波，无直流 B. 正弦项的奇次谐波,无直流 C 。

余弦项的偶次谐波,直流 D. 正弦项的偶次谐波，直流 3。

当周期矩形信号的脉冲宽度缩小一半时，以下说法正确的是_____.A 。

谱线间隔增加一倍 B. 第一个过零点增加一倍 C. 幅值不变 D. 谱线变成连续的 4。

图3所示的变化过程，依据的是傅立叶变换的_____。

图3A. 时移性 B. 频移性 C. 尺度变换 D 。

对称性 5. 对抽样信号进行恢复,需将信号通过_____。

A. 理想带通滤波器 B 。

理想电源滤波器C. 理想高通滤波器 D 。

理想低通滤波器 6. 连续周期信号的频谱有_____。

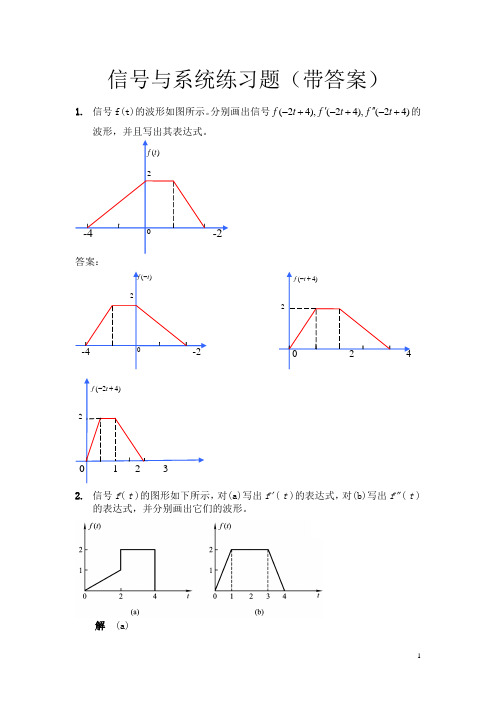
信号与系统练习题（带答案）1. 信号f(t)的波形如图所示。

分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形，并且写出其表达式。

答案：2. 信号f ( t )的图形如下所示，对(a)写出f ' ( t )的表达式，对(b)写出f " ( t )的表达式，并分别画出它们的波形。

解 (a)20,21≤≤tf ' (t)= δ(t -2)， t = 2-2δ(t -4)， t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示，试画出f(t)的波形。

52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析（）右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得－2t ，即f(5-2t)左移(52)(2)f t f t -−−−→-时移由（2）反转：f(-2t)中以-t 代替t ，可求得f(2t),表明f(-2t)的波形 以t ＝0的纵轴为中心线对褶，注意()t δ是偶数，故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由（3）尺度变换：以12t 代替f(2t)中的t ，所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。

4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。

解：{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。

信号与系统复习题（答案全）1、若系统的输⼊f (t)、输出y (t) 满⾜()3()4t y t e ft -=，则系统为线性的（线性的、⾮线性的）、时变的（时变的、时不变）、稳定的（稳定的、⾮稳定的）。

2、⾮周期、连续时间信号具有连续、⾮周期频谱；周期、连续时间信号具有离散、⾮周期频谱；⾮周期、离散时间信号具有连续、周期频谱；周期、离散时间信号具有离散、周期频谱。

3、信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最⼤采样周期为 5×10-5 s . 4、 )100()(2t Sa t f =是能量信号（功率信号、能量信号、既⾮功率亦⾮能量信号）。

5、 ()2cos()f t t =+是功率信号（功率信号、能量信号、既⾮功率亦⾮能量信号）。

6、连续信号f(t)=sint 的周期T 0=,若对f(t)以fs=1Hz 进⾏取样，所得离散序列f(k)=sin(k) ,该离散序列是周期序列？否。

7、周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑，此信号的周期为 1s 、直流分量为 2/π、频率为5Hz 的谐波分量的幅值为 2/5 。

8、 f (t) 的周期为0.1s 、傅⽴叶级数系数**03355532F F F F F j --=====、其余为0。

试写出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。

9、 f (k) 为周期N=5的实数序列，若其傅⽴叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、则F 5 (3 )= ()54512πjeF +=- 、F 5 (4 )= ()52511πj eF +=- 、F 5 (5 )= 2 ；f(k) =())1.7254cos(62.052)9.3552cos(62.152525140525?-?+?-?+=∑=k k e n F n k jn πππ。

信号与系统考试题及答案第一题：问题描述：什么是信号与系统？答案：信号与系统是电子工程和通信工程中重要的基础学科。

信号是信息的传递载体，可以是电流、电压、声音、图像等形式。

系统是对信号进行处理、传输和控制的装置或网络。

信号与系统的研究内容包括信号的产生、变换、传输、处理和控制等。

第二题：问题描述：信号的分类有哪些？答案：信号可以根据多种特征进行分类。

按照时间域和频率域可以将信号分为连续时间信号和离散时间信号；按照信号的能量和功率可以分为能量信号和功率信号；按照信号的周期性可以分为周期信号和非周期信号；按照信号的波形可以分为正弦信号、方波信号、脉冲信号等。

第三题：问题描述：什么是线性时不变系统？答案：线性时不变系统是信号与系统领域中重要的概念。

线性表示系统满足叠加性原理，即输入信号的线性组合经过系统后，输出信号也是输入信号的线性组合。

时不变表示系统的性质不随时间变化而改变。

线性时不变系统具有许多重要的性质和特点，可以通过线性时不变系统对信号进行处理和分析。

第四题：问题描述：系统的冲激响应有什么作用？答案：系统的冲激响应是描述系统特性的重要参数。

当输入信号为单位冲激函数时，系统的输出即为系统的冲激响应。

通过分析冲激响应可以得到系统的频率响应、幅频特性、相频特性等，从而对系统的性能进行评估和优化。

冲激响应还可以用于系统的卷积运算和信号的滤波等应用。

第五题：问题描述：如何对信号进行采样？答案：信号采样是将连续时间信号转换为离散时间信号的过程。

常用的采样方法包括周期采样和非周期采样。

周期采样是将连续时间信号按照一定的时间间隔进行等间隔采样；非周期采样是在信号上选取一系列采样点，采样点之间的时间间隔可以不相等。

采样频率和采样定理是采样过程中需要考虑的重要因素。

第六题：问题描述：什么是离散傅里叶变换（DFT）？答案：离散傅里叶变换是对离散时间信号进行频域分析的重要工具。

通过计算离散傅里叶变换可以将离散时间信号转换为复数序列，该复数序列包含了信号的频率成分和相位信息。