2018年中国计量大学821自动控制原理2考研真题

《自动控制原理1》试卷 第1 页 共4 页中国计量大学2019年硕士研究生招生考试试题考试科目代码：801 考试科目名称：自动控制原理1所有答案必须写在报考点提供的答题纸上，做在试卷或草稿纸上无效。

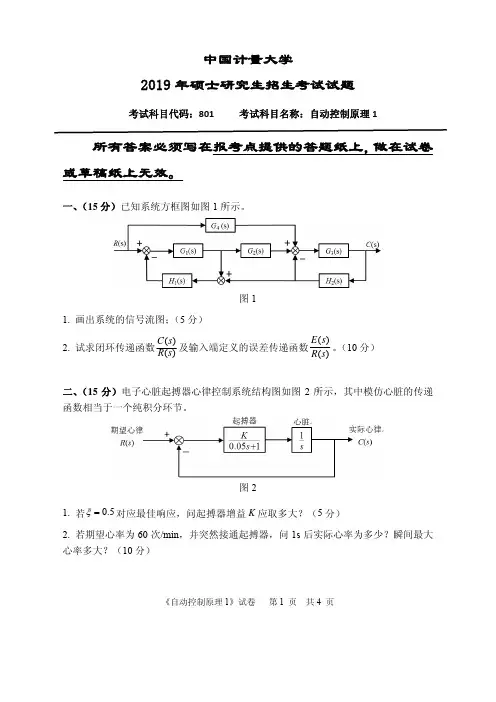
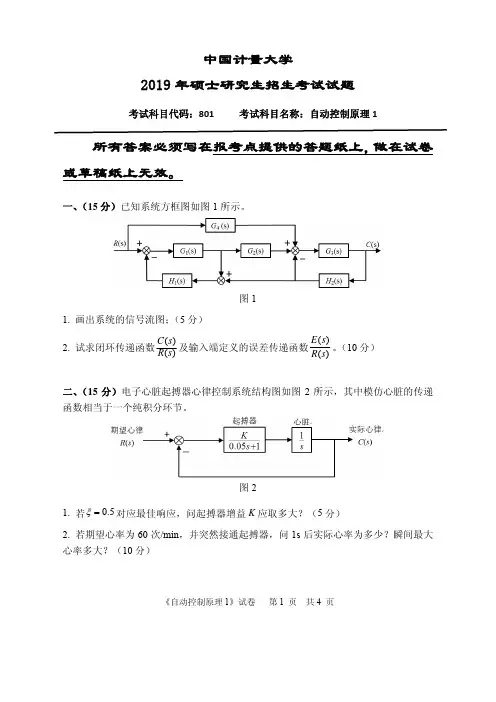
一、（15分）已知系统方框图如图1所示。

图11. 画出系统的信号流图；（5分）2. 试求闭环传递函数)()(s R s C 及输入端定义的误差传递函数)()(s R s E 。

（10分）二、（15分）电子心脏起搏器心律控制系统结构图如图2所示，其中模仿心脏的传递函数相当于一个纯积分环节。

图21. 若5.0=ξ对应最佳响应，问起搏器增益K 应取多大？（5分）2. 若期望心率为60次/min ，并突然接通起搏器，问1s 后实际心率为多少？瞬间最大心率多大？（10分）《自动控制原理1》试卷 第2 页 共4 页三、（15分）系统结构图如图3所示，[]()()()e t r t b t =−。

图31. 已知G 1(s )的单位阶跃响应为21e t −−，试求G 1(s )；（5分） 2. 利用求出的G 1(s )，当r (t )=10·1(t )时，试求：①系统的稳态输出；②系统的超调量、调节时间和稳态误差。

（10分）四、（15分）已知系统结构图如图4所示：图41. 绘出K *从0→+∞变化时系统的根轨迹；（8分）2. 确定系统处于欠阻尼条件下的K *范围；（4分）3. 确定系统稳定时的最小阻尼比。

（3分）五、（15分）已知系统传递函数为)52)(2()(2+++=s s s K s G ，1. 画出奈奎斯特图；（10分） 2. 当K =52，利用奈奎斯特稳定判据判断其闭环系统的稳定性。

（5分）六、（15分）已知最小相位开环系统的渐近对数幅频特性如图5所示，试求： 1. 系统的开环传递函数；（4分） 2. 截止频率c ω和相角裕量γ；（8分）3. 若使截止频率s rad c /10=ω，其放大倍数应取多少？（3分）《自动控制原理1》试卷 第3 页 共4 页七、（20分）已知采样系统结构如图6所示，其中采样周期s T 4.0=。

《自动控制原理1》试卷 第1 页 共3页
中国计量大学
2018年硕士研究生招生考试试题
考试科目代码：801 考试科目名称：自动控制原理1
所有答案必须写在报考点提供的答题纸上，做在试卷或草稿纸上无效。

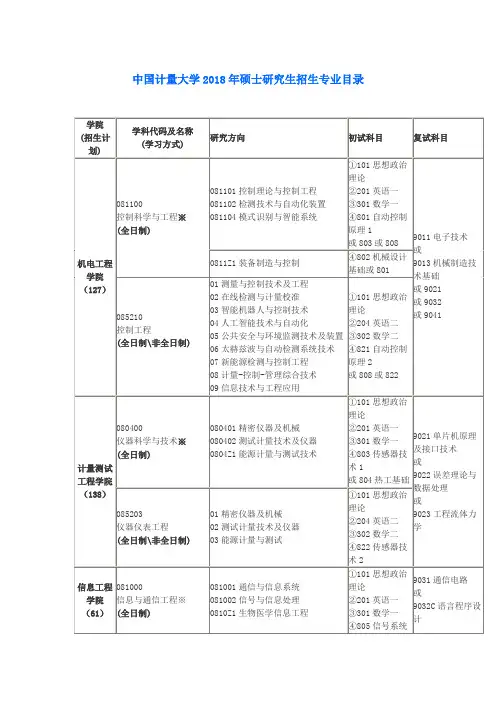
一、（15分）某系统结构图如图1所示，R(s)为输入，N(s)为扰动，C(s)为输出。

试要求：
1. 画出系统的信号流图；（5分）
2. 用梅逊公式求出其传递函数)()(s R s C ；（5分）
3. 说明在什么条件下，输出C(s)不受扰动N(s)的影响。

（5分）
图1
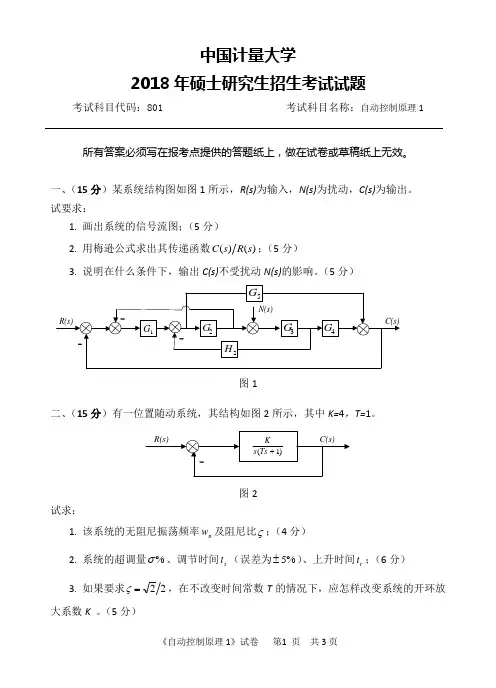
二、（15分）有一位置随动系统，其结构如图2所示，其中K=4，T=1。

图2
试求：
1. 该系统的无阻尼振荡频率n w 及阻尼比ς；（4分）
2. 系统的超调量%σ、调节时间s t （误差为%5±）、上升时间r t ；（6分）
3. 如果要求22=ς，在不改变时间常数T 的情况下，应怎样改变系统的开环放大系数K 。

（5分）。

目录
2018 年中国计量大学822传感器技术2考研真题试题试卷 (2)
2018年中国计量大学考研真题试题试卷
一、名词解释（每题3分，共30分）
1.热电阻传感器
2.磁致伸缩效应
3.涡流效应
4.传感器的迟滞
5.压阻效应
6.光生伏特效应
7.电容的边缘效应
8.气敏传感器
9.不等位电势
10.光电耦合器件
二、填空题（每空0.5分，共20分）
1.将两种不同的导体或半导体两端相接组成闭合回路，当两接点的温度不同时，则在回路中产生，并形成。

这种现象称塞贝克效应，即热电效应。

实验指出，当组成热电偶的材料A、B为均质材料时，回路电动势只与有关，与有关，而与热电偶的和无关。

这样我们就可以将热电偶做成传感器，也可以做成测量与之有关的其他物理量的传感器。

热电偶回路产生的热电动势由和两部分组成。

2.感应同步器是利用两个的互感随不同而变化的原理组成的，可用来测量或，对应的感应同步器分别称为和。

感应同步器的信号处理方式分为
和两大类。

3.光电式传感器的工作原理，是首先把被测量的变化转换成的变化，然后通过变换成。

光电式传感器一般由、和三部分组成。

被测量作用于
《传感器技术2》试卷第1页共5页。

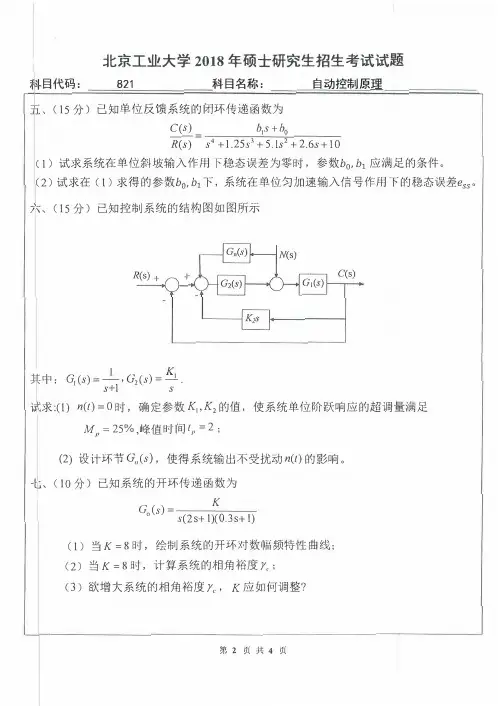
北京工业大学2018年硕士研究生招生考试试题目代码：821 科目名称：
、(15分）已知单位反馈系统的闭环传递函数为
C(s ) =沁+b 。

自动控制原理R (s ) s 4 +l.25s 3 +5.1s 2 +2.6s+l O Cl)试求系统在单位斜坡输入作用下稳态误差为零时，参数b。

,h 1应满足的条件。

(2)试求在(1)求得的参数b。

,h 1下，系统在单位匀加速输入信号作用下的稳态误差esso 六、(15分）已知控制系统的结构图如图所示其K 中：G 1(s ) =—, G 2(s ) = _J_. k s+l
s i求：(1) n (t )=O 时，确定参数K i ,K 2的值，使系统单位阶跃响应的超调量满足M" =25%, 峰值时间t,,=2: (2)设计环节G ,(s ),使得系统输出不受扰动n (t )的影响。

t 、(10分）已知系统的开环传递函数为
G 。

(s )= K s (2s+ 1)(0.3s+ 1) (1)当K=8时，绘制系统的开环对数幅频特性曲线；
(2)当K=8时，计算系统的相角裕度Y e :(3)欲增大系统的相角裕度Y e ,K 应如何调整？第2页共4页。

本试卷共8大题，共3页。

图1是液面自动控制系统的两种原理示意图。

在运行中，希望液面高度0H 维持不变。

（1）试说明各系统的工作原理。

（2）画出各系统的方框图，并说明被控对象、给定值、被控量和干扰信号是什么?二、（15分）试用梅逊公式列写图2所示系统的传递函数)(/)(s R s C 。

单位反馈开环传递函数为)10)(2()(10)(+++=s s s a s s G ，(1)试确定使系统稳定的a 值；(2)使系统特征值均落在S 平面中1Re -=这条线左边的a 值。

四、（20分）设单位负反馈系统开环传递函数为1)(+=Ts K K s G g p 。

如果要求系统的位置稳态误差0e ss =，单位阶跃响应的超调量%3.4=Mp ，试问p K 、g K 、T 各参数之间应保持什么关系？五、（20分）单位反馈系统的开环传递函数为：)1)(2()52()(2-++-=s s s s K s G （1）绘制系统的根轨迹（2）确定使系统闭环传递函数具有阻尼比0.5的K 值六、（20分）一控制系统如图3所示。

当t t r =)(，要求系统的稳态误差小于0.2，且增益裕量不小于6dB。

试求增益K 的取值范围。

七、（20分）已知最小相位系统的开环对数幅频特性)(0ωL 和串联校正装置的对数幅频特性)(ωc L 如图4所示，原系统的幅值穿越频率为s rad c /3.24=ω；(1)写出原系统的开环传递函数)(0s G ；(2)写出校正装置的传递函数)(s G c ；(3)写出校正后的开环传递函数)()(0s G s G c ，画出校正后系统的开环对数幅频特性)(ωGC L 。

图4八、（20分）求图5所示系统的闭环脉冲传递函数。

图50.010.11101000.322024.340-20dB/dec-20dB/dec -40dB/dec -60dB/dec L(ω)ωL 0L c。

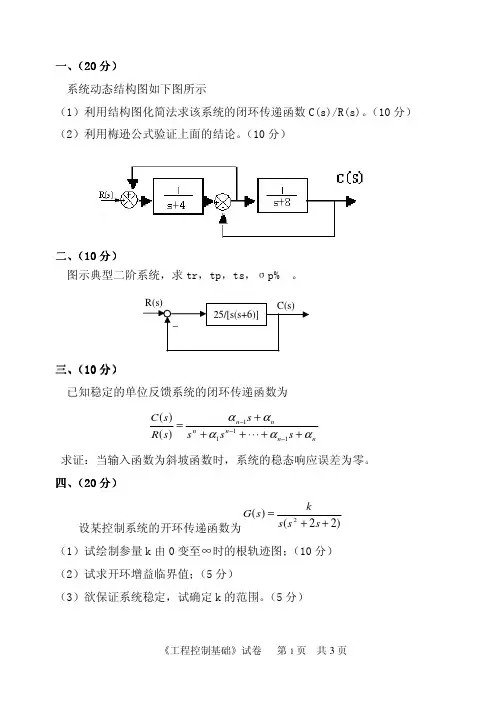
系统动态结构图如下图所示（1）利用结构图化简法求该系统的闭环传递函数C(s)/R(s)。

（10分）（2）利用梅逊公式验证上面的结论。

（10分）二（、（110分）图示典型二阶系统，求tr，tp，ts，σp% 。

三（、（110分） 已知稳定的单位反馈系统的闭环传递函数为n n n n n n s s s s s R s C ααααα++⋅⋅⋅+++=−−−1111)()(求证：当输入函数为斜坡函数时，系统的稳态响应误差为零。

四（、（2020分）设某控制系统的开环传递函数为)22()(2++=s s s ks G （1）试绘制参量k 由0变至∞时的根轨迹图；（10分）（2）试求开环增益临界值；（5分）（3）欲保证系统稳定，试确定k 的范围。

（5分）已知反馈控制系统的开环传递函数为：)15)(5()1(250)(2+++=s s s s s G ，绘制其乃氏图，并应用Nyquist 稳定判据说明此时闭环系统的稳定性。

六（、（1515分）已知系统特征方程如下，试求系统在s 右半平面的根数及虚根值。

（1）04832241232345=+++++S S S S S ；（8分）（2）0160161023=+++S S S 。

（7分）七（、（2020分）已知一阶系统的方框图如图所示。

设()t t r =，试求：（1）系统具有几型精度？（5分）（2）单位斜坡输出响应；（10分）（3）系统能否跟踪斜坡输入？（5分）八（、（2020分）单位负反馈系统的开环传递函数为120()(2)(10)G s s s s =++ ， （1） 绘制系统开环bode 图；（10分）（2） 求出系统的截止频率和相位裕度；（6分）（3） 判别闭环系统的稳定性。

（4分）九（、（110分） 试求下列函数的初值和终值：)8.0)(18.0()1()(2222+++−++=z z z z z z z z E十（、（110分）已知离散系统的特征方程为32()17292770F z z z z =+++=，应用劳斯判据确定系统的稳定性。

西工大821自动控制原理第二章 控制系统的数学模型习题及答案2-1 试建立图2-27所示各系统的微分方程。

其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dty d m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dt t y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I cs R cs R s U c r ++= （3） 2)()(R s Uc s I = （4）联立式（3）、（4），可解得： CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++(d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明图2-28中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。