解直角三角形题型归纳-2023年中考数学拉分专题(教师版含解析)
- 格式:docx
- 大小:4.50 MB
- 文档页数:23

2023年中考数学一轮复习:解直角三角形及其应用一、单选题1.如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线kyx=(k≠0)上,则k的值为()A.4B.﹣2C D.2.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AE平分△BAD,分别交BC,BD于点E,P,连接OE,△ADC=60°,122AB BC==,则下列结论:①△CAD=30°;②14OE AD=;③S平行四边形ABCD=AB·AC;④27BD=⑤S△BEP=S△APO;其中正确的个数是()A.2B.3C.4D.5 3.如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒。
若△BAC=α,则此车的速度为()A.5tanα米/秒B.80tanα米/秒C.5tanα米/秒D.80tanα米/秒二、填空题4.如图,在 ABC 中,AD 是BC 上的高, cos tanB DAC =∠ ,若 1213sinC =, 12BC = ,则AD 的长 .5.某人沿着坡角为α的斜坡前进80m ,则他上升的最大高度是 m . 6.如图,建筑物BC 上有一旗杆AB ,点D 到BC 的距离为20m ,在点D 处观察旗杆顶部A 的仰角为52°,观察底部B 的仰角为45°,则旗杆的高度为 m .(精确到0.1m ,参考数据:520.79sin ︒≈,52 1.28tan ︒≈ 1.41≈ 1.73≈.)三、综合题7.在Rt△ACB 中,△C=90°,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AB 、AC 分别交于点D 、E ,且△CBE=△A.(1)求证:BE 是△O 的切线; (2)连接DE ,求证:△AEB△△EDB ;(3)若点F 为 AE 的中点,连接OF 交AD 于点G ,若AO=5,3sin 5CBE ∠= ,求OG 的长.8.如图(1)放置两个全等的含有30°角的直角三角板 ABC 与(30)DEF B E ∠=∠=︒ ,若将三角板 ABC 向右以每秒1个单位长度的速度移动(点C 与点E 重合时移动终止),移动过程中始终保持点B 、F 、C 、E 在同一条直线上,如图(2), AB 与 DF 、 DE 分别交于点P 、M , AC 与 DE 交于点Q ,其中 AC DF ==,设三角板 ABC 移动时间为x 秒.(1)在移动过程中,试用含x 的代数式表示AMQ 的面积;(2)计算x 等于多少时,两个三角板重叠部分的面积有最大值?最大值是多少?9.已知AB 是△O 的切线,切点为B 点,AO 交△O 于点C ,点D 在AB 上且DB=DC .(1)求证:DC 为△O 的切线;(2)当AD=2BD ,CD=2时,求AO 的长.10.脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 AB 所在的直线.为了测量房屋的高度,在地面上C 点测得屋顶 A 的仰角为 35︒ ,此时地面上C 点、屋檐上 E 点、屋顶上A 点三点恰好共线,继续向房屋方向走 8m 到达点D 时,又测得屋檐 E 点的仰角为 60︒ ,房屋的顶层横梁 12EF m = ,//EF CB , AB 交 EF 于点G (点C ,D , B 在同一水平线上).(参考数据:sin350.6︒≈ , cos350.8︒≈ , tan350.7︒≈ ,1.7≈ )(1)求屋顶到横梁的距离 AG ;(2)求房屋的高 AB (结果精确到 1m ).11.如图,直线 (0)y mx n m =+≠ 与双曲线 (0)ky k x=≠ 交于 A B 、 两点,直线AB 与坐标轴分别交于 C D 、 两点,连接 OA ,若 OA = ,1tan 3AOC ∠= ,点 (3,)B b - .(1)分别求出直线 AB 与双曲线的解析式; (2)连接 OB ,求 AOBS.12.如图,某港口O 位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.(1)若它们离开港口一个半小时后分别位于A 、B 处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?说明理由.(2)若“远航”号沿北偏东60︒方向航行,经过两个小时后位于F 处,此时船上有一名乘客需要紧急回到PE 海岸线上,若他从F 处出发,乘坐的快艇的速度是每小时80海里.他能在半小时内回到海岸线吗?说明理由.13.如图,某人在山坡坡脚A 处测得电视塔尖点 C 的仰角为 60︒ ,沿山坡向上走到p 处再测得点C 的仰角为 45︒ ,已知 100OA = 米,山坡坡度 1:2i = ,且O A B 、、 在同一条直线上,其中测倾器高度忽略不计.(1)求电视塔OC 的高度;(计算结果保留根号形式)(2)求此人所在位置点 P 的铅直高度.(结果精确到0.1米,参考数据:1.41= , 1.73= )14.我国于2019年6月5日首次完成运载火箭海上发射,达到了发射技术的新高度.如图,运载火箭海面发射站点M 与岸边雷达站N 处在同一水平高度。


2023年安徽中考数学总复习专题:解直角三角形的实际应用1.超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO =45°.(1)求A、B之间的路程;(2)请判断此车是否超过了万丰路每小时70千米的限制速度?(参考数据:2≈1.41,3≈1.73).2.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.8m和2.4m,∠BOC=90°.(1)△CEO与△ODB全等吗?请说明理由.(2)爸爸在距离地面多高的地方接住小丽的?(3)秋千的起始位置A处与距地面的高是 m.3.投影仪,又称投影机,是一种可以将图象或视频投射到幕布上的设备.如图①是屏幕投影仪投屏情景图,如图②是其侧面示意图,已知支撑杆AD与地面FC垂直,且AD的长为12cm,脚杆CD的长为50cm,AD距墙面EF的水平距离为240cm,投影仪光源散发器与支撑杆的夹角∠EAD=120°,脚杆CD与地面的夹角∠DCB=42°,求光源投屏最高点与地面间的距离EF.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,3≈1.73)4.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移多少m时,才能确保山体不滑坡.(取tan50°≈1.2)5.小华在网上看到一个如图(1)的躺椅,他决定自己动手用木条制作一个简易的躺椅,如图(2)是简易躺椅的侧面,其中∠B=44°,∠ACB=17°,∠DEC=∠DCE=48°,AE=13AC,若木条AB=5dm,请你计算木条AC,DE,DC的长.(相关数据:sin44°=0.69,cos44°=0.72,tan44°=0.97,sin17°=0.29,cos17°=0.96,tan17°=0.31,sin48°=0.74,cos48°=0.67,tan48°=1.11,结果保留一位小数)6.“蛟龙号”载人潜水器是中国探索深蓝的利器.如图,在某次任务中,当蛟龙号下潜到点B处时,科研人员在海面的观察点A测得点B的俯角为60°,当蛟龙号继续垂直下潜2千米到达海底C处时,在观察点A测得点C的俯角为75.97°,求点C到海面的深度.(结果精确到0.1千米)参考数据:3≈1.73,sin75.97°=0.97,cos75.97°≈0.24,tan75.97°≈4.007.图1是重庆欢乐谷的一个大型娱乐设施——“重庆之眼”摩天轮,它是全球第六、西南最高的观光摩天轮.如图2,小嘉从摩天轮最低处B出发先沿水平方向向左行走37米到达点C,再经过一段坡度(坡面的垂直高度与水平方向的距离的比)为i=1:2.4,坡长为26米的斜坡CD到达点D,然后再沿水平方向向左行走50米到达点E.在E处小嘉操作一架无人勘测机,当无人勘测机飞行至点E的正上方点F时,测得点D处的俯角为58°,摩天轮最高处A的仰角为24°.AB所在的直线垂直于地面,垂足为O,点A、B、C、D、E、F、O在同一平面内,求AB的高度.(结果精确到1米,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)8.一艘渔船在海中自西向东航行,速度为28海里/小时,船在A处测得灯塔C在北偏东60°方向,半小时后渔船到达B点,测得灯塔C在北偏东15°方向,求船与灯塔间的最近距离.9.海洋安全预警系统为海洋安全管理起到了巨大作用,某天海洋监控中心收到信息,在A 的北偏西60°方向的120海里的C处,疑似有海盗船在沿CB方向行驶,C在B的北偏西30°方向上,监控中心向A正西方向的B处海警船发出指令,海警船立即从B出发沿BC方向行驶,在距离A为602海里的D处拦截到该可疑船只.(1)求点A到直线CB的距离;(2)若海警船的速度是30海里/小时,那么海警船能否在1小时内拦截到可疑船只?请说明理由.(结果保留一位小数,参考数据:3≈1.73)10.如图1,图2分别是某款篮球架的实物图与侧面示意图,已知底座矩形BCLK的高BK=19cm,宽BC=40cm,底座BC与支架AC所成的角∠ACB=76°,支架AF的长为240cm,篮板顶端F到篮筐D的距离FD=90cm(FE与地面LK垂直,支架AK与地面LK 垂直,支架HE与FE垂直),篮板底部支架HE与支架AF所成的角∠FHE=66°,求篮筐D到地面的距离(精确到1cm).(参考数据:sin66°≈910,cos66°≈25,tan66°≈94,sin76°≈0.96,cos76°≈0.24,tan76°≈4.0)参考答案1.解:(1)在Rt△BOP中,∠BOP=90°,∵∠BPO=45°,OP=100,∴OB=OP=100.在Rt△AOP中,∠AOP=90°,∵∠APO=60°,∴AO=OP•tan∠APO.∴AO=1003(米),∴AB=100(3―1)(米);(2)∵此车的速度=100(3―1)4=25(3―1)≈25×0.73=18.25米/秒,70千米/小时=700003600米/秒≈19.4米/秒,18.25米/秒<19.4米/秒,∴此车没有超过了万丰路每小时70千米的限制速度.2.解:(1)△OBD与△COE全等.理由如下:由题意可知∠CEO=∠BDO=90°,OB=OC,∵∠BOC=90°,∴∠COE+∠BOD=∠BOD+∠OBD=90°.∴∠COE=∠OBD,在△COE和△OBD中,∠COE=∠OBD∠CEO∠ODBOC=OB,∴△COE≌△OBD(AAS);(2)∵△COE≌△OBD,∴CE=OD,OE=BD,∵BD、CE分别为1.8m和2.4m,∴OD=2.4m,OE=1.8m,∴DE=OD﹣OE=CE﹣BD=2.4﹣1.8=0.6(m),∵妈妈在距地面1.2m高的B处,即DM=1.2m,∴EM=DM+DE=1.8(m),答:爸爸是在距离地面1.8m的地方接住小丽的;(3)∵OA=OB=OD2+BD2=2.42+1.82=3(m),∴AM=OD+DM﹣OA=2.4+1.2﹣3=0.6(m).∴秋千的起始位置A处与距地面的高0.6m.故答案为:0.6.3.解:过点A作AG⊥EF,垂足为G,过点D作DH⊥EF,垂足为H,则AB=GF,AG=BF=240cm,∠GAB=90°,在Rt△DBC中,∠DCB=42°,CD=50cm,∴DB=CD•sin42°≈50×0.67=33.5(cm),∵AD=12cm,∴GF=AB=AD+DB=45.5(cm),∵∠EAD=120°,∴∠EAG=∠EAD﹣∠GAB=30°,在Rt△EAG中,EG=AG•tan30°=240×33=803(cm),∴EF=EG+GF=803+45.5≈183.9(cm),∴光源投屏最高点与地面间的距离EF约为183.9cm.4.解:作∠DAG=50°,AG交BC于G,过点G作GH⊥AD于H,则BEGH为矩形,∴GH=BE,BG=EH,设BE=12xm,∵斜坡AB的坡比为12:5,∴AE=5xm,由勾股定理得:(5x)2+(12x)2=262,解得:x=2(负值舍去),∴BE=24m,AE=12m,∴GH=BE=24m,在Rt△GAH中,tan∠GAH=GH AH,则24AH≈1.2,解得:AH=20,∴EH=AH﹣AE=10(m),∴BG=EH=10m,答:坡顶B沿BC至少向右移10m时,才能确保山体不滑坡.5.解:过点A作AM⊥BC于点M,过点D作DN⊥FC于点N,如图,在Rt△ABM中,AB=5dm,∠ABC=44°,∵sin∠ABM=AM AB,∴AM=AB•sin∠ABM=5•sin44°=5×0.69=3.45dm,在Rt△ACM中,∠ACM=17°,∵sin∠ACM=AM AC∴AC=AMsin∠ACM=AMsin17°=3.450.29≈11.9dm;∵AE=13 AC,∴EC=AC―AE=23AC=23×11.9≈7.93dm,∵∠DEC=∠DCE=48°,∴DE=DC,∵DN⊥FC∴FN=CN=12EC≈3.97dm,在Rt△DEN中,EN=3,97dm,∠DEN=48°,∵cos∠DEN=EN DE,∴DE=ENcos∠DEN=3.97cos48°=3.970.67≈5.9dm答:AC的长为11.9dm,DE的长为5.9dm,DC的长为5.9dm.6.解:延长CB,交AE于点D,由题意得,∠DAB=60°,∠DAC=75.97°,∠ADC=90°,BC=2千米,设BD=x千米,则CD=(x+2)千米,在Rt△ABD中,tan60°=BDAD=xAD=3,解得AD=33 x,在Rt△ACD中,tan75.97°=CDAD=x+233x≈4.00,解得x≈1.5,经检验,x≈1.5是原方程的解且符合题意,∴CD≈3.5千米.∴点C到海面的深度约为3.5千米.7.解:过C作CM⊥OD于M,过F作FN⊥AB于N,如图所示:则FN=EO,ON=EF,OM=BC=37米,BO=CM,FN∥EO,∴∠EDF=∠DFN=58°,∵斜坡CD的坡度为i=1:2.4,CD=26米,∴BO=CM=10(米),MD=24(米),∵DE=50米,∴FN=EO=DE+MD+OM=50+24+37=111(米),在Rt△DEF中,tan∠EDF=EFDE=tan58°≈1.60,∴EF≈1.60DE=1.60×50=80(米),∴ON=EF≈80米,∴BN=ON﹣BO≈70(米),在Rt△AFN中,∠AFN=24°,∵tan∠AFN=ANFN=tan24°≈0.45,∴AN≈0.45FN=0.45×111=49.95(米),∴AB=AN+BN=49.95+70≈120(米),即AB的高度约为120米.8.解:过点C作CD⊥AB,交AB的延长线于点D,过点B作BE⊥AC于点E,由题意得,∠CAB=90°﹣60°=30°,∠CBD=90°﹣15°=75°,AB=28×0.5=14(海里),∴∠ACB=∠CBD﹣∠CAB=45°,在Rt△ABE中,sin30°=BEAB=BE14=12,cos30°=AEAB=AE14=32,解得BE=7,AE=73,在Rt△BCE中,∠BCE=45°,∴BE=CE=7海里,∴AC=AE+CE=(7+73)海里,在Rt△ACD中,sin30°=CDAC=CD7+73=12,解得CD=72+732.∴船与灯塔间的最近距离为(72+732)海里.9.解:(1)过点A作AH⊥CB于点H,如图.由题意得:∠CAB=90°﹣60°=30°,∠ABC=180°﹣60°=120°,∴∠C=180°﹣30°﹣120°=30°,∴AH=12AC=12×120=60(海里).答:点A到直线CB的距离是60海里;(2)海警船能否在1小时内拦截到可疑船只,理由:在Rt△ADH中,AD=602海里,AH=60海里,∴DH=AD2―AH2=60(海里),∵∠ABH=∠BAC+∠C=60°,在Rt△ABH中,∠BAH=90°﹣∠ABH=30°,∴BH=12 AB,∴AB=2BH,∵BH2+AH2=AB2,∴BH2+602=(2BH)2,∴BH=203,∴BD=DH﹣BH=(60﹣203)海里,∵海警船的速度是30海里/小时,∴(60﹣203)÷30≈0.9<1,答:海警船能否在1小时内拦截到可疑船只.10.解:延长FE交地面LK于点M,过点A作AG⊥FM,垂足为G,则∠FML=90°,AK=GM,HE∥AG,∴∠FHE=∠FAG=66°,在Rt△ACB中,∠ACB=76°,BC=40cm,∴AB=BC•tan76°≈40×4=160(cm),∵BK=19cm,∴GM=AK=AB+BK=179(cm),在Rt△AFG中,AF=240cm,∴FG=AF•sin66°≈240×910=216(cm),∵FD=90cm,∴DM=FG+GM﹣FD=216+179﹣90=305(cm),∴篮筐D到地面的距离约为305cm.。


精练10--解直角三角形1.如图,某辆自行车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,测得AB=54cm,AC、BC与AB的夹角分别为45°与60°.(1)求点C到AB的距离(结果保留一位小数).(2)若点C到地面的距离CD为30cm,坐垫中轴E与点B的距离BE为4cm(坐垫E 可按轴线BC上下伸缩调节).茜茜根据自己身高比例,坐垫E到地面的距离为70cm 时,乘坐该自行车最舒适.茜茜坐上该自行车,感觉不是很舒适,问:如果要达到最佳舒适高度,茜茜应该如何调节坐垫E的位置?(结果保留一位小数)(参考数据:≈1.4,≈1.7)【解答】解:过点C 作CM⊥AB于点M,则∠CMA=∠CMB=90°,∵∠CAM=45°,∠CBM=60°,∴AM=CM,BM=,∵AB=54(cm),∴CM+=54,∴CM=27(3﹣)≈35.1(cm),∴点C到AB的距离为35.1cm;(2)∵坐垫E到地面的距离为70cm时,乘坐该自行车最舒适,∴点E到AB的距离为70﹣30﹣35.1=4.9(cm),过点E作EN⊥AB于点N,则EN=4.9(cm),∠ENB=90°,∵∠EBN=∠CBM=60°,∴BE==≈5.8(cm)∵原BE为4cm,∴需将BE调长5.8﹣4=1.8(cm).2.某小区拟建设地下停车库入口,将原步行楼梯入口AC改造为斜坡AD.已知入口高AB =3m,坡面AC的坡度i=1:1,新坡面坡角∠ADB=30°.(1)求斜坡底部增加的长度CD为多少米?(保留根号)(2)入口处水平线AE=5m,地下停车库坡道入口上方点E处有悬挂广告牌EF,EF⊥BD,EF=0.5m.若一辆高度为2米的货车沿斜坡AD驶入车库,行进中是否会碰到广告牌的下端F?请说明理由.(参考数据:≈1.4,≈1.7)【解答】解:(1)∵坡面AC的坡度i=1:1,∴AB:BC=1:1,∴BC=AB=3m,∵∠ADB=30°,∴tan∠ADB==tan30°=,∴BD=AB=3m),∴CD=BD﹣BC=(3﹣3)(m),答:斜坡底部增加的长度CD为(3﹣3)米;(2)若一辆高度为2米的货车沿斜坡AD驶入车库,行进中不会碰到广告牌的下端F,理由如下:如图,延长EF交AD于G,过F作FH⊥AD于H,由题意得:∠AEG=90°,AE∥BD,∴∠EAG=∠ADB=30°,∵tan∠EAG==tan30°=,AE=5m,∴EG=AE=(m),∴FG=EG﹣EF=﹣0.5=(﹣)(m),在Rt△FGH中,∠FGH=90°﹣∠EAG=90°﹣30°=60°,∵sin∠FGH==sin60°=,∴FH=FG=×(﹣)=﹣≈2.075(m)>2m,∴若一辆高度为2米的货车沿斜坡AD驶入车库,行进中不会碰到广告牌的下端F.3.如图,在同一剖面内,小明在点A处用测角仪测得居民楼的顶端F的仰角为27°,他水平向右前进了30米来到斜坡的坡脚B处,沿着斜坡BC上行25米到达C点,用测角仪测得点F的仰角为54°,然后,水平向右前进一段路程来到了居民楼的楼底E处,若斜坡BC的坡度为3:4,请你求出居民楼EF 的高度.(测角仪的高度忽略不计,计算结果精确到0.1米.)参考数据:sin27°≈0.45,tan27°≈0.51,sin54°≈0.81,tan54°≈1.38)【解答】解:如图,过点C作CG⊥AD于点G,EH⊥AD于点H,得矩形CGHE,∴CE=GH,CG=EH,在Rt△BCG中,BC=25米,CG:BG=3:4,∴CG=EH=15米,BG=20米,在Rt△AFH中,AH=AB+BC+GH =30+20+GH=50+CE,∵∠F AG=27°,∴FH=AH•tan27°,∴EF+15≈(50+CE)×0.51,在Rt△FCE中,∵∠FCE=54°,∴EF=CE×tan54°≈1.38CE,∴1.38CE+15≈(50+CE)×0.51,解得CE=,∴EF≈1.38CE≈16.7(米),∴居民楼EF的高度约为16.7米.4.如图,在某海域内有一小岛P,在以P为圆心,半径r为6海里的圆形海域内有暗礁,一轮船自东向西航行,它在A处测得小岛P位于北偏西45°的方向上,当这艘轮船行驶4海里后到达B地,此时观测小岛P位于B地北偏西30°的方向上.(1)求A、P之间的距离;(结果精确到0.1海里,参考数据:≈1.41,≈2.45)(2)该轮船由B地继续向西行驶(4﹣4)海里到达C地,此时观测小岛P位于C地北偏西15°的方向上,同时接到总部通知,由于突发状况,该轮船必须驶离东西航线并沿北偏西某航向行驶,那么该轮船由C处开始沿北偏西至少多少度的方向航行才能避开小岛P周围的暗礁安全通过这一海域?【解答】解:(1)过点P作PD⊥AB,交AB的延长线于点D,由题意得,∠BPD=30°,∠P AD=45°,AB=4海里,设PD=x海里,则AD=x海里,∴BD=AD﹣AB=(x﹣4)海里,在Rt△PBD中,∵BD=PD tan30°,∴x﹣4=x,∴x=2(3+),∴P A=PD=x=6+2≈13.4(海里),答:A,P之间的距离约为13.4海里;(2)因为r﹣PD=6﹣2(3+)=6﹣6﹣2≈﹣1<0,所以无触礁的危险;设轮船无触礁危险的新航线为射线CH,作PE⊥CH,垂足为E,当P到CH的距离PE=6海里时,有sin∠PCE=,设CD=y海里,∵BC=(4﹣4)海里,在Rt△PBD中,PD=2(3+)海里,∠BPD=30°,∴BD=PD tan30°,∴y+4﹣4=2(3+)×,解得y=6﹣2,∴CD=(6﹣2)海里,∴PC===4,∴sin∠PCE===,∴∠PCE=60°,∴60°+15°=75°,∴该轮船由C处开始沿北偏西至少75度的方向航行才能避开小岛P周围的暗礁安全通过这一海域.5.如图,某渔船向正东方向以14海里/时的速度航行,在A处测得小岛C在北偏东70°方向,2小时后渔船到达B处,测得小岛C在北偏东45°方向,已知该岛周围20海里范围内有暗礁.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41)(1)求B处距离小岛C的距离(精确到0.1海里);(2)为安全起见,渔船在B处向东偏南转了25°继续航行,通过计算说明船是否安全?【解答】解:(1)如图,过点C作CN⊥AD于M,CN ⊥BE于N,由题意得,∠CAD=90°﹣70°=20°,∠CBD=90°﹣45°=45°,AB=14×2=28海里,∵∠CBD=45°,∴CM=BM,在Rt△CAM中,∵tan∠ACM=,∴tan70°=,解得CM≈16,在Rt△BCM中,BC=CM=16≈22.6(海里),答:B处距离小岛C的距离约为22.6海里;(2)在Rt△BCN中,∠CBN=45°+25°=70°,BC=16海里,∴CN=BC•sin∠CBN≈16×0.94≈21.2(海里),∵21.2>20,∴能安全通过,答:能安全通过.6.首钢滑雪大跳台是世界上首个永久性的单板大跳台,其优美的造型,独特的设计给全球观众留下深刻的印象,大跳台场地分为助滑区、起跳台、着陆坡和终点区域4个都分,现将大跳台抽象成如图的简图,FC表示运送运动员上跳台的自动扶梯,CD表示助滑区,Rt△DEH表示起跳台,EB表示着陆坡.已知∠CF A =60°,∠EBF=30°,在助滑区D处观察到顶点C处的仰角是30°,且自动扶梯的速度是2m/s,运送运动员到达跳台顶端C点处需要30秒,BE=24m,DE∥BF,CA、DG、EF都垂直于BF.(1)求大跳台AC的高度是多少米(结果精确到0.1m);(2)首钢滑雪大跳台主体结构采用装配式钢结构体系和预制构件,“助滑区”和“着陆坡”赛道面宽35米,面板采用10mm耐候钢,密度为7850kg/m3,求铺装“助滑区”和“着陆坡”赛道的耐候钢总重量是多少吨(结果精确到1吨).(≈1.41,≈1.73)【解答】解:(1)根据题意可知:AC=2×30=60(m),答:大跳台AC的高度是60米;(2)如图,过点D作DM⊥CA于点M,得矩形AMDG,矩形DGNE,在Rt△ACF中,CF=60m,∠CF A =60°,∴AC=CF•sin60°=60×=30(m),在Rt△EBN中,∠EBN=30°,BE=24m,∴EN=BE=12m,∴AM=DG=EN=12m,∴CM=AC﹣AM=(30﹣12)m,∵DE∥BF,∴∠CDM=∠E=30°,∴CD=2CM=2(30﹣12)=60﹣24≈79.8m,∴耐候钢的体积=79.8×35×10﹣2+24×35×10﹣2=36.33(m3),∴耐候钢总重量=36.33×7850≈285190(吨).答:赛道的耐候钢总重量约为285190吨.7.5G时代,万物互联.互联网、大数据、人工智能与各行业应用深度融合,助力数字经济发展,共建智慧生活.网络公司在改造时,把某一5G信号发射塔MN建在了山坡BC 的平台CD上,已知山坡BC的坡度为1:2.4.眼睛距地面1.6米的小明站在A处测得塔顶M的仰角是37°.向前步行6米到达B处,再延斜坡BC步行6.5米至平台点C处,测得塔顶M的仰角是50°.若A.B、C、D、M、N在同一平面内,且A、B和C、D、N分别在同一水平线上.(1)求平台CD距离地面的高度;(2)求发射塔MN的高度.(结果精确到0.1米.参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)【解答】(1)解:如图,过点Q作QP⊥MN 于P,过点F作FE⊥MN于E,∵山坡BC的坡度为1:2.4,BC=6.5米,设CG=x,则BG=2.4x,∴x2+(2.4x)2=6.52,解得x=,∴CG=HN=米,BG=6米,(2)解:∵CG=HN=米,BG=6米,∴AG=12米,由题意知∠MQP=37°,∠MFE=50°,设EF=a米,则PQ=AH=(a+12)(米),∵tan50°=≈1.20,∴ME=1.2a,∵tan37°=≈0.75,∴MP=(a+12),∵ME+EN+NH=MP+PH,∴1.2a+1.6+=(a+2)+1.6,解得a=米,∴MN=1.2a+1.6≈18.9(米).8.如图,为了测量陶行知纪念馆AB的高度,小李在点C处放置了高度为1.5米的测角仪CD,测得纪念馆顶端A点的仰角∠ADE=51°,然后他沿着坡度i=1:2.4的斜坡CF 走了6.5米到达点F,再沿水平方向走4米就到达了纪念馆底端点B.(结果精确到0.1,参考数据:sin51°≈0.78,cos51°≈0.63,tan51°≈1.23)(1)求点D到纪念馆AB的水平距离;(2)求纪念馆AB的高度约为多少米?【解答】解:(1)延长AB交水平线于点M,过F作FN⊥CM 于N,延长DE交AM于H,则四边形HMCD为矩形,∴HM=CD=1.5米,DH=CM,∵斜坡CF的坡度i=1:2.4,∴=,∴CN=2.4FN,∵CF=6.5米,∴BM=FN=2.5(米),CN=6(米),∵MN=BF=4米,∴DH=CM=6+4=10(米),答:点D到纪念馆AB的水平距离为10米;(2)在Rt△ADH中,tan∠ADE=则AH=DH•tan∠ADE=10×tan51°≈12.3(米),∴AB=AM﹣BM=AH+HM﹣BM=12.3+1.5﹣2.5≈11.3(米),答:纪念馆AB的高度约为11.3米.9.2022北京冬奥会已正式闭幕,但因冬奥燃起的冰雪消费热潮仍在持续中国滑雪场、冰雪产业正在逐步形成.如图,是某度假村兴建的专业滑雪场地,小南在观景台A处向前走15米到达观景点B处,测得滑雪场顶端E的仰角为22°,沿着坡度为1:2.4的斜坡走了26米到达坡底C处,然后往前走93米到达滑雪场底端D处.A、B、C、D、E、M、N在同一平面内,ED⊥MD,BN⊥MD,AM⊥MD,AB∥MD.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)(1)求观景台A 处到坡底C的水平距离CM;(2)求滑雪场顶端E到CD的距离ED的长(结果精确到1米).【解答】解:(1)延长AB 交DE于F,∵ED⊥MD,BN⊥MD,AM⊥MD,AB∥MD,∴AM∥BN∥FD,BF⊥EF,∴四边形AMNB和四边形BNDF是平行四边形,∴▱AMNB和▱BNDF是矩形,在Rt△BCN中,=,BC=26,BN2+CN2=BC2,设BN=x,CN=2.4x,∴x2+(2.4x)2=262,解得:x=10,∴BN=10,CN=24,∵四边形AMNB是矩形,AB=15,∴MN=AB=15,∴CM=MN+CN=15+24=39(米),答:观景台A处到坡底C的水平距离CM为39米;(2)∵四边形BNDF是矩形,BN=10,CD=93,CN=24,∴FD=BN=10,BF=DN=CN+CD=24+93=117,在Rt△BEF中,tan∠EBF==tan22°,∴EF=BF•tan22°≈117×0.40=46.8,∴ED=EF+FD=56.8≈57(米).答:滑雪场顶端E到CD的距离ED的长约为57米.10.如图,梯形ABCD是一个拦河坝的截面图,坝高5米,背水坡AD的坡度为1:1.2.为了提高河坝抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽1米,新的背水坡EF 的坡角α为30°,河坝总长400米.(1)求大坝底端AF需加宽多少米?(精确到0.1米,参考数据:≈1.73,≈1.41)(2)某工程队每天加固150立方米,工程队能否在30天内完成河坝加固?(体积=底面积×高)【解答】解:(1)过点D作DG⊥AB于G,过点E作EH⊥AB于H,则四边形EHGD为矩形,∴HG=ED=1米,∵坡AD的坡度为1:1.2,DG=5米,∴AG=5×1.2=6米,∴AH=AG﹣GH=6﹣1=5(米),在Rt△EFH中,∠F=30°,∴FH===5≈8.65(米),∴AF=FH﹣AH=8.65﹣5=3.65≈3.7(米),答:大坝底端AF需加宽约为3.7米;(2)需加固的土方量为:×(1+3.7)×5×400=4700(立方米),工程队每天加固150立方米,工程队30天内完成的土方量为:150×30=4500(立方米),∵4500<4700,∴工程队不能在30天内完成河坝加固,答:工程队不能在30天内完成河坝加固.11.图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管CE的长度为0.5米.(1)真空管上端B到水平线AD的距离.(2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米).(参考数据:sin37°≈,cos37°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈0.4)【解答】解:(1)过B作BF⊥AD于F.在Rt△ABF中,sin∠BAF=,则BF=AB sin∠BAF=3sin37°≈3×=1.8(米).答:真空管上端B到AD的距离约为1.8米;(2)在Rt△ABF中,cos∠BAF=,则AF=AB cos∠BAF=3×cos37°≈2.25(米),∵BF⊥AD,CD⊥AD,BC∥FD,∴四边形BFDC是矩形.∴BF=CD,BC=FD,∵EC=0.5米,∴DE=CD﹣CE=1.3米,在Rt△EAD中,tan∠EAD=,则AD=≈=3.25(米),∴BC=DF=AD﹣AF=3.25﹣2.25≈1.0(米),答:安装热水器的铁架水平横管BC的长度约为1.0米.12.如图所示,已知BC是水平面,AB、AD、CD是斜坡.AB的坡角为42°,坡长为200米,AD的坡角为60°,坡长为100米,CD的坡比i=1:2.(1)求坡顶A到水平面BC的距离;(2)求斜坡CD的长度.(结果精确到1米,参考数据:sin42°≈0.70,≈1.73)【解答】解:(1)过点A作AE⊥BC于E,在Rt△ABE中,∠B=42°,AB=200米,则AE=AB•sin B≈200×0.70=140(米),答:坡顶A到水平面BC的距离约为140米;(2)过点D作DF⊥BC于F,DG⊥AE于G,则四边形EFDG为矩形,∴GE=DF,在Rt△AGD中,∠ADG=60°,AD=100米,则AG=AD•sin∠ADG=100×≈86.5(米),∴DF=GE=AE﹣AG=53.5(米),∵CD的坡比i=1:2,∴DF:FC=1:2,∴DF:CD=1:3,∴CD=3DF=160.5≈161(米),答:斜坡CD的长度约为161米.13.数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB =10m,请你根据以上数据计算GH的长.(参考数据sin67,cos67°,tan67°,cos37°,sin37°,tan37°)【解答】解:延长CD交AH于点E,则CE⊥AH,如图所示.设DE=xm,则CE=(x+2)m,在Rt△AEC和Rt△BED中,tan37°=,tan67°=,∴AE=,BE=.∵AE﹣BE=AB,∴﹣=10,即﹣=10,解得:x=8,∴DE=8m,∴GH=CE=CD+DE=2m+8m=10m.答:GH的长为10m.。

人教版备考2023中考数学二轮复习 专题20 解直角三角形一、单选题1.(2021九上·莘县期中)河堤横断面如图所示,堤高BC =6米,迎水坡AB 的坡比是1∶√3,则AC的长是( )A .6√2米B .12米C .3√3米D .6√3米【答案】D【知识点】解直角三角形的应用﹣坡度坡角问题 【解析】【解答】解:∵迎水坡AB 的坡比为1∶√3, ∴BC AC =1√3,∵堤高BC=6米,∴AC =√3BC =6√3(米). 故答案为:D.【分析】根据坡度比可得BC AC =√3,再将数据代入求出AC 的长即可。
2.(2021九上·莘县期中)如图,一艘海轮位于灯塔P 的北偏东55°方向的A 处,已知PA =6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB 的长是( )A .6海里B .6cos55°海里C .6sin55°海里D .6tan55°海里【答案】B【知识点】解直角三角形的应用﹣方向角问题【解析】【解答】由题意可知∠NPA =55°,PA =6海里,∠ABP =90°.∵AB ∥NP ,∴∠A =∠NPA =55°.在Rt△ABP中,∵∠ABP=90°,∠A=55°,PA=6海里,∴AB=AP•cosA=6cos55°海里.故答案为:B.【分析】先利用平行线的性质可得∠A=∠NPA=55°,再利用解直角三角形的方法求出AB=AP•cosA =6cos55°海里即可。
3.(2022九上·襄汾期中)一配电房示意图如图所示,它是一个轴对称图形,已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为()A.(4+3sinα)m B.(4+3tanα)m C.(4+3sinα)m D.(4+3tana)m【答案】B【知识点】解直角三角形的应用【解析】【解答】解:过点A作AD⊥BC于D,如图所示:∵它是一个轴对称图形,∴BD=DC=12BC=3m,∴tanα=ADBD=AD3,即AD=3tanα,∴房顶A离地面EF的高度为(4+3tanα)m,故答案为:B.【分析】过点A作AD⊥BC于D,根据tanα=ADBD=AD3,求出AD=3tanα,再求出EF的长即可。

第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义:在Rt△ABC中,∠C=900, ∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA= ,∠A的余弦可表示为cosA= ∠A的正切:tanA= ,它们统称为∠A的锐角三角函数【名师提醒:1、sinA、∠cosA、tanA表示的是一个整体,是两条线段的比,没有单位,这些比值只与有关,与直角三角形的无关2、取值范围<sinA< ,cosA< ,tanA> 】二、特殊角的三角函数值:在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系:⑴sinA+cos2A= ,tanA=sin A()⑵若∠A+∠B=900,则sinA= ,tanA.tanB= 】三、解直角三角形:1、定义:由直角三角形中除直角外的个已知元素,求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据:Rt∠ABC中,∠C=900 三边分别为a、b、c⑴三边关系:⑵两锐角关系⑶边角之间的关系:sinA cosA tanAsinBcosB tanB【名师提醒:解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形,再利用相应的边角关系解决】3、解直角三角形应用中的有关概念⑴仰角和俯角:如图:在图上标上仰角和俯角⑵坡度坡角:如图:斜坡AB的垂直度h和水平宽度l的比叫做坡度,用i表示,即i=坡面与水平面得夹角为用字母α表示,则i=tanα=hl。
铅直水平线⑶方位角:是指南北方向线与目标方向所成的小于900的水平角如图:OA表示OB表示OC表示OD表示(也可称东南方向)3、利用解直角三角形知识解决实际问题的一般步骤:⑴把实际问题抓化为数学问题(画出平面图形,转化为解直角三角形的问题)⑵根据条件特点,选取合适的锐角三角函数去解直角三角形⑶解出数学问题答案,从而得到实际问题的答案【名师提醒:在解直角三角形实际应用中,先构造符合题意的三角形,解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决】【重点考点例析】考点一:锐角三角函数的概念例1 (2013•贵阳)如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于()A.513B.1213C.512D.1251.(2013•宿迁)如图,将∠AOB 放置在5×5的正方形网格中,则tan ∠AOB 的值是( )A .23B .32C D1.B2.(2013•重庆)计算6tan45°-2cos60°的结果是()A.B.4 C.D.52.D考点三:化斜三角形为直角三角形3.(2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为.(结果保留根号)3.考点四:解直角三角形的应用例4 (2013•舟山)某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).思路分析:先求出校门关闭时,20个菱形的宽即大门的宽;再求出校门打开时,20个菱形的宽即伸缩门的宽;然后将它们相减即可.解:如图,校门关闭时,取其中一个菱形ABCD.根据题意,得∠BAD=60°,AB=0.3米.∵在菱形ABCD中,AB=AD,∴△BAD是等边三角形,∴BD=AB=0.3米,∴大门的宽是:0.3×20≈6(米);如图,校门打开时,取其中一个菱形A1B1C1D1.根据题意,得∠B1A1D1=10°,A1B1=0.3米.∵在菱形A1B1C1D1中,A1C1⊥B1D1,∠B1A1O1=5°,∴在Rt△A1B1O1中,B1O1=sin∠B1A1O1•A1B1=sin5°×0.3=0.02616(米),∴B1D1=2B1O1=0.05232米,∴伸缩门的宽是:0.05232×20=1.0464米;∴校门打开的宽度为:6-1.0464=4.9536≈5(米).故校门打开了5米.点评:本题考查了菱形的性质,解直角三角形的应用,难度适中.解题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,一切将迎刃而解.对应训练【聚焦山东高考】1.2A.12 B.C.米D.米2.A3.(2013•潍坊)一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A./小时B.30海里/小时C./小时D.海里/小时3.D4.(2013•东营)某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为米.4.9tan11°≈0.19)4【备考真题过关】一、选择题1.(2013•天津)tan60°的值等于()A.1 B C D.21.C2.(2013•温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是()A.34B.43C.35D.452.CA.12B.13C.3D.133.DA.5B.4C.5D.34.AA.B.0 C.D.25.BA.30°B.45°C.60°D.90°6.D7.(2013•宁夏)如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h是()A.B.25m C.m D m7.A8.(2013•山西)如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m 到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为()mA. m B. m C.m D.38.A二、填空题10.(2013•淮安)sin30°的值为.110.11.412.(2013•铜仁地区)如图,在直角三角形ABC中,∠C=90°,AC=12,AB=13,则sinB 的值等于.12.1213.14.215.(2013•荆门)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA= 35,则DE= .15.15 416.(2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为米.16.10017.(2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米.17.18.(2013•荆州)如图,在高度是21米的小山A处没得建筑物CD顶部C处的仰角为30°,底部D处的俯角为何45°,则这个建筑物的高度CD= 米(结果可保留根号)- 21 -。

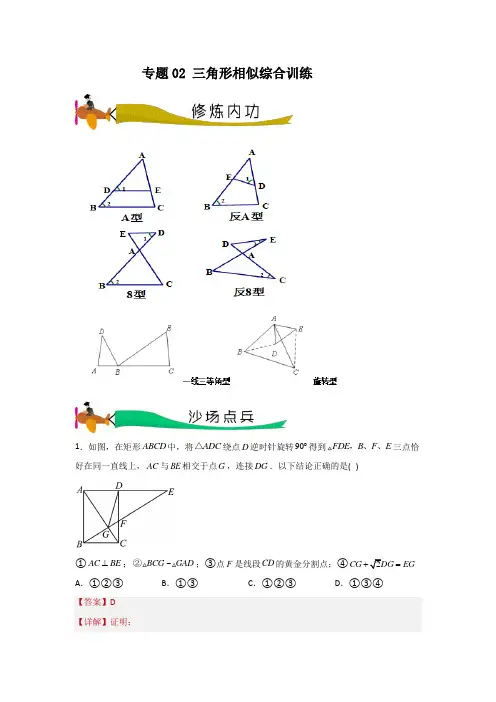
专题02 三角形相似综合训练1.如图,在矩形ABCD 中,将ADC △绕点D 逆时针旋转90︒得到FDE B F E ,、、三点恰好在同一直线上,AC 与BE 相交于点G ,连接DG .以下结论正确的是( )①AC BE ⊥;BCG GAD ~②;③点F 是线段CD 的黄金分割点;④CG EG = A .①②③ B .①③C .①②③D .①③④【答案】D 【详解】证明:FDE ADC ≌,∴AD DF DC DE ==,又∴四边形ABCD 是矩形,∴90ADC ∠=︒, ∴90DAC DCA ∠+∠=即DAG DEF ∠+∠=即BGC 是直角三角形,而AGD 不是直角三角形,∴②错误;Rt FCB 和Rt 中, BFC EFC ∠=∠Rt FCB Rt FDE ∽, FC BCDF DE=, BC AD DF DE DC ===,FC DFDF DC=, F 是线段CD 的黄金分割点,和DEG '中,∴SAS DCG DEG '≌(DG DG CDG ='∠=,90CDG GDA ∠+∠=︒90EDG GDA ∠'+∠=90GDG ∠'=︒,∴GDG '是等腰直角三角形,2GG DG '=EG CG '=EG EG ='故选:D .【我思故我在】2.如图,在ABC 中,D 、E 分别在AB 边和AC 边上,//DE BC ,M 为BC 边上一点(不与B 、C 重合),连结AM 交DE 于点N ,则( )A .ADANANAEB .BD MNMN CEC .DN NEBM MCD .DN NEMC BM,AN ANNE DN NEAM AMMCBMMC,故选相似三角形的判定和性质,解题的关键是熟练掌握3.如图,在ABC ∆中,2AC =,4BC =,D 为BC 边上的一点,且CAD B ∠=∠.若ADC ∆的面积为a ,则ABD ∆的面积为( )A .2aB .52aC .3aD .72aACD BCA ∆,再由相似三角形的性质得到答案ACD BCA ∆,2AC BC ⎛⎫= ⎪⎝⎭,即BCA ∆的面积为的面积为:.4.如图,在矩形ABCD 中,E,F分别为边BC 、CD 中点,线段AE ,AF 与对角线BD 分别交于点G ,H .设矩形ABCD 的面积为S ,则以下4个结论中:①AG :GE =2:1 ②BG :GH :HD =1:1:1;③12325S S S S ++=;④ 246124S S S =::::正确的结论有( )A .1个B .2个C .3个D .4个【答案】C∴,BGE DGA ∽ 2,AG AD BGGE BE DG===②∴AG AD BGGE BE DG==13BG BD =,1所以本题的3个结论符合题意; 故选:C .【我思故我在】本题考查了矩形的性质,三角形相似的性质和判定,三角形面积等知识,解题的关键是理解题意,等底同高三角形面积相等,相似三角形面积的比等于相似比的平方. 5.如图,在正方形ABCD 中,BPC △是等边三角形,BP 、CP 的延长线分别交AD 于E 、F ,连接BD 、DP ,BD 与CF 相交于点H .给出以下结论:①3BE AE =;②DFP BPH ;③2DP PH PC =⋅;④若2AB =,则1BPD S △.其中正确结论的是( )A .①②③④B .②③④C .①②④D .①③④从而证明DFP BPH ,正确;利用DPH CPD ~,得DP PC ,将ΔBPD S 转化为S 四边形解:BPC ∆是等边三角形,BC ,60PBC PCB BPC ∠=∠=∠=ABCD 中,AB BC CD =,A ∠30ABE DCF ∴∠==︒2BE AE ∴=故①错误PC CD =PDC ∴∠=FDP ∴∠=DBA =∠DFP ∠=DFP BPH ∴~,故②正确;30PDH PCD ∠=∠=︒DPH CPD ∴~,∴DP PHPC DP=, 2DP PH PC ∴=⋅,故③正确;如图,过点P 作PM正方形的边长6.如图, 在平行四边形ABCD 中, 点,M N 分别是AD BC 、上的点, 且22AM DM BN CN ==,, 点O 是CM , DN 的交点, 直线AB 分别与CM DN ,的延长线交于点,P Q . 若平行四边形ABCD 的面积为144 , 则POQ △的面积为( )A .72B .216C .268D .300∴AMP DMC ∽, AP AMDC DM=, 2AM DM = 2AP AMDC DM==, 2AP CD =, ∴COD POQ ∽, 1215h CD h PQ ==, ∴∴POQ 的高为56h ,144ABCDS CD h =⋅=151POQS=故选:D 【我思故我在】的性质及平行四边形的性质是解题的关键.7.如图,在正方形ABCD 中,点G 是BC 上一点,且12GC BG =,连接DG 交对角线AC 于F 点,过D 点作DE DG ⊥交CA 的延长线于点E ,若5AE =,则DF 的长为( )A .BC .92D ,证明DEH DGC ∽,推出,求出5EH HA ==延长线于H ,DE DG ⊥EDG ∠∴21∴∠+∠1∠∠∴=DEH DGC ∴∽,∴EH DHGC DC =, 12GC BG =, ∴设GC x =,则BG =∴3EH DHGC x=, AC 是正方形DAC ∴∠EAH ∠=HEA ∴∠=EH HA ∴=2EH HA ∴+EH HA ∴=在正方形8.已知,如图,平行四边形ABCD 中,:1:3=CE BE ,且1EFC S =△,那么ABCS=_____.ACD ABC SS =,证明1:4AD =,则CE AD =. 9.P 是ABC 边上的任一点(P 不与A 、B 、C 重合),过点P 的一条直线截ABC ,如果截得的三角形与ABC 相似,我们称这条直线为过点P 的∴ABC 的“相似线”.Rt ABC △中,90C ∠=︒,30B ∠=︒,当点P 是边BC 上一个三等分点时(PB PC >),过点P 的ABC 的“相似线”最多有___________条.【答案】4【分析】根据相似线的定义,可知截得的三角形与ABC 有一个公共角,分①公共角为A ∠时;②公共角为B ∠时;③公共角为C ∠时;三种情况进行讨论,即可得出答案.【详解】解:①当公共角为A ∠时,不存在;②公共角为B ∠时,过点P 作PD BC ⊥,交AB 于点D ,如图所示:∴90DPB C ∠=∠=︒,B B ∠=∠,∴BPD BCA ∽;过点P 作PD AB ⊥于点D ,如图所示:∴90PDB C ∠=∠=︒,B B ∠=∠,∴BPD BAC ∽△△;③公共角为C ∠时,连接AP ,如图所示:∴30B ∠=︒,∴2AB AC =,设AC a =,则2AB a =,∴ACP BCA∽;过点P作PD AB∥,交∴CDP CAB∽;综上分析可知,过点的ABC的“相似线故答案为:4.【我思故我在】本题主要考查了相似三角形的判定,平行线的性质,勾股定理,解题的关键是熟练掌握三角形相似的判定方法.10.如图,在ABC中,6BC=,AE AFEB FC=,动点P在射线EF上,BP交CE于点D,CBP∠的平分线交CE于点Q,当14CQ CE=时,EP BP+的值为______.【答案】18【分析】如图,延长EF交BQ的延长线于G.首先证明PB PG=,EP PB EG+=,由EG BC∥,11.如图,在矩形ABCD中,点E,F分别是,==∠=︒∠=︒,则BC的长度是___________.3,6,30,45BE CD FED FDE【答案】3##3+【分析】作FN DE ⊥于点N ,延长DE 交CB 的延长线于点M ,先证FND ∆是等腰直角三角形,设FN x =,利用勾股定理、含30度角的直角三角形的性质求出DN ,EF ,NE 的长度,FDE ∠=DFN ∴∠FND ∴∆是等腰直角三角形.由题意得:设FN x =FED ∠=2EF FN ∴=NE ∴=DE DN ∴=3BE =,AE BE ∴=又EAD ∠=EAD ∴∆∆≌AD BM ∴=EBM ∠=EBM ∴∆∽BM BE MN NF ∴=解得:BM 12.如图,在ABC 中,146AB AC ==,,在AC 上取一点D ,使2AD =,如果在AB 上取点E ,使ADE 和ABC 相似,则AE =___________.①ABC AED ;②ABC ADE ;可根据各四条线段的比例关系式求出AE 的长.此时ADE ACB ,::AC AE AD =,146AC AD ==,,此时ADE ABC ,::AC AD AE =,146AC AD ==,,67=, 故答案为:143或67.13.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M 在旋转中心O 的正下方,某一时刻,太阳光线恰好垂直照射叶片OA 、OB ,此时各叶片影子在点M 右侧成线段CD .测得8.5m MC =,13m CD =,垂直于地面的木棒EF 与影子FG 的比为23:.则点O 、M 之间的距离等于___________m ;【答案】10【分析】连接OM 交AC 于点H ,过点C 作CN BD ⊥,通过证明HMC EFG HAO ∽∽△△△,通过相似三角形对应边成比例即可解答.【详解】解:连接OM 交AC 于点H ,过点C 作CN BD ⊥,14.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE 并延长,交对角线BD 于点F 、DC 的延长线于点G .如果23CE BE =,求FE EG的值.15.矩形ABCD 中,AC BD ,为对角线,6cm 8cm AB BC ==,,E 为DC 中点,动点P 从点A 出发沿AB 方向,向点B 运动,动点Q 同时以相同速度,从点B 出发沿BC 方向向点C 运动,P 、Q 的速度都是1cm/秒,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为x 秒.()06t <<(1)PQ AC ∥时,求运动时间t ;(2)PQ BD ⊥时,求运动时间t ;(3)当t 为何值时,以点P ,B ,Q 为顶点的三角形与QCE 相似?(4)连接PE PQE ,△的面积能否达到矩形ABCD 面积的三分之一,若能求出t 的值;若不能,说明理由.7BP BQBP BQ为顶点的三角形与QCE相似216.解答题=;(1)如图1,ABC和ADE都是等边三角形,连接BD、CE,求证,BD CE[类比探究](2)如图2,ABC 和ADE 都是等腰直角三角形,90ABC ADE ∠=∠=︒,连接BD CE ,.求BD CE的值.[拓展提升](3)如图3,ABC 和ADE 都是直角三角形,90ABC ADE ∠=∠=︒,2AC AE AB AD==.连接BD CE 、,延长CE 交BD 于点F ,连接AF .若AFC ∠恰好等于90︒,请直接写出此时AF BF CF ,,之间的数量关系.证明BAD CAE ∽,从而得出结果;B 作BH CF ⊥,垂足为点AOF BOH ∆∽,根据对应边成比例,【详解】(1)解:∴ABC 和ADE 都是等边三角形,AC ,AD AE =,∠∠DAE BAC =BAC BAE ∠-∠,即:在BAD 和CAE 中,AB AC DAB EAC AD AE =∠=∠=,(SAS BAD CAE ≌△△BD CE =.∴ABC 和ADE 都是等腰直角三角形,45BAC =∠=︒,ADE ∠ADE △∽,AE AC ,则AD AB AE AC=,BAE BAC -∠=∠-∠在BAD 和CAE 中,DAB EAC =∠,AD AE ∴BAD CAE ∽,BD AB CE AC =, 令AB x =,根据勾股定理可得:2BD AB x CE AC x===(3)∴BAD CAE ∽,ACE ABD ∠=∠,在FOB ∆和AOC ∆中,ACE ABD ∠=∠,∠60OFB OAC ∠=∠=设FH x =,OH y =,则17.在△ABC 中,90ACB ∠=,BE 是AC 边上的中线,点D 在射线BC 上.(1)如图1,点D 在BC 边上,:1:2CD BD =,AD 与BE 相交于点P ,过点A 作AF BC ,交BE 的延长线于点F ,易得AP PD的值为 ; (2)如图2,在△ABC 中,90ACB ∠=,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,:1:2DC BC =,求AP PD的值; (3)在(2)的条件下,若CD=2,AC=6,则BP= .18.在∴ABC 中,CA CB =,ACB α∠=,点P 在平面内不与点A ,C 重合,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接,,AD BD CP .(1)如图①,当60α=︒,BD CP的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 . (2)如图②,当90α=︒时,请写出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数,并说明理由. (3)当90α=︒时,若点E ,F 分别是,CA CB 中点,点P 在直线EF 上,请直接写出当C ,P ,D 在同一直线上时,求AD CP 的值. ,ABC 是等腰直角三角形,根据等腰直角三角形的性质证明,利用相似的性质即可得解;上,和P 在线段解:如图,延长CP 交60︒,∴ABC 是等边三角形,由题意可知∴PAD 是等边三角形,PAD ∠=∠CAP ∠+∠在CAP 和BAD 中,CA BA CAP BAD AP AD =⎧⎪∠=∠⎨⎪=⎩,CAP BAD △≌△ (SAS),PC BD ACP =∠=∠在AOC 和△1BD PC=,直线BD ∴ABC 是等腰直角三角形,CAB ∠=∠∴ AB AC =AB AD AC AP∴=CAB ∠+∠AD是ABC的中位线,2219.如图,点E是矩形ABCD的边AB的中点,F是BC边上一动点(点F与点B,点C不重合),线段DE和:AF相交于点P,连接PC.(1)若在线段DP 上取一点Q ,使得2DP EQ =,连接AQ ,猜想PC 与AQ 的关系并证明;(2)若AF DE ⊥时,8,10AB AD ==,求BF 的长;(3)当点F 为BC 的中点时,求AP PF 的值. AEQCDP ∆,即可得出结论;,再判断出DAE ABF ,即可得出结论;,先判断出(AAS)ADE BGE ∆≅∆,再判断出2,2AD BF BG BF ==,进而判断出,即可得出结论.∴90BAF AED .90BAF AFB ∠+∠=︒,AED AFB ∠=∠,90DAE ABF ∠=∠=︒,∴DAEABF , AD AE AB BF =,即1083.2BF =;(3)解:如图,延长AD GC ,APD FPG ∆,23AD GF ==.【我思故我在】此题查了矩形的性质,构造出相似三角形是解本题的关键.。


第九讲直角三角形、锐角三角函数及其应用专项一直角三角形知识清单1. 直角三角形的性质(1)直角三角形的两个锐角;(2)直角三角形斜边上的中线等于斜边的;(3)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a,b,c满足;(4)直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的.2. 直角三角形的判定(1)有一个角是直角的三角形是直角三角形;(2)有两个角的三角形是直角三角形;(3)勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形;(4)如果一个三角形一边上的中线等于这条边的,那么这个三角形是直角三角形.(这个结论在做填空、选择题时可直接用)3. 勾股数:能够成为的三个正整数,称为勾股数.考点例析例1 如图1,AB∥CD,CE⊥AD,垂足为E.若∠A=40°,则∠C的度数为()A.40°B.50°C.60°D.90°图1分析:根据平行线的性质,得∠D=∠A=40°,再在Rt△CED中,根据“直角三角形的两个锐角互余”即可求得∠C的度数.例2 如图2,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线.若DE=6,则BF的长为()A.6 B.4 C.3 D.5图2分析:根据三角形的中位线定理可求出AC 的长,再根据“直角三角形斜边上的中线等于斜边的一半”即可求得BF 的长.例3 如图3,在Rt △ABC 中,∠C =90°,∠B =30°,AB =8.若E ,F 是BC 边上的两个动点,以EF 为边的等边三角形EFP 的顶点P 在△ABC 的内部或边上,则等边三角形EFP 的周长的最大值为 .图3分析:当点F 与点C 重合,点P 落在AB 边上时,△EFP 的边长最长,周长也最长,根据“直角三角形中,30°角所对的直角边等于斜边的一半”可求出AC 的长,再利用三角函数,或求出AP 利用勾股定理均可求得△EFP 边长的最大值,进而得解.例4 如图4,某港口P 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A ,B 处,且相距20海里.若甲船沿北偏西40°方向航行,则乙船沿 方向航行.图4分析:由题意,知AP =12,BP =16,AB =20,根据勾股定理的逆定理,可推出△APB 是直角三角形,且∠APB =90°,结合甲船的航行方向可推出乙船的航行方向.例5 如图5,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形,正方形的顶点E ,F ,G ,H ,M ,N 都在同一个圆上.记该圆的面积为S 1,△ABC 的面积为S 2,则12S S 的值是( ) A .5π2 B .3π C .5π D .11π2图5分析:设Rt △ABC 的三边长为a ,b ,c ,其中c 为斜边,设⊙O 的半径为r ,根据图形的特点找出a ,b ,c,r的等量关系,用含c的式子表示S1和S2,即可求出比值.跟踪训练1.如图,△ABC中,∠ACB=90°,AC=8,BC=6,将△ADE沿DE翻折,使点A与点B重合,则CE的长为()A.198B.2 C.254D.74第1题图第2题图第3题图2.如图,已知A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B 的坐标为()A.(0,5)B.(5,0)C.(6,0)D.(0,6)3.(2021·成都)如图,图中数字代表所在正方形的面积,则A所代表的正方形的面积为.4.(2021·西宁)如图,在Rt△ABC中,∠BAC=90°,D,E分别是AB,BC的中点,连接AE,DE.若DE=92,AE=152,则点A到BC的距离是.第4题图第5题图5.如图,在▱ABCD中,点E在AD上,且EC平分∠BED.若∠EBC=30°,BE=10,则▱ABCD的面积为.6.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=4,则AB2+CD2=.第6题图第7题图7.如图,在四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4.若M是四边形ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为.专项二锐角三角函数知识清单1. 锐角三角函数如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边长分别为a,b,c,则∠A的正弦:sin A=ac;∠A的余弦:cos A=;∠A的正切:tan A=.∠A的正弦、余弦、正切都是∠A的锐角三角函数.2. 特殊角的三角函数值考点例析例1如图1,点A,B,C在边长为1的正方形网格格点上,下列结论错误的是()A.1sin3B=B.25sin C C.1tan2B=D.22sin sin1B C+=图1分析:利用正方形网格的特点,由勾股定理得出AB,AC,BC的长,进而利用勾股定理的逆定理推出△ABC 是直角三角形,最后根据锐角三角函数的定义对选项逐一判断即可.归纳:锐角三角函数使用的前提一定是直角三角形,并能准确地找出某个角的对边、邻边和斜边.例2 如图2,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为()A.35B5C.45D25三角函数α30°45°60°sin αcos αtan α图2分析:根据“直角三角形斜边上的中线等于斜边的一半”,得CE =AE =BE ,进而得到∠BEC =2∠A ,连接BF ,由EF ⊥AB ,得∠BFC =2∠A ,所以∠BEC =∠BFC ,从而有∠CEF =∠CBF .根据三角形的面积公式求出AF 的长,在Rt △BCF 中,利用勾股定理求出CF ,再根据锐角三角函数的定义求解即可.归纳:一个锐角的三角函数值仅与这个锐角的大小有关,而与这个锐角在何处、在何种三角形中无关(即与三角形三边的长短无关).当一个锐角的三角函数值求解较烦琐或不易直接求得时,可转化为求与其相等的角的三角函数值.跟踪训练1.tan 30°的值等于( )A B C .1 D .22.如图,在平面直角坐标系内有一点P (3,4),连接OP ,则OP 与x 轴正方向所夹锐角α的正弦值是( )A .34B .43C .35D .45第2题图 第3题图 第4题图3.如图,在△ABC 中,O 是角平分线AD ,BE 的交点.若AB =AC =10,BC =12,则tan ∠OBD 的值是( )A .12B .2CD 4.如图,在正方形网格中,每个小正方形的边长都是1,⊙O 是△ABC 的外接圆,点A ,B ,O 在网格线的交点上,则sin ∠ACB 的值是 .专项三 解直角三角形知识清单解直角三角形的几种常见类型及解法:考点例析例1 在△ABC 中,∠ABC =90°.若AC =100,sin A =35,则AB 的长是( ) A .5003 B .5035 C .60 D .80分析:利用锐角三角函数的定义求出BC 的长,然后再利用勾股定理即可求得AB 的长.例2 如图,△ABC 底边BC 上的高为h 1,△PQR 底边QR 上的高为h 2,则有( )A .h 1=h 2B .h 1<h 2C .h 1>h 2D .以上都有可能分析:分别作出△ABC 底边BC 上的高和△PQR 底边QR 上的高,再利用锐角三角函数分别表示出h 1和h 2,即可确定其大小关系.跟踪训练1.如图,在△ABC 中,∠B =45°,∠C =60°,AD ⊥BC 于点D ,BD 若E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D第1题图 第2题图2.如图,△ABC 的顶点B ,C 的坐标分别是(1,0),(,且∠ABC =90°,∠A =30°,则顶点A 的坐标是 .3.在△ABC 中,∠A =45°,AB =BC =5,则△ABC 的面积为 .4.在锐角三角形ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,边角总满足关系式:sin sin sin a b c A B C ==. (1)如图①,若a =6,∠B =45°,∠C =75°,求b 的值;(2)某公园准备在园内一个锐角三角形水池ABC 中建一座小型景观桥CD (如图②所示).若CD ⊥AB ,AC =14米,AB =10米,sin ∠ACB ,求景观桥CD 的长度.① ②第4题图专项四 锐角三角函数的实际应用知识清单锐角三角函数的实际应用主要是测量物体的高度、测量两点之间的距离等,常用到下面几个概念:1. 仰角、俯角如图1,在视线与水平线所成的锐角中,视线在水平线上方的角叫做 ,视线在水平线下方的角叫做 .图1 图2 图32. 坡度、坡角如图2,坡面的铅直高度h 和水平宽度l 的比叫做坡面的坡度(或坡比),用字母i 表示;坡面与水平面的夹角α叫做坡角,i = = ,坡度越大,α越 ,坡面越 .3. 方位角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向所成的小于90°的角.如图3,点A位于点O的北偏东方向,点B位于点O的60°方向,点C位于点O的(或)方向.考点例析例1 无人机低空遥感技术已广泛应用于农作物监测.如图1,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135 m的A处测得试验田右侧边界N处的俯角为43°,无人机垂直下降40 m至B处,又测得试验田左侧边界M处的俯角为35°,则M,N之间的距离为(参考数据:tan 43°≈0.9,sin 43°≈0.7,cos 35°≈0.8,tan 35°≈0.7)()A.188 m B.269 m C.286 m D.312 m图1分析:在Rt△AON中,由AO的长和∠N的度数求出ON的长,再在Rt△BOM中,由BO的长和∠M的度数求出MO的长,结合MN=MO+ON即可求得M,N之间的距离.例2 某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°.已知原楼梯长为5米,调整后的楼梯会加长(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)()A.6米B.3米C.2米D.1米分析:画出示意图如图2所示,在Rt△BAD中,由AB=5,∠BAD=37°,求出BD的长,在Rt△BCD中,根据“直角三角形中,30°角所对的直角边等于斜边的一半”求出BC的长,进而得解.图2例3 如图3,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为海里.(结果保留根号)图3分析:过点P作PC⊥AB于点C,在Rt△APC中,由P A的长和∠A的度数求出PC的长,再在Rt△BPC 中,由PC的长和∠B的度数即可求得PB的长.跟踪训练1.如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E处,即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为()A.15sin 32°B.15tan 64°C.15sin 64°D.15tan 32°第1题图第2题图第3题图2.如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A 点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1∶2.4.根据小颖的测量数据,计算筑物BC)()A.136.6米B.86.7米C.186.7米D.86.6米3.某景区A,B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°方向,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.(1)求景点B和C处之间的距离;(结果保留根号)(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B)专项五锐角三角函数中的建模思想知识清单根据实际问题建立数学模型,再通过解决数学问题达到解决实际问题的目的,这种思想被称为建模思想.考点例析例一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为△ABC,点B,C,D在同一条直线上,测得∠ACB=90°,∠ABC=60°,AB=32 cm,∠BDE=75°,其中一段支撑杆CD=84 cm,另一段支撑杆DE=70 cm.求支撑杆上的点E到水平地面的距离EF是多少?(结果保留整数;参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27)分析:过点D作DM⊥EF于点M,DN⊥BA交BA的延长线于点N,解Rt△ABC求出BC的长,再解Rt△BDN 求出DN的长,易得四边形MFND是矩形,利用矩形的性质可得MF=DN及∠BDM的度数,进而求得∠EDM,最后解Rt△EMD求出EM的长,进而得解.解:归纳:解直角三角形的前提是在直角三角形中进行,对于非直角三角形问题,要注意观察图形特点,作恰当的辅助线,将其转化为直角三角形求解.跟踪训练1.如图①是一台手机支架,图②是其侧面示意图,AB,BC可分别绕点A,B转动,测量知BC=8 cm,AB =16 cm.当AB,BC转动到∠BAE=60°,∠ABC=50°时,点C到AE的距离为cm.(结果精确到0.1 cm;参考数据:sin 70°≈0.94)①②①②③第1题图第2题图2.某种落地灯如图①所示,AB为立杆,其高为84 cm;BC为支杆,可绕点B旋转,其中BC长为54 cm;DE为悬杆,滑动悬杆可调节CD的长度.已知支杆BC与悬杆DE之间的夹角∠BCD为60°.(1)如图②,当支杆BC与地面垂直,且CD的长为50 cm时,求灯泡悬挂点D距离地面的高度;(2)在图②所示的状态下,将支杆BC绕点B顺时针旋转20°,同时调节CD的长(如图③),此时测得灯泡悬挂点D到地面的距离为90 cm,求CD的长.(结果精确到1 cm;参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)参考答案专项一直角三角形例1 B 例2 A 例3例4 北偏东50°例5 C 解析:如图,取AB的中点O,AC的中点D,连接OC,OD,OE,OG.因为圆心在线段EF和MN的垂直平分线上,所以点O为圆心.设AC=a,BC=b,AB=c,则a2+b2=c2.在Rt△ABC中,O为AB的中点,所以OA=OB=OC.又D为AC的中点,所以OD∥BC.所以OD⊥AC.因为OG,OE为⊙O的半径,所以OD2+DG2=OB2+BE2,即2222222a cb cb⎛⎫⎛⎫⎛⎫++=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.整理,得a=b.所以215π4Sc=,224Sc=.所以12SS=5π.1.D 2.D 3.100 4.3655.50 6.20 7.2专项二锐角三角函数例1 A例2 A 解析:连接BF.在Rt△ABC中,CE是斜边AB上的中线,所以CE=AE=BE,所以∠A=∠ACE.所以∠BEC=2∠A.因为EF⊥AB,所以EF是AB的垂直平分线.所以S△BEF=S△AEF=5,∠FBA=∠A.所以∠BFC=2∠A.所以∠BEC=∠BFC.又∠BEF=∠BCF=90°,所以∠CEF=∠CBF.因为S △AFB =2S △AEF =10,所以12AF ·BC =10.因为BC =4,所以AF =BF =5.所以CF 3. 所以sin ∠CEF =sin ∠CBF =35CF BF =.1.A 2.D 3.A 4 专项三 解直角三角形例1 D 例2 A1.C 2.( 3.2或144.解:(1)因为∠B =45°,∠C =75°,所以∠A =180°-∠B -∠C =60°.所以6sin 60sin 45b =︒︒,解得b =(2)因为sin sin AB AC ACB B =∠14sin B =,解得sin B .所以∠B =60°.所以tan B =CD BD =BD CD .在Rt △ACD 中,AC 2=CD 2+AD 2,即196=CD 2+210⎛⎫ ⎪ ⎪⎝⎭,解得CD =CD =-(舍去). 所以景观桥CD 的长度为专项四 锐角三角函数的实际应用例1 C 例2 D 例3 1.C 2.A3.解:(1)过点C 作CD ⊥AB 于点D .在Rt △ACD 中,∠A =30°,AC =600,所以CD =12AC =300.在Rt △BCD 中,∠B =75°-∠A =45°,所以BC =sin 45CD ︒=.答:景点B 和C 处之间的距离为m .(2)在Rt △ACD 中,∠A =30°,AC =600,所以AD =AC ·cos 30°=.在Rt △BCD 中,∠B =45°,所以BD =CD =300.所以AB =AD +BD =.所以AC +BC -AB =600+-(300+≈205(m ).答:大桥修建后,从景点A 到景点B 比原来少走约205 m .专项五 锐角三角函数中的建模思想例 过点D 作DM ⊥EF 于点M ,DN ⊥BA 交BA 的延长线于点N .在Rt △ABC 中,∠ABC =60°,AB =32,所以BC =AB ·cos 60°=16.因为CD =84,所以BD =BC +CD =16+84=100.在Rt △BDN 中,DN =BD ·sin 60°==.易得四边形MFND 是矩形,所以MF =DN =,MD ∥FN .所以∠BDM =∠ABC =60°.因为∠BDE =75°,所以∠EDM =∠BDE -∠BDM =75°-60°=15°.在Rt △EMD 中,DE =70,所以EM =DE ·sin 15°≈70×0.26=18.2.所以EF =EM +MF =18.2+≈105.答:支撑杆上的点E 到水平地面的距离EF 约是105 cm .1.6.32.解:(1)如图①,过点D 作DF ⊥BC 于点F .在Rt △DCF 中,CD =50,∠FCD =60°,所以FC =CD ·cos 60°=25.所以F A =AB +BC -FC =84+54-25=113(cm ).答:灯泡悬挂点D 距离地面的高度为113 cm .(2)如图②,过点C 作CG 垂直于地面于点G ,过点B 作BN ⊥CG 于点N ,过点D 作DM ⊥CG 于点M . 在Rt △BCN 中,BC =54,∠BCN =20°,所以CN =BC ·cos 20°≈54×0.94=50.76.所以CM =CN +NG -MG =CN +AB -MG =50.76+84-90=44.76.在Rt △DCM 中,∠DCM =∠BCD -∠BCN =40°,所以CD =cos40CM ≈44.760.77≈58(cm ). 答:CD 的长约为58 cm .① ②第2题图。
知识回顾微专题专题21直角三角形考点一:直角三角形1. 直角三角形的概念:有一个角是90°的三角形叫做直角三角形。
2. 直角三角形的性质:①直角三角形的两锐角互余。
②直角三角形斜边上的中线等于斜边的一半。
③含30°的直角三角形中,30°角所对的直角边等于斜边的一半。
④直角三角形的两直角边的成绩等于斜边乘以斜边上的高线。
⑤直角三角形的勾股定理。
1.(2022•贺州)如图,在Rt △ABC 中,∠C =90°,∠B =56°,则∠A 的度数为( )第1题 第2题 A .34° B .44° C .124° D .134°2.(2022•岳阳)如图,已知l ∥AB ,CD ⊥l 于点D ,若∠C =40°,则∠1的度数是( )A .30°B .40°C .50°D .60°3.(2022•绍兴)如图,把一块三角板ABC 的直角顶点B 放在直线EF 上,∠C =30°,AC ∥EF ,则∠1=( )A .30°B .45°C .60°D .75°4.(2022•大连)如图,在△ABC 中,∠ACB =90°.分别以点A 和点C 为圆心,大于21AC 的长为半径作弧,两弧相交于M ,N 两点,作直线MN .直线MN 与AB 相交于点D ,连接CD ,若AB =3,则CD 的长是( )第4题第5题A.6B.3C.1.5D.1 5.(2022•永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为()A.3B.23C.2D.4 6.(2022•青海)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF.若AC=16,BC=12,则BF的长为()第6题第7题A.5B.4C.6D.8 7.(2022•镇江)如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点,若DE=1,则FG=.8.(2022•西宁)如图,△ABC中,AB=6,BC=8,点D,E分别是AB,AC的中点,点F 在DE上,且∠AFB=90°,则EF=.9.(2022•梧州)如图,在△ABC中,∠ACB=90°,点D,E分别是AB,AC边上的中点,连接CD,DE.如果AB=5m,BC=3m,那么CD+DE的长是m.知识回顾微专题第9题 第10题10.(2022•台州)如图,在△ABC 中,∠ACB =90°,D ,E ,F 分别为AB ,BC ,CA 的中点.若EF 的长为10,则CD 的长为 .考点二:勾股定理1. 勾股定理的内容:在直角三角形中,两直角边的平方的和等于斜边的平方。
专题06解直角三角形的应用目录热点题型归纳 (1)题型01仰角与俯角问题 (1)题型02坡度问题 (6)题型03方位角问题 (14)中考练场 (23)题型01仰角与俯角问题【解题策略】仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.【典例分析】例.(2023·湖北襄阳·中考真题)在襄阳市诸葛亮广场上矗立着一尊诸葛亮铜像.某校数学兴趣小组利用热气球开展综合实践活动,测量诸葛亮铜像的高度.如图,在点C 处,探测器显示,热气球到铜像底座底部所在水平面的距离CE 为32m ,从热气球C 看铜像顶部A 的俯角为45︒,看铜像底部B 的俯角为63.4︒.已知底座BD 的高度为4m ,求铜像AB 的高度.(结果保留整数.参考数据:sin 63.40.89︒≈,cos 63.40.45︒≈,tan 63.4 2.00︒≈ 1.41≈)【答案】铜像AB 的高度是14m ;1.(2024·山西朔州·一模)山西“应县木塔”,又名山西“应县佛宫寺释迦塔”,它是当今世界上的第一奇塔.它不仅是中国,而且是世界上现存最古老、最高峻的木构建筑物,所以它在世界建筑中占有突出的地位.已知“应县木塔”的高度AB 为67.3米,塔前“女神雕像”的高度CD 为10.3米,木塔与雕像之间有障碍物,不能直接测量,某测量小组为了测量“应县木塔”与塔前“女神雕像”之间的距离,采用了如下测量方案(如图所示):①他们在“木塔”和“雕像”之间选择一观景平台E ,测得“木塔”顶部A 的仰角为30︒,测得“雕像”顶部C 的仰角为45︒;②测得测角仪的高度EF 为1.3米;③测得点,,B F D 在同一条直线上,,,AB BD EF BD CD BD ⊥⊥⊥,垂足分别是,,B F D .求“应县木塔”与塔前“女神雕像”之间的距离BD .(结果精确到0.1 1.7≈)【答案】121.2米【分析】本题主要考查解直角三角形的实际应用,矩形的判定和性质,过点E 作MN BD ∥,交AB 于M ,交CD 于M ,构造矩形MBFE ,NDFE ,MBDN ,再利用三角函数解Rt AME △和Rt CNE △即可.,,AB BD EF BD CD BD ⊥⊥⊥,MN∴四边形MBFE ,NDFE,MBDN ∴67.3 1.366AM AB MB =-=-=,长安城保留至今的重要标志.小港为测量小雁塔的高度、制定了如下测量方案:如图所示,当小港站在点A 处仰望塔顶,测得仰角为30︒,再往塔的方向前进50m 至B 处,测得仰角为60︒、小港的身高忽略不计,请根据题目信息,求出小雁塔的高度CD 1.73≈,结果精确到0.1m )学楼顶部A 处测得办公楼顶部D 处的俯角30α=︒,测得办公楼底部C 处俯角60β=︒,求办公楼高CD (结果保留根号)过A 作AE CD ⊥交CD 在Rt AED 中,∵DAE ∠机在A 处测得正前方河流的左岸C 处的俯角为α,无人机沿水平线AF 方向继续飞行60米至B 处,测得正前方河流右岸D 处的俯角为30︒,线段AM 的长为无人机距地面的铅直高度,点M 、C 、D 在同一条直线上,其中tan α=MC =(1)填空:ACM ∠=度,BDC ∠=度;(2)求无人机的飞行高度AM ;(3)求河流的宽度CD .(结果保留根号)则180BE AM ==米,60ME AB ==米,在Rt BDE △中,30BDE ∠=︒,则180180tan 33BE DE BDE ===∠(601803)MD ME DE ∴=+=+米,603MC = 米,()601203CD MD MC ∴=-=+米,【解题策略】坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i 表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有tan i α=.【典例分析】例.(2023·江苏泰州·中考真题)如图,堤坝AB 长为10m ,坡度i 为1:0.75,底端A 在地面上,堤坝与对面的山之间有一深沟,山顶D 处立有高20m 的铁塔CD .小明欲测量山高DE ,他在A 处看到铁塔顶端C 刚好在视线AB 上,又在坝顶B 处测得塔底D 的仰角α为2635︒'.求堤坝高及山高DE .(sin 26350.45'︒≈,cos 26350.89'︒≈,tan 26350.50'︒≈,小明身高忽略不计,结果精确到1m )∵坡度i 为1:0.75,∴设BH 过B 作BF CE ⊥于F ,则EF 设DF a =,∵2635α'=︒.∴∵坡度i 为1:0.75,∴CE :答:堤坝高为8米,山高DE 为20米.【点睛】本题考查了解直角三角形的应用-俯角仰角,解直角三角形的应用-坡角坡度,正确地作出辅助线是解题的关键.【变式演练】1.(2023·安徽·模拟)如图,一栋楼房AB 后有一个小山坡CD ,其坡度3:4i =.某一时刻太阳光线与水平线的夹角为40︒时,楼房AB 在小山坡CD 上的影长为25米,测得坡脚C 与楼房的水平距离40BC =米,求楼房AB 的高度.(结果精确到1米,参考数据:sin 400.64,cos 400.77,tan 400.84︒≈︒≈︒≈)【答案】65米【分析】本题主要考查了勾股定理,解直角三角形以及矩形的判定及性质,通过作恰当的辅助线,构造直角三角形,将实际问题转化成解直角三角形求解是解题的关键.过点D 分别作DE BC ⊥,交BC 的延长线于点E ,DF AB ⊥于点F ,则四边形BFDE 是矩形,,DF BE DE BF ==.设3DE x =,可得4CE x =,由勾股定理得222(3)(4)25x x +=,解得5x =,从而20,15CE BF DE ===,在Rt ADF 中,解直角三角形得tan 40600.8450.4AF DF =︒≈⨯=米,从而即可得解.【详解】解:过点D 分别作DE BC ⊥,交BC 的延长线于点E ,DF AB ⊥于点F ,则四边形BFDE 是矩形,,DF BE DE BF ∴==.在Rt DCE V 中,B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45︒,然后沿坡面CF上行了D处,此时在D处测得楼顶A的仰角为30︒.(1)求DE的值.(2)求楼AB的高度.∵20m DE =,∴40m EC =,∵45ACB ∠=︒,AB BC ⊥,∴AB BC =,有一斜坡,坡长10m AB =,坡比34i =,李东在A 点处测得楼顶端C 的仰角为45︒,在B 点处测得楼顶端C 的仰角为61︒(点A ,B ,C ,D 在同一平面内).求教学楼CD 的高度(结果精确到0.1m ,参考数据:tan 61 1.80≈︒)【答案】教学楼CD 的高度约为31.5m .【分析】本题考查了解直角三角形的应用-仰角俯角问题,坡度坡角问题,正确地作出辅助线是解题的关键.过点A 作AF BD ⊥,垂足为F ,过点A 作AE CD ⊥,垂足为E ,根据矩形的性质得到AF DE =,AE DF =,设34AF t BF t ==,,根据勾股定理得到6AF =,8BF =,在Rt ACE 中,45CAE ∠=︒,设AE CE x ==,求得6DF x CD x ==+,,得到8BD x =-,根据三角函数的定义即可得到结论.【详解】解:过点A 作AF BD ⊥,垂足为F ,过点A 作AE CD ⊥,垂足为E ,CD BD ⊥ ,小河阻碍,无法直接从山脚B处测得山顶A的仰角,于是小明和同学们展开了如下的测量:第一步:从小河边的C 处测得山顶A 的仰角为37︒;第二步:从C 处后退30米,在D 处测得山顶A 的仰角为266︒.;第三步:测得小河宽BC 为33米.已知点B 、C 、D 在同一水平线上,请根据小明测量的数据求山坡AB 的坡度.(参考数据:sin 22.60.45︒≈,cos26.60.89︒≈,tan 26.60.5≈°,sin 370.6︒≈,cos370.8︒≈,tan370.75︒≈)在Rt ADH 中,.ADH ∠=︒266,∵tan AH ADH DH∠=,题型03方位角问题【解题策略】方向角:平面上,通过观察点O作一条水平线(向右为东向)和一条铅垂线(向上为北向),则从点O出发的视线与水平线或铅垂线所夹的角,叫做观测的方向角.【典例分析】例.(2023·海南·中考真题)如图,一艘轮船在A处测得灯塔M位于A的北偏东30︒方向上,轮船沿着正北方向航行20海里到达B处,测得灯塔M位于B的北偏东60︒方向上,测得港口C位于B的北偏东45︒方向上.已知港口C在灯塔M的正北方向上.∠=度;(1)填空:AMB∠=度,BCM(2)求灯塔M到轮船航线AB的距离(结果保留根号);(3)求港口C与灯塔M的距离(结果保留根号).DBM A AMB∠=∠+∠=、都是正北方向,AB CM,BCM∴∠∠=︒DBC45(2)解:如图,作CD⊥由(1)可得:A BMA ∠=∠在Rt BEM 中,EBM ∠=sin 20EM BM EBM ∴=⋅∠=∴灯塔M 到轮船航线AB 的距离为(3)解:如图,作CD ⊥ CD AB ⊥,ME AB ⊥,∴四边形CDEM 是矩形,103CD EM ∴==海里,在Rt BEM 中,EBM ∠=1.(2024·陕西西安·一模)如图,我国某海域上有A、B两个小岛,B在A的正东方向.有一艘渔船在点C处捕鱼,在A岛测得渔船在东北方向上,在B岛测得渔船在北偏西60︒的方向上,且测得B、C两处的距离为(1)求A、C两处的距离;(2)突然,渔船发生故障,而滞留C处等待救援.此时,在D处巡逻的救援船立即以每小时40海里的速度沿DC方向前往C处,测得D在小岛A的北偏西15︒方向上距A岛30海里处.求救援船到达C处所用的时间.(结果保留根号)由题意得:202BC =海里,CBE ∠1120210222CE BC ∴==⨯=(海里),2210220AC CE ∴==⨯=(海里),答:A 、C 两处的距离为20海里;在Rt ADF 中,30AD =海里,DAF ∠1cos 30152AF AD DAF ∴=⋅∠=⨯=(海里),3sin 301532DF AD DAF =⋅∠=⨯=(海里),20155CF AC AF ∴=-=-=(海里),B 的正东方向,且,BC 之间的距离为10km .一艘轮船从港口A 出发,沿正南方向航行到达D 处,测得灯塔C 在北偏东37︒方向上,灯塔B 到直线AD 的距离为BE .(1)求BE 的长;(2)求DE 的长(结果精确到0.1).(参考数据:sin580.85,cos580.53,tan58 1.60,sin370.60,cos370.80,tan370.75︒≈︒≈︒≈︒≈︒≈︒≈)【答案】(1)25.5km(2)47.3km【分析】本题考查了解直角三角形的应用,熟悉掌握三角函数是解题的关键.(1)用正弦三角函数求解即可.(2)结合第一问,求解CE 长度,用正切三角函数求解即可.【详解】(1)解:由题意得,90E ∠=︒,58,30km BAE AB ∠=︒= ,()sin 58300.8525.5km BE AB ∴=⋅︒≈⨯=.(2)10km BC = ,()35.5km CE BE BC ∴=+=()tan 3735.50.7547.3km DE CE ∴=÷︒≈÷≈.4.(2023·山东青岛·模拟预测)如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的距离为2km ,点B 位于点A 北偏东60︒方向且与A 相距10km 处.现有一艘轮船从位于点B 南偏西76︒方向的C 处,正沿该航线自西向东航行,5min 后该轮船行至点A 的正北方向的D 处.(1)求观测点B 到航线l 的距离;(2)求该轮船航行的距离CD 的长(结果精确到0.1km).( 1.732=,sin760.97︒≈,cos760.24︒≈,tan76 4.01)︒≈【答案】(1)3km (2)3.4km【分析】本题考查解直角三角形应用的问题.(1)图中已将观测点B 到航线l 的距离用辅助线BE 表示出来,要求BE ,先求出OA ,OB ,再在Rt OBE 中,求出BE 即可.(2)Rt AOD 中求出OD ,在Rt BOE 中求出OE ,进而可求出DE ,在Rt CBE △中,根据76CBE ∠=︒,3km BE =,求出CE ,则CD CE DE =-.【详解】(1)解:设AB 与l 交于点O .在Rt AOD 中,60OAD ∠=︒ ,()2km AD =,的北偏东45︒方向3.6km 处,点C 在点B 的正东方2.4km 处,点D 在点C 的南偏东30︒方向,点D 在点A 的正东方.(参1.414≈ 1.732≈2.449≈)(1)求线段CD 的长度;(结果精确到0.01km)(2)已知送货司机在送货过程中全程保持10m /s 的速度匀速行驶,若现在有急件需要在16分钟内从A 点运送到D 点,则送货司机按既定路线A B C D ---进行运送能否按时送达?(送货司机在各站点停留的时间忽略不计)依题意可知:BC AD ∥,45BAE ∠=︒,30DCF ∠=︒, 3.6km AB =∴90CBE AEB BEF EFC CFD BCF ∠=∠=∠=∠=∠==︒,∴四边形∵ 3.6km AB =,45BAE ∠=︒,∴sin 3.6BE CF AB BAE ==∠=⨯又∵30DCF ∠=︒,---进行运送能按时送达.∴送货司机按既定路线A B C D1.(2023·湖北恩施·中考真题)小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点A,B处测出点D的仰角度数,可以求出信号塔DE的高.如图,AB的长为5m,高BC,,,,在同一平面内.你认为为3m.他在点A处测得点D的仰角为45︒,在点B处测得点D的仰角为38.7︒,A B C D E︒≈,小王同学能求出信号塔DE的高吗?若能,请求出信号塔DE的高;若不能,请说明理由.(参考数据:sin38.70.625︒≈,tan38.70.80cos38.70.780︒≈,结果保留整数)∴能求出信号塔DE 的高,信号塔DE 的高为31m .【点睛】本题考查了勾股定理,等腰直角三角形性质,锐角三角函数,掌握锐角三角函数是解题的关键.2.(2023·辽宁·中考真题)暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶600m 高的山峰,由山底A 处先步行300m 到达B 处,再由B 处乘坐登山缆车到达山顶D 处.已知点A ,B .D ,E ,F 在同一平面内,山坡AB 的坡角为30︒,缆车行驶路线BD 与水平面的夹角为53︒(换乘登山缆车的时间忽略不计)(1)求登山缆车上升的高度DE ;(2)若步行速度为30m/min ,登山缆车的速度为60m/min ,求从山底A 处到达山顶D 处大约需要多少分钟(结果精确到0.1min )(参考数据:sin 530.80cos530.60tan 53 1.33︒≈︒≈︒≈,,)【答案】(1)登山缆车上升的高度450m DE =;(2)从山底A 处到达山顶D 处大约需要19.4min .【分析】(1)过B 点作BC AF ⊥于C ,BE DF ⊥于E ,则四边形BEFC 是矩形,在Rt ABC △中,利用含30度的直角三角形的性质求得BC 的长,据此求解即可;(2)在Rt BDE △中,求得BD 的长,再计算得出答案.【详解】(1)解:如图,过B 点作BC AF ⊥于C ,BE DF ⊥于E ,则四边形BEFC 是矩形,道.设计示意图如图②所示,以山脚A 为起点,沿途修建AB 、CD 两段长度相等的观光索道,最终到达山顶D 处,中途设计了一段与AF 平行的观光平台BC 为50m .索道AB 与AF 的夹角为15︒,CD 与水平线夹角为45︒,A B 、两处的水平距离AE 为576m ,DF AF ⊥,垂足为点F .(图中所有点都在同一平面内,点A E F 、、在同一水平线上)(1)求索道AB 的长(结果精确到1m );(2)求水平距离AF 的长(结果精确到1m ).(参考数据:sin150.25︒≈,cos150.96︒≈,tan150.26︒≈ 1.41≈)【答案】(1)600m (2)1049m【点睛】本题考查解直角三角形解决实际应用题,解题的关键是熟练掌握几种三角函数.4.(2023·辽宁丹东·中考真题)一艘轮船由西向东航行,行驶到东航行10nmile 到达C 港,此时测得灯塔B 在它北偏西61︒方向上,求轮船在航行过程中与灯塔B 的最短距离.(结果精确到0.1nmile )(参考数据:sin310.52︒≈,cos310.86︒≈,tan310.60︒≈,sin610.87≈︒,cos610.48︒≈,tan61 1.80︒≈).【答案】轮船在航行过程中与灯塔B 的最短距离为4.2nmile【分析】过点B 作BD AC ⊥于点D ,则31,61ABD CBD ∠=︒∠=︒,进而得出0.6AD BD ≈, 1.8CD BD ≈,根据10nmile AC =,得出0.6 1.810AD CD BD BD +=+=,即可求解.【详解】解:过点B 作BD AC ⊥于点D ,∵,AE AC CF AC ⊥⊥,【点睛】本题主要考查了解直角三角形的实际应用,解题的关键是正确画出辅助线,构造直角三角形,熟练掌握解直角三角形的方法和步骤.5.(2023·湖北·中考真题)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形度3:4i =是指坡面的铅直高度AF 与水平宽度BF 的比.已知斜坡CD 长度为20米,18C ∠=︒,求斜坡AB 的长.(结果精确到米)(参考数据:sin180.31,cos180.95,tan180.32︒≈︒≈︒≈)【答案】斜坡AB 的长约为10米【分析】过点D 作DE BC ⊥于点E ,在Rt DEC △中,利用正弦函数求得 6.2DE =,在Rt ABF 中,利用勾股定理即可求解.【详解】解:过点D 作DE BC ⊥于点E ,则四边形ADEF 是矩形,在Rt DEC △中,2018CD C ︒=∠=,,sin 20sin18200.31 6.2DE CD C =⋅∠=⨯︒≈⨯=综合实践活动——测量太阳能路灯电池板的宽度.如图,太阳能电池板宽为AB ,点O 是AB 的中点,OC 是灯杆.地面上三点D ,E 与C 在一条直线上, 1.5m DE =,5m EC =.该校学生在D 处测得电池板边缘点B 的仰角为37︒,在E 处测得电池板边缘点B 的仰角为45︒.此时点A 、B 与E 在一条直线上.求太阳能电池板宽AB 的长度.(结果精确到0.1m .参考数据:3sin 375︒≈,4cos375≈︒,3tan 374︒≈ 1.41≈)依题意得:OC DC ⊥,37BDH ∠=︒,45NEH ∠=又BH DC⊥B E H ∴ 和OEC △均为等腰直角三角形,EH BH ∴=,EC OC =,机在A 处测得河流左岸C 处的俯角为α,无人机沿水平线AF 方向继续飞行12米至B 处,测得河流右岸D 处的俯角为30︒,线段AM =点M ,C ,D 在同一条直线上,其中tan 2α=.求河流的宽度CD(结果精确到1 1.7≈).【答案】河流的宽度CD 约为64米【分析】过点B 作BE MD ⊥于点E ,分别解Rt AMC △、Rt BDE △即可.【详解】解:过点B 作BE MD ⊥于点E .则四边形AMEB 是矩形.∴243BE AM ==,12ME AB ==∵AF MD∥∴ACM α∠=123ABC ∠=︒,该车的高度 1.7m AO =.如图2,打开后备箱,车后盖ABC 落在AB C ''处,AB '与水平面的夹角27B AD '∠=︒.(1)求打开后备箱后,车后盖最高点B '到地面l 的距离;(2)若小琳爸爸的身高为1.8m ,他从打开的车后盖C '处经过,有没有碰头的危险?请说明理由.(结果精确到.....001m .,参考数据:sin 270.454︒≈,cos 270.891︒≈,tan 270.510︒≈ 1.732≈)在Rt AB E '△中∵27B AD '∠=︒,AB ∴sin 27B EAB '︒='∴sin 27B E AB ''=︒≈∵平行线间的距离处处相等∴0.454B E AO '+=答:车后盖最高点B(2)没有危险,理由如下:过C '作C F B E ''⊥,垂足为点F∵27B AD '∠=︒,90B EA '∠=︒∴63AB E '∠=︒∵123AB C ABC ''∠=∠=︒∴60C B F AB C AB E '''''∠=∠-∠=︒在Rt B FC '' 中,0.6B C BC ''==∴cos600.3B F B C '''=⋅︒=.∵平行线间的距离处处相等∴C '到地面的距离为2.150.3 1.85-=.∵1.85 1.8>∴没有危险.【点睛】本题主要考查了解直角三角形的应用,掌握直角三角形的边角关系是解题的关键.9.(2023·江苏宿迁·中考真题)【问题背景】由光的反射定律知:反射角等于入射角(如图,即CEF AEF ∠=∠).小军测量某建筑物高度的方法如下:在地面点E 处平放一面镜子,经调整自己位置后,在点D 处恰好通过镜子看到建筑物AB 的顶端A .经测得,小军的眼睛离地面的距离 1.7m CD =,20m BE =,2m DE =,求建筑物AB 的高度.【活动探究】观察小军的操作后,小明提出了一个测量广告牌高度的做法(如图):他让小军站在点D 处不动,将镜子移动至1E 处,小军恰好通过镜子看到广告牌顶端G ,测出12m DE =;再将镜子移动至2E 处,恰好通过镜子看到广告牌的底端A ,测出2 3.4m DE =.经测得,小军的眼睛离地面距离 1.7m CD =,10m BD =,求这个广告牌AG 的高度.【应用拓展】小军和小明讨论后,发现用此方法也可测量出斜坡上信号塔AB 的高度.他们给出了如下测量步骤(如图):①让小军站在斜坡的底端D 处不动(小军眼睛离地面距离 1.7m CD =),小明通过移动镜子(镜子平放在坡面上)位置至E 处,让小军恰好能看到塔顶B ;②测出 2.8m DE =;③测出坡长17m AD =;④测出坡比为8:15(即8tan 15ADG ∠=).通过他们给出的方案,请你算出信号塔AB 的高度(结果保留整数).CEF AEF ∠=∠,,AB BD FE ⊥⊥,90AEB CED B D ∴∠=∠∠=∠=︒,ABE CDE ∴△∽△,AB CD BE DE∴=, 1.7m CD =,20m BE =,2m DE =1.7202AB ∴=,解得17m AB =;[活动探究]如图所示:,GB BD CD BD ⊥⊥,90B D ∴∠=∠=︒,11GE B CE D∠=∠Q由题意得:BG DG ⊥,CD DG ⊥,AGD CDG BMA CND ∴∠=∠=∠=∠BAM GAD ∠=∠ ,9090BAM GAD ∴︒-∠=︒-∠,即ABM ADG ∠=∠,90ADG DAG ∠∠+=︒ ,ADG ∠+。
专题18 解直角三角形1.理解正弦、余弦、正切的概念,并能运用.2.掌握特殊角三角函数值,并能运用特殊角的三角函数值进行计算和化简;3.理解直角三角形的概念,灵活运用直角三角形中边与角的关系和勾股定理解直角三角形,提高把实际问题转化为解直角三角形问题的能力;一、直角三角形的性质1、直角三角形的两个锐角互余 可表示如下:∠C=90°⇒∠A+∠B=90°2、在直角三角形中,30°角所对的直角边等于斜边的一半。
可表示如下:3、直角三角形斜边上的中线等于斜边的一半可表示如下:4、勾股定理 直角三角形两直角边a ,b 的平方和等于斜边c 的平方,即222c b a =+ 5、射影定理在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项6、常用关系式由三角形面积公式可得: AB •CD=AC •BC二、直角三角形的判定1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理如果三角形的三边长a ,b ,c 有关系222c b a =+,那么这个三角形是直角三角形。
三、锐角三角函数的概念 1、如图,在∠ABC 中,∠C=90°∠锐角A 的对边与斜边的比叫做∠A 的正弦,记为sinA ,即casin =∠=斜边的对边A A∠锐角A 的邻边与斜边的比叫做∠A 的余弦,记为cosA ,即cbcos =∠=斜边的邻边A A∠锐角A 的对边与邻边的比叫做∠A 的正切,记为tanA ,即b atan =∠∠=的邻边的对边A A A∠锐角A 的邻边与对边的比叫做∠A 的余切,记为cotA ,即abcot =∠∠=的对边的邻边A A A2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值 三角函数 0° 30°45°60° 90° sinα21 22 23 1cosα 123 22 21 0tanα 0 33 13 不存在cotα 不存在31 33 04、各锐角三角函数之间的关系 (1)互余关系sinA=cos(90°—A),cosA=sin(90°—A) tanA=cot(90°—A),cotA=tan(90°—A) (2)平方关系1cos sin 22=+A A(3)倒数关系 tanA •tan(90°—A)=1 (4)弦切关系 tanA=AAcos sin 5、锐角三角函数的增减性 当角度在0°~90°之间变化时,(1)正弦值随着角度的增大(或减小)而增大(或减小) (2)余弦值随着角度的增大(或减小)而减小(或增大) (3)正切值随着角度的增大(或减小)而增大(或减小) (4)余切值随着角度的增大(或减小)而减小(或增大) 四、解直角三角形 1、解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
专题06 解直角三角形题型归纳1.如图是某小区地下停车场入口处栏杆的示意图,MQ、PQ分别表示地面和墙壁的位置,OM表示垂直于地面的栏杆立柱,OA、AB是两段式栏杆,其中OA段可绕点O旋转,AB 段可绕点A旋转.图1表示栏杆处于关闭状态,此时O、A、B在与地面平行的一直线上,并∥,OA段与竖直方向夹角为且点B接触到墙壁;图2表示栏杆处于打开状态,此时AB MQAB=.OA=,150cm 30︒.已知立柱宽度为30cm,点O在立柱的正中间,120cmOM=,120cm(1)求栏杆打开时,点A到地面的距离;(2)为确保通行安全,要求汽车通过该入口时,车身与墙壁间需至少保留10cm的安全距离,问一辆最宽处为2.1m,最高处为2.1m的货车能否安全通过该入口?(取1.73)【详解】(1)(2)2.如图,株洲市炎陵县某中学在实施“五项管理”中,将学校的“五项管理”做成宣传牌(CD),放置在教学楼A栋的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿芙蓉小学围墙边坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:3,AB m,AE=8m.(1)求点B距水平面AE的高度BH.(2)求宣传牌CD的高度.(结果精确到0.1【答案】(1)点B距水平面AE的高度BH是2米【我思故我在】本题考查了解直角三角形的应用-仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.3.如图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC 与手臂MC 始终在同一直线上,枪身BA 与额头保持垂直量得胳膊28cm MN =,枪柄与枪身之间的夹角为120°(即120MBA ∠=︒),肘关节M 与枪身端点A 之间的水平宽度为25.3cm(即MP 的长度),枪身8.5cm BA =.(1)求M B 的长;(2)测温时规定枪身端点A 与额头距离范围为3~5cm .在图2中,若测得75BMN ∠=︒,小红与测温员之间距离为50cm 问此时枪身端点A 与小红额头的距离是否在规定范围内?并说明理由.(结果精确到0.1cm 1.4≈ 1.7≈) 【答案】(1)33.6cm ;(2)在规定范围内,理由见详解.【分析】(1)过点B 作BH MP ⊥于点H ,在Rt BMH 中,利用含30°直角三角形三边关系,即可解答;(2)延长PM 交FG 于点I ,45NMI ∠=︒,在Rt NMI 中,利用三角函数的定义即可求出MI 的长,比较即可判断.(1)解:过点B 作BH MP ⊥于点H ,由题可知四边形ABHP 为矩形,如下图:Rt BMH Rt NMI 4.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B ,如图所示.于是他们先在古树周围的空地上选择一点D ,并在点D 处安装了测量器CD ,测得=135ACD ∠︒;再在BD 的延长线上确定一点G ,使5DG =米,并在G 处的地面上水平放置了一个小平面镜,小明沿着BG 方向移动,当移动到点F 时,他刚好在小平面镜内看到这棵古树的顶端A 的像,此时,测得2FG =米,小明眼睛与地面的距离=1.6EF 米,测量器的高度=0.5CD 米.已知点F 、G 、D 、B 在同一水平直线上,且EF 、CD 、AB 均垂直于FB ,则这棵古树的高度AB 为多少米?(小平面镜的大小忽略不计)ACH ,得出ABG ∽△,因此得出米,ACH 中,5.广场上有一个充满氢气的气球P ,被广告条拽着悬在空中,甲乙二人分别站在E 、F 处,他们看气球的仰角分别是30度、45度,E 点与F 点的高度差AB 为1米,水平距离CD 为5米,FD 的高度为0.5米,请问此气球有多高?(结果保留到0.1米).Rt PEA AE tan30°6.综合与实践小明为自己家设计了一个在水平方向可以伸缩的遮阳蓬,如图所示,已知太原地区在夏至日的正午太阳高度角(即正午太阳光线与地平面的夹角)为75︒ ,冬至日的正午太阳高度角为29.5︒ ,小明家的玻璃窗户()AB 高为190cm ,在A 点上方20cm 的C 处安装与墙垂直的宽为CD 的遮阳蓬,并且该遮阳蓬可伸缩(CD 可变化);为了保证在夏至日正午太阳光不射到屋内,冬至日正午整块玻璃都能受到太阳光照射,求可伸缩的遮阳蓬CD 宽度的范围.(结果精确到0.1,参考数据:sin750.97︒=,cos750.26︒=,tan75 3.73︒=,sin29.50.49︒=,cos29.50.87︒=,tan29.50.57︒=)t R BCD ,求出t R BCD 中,cm 210 ,DBE ∠cm7.如图,在航线l 的两侧分别有两个灯塔A 和B ,灯塔A 到航线l 的距离为3AC =千米,灯塔B 到航线l 的距离为4BD =千米,灯塔B 位于灯塔A 南偏东60︒方向.现有一艘轮船从位于灯塔B 北偏西53︒方向的N (在航线l 上)处,正沿该航线自东向西航行,10分钟后该轮船行至灯塔A 正南方向的点C (在航线l 上)处.( 1.73≈,sin530.80≈︒,cos530.60≈︒,tan53 1.33≈︒ )(1)求两个灯塔A 和B 之间的距离;(2)求该轮船航行的速度(结果精确到0.1千米/小时). Rt ACM 中,3cos60=AM ︒,6AM = ,Rt BDM 中,cos60=BD BM ︒,8BM =,AM BM =+答:两个灯塔Rt ACM 中,tan60=3MC ︒,33=MC ,Rt BDM 中,tan60=4DM ︒,MC DM =+Rt BDN △中,由题意,得DBN ∠8.风能作为一种清洁能源越来越受到世界各国的重视,我市结合自身地理优势架设风力发电机利用风能发电.王芳和李华假期去明月峰游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇的想知道风力发电机塔架的高度.如图,王芳站在C 点测得C 点与塔底D 点的距离为25m ,李华站在斜坡BC 的坡顶B 处,已知斜坡BC 的坡度i =,坡面BC 长30m ,李华在坡顶B 处测得轮毂A 点的仰角38α=︒,请根据测量结果帮他们计算:(1)斜坡顶点B 到CD 所在直线的距离;(2)风力发电机塔架AD 的高度.(结果精确到0.1m ,参考数据sin380.62︒≈,cos380.79︒≈,tan380.78︒≈ 1.41 1.73)≈BC︒=153由题意得,四边形BEDF由勾股定理得:EC=,ABF BF=︒≈⨯Rt ABF中,tan38400.7840=+AD AF FD答:塔架高度【我思故我在】本题考查了解直角三角形的实际应用以及勾股定理,根据题意构造直角三角形是解本题的关键.9.小明和小亮利用数学知识测量学校操场边升旗台上的旗杆高度.如图,旗杆AB立在水平的升旗台上,两人测得旗杆底端B到升旗台边沿C的距离为2m,升旗台的台阶所在的斜坡CD长为2m,坡角为30,小明又测得旗杆在太阳光下的影子落在水平地面MN上的部分DE的长为6m,同一时刻,小亮测得长1.6m的标杆直立于水平地面时的影子长为1.2m.请你帮小明和小亮求出旗杆AB 的高度( 1.732)CDG ∠=12CG ∴=HE HG ∴=同一时刻,物高和影长成正比,1.61.2AH HE ∴=握同一时刻,物高和影长成正比是解决本题的关键.10.某项目学习小组用测倾仪、皮尺测量小山的高度MN ,他们设计了如下方案(如图):①在点A 处安置测倾仪,测得小山顶M 的仰角MCE ∠的度数;②在点A 与小山之间的B 处安置测倾仪,测得小山顶M 的仰角MDE ∠的度数(点A ,B 与N 在同一水平直线上);③量出测点A ,B 之间的距离.已知测倾仪的高度 1.5AC BD ==米,为减小误差,他们按方案测量了两次,测量数据如下表(不完整):(1)写出MCE ∠的度数的平均值.(2)根据表中的平均值,求小山的高度.(参考数据:sin 220.37,cos 220.93,tan 220.40︒≈︒≈︒≈) (3)该小组没有利用物体在阳光下的影子来测量小山的高度,你认为原因可能是什么?(写出一条即可)【答案】(1)22°(2)101.5米(3)小山的影子长度无法测量【分析】(1)根据平均数公式,用两次测量得的MCE ∠的度数和除以2即可求解;(2)在Rt △MDE 中,利用仰角⊥MDE 的45°,即可求得ME =DE ,在Rt △MCE 中,利用仰角⊥MCE 的正切值,可得ME =CE ⋅tan⊥MCE ,进而由CE =CD +DE =CD +ME ,易知四边形CANE 、四边形ABDC 是矩形,可得EN =AC =1.5米,CD =AB =150米,代入即可求出ME 的值,然后由MN =ME +NE 求解;11.小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF =34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm(参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).(1)求证:AC⊥BD .(2)求扣链EF 与立杆AB 的夹角⊥OEF 的度数(结果精确到0.1°).(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm ,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由. 证明:证法一:,AB CDOA OC =1(1802OAC ∴∠==︒﹣同理可证:ODB =∠=OAC ∴∠=.AC BD ∴证法二:AB =85cm OD ==OA OC OB OD ==又,AOC BODAOC BOD ∴∽,OAC OBD ∴∠=∠,.AC BD ∴(2)解:在OEF 中,EF BD ,OEM ,Rt Rt OEM ABH ∽,,OE OM OM AB AH AB AH OE ⋅===所以:小红的连衣裙垂挂在衣架后的总长度解法二:小红的连衣裙会拖落到地面)可证:EF BD ,ABD ∴∠BD ⊥于点, 136ABD =所以:小红的连衣裙垂挂在衣架后的总长度12.开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC 的高度,如图,在A 处用测角仪测得拂云阁顶端D 的仰角为34°,沿AC 方向前进15m 到达B 处,又测得拂云阁顶端D 的仰角为45°.已知测角仪的高度为1.5m ,测量点A ,B 与拂云阁DC 的底部C 在同一水平线上,求拂云阁DC 的高度(结果精确到1m .参考数据:sin340.56︒≈,cos340.83︒≈,tan340.67︒≈).EG FG -即0.67DG -解得DG ≈DC DG ∴=∴拂云阁13.如图,为测量某建筑物AB 的高度,小刚采用了如下的方法:先从与建筑物底端B 在同一水平线上的C 点出发,沿斜坡CD 行走60米至坡顶D 处,再从D 处沿水平方向继续前行若干米后至E 点处,在E 点测得该建筑物顶端A 的仰角为60︒,建筑物底端B 的俯角为45︒,点AB C D E 、、、、在同一平面内,斜坡CD 的坡度34i =:.请根据小刚的测量数据,计算出建筑物AB 的高度.( 1.73≈)Rt DFC 中,利用勾股定理求出Rt GEB 中,利用锐角三角函数的定义求出Rt AGE 中,利用锐角三角函数的定义求出的长,进行计算即可解答.【详解】解:过点,垂足为F 交AB 于点GRt DFC 中,60DC =,⊥560a =解得12a =,⊥336DF a ==,36GB DF =∴=Rt GEB 中,Rt AGE 中,tan EG =⋅AG GB =+建筑物AB 的高度约为【我思故我在】本题考查了解直角三角形的应用14.如图1,2分别是某款篮球架的实物图与示意图,AB BC ⊥于点B ,底座=1BC 米,底座BC 与支架AC 所成的角60ACB ∠=︒,点H 在支架AF 上,篮板底部支架EH BC .EF EH ⊥于点E ,已知AH HF 3=2HE 米.(1)求篮板底部支架HE 与支架AF 所成的FHE ∠的度数.(2)求篮板底部点E 到地面的距离,(精确到0.1米)( 1.41≈ 1.73≈) 【答案】(1)篮板底部支架HE 与支架AF 所成的角⊥FHE 的度数为45°;(2)篮板底部点E 到地面的距离约为2.2米【分析】(1)在Rt ⊥HEF 中,利用锐角三角函数的定义进行计算即可解答;(2)延长FE 交直线BC 与点M ,过点A 作AG ⊥FM ,垂足为G ,根据题意易证四边形ABMG 是矩形,从而得AB =GM ,然后在Rt ⊥AGF 中求出FG ,从而求出EG ,最后在Rt ⊥ABC 中,求出AB ,进行计算即可解答.(1)⊥EF ⊥EH ,⊥⊥HEF =90°,【我思故我在】本题考查了解直角三角形的应用,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.。