DSP实验报告
- 格式:doc
- 大小:683.00 KB
- 文档页数:26


dsp原理与应用实验报告总结DSP(Digital Signal Processing)数字信号处理是利用数字技术对信号进行处理和分析的一种方法。
在本次实验中,我们探索了DSP的原理和应用,并进行了一系列实验以验证其在实际应用中的效果。
以下是对实验结果的总结与分析。
实验一:数字滤波器设计与性能测试在本实验中,我们设计了数字滤波器,并通过性能测试来评估其滤波效果。
通过对不同类型的滤波器进行设计和实现,我们了解到数字滤波器在信号处理中的重要性和应用。
实验二:数字信号调制与解调本实验旨在通过数字信号调制与解调的过程,了解数字信号的传输原理与方法。
通过模拟调制与解调过程,我们成功实现了数字信号的传输与还原,验证了调制与解调的可行性。
实验三:数字信号的傅里叶变换与频谱分析傅里叶变换是一种重要的信号分析方法,可以将信号从时域转换到频域,揭示信号的频谱特性。
本实验中,我们学习了傅里叶变换的原理,并通过实验掌握了频谱分析的方法与技巧。
实验四:数字信号的陷波滤波与去噪处理陷波滤波是一种常用的去除特定频率噪声的方法,本实验中我们学习了数字信号的陷波滤波原理,并通过实验验证了其在去噪处理中的有效性。
实验五:DSP在音频处理中的应用音频处理是DSP的一个重要应用领域,本实验中我们探索了DSP在音频处理中的应用。
通过实验,我们成功实现了音频信号的降噪、均衡和混响处理,并对其效果进行了评估。
实验六:DSP在图像处理中的应用图像处理是另一个重要的DSP应用领域,本实验中我们了解了DSP在图像处理中的一些基本原理和方法。
通过实验,我们实现了图像的滤波、边缘检测和图像增强等处理,并观察到了不同算法对图像质量的影响。
通过以上一系列实验,我们深入了解了DSP的原理与应用,并对不同领域下的信号处理方法有了更深刻的认识。
本次实验不仅加深了我们对数字信号处理的理解,也为日后在相关领域的研究与实践提供了基础。
通过实验的结果和总结,我们可以得出结论:DSP作为一种数字信号处理的方法,具有广泛的应用前景和重要的实际意义。

DSP第六、七次实验报告1. 实验目的:(1)进一步熟悉Matlab实验环境和语言。
(2)熟悉各种滤波器的结构及Matlab实现语言。
(3)掌握用冲击响应不变法和双线性变换法设计IIR滤波器的方法。
(4)掌握用窗函数法和频率抽样法设计FIR滤波器的方法。
2. 实验内容及总结:1.滤波器结构:(1)IIR滤波器各种结构1、直接型结构例如直接型滤波器系统函数, 则有系数向量a=[1,a1,a2,a3],b=[b0,b1,b2], 利用:Y=filter[b,a,x]求信号x(n)通过此滤波器的输出。
2、由系统函数或差分方程求系统的二阶分式(含一阶分式)的级联结构将例如的系统函数重写为二阶分式节的级联型, 利用:[sos,G]=tf2sos(b,a)3、由二阶分式的级联结构转换成系统函数的直接结构是第二步的逆运算, 调用函数:[b,a] = sos2tf(sos)可以求得系数向量a,b, 从而得到H(z)4、由系统函数求部分分式展开(留数及其极点计算)即求z反变换的部分分式展开法, 利用:[r,p,c]=residuez(b,a)其中极点为p, 留数为r, 直接项系数为c。
5、由r,p,c求系统函数即第4步的逆运算, 利用:[b,a]=residuez(r,p,c)6、由直接型结构转换为并联型结构需开发函数:[C,B,A]=tf2par(b,a)其中, b,a为直接型的系数向量, C,B,A为并联型实系数向量, 基本思想是: 1.反复调用[r,p,c]=residuez(b,a)求出极点及留数;2.利用cplxpair函数把极点、留数对按复共轭极点-留数对, 实极点-留数对的顺序排列;3.开发cplxcomp函数, 保证极点和留数相互对应;4.调用[b,a]=residuez(r,p,c)计算并联二阶节的分子分母。
7、由并联型结构转换成直接型结构开发函数:[b,a]=par2tf(C,B,A)为[C,B,A]=tf2par(b,a)的逆函数。

实验一: 闪灯实验熟悉DSP 软硬件测试系统实验目的1.了解SHARC 系列高性能数字信号处理器的程序开发过程和编程语言;2.熟悉集成开发工具VisualDSP++, 学会使用VisualDSP++进行SHARC 系列ADSP 的程序开发、编译与调试;3.掌握SHARC 系列ADSP 的程序加载设计和加载过程。
实验内容利用波形产生信号板, 结合FPGA 编程技术和程序编程器, 编写测试ADSP21065L 和FPGA 之间硬件连接的应用程序, 同时完成应用程序的加载和脱机操作, 在信号指示灯“HL2”上产生可调周期的脉冲信号, “点亮”与“熄灭”指示灯HL2。
实验要求通过DSP 编程, 在其FLAG11引脚上模拟如下波形的周期信号:要求:(1) 500H T ms >,500L T ms >. (2) 并用示波器查看波形, 测量信号周期。
实验步骤1. 熟悉电路图, 清楚波形产生电路板ADSP21065L 与可编程FPGA 器件之间的连接关系;2. 编写FPGA 程序。
在FPGA 内部将ADSP21065L 的标志引脚FLAG11(引脚号26)设置为输出, 作为FPGA 的输入信号, 在FPGA 内部编程将该信号直接输出在发FPGA 的37引脚号上, 设置37引脚为输出信号, 驱动板上的HL2 LED 指示灯;3. 启动VisualDsp++4.5,选择project 工程选项菜单, 创建一个名称为Test.dpj 的工程文件, 选择处理器的型号为ADSP-21065L ;4.弹出一个对话框, 选择是否需要加入VDSP kernel ,选择“NO ”;5. 在工程中加入以下参考源文件:\exp1\test(boot)\ boot1.asm 和boot1.ldf 6.编译, 链接调试, 生成可执行文件。
7.运行程序, 可以看到波形发生电路板上的指示灯“HL2”不断闪动。
8. 利用示波器观测系统时钟,并测量产生信号的波形和周期。

一、综合实验内容和目的1、实验目的(1) 通过实验学习掌握TMS320F28335的浮点处理; (2) 学习并掌握A/D 模块的使用方法;(3) 学习并掌握中断方式和查询方式的相关知识及其相互之间的转换; (4) 学习信号时域分析的方法,了解相关电量参数的计算方法; (5) 了解数字滤波的一些基本方法。
2、实验内容要求1:对给定的波形信号,采用TMS320F28335的浮点功能计算该信号的以下时域参数:信号的周期T ,信号的均方根大小V rms 、平均值V avg 、峰-峰值V pp 。
其中,均方根V rms 的计算公式如下:()21N rms iV u i N =∑ 式中N 为采样点数,()u i 为采样序列中的第i 个采样点。
要求2:所设计软件需要计算采样的波形周期个数,并控制采样点数大于1个波形周期,且小于3个波形周期大小。
要求3:对采集的数据需要加一定的数字滤波。
二、硬件电路相关硬件:TMS320F28335DSP 实验箱,仿真器。
硬件结构图三、程序流程图1、主程序流程图程序的主流程图2、子程序流程图参数计算的流程图四、实验结果和分析1、实验过程分析(1) 使用的函数原型声明对ADC模件相关参数进行定义:ADC时钟预定标,使外设时钟HSPCLK 为25MHz,ADC模块时钟为12.5MHz,采样保持周期为16个ADC时钟。
(2) 定义全局变量根据程序需要,定义相关变量。
主要有:ConversionCount、Voltage[1024]、Voltage1[1024]、Voltage2[1024]、filter_buf[N]、filter_i、Max、Min、T、temp、temp1、temp2、temp3、Num、V、Vav、Vpp、Vrm、fre。
这些变量的声明请见报告后所附的源程序。
(3) 编写主函数完成系统寄存器及GPIO初始化;清除所有中断,初始化PIE向量表,将程序中使用的ADC中断重新映射到ISR;对外部设备ADC模块进行初始化;使能PIE中ADCINT中断;配置ADC模块;等待ADC中断。

dsp实验报告实验一:CCS入门实验实验目的:1. 熟悉CCS集成开发环境,掌握工程的生成方法;熟悉SEED-DEC643实验环境; 掌握CCS集成开发环境的调试方法。
2.学习用标准C 语言编写程序;了解TI CCS开发平台下的C 语言程序设计方法和步骤; 熟悉使用软件仿真方式调试程序。
3. 学习用汇编语言编写程序; 了解汇编语言与 C 语言程序的区别和在设置上的不同;了解TMS320C6000 汇编语言程序结果和一些简单的汇编语句用法学习在CCS 环境中调试汇编代码。
4. 在了解纯C 语言程序工程和汇编语言程序工程结构的基础上,学习在C 工程中加入汇编编程的混合编程方法; 了解混合编程的注意事项;理解混合编程的必要性和在什么情况下要采用混合编程5. 熟悉CCS集成开发环境,掌握工程的生成方法; 熟悉SEED-DEC643实验环境;掌握CCS集成开发环境的调试方法。
实验原理:CCS 提供了配置、建立、调试、跟踪和分析程序的工具,它便于实时、嵌入式信号处理程序的编制和测试,它能够加速开发进程,提高工作效率。
CCS 提供了基本的代码生成工具,它们具有一系列的调试、分析能力序。
使用此命令后,要重新装载.out 文件后,再执行程序。
使用 CCS常遇见文件简介1. program.c: C 程序源文件;2. program.asm: 汇编程序源文件;3. filename.h: C 程序的头文件,包含DSP/BIOS API模块的头文件;4. filename.lib: 库文件;5. project.cmd: 连接命令文件;6. program.obj: 由源文件编译或汇编而得的目标文件;7. program.out: 经完整的编译、汇编以及连接后生成可执行文件; 8. program.map: 经完整的编译、汇编以及连接后生成空间分配文件; 9.project.wks: 存储环境设置信息的工作区文件。
P.S(CMD文件中常用的程序段名与含义1. .cinit 存放C程序中的变量初值和常量;2. .const 存放C程序中的字符常量、浮点常量和用const声明的常量;3. .text 存放C程序的代码;4. .bss 为C 程序中的全局和静态变量保留存储空间;5. .far 为C 程序中用far声明的全局和静态变量保留空间;6. .stack 为 C 程序系统堆栈保留存储空间,用于保存返回地址、函数间的参数传递、存储局部变量和保存中间结果;7. .sysmem 用于 C 程序中malloc、calloc 和 realloc 函数动态分配存储空间。


dsp实验报告DSP实验报告一、引言数字信号处理(Digital Signal Processing,DSP)是一种对数字信号进行处理和分析的技术。
它在许多领域中被广泛应用,如通信、音频处理、图像处理等。
本实验旨在通过实际操作,探索和理解DSP的基本原理和应用。
二、实验目的1. 理解数字信号处理的基本概念和原理;2. 掌握DSP实验平台的使用方法;3. 进行一系列DSP实验,加深对DSP技术的理解。
三、实验器材和软件1. DSP开发板;2. 电脑;3. DSP开发软件。
四、实验内容1. 实验一:信号采集与重构在此实验中,我们将通过DSP开发板采集模拟信号,并将其转换为数字信号进行处理。
首先,我们需要连接信号源和开发板,然后设置采样频率和采样时间。
接下来,我们将对采集到的信号进行重构,还原出原始模拟信号,并进行观察和分析。
2. 实验二:滤波器设计与实现滤波器是DSP中常用的模块,用于去除或增强信号中的特定频率成分。
在此实验中,我们将学习滤波器的设计和实现方法。
首先,我们将选择合适的滤波器类型和参数,然后使用DSP开发软件进行滤波器设计。
最后,我们将将设计好的滤波器加载到DSP开发板上,并进行实时滤波处理。
3. 实验三:频谱分析与频域处理频谱分析是DSP中常用的方法,用于分析信号的频率成分和能量分布。
在此实验中,我们将学习频谱分析的基本原理和方法,并进行实际操作。
我们将采集一个包含多个频率成分的信号,并使用FFT算法进行频谱分析。
然后,我们将对频谱进行处理,如频率选择、频率域滤波等,并观察处理后的效果。
4. 实验四:音频处理与效果实现音频处理是DSP中的重要应用之一。
在此实验中,我们将学习音频信号的处理方法,并实现一些常见的音频效果。
例如,均衡器、混响、合唱等。
我们将使用DSP开发软件进行算法设计,并将设计好的算法加载到DSP开发板上进行实时处理。
五、实验结果与分析通过以上实验,我们成功完成了信号采集与重构、滤波器设计与实现、频谱分析与频域处理以及音频处理与效果实现等一系列实验。

dsp信号处理实验报告DSP信号处理实验报告一、引言数字信号处理(DSP)是一种将连续信号转换为离散信号,并对其进行处理和分析的技术。
在现代通信、音频处理、图像处理等领域中,DSP技术被广泛应用。
本实验旨在通过对DSP信号处理的实践,加深对该技术的理解与应用。
二、实验目的本实验旨在通过对DSP信号处理的实践,掌握以下内容:1. 学习使用DSP芯片进行信号采集和处理;2. 理解离散信号的采样和重构过程;3. 掌握常见的DSP信号处理算法和方法。
三、实验原理1. 信号采集与重构在DSP信号处理中,首先需要对模拟信号进行采样,将连续信号转换为离散信号。
采样过程中需要注意采样频率的选择,以避免混叠现象的发生。
采样完成后,需要对离散信号进行重构,恢复为连续信号。
2. DSP信号处理算法DSP信号处理涉及到多种算法和方法,如滤波、频谱分析、时域分析等。
其中,滤波是一种常见的信号处理方法,可以通过滤波器对信号进行去噪、增强等处理。
频谱分析可以将信号在频域上进行分析,了解信号的频率成分和能量分布。
时域分析则关注信号的时序特征,如幅值、相位等。
四、实验步骤1. 信号采集与重构在实验中,我们使用DSP芯片进行信号采集与重构。
将模拟信号输入DSP芯片的模拟输入端口,通过ADC(模数转换器)将模拟信号转换为数字信号。
然后,通过DAC(数模转换器)将数字信号转换为模拟信号输出。
2. 滤波处理为了演示滤波处理的效果,我们选择了一个含有噪声的信号进行处理。
首先,使用FIR滤波器对信号进行低通滤波,去除高频噪声。
然后,使用IIR滤波器对信号进行高通滤波,增强低频成分。
3. 频谱分析为了对信号的频率成分和能量分布进行分析,我们使用FFT(快速傅里叶变换)算法对信号进行频谱分析。
通过观察频谱图,可以了解信号的频率特性。
4. 时域分析为了对信号的时序特征进行分析,我们使用时域分析方法对信号进行处理。
通过计算信号的均值、方差、峰值等指标,可以了解信号的幅值、相位等特性。

DSP课程设计实验报告学院班级姓名学号指导教师2010年 6月课程设计第一部分:学习程序实例[实验4.1] 卷积运算一、 实验目的1. 掌握卷积运算的基本原理;2. 掌握用C 语言编写DSP 程序的方法。
二、 实验设备1. 一台装有CCS 软件的计算机;2. DSP 实验箱的TMS320C5410主控板;3. DSP 硬件仿真器。
三、 实验原理卷积是数字信号处理中经常用到的运算。
其基本的表达式为:()()()∑=-=nm m n x m h n y 0写实现程序时需要注意两点:(1)序列数组长度的分配,尤其是输出数组y (n) 要有足够的长度;(2)循环体中变量的位置,即n 和m 的关系。
四、 实验结果打开工程Ex5_1.pjt 修改程序:将输入序列x 的长度改为N1=15,h 的长度改为N2=20,将输入序列x 的函数改为x[i]=i+1,Run 之后出现问题,发现可能是由于x 长度15,h 长度20,卷积运算之后y 的长度为34,超出了之前程序定义好的三个都是20,存储长度没有改导致出错,于是将原来的float y[20]改为float y[100];改之后发现程序运行无误。
绘制波形图的方式:波形图如下:H 图:X图:Y图:该CCS程序用C语言编写,实现得功能较为简单,在源程序的基础上可以很快地实现数据的修改从而得到新的结果,通过运行该程序,对于CCS的操作和使用方法有了初步的认识,同时也熟悉了利用C语言开发DSP程序的过程和所需要的条件。
§4.2 [实验4.2] 相关运算一、实验目的1.掌握相关系数的估计方法;2.掌握用C语言编写DSP程序的方法。
二、实验设备1. 一台装有CCS软件的计算机;2. DSP实验箱的TMS320C5410主控板;3. DSP硬件仿真器。
三、实验结果打开工程Ex5_2.pjt修改程序:修改了m和n的长度:m=15; //10n=45; //40修改了for循环:for(i=0;i<n;i++){x[i]=2; //1y[i]=i+1; //i绘制出更改之后r的波形图:[实验4.3] 快速傅里叶变换(FFT) 实现一、实验目的1. 掌握FFT算法的基本原理;2. 掌握用C语言编写DSP程序的方法。
实验一:CPU 定时器实验一:实验目的1、熟悉F2812 的CPU 定时器;2、掌握F2812 的CPU 定时器的控制方法;3、学会使用CPU 定时器中断方式控制程序流程。
二:实验设备计算机,CCS 3.1 版软件,DSP 硬件仿真器,E300 实验箱,2812CPU 板。
三:实验原理样例实验是采用CPU 定时器来定时使LED 亮灭的。
F2812 的CPU 定时器不同于事件管理器模块(EVA、EVB)中的通用定时器(GP)。
F2812 的CPU共有三个定时器,其中,CPU 定时器 1 和 2 被保留用作实时操作系统OS(例如DSPBIOS),CPU 定时器0 可以供用户使用。
定时器的一般操作如下:将周期寄存器PRDH:PRD 中的值装入32 为计数器寄存器TIMH:TIM。
然后计数器寄存器以F281x 的SYSCLKOUT 速率递减。
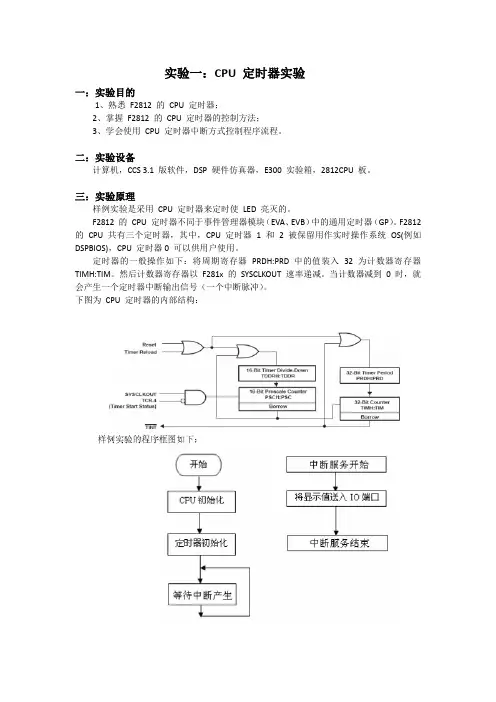
当计数器减到0 时,就会产生一个定时器中断输出信号(一个中断脉冲)。
下图为CPU 定时器的内部结构:四:实验步骤1 、F2812CPU 板的JUMP1 的1 和2 脚短接,拨码开关SW1 的第二位置ON;其余置OFF。
2 、E300 底板的开关SW4 的第2 位置ON,其余位置OFF。
其余开关设置为OFF。
3 、运行CCS 软件,调入样例程序,装载并运行;(进入CCS 界面后需要点“Debug--Connect”)4 、加载“..\ e300_03_cpu_timer\Debug\Example_281x_cpu_timer.out”;5 、单击“Debug \ Animate”运行,可观察到灯LED1~LED8 的变化规律:6 、单击“Debug \ Halt”,暂停程序运行,LED 灯停止闪烁;单击“Debug \ Run”,运行程序,LED 灯又开始按上述规律变化;五:实验程序及结果修改后程序如下:/*;**************************************************************;* 北京达盛科技有限公司;* 研发部;*;* ;*************************************************************//*----------------------- 文件信息----------------------------;*;* 文件名称: Example_DSP281x_e300_switch.c;* 适用平台: DSP E300 实验箱;;* CPU类型: DSP TMS320F2812;* 软件环境: CCS3.1;* 试验接线: 1、F2812CPU板上:JUMP1的1和2脚短接,拨码开关SW1的第二位置ON;;* 2、E300底板的开关SW4的第2位置ON,其余置OFF。
实验0 实验设备安装才CCS调试环境实验目的:按照实验讲义操作步骤,打开CCS软件,熟悉软件工作环境,了解整个工作环境内容,有助于提高以后实验的操作性和正确性。
实验步骤:以演示实验一为例:1.使用配送的并口电缆线连接好计算机并口与实验箱并口,打开实验箱电源;2.启动CCS,点击主菜单“Project->Open”在目录“C5000QuickStart\sinewave\”下打开工程文件sinewave.pjt,然后点击主菜单“Project->Build”编译,然后点击主菜单“File->Load Program”装载debug目录下的程序sinewave.out;3.打开源文件exer3.asm,在注释行“set breakpoint in CCS !!!”语句的NOP处单击右键弹出菜单,选择“Toggle breakpoint”加入红色的断点,如下图所示;4.点击主菜单“View->Graph->Time/Frequency…”,屏幕会出现图形窗口设置对话框5.双击Start Address,将其改为y0;双击Acquisition Buffer Size,将其改为1;DSP Data Type设置成16-bit signed integer,如下图所示;6.点击主菜单“Windows->Tile Horizontally”,排列好窗口,便于观察7.点击主菜单“Debug->Animate”或按F12键动画运行程序,即可观察到实验结果:心得体会:通过对演示实验的练习,让自己更进一步对CCS软件的运行环境、编译过程、装载过程、属性设置、动画演示、实验结果的观察有一个醒目的了解和熟悉的操作方法。
熟悉了DSP实验箱基本模块。
让我对DSP课程产生了浓厚的学习兴趣,课程学习和实验操作结合为一体的学习体系,使我更好的领悟到DSP课程的实用性和趣味性。
实验二基本算数运算2.1 实验目的和要求加、减、乘、除是数字信号处理中最基本的算术运算。
DSP实验报告班级:11050641学号:姓名:指导教师:实验一、二 DSP芯片的开发工具及应用实验1.实验目的(1)熟悉CCS集成开发环境,掌握工程的生成方法;(2)熟悉SEED-DTK DAD实验环境;(3)掌握CCS集成开发环境的调试方法。
2.实验设备DSP实验箱,计算机,CCS软件。
3.实验内容及步骤(1)CCS软件的安装;(2)了解SEED-DTK5416实验环境;(3)打开CCS集成开发环境,进入CCS的操作环境;(4)新建一个工程文件○1在c:\ti\myprojects中建立文件夹volume1(如果CCS安装在其他d:\ti ,则在d:\ti\myprojects中);○2将c:\ti\tutorial\target\volume1拷贝到c:\ti\myprojects\ volume1;○3从在CCS 中的Project 菜单,选择 New;○4在Project Name域中,键入volume1;○5在Location区域中,浏览步骤1所建立的工作文件夹;○6在Project Type 域中,选择Executable(.out);○7在Target域中,选择CCS配置的目标,并单击完成。
(5)向工程中添加文件○1从Project/Add Files to Project,选择 volume.c,单击Open(或右击Project View图标,选择Add Files to Project );○2选择Project/Add Files to Project,在Files of type对话框中,选择Asm Source Files (*.a*, *.s*)。
选择vectors.asm 和 load.asm, 单击Open;○3选择 Project/Add Files to Project,在Files of type 对话框中选择 Linker Command File (*.cmd),选择volume.cmd,单击Open。
dsp图像处理实验报告DSP图像处理实验报告一、引言数字信号处理(DSP)是一种用于处理数字信号的技术,广泛应用于各个领域。
图像处理是DSP的一个重要应用,通过对图像进行数字化处理,可以实现图像增强、边缘检测、目标识别等功能。
本实验旨在通过DSP技术对图像进行处理,探索图像处理算法的实际应用。
二、实验目的1. 了解数字信号处理在图像处理中的应用;2. 掌握DSP平台的基本操作和图像处理算法的实现;3. 进一步熟悉MATLAB软件的使用。
三、实验环境和工具本实验使用的DSP平台为TMS320C6713,开发环境为Code Composer Studio (CCS)。
图像处理算法的实现主要依赖于MATLAB软件。
四、实验步骤1. 图像采集与预处理首先,通过CCD摄像头采集一张待处理的图像,并将其转化为数字信号。
然后,对图像进行预处理,包括去噪、灰度化等操作,以提高后续处理的效果。
2. 图像增强图像增强是指通过一系列算法和技术,提高图像的质量、清晰度和对比度。
在本实验中,我们采用了直方图均衡化算法对图像进行增强。
该算法通过对图像像素值的统计分析,调整像素值的分布,使得图像的对比度更加明显,细节更加突出。
3. 边缘检测边缘检测是图像处理的重要环节,可以用于目标识别、图像分割等应用。
在本实验中,我们采用了Canny算法进行边缘检测。
Canny算法是一种经典的边缘检测算法,通过对图像进行多次滤波和梯度计算,得到图像的边缘信息。
4. 目标识别目标识别是图像处理中的关键任务之一,可以应用于人脸识别、车牌识别等领域。
在本实验中,我们以人脸识别为例,使用了Haar特征分类器进行目标识别。
Haar特征分类器是一种基于图像特征的分类器,通过对图像进行特征提取和分类器训练,可以实现对目标的快速准确识别。
五、实验结果与分析通过对图像进行处理,我们得到了增强后的图像、边缘检测结果和目标识别结果。
经过对比分析,我们发现图像增强算法能够有效提高图像的对比度和清晰度,使得图像更加易于观察和分析。
一、综合实验内容和要求1. 实验目的(1) 学习掌握CCS3.3编译器的使用;(2) 通过实验学习掌握TMS320F28335的GPIO ,浮点计算; (3) 学习并掌握A/D 模块的使用方法;(4) 学习并掌握中断方式和查询方式的串口通信; (5) 学习并掌握28335DSP 的定时器相关的设置与运用; (6) 学习信号时域分析的方法,了解相关波形参数的计算方法; (7) 了解数字滤波的一些基本方法; (8) 学习数码管的驱动及运用。
(9) 学习MATLAB 串口以及画图的运用。
2. 实验设计内容与要求:(1) 对给定的周期波形信号采用TI 公司的TMS320F28335DSP ,利用试验箱上的相关资源计算出波形的周期T ,波形的有效值rms V ,平均值avg V 。
其中,有效值和平均值的计算公式(数字量的离散公式)如下:rms V =1()NavgiV u i N =∑式中N 为一个周期采样点数,()u i 为采样序列中的第i 个采样点。
(2) 通过算法计算出波形的有效值和平均值,利用串口通信把测得的数据发送到串口助手查看,或者在MATLAB 上编写上位机程序,把发送的数据在MATLAB 上画出来。
(3) 把测得的数据实时显示在数码管上。
二、硬件电路图1为试验系统的硬件图,硬件电路主要包括TMS320F28335DSP 实验箱,SEED-XDS510仿真器,数码管,SCI,信号发生器,电脑,串口线等。
图1 硬件电路图三、实验原理本试验主要是通过程序去测量一个周期波形的有效值、平均值、峰值等相关参数。
计算离散数据的有效值可用公式rms V =,平均值可用公式1()N avgiV u i N=∑。
所以首先需要测出波形的周期,然后确定每个周期需要采样的点数N ,最后去计算平均值和有效值。
v mv 1图2 理想输入采样波形如图2所示为一个正弦输入波形,m V 为输入波形的峰值,1V 是介于0~ m V 的一个值。
实验一 离散系统的时域分析一、实验目的1、掌握离散时间信号的MATLAB 表示;2、信号运算;3、差分方程的求解;4、离散时间信号的卷积运算。
二、实验原理1、离散时间信号离散时间信号只在某些离散的瞬时给出函数值,而在其他时刻无定义。
它是时间上不连续按一定先后次序排列的一组数的集合,称为时间序列,用x(n)表示,n 取整数代表时间的离散时刻。
在matlab 中用向量来表示一个有限长度的序列。
2、序列的类型为了分析的方便,在数字信号处理中规定了一些基本的序列。
a) 单位采样序列function [x,n]=impseq(n1,n2,n0) n=[n1:n2]; x=[(n-n0)==0];调用该函数[x,n]=impseq(-2,8,2); stem(n,x)0010()001()0n n n n n n n n n δδ =⎧=⎨ ≠⎩ =⎧-⎨≠⎩单位采样序列的另一种生成方法n0=-2; n=[-10:10]; nc=length(n); x=zeros(1,nc); for i=1:nc if n(i)==n0 x(i)=1 end endstem(n,x)b) 单位阶跃序列function [x,n]=stepseq(n1,n2,n0) n=[n1:n2]; x=[(n-n0)>=0];调用该函数[x,n]=stepseq(-2,8,2); stem(n,x)00010()001()0n n n n n n n n nεε >=⎧=⎨<⎩ >=⎧-⎨ <⎩c) 实数指数序列x(n)=an (运算符“.^”)n=[0:10]; x=0.9.^n; stem(n,x)d) 复数指数序列n=[-10:10]; alpha=-0.1+0.3*j; x=exp(alpha*n);real_x=real(x); image_x=imag(x); mag_x=abs(x); phase_x=angle(x); subplot(2,2,1); stem(n,real_x) subplot(2,2,2); stem(n,image_x) subplot(2,2,3); stem(n,mag_x) subplot(2,2,4); stem(n,phase_x)()()j nx n e αω+=(0.1j0.3)n x(n)e (10n 10)-+= -<<e) 正弦和余弦序列 n=[0:10]; x=3*cos(0.1*pi*n+pi/3);stem(n,x)f)随机序列rand(1,N)产生其元素在[0,1]之间均匀分布长度为N 的随机序列。
实验报告利用DSP实现实时滤波姓名:班级:学号:一、实验任务1、实验背景在信号与信息处理中,提取有用信息就要对信号进行滤波。
利用DSP可以实时地对信号进行数字滤波。
本设计要求利用DSP的DMA方式进行信号采集和信号输出,同时对外部输入的信号进行数字滤波。
自适应滤波不仅能够选择信号,而且能够控制信号的特性。
自适应滤波器具有跟踪信号和噪声变化的能力,它的系数能够被一种自适应算法所修改。
利用DSP可以实时地对信号进行自适应滤波。
DSP利用直接存储器访问方式DMA采集数据时不打扰CPU,因此CPU可以对信号进行实时地滤波。
本设计要求利用DSP的DMA方式进行信号采集和信号输出,同时对外部输入的信号进行数字滤波。
2、实验要求1.建立信号处理系统的概念,学会使用DSP处理器;2.了解DSP处理系统的关键器件的使用方法;3.掌握DSP课程设计的基本方法,巩固信号处理的基本理论4.掌握查阅有关资料和使用器件手册的基本方法,学会阅读原版英文资料;5.掌握DSP集成开发环境的使用和调试方法;6.掌握DSP片外资源和片上资源访问的基本方法,如存储器、McBSP、DMA、A/D 和D/A转换器等。
二、设计内容1、基本部分:(1)对DMA进行初始化;(2)对A/D、D/A进行初始化;(3)编写DMA中断服务程序,实现信号的实时滤波;(4)利用CCS信号分析工具分析信号的频谱成分,确定滤波器的参数,利用MATLAB设计数字滤波器,提取滤波器参数;(5)设计数字滤波算法,或调用DSPLIB中的滤波函数,实现对信号的滤波。
(6)比较加不同窗和阶数时滤波器的滤波效果;(7)测试所设计滤波器的幅频特性和相频特性,并与MATLIB下的设计结果进行比较。
2、拓展部分:(1)滤波后信号实时输出的同时,将数据存放在数据文件中;(2)利用自适应滤波实现语音信号回波对消。
三、设计方案、算法原理说明1、设计方案流图如下:主程序简要说明:模拟音频进过codec电路(codec已设置好初值),转化为数据流,存放于缓冲区中,用于对数据处理。
实验一 离散系统的时域分析一、实验目的1、掌握离散时间信号的MATLAB 表示;2、信号运算;3、差分方程的求解;4、离散时间信号的卷积运算。
二、实验原理1、离散时间信号离散时间信号只在某些离散的瞬时给出函数值,而在其他时刻无定义。
它是时间上不连续按一定先后次序排列的一组数的集合,称为时间序列,用x(n)表示,n 取整数代表时间的离散时刻。
在matlab 中用向量来表示一个有限长度的序列。
2、序列的类型为了分析的方便,在数字信号处理中规定了一些基本的序列。
a) 单位采样序列function [x,n]=impseq(n1,n2,n0) n=[n1:n2]; x=[(n-n0)==0];调用该函数[x,n]=impseq(-2,8,2); stem(n,x)0010()001()0n n n n n n n n n δδ =⎧=⎨ ≠⎩ =⎧-⎨≠⎩单位采样序列的另一种生成方法n0=-2; n=[-10:10]; nc=length(n); x=zeros(1,nc); for i=1:nc if n(i)==n0 x(i)=1 end endstem(n,x)b) 单位阶跃序列function [x,n]=stepseq(n1,n2,n0) n=[n1:n2]; x=[(n-n0)>=0];调用该函数[x,n]=stepseq(-2,8,2); stem(n,x)00010()001()0n n n n n n n n nεε >=⎧=⎨<⎩ >=⎧-⎨ <⎩c) 实数指数序列x(n)=an (运算符“.^”)n=[0:10]; x=0.9.^n; stem(n,x)d) 复数指数序列n=[-10:10]; alpha=-0.1+0.3*j; x=exp(alpha*n);real_x=real(x); image_x=imag(x); mag_x=abs(x); phase_x=angle(x); subplot(2,2,1); stem(n,real_x) subplot(2,2,2); stem(n,image_x) subplot(2,2,3); stem(n,mag_x) subplot(2,2,4); stem(n,phase_x)()()j nx n e αω+=(0.1j0.3)n x(n)e (10n 10)-+= -<<e) 正弦和余弦序列 n=[0:10]; x=3*cos(0.1*pi*n+pi/3);stem(n,x)f)随机序列rand(1,N)产生其元素在[0,1]之间均匀分布长度为N 的随机序列。
randn(1,N)产生均值为0,方差为1,长度为N 的高斯随机序列。
3、信号运算a) 信号时移 b) 信号倒置 c) 信号加 d) 信号乘 e) 信号微分 f)信号积分等0()sin()x n n ωθ=+0()cos()x n n ωθ=+4、序列运算在matlab 中进行序列运算要求参与运算的序列的长度要一样,如果出现长度不一样或者长度相同但采样位置不同时,不能直接利用加减运算符,利用matlab 中的下标运算使其具有相同的长度。
function [y,n]=sigadd(x1,n1,x2,n2)n=min(min(n1),min(n2)) : max(max(n1),max(n2)); y1=zeros(1,length(n)); y2=y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; y=y1+y2;移位function [y,n]=sigshift(x,m,n0) n=m+n0; y=x;例: 求出下列波形x1(n)=2x(n-5)-3x(n+4)n=[-2:10]; x=[1:7,6:-1:1];[x11,n11]=sigshift(x,n,5); [x12,n12]=sigshift(x,n,-4);[x1,n1]=sigadd(2*x11,n11,-3*x12,n12); stem(n1,x1)5、差分方程在《信号与系统》和《数字信号处理》课程中,我们知道描述线性移不变离散时间系统的数学模型是常系数差分方程,它与系统的结构流图之间可以互相推导。
迭代解法(也称递推解法)是求解差分方程的最简单也最适用的方法,也是实现数字滤波器的一种基本方法。
差分方程通式为:(){1,2,3,4,5,6,7,6,5,4,3,2,1}x n =0[]()[]()N Nk r a k y n k b r x n r ==-=-∑∑x(n)与y(n)分别为系统的激励和响应。
6、差分方程MATLAB 实现MATLAB 以函数filter(num , den , x),来计算在给定输入和差分方程系数时求差分方程的数值解。
num,den 分别为系统方程的系数向量。
x 是输入序列。
已知某一系统方程为:y[n]-y[n-1]+0.9y[n-2]=x[n]计算并画出脉冲响应h(n),n=(-20,100)n=[-20:100];num=[1]; den=[1 -1 0.9]; x=impseq(-20,100,0); h=filter(num,den,x); stem(n,h)xlabel('时间序号N'); ylabel('脉冲响应h'); title('脉冲响应');离散卷积的计算公式如下:序列x(n)、h(n) 可以是有限长或无限长,但为了在计算机上绘图观察方便,我们主要讨论有限长序列。
如果x(n) 和h(n)长度分别为M 和N ,则响应序列y(n) 也为有限长序列,其长度为 L=M+N-1 。
于是,上式可以“形象”地描述为两个有限长序列的反褶、移位、相乘、累加过程,这使计算机编程十分方便。
卷积函数conv(a,b)实现两个序列a,b 的卷积。
例:假定两个序列。
x=[3,11,7,0,-1,4,2]; y=[2,3,0,-5,2,1]; c=conv(x,y); stem(c)()()*()()()m y n x n h n x m h n m +∞=-∞==-∑将函数conv 稍加扩展为函数conv-m ,它可以对任意的序列求卷积。
格式如下:function [y,ny]= conv_m(x,nx,h,nh,p) %信号处理的改进卷积程序 nyb=nx(1)+nh(1);nyc=nx(length(x))+nh(length(h)); ny=[nyb:p:nyc]; y=conv(x , h);♦ 已知试求卷积C(t)=f1(t)*f2(t),并绘制出f1、f2及卷积以后的波形。
p=0.1; t1= [0:p:1]; f1=t1.*(t1>0); t2= [-1:p:2];f2=t2.*exp(-t2).*(t2>=0)+exp(t2).*(t2<0); [y,ny]=conv_m(f1,t1,f2,t2,p); Subplot(3,1,1); stem(t1,f1) Subplot(3,1,2); stem(t2,f2) Subplot(3,1,3); stem(ny,y)12()()01,0()12,0t t f t t t t te t f t t e t ε-= ≤≤⎧>=⎪= -≤≤⎨<⎪⎩四、实验报告要求1、简述实验目的和实验原理。
2、用笔算求出你选定的序列x(n)、h(n)的卷积结果并与计算机计算结果相比较。
实验二 离散傅立叶变换一、实验目的1. 掌握离散傅里叶变换的有关性质。
2. 利用matlab 验证有关性质。
3. 利用傅立叶变换进行相关运算。
二、实验原理及方法在工程技术的许多分支中,要掌握的基本内容之一就是正确理解时域和频域的关系。
对于数字系统来说,就是要精通离散傅立叶变换,因此离散傅立叶变换在数字信号处理中占有十分重要的地位。
在实际应用中,有限长序列有相当重要的地位,由于计算机容量的限制,只能对过程进行逐段分析。
由于有限长序列,引入DFT(离散付里叶变换)。
傅里叶变换建立以时间t 为自变量的“信号”与以频率f 为自变量的“频率函数”(频谱)之间的某种变换关系。
所以“时间”或“频率”取连续还是离散值, 就形成各种不同形式的傅里叶变换对。
四种不同傅里叶变换对1. 傅里叶级数(FS):连续时间, 离散频率的傅里叶变换。
周期连续时间信号傅里叶级数(FS)得到非周期离散频谱密度函数。
2. 傅里叶变换(FT):连续时间, 连续频率的傅里叶变换。
非周期连续时间信号通过连续付里叶变换(FT)得到非周期连续频谱密度函数。
3. 序列的傅里叶变换(DTFT):离散时间,连续频率的傅里叶变换。
非周期离散的时间信号(单位园上的Z 变换(DTFT))得到周期性连续的频率函数。
4. 离散傅里叶变换(DFT):离散时间, 离散频率的傅里叶变换。
上面讨论的前三种傅里叶变换对,都不适用在计算机上运算, 因为至少在一个域( 时域或频域)中, 函数是连续的。
因为从数字计算角度我们感兴趣的是时域及频域都是离散的情况, 这就是第四种离散傅里叶变换。
离散傅里叶级数(DFS)设 为周期为N 的周期序列, 则其离散傅里叶级数(DFS) 变换对为: 正变换逆变换其中利用MATLAB 实现傅立叶级数计算编写函数实现DFS 计算function xk=dfs(xn,N) n=[0:1:N-1]; k=n;WN=exp(-j*2*pi/N);21100()[()]()()---=====∑∑N N j nknkN N n n X k DFS x n x n e x n W π2110011()[()]()()---=====∑∑N N j nk nkN N n k x n IDFS X k X k e X k W N N π2jNN W e π-=()x nnk=n'*k; WNnk=WN.^nk; xk=xn* WNnk;例:xn=[0,1,2,3],N=4xn=[0,1,2,3]; N=4;xk=dfs(xn,N)'逆运算IDFSfunction xn=idfs(xk,N) n=[0:1:N-1]; k=n;WN=exp(-j*2*pi/N); nk=n'*k; WNnk=WN.^(-nk); xn=xk*WNnk/N;离散傅立叶变换的正、逆变换定义为:比较正、逆变换的定义式可以看出,只要把DFT 公式中的系数 改为 ,并最后乘以1/N ,那么,DFT 的计算程序就可以用来计算IDFT 。