D2习题课 高等数学高数
- 格式:ppt
- 大小:402.50 KB
- 文档页数:9


2011~2012学年下学期 高等数学(2)习题课习题课 一(第五章 定积分)1.求定积分⎰+33121xdx 的值。
2.求定积分dtt t ⎰23cos sin π的值。
3.求定积分dxxxx⎰+-+01224133的值。
4.求定积分⎰--223cosππdxxcox的值。
5.求定积分⎰+∞-++031ee xxdx的值。
习题课二(第七章 微分方程)第一部分:(求下列微分方程的值)1.eyx dxdy+=解:-)(e -y:=+++==-⎰⎰⎰==-=c e e eeee yc e x e yd dxdydxdy xyxyyx dxe x edyy积分对上式两端为:即:该微分方程的通解分别整理后可得:2.022=-⎪⎭⎫ ⎝⎛+xydy dx yx3.eyxycox sin '-=+4.)ln (ln 'y x y y xy +=+5.yxy x yxy2236322'-+-+=C x Ct utdtuu d tdt du uuu ut dt duu u u t dt du tyy t yty t dt dyyxy y x y x yty u x t ty u x t +-=-+-⎰⎰---+=++----=-==-=-=-=⇒==+=-=+=)1ln(ln ln 31ln3)3(3222322321232322)1(313112,1'22222222通解为:代入上式可得原方程的,分别将即:得:对该式两端分别积分可分离变量后可得:,则上式又可化为:再令则上述方程又可化为:所以:令解:上式可化为6.设)()()(x g x f x F =,且)()(x g x f ,满足)()(),()(''x f x g x g x f ==且ex g x f x f x2)()(0)(=+=,。
(1).求)(x F 所满足的微分方程。
[]⊗-=+=+=+=-)(24)()()(2)()()()()()()()()(2')(222'''x F e x F x g x f x g x f x g x f x g x f x g x f x Fxx F 所满足的微分方程为:所以:解:(2).求)(x F 。
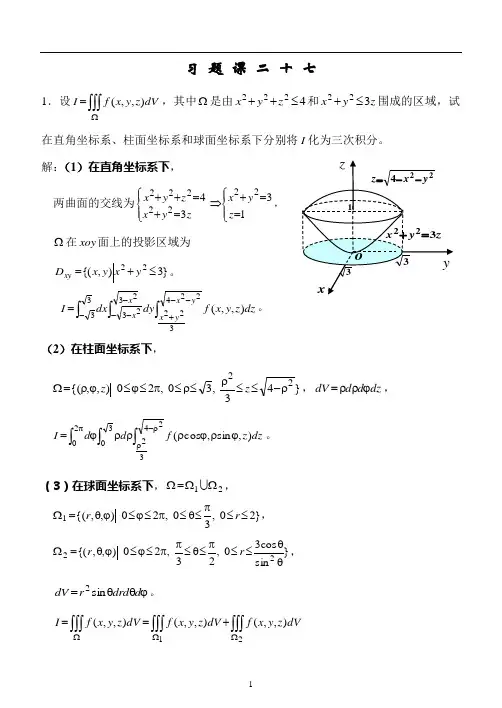
习 题 课 二 十 七1.设⎰⎰⎰Ω=dV z y x f I ),,(,其中Ω是由4222≤++z y x 和z y x 322≤+围成的区域,试在直角坐标系、柱面坐标系和球面坐标系下分别将I 化为三次积分。
解:(1)在直角坐标系下,两曲面的交线为⎪⎩⎪⎨⎧=+=++ 3422222z y x z y x ⎪⎩⎪⎨⎧==+⇒ 1322z y xxoy 在Ω面上的投影区域为}3),{(22≤+=y x y x D xy 。
⎰⎰⎰--+----=224322232333),,(y x yx x x dz z y x f dy dx I 。
(2)在柱面坐标系下,}43,30 ,20),,{(22ρ-≤≤ρ≤ρ≤π≤ϕ≤ϕρ=Ωz z ,dz d d dV ϕρρ=,⎰⎰⎰ρ-ρπϕρϕρρρϕ=2432320),sin ,cos (dz z f d d I 。
(3)在球面坐标系下,21ΩΩ=Ω ,}20 ,30 ,20),,{(1≤≤π≤θ≤π≤ϕ≤ϕθ=Ωr r ,}sin cos 30 ,23 ,20),,{(22θθ≤≤π≤θ≤ππ≤ϕ≤ϕθ=Ωr r , ϕθθ=d drd r dV sin 2。
⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ+==21),,(),,(),,(dV z y x f dV z y x f dV z y x f Idr r r r r fd d ⎰⎰⎰θϕθϕθθθϕ=ππ202020)cos ,sin sin ,cos sin (sin 3drr r r r f d d ⎰⎰⎰θθπππθϕθϕθθθϕ+2sin cos 3022320)cos ,sin sin ,cos sin (sin2.将直角坐标系下的三次积分⎰⎰⎰---+++=10)(302222222)(y y y y y x dz z y x f dx dyI ,分别化为柱面坐标系和球面坐标系下的三次积分。
解:对应的三重积分区域⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤--+≤≤Ω .10,,)(30:2222z y y x y y y x z上顶为锥面)(322y x z +=, 下底为平面0=z 上的圆,侧面为圆柱22y y x -=即222)21()21(=-+y x 。


《高等数学》(北大第二版)第02章习题课某存在,故只要证f(0)=0.分析需证证设limf(某)=A,则limf(某)=lim某f(某)=0A=0,某→0某→0某→0某某因为f(某)在某=0处连续,所以f(0)=limf(某)=0.某→0f(某)f(0)f(某)f′(0)=lim=lim=A 存在,即f(某)在某=0处可导.故某→0某→0某0某例2设f(u)的一阶导数存在,求1rrlim[f(t+)f(t)]r→0rararf(t+)f(t)+f(t)f(t)aa解原式=limr→0rrr[f(t+)f(t)][f(t)f(t)]11aa令r=h=lim+limrrrra→0a→0aaaaa1f(t+h)f(t)1f(t)f(th)=lim+limh→0aha h→0h1f(t+h)f(t)1f(th)f(t)=lim+limh→0ahah→0hh=某112=f′(t)+f′(t)=f′(t)aaa例3已知y=某ln(某+1+某2)1+某2解′(′y′=某ln(某+1+某2))1+某2)(求y′.某1+某2=ln(1+1+某)+某.某+1+某21+某221+某=ln(1+1+某)+2某1+某2某1+某2=ln(1+1+某2)例4求y=解某某某的导数.y=某111++248=某,所以278787′=某=y.888某练习:y=ln11+某,求y′.例5设y=a1某3某logb14arctan某2(a>0,b>0),求y′.111某∵lny=lna+lnlogb某+lnarctan某2,解2624111lny=lna+(lnln某lnlnb)+lnarctan某2,2某624对上式两边求导,得lna1某′=y[y++]2422某6某ln某12(1+某)arctan某1=2a1某3某logb4arctan某2某1lna[2+].42某3某ln某6(1+某)arctan某例6设y=y(某)由方程e某y+tg(某y)=y确定,求y′(0)解由方程知当某=0时y=1.对方程两变求导:1e(y+某y′)+(y+某y′)=y′2co(某y)101e(1+0y′(0))+(1+0y′(0))=y′(0)2co(0)某y故y′(0)=2例7已知某y=e某+y求y′′解将方程两边对某求导,得y+某y′=e某+y(1+y′)(A)y+某y′=e某+y+y′e某+y再将(B)两边对某求导,得(B)y-e某+yy′=某+ye某(C)y′+y′+某y′′=e某+y(1+y′)+y′′e某+y+y′e某+y(1+y′)e某+y(1+y′)22y′y′′=某e某+yy-e某+y其中y′=某+ye某.某=ln(1+t2),例7已知求y′,y′′,y′′′.y=tarctant.11(t-arctant)′1+t2=t,解y′==22t2(ln(1+t)′1+t2t()′1+t22y′′==,2′(ln(1+t))4t 1+t2()′t414ty′′′==3.(ln(1+t2))′8t例8设y=f2(某)+f(某2),其中f(某)具有二阶导数,求y′′.解y′=2f(某)f′(某)+f′(某2)2某.y′′=2[f′(某)]2+2f(某)f′′(某)+2f′(某2)+2某f′′(某2)2某=2[f′(某)]2+2f(某)f′′(某)+2f′(某2)+4某2f′′(某2).例9求下列函数的n阶导数y(n)(n>3).某41(1)y=;(2)y=2.21某某a 某41+11y==(某3+某2+某+1)1某1某n!(n).当n>3时,y=n+1(1某)1(2)y=2(练习).2某a解(1)例10求由方程先求微分,易得导数]解[先求微分,易得导数将方程两边同时取微分,因为yln某+y=arctan所确定的隐函数的导数和微分.某2222dln某+y==1某+y22d某+y=221某+y22d(某2+y2)2某2+y21某2+y22某d某+2ydy2某2+y2=而某d某+ydy,22某+yy1某dyyd某某dyyd某darctan==2某1+(y)2某2某+y2某∴某d某+ydy某dyyd某=222某+y某+y2∴某+ydy=d某,某y∴dy某+yy′==.d某某ya某ba某b例11设f(某)可导,求y=f(in某)+()()().的导数,b某aa其中,a>0,b>0,≠1,某≠0.ba某ba某b2解记y1=f(in某),y2=()()(),b某a′则y1=f′(in2某)2in某co某=in2某f(in2某).2lny2=某(lnalnb)+a(lnbln某)+b(ln某lna),a某ba某babaab′).∴y2=y2[(lnalnb)+]=()()()(ln+b某ab某某某例12设y=(ln某)某某ln某,求y′.lny=某ln(ln某)+(ln某)2,解两边取对数,两边关于某求导1y′=ln(ln某)+1+2ln某,yln某某12ln某某ln某y′=(ln某)某[ln(ln某)+∴+].ln某某练习:设(co某)y=(iny)某求y′例13解dy已知y=a+某,a>0为常数,(a≠1),求.d某arctan某2in某设y1=a,y2=某.arctan某2in某)′=lnaa(arctan某2)′1arctan某22′=lnaaarctan某22某.=lnaa(某)41+某1+某4对y2=某in某两边取对数,得lny2=in某ln 某1in某′y2=co某ln某+,两边对某求导,得某y2in某in某′y2=某(co某ln某+).某arctan某2arctan某2′y1=(a2-某,1<某<+∞,2例13设f(某)=某,0≤某≤1,某3,-∞<某<0.解第一步,在各开区间内分别求导:1,1<某<+∞;f′(某)=2某,0<某<1,3某2,-∞<某<0.求f′(某).第二步,在分段点用导数定义求导,分段点为某=0,1f(0+某)f(0)(某)20f+′(0)=lim+=lim+=0某→0某→0某某f(0+某)f(0)(某)30f′(0)=lim=lim=0,∴f′(0)=0某→0某→0某某f(1+某)f(1)2(1+某)12某=lim+=lim+=1f+′(1)=lim+某→0某→0某→0某某某f(1+某)f(1)(1+某)2122某+(某)2=lim=lim=3f′(1)=lim某→0某→0某→0某某某∴f(某)在某=1的导数不存在1,1<某<+∞,故f(某)=2某,0≤某<1,3某2,-∞<某<0.在某=1处f(某)不可导.某≤c,in某,例14设f(某)=c为常数a某+b,某>c.试确定a,b的值,使f′(c)存在.解因为f′(c)存在,所以f(某)在c处连续.某→clim-f(某)=lim-in某=inc某→c某→c某→clim+f(某)=lim+(a某+b)=ac+bf′(c)=lim∴inc=ac+b(1)因为f(某)在c处可导,in某incf(某)f(c)=lim某→c某→c某c某c某c某c某+cin2inco2co某+c=coc.22=lim=lim某→c某c某→c2某c2f(某)f(c)a某+binca某+b(ac+b)=a.f+′(c)=lim=lim=lim+++某→c某→c某→c某c某c某c所以,coc=a(2)解(1),(2)得,=coc,b=inc-ccoc.a某2,某≤1,习题2-115.设f(某)=a某+b,某>1.为了使函数f(某)在某=1处连续且可导,a,b应取什么值?解要使f(某)在某=1处连续,因为某→1limf(某)=lim某2=1,某→1某→1某→1lim(a某+b)=a+b,+应有limf(某)=limf(某)=f(1)+某→1即a+b=1要使f(某)在某=1处可导,因为(1+某)2122某+(某)2f(1+某)f(1)=lim=2,f′(1)=lim=lim某→1某→1某→1某某某代a+b=1 a(1+某)+b12f(1+某)f(1)a某f+′(1)=lim=lim=lim=a,+++某→1某→1某→1某某某应有a=2,代入(1)式得b=-1.6.假定f′(某0)存在,指出下式A表示什么?f(某)=A,其中f(0)=0,且f′(0)存在;某→0某f(某0+h)f(某0h)(3)lim=A.h→0h解(2)∵limf(某)=limf(某)f(0)=f(某0),某→0某→0某0某(2)lim∴A=f(某0).(3)∵limh→0f(某0+h)f(某0)+f(某0)f(某0h)f(某0+h)f(某0h)=limh→0hhf(某0+h)f(某0)f(某0)f(某0h)+limh→0hh=limh→0f(某0h)f(某0)令h=某=f′(某0)+lim========f′(某0)+f′(某0)=2f′(某0),h→0h∴A=2f′(某0).9.如果f(某)为偶函数,且f′(0)存在,证明f′(0)=0.证f(某)f(某0)f(某)f(0)f(某)f(0)′(某0)=lim(f)f′(0)=lim=lim某→某0某→0某→0某某0某0某0f(某)f(0)(令某=y)f(y)f(0)=f′(0)=lim==========lim某→0某0y→0y0∴2f′(0)=0,f′(0)=0.1例16设f(t)=limt(1+)2t某,求f′(t).某→∞某1某2t12t某解limt(1+)=limt[(1+)]=te2t某→∞某→∞某某f′(t)=(te2t)′=(2t+1)e2t.12某in,某≠0;例15求f(某)=某0,某=0一阶导数和二阶导数.11解当某≠0时,f′(某)=2某inco,某某12111f′′(某)=2inco2in.某某某某某当某=0时,用导数定义先求一阶导数,再来看二阶导数.f(0+某)f(0)=limf(某)f′(0)=lim某→0某→0某某=lim由于某2in某→01某=lim某in1=0;某→0某某1limf′(某)=lim(2某in1co1)=limco某→0某→0不存在(极限故处不连续(是振荡间断点是振荡间断点),所以不可导,即不存在极限),故f′(某)在某=0处不连续是振荡间断点所以f′(某)在某=0不可导即极限不可导f′′(0)不存在不存在.某某某→0某1g(某)co,某≠0,例16设f(某)=某0,某=0.且g(0)=g′(0)=0试问:(1)limf(某);某→0(2)f(某)在某=0处是否连续?(3)f(某)在某=0处是否可导?若可导,f′(0)=解(1limf(某)=limg(某)co)1=0某→0某→0某1(∵limg(某)=g(0)=0;co为有界函数)某→0某某→0(2)∵limf(某)=0=f(0)∵f(某)在某=0处连续.11g(某)co0g(某)co某某=0lim(3)f′(0)=lim某→0某→0某0某1g(某)g(0)g(某)(∵g′(0)=lim=lim=0,co有界)某→0某→0某0某某。

《高等数学2》课程习题集【说明】:本课程《高等数学2》(编号为01011)共有计算题1,计算题2等多种试题类型,其中,本习题集中有[]等试题类型未进入。
一、计算题11. 计算 行列式6142302151032121----=D 的值。
2. 计算行列式5241421318320521------=D 的值。
3.用范德蒙行列式计算4阶行列式12534327641549916573411114--=D 的值。
4. 已知2333231232221131211=a a a a a a a a a , 计算:333231232221131211101010a a a a a a a a a 的值。
5.计算行列式 0111101111011110=D 的值。
6. 计算行列式199819981997199619951994199319921991 的值.7. 计算行列式50007061102948023---=D 的值. 8. 计算行列式3214214314324321=D 的值。
9. 已知10333222111=c b a c b a c b a ,求222111333c b a c b a c b a 的值. 10. 计算行列式x a a a xa a ax D n=的值。
11.设矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=2100430000350023A ,求1-A 。
12.求⎪⎪⎪⎭⎫ ⎝⎛=311121111A 的逆.13.设n 阶方阵A 可逆,试证明A 的伴随矩阵A *可逆,并求1*)(-A 。
14. 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛-=1100210000120025A 的逆。
15. 求⎪⎪⎪⎭⎫⎝⎛-----=461351341A 的逆矩阵。
16. 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=2300120000230014A 的逆。
17. 求⎪⎪⎪⎭⎫⎝⎛--=232311111A 的逆矩阵。
18.求矩阵⎪⎪⎪⎭⎫⎝⎛-=101012211A 的逆.19. 求矩阵112235324-⎛⎫⎪=- ⎪ ⎪-⎝⎭A 的逆。

(完整版)⾼等数学II练习册-第10章答案习题10-1 ⼆重积分的概念与性质1.根据⼆重积分的性质,⽐较下列积分的⼤⼩:(1)2()D x y d σ+??与3()Dx y d σ+??,其中积分区域D 是圆周22(2)(1)2x y -+-=所围成;(2)ln()Dx y d σ+??与2[ln()]Dx y d σ+??,其中D 是三⾓形闭区域,三顶点分别为(1,0),(1,1),(2,0);2.利⽤⼆重积分的性质估计下列积分的值:(1)22sin sin DI x yd σ=,其中{(,)|0,0}D x y x y ππ=≤≤≤≤;(2)22(49)DI x y d σ=++??,其中22{(,)|4}D x y x y =+≤.(3).DI =,其中{(,)|01,02}D x y x y =≤≤≤≤解 (),f x y =Q 2,在D 上(),f x y 的最⼤值()14M x y ===,最⼩值()11,25m x y ====故0.40.5I ≤≤习题10-2 ⼆重积分的计算法1.计算下列⼆重积分:(1)22()Dx y d σ+??,其中{(,)|||1,||1}D x y x y =≤≤;(2)cos()Dx x y d σ+??,其中D 是顶点分别为(0,0),(,0)π和(,)ππ的三⾓形闭区域。
2.画出积分区域,并计算下列⼆重积分:(1)x y De d σ+??,其中{(,)|||1}D x y x y =+≤(2)22()Dxy x d σ+-??,其中D 是由直线2y =,y x =及2y x =所围成的闭区域。
3.化⼆重积分(,)DI f x y d σ=为⼆次积分(分别列出对两个变量先后次序不同的两个⼆次积分),其中积分区域D 是:(1)由直线y x =及抛物线24y x =所围成的闭区域;(2)由直线y x =,2x =及双曲线1(0)y x x=>所围成的闭区域。



习题9-11. 设有一平面薄板(不计其厚度), 占有xOy 面上的闭区域D , 薄板上分布有密度为μ =μ(x , y )的电荷, 且μ(x , y )在D 上连续, 试用二重积分表达该板上全部电荷Q .解 板上的全部电荷应等于电荷的面密度μ(x , y )在该板所占闭区域D 上的二重积分⎰⎰=Dd y x Q σμ),(.2. 设⎰⎰+=13221)(D d y x I σ, 其中D 1={(x , y )|-1≤x ≤1, -2≤y ≤2};又⎰⎰+=23222)(D d y x I σ, 其中D 2={(x , y )|0≤x ≤1, 0≤y ≤2}.试利用二重积分的几何意义说明I 1与I 2的关系.解 I 1表示由曲面z =(x 2+y 2)3与平面x =±1, y =±2以及z =0围成的立体V 的体积.I 2表示由曲面z =(x 2+y 2)3与平面x =0, x =1, y =0, y =2以及z =0围成的立体V 1的体积.显然立体V 关于yOz 面、xOz 面对称, 因此V 1是V 位于第一卦限中的部分, 故V =4V 1, 即I 1=4I 2.3. 利用二重积分的定义证明: (1)⎰⎰=Dd σσ (其中σ为D 的面积);证明 由二重积分的定义可知,⎰⎰∑=→∆=Dni iiif d y x f 1),(lim ),(σηξσλ其中∆σi 表示第i 个小闭区域的面积. 此处f (x , y )=1, 因而f (ξ, η)=1, 所以,σσσσλλ==∆=→=→⎰⎰∑01lim lim Dni id .(2)⎰⎰⎰⎰=DDd y x f k d y x kf σσ),(),( (其中k 为常数);证明∑⎰⎰∑=→=→∆=∆=ni i i i Dni iiif k kf d y x kf 11),(lim ),(lim ),(σηξσηξσλλ⎰⎰∑=∆==→Dn i i i i d y x f k f k σσηξλ),(),(lim 10. (3)⎰⎰⎰⎰⎰⎰+=21),(),(),(D DD d y x f d y x f d y x f σσσ,其中D =D 1⋃D 2, D 1、D 2为两个无公共内点的闭区域.证明 将D 1和D 2分别任意分为n 1和n 2个小闭区域1i σ∆和2i σ∆, n 1+n 2=n , 作和∑∑∑===∆+∆=∆2222211111111),(),(),(n i i i i n i i i i ni iiif f f σηξσηξσηξ.令各1i σ∆和2i σ∆的直径中最大值分别为λ1和λ2, 又λ=ma x (λ1λ2), 则有∑=→∆ni i i i f 10),(lim σηξλ∑∑=→=→∆+∆=22222211111111),(lim ),(lim n i i i i n i i i i f f σηξσηξλλ,即 ⎰⎰⎰⎰⎰⎰+=21),(),(),(D D Dd y x f d y x f d y x f σσσ.4. 根据二重积分的性质, 比较下列积分大小:(1)⎰⎰+Dd y x σ2)(与⎰⎰+Dd y x σ3)(, 其中积分区域D 是由x 轴, y 轴与直线x +y =1所围成;解 区域D 为: D ={(x , y )|0≤x , 0≤y , x +y ≤1}, 因此当(x , y )∈D 时, 有(x +y )3≤(x +y )2, 从而⎰⎰+Dd y x σ3)(≤⎰⎰+Dd y x σ2)(. (2)⎰⎰+Dd y x σ2)(与⎰⎰+Dd y x σ3)(, 其中积分区域D 是由圆周(x -2)2+(y -1)2=2所围成;解 区域D 如图所示, 由于D 位于直线x +y =1的上方, 所以当(x , y )∈D 时, x +y ≥1, 从而(x +y )3≥(x +y )2, 因而⎰⎰⎰⎰+≤+DDd y x d y x σσ32)()(. (3)⎰⎰+Dd y x σ)ln(与⎰⎰+Dd y x σ3)(, 其中D 是三角形闭区域, 三角顶点分别为(1, 0), (1, 1), (2, 0);解 区域D 如图所示, 显然当(x , y )∈D 时, 1≤x +y ≤2, 从而0≤ln(x +y )≤1, 故有[ln(x +y )]2≤ ln(x +y ), 因而⎰⎰⎰⎰+≥+DDd y x d y x σσ)ln()][ln(2. (4)⎰⎰+Dd y x σ)ln(与⎰⎰+Dd y x σ3)(, 其中D ={(x , y )|3≤x ≤5. 0≤y ≤1}.解 区域D 如图所示, 显然D 位于直线x +y =e 的上方, 故当(x , y )∈D 时, x +y ≥e , 从而ln(x +y )≥1, 因而 [ln(x +y )]2≥ln(x +y ), 故⎰⎰⎰⎰+≤+DDd y x d y x σσ2)][ln()ln(. 5. 利用二重积分的性质估计下列积分的值: (1)⎰⎰+=Dd y x xy I σ)(, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解 因为在区域D 上0≤x ≤1, 0≤y ≤1, 所以 0≤xy ≤1, 0≤x +y ≤2, 进一步可得0≤xy (x +y )≤2, 于是⎰⎰⎰⎰⎰⎰≤+≤DDDd d y x xy d σσσ2)(0,即 ⎰⎰≤+≤Dd y x xy 2)(0σ.(2)⎰⎰=Dyd x I σ22sin sin , 其中D ={(x , y )| 0≤x ≤π, 0≤y ≤π};解 因为0≤sin 2x ≤1, 0≤sin 2y ≤1, 所以0≤sin 2x sin 2y ≤1. 于是⎰⎰⎰⎰⎰⎰≤≤DDDd yd x d σσσ1sin sin 022, 即 ⎰⎰≤≤Dyd x 222sin sin 0πσ.(3)⎰⎰++=Dd y x I σ)1(, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤2};解 因为在区域D 上, 0≤x ≤1, 0≤y ≤2, 所以1≤x +y +1≤4, 于是⎰⎰⎰⎰⎰⎰≤++≤DDDd d y x d σσσ4)1(,即 ⎰⎰≤++≤Dd y x 8)1(2σ.(4)⎰⎰++=Dd y x I σ)94(22, 其中D ={(x , y )| x 2+y 2 ≤4}.解 在D 上, 因为0≤x 2+y 2≤4, 所以 9≤x 2+4y 2+9≤4(x 2+y 2)+9≤25. 于是⎰⎰⎰⎰⎰⎰≤++≤DDDd d y x d σσσ25)94(922, ⎰⎰⋅⋅≤++≤Dd y x 2222225)94(29πσπ,即 ⎰⎰≤++≤Dd y x πσπ100)94(3622.习题9-21. 计算下列二重积分:(1)⎰⎰+Dd y x σ)(22, 其中D ={(x , y )| |x |≤1, |y |≤1};解 积分区域可表示为D : -1≤x ≤1, -1≤y ≤1. 于是⎰⎰+Dd y x σ)(22y d y x dx ⎰⎰--+=111122)(x d y y x ⎰--+=111132]31[ x d x ⎰-+=112)312(113]3232[-+=x x 38=. (2)⎰⎰+Dd y x σ)23(, 其中D 是由两坐标轴及直线x +y =2所围成的闭区域:解 积分区域可表示为D : 0≤x ≤2, 0≤y ≤2-x . 于是⎰⎰+Dd y x σ)23(y d y x dx x⎰⎰-+=2020)23(dx y xy x ⎰-+=222]3[ dx x x ⎰-+=202)224(0232]324[x x x -+=320=. (3)⎰⎰++Dd y y x x σ)3(223, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解⎰⎰++Dd y y x x σ)3(323⎰⎰++=1032310)3(dx y y x x dy ⎰++=1001334]4[dy x y y x x⎰++=103)41(dy y y 0142]424[y y y ++=1412141=++=.(4)⎰⎰+Dd y x x σ)cos(, 其中D 是顶点分别为(0, 0), (π, 0), 和(π, π)的三角形闭区域.解 积分区域可表示为D : 0≤x ≤π, 0≤y ≤x . 于是,⎰⎰+D d y x x σ)cos(⎰⎰+=x dy y x xdx 00)cos(π⎰+=π)][sin(dx y x x x⎰-=π0)sin 2(sin dx x x x ⎰--=π0)cos 2cos 21(x x xd+--=0|)cos 2cos 21(πx x x dx x x ⎰-π0)cos 2cos 21(π23-=. .2. 画出积分区域, 并计算下列二重积分:(1)⎰⎰Dd y x σ, 其中D 是由两条抛物线x y =, 2x y =所围成的闭区域;解 积分区域图如, 并且D ={(x , y )| 0≤x ≤1, x y x ≤≤2}. 于是⎰⎰D d y xσ⎰⎰=102dy y x dx xx⎰=10223]32[dx y x x x 556)3232(10447=-=⎰dx x x .(2)⎰⎰Dd xy σ2, 其中D 是由圆周x 2+y 2=4及y 轴所围成的右半闭区域; 解 积分区域图如, 并且D ={(x , y )| -2≤y ≤2, 240y x -≤≤}. 于是⎰⎰⎰⎰⎰----=22402240222222]21[dy y x dx xy dy d xy y y Dσ1564]10132[)212(22225342=-=-=--⎰y y dy y y . (3)⎰⎰+Dy x d e σ, 其中D ={(x , y )| |x |+|y |≤1};解 积分区域图如, 并且D ={(x , y )| -1≤x ≤0, -x -1≤y ≤x +1}⋃{(x , y )| 0≤x ≤1, x -1≤y ≤-x +1}. 于是⎰⎰⎰⎰⎰⎰+--+---++=11101101x x y x x x y x Dy x dy e dx e dy e dx e d e σ⎰⎰+---+--+=1110111][][dy e e dx e e x x y x x x y x ⎰⎰---+-+-=11201112)()(dx e e dx e ex x 101201112]21[]21[---+-+-=x x e ex x e e =e -e -1. (4)⎰⎰-+Dd x y x σ)(22, 其中D 是由直线y =2, y =x 及y =2x 轴所围成的闭区域.解 积分区域图如, 并且D ={(x , y )| 0≤y ≤2, y x y ≤≤21}. 于是⎰⎰⎰⎰⎰-+=-+=-+2022232222022]2131[)()(dy x x y x dx x y x dy d x y x y y y y Dσ613)832419(2023=-=⎰dy y y .3. 如果二重积分⎰⎰Ddxdy y x f ),(的被积函数f (x , y )是两个函数f 1(x )及f 2(y )的乘积,即f (x , y )= f 1(x )⋅f 2(y ), 积分区域D ={(x , y )| a ≤x ≤b , c ≤ y ≤d }, 证明这个二重积分等于两个单积分的乘积, 即 ])([])([)()(2121dy y f dx x f dxdy y f x f dcb aD⎰⎰⎰⎰⋅=⋅证明dx dy y f x f dy y f x f dx dxdy y f x f dcb a d cb aD⎰⎰⎰⎰⎰⎰⋅=⋅=⋅])()([)()()()(212121,而 ⎰⎰=⋅dcdcdy y f x f dy y f x f )()()()(2121,故dx dy y f x f dxdy y f x f b adcD⎰⎰⎰⎰=⋅])()([)()(2121.由于⎰dcdy y f )(2的值是一常数, 因而可提到积分号的外面, 于是得])([])([)()(2121dy y f dx x f dxdy y f x f dcb a D⎰⎰⎰⎰⋅=⋅4. 化二重积分⎰⎰=Dd y x f I σ),(为二次积分(分别列出对两个变量先后次序不同的两个二次积分), 其中积分区域D 是:(1)由直线y =x 及抛物线y 2=4x 所围成的闭区域; 解积分区域如图所示, 并且D ={(x , y )|x y x x 2 ,40≤≤≤≤}, 或D ={(x , y )| y x y y ≤≤≤≤241 ,40},所以 ⎰⎰=xxdy y x f dx I 240),(或⎰⎰=yy dx y x f dy I 4402),(.(2)由x 轴及半圆周x 2+y 2=r 2(y ≥0)所围成的闭区域; 解积分区域如图所示, 并且D ={(x , y )|220 ,x r y r x r -≤≤≤≤-},或D ={(x , y )| 2222 ,0y r x y r r y -≤≤--≤≤}, 所以 ⎰⎰--=220),(x r rr dy y x f dx I , 或⎰⎰---=2222),(0y r y r r dx y x f dy I .(3)由直线y =x , x =2及双曲线x y 1=(x >0)所围成的闭区域;解积分区域如图所示, 并且D ={(x , y )|x y xx ≤≤≤≤1 ,21},或D ={(x , y )| 21 ,121≤≤-≤≤x y y }⋃{(x , y )|2 ,21≤≤≤≤x y y },所以 ⎰⎰=x xdy y x f dx I 1),(21, 或⎰⎰⎰⎰+=22121121),(),(yydx y x f dy dx y x f dy I .(4)环形闭区域{(x , y )| 1≤x 2+y 2≤4}.解 如图所示, 用直线x =-1和x =1可将积分区域D 分成四部分, 分别记做D 1, D 2,D 3, D 4. 于是⎰⎰⎰⎰⎰⎰⎰⎰+++=4321),(),(),(),(D D D D d y x f d y x f d y x f d y x f I σσσσ⎰⎰⎰⎰--------+=222244411112),(),(x x x x dy y x f dx dy y x f dx ⎰⎰⎰⎰--------++222214442111),(),(x x x x dy y x f dx dy y x f dx用直线y =1, 和y =-1可将积分区域D 分成四部分, 分别记做D 1, D 2, D 3, D 4, 如图所示. 于是⎰⎰⎰⎰⎰⎰⎰⎰+++=4321),(),(),(),(D D D D d y x f d y x f d y x f d y x f I σσσσ⎰⎰⎰⎰--------+=222244141121),(),(y y y y dx y x f dy dx y x f dy⎰⎰⎰⎰--------++222241441211),(),(y y y y dx y x f dy dx y x f dy5. 设f (x , y )在D 上连续, 其中D 是由直线y =x 、y =a 及x =b (b >a )围成的闭区域, 证明:⎰⎰⎰⎰=bybaxabadx y x f dy dy y x f dx ),(),(.证明 积分区域如图所示, 并且积分区域可表示为 D ={(x , y )|a ≤x ≤b , a ≤y ≤x }, 或D ={(x , y )|a ≤y ≤b , y ≤x ≤b }. 于是⎰⎰Dd y x f σ),(⎰⎰=x a b a dy y x f dx ),(, 或⎰⎰Dd y x f σ),(⎰⎰=by b a dx y x f dy ),(.因此⎰⎰⎰⎰=byb ax abadx y x f dy dy y x f dx ),(),(.6. 改换下列二次积分的积分次序: (1)⎰⎰ydx y x f dy 01),(;解 由根据积分限可得积分区域D ={(x , y )|0≤y ≤1, 0≤x ≤y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤1, x ≤y ≤1}, 所以⎰⎰⎰⎰=1101),(),(xy dy y x f dx dx y x f dy .(2)⎰⎰y ydx y x f dy 2202),(;解 由根据积分限可得积分区域D ={(x , y )|0≤y ≤2, y 2≤x ≤2y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤4, x y x ≤≤2}, 所以⎰⎰y ydx y x f dy 222),(⎰⎰=402),(xx dy y x f dx .(3)⎰⎰---221110),(y y dx y x f dy ;解 由根据积分限可得积分区域}11 ,10|),{(22y x y y y x D -≤≤--≤≤=, 如图. 因为积分区域还可以表示为}10 ,11|),{(2x y x y x D -≤≤≤≤-=, 所以⎰⎰⎰⎰-----=22210111110),(),(x y ydy y x f dx dx y x f dy(4)⎰⎰--21222),(x x xdy y x f dx ;解 由根据积分限可得积分区域}22 ,21|),{(2x x y x x y x D -≤≤-≤≤=, 如图. 因为积分区域还可以表示为}112 ,10|),{(2y x y y y x D -+≤≤-≤≤=, 所以⎰⎰--21222),(x x x dy y x f dx ⎰⎰-+-=11122),(y ydx y x f dy .(5)⎰⎰e xdy y x f dx 1ln 0),(;解 由根据积分限可得积分区域D ={(x , y )|1≤x ≤e , 0≤y ≤ln x }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤y ≤1, e y ≤x ≤ e }, 所以⎰⎰e xdy y x f dx 1ln 0),(⎰⎰=10),(eey dx y x f dy(6)⎰⎰-xxdy y x f dx sin 2sin 0),(π(其中a ≥0).解 由根据积分限可得积分区域}sin 2sin ,0|),{(x y x x y x D ≤≤-≤≤=π, 如图.因为积分区域还可以表示为}arcsin 2 ,01|),{(π≤≤-≤≤-=x y y y x D}arcsin arcsin ,10|),{(y x y y y x -≤≤≤≤⋃π, 所以⎰⎰⎰⎰⎰⎰----+=yyyxxdx y x f dy dx y x f dy dy y x f dx arcsin arcsin 10arcsin 201sin 2sin 0),(),(),(πππ.7. 设平面薄片所占的闭区域D 由直线x +y =2, y =x 和x 轴所围成, 它的面密度为μ(x , y )=x 2+y 2, 求该薄片的质量. 解 如图, 该薄片的质量为⎰⎰=D d y x M σμ),(⎰⎰+=Dd y x σ)(22⎰⎰-+=10222)(yydx y x dy⎰-+-=10323]372)2(31[dy y y y 34=.8. 计算由四个平面x =0, y =0, x =1, y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体的体积.解 四个平面所围成的立体如图, 所求体积为 ⎰⎰--=Ddxdy y x V )326(⎰⎰--=101)326(dy y x dx⎰--=10102]2326[dx y xy y ⎰=-=1027)229(dx x .9. 求由平面x =0, y =0, x +y =1所围成的柱体被平面z =0及抛物面x 2+y 2=6-z 截得的立体的体积.解 立体在xOy 面上的投影区域为D ={(x , y )|0≤x ≤1, 0≤y ≤1-x }, 所求立体的体积为以曲面z =6-x 2-y 2为顶, 以区域D 为底的曲顶柱体的体积, 即⎰⎰--=Dd y x V σ)6(22⎰⎰---=101022)6(xdy y x dx 617=.10. 求由曲面z =x 2+2y 2及z =6-2x 2-y 2所围成的立体的体积.解 由⎩⎨⎧--=+=2222262y x z y x z 消去z , 得x 2+2y 2=6-2x 2-y 2, 即x 2+y 2=2, 故立体在x O y 面上的投影区域为x 2+y 2≤2, 因为积分区域关于x 及y 轴均对称, 并且被积函数关于x , y都是偶函数, 所以⎰⎰+---=Dd y x y x V σ)]2()26[(2222⎰⎰--=Dd y x σ)336(22⎰⎰---=2202220)2(12x dy y x dx π6)2(8232=-=⎰dx x .11. 画出积分区域, 把积分⎰⎰Ddxdy y x f ),(表示为极坐标形式的二次积分, 其中积分区域D 是:(1){(x , y )| x 2+y 2≤a 2}(a >0);解积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤a }, 所以⎰⎰⎰⎰=D Dd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (d f d a.(2){(x , y )|x 2+y 2≤2x };解 积分区域D 如图. 因为}cos 20 ,22|),{(θρπθπθρ≤≤≤≤-=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰-=22cos 20)sin ,cos (ππθρρθρθρθd f d .(3){(x , y )| a 2≤x 2+y 2≤b 2}, 其中0<a <b ;解 积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以⎰⎰⎰⎰=D Dd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (bad f d .(4){(x , y )| 0≤y ≤1-x , 0≤x ≤1}.解 积分区域D 如图. 因为}sin cos 10 ,20|),{(θθρπθθρ+≤≤≤≤=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰+=θθρρθρθρθπsin cos 1020)sin ,cos (d f d .12. 化下列二次积分为极坐标形式的二次积分: (1)⎰⎰11),(dy y x f dx ;解 积分区域D 如图所示. 因为}csc 0 ,24|),{(}sec 0 ,40|),{(θρπθπθρθρπθθρ≤≤≤≤⋃≤≤≤≤=D ,所以⎰⎰⎰⎰⎰⎰==DDd d f d y x f dy y x f dx θρρθρθρσ)sin ,cos (),(),(0⎰⎰=4sec 0)sin ,cos (πθρρθρθρθd f d ⎰⎰+24csc 0)sin ,cos (ππθρρθρθρθd f d .(2)⎰⎰+xxdy y x f dx 3222)(;解 积分区域D 如图所示, 并且 }sec 20 ,34|),{(θρπθπθρ≤≤≤≤=D ,所示⎰⎰⎰⎰⎰⎰=+=+xxDDd d f d y x f dy y x f dx 3222220)()()(θρρρσ⎰⎰=34sec 20)(ππθρρρθd f d .(3)⎰⎰--2111),(x xdy y x f dx ;解 积分区域D 如图所示, 并且}1sin cos 1 ,20|),{(≤≤+≤≤=ρθθπθθρD ,所以⎰⎰⎰⎰⎰⎰--==10112)sin ,cos (),(),(x xDDd d f d y x f dy y x f dx θρρθρθρσ⎰⎰+=2sin cos 101)sin ,cos (πθθρρθρθρθd f d(4)⎰⎰21),(x dy y x f dx .解 积分区域D 如图所示, 并且}sec tan sec ,40|),{(θρθθπθθρ≤≤≤≤=D ,所以⎰⎰210),(x dy y x f dx ⎰⎰⎰⎰==DDd d f d y x f θρρθρθρσ)sin ,cos (),(⎰⎰=40sec tan sec )sin ,cos (πθθθρρθρθρθd f d13. 把下列积分化为极坐标形式, 并计算积分值: (1)⎰⎰-+2202220)(x ax ady y x dx ;解 积分区域D 如图所示. 因为}cos 20 ,20|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰-+2202220)(x ax ady y x dx ⎰⎰⋅=Dd d θρρρ2⎰⎰⋅=20cos 202πθρρρθa d d ⎰=2044cos 4πθθd a 443a π=.(2)⎰⎰+dy y x dx 0220;解 积分区域D 如图所示. 因为}sec 0 ,40|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰⎰⎰⋅=+Dxad d dy y x dx θρρρ0220⎰⎰⋅=40sec 0πθρρρθa d d ⎰=4033sec 3πθθd a )]12ln(2[63++=a .(3)⎰⎰-+xxdy y xdx 2212210)(;解 积分区域D 如图所示. 因为}tan sec 0 ,40|),{(θθρπθθρ≤≤≤≤=D , 所以⎰⎰⎰⎰⋅=+--Dxx d d dy y xdx θρρρ212122102)(12tan sec 40tan sec 02140-==⋅=⎰⎰⎰-πθθπθθθρρρθd d d .(4)⎰⎰-+220220)(y a a dx y x dy .解 积分区域D 如图所示. 因为}0 ,20|),{(a D ≤≤≤≤=ρπθθρ, 所以⎰⎰⎰⎰⋅=+-Dy a ad d dx y x dy θρρρ2022022)(420028a d d aπρρρθπ=⋅=⎰⎰.14. 利用极坐标计算下列各题: (1)⎰⎰+Dy xd e σ22,其中D 是由圆周x 2+y 2=4所围成的闭区域;解 在极坐标下D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤2}, 所以⎰⎰⎰⎰=+DDy x d d e d e θρρσρ222)1()1(2124420202-=-⋅==⎰⎰e e d e d ππρρθπρ. (2)⎰⎰++Dd y x σ)1ln(22,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解 在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰+=++DDd d d y x θρρρσ)1ln()1ln(222)12ln 2(41)12ln 2(212)1ln(2012-=-⋅=+=⎰⎰πρρρθπd d .(3)σd xyDarctan⎰⎰, 其中D 是由圆周x 2+y 2=4, x 2+y 2=1及直线y =0, y =x 所围成的第一象限内的闭区域.解 在极坐标下}21 ,40|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⎰⎰⋅=⋅=DDDd d d d d xyθρρθθρρθσ)arctan(tan arctan⎰⎰⋅=4021πρρθθd d ⎰⎰==40321643ππρρθθd d . 15. 选用适当的坐标计算下列各题:(1)dxdy yx D 22⎰⎰,其中D 是由直线x =2,y =x 及曲线xy =1所围成的闭区域.解 因为积分区域可表示为}1 ,21|),{(x y xx y x D ≤≤≤≤=, 所以dxdy yx D 22⎰⎰dy y dx x x x ⎰⎰=211221⎰-=213)(dx x x 49=.(2)⎰⎰++--Dd yx y x σ222211, 其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解 在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⋅+-=++--DD d d d y x y x θρρρρσ2222221111)2(811102220-=+-=⎰⎰ππρρρρθπd d .(3)⎰⎰+Dd y x σ)(22, 其中D 是由直线y =x , y =x +a , y =a , y =3a (a >0)所围成的闭区域;解 因为积分区域可表示为D ={(x , y )|a ≤y ≤3a , y -a ≤x ≤y }, 所以⎰⎰+D d y x σ)(22⎰⎰-+=a a ya y dx y x dy 322)(4332214)312(a dy a y a ay a a =+-=⎰.(4)σd y x D22+⎰⎰, 其中D 是圆环形闭区域{(x , y )| a 2≤x 2+y 2≤b 2}.解 在极坐标下D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以 σd y x D22+⎰⎰)(3233202a b dr r d b a -==⎰⎰πθπ.16. 设平面薄片所占的闭区域D 由螺线ρ=2θ上一段弧(20πθ≤≤)与直线2πθ=所围成, 它的面密度为μ(x , y )=x 2+y 2. 求这薄片的质量.解 区域如图所示. 在极坐标下}20 ,20|),{(θρπθθρ≤≤≤≤=D , 所以所求质量⎰⎰⎰⎰⋅==Dd d d y x M 20202),(πθρρρθσμ⎰==254404ππθθd .17. 求由平面y =0, y =kx (k >0), z =0以及球心在原点、半径为R 的上半球面所围成的在第一卦限内的立体的体积.解 此立体在xOy 面上的投影区域D ={(x , y )|0≤θ≤arctan k , 0≤ρ≤R }.⎰⎰--=D dxdy y x R V 222k R d R d k Rarctan 313arctan 0022=-=⎰⎰ρρρθ.18. 计算以xOy 平面上圆域x 2+y 2=ax 围成的闭区域为底, 而以曲面z =x 2+y 2为顶的曲顶柱体的体积.解 曲顶柱体在xOy 面上的投影区域为D ={(x , y )|x 2+y 2≤ax }. 在极坐标下}cos 0 ,22|),{(θρπθπθρa D ≤≤≤≤-=, 所以⎰⎰≤++=axy x dxdy y xV 22)(22πθθρρρθππθππ422cos 022442323cos 4a d a d d a ==⋅=⎰⎰⎰--. 习题9-31. 化三重积分dxdydz z y x f I ),,(Ω⎰⎰⎰=为三次积分, 其中积分区域Ω分别是:(1)由双曲抛物面xy =z 及平面x +y -1=0, z =0所围成的闭区域; 解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤xy , 0≤y ≤1-x , 0≤x ≤1}, 于是 ⎰⎰⎰-=xyx dz z y x f dy dx I 01010),,(.(2)由曲面z =x 2+y 2及平面z =1所围成的闭区域; 解 积分区域可表示为}11 ,11 ,1|),,{(2222≤≤--≤≤--≤≤+=Ωx x y x z y x z y x , 于是 ⎰⎰⎰+----=111112222),,(y x x x dz z y x f dy dx I .(3)由曲面z =x 2+2y 2及z =2-x 2所围成的闭区域;解 曲积分区域可表示为}11 ,11 ,22|),,{(22222≤≤--≤≤---≤≤+=Ωx x y x x z y x z y x , 于是 ⎰⎰⎰-+----=22222221111),,(x y x x x dz z y x f dy dx I .提示: 曲面z =x 2+2y 2与z =2-x 2的交线在xOy 面上的投影曲线为x 2+y 2=1.(4)由曲面cz =xy (c >0), 12222=+by a x , z =0所围成的在第一卦限内的闭区域. 解 曲积分区域可表示为}0 ,0 ,0|),,{(22a x x a a b y c xyz z y x ≤≤-≤≤≤≤=Ω,于是 ⎰⎰⎰-=cxy abdz z y x f dy dx I x a a0),,(22.提示: 区域Ω的上边界曲面为曲面c z =xy , 下边界曲面为平面z =0.2. 设有一物体, 占有空间闭区域Ω={(x , y , z )|0≤x ≤1, 0≤y ≤1, 0≤z ≤1}, 在点(x , y , z )处的密度为ρ(x , y , z )=x +y +z , 计算该物体的质量.解 ⎰⎰⎰⎰⎰⎰++==Ω101010)(dz z y x dy dx dxdydz M ρ⎰⎰++=1010)21(dy y x dx⎰⎰+=++=1010102)1(]2121[dx x dx y y xy 23)1(21102=+=x .3. 如果三重积分dxdydz z y x f ),,(Ω⎰⎰⎰的被积函数f (x , y , z )是三个函数f 1(x )、f 2(y )、f 3(z )的乘积, 即f (x , y , z )= f 1(x )⋅f 2(y )⋅f 3(z ), 积分区域Ω={(x , y , z )|a ≤x ≤b , c ≤y ≤d , l ≤z ≤m }, 证明这个三重积分等于三个单积分的乘积, 即⎰⎰⎰⎰⎰⎰=Ωmldcbadz z f dy y f dx x f dxdydz z f y f x f )()()()()()(321321.证明dxdydz z f y f x f )()()(321Ω⎰⎰⎰dx dy dz z f y f x f b a d c ml]))()()(([321⎰⎰⎰=dx dy dz z f y f x f ba dc ml]))()()(([321⎰⎰⎰=⎰⎰⎰=mldcbadx dy y f dz z f x f )])()()()([(231dx x f dy y f dz z f b a mldc)]())()()([(123⎰⎰⎰=⎰⎰⎰=d cbam ldx x f dy y f dz z f )())()()((123 ⎰⎰⎰=dcmlbadz z f dy y f dx x f )()()(321.4. 计算dxdydz z xy 32Ω⎰⎰⎰, 其中Ω是由曲面z =xy , 与平面y =x , x =1和z =0所围成的闭区域.解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤xy , 0≤y ≤x , 0≤x ≤1}, 于是dxdydz z xy 32Ω⎰⎰⎰⎰⎰⎰=xyxdz z dy y xdx 030210⎰⎰=xxy dy z y xdx 004210]4[⎰⎰=x dy y dx x 051054136412811012==⎰dx x .5. 计算3)1(z y x dxdydz+++Ω⎰⎰⎰, 其中Ω为平面x =0, y =0, z =0, x +y +z =1所围成的四面体. 解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤1-x -y , 0≤y ≤1-x , 0≤x ≤1},于是 3)1(z y x dxdydz +++Ω⎰⎰⎰⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰--++=x dy y x dx 10210]81)1(21[dx x x ⎰+-+=10]8183)1(21[)852(ln 21-=.提示: ⎰⎰⎰Ω+++3)1(z y x dxdydz ⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰---+++-=xyx dy z y x dx 1010210])1(21[⎰⎰--++=x dy y x dx 10210]81)1(21[ dx y y x x -⎰-++-=1010]81)1(21[dx x x ⎰+-+=10]8183)1(21[ 102]16183)1ln(21[x x x +-+= )852(ln 21-=.6. 计算xyzdxdydz Ω⎰⎰⎰, 其中Ω为球面x 2+y 2+z 2=1及三个坐标面所围成的在第一卦限内的闭区域.解 积分区域可表示为}10 ,10 ,10|),,{(222≤≤-≤≤--≤≤=Ωx x y y x z z y x 于是xyzdxdydz Ω⎰⎰⎰⎰⎰⎰---=222101010x y x xyzdz dy dx⎰⎰---=210221)1(21x dy y x xy dx ⎰-=1022)1(81dx x x 481=.7. 计算xzdxdydz Ω⎰⎰⎰, 其中Ω是由平面z =0, z =y , y =1以及抛物柱面y =x 2所围成的闭区域.解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤y , x 2≤y ≤1, -1≤x ≤1}, 于是xzdxdydz Ω⎰⎰⎰⎰⎰⎰-=yx zdz dy xdx 01112⎰⎰-=1211221x dy y xdx 0)1(61116=-=⎰-dx x x .8. 计算zdxdydz Ω⎰⎰⎰, 其中Ω是由锥面22y x R h z +=与平面z =h (R >0, h >0)所围成的闭区域.解 当0≤z ≤h 时, 过(0, 0, z )作平行于xOy 面的平面, 截得立体Ω的截面为圆D z :222)(z h R y x =+, 故D z的半径为z h R , 面积为222z h R π, 于是 zdxdydz Ω⎰⎰⎰=dxdy zdz zD h ⎰⎰⎰0⎰==h h R dz z h R 0223224ππ. 9. 利用柱面坐标计算下列三重积分:(1)zdv Ω⎰⎰⎰, 其中Ω是由曲面222y x z --=及z =x 2+y 2所围成的闭区域;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ρ≤1, 222ρρ-≤≤z , 于是zdv Ω⎰⎰⎰⎰⎰⎰-=122022ρρπρρθzdz d d⎰--=1042)2(212ρρρρπdπρρρρπ127)2(1053=--=⎰d .(2)dv y x )(22+Ω⎰⎰⎰, 其中Ω是由曲面x 2+y 2=2z 及平面z =2所围成的闭区域.解 在柱面坐标下积分区域Ω可表示为0≤θ≤2π, 0≤ρ≤2, 222≤≤z ρ,于是dv y x)(22+Ω⎰⎰⎰dz d d θρρρ⋅=Ω⎰⎰⎰2⎰⎰⎰=22123202ρπρρθdz d d⎰⎰-=205320)212(ρρρθπd d ⎰==ππθ2031638d .10. 利用球面坐标计算下列三重积分:(1)dv z y x )(222++Ω⎰⎰⎰, 其中Ω是由球面x 2+y 2+z 2=1所围成的闭区域.解 在球面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ϕ≤π, 0≤r ≤1,于是 dv z y x )(222++Ω⎰⎰⎰θϕϕd drd r sin 4⋅=Ω⎰⎰⎰⎰⎰⎰=104020sin dr r d d ππϕϕθπ54=.(2)zdv Ω⎰⎰⎰, 其中闭区域Ω由不等式x 2+y 2+(z -a )2≤a 2, x 2+y 2≤z 2 所确定.解 在球面坐标下积分区域Ω可表示为 ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤,于是 zdv Ω⎰⎰⎰θϕϕϕd drd r r sin cos 2⋅=Ω⎰⎰⎰⎰⋅=404)cos 2(41cos sin 2πϕϕϕϕπd a4405467cos sin 8a d a πϕϕϕππ==⎰.11. 选用适当的坐标计算下列三重积分:(1)xydv Ω⎰⎰⎰, 其中Ω为柱面x 2+y 2=1及平面z =1, z =0, x =0, y =0所围成的在第一卦限内的闭区域;解 在柱面坐标下积分区域Ω可表示为 10 ,10 ,20≤≤≤≤≤≤z ρπθ,于是 xydv Ω⎰⎰⎰dz d d θρρθρθρ⋅⋅=Ω⎰⎰⎰sin cos⎰⎰⎰==101032081cos sin dz d d ρρθθθπ.别解: 用直角坐标计算⎰⎰⎰Ωxydv ⎰⎰⎰-=1010102dz ydy xdx x ⎰⎰-=21010x ydy xdx ⎰-=103)22(dx x x 81]84[1042=-=x x . (2)dv z y x 222++Ω⎰⎰⎰, 其中Ω是由球面x 2+y 2+z 2=z 所围成的闭区域;解 在球面坐标下积分区域Ω可表示为 ϕπϕπθcos 0 ,20 ,20≤≤≤≤≤≤r ,于是dv z y x 222++Ω⎰⎰⎰⎰⎰⎰⋅=ϕππϕϕθcos 022020sin dr r r d d10cos 41sin 2204πϕϕϕππ=⋅=⎰d .(3)dv y x )(22+Ω⎰⎰⎰, 其中Ω是由曲面4z 2=25(x 2+y 2)及平面z =5所围成的闭区域;解 在柱面坐标下积分区域Ω可表示为 525 ,20 ,20≤≤≤≤≤≤z ρρπθ,于是dv y x )(22+Ω⎰⎰⎰⎰⎰⎰=52520320ρπρρθdz d dπρρρπ8)255(2203=-=⎰d .(4)dv y x )(22+Ω⎰⎰⎰, 其中闭区域Ω由不等式A z y x a ≤++≤<2220, z ≥0所确定.解 在球面坐标下积分区域Ω可表示为A r a ≤≤≤≤≤≤ ,20 ,20πϕπθ,于是 dv y x )(22+Ω⎰⎰⎰θϕϕθϕϕϕd drd r r r sin )sin sin cos sin (2222222+=Ω⎰⎰⎰)(154sin 55420320a A dr r d d Aa-==⎰⎰⎰πϕϕθππ.12. 利用三重积分计算下列由曲面所围成的立体的体积:(1)z =6-x 2-y 2及22y x z +=;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2 π, 0≤ρ≤2, ρ≤z ≤6-ρ2,于是 dz d d dv V θρρΩΩ⎰⎰⎰⎰⎰⎰==⎰⎰⎰-=262020ρρπρρθdz d d⎰=--=2032332)6(2πρρρρπd .(2)x 2+y 2+z 2=2az (a >0)及x 2+y 2=z 2(含有z 轴的部分); 解 在球面坐标下积分区域Ω可表示为ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤,于是 θϕϕd drd r dv V sin 2ΩΩ⎰⎰⎰⎰⎰⎰==⎰⎰⎰=ϕππϕϕθcos 2024020sin a dr r d d34033sin cos 382a d a πϕϕϕππ==⎰. (3)22y x z +=及z =x 2+y 2;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ρ≤1, ρ2≤z ≤ρ,于是 6)(2103210202πρρρπρρθρρπ=-===⎰⎰⎰⎰⎰⎰⎰Ωd dz d d dv V .(4)225y x z --=及x 2+y 2=4z .解 在柱面坐标下积分区域Ω可表示为 22541 ,20 ,20ρρρπθ-≤≤≤≤≤≤z ,于是 ⎰⎰⎰-=22541220ρρπρρθdz d d V)455(32)45(22022-=--=⎰πρρρρπd .13. 球心在原点、半径为R 的球体, 在其上任意一点的密度的大小与这点到球心的距离成正比, 求这球体的质量.解 密度函数为222),,(z y x k z y x ++=ρ. 在球面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ϕ≤π, 0≤r ≤R ,于是 dv z y x k M 222++=Ω⎰⎰⎰40220sin R k dr r kr d d Rπϕϕθππ=⋅=⎰⎰⎰.习题9-41. 求球面x 2+y 2+z 2=a 2含在圆柱面x 2+y 2=ax 内部的那部分面积. 解 位于柱面内的部分球面有两块, 其面积是相同的.由曲面方程z =222y x a --得222y x a x x z ---=∂∂, 222y x a y y z ---=∂∂, 于是 dxdy yz x z A axy x ⎰⎰≤+∂∂+∂∂+=2222)()(12dxdy yx a a axy x ⎰⎰≤+--=222222⎰⎰-=20cos 02214πθρρρθa d a d a )2(2)sin (4220-=-=⎰πθθπa d a a a .2. 求锥面z =22y x +被柱面z 2=2x 所割下的部分的曲面的面积.解 由z =22y x +和z 2=2x 两式消z 得x 2+y 2=2x , 于是所求曲面在xOy 面上的投影区域D 为x 2+y 2≤2x .由曲面方程22y x +得22y x x x z +=∂∂, 22y x y y z +=∂∂, 于是 dxdy y z x z A y x ⎰⎰≤+-∂∂+∂∂+=1)1(2222)()(1π221)1(22==⎰⎰≤+-dxdy y x .3. 求底面半径相同的两个直交柱面x 2+y 2=R 2及x 2+z 2=R 2所围立体的表面积.解 设A 1为曲面22x R z -=相应于区域D : x 2+y 2≤R 2上的面积. 则所求表面积为A =4A 1.dxdy y z x z A D ⎰⎰∂∂+∂∂+=22)()(14dxdy x R x D ⎰⎰+--+=22220)(14dxdy x R R D⎰⎰-=2242221681422R dx R dy x R dx R R R R R xR x R ==-=⎰⎰⎰-------. 4. 设薄片所占的闭区域D 如下, 求均匀薄片的质心:(1)D 由px y 2=, x =x 0, y =0所围成;解 令密度为μ=1.因为区域D 可表示为px y x x 20 ,00≤≤≤≤, 所以 3002023220px dx px dy dx dxdy A x x px D====⎰⎰⎰⎰⎰, 0002053211100x dx px x A xdy dx A xdxdy A x x x px D====⎰⎰⎰⎰⎰,000208311100y pxdx A ydy dx A ydxdy A y x x px D====⎰⎰⎰⎰⎰,所求质心为)83 ,53(00y x(2)D 是半椭圆形闭区域}0 ,1 |),{(2222≥≤+y by a x y x ; 解 令密度为μ=1. 因为闭区域D 对称于y 轴, 所以0=x . ab dxdy A Dπ21==⎰⎰(椭圆的面积),π34)(21112222022b dx x a a b A ydy dx A ydxdy A y aa aa x a Dab=-⋅===⎰⎰⎰⎰⎰---, 所求质心为)34 ,0(πb .(3)D 是介于两个圆r =a cos θ, r =b cos θ(0<a <b )之间的闭区域. 解 令密度为μ=1. 由对称性可知0=y .)(4)2()2(2222a b a b dxdy A D-=-==⎰⎰πππ(两圆面积的差),)(2cos 212220cos cos b a ab b a dr r r d A xdxdy A x b a D+++=⋅⋅==⎰⎰⎰⎰πθθθθ, 所求质心是)0 ,)(2(22b a ab b a +++. 5. 设平面薄片所占的闭区域D 由抛物线y =x 2及直线y =x 所围成, 它在点(x , y )处的面密度μ(x , y )=x 2y , 求该薄片的质心.解 351)(21),(10641022=-===⎰⎰⎰⎰⎰dx x x ydy x dx dxdy y x M x x Dμ4835)(2111),(110751032=-===⎰⎰⎰⎰⎰dx x x M ydy x dx Mdxdy y x x M x x x Dμ, 5435)(3111),(1108510222=-===⎰⎰⎰⎰⎰dx x x Mdy y x dx Mdxdy y x y My x x Dμ, 质心坐标为)5435 ,4835(.6. 设有一等腰直角三角形薄片, 腰长为a , 各点处的面密度等于该点到直角顶点的距离的平方, 求这薄片的质心.解 建立坐标系, 使薄片在第一象限, 且直角边在坐标轴上. 薄片上点(x , y )处的函数为μ=x 2+y 2. 由对称性可知y x =.4022061)(),(a dy y x dx dxdy y x M xa a D=+==⎰⎰⎰⎰-μ,a dy y x xdx Mdxdy y x x M y x xa aD52)(1),(1220=+===⎰⎰⎰⎰-μ,薄片的质心坐标为)52 ,52(a a .7. 利用三重积分计算下列由曲面所围成立体的质心(设密度ρ=1): (1)z 2=x 2+y 2, z =1;解 由对称性可知, 重心在z 轴上, 故0==y x . π31==⎰⎰⎰Ωdv V (圆锥的体积),431120101===⎰⎰⎰⎰⎰⎰Ωπθr zdz rdr d V zdv V z ,所求立体的质心为)43 ,0 ,0(. (2)222y x A z --=, 222y x a z --=(A >a >0), z =0; 解 由对称性可知, 重心在z 轴上, 故0==y x .)(3232323333a A a A dv V -=-==⎰⎰⎰Ωπππ(两个半球体体积的差),)(8)(3cos sin 1cos sin 133442000332a A a A dr r d d V d drd r V z A --===⎰⎰⎰⎰⎰⎰Ωππϕϕϕθθϕϕϕ,所求立体的质心为))(8)(3 ,0 ,0(3344a A a A --.(3)z =x 2+y 2, x +y =a , x =0, y =0, z =0.解 ⎰⎰⎰-+=a xa y x dz dy dx V 0022⎰⎰-+=a xa dy y x dx 022)(⎰-+-=adx x a x a x 032])(31)([461a =,⎰⎰⎰Ω=xdv V x 1a a a dz dy xdx V a x a yx52611511450022===⎰⎰⎰-+,a x y 52==,⎰⎰⎰Ω=zdv V z 1⎰⎰⎰-+=a x a y x zdz dy dx V 0002212307a =,所以立体的重心为)307,52,52(2a a a .8. 设球体占有闭区域Ω={(x , y , z )|x 2+y 2+z 2≤2Rz }, 它在内部各点的密度的大小等于该点到坐标原点的距离的平方, 试求这球体的质心.解 球体密度为ρ=x 2+y 2+z 2. 由对称性可知质心在z 轴上, 即0==y x . 在球面坐标下Ω可表示为: ϕπϕπθcos 20 ,20 ,20R r ≤≤≤≤≤≤, 于是⎰⎰⎰⎰⎰⎰⋅==Ωππϕϕϕθρ2020cos 2022sin R dr r r d d dv M⎰=2055cos sin 5322πϕϕϕπd R 51532R π=,⎰⎰⎰⎰⎰⎰Ω==ππϕϕϕϕθρ2020cos 205cos sin 11R dr r d d M zdv Mz R r R d R M 45153238cos sin 6642562076===⎰ππϕϕϕππ,故球体的质心为)45 ,0 ,0(R .9. 设均匀薄片(面密度为常数1)所占闭区域D 如下, 求指定的转动惯量:(1)}1 |),{(2222≤+=by a x y x D , 求I y ; 解 积分区域D 可表示为22 ,x a ab y x a a b a x a -≤≤--≤≤-,于是 ⎰⎰⎰⎰⎰------===aa x a ab x a ab aaDy dx x a x a b dy dx x dxdy x I 2222222222b a 341π=.提示: 4202422282sin 2 sina tdt a t a x dx x a x aa ππ==-⎰⎰-. (2)D 由抛物线x y 292=与直线x =2所围成, 求I x 和I y ;解 积分区域可表示为2/32/3 ,20x y x x ≤≤-≤≤,于是 57222273220232/32/32202====⎰⎰⎰⎰⎰-dx x dy y dx dxdy y I Dx x x , 796262252/32/32022====⎰⎰⎰⎰⎰-dx x dy dx x dxdy x I Dx x y . (3)D 为矩形闭区域{(x , y )|0≤x ≤a , 0≤y ≤b }, 求I x 和I y .解 331330202ab b a dy y dx dxdy y I Db a x =⋅===⎰⎰⎰⎰,331330022b a b a dy dx x dxdy x I Dba y =⋅===⎰⎰⎰⎰.10. 已知均匀矩形板(面密度为常量μ)的长和宽分别为b 和h , 计算此矩形板对于通过其形心且分别与一边平行的两轴的转动惯量.。
《高等数学(二)》作业一、填空题1.点A (2,3,-4)在第 卦限。
2.设22(,)sin,(,)yf x y x xy y f tx ty x=--=则 .3。
4.设25(,),ff x y x y y x y∂=-=∂则。
5.设共域D 由直线1,0x y y x ===和所围成,则将二重积分(,)Df x y d σ⎰⎰化为累次积分得 。
6.设L 为连接(1,0)和(0,1)两点的直线段,则对弧长的曲线积分()Lx y ds +⎰= 。
7.平面2250x y z -++=的法向量是 。
8.球面2229x y z ++=与平面1x y +=的交线在0x y 面上的投影方程为 。
9.设22,z u v ∂=-=∂z而u=x-y,v=x+y,则x。
10.函数z =的定义域为 。
11.设n 是曲面22z x y =+及平面z=1所围成的闭区域,化三重积为(,,)nf x y z dx dy dz ⎰⎰⎰为三次积分,得到 。
12.设L 是抛物线2y x =上从点(0,0)到(2,4)的一段弧,则22()Lx y dx -=⎰。
13.已知两点12(1,3,1)(2,1,3)M M 和。
向量1212M M M M =的模 ;向量12M M 的方向余弦cos α= ,cos β= ,cos γ= 。
14.点M (4,-3,5)到x 轴的距离为 。
15.设sin ,cos ,ln ,dzz uv t u t v t dt=+===而则全导数。
16.设积分区域D 是:222(0)x y a a +≤>,把二重积分(,)Df x y dx dy ⎰⎰表示为极坐标形式的二次积分,得 。
17.设D 是由直线0,01x y x y ==+=和所围成的闭区域,则二重积分Dx d σ⎰⎰= 。
18.设L 为XoY 面内直线x=a 上的一段直线,则(,)Lp x y dx ⎰= 。
19.过点0000(,,)p x y z 作平行于z 轴的直线,则直线方程为 。