2015-2016学年四川岳池一中八年级数学学案：19.2《一次函数》(无答案)(新人教版下)

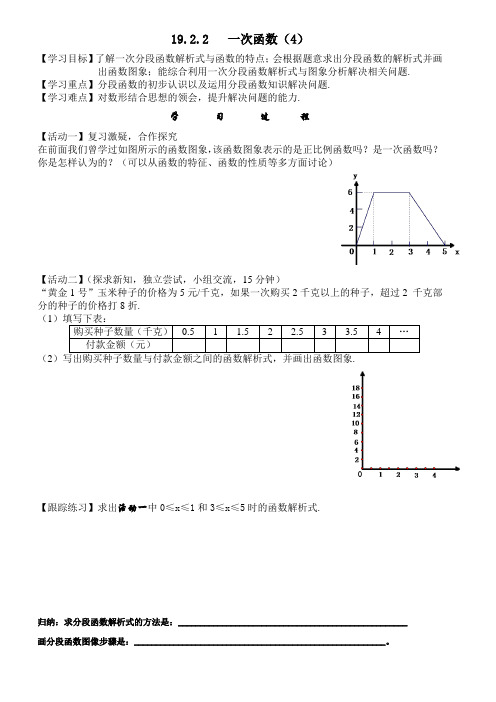
19.2.2 一次函数（4）【学习目标】了解一次分段函数解析式与函数的特点；会根据题意求出分段函数的解析式并画出函数图象；能综合利用一次分段函数解析式与图象分析解决相关问题.【学习重点】分段函数的初步认识以及运用分段函数知识解决问题.【学习难点】对数形结合思想的领会，提升解决问题的能力.学习过程【活动一】复习激疑，合作探究在前面我们曾学过如图所示的函数图象，该函数图象表示的是正比例函数吗？是一次函数吗？你是怎样认为的？（可以从函数的特征、函数的性质等多方面讨论）【活动二】（探求新知，独立尝试，小组交流，15分钟）“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2 千克部分的种子的价格打8折.（1购买种子数量（千克）0.5 1 1.5 2 2.5 3 3.5 4 …付款金额（元）（2【跟踪练习】求出活动一中0≤x≤1和3≤x≤5时的函数解析式.归纳：求分段函数解析式的方法是：____________________________________________________ 画分段函数图像步骤是：_________________________________________________________。

【活动三】巩固强化，独立尝试，小组交流1、为缓解用电紧张矛盾，某电力公司制定了新的用电收费标准，每月用电x（度）与应付电费y（元）的关系如图所示.（1）根据图象，请分别求出当0≤x≤50和x＞50，y与x的函数关系式.（2）当每月用电量不超过50度时，收费标准是_______；当每月用电量超过50度时，收费标准是_______.2、一个有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（升）与时间x（分）之间的关系如图所示.（1）求0≤x≤4时y随x变化的函数关系式.（2）求4≤x≤12时y随x变化的函数关系式.※（3）每分钟进水、出水各多少升？19.2.2一次函数（4）检测题1、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量较高，达到每毫升6微克，接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升中含药量y(微克)随着时间（小时）的变化如下图所示，当成人按规定剂量服药后，（1） 分别求出x ≤2和x ＞2时，y 与x 之间的函数关系式；（2） 如果每毫升血液中含药量为4微克或4微克以上时，治疗疾病是有效的，那么这个有效时间是多长？2、如图，某同学由甲地出发去乙地，去时以每小时6千米速度步行2小时到达乙地，在乙地耽搁一小时后，以每小时4千米的速度步行返回甲地.（1）分别指出图中点A 、B 、C 、D 各表示的数是什么？（2）试写出该同学在上述过程中离甲地的距离s （千米）和时间t （小时）的函数关系式，并求出自变量t的取值范围. A B C D。

19.2.2 —次函数（第1课时）教学设计河北省沽源县白土窑乡寄宿制学校郝小纲教学目标：1结合具体情境理解一次函数的意义，能结合实际问题中的数量关 系写出一次函数的解析式；2. 能辨别正比例函数与一次函数的区别与联系；3. 初步体会用待定系数法求一次函数解析式的方法.教学重点：一次函数的概念. 教学难点：一次函数的概念 教学过程： 一、温故而知新：1. 下列函数中哪些是正比例函数？、••82(1) y =「8x,(2)y=」(3)y=5x 6 (4)y =「0.5x -1x2⑹ y = —-13 (7)y =2(x-4)x问题1:某登山队大本营所在地的气温为 5 C.海拔每升高1 km气温下降6C,登山队员由大本营向上登高 x km 时，他们所在位置 的气温是y C.试用解析式表示y 与x 的关系.当登山队员由大本 营向上登高0.5km时，他们所在位置的气温是多少？ 三、新知探究问题2:下列问题中，变量之间的对应关系是函数关系吗？如果 是，请x ⑸ y — 一1（8）厂宁、情境引入写出函数解析式，这些函数解析式有哪些共同特征?(1)有人发现，在20 C〜25 C时蟋蟀每分鸣叫次数c与温度t (单位：C)有关，且c的值约是t的7倍与35的差；(2)一种计算成年人标准体重G (单位：kg )的方法是，以厘米为单位量出身高值h，再减常数105,所得差是G的值；(3)某城市的市内电话的月收费额y (单位：元)包括月租费22元和拨打电话x min 的计时费(按0.1元/min收取)；(4)把一个长10 cm,宽5 cm的矩形的长减少x cm，宽不变，矩形面积y (单位：cm2随x的值而变化.问题3观察以上出现的四个函数解析式，很显然它们不是正比例函数，那么它们有什么共同特征呢？1. 一次函数的定义：一般地，形如( ) 的函数叫一次函数.2. 注意：①常数k, b的要求：②当b = 0时，y=kx+b即( )所以说正比例函数是一种特殊的一次函数.辨一辨：1•下列函数中哪些函数是一次函数，哪些函数也是正比例函数？--8 2(1)y =「8x, (2)y=」(3)y=5x 6 (4)y =「0.5x-1xx 2 x—'3⑸y 1 (6)y 13 (7)y=2(x-4) (8)^- 32 x 2四、新知应用：例1.已知函数y = (k —2)x + 2k +1,若它是正比例函数，求k的值;若它是一次函数，求k的取值范围.例2: 一种移动通讯服务的收费标准为：每月基本服务费30元，每月免费通话时间为120分，以后每分收费0.4元。

一次函数（第1 课时）导学案【学习目标】１．掌握一次函数解析式的特点及意义．２．理解一次函数与正比例函数的关系．【重点难点】重点：理解和掌握一次函数解析式特点难点：一次函数与正比例函数关系的正确理解.【学习过程】一、自主学习：【问题1】问题：某登山队大本营所在地的气温为15℃，海拔每升高1km 气温下降6℃．登山队员由大本营向上登高xkm 时，他们所处位置的气温是y ℃．(1)试用解析式表示y•与x 的关系．(2)当登山队员由大本营出发向上登高0.5km 是,气温是多少?二、合作探究：【问题2】在下列问题中的变量间的对应关系可用怎样的函数表示？(1)有人发现,在20:50℃时蟋蟀每分鸣叫的次数c 与温度t(单位：℃)有关，即c 的值约是t 的7倍与35的差；(2)一种计算成年人标准体重G(单位：千克)的方法是，以厘米为单位量出身高值h ，再减去常数105，所得差是G 的值；(3)某城市的市内电话的月收费额y(单位：元)包括：月租费22元，拔打电话x 分的计时费(按0.1元/分收取)；(4)把一个长10cm 、宽5cm 的长方形的长减少xcm,宽不变，长方形的面积y(单位：2cm )随x 的值而变化.【问题3】请你认真观察我们得到的这几个函数解析式，看看它们有什么共同的特点？完成下列填空：共同特点： .【形成概念】一般地，形如 的函数，叫做一次函数.【问题4】一次函数b k b kx y ),0(≠+=能等于零吗？b=0时，解析式变成了什么？正比函数与一次函数有什么关系？三、例题探究：例1.下列哪些函数是一次函数，哪些又是正比例函数？（1）y=-3x-4 (2)x y 7-= (3)y=9x (4)y=4x 2+1例2. 汽车油箱中原有汽油50升，如果行驶中每小时用油5升，求油箱中的汽油y(单位：升)随行驶时间x(单位：时)变化的函数关系式，并写出自变量x 的取值范围，y 是x 的一次函数吗？四、尝试应用1.下列说法正确的是（ ）A.一次函数是正比例函数B.正比例函数不是一次函数C.不是正比例函数就不是一次函数D.正比例函数是一次函数。

19.2.2课题：一次函数的应用课型：新授主备：审核: 八年级数学组班级：姓名:教学目标：1、使学生熟练掌握一次函数图象的画法。

2、用待定系数法求解析式教学重点：用待定系数法求解析式教学难点：用待定系数法求解析式教学过程：一．学前准备告诉我们有关一次函数的某些特征能否求出其解析式，如果能怎么做？二．自学、合作探究（一）考考你已知一次函数的图象过点（3，5）与（-4，-9）。

求这个函数的解析式。

（二）思索、交流总结归纳：怎样用待定系数法求函数解析式？（三）应用、探究1、小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分.试写出这段时间她的跑步速度y(单位:米/分)随跑步时间x(单位:分)变化的函数关系式,并画出函数图像.2、A城有肥料200吨,B城有肥料300吨,现要把这些肥料运往C、D两乡。

从A城往C、D两乡运肥料的费用分别为每吨20元和25元；从B城往C、D两乡运肥料的费用分别为每吨15元和24元，现C乡需肥料240吨，D乡需肥料260吨，怎样调运总用费最少？3、下图的图象所表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?你能写出它的解析式吗？三、课堂检测：1、某风景区集体门票收费标准是:20人以内(含20人)每人收25元,超过20人的部分,每人收10元.（1）求应收门票y(元)与游览人数x(人)之间的函数关系式（2） “十·一黄金周”某班有54名学生去该风景区游览,那么购买门票需要多少费用？2、陈华暑假去某地旅游，导游要大家上山时多带一件衣服，并介绍当地山区海拔每增加100米，气温下降0.6℃．陈华在山脚下看了一下随带的温度计，气温为34℃，乘缆车到山顶发现温度为32.2℃．求山高．3、已知两条直线y 1＝2x -3和y 2＝5-x ．(1)在同一坐标系内作出它们的图象；(2)求出它们的交点A 坐标；(3)求出这两条直线与x 轴围成的三角形ABC 的面积；(4)k 为何值时，直线2k ＋1＝5x ＋4y 与k ＝2x ＋3y 的交点在每四象限．4、某年夏天，湖南省由于持续高温和连日无雨，水库蓄水量普遍下降，如图，这是某水库的蓄水量V （万米3）与干旱持续时间t （天）之间的关系图，请根据此图回答下列问题：⑴该水库原蓄水量为多少万米3？持续干旱10天后，水库蓄水量为多少万米3？ ⑵若水库的蓄水量小于400万米3时，将发出严重干旱警报，请问：持续干旱多少天后，将发出严重干旱警报？V/(万米3) ⑶按此规律，持续干旱多少天时，水库将干涸？5、在弹性限度内，弹簧的长度 y （厘米）是所挂物体质量 x （千克）的一次函数。

一次函数（一）【学习目标】：本节课主要内容是探索一次函数的概念，感受一次函数解析式的特征，学会从实际问题中建立一次函数的模型，体会一次函数在实际生活中的应用价值．一、创设情境，揭示课题【问题思索1】：1、小张准备将平时的零用钱节约一些储存起来．他已存有50元,从现在起每个月节存12元．试写出小张的存款y与从现在开始的月份x之间的函数关系式．2、某登山队大本营所在地的气温为5℃，海拔每升高1km，气温下降6℃，登山队员由大本营向上登高xkm时，他们所在位置的气温是y℃，试用解析式表示y•与x的关系．【问题思索2】：下列问题中变量间的对应关系可用怎样的函数表示？这些函数有什么共同点？（1）有人发现，在20～30℃时蟋蟀每分鸣叫次数C与温度t（单位：℃）有关，即C•的值约是t的7 倍与35的差；（）（2）一种计算成年人标准体重G（单位：千克）的方法是，以厘米为单位量出身高值h 减常数105，所得差是G的值；（）（3）某城市市内电话的月收费额y（单位：元）包括：月租费22元，拨打电话x分的计时费按0.01元/分收取；（）（4）把一个长10cm，宽5cm的长方形的长减少x，宽不变，长方形的面积y（单位：cm2）随x的值而变化．（）以上函数解析式的共同点是：【形成概念】一般地，形如的函数，叫做一次函数，当b=0时，y=kx+b即y=kx，所以说函数是一种特殊的一次函数．二、范例点击，提高认知【例3】已知函数y＝(k－2)x＋2k＋1，若它是正比例函数，求k的值．若它是一次函数，求k的值．【例4】已知y与x－3成正比例，当x＝4时，y＝3．(1)写出y与x之间的函数关系式；(2)y与x之间是什么函数关系；(3)求x＝2.5时，y的值．【例5】 已知A 、B 两地相距30千米，B 、C 两地相距48千米．某人骑自行车以每小时12千米的速度从A 地出发，经过B 地到达C 地．设此人骑行时间为x （时），离B 地距离为y （千米）．(1)当此人在A 、B 两地之间时，求y 与x 的函数关系及自变量x 取值范围．(2)当此人在B 、C 两地之间时，求y 与x 的函数关系及自变量x 的取值范围．三、课堂总结，发展潜能1．y=kx+b （k ，b 是常数，k ≠0）是一次函数．2．一次函数包含了正比例函数，即正比例函数是一次函数在b=0时的特例． ※ 练习：下列函数中，是一次函数的有_____________，是正比例函数的有______________（1）x y 8-= （2）xy 8-=（3）652+=x y （4）15.0--=x y （5）x y = （6）)3(2+=x y （7）x y 34-=2、若函数9)3(2-+-=b x b y 是正比例函数，则b = _________3、在一次函数53--=x y 中，k =_______，b =________4、若函数m x m y -+-=2)3(是一次函数，则m__________5、在一次函数32+-=x y 中，当3=x 时，=y ______；当=x _____时，5=y 。

学习目标知识：会应用一次函数与一元一次方程和一元一次不等式的关系，解决实质生活中的方案问题。

能力：培育学生剖析问题、解决问题的能力感情：解决实质生活中的方案问题。

学习要点：会应用一次函数与一元一次方程和一元一次不等式的关系，解决实质生活中的方案问题。

学习难点：会应用一次函数与一元一次方程和一元一次不等式的关系，解决实质生活中的方案问题。

教课流程【导课】做一件事情，有时有不一样的实行方案，比较这些方案，从中选择最正确方案作为行动计划是特别有必需的。

【多元互动合作研究】问题一如何选用上网收费方式？下表给出了A、 B、 C三种上宽带网的收费方式。

收费方式月使用费∕元包时上网时间∕h超时费∕ (元∕ min) A30250.05B50500.05C120不限时选用哪一种方式能结省上网费？练习：下边有两处挪动电话计费方式全世界通神州行月租费50元/月0当地通话0.40 元/ 分0.60 元 / 分你知道如何选择计费方式更省钱吗？问题二如何租车某学校计划在总花费 2 300 元的限额内，利用汽车送 234 名学生和 6 名教师集体出门活动，每辆汽车上起码有 1 名教师。

现有甲、乙两种大客车，它们的载客量和租金如表：甲种客车乙种客车载客量（单位：人/辆）4530租金（单位：元/ 辆）400280（1）共需租多少辆汽车？（2）给出最节俭花费的租车方案。

剖析：（ 1）要保证240 名师生有车坐（2）要使每辆汽车上起码要有 1 名教师依据（ 1）可知，汽车总数不可以小于＿＿＿＿；依据（2）可知，汽车总数不可以大于＿＿＿＿。

综合起来可知汽车总数为＿＿＿＿＿。

议论：依据问题中的条件，自变量x 的取值应有几种可能？为使 240 名师生有车坐， x 不可以小于＿＿＿＿；为使租车花费不超出2300 元， X 不可以超出1＿＿＿＿。

综合起来可知x 的取值为＿＿＿＿。

在考虑上述问题的基础上，你能得出几种不一样的租车方案？为节俭花费应选择此中的哪一种方案？试说明原因。

2014-2015学年第二学期八年级数学第19章单元计划授课时间： 年 月 日 第 周 星期 课时序号 一、课前导学：学生自学课本71-73页内容，并完成下列问题[问题一]：一辆汽车以60千米／小时的速度匀速行驶，行驶里程为s 千米，行驶时间为t 小时．２．在以上这个过程中，变化的量是_____________．不变化的量是__________． ３．试用含t 的式子表示s ，s=_____________ ，t 的取值X 围是.这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程． [问题二]：每X 电影票的售价为10元，如果早场售出票150X ，午场售出205X ，晚场售出310X ，三场电影的票房收入各多少元？设一场电影售票xX ，票房收入y 元．•怎样用含x 的式子表示y ?2．在以上这个过程中，变化的量是_____________．不变化的量是__________． ３．试用含x 的式子表示y ，y=_________________ ，x的取值X 围是这个问题反映了票房收入_________随售票X 数_________的变化过程． [问题三]：圆的面积和它的半径之间的关系是什么？ 1中国人口数统计表 年份 人口数／亿 1984 10．34 1989 11．06 1994 11．76 201013．71２．在以上这个过程中，变化的量是_____________．不变化的量是__________． ３．试用含r 的式子表示s ．s=______________ ，r 的取值X 围是 这个问题反映了____ 随___的变化过程．[问题四]：用10m 长的绳子围成矩形，试改变矩形一边的长度，观察矩形的面积怎样变化． １．请同学们根据题意填写下表：一边长x 〔m 〕 1 2 3 4 x 面积s 〔m 2〕２．在以上这个过程中，变化的量是_____________．不变化的量是__________． ３．试用含x 的式子表示s ，s =_______________ ，x 的取值X 围是 这个问题反映了矩形的____ 随___的变化过程．[归纳]：在一个变化过程中，我们称数值发生变化的量为________； 在一个变化过程中，我们称数值始终不变的量为________； 二、合作、交流、展示： 〔一 〕[交流1]1．在前面研究的每个问题中，都出现了______个变量，它们之间是相互影响，相互制约的． 2．同一个问题中的变量之间有什么联系？归纳：上面每个问题中的两个变量相互联系，当其中一个变量取定一个值时，另一个变量就有________确定的值与其对应.3．其实，在一些用图或表格表达的问题中，也能看到两个变量间有上述这样的关系．我们来看下面两个问题，通过观察、思考、讨论后回答：〔1〕下图是体检时的心电图．其中图上点的横坐标x 表示时间，纵坐标y•表示心脏部位的生物电流，它们是两个变量．在心电图中，对于x 的每一个确定的值，y 都有唯一确定的对应值吗？〔2〕在下面的我国人口数统计表中，年份与人口数 可以记作两个变量x 与y ，•对于表中每一个确定的年 份〔x 〕，都对应着一个确定的人口数〔y 〕吗？中国人口数统计表 〔二 〕[交流2]归纳概念一般地，在一个变化过程中，如果有两个变量x 与y ，并且对于x•的每一个确定的值，y•都有唯一确定的值与其对应，•那么我们就说x•是_________，y 是x 的________．如果当x=a 时y=b ，那么b•叫做当自变量的值为a 时的_________． 三、巩固与应用1．说出上述四个问题中的函数、自变量；2.课本第71页练习； 四、小结： 本节课学了哪些概念？五、作业：必做：P81练习T1、2. 选做：《全效》或《点睛》相应练习.授课时间： 年 月 日 第 周 星期 课时序号 一、课前导学：学生自学课本73-74页内容，并完成下列问题 1．在一个变化过程中，我们称数值发生变化的量为________； 在一个变化过程中，我们称数值始终不变的量为________。

河北省承德市平泉县七沟镇八年级数学下册19.2.2 一次函数学案1（无答案）（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河北省承德市平泉县七沟镇八年级数学下册19.2.2 一次函数学案1（无答案）（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河北省承德市平泉县七沟镇八年级数学下册19.2.2 一次函数学案1（无答案）（新版）新人教版的全部内容。

19。

2.2一次函数学习目标1、掌握一次函数解析式的特点及意义，从各种问题情境中寻找条件，确定一次函数的表达式。

2、理解一次函数与正比例函数的关系。

3、会画一次函数的图象重难点1、理解和掌握一次函数解析式特点2、一次函数与正比例函数关系的正确理解学习过程以及学习方法一、创设情境独立思考（课前20分钟）1、阅读课本P 89～91 页,思考下列问题:（1）什么叫一次函数？（2）一次函数和正比例函数有什么关系?（3）课本P91页例2你能独立完成吗？（4)课本P90-91页练习你能独立完成吗？2、独立思考后我还有以下疑惑：（课前写在小组的小黑板上）二、答疑解惑我最棒（约8分钟）甲：乙:丙：丁：三、合作学习探索新知（约15分钟）1、小组合作分析问题2、小组合作答疑解惑同伴互助答疑解惑3、师生合作解决问题1】问题:某登山队大本营所在地的气温为15℃，海拔每升高1km气温下降6℃．登山队员由大本营向上登高xkm时,他们所处位置的气温是y℃．(1)试用解析式表示y•与x的关系．（2)当登山队员由大本营出发向上登高0。

5km是,气温是多少？2】这个函数与我们上节所学的正比例函数有何不同？它的图象又具备什么特征？我们这节课将研究这些问题．3】（1)有人发现，在20~25℃时蟋蟀每分钟鸣叫次数C与温度t（℃）有关，即C•的值约是t的7倍与35的差．（2）一种计算成年人标准体重G（kg)的方法是：以厘米为单位量出身高值h减常数105，所得差是G的值．(3）某城市的市内电话的月收费额y(元）包括：月租费22元，拨打电话x分的计时费（按0．1分收取）．（4）把一个长10cm,宽5cm的矩形的长减少xcm,宽不变，矩形面积y（cm2)随x的值而变化.可以得出上面问题中的函数解析式分别为：四、归纳总结巩固新知(约15分钟)1、知识点的归纳总结：※一般地，形如y=kx+b（k、b是常数，k≠0•）的函数，•叫做一次函数．当b=0时，y=kx+b即y=kx．所以说正比例函数是一种特殊的一次函数．※对一次函数概念内涵和外延的把握： （1)自变量系数（常数）k ≠0； （2）自变量x 的次数为1；※一次函数与正比例函数的辨证关系可以用下图来表示：2、运用新知解决问题：（重点例习题的强化训练） （1）例1：下列函数关系式中，哪些是一次函数，哪些是 正比例函数？① y=-x-4 ② y=5x 2+6 ③ y=2πx ④ xy 8-= ⑤ y=—8x2）一个小球由静止开始在一个斜坡向下滚动，其速度每秒增加2米.①求小球速度v 随时间t 变化的函数关系式，它是一次函数吗?②求第2。