下载文档原格式
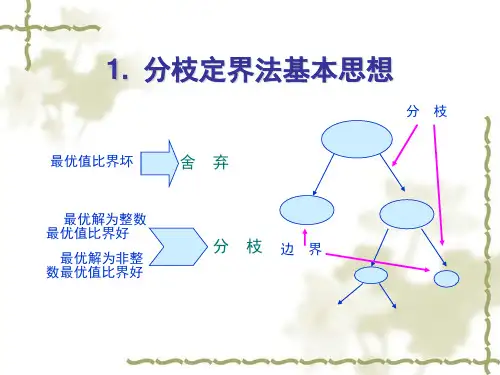
§3.3 分支定界法引入：复习割平面的思想⎪⎪⎩⎪⎪⎨⎧≥=为整数向量x x b Ax t s x c T 0..min （P ） ⎪⎩⎪⎨⎧≥=0..min x b Ax t s x c T （P 0）1、分支定界法的基本思想⎪⎪⎩⎪⎪⎨⎧≥≤为整数向量x x b Ax t s x c T 0..min（P ） ⎪⎩⎪⎨⎧≥≤0..min x b Ax t s x c T （P 0）设原问题（P ）的松弛问题（P 0）的最优解为0x 。
若 0x 的某个分量 0i x 不是整数，由于（P ）的整数最优解的第i 个分量必定落在区域 ][0i i x x ≤ 或 1][0+≥i i x x 中，因此可将原问题（P ）分解为两个子问题来求解，⎪⎪⎩⎪⎪⎨⎧≤≥≤][,0..min 0i i T x x x x b Ax t s x c 为整数向量（P 1） ⎪⎪⎩⎪⎪⎨⎧+≥≥≤1][,0..min 0i i T x x x x bAx t s x c 为整数向量（P 2）某个点不需要分支的条件：（1）相应的松弛问题的最优解是整数向量，或（2）相应的松弛问题没有可行解记 1x c z T m =， 若 m T z x c ≥2，则对 )(2P 的任何一个整数可行解 x 都有 m T T z x c x c ≥≥2x 1][0+≥i i x x ][0i i x x ≤)(1P )(2P 2x 或无解整数1x ][2k k x x ≤1][2+≥k k x x )(3P )(4P 3x 或无解整数4x ][3l l x x ≤1][3+≥l l x x )(1P )(6P )(P所以原问题的最优整数解一定不在)(2P 中，所以对 )(2P 就无须继续分支，在这种情况下，我们说)(2P 被剪枝，并把它称为死点（也称为已查明），尚未查明的点称为活点。
若 m T z x c <2，则对 )(2P 需继续考察。
