POJ经典题答案(20201109141908)

1000 A+B Problem 送分题1001 Exponentiation 高精度1003 Hangover 送分题1004 Financial Management 送分题1005 I Think I Need a Houseboat 几何1006 Biorhythms 送分题1007 DNA Sorting 送分题1008 Maya Calendar 日期处理1010 STAMPS 搜索＋DP1011 Sticks 搜索1012 Joseph 模拟/数学方法1014 Dividing 数论/DP?/组合数学->母函数?1015 Jury Compromise DP1016 Numbers That Count 送分题1017 Packets 贪心1018 Communication System 贪心1019 Number Sequence 送分题1020 Anniversary Cake 搜索1023 The Fun Number System 数论1025 Department 模拟1026 Cipher 组合数学1027 The Same Game 模拟1028 Web Navigation 送分题1031 Fence 计算几何1034 The dog task 计算几何1037 A decorative fence DP/组合数学1039 Pipe 几何1042 Gone Fishing 贪心/DP1045 Bode Plot 送分题(用物理知识)1046 Color Me Less 送分题1047 Round and Round We Go 高精度1048 Follow My Logic 模拟1049 Microprocessor Simulation 模拟1050 To the Max DP1053 Set Me 送分题1054 The Troublesome Frog 搜索1060 Modular multiplication of polynomials 高精度1061 青蛙的约会数论1062 昂贵的聘礼DP1064 Cable master DP/二分查找1065 Wooden Sticks DP1067 取石子游戏博弈论1068 Parencodings 送分题1069 The Bermuda Triangle 搜索1070 Deformed Wheel 几何1071 Illusive Chase 送分题1072 Puzzle Out 搜索1073 The Willy Memorial Program 模拟1074 Parallel Expectations DP1075 University Entrance Examination 模拟1080 Human Gene Functions DP->LCS变形1082 Calendar Game 博弈论1084 Square Destroyer 搜索？1085 Triangle War 博弈论1086 Unscrambling Images 模拟?1087 A Plug for UNIX 图论->最大流1088 滑雪DFS/DP1090 Chain ->格雷码和二进制码的转换1091 跳蚤数论1092 Farmland 几何1093 Formatting Text DP1094 Sorting It All Out 图论->拓扑排序1095 Trees Made to Order 组合数学1096 Space Station Shielding 送分题1097 Roads Scholar 图论1098 Robots 模拟1099 Square Ice 送分题1100 Dreisam Equations 搜索1101 The Game 搜索->BFS1102 LC-Display 送分题1103 Maze 模拟1104 Robbery 递推1106 Transmitters 几何1107 W's Cipher 送分题1110 Double Vision 搜索1111 Image Perimeters 搜索1112 Team Them Up! DP1113 Wall 计算几何->convex hull1119 Start Up the Startup 送分题1120 A New Growth Industry 模拟1122 FDNY to the Rescue! 图论->Dijkstra 1125 Stockbroker Grapevine 图论->Dijkstra 1128 Frame Stacking 搜索1129 Channel Allocation 搜索（图的最大独立集）1131 Octal Fractions 高精度1135 Domino Effect 图论->Dijkstra1137 The New Villa 搜索->BFS1141 Brackets Sequence DP1142 Smith Numbers 搜索1143 Number Game 博弈论1147 Binary codes 构造1148 Utopia Divided 构造1149 PIGS 图论->网络流1151 Atlantis 计算几何->同等安置矩形的并的面积->离散化1152 An Easy Problem! 数论1157 LITTLE SHOP OF FLOWERS DP1158 TRAFFIC LIGHTS 图论->Dijkstra变形1159 Palindrome DP->LCS1160 Post Office DP1161 Walls 图论1162 Building with Blocks 搜索1163 The Triangle DP1170 Shopping Offers DP1177 Picture 计算几何->同等安置矩形的并的周长->线段树1179 Polygon DP1180 Batch Scheduling DP1182 食物链数据结构->并查集1183 反正切函数的应用搜索1184 聪明的打字员搜索1185 炮兵阵地DP->数据压缩1187 陨石的秘密DP（BalkanOI99 Par的拓展）1189 钉子和小球递推?1190 生日蛋糕搜索/DP1191 棋盘分割DP1192 最优连通子集图论->无负权回路的有向图的最长路->BellmanFord 1193 内存分配模拟1194 HIDDEN CODES 搜索+DP1197 Depot 数据结构->Young T ableau1201 Intervals 贪心/图论->最长路->差分约束系统1202 Family 高精度1209 Calendar 日期处理1217 FOUR QUARTERS 递推1218 THE DRUNK JAILER 送分题1233 Street Crossing 搜索->BFS1245 Programmer, Rank Thyself 送分题1247 Magnificent Meatballs 送分题1248 Safecracker 搜索1250 T anning Salon 送分题1251 Jungle Roads 图论->最小生成树1271 Nice Milk 计算几何1273 Drainage Ditches 图论->最大流1274 The Perfect Stall 图论->二分图的最大匹配1275 Cashier Employment 图论->差分约束系统->无负权回路的有向图的最长路->Bellman-Ford1280 Game 递推1281 MANAGER 模拟1286 Necklace of Beads 组合数学->Polya定理1288 Sly Number 数论->解模线性方程组1293 Duty Free Shop DP1298 The Hardest Problem Ever 送分题1316 Self Numbers 递推同Humble Number一样1322 Chocolate 递推/组合数学1323 Game Prediction 贪心1324 Holedox Moving BFS+压缩储存1325 Machine Schedule 图论->二分图的最大匹配1326 Mileage Bank 送分题1327 Moving Object Recognition 模拟?1328 Radar Installation 贪心（差分约束系统的特例）1338 Ugly Numbers 递推(有O(n)算法)1364 King 图论->无负权回路的有向图的最长路->BellmanFord1370 Gossiping (数论->模线性方程有无解的判断)+(图论->DFS)2184 Cow Exhibition DP2190 ISBN 送分题2191 Mersenne Composite Numbers 数论2192 Zipper DP->LCS变形2193 Lenny's Lucky Lotto Lists DP2194 Stacking Cylinders 几何2195 Going Home 图论->二分图的最大权匹配2196 Specialized Four-Digit Numbers 送分题2197 Jill's Tour Paths 图论->2199 Rate of Return 高精度2200 A Card Trick 模拟2210 Metric Time 日期处理2239 Selecting Courses 图论->二分图的最大匹配2243 Knight Moves 搜索->BFS2247 Humble Numbers 递推(最优O(n)算法)2253 Frogger 图论->Dijkstra变形(和1295是一样的)2254 Globetrotter 几何2261 France '98 递推2275 Flipping Pancake 构造2284 That Nice Euler Circuit 计算几何2289 Jamie's Contact Groups 图论->网络流?2291 Rotten Ropes 送分题2292 Optimal Keypad DP2299 Ultra-QuickSort 排序->归并排序2304 Combination Lock 送分题2309 BST 送分题2311 Cutting Game 博弈论2312 Battle City 搜索->BFS2314 POJ language 模拟2315 Football Game 几何2346 Lucky tickets 组合数学2351 Time Zones 时间处理2379 ACM Rank T able 模拟+排序2381 Random Gap 数论2385 Apple Catching DP(像NOI98“免费馅饼”)2388 Who's in the Middle 送分题(排序)2390 Bank Interest 送分题2395 Out of Hay 图论->Dijkstra变形2400 Supervisor, Supervisee 图论->二分图的最大权匹配?2403 Hay Points 送分题2409 Let it Bead 组合数学->Polya定理2416 Return of the Jedi 图论->2417 Discrete Logging 数论2418 Hardwood Species 二分查找2419 Forests 枚举2421 Constructing Roads 图论->最小生成树2423 The Parallel Challenge Ballgame 几何2424 Flo's Restaurant 数据结构->堆2425 A Chess Game 博弈论2426 Remainder BFS2430 Lazy Cows DP->数据压缩1375 Intervals 几何1379 Run Away 计算几何->1380 Equipment Box 几何1383 Labyrinth 图论->树的最长路1394 Railroad 图论->Dijkstra1395 Cog-Wheels 数学->解正系数的线性方程组1408 Fishnet 几何1411 Calling Extraterrestrial Intelligence Again 送分题1430 Binary Stirling Numbers 日期处理1431 Calendar of Maya 模拟1432 Decoding Morse Sequences DP1434 Fill the Cisterns! 计算几何->离散化/1445 Random number 数据结构->碓1447 Ambiguous Dates 日期处理1450 Gridland 图论(本来TSP问题是NP难的，但这个图比较特殊，由现成的构造方法)1458 Common Subsequence DP->LCS1459 Power Network 图论->最大流1462 Random Walk 模拟+解线性方程组1463 Strategic game 贪心1466 Girls and Boys 图论->n/a1469 COURSES 贪心1475 Pushing Boxes DP1476 Always On the Run 搜索->BFS1480 Optimal Programs 搜索->BFS1481 The Die Is Cast 送分题1482 It's not a Bug, It's a Feature! 搜索->BFS1483 Going in Circles on Alpha Centauri 模拟1484 Blowing Fuses 送分题1485 Fast Food DP(似乎就是ioi2000的postoffice)1486 Sorting Slides 图论->拓扑排序1505 Copying Books DP+二分查找1510 Hares and Foxes 数论1512 Keeps Going and Going and ... 模拟1513 Scheduling Lectures DP1514 Metal Cutting 几何1515 Street Directions 图论->把一个无向连通图改造成为有向强连通图1517 u Calculate e 送分题1518 Problem Bee 几何1519 Digital Roots 送分题(位数可能很大)1520 Scramble Sort 排序1547 Clay Bully 送分题1555 Polynomial Showdown 送分题(非常阴险)1563 The Snail 送分题1601 Pizza Anyone? 搜索1604 Just the Facts 送分题1605 Horse Shoe Scoring 几何1606 Jugs 数论/搜索1631 Bridging signals DP+二分查找1632 Vase collection 图论->最大完全图1633 Gladiators DP1634 Who's the boss? 排序1635 Subway tree systems 图论->不同表示法的二叉树判同1637 Sightseeing tour 图论->欧拉回路1638 A number game 博弈论1639 Picnic Planning 图论->1641 Rational Approximation 数论1646 Double Trouble 高精度1654 Area 几何1657 Distance on Chessboard 送分题1658 Eva's Problem 送分题1660 Princess FroG 构造1661 Help Jimmy DP1663 Number Steps 送分题1664 放苹果组合数学->递推1677 Girls' Day 送分题1688 Dolphin Pool 计算几何1690 (Your)((Term)((Project))) 送分题1691 Painting A Board 搜索/DP1692 Crossed Matchings DP1693 Counting Rectangles 几何1694 An Old Stone Game 博弈论?1695 Magazine Delivery 图论->1712 Flying Stars DP1713 Divide et unita 搜索1714 The Cave 搜索/DP1717 Dominoes DP1718 River Crossing DP1719 Shooting Contest 贪心1729 Jack and Jill 图论->1730 Perfect Pth Powers 数论1732 Phone numbers DP1734 Sightseeing trip 图论->Euler回路1738 An old Stone Game 博弈论?1741 Tree 博弈论?1745 Divisibility DP1751 Highways 图论->1752 Advertisement 贪心/图论->差分约束系统1753 Flip Game 搜索->BFS1755 Triathlon 计算几何?1770 Special Experiment 树形DP1771 Elevator Stopping Plan DP1772 New Go Game 构造?1773 Outernet 模拟1774 Fold Paper Strips 几何1775 Sum of Factorials 送分题1776 T ask Sequences DP1777 Vivian's Problem 数论1870 Bee Breeding 送分题1871 Bullet Hole 几何1872 A Dicey Problem BFS1873 The Fortified Forest 几何+回溯1874 Trade on Verweggistan DP1875 Robot 几何1876 The Letter Carrier's Rounds 模拟1877 Flooded! 数据结构->堆1879 Tempus et mobilius Time and motion 模拟+组合数学->Polya定理1882 Stamps 搜索+DP1883 Theseus and the Minotaur 模拟1887 Testing the CATCHER DP1889 Package Pricing DP1893 Monitoring Wheelchair Patients 模拟+几何1915 Knight Moves 搜索->BFS1916 Rat Attack 数据结构->?1936 All in All DP?1946 Cow Cycling DP1947 Rebuilding Roads 二分1985 Cow Marathon 图论->有向无环图的最长路1995 Raising Modulo Numbers 数论->大数的幂求余2049 Finding Nemo 图论->最短路2050 Searching the Web 模拟(需要高效实现)2051 Argus 送分题(最好用堆，不用也可以过)2054 Color a Tree 贪心2061 Pseudo-random Numbers 数论2080 Calendar 日期处理2082 Terrible Sets 分治/2083 Fractal 递归2084 Game of Connections 递推(不必高精度)2105 IP Address 送分题2115 C Looooops 数论->解模线性方程2136 Vertical Histogram 送分题2165 Gunman 计算几何2179 Inlay Cutters 枚举2181 Jumping Cows 递推2182 Lost Cows ->线段树/＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝1370 Gossiping (数论->模线性方程有无解的判断)+(图论->DFS)1090 Chain ->格雷码和二进制码的转换2182 Lost Cows ->线段树/2426 Remainder BFS1872 A Dicey Problem BFS1324 Holedox Moving BFS+压缩储存1088 滑雪DFS/DP1015 Jury Compromise DP1050 To the Max DP1062 昂贵的聘礼DP1065 Wooden Sticks DP1074 Parallel Expectations DP1093 Formatting Text DP1112 Team Them Up! DP1141 Brackets Sequence DP1157 LITTLE SHOP OF FLOWERS DP1160 Post Office DP1163 The Triangle DP1170 Shopping Offers DP1179 Polygon DP1180 Batch Scheduling DP1191 棋盘分割DP1293 Duty Free Shop DP2184 Cow Exhibition DP2193 Lenny's Lucky Lotto Lists DP2292 Optimal Keypad DP1432 Decoding Morse Sequences DP1475 Pushing Boxes DP1513 Scheduling Lectures DP1633 Gladiators DP1661 Help Jimmy DP1692 Crossed Matchings DP1712 Flying Stars DP1717 Dominoes DP1718 River Crossing DP1732 Phone numbers DP1745 Divisibility DP1771 Elevator Stopping Plan DP1776 T ask Sequences DP1874 Trade on Verweggistan DP1887 Testing the CATCHER DP1889 Package Pricing DP1946 Cow Cycling DP1187 陨石的秘密DP（BalkanOI99 Par的拓展）1485 Fast Food DP(似乎就是ioi2000的postoffice) 2385 Apple Catching DP(像NOI98“免费馅饼”) 1064 Cable master DP/二分查找1037 A decorative fence DP/组合数学1936 All in All DP?1505 Copying Books DP+二分查找1631 Bridging signals DP+二分查找1159 Palindrome DP->LCS1458 Common Subsequence DP->LCS1080 Human Gene Functions DP->LCS变形2192 Zipper DP->LCS变形1185 炮兵阵地DP->数据压缩2430 Lazy Cows DP->数据压缩1067 取石子游戏博弈论1082 Calendar Game 博弈论1085 Triangle War 博弈论1143 Number Game 博弈论2311 Cutting Game 博弈论2425 A Chess Game 博弈论1638 A number game 博弈论1694 An Old Stone Game 博弈论?1738 An old Stone Game 博弈论?1741 Tree 博弈论?2083 Fractal 递归1104 Robbery 递推1217 FOUR QUARTERS 递推1280 Game 递推2261 France '98 递推2181 Jumping Cows 递推1316 Self Numbers 递推同Humble Number一样2084 Game of Connections 递推(不必高精度) 1338 Ugly Numbers 递推(有O(n)算法)2247 Humble Numbers 递推(最优O(n)算法)1322 Chocolate 递推/组合数学1189 钉子和小球递推?1947 Rebuilding Roads 二分2418 Hardwood Species 二分查找2082 Terrible Sets 分治/1001 Exponentiation 高精度1047 Round and Round We Go 高精度1060 Modular multiplication of polynomials 高精度1131 Octal Fractions 高精度1202 Family 高精度2199 Rate of Return 高精度1646 Double Trouble 高精度1147 Binary codes 构造1148 Utopia Divided 构造2275 Flipping Pancake 构造1660 Princess FroG 构造1772 New Go Game 构造?1005 I Think I Need a Houseboat 几何1039 Pipe 几何1070 Deformed Wheel 几何1092 Farmland 几何1106 Transmitters 几何2194 Stacking Cylinders 几何2254 Globetrotter 几何2315 Football Game 几何2423 The Parallel Challenge Ballgame 几何1375 Intervals 几何1380 Equipment Box 几何1408 Fishnet 几何1514 Metal Cutting 几何1518 Problem Bee 几何1605 Horse Shoe Scoring 几何1654 Area 几何1693 Counting Rectangles 几何1774 Fold Paper Strips 几何1871 Bullet Hole 几何1875 Robot 几何1873 The Fortified Forest 几何+回溯1031 Fence 计算几何1034 The dog task 计算几何1271 Nice Milk 计算几何2284 That Nice Euler Circuit 计算几何1688 Dolphin Pool 计算几何2165 Gunman 计算几何1755 Triathlon 计算几何?1379 Run Away 计算几何->1113 Wall 计算几何->convex hull1434 Fill the Cisterns! 计算几何->离散化/1151 Atlantis 计算几何->同等安置矩形的并的面积->离散化1177 Picture 计算几何->同等安置矩形的并的周长->线段树2419 Forests 枚举2179 Inlay Cutters 枚举1025 Department 模拟1027 The Same Game 模拟1048 Follow My Logic 模拟1049 Microprocessor Simulation 模拟1073 The Willy Memorial Program 模拟1075 University Entrance Examination 模拟1098 Robots 模拟1103 Maze 模拟1120 A New Growth Industry 模拟1193 内存分配模拟1281 MANAGER 模拟2200 A Card Trick 模拟2314 POJ language 模拟1431 Calendar of Maya 模拟1483 Going in Circles on Alpha Centauri 模拟1512 Keeps Going and Going and ... 模拟1773 Outernet 模拟1876 The Letter Carrier's Rounds 模拟1883 Theseus and the Minotaur 模拟2050 Searching the Web 模拟(需要高效实现)1012 Joseph 模拟/数学方法1086 Unscrambling Images 模拟?1327 Moving Object Recognition 模拟?1893 Monitoring Wheelchair Patients 模拟+几何1462 Random Walk 模拟+解线性方程组2379 ACM Rank T able 模拟+排序1879 Tempus et mobilius Time and motion 模拟+组合数学->Polya定理1520 Scramble Sort 排序1634 Who's the boss? 排序2299 Ultra-QuickSort 排序->归并排序1008 Maya Calendar 日期处理1209 Calendar 日期处理2210 Metric Time 日期处理1430 Binary Stirling Numbers 日期处理1447 Ambiguous Dates 日期处理2080 Calendar 日期处理2351 Time Zones 时间处理1770 Special Experiment 树形DP1916 Rat Attack 数据结构->?1197 Depot 数据结构->Young T ableau1182 食物链数据结构->并查集2424 Flo's Restaurant 数据结构->堆1877 Flooded! 数据结构->堆1445 Random number 数据结构->碓1023 The Fun Number System 数论1061 青蛙的约会数论1091 跳蚤数论1152 An Easy Problem! 数论2191 Mersenne Composite Numbers 数论2381 Random Gap 数论2417 Discrete Logging 数论1510 Hares and Foxes 数论1641 Rational Approximation 数论1730 Perfect Pth Powers 数论1777 Vivian's Problem 数论2061 Pseudo-random Numbers 数论1014 Dividing 数论/DP?/组合数学->母函数?1606 Jugs 数论/搜索1995 Raising Modulo Numbers 数论->大数的幂求余2115 C Looooops 数论->解模线性方程1288 Sly Number 数论->解模线性方程组1395 Cog-Wheels 数学->解正系数的线性方程组1000 A+B Problem 送分题1003 Hangover 送分题1004 Financial Management 送分题1006 Biorhythms 送分题1007 DNA Sorting 送分题1016 Numbers That Count 送分题1019 Number Sequence 送分题1028 Web Navigation 送分题1046 Color Me Less 送分题1053 Set Me 送分题1068 Parencodings 送分题1071 Illusive Chase 送分题1096 Space Station Shielding 送分题1099 Square Ice 送分题1102 LC-Display 送分题1107 W's Cipher 送分题1119 Start Up the Startup 送分题1218 THE DRUNK JAILER 送分题1245 Programmer, Rank Thyself 送分题1247 Magnificent Meatballs 送分题1250 T anning Salon 送分题1298 The Hardest Problem Ever 送分题1326 Mileage Bank 送分题2190 ISBN 送分题2196 Specialized Four-Digit Numbers 送分题2291 Rotten Ropes 送分题2304 Combination Lock 送分题2309 BST 送分题2390 Bank Interest 送分题2403 Hay Points 送分题1411 Calling Extraterrestrial Intelligence Again 送分题1481 The Die Is Cast 送分题1484 Blowing Fuses 送分题1517 u Calculate e 送分题1547 Clay Bully 送分题1563 The Snail 送分题1604 Just the Facts 送分题1657 Distance on Chessboard 送分题1658 Eva's Problem 送分题1663 Number Steps 送分题1677 Girls' Day 送分题1690 (Your)((Term)((Project))) 送分题1775 Sum of Factorials 送分题1870 Bee Breeding 送分题2105 IP Address 送分题2136 Vertical Histogram 送分题1555 Polynomial Showdown 送分题(非常阴险) 2388 Who's in the Middle 送分题(排序)1519 Digital Roots 送分题(位数可能很大)1045 Bode Plot 送分题(用物理知识)2051 Argus 送分题(最好用堆，不用也可以过) 1011 Sticks 搜索1020 Anniversary Cake 搜索1054 The Troublesome Frog 搜索1069 The Bermuda Triangle 搜索1072 Puzzle Out 搜索1100 Dreisam Equations 搜索1110 Double Vision 搜索1111 Image Perimeters 搜索1128 Frame Stacking 搜索1142 Smith Numbers 搜索1162 Building with Blocks 搜索1183 反正切函数的应用搜索1184 聪明的打字员搜索1248 Safecracker 搜索1601 Pizza Anyone? 搜索1713 Divide et unita 搜索1129 Channel Allocation 搜索（图的最大独立集）1190 生日蛋糕搜索/DP1691 Painting A Board 搜索/DP1714 The Cave 搜索/DP1084 Square Destroyer 搜索？1010 STAMPS 搜索＋DP1194 HIDDEN CODES 搜索+DP1882 Stamps 搜索+DP1101 The Game 搜索->BFS1137 The New Villa 搜索->BFS1233 Street Crossing 搜索->BFS2243 Knight Moves 搜索->BFS2312 Battle City 搜索->BFS1476 Always On the Run 搜索->BFS1480 Optimal Programs 搜索->BFS1482 It's not a Bug, It's a Feature! 搜索->BFS 1753 Flip Game 搜索->BFS1915 Knight Moves 搜索->BFS1017 Packets 贪心1018 Communication System 贪心1323 Game Prediction 贪心1463 Strategic game 贪心1469 COURSES 贪心1719 Shooting Contest 贪心2054 Color a Tree 贪心1328 Radar Installation 贪心（差分约束系统的特例）1042 Gone Fishing 贪心/DP1752 Advertisement 贪心/图论->差分约束系统1201 Intervals 贪心/图论->最长路->差分约束系统1097 Roads Scholar 图论1161 Walls 图论1450 Gridland 图论(本来TSP问题是NP难的，但这个图比较特殊，由现成的构造方法)2197 Jill's Tour Paths 图论->2416 Return of the Jedi 图论->1639 Picnic Planning 图论->1695 Magazine Delivery 图论->1729 Jack and Jill 图论->1751 Highways 图论->1122 FDNY to the Rescue! 图论->Dijkstra1125 Stockbroker Grapevine 图论->Dijkstra1135 Domino Effect 图论->Dijkstra1394 Railroad 图论->Dijkstra1158 TRAFFIC LIGHTS 图论->Dijkstra变形2395 Out of Hay 图论->Dijkstra变形2253 Frogger 图论->Dijkstra变形(和1295是一样的)1734 Sightseeing trip 图论->Euler回路1466 Girls and Boys 图论->n/a1515 Street Directions 图论->把一个无向连通图改造成为有向强连通图1635 Subway tree systems 图论->不同表示法的二叉树判同1275 Cashier Employment 图论->差分约束系统->无负权回路的有向图的最长路->Bellman-Ford1274 The Perfect Stall 图论->二分图的最大匹配1325 Machine Schedule 图论->二分图的最大匹配2239 Selecting Courses 图论->二分图的最大匹配2195 Going Home 图论->二分图的最大权匹配2400 Supervisor, Supervisee 图论->二分图的最大权匹配?1637 Sightseeing tour 图论->欧拉回路1383 Labyrinth 图论->树的最长路1094 Sorting It All Out 图论->拓扑排序1486 Sorting Slides 图论->拓扑排序1149 PIGS 图论->网络流2289 Jamie's Contact Groups 图论->网络流?1192 最优连通子集图论->无负权回路的有向图的最长路->BellmanFord 1364 King 图论->无负权回路的有向图的最长路->BellmanFord1985 Cow Marathon 图论->有向无环图的最长路1087 A Plug for UNIX 图论->最大流1273 Drainage Ditches 图论->最大流1459 Power Network 图论->最大流1632 Vase collection 图论->最大完全图2049 Finding Nemo 图论->最短路1251 Jungle Roads 图论->最小生成树2421 Constructing Roads 图论->最小生成树1026 Cipher 组合数学1095 Trees Made to Order 组合数学2346 Lucky tickets 组合数学1286 Necklace of Beads 组合数学->Polya定理2409 Let it Bead 组合数学->Polya定理1664 放苹果组合数学->递推。

POJ Grids基本练习题资料POJ——1004 Financial Management .............................................. - 3 -POJ——1664 放苹果 ........................................................................ - 5 -POJ——2675 计算书费...................................................................... - 7 -POJ——2676 整数的个数................................................................... - 9 -POJ——2679 整数的立方和.............................................................. - 11 -POJ——2680化验诊断 .................................................................... - 12 -POJ——2684 求阶乘的和................................................................. - 15 -POJ——2687数组逆序重放............................................................... - 16 -POJ——2688求字母的个数............................................................... - 17 -POJ——2689 大小写字母互换 ........................................................... - 18 -POJ——2694逆波兰表达式............................................................... - 19 -POJ——2696 计算表达式的值 ........................................................... - 20 -POJ——2699自整除数 .................................................................... - 22 -POJ——2701 与7无关的数 ............................................................. - 23 -POJ——2702密码翻译 .................................................................... - 24 -POJ——2703骑车与走路.................................................................. - 26 -POJ——2707求一元二次方程的根....................................................... - 27 -POJ——2714求平均年龄.................................................................. - 29 -POJ——2715 谁拿了最多的奖学金...................................................... - 30 -POJ——2718晶晶赴约会.................................................................. - 32 -POJ——2719陶陶摘苹果.................................................................. - 33 -POJ——2720 大象喝水.................................................................... - 34 -POJ——2722 学分绩点.................................................................... - 35 -POJ——2733判断闰年 .................................................................... - 37 -POJ——2734十进制到八进制............................................................ - 38 -POJ——2750 鸡兔同笼.................................................................... - 39 -POJ——2753菲波那契数列............................................................... - 40 -POJ——2758 菲波那契数列(2) ......................................................... - 41 -POJ——2764数根.......................................................................... - 42 -POJ——2767简单密码 .................................................................... - 44 -POJ——2780 Eva’s Problem ......................................................... - 47 -POJ——2786 Pell数列................................................................... - 48 -POJ——2796数字求和 .................................................................... - 49 -POJ——2807两倍.......................................................................... - 50 -POJ ——2808校门外的树................................................................. - 52 -POJ——2856 计算邮资.................................................................... - 54 -POJ——2870 求矩阵的加法.............................................................. - 56 -POJ——2871 整数奇偶排序.............................................................. - 58 -POJ——2882 Program I ............................................................... - 60 -POJ——2883 checking order ........................................................ - 62 -POJ——2886能被3除尽的数之和...................................................... - 64 -POJ——2887 能被3、5、7整除的数 ................................................. - 65 -POJ——2888字符串中的数字............................................................ - 67 -POJ——2926算数运算 .................................................................... - 69 -POJ——2927判断数字个数............................................................... - 70 -POJ——2930 加减乘除.................................................................... - 72 -POJ——2933停车场收费.................................................................. - 74 -POJ——2938 按顺序输出................................................................. - 76 -POJ——2943 小白鼠排队................................................................. - 77 -POJ——3142 球弹跳高度的计算......................................................... - 79 -POJ——3164 奇偶排序.................................................................... - 80 -POJ——3195最大公约数.................................................................. - 81 -POJ——3248 最大公约数................................................................. - 82 -POJ——3255 十进制到六进制 ........................................................... - 84 -POJ——3670 计算鞍点.................................................................... - 86 -POJ——3708 1的个数.................................................................... - 88 -POJ——3756多边形内角和............................................................... - 90 -POJ——1004 Financial Management思路：这道题就是计算一下12个月的平均工资。

一、选择题1.设θ∈R ，则“ππ||1212θ-<”是“1sin 2θ<”的（ ） （A ）充分而不必要条件 （B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件 【答案】A【解析】πππ||012126θθ-<⇔<< 1sin 2θ⇒<，但10,sin 2θθ=<，不满足 ππ||1212θ-<，所以是充分不必要条件，选A. 【考点】 充要条件件，若B 是A 的真子集，则A 是B 的必要不充分条件。

2.已知命题p:；命题q ：若a ＞b ，则，下列命题为真命题的是（ ）（A ） ∧p q （B ）⌝∧p q （C ） ⌝∧p q （D ）⌝⌝∧p q 【答案】B【解析】试题分析：由时有意义，知p 是真命题，由可知q 是假命题，即均是真命题，故选B.【考点】1.简易逻辑联结词.2.全称命题.【名师点睛】解答简易逻辑联结词相关问题，关键是要首先明确各命题的真假，利用或、且、非真值表，进一步作出判断.3.命题“*x n ∀∈∃∈，R N ，使得2n x >”的否定形式是（ ）A ．*x n ∀∈∃∈，R N ，使得2n x < B ．*x n ∀∈∀∈，R N ，使得2n x < C ．*x n ∃∈∃∈，R N ，使得2n x < D ．*x n ∃∈∀∈，R N ，使得2n x <【答案】D 【解析】试题分析：∀的否定是∃，∃的否定是∀，2n x ≥的否定是2n x <．故选D ． 考点：全称命题与特称命题的否定．【方法点睛】全称命题的否定是特称命题，特称命题的否定是全称命题．对含有存在（全称）量词的命题进行否定需要两步操作：①将存在（全称）量词改成全称（存在）量词；②将结论加以否定．4.已知直线a ，b 分别在两个不同的平面α，β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的（ ） （A ）充分不必要条件（B ）必要不充分条件 （C ）充要条件（D ）既不充分也不必要条件【答案】A 【解析】 试题分析：“直线a 和直线b 相交”⇒“平面α和平面β相交”，但“平面α和平面β相交”⇒“直线a 和直线b 相交”，所以“直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件，故选A ．考点：1.充要条件；2.直线与平面的位置关系.能力等。

定积分典型例题20例答案欧阳家百（2021.03.07）例1 求3321lim )n n n→∞+．分析 将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解 将区间[0,1]n 等分，则每个小区间长为1i x n∆=，然后把2111n n n=⋅的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即3321lim)n n n →∞+=31lim )n n n n →∞+=34=⎰．例2 0⎰=_________．解法 1 由定积分的几何意义知，0⎰等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故0⎰=2π．解法 2 本题也可直接用换元法求解．令1x -=sin t（22t ππ-≤≤），则0⎰=22tdt ππ-⎰=2tdt =2202cos tdt π⎰=2π 例3 （1）若22()x t x f x e dt -=⎰，则()f x '=___；（2）若0()()xf x xf t dt =⎰，求()f x '=___．分析 这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-⎰．解 （1）()f x '=422xxxe e ---；（2） 由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =⎰，则可得()f x '=0()()xf t dt xf x +⎰．例4 设()f x 连续，且31()x f t dt x -=⎰，则(26)f =_________．解 对等式31()x f t dt x -=⎰两边关于x 求导得32(1)31f x x -⋅=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =． 例5函数1()(3(0)xF x dt x =>⎰的单调递减开区间为_________．解()3F x '=，令()0F x '<得3>，解之得109x <<，即1(0,)9为所求．例6 求0()(1)arctan xf x t tdt =-⎰的极值点．解 由题意先求驻点．于是()f x '=(1)arctan x x -．令()f x '=0，得x 故1x =为()f x 的极大值点，0x =为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()x t g x e dt -=⎰，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ''=．解 由已知条件得2(0)(0)0t f g e dt -===⎰，且由两曲线在(0,0)处切线斜率相同知(0)(0)1f g =''===．故所求切线方程为y x =．而3()(0)3lim ()lim33(0)330n n f f n nf f n n→∞→∞-'=⋅==-． 例8 求 22000sin lim(sin )x x xtdtt t t dt→-⎰⎰；分析 该极限属于00型未定式，可用洛必达法则．解 22000sin lim (sin )x x xtdtt t t dt→-⎰⎰=2202(sin )lim (1)(sin )x x x x x x →-⋅⋅-=220()(2)limsin x x x x→-⋅-=304(2)lim 1cos x x x→-⋅-=2012(2)limsin x x x→-⋅=0．注 此处利用等价无穷小替换和多次应用洛必达法则． 例9 试求正数a 与b，使等式201lim1sin x x x b x →=-⎰成立． 分析 易见该极限属于00型的未定式，可用洛必达法则．解2001lim sin x x x b x →-⎰=20x →=20lim 1cos x x x b x →→-2011cos x x b x →==-，由此可知必有0lim(1cos )0x b x →-=，得1b =．又由2011cos x x x →==-， 得4a =．即4a =，1b =为所求． 例10 设sin 20()sin x f x t dt =⎰，34()g x x x =+，则当0x →时，()f x 是()g x 的（ ）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小． D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→⋅=+ 22011lim 33x x x →==． 故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+⎰，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++． 例11 计算21||x dx -⎰．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -⎰＝0210()x dx xdx --+⎰⎰＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如33222111[]6dx x x --=-=⎰，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界.例12 设()f x 是连续函数，且10()3()f x x f t dt =+⎰，则()________f x =．分析 本题只需要注意到定积分()b af x dx ⎰是常数（,a b 为常数）．解 因()f x 连续，()f x 必可积，从而10()f t dt ⎰是常数，记1()f t dt a =⎰，则()3f x x a =+，且11(3)()x a dx f t dt a +==⎰⎰．所以2101[3]2x ax a +=，即132a a +=，从而14a =-，所以 3()4f x x =-．例13 计算21-⎰．分析 由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解 21-⎰=211--+⎰⎰2是偶是奇函数，有10-=⎰, 于是21-⎰=214⎰=04⎰=1044dx -⎰⎰ 由定积分的几何意义可知4π=⎰, 故2114444dx ππ-=-⋅=-⎰⎰．例14 计算220()xd tf x t dt dx -⎰，其中()f x 连续． 分析 要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解 由于220()xtf x t dt -⎰=2221()2x f x t dt -⎰．故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()xtf x t dt -⎰=201()()2x f u du -⎰=201()2x f u du ⎰， 故220()x d tf x t dt dx -⎰=201[()]2x d f u du dx ⎰=21()22f x x ⋅=2()xf x ． 错误解答220()xd tf x t dt dx -⎰22()(0)xf x x xf =-=． 错解分析 这里错误地使用了变限函数的求导公式，公式 中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元． 例15 计算30sin x xdx π⎰．分析 被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解 30sin x xdx π⎰30(cos )xd x π=-⎰330[(cos )](cos )x x x dx ππ=⋅---⎰30cos 6xdx ππ=-+⎰6π=-． 例16 计算120ln(1)(3)x dx x +-⎰．分析 被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-⎰=101ln(1)()3x d x+-⎰=1100111[ln(1)]3(3)(1)x dx x x x +-⋅--+⎰=101111ln 2()2413dx x x-++-⎰ 11ln 2ln324=-． 例17 计算20sin x e xdx π⎰．分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解 由于20sin xe xdx π⎰20sin xxde π=⎰220[sin ]cos xx e x e xdx ππ=-⎰220cos x e e xdxππ=-⎰，（1） 而20sin 1x e xdx π=-⎰， （2）将（2）式代入（1）式可得20sin xe xdx π⎰220[sin 1]x e e xdx ππ=--⎰,故20sin xe xdx π⎰21(1)2e π=+．例18 计算10arcsin x xdx ⎰．分析 被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdx ⎰210arcsin ()2x xd =⎰221100[arcsin ](arcsin )22x x x d x =⋅-⎰21142π=-⎰． （1）令sin x t =，则201cos22t dt π-==⎰20sin 2[]24t t π-4π=． （2）将（2）式代入（1）式中得1arcsin x xdx =⎰8π．例19设()f x [0,]π上具有二阶连续导数，()3f π'=且[()()]cos 2f x f x xdx π''+=⎰，求(0)f '．分析 被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．解 由于0[()()]cos f x f x xdx π''+⎰0()sin cos ()f x d x xdf x ππ'=+⎰⎰()(0)2f f π''=--=．故 (0)f '=2()235f π'--=--=-． 例20 计算243dxx x +∞++⎰． 分析 该积分是无穷限的的反常积分，用定义来计算． 解 2043dx x x +∞++⎰=20lim 43t t dx x x →+∞++⎰=0111lim ()213t t dx x x →+∞-++⎰=011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32．。

[1]POJ 动态规划题目列表容易：1018, 1050, 1083, 1088, 1125, 1143, 1157, 1163, 1178, 1179, 1189, 1208, 1276, 1322, 1414, 1456, 1458, 1609, 1644, 1664, 1690, 1699, 1740(博弈), 1742, 1887, 1926(马尔科夫矩阵，求平衡）, 1936, 1952, 1953, 1958, 1959, 1962, 1975, 1989, 2018, 2029, 2039, 2063, 2081, 2082, 2181, 2184, 2192, 2231, 2279, 2329, 2336, 2346, 2353, 2355, 2356, 2385, 2392, 2424,不易：1019, 1037, 1080, 1112, 1141, 1170, 1192, 1239, 1655, 1695, 1707, 1733(区间减法加并查集), 1737, 1837, 1850, 1920(加强版汉罗塔), 1934(全部最长公共子序列), 1937(计算几何), 1964(最大矩形面积，O(n)算法), 2138, 2151, 2161, 2178,推荐：1015, 1635, 1636(挺好的), 1671, 1682, 1692(优化), 1704, 1717, 1722, 1726, 1732, 1770, 1821, 1853, 1949, 2019, 2127, 2176, 2228, 2287, 2342, 2374, 2378, 2384, 24111015 Jury Compromise1029 False coin1036 Gangsters1037 A decorative fence1038 Bugs Integrated, Inc.1042 Gone Fishing1050 To the Max1062 昂贵的聘礼1074 Parallel Expectations1080 Human Gene Functions1088 滑雪1093 Formatting Text1112 Team Them Up!1141 Brackets Sequence1143 Number Game1157 LITTLE SHOP OF FLOWERS1159 Palindrome1160 Post Office1163 The Triangle1170 Shopping Offers1178 Camelot1179 Polygon1180 Batch Scheduling1185 炮兵阵地1187 陨石的秘密1189 钉子和小球1191 棋盘分割1192 最优连通子集1208 The Blocks Problem1239 Increasing Sequences1240 Pre-Post-erous!1276 Cash Machine1293 Duty Free Shop1322 Chocolate1323 Game Prediction1338 Ugly Numbers1390 Blocks1414 Life Line1432 Decoding Morse Sequences 1456 Supermarket1458 Common Subsequence1475 Pushing Boxes1485 Fast Food1505 Copying Books1513 Scheduling Lectures1579 Function Run Fun1609 Tiling Up Blocks1631 Bridging signals 2分+DP NLOGN 1633 Gladiators1635 Subway tree systems1636 Prison rearrangement1644 To Bet or Not To Bet1649 Market Place1651 Multiplication Puzzle1655 Balancing Act1661 Help Jimmy1664 放苹果1671 Rhyme Schemes1682 Clans on the Three Gorges 1690 (Your)((Term)((Project)))1691 Painting A Board1692 Crossed Matchings1695 Magazine Delivery1699 Best Sequence1704 Georgia and Bob1707 Sum of powers1712 Flying Stars1714 The Cave1717 Dominoes1718 River Crossing1722 SUBTRACT1726 Tango Tango Insurrection 1732 Phone numbers1733 Parity game1737 Connected Graph1740 A New Stone Game1742 Coins P1745 Divisibility1770 Special Experiment1771 Elevator Stopping Plan 1776 Task Sequences1821 Fence1837 Balance1848 Tree1850 Code1853 Cat1874 Trade on Verweggistan 1887 Testing the CATCHER 1889 Package Pricing1920 Towers of Hanoi1926 Pollution1934 Trip1936 All in All1937 Balanced Food1946 Cow Cycling1947 Rebuilding Roads1949 Chores1952 BUY LOW, BUY LOWER 1953 World Cup Noise1958 Strange Towers of Hanoi 1959 Darts1962 Corporative Network 1964 City Game1975 Median Weight Bead 1989 The Cow Lineup2018 Best Cow Fences2019 Cornfields2029 Get Many Persimmon Trees 2033 Alphacode2039 To and Fro2047 Concert Hall Scheduling 2063 Investment2081 Recaman's Sequence 2082 Terrible Sets2084 Game of Connections2127 Greatest Common Increasing Subsequence 2138 Travel Games2151 Check the difficulty of problems2152 Fire2161 Chandelier2176 Folding2178 Heroes Of Might And Magic2181 Jumping Cows2184 Cow Exhibition2192 Zipper2193 Lenny's Lucky Lotto Lists2228 Naptime2231 Moo Volume2279 Mr. Young's Picture Permutations2287 TianJi -- The Horse Racing2288 Islands and Bridges2292 Optimal Keypad2329 Nearest number - 22336 Ferry Loading II2342 Anniversary party2346 Lucky tickets2353 Ministry2355 Railway tickets2356 Find a multiple2374 Fence Obstacle Course2378 Tree Cutting2384 Harder Sokoban Problem2385 Apple Catching2386 Lake Counting2392 Space Elevator2397 Spiderman2411 Mondriaan's Dream2414 Phylogenetic Trees Inherited2424 Flo's Restaurant2430 Lazy Cows2915 Zuma3017 Cut the Sequence3028 Shoot-out3124 The Bookcase3133 Manhattan Wiring3345 Bribing FIPA3375 Network Connection3420 Quad Tiling ?/?cat=5[2]动态规划方法总结1. 按状态类型分写在前面：从状态类型分，并不表示一题只从属于一类。

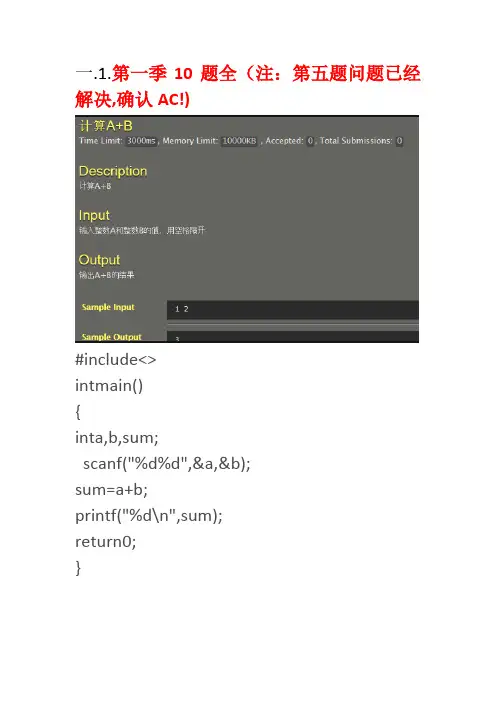
一.1.第一季10题全（注：第五题问题已经解决,确认AC!)#include<>intmain(){inta,b,sum;scanf("%d%d",&a,&b);sum=a+b;printf("%d\n",sum);return0;}2.#include<>#definePIintmain(){ doubler,h,l,s,sq,vq,vz; scanf("%lf%lf",&r,&h); l=2*PI*r;s=PI*r*r;sq=4*PI*r*r;vq=4*PI*r*r*r/3;vz=s*h;printf("%.2lf\n%.2lf\n%.2lf\n%.2lf\n%.2lf\n",l, s,sq,vq,vz);return0;}3.#include<>intmain(){inta,b,c;doubled,e;scanf("%d%d%d",&a,&b,&c); d=a+b+c;e=d/3;printf("%lf\n%lf\n",d,e); return0;} 4.#include<>intmain(){inta,b,c;scanf("%d%d%d",&a,&b,&c); if(a<b)a=b;if(a<c)a=c;printf("%d\n",a);return0; }5.#include<> intmain()inti=0,j=0,k=1;chara[6];while((a[i]=getchar())!='\n') {i++;}for(;i>0;i--){if(a[j]==a[i-1]){j++;continue;}else{k=0;break;}}if(k==1)printf("yes\n");elseprintf("no\n");}6.#include<> intmain(){doublea,c; scanf("%lf",&a); switch((int)a/10) {case0:c=a*;break;case1:c=(a-10)*+10*;break;case2:case3:c=(a-20)*+10*+10*;break;case4:case5:c=(a-40)*+20*+10*+10*;break; case6:case7:case8:case9:c=(a-60)*+20*+20*+10*+10*;break; default:c=(a-100)*+40*+20*+20*+10*+10*; }printf("%lf\n",c);return0;}7.#include<> intmain(){doublea,b,c; scanf("%lf",&a); c=(int)a;if(a>c)a=c+1;if(a>15)b=(a-15)*+7+13*; else{if(a>2)b=(a-2)*+7; elseb=7;}printf("%lf\n",b); return0;}8.#include<>intmain(){inta,b,c,e,f=30,g=31,n;scanf("%d-%d-%d",&a,&b,&c);if((a%400==0)||(a%100!=0&&a%4==0)) e=29;elsee=28;switch(b){case1:n=c;break;case2:n=g+c;break;case3:n=g+e+c;break;case4:n=g+e+g+c;break;case5:n=g+e+g+f+c;break;case6:n=g+e+g+f+g+c;break;case7:n=g+e+g+f+g+f+c;break;case8:n=g+e+g+f+g+f+g+c;break;case9:n=g+e+g+f+g+f+g+g+c;break; case10:n=g+e+g+f+g+f+g+g+f+c;break; case11:n=g+e+g+f+g+f+g+g+f+g+c;break; default:n=g+e+g+f+g+f+g+g+f+g+f+c;}printf("%d\n",n);return0;}9.#include<>intmain(){intx;scanf("%d",&x);if(x>=90&&x<=100) printf("A\n"); elseif(x>=80) printf("B\n"); elseif(x>=70) printf("C\n"); elseif(x>=60) printf("D\n");elseprintf("E\n"); return0;}10.#include<> intmain() {doublex,y,s;scanf("%lf,%lf",&x,&y);s=(x+2)*(x+2)+(y-2)*(y-2);if(s>1){s=(x+2)*(x+2)+(y+2)*(y+2); if(s>1){s=(x-2)*(x-2)+(y+2)*(y+2);if(s>1){s=(x-2)*(x-2)+(y-2)*(y-2);if(s>1){printf("0\n");return1;} }}}printf("10\n");return0;}二。

1·计算A+B2·圆及圆球等的相关计算3·计算成绩4·找最大数5·找幸运数6·奖金发放7·出租车费8·是该年的第几天9·成绩转换10·求建筑高度11·区间内素数12·计算π13·两个整数之间所有的素数14·最次方数15·自然数立方的乐趣16·五猴分桃17·完全数18·二分求根19·你会存钱吗？20·级数和21·幸运数字722·粒子裂变23·特殊整数24·最大乘积25·解不等式26·危险的组合27·子序列的和29·探索合数世纪30·韩信点兵31·亲和数32·高低交换33·循环移位35·组合数36·积分计算37·数据加密38·获取指定二进制位39·ACKERMAN40·不会吧，又是A+B 41·平均值函数42·插入排序43·一维数组赋值44·右下角45·右上角46·山迪的麻烦47·冒泡排序48·恐怖水母49·左上角50·一维数组加法51·字符串排序52·字符串左中右53·文章统计54·找出数字55·字符串比较56·THE CLOCK 57·合并字符串58·特殊要求的字符串59·字符串逆序60·COIN TEST 61·小型数据库62·单词频次65·检测位图长宽67·子字符串替换68·复数69·字符串加密编码70·重组字符串71·大数除法72·创建与遍历职工链表73·大数加法74·大数减法75·链表节点删除76·链表动态增长或缩小77·大数乘法78·精确乘幂80·火车站81·操场训练82·HAILSTONE84·阶乘合计85·王的对抗86·三点顺序87·公园喷水器88·勇闯天涯89·不屈的小蜗90·THE RATIO OF GAINERS TO LOSERS 91·GRAVEYARD92·ARITHMETIC PROGRESSIONS 93·SCORING94·HOUSEBOAT97·BEE98·CHECKSUM ALGORITHM99·Hanoi 2100·Specialized number1·计算A+B#include<stdio.h>int main(){int a,b,sum;scanf("%d %d",&a,&b);sum=a+b;printf("%d",sum);}2·圆及圆球等的相关计算#include<stdio.h>int main(){float r,h,l,s,sq,vq,vz,pi=3.141592653;scanf("%f %f",&r,&h);l=2*pi*r;s=pi*r*r;sq=4*pi*r*r;vq=4.0/3*pi*r*r*r;vz=pi*r*r*h;printf("%.2f\n%.2f\n%.2f\n%.2f\n%.2f\n",l,s,sq,v q,vz);return 0;}3·计算成绩#include <stdio.h>int main(){float a,b,c,sum,ave;scanf("%f %f %f",&a,&b,&c);sum=a+b+c;ave=sum/3.0;printf("%.6f\n%.6f",sum,ave);return 0;}4·找最大数#include<stdio.h>int main(){int a,b,c,t;scanf("%d %d %d",&a,&b,&c);if (a<b) t=a,a=b;if(a<c) t=a,a=c;printf("%d",a);return 0;}5·找幸运数#include <stdio.h>int main(){int i,j,a;scanf("%d",&a);i=0;j=a;while(j){i=10*i+(j%10);j=j/10;}if(i==a)printf("yes\n");else printf("no\n");return 0;}6·奖金发放#include<stdio.h>int main (){float l;scanf("%f",&l);if (l<=10)l=l*0.1;else if(l<=20)l=10*0.1+(l-10)*0.075;else if(l<=40)l=10*0.1+10*0.075+(l-20)*0.05;elseif(l<=60)l=10*0.1+10*0.075+20*0.05+(l-40)*0.03;elseif(l<=100)l=10*0.1+10*0.075+20*0.05+20*0.03+(l-60)* 0.015;elsel=10*0.1+10*0.075+20*0.05+20*0.03+40*0.015+(l-100)* 0.01;printf("%.6f",l);return 0;}7·出租车费#include<stdio.h>#include<math.h>int main(){float a,n,t;scanf("%f",&a);if (a<=2) n=7;else if (a<=15) {t=a-floor(a);if(t==0)n=7+(floor(a)-2)*1.5;else n=7+(floor(a)-1)*1.5;}else {t=a-floor(a);if(t==0) n=7+13*1.5+(floor(a)-15)*2.1;else n=7+13*1.5+(floor(a)-14)*2.1;} printf("%.6f",n);return 0;}8·是该年的第几天#include<stdio.h>int main(){int y,m,d,n,a;scanf("%d-%d-%d",&y,&m,&d);if((y%4==0&&y%100!=0)||(y%400==0)) a=29;else a=28;switch(m){case 1:n=d;break;case 2:n=31+d;break;case 3:n=31+a+d;break;case 4:n=62+a+d;break;case 5:n=92+a+d;break;case 6:n=123+a+d;break;case 7:n=153+a+d;break;case 8:n=184+a+d;break;case 9:n=215+a+d;break;case 10:n=245+a+d;break;case 11:n=276+a+d;break;case 12:n=306+a+d;break;}printf("%d",n);return 0;}9·成绩转换#include<stdio.h>int main(){int n;scanf("%d",&n);if(n<60)printf("E\n");else if(n<70)printf("D\n");else if(n<80)printf("C\n");else if(n<90)printf("B\n");else printf("A\n");return 0;}10·求建筑高度#include<stdio.h>int main(){float x,y,a,b,c,d;scanf("%f,%f",&x,&y);a=(x-2)*(x-2)+(y-2)*(y-2);b=(x-2)*(x-2)+(y+2)*(y+2);c=(x+2)*(x+2)+(y-2)*(y-2);d=(x+2)*(x+2)+(y+2)*(y+2);if(a<=1||b<=1||c<=1||d<=1)printf("10");else printf("0");return 0;}11·区间内素数#include<stdio.h>#include<math.h>int main(){int i,n=500,cnt=0,sum=0;while(n<=800){for (i=2;i<=n-1;i++)if (n%i==0)break;if (i==n)cnt=cnt+1,sum=sum+pow((-1),cnt)*n; n=n+1;}printf("%d %d",cnt,sum);return 0;}12·计算π#include<stdio.h>#include<math.h>int main(){int s=1;double pi=0,n=1,t=1;while (fabs(t)>1e-6)pi=pi+t,n=n+2,s=-s,t=s/n;pi=pi*4;printf("%.6f",pi);return 0;}13·两个整数之间所有的素数#include<stdio.h>int main(){int a,b,t,i;scanf("%d%d",&a,&b);if(a>b)t=a,a=b,b=t;while (a<=b){for (i=2;i<=a-1;i++)if (a%i==0)break;if(i==a)printf("%d ",a);a++;}return 0;}14·最次方数#include<stdio.h>int main(){int x,a,m=1,n=1;scanf("%d %d",&x,&a);while (m<=a){n=n*x;n=n%1000;m=m+1;}printf("%d",n);return 0;}15·自然数立方的乐趣#include<stdio.h>int main(){int n,a,i,t;scanf("%d",&n);a=n*(n-1)+1;t=n*n*n;printf("%d*%d*%d=%d=",n,n,n,t);for(i=1;i<n;i++){printf("%d+",a);a=a+2;}printf("%d",a);return 0;}16·五猴分桃#include<stdio.h>int divides(int n,int m){if (n/5==0||n%5!=1)return 0;if (m==1)return 1;return divides(n-n/5-1,m-1);}int main(){int n,a;for (n=1;;n++)if(divides(n,5)){printf("%d ",n);break;}a=(((((n-1)*4/5-1)*4/5-1)*4/5-1)*4/5-1)*4/5;printf("%d",a);return 0;}17·完全数#include<stdio.h>int main(){int i,n,sum=0;for(n=2;n<1000;n++){sum=0;for (i=1;i<=n/2;i++){if(n%i==0)sum=sum+i;}if(sum==n){printf("%d=",n);for(i=1;i<n/2;i++)if(n%i==0)printf("%d+",i);i=n/2;printf("%d\n",i);}}return 0;}18·二分求根#include<math.h>#include<stdio.h>double fun(double x) {return 2*x*x*x-4*x*x+3*x-6;} double root(double a,double b,double e){double x1,x2,y1,x,y;x1=a;x2=b;do {x=(x1 + x2)/2;y=fun(x);y1=fun(x1);if((y<0&&y1<0)||(y>0&&y1>0))x1=x;elsex2=x;/*end if*/}while(fabs(y) > e);return x;}int main(void){double m,n;scanf("%f %f",&m,&n);double x=root(m,n,1e-8);printf("%.2f\n",x);return 0;}19·你会存钱吗？#include<stdio.h>#include<math.h>int main(){int i8,i5,i3,i2,i1,n8,n5,n3,n2,n1;float max=0,term;for(i8=0;i8<3;i8++) /*穷举所有可能的存款方式*/for(i5=0;i5<=(20-8*i8)/5;i5++)for(i3=0;i3<=(20-8*i8-5*i5)/3;i3++)for(i2=0;i2<=(20-8*i8-5*i5-3*i3)/2;i2++){i1=20-8*i8-5*i5-3*i3-2*i2;term=2000.0*pow((double)(1+0.0063*12),(double)i1) *pow((double)(1+2*0.0063*12),(double)i2)*pow((double)(1+3*0.0069*12),(double)i3)*pow((double)(1+5*0.0075*12),(double)i5)*pow((double)(1+8*0.0084*12),(double)i8);/*计算到期时的本利合计*/if(term>max){max=term;n1=i1;n2=i2;n3=i3;n5=i5;n8=i8;}}printf("%d ",n8);printf("%d ",n5);printf("%d ",n3);printf("%d ",n2);printf("%d\n",n1);printf("%.2f",max);/*输出存款方式*/}20·级数和#include<stdio.h>#include<math.h>int main(){ int j,t,i,a,n;double s=0;scanf("%d",&n);j=-1; i=1; t=1;for (a=0;a<n;a++){t=t*2; j*=-1; i*=-1; s=s+j*t/((t+i)*(2*t+j)+0.0);}printf("%.6lf\n",s);return 0;}21·幸运数字7#include<stdio.h>int main(){int n,i;scanf("%d",&n);//n不大于30000if(n<7);else {for (i=7;i<=n;i++)if(i%7==0||i%10==7||i/1000%10==7||i/100%10==7||i/10 %10==7)printf("%d ",i);}return 0;}22·粒子裂变#include<stdio.h>int main(){int n[100],m[100],t,i;n[0]=1;m[0]=0;scanf("%d",&t);for(i=1;i<=t;i++){n[i]=m[i-1];m[i]=3*n[i-1]+2*m[i-1]; }printf("%d %d",n[t],m[t]); return 0;}23·特殊整数#include<stdio.h>#include <stdlib.h>#include<math.h>int main(){int m,n,g=0,s=0,i,j,x,x1,x2;scanf("%d %d",&m,&n);x1=(int)(pow(10.0,n)/10);x2=(int)(pow(10.0,n)-1);for(i=x1;i<=x2;i++){j=i;do{x=j%10;if(x==m){if(i%m!=0)g++,s=s+i;break;}else j=j/10;}while(j!=0);}printf("%d %d\n",g,s);return 0;}24·最大乘积#include<stdio.h>int main(){int A[18],i,j,n,x,y=0;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&A[i]);for(i=0;i<n;i++){x=1;for(j=i;j<n;j++){x=x*A[j];if(x>y) y=x;}}if(y>0)printf("%d",y);else printf("-1");return 0;}25·解不等式#include<stdio.h>int main(){int a,b;float n,s=0,sum=0;scanf("%d %d",&a,&b);for (n=1;sum<=a;n++){s=s+1/n;sum=sum+1/s;}printf("%.0f ",n=n-1); for (n;sum<=b;n++){s=s+1/n;sum=sum+1/s;}printf("%.0f",n=n-1); return 0;}26·危险的组合#include<stdio.h>#include<math.h>int main(){int n;int f(int);scanf("%d",&n);printf("%d",f(n));return 0;}int f(int n){int a;if(n==1||n==2)a=0;else if(n==3)a=1;else if(n==4)a=3;else a=f(n-1)*2+pow(2,n-4)-f(n-4);return a;}27·子序列的和#include<stdio.h>#include<math.h>int main(){int m,n,i; //n<m<1000000double a,sum=0;scanf("%d %d",&n,&m);for (i=n;i<=m;i++){a=pow(i,2.0);sum=sum+1/a;}printf("%.5lf",sum);return 0;}29·探索合数世纪#include<stdio.h>int main(){int n,i=500,s,x,count=0;long j,k;scanf("%d",&n);while(count<n){s=0;for(j=i*100-99;j<i*100;j+=2){x=0;for(k=3;k*k<=j;k+=2)if(j%k==0){x=1;break;}s+=x;}if(s==50)count++;i++;}printf("%d %d",j-101,j-2);return 0;}30·韩信点兵include<stdio.h>int main(){int a,b,c,n;//a<3,b<5,c<7scanf("%d %d %d",&a,&b,&c);for (n=10;n<=100;n++){if((n-a)%3==0&&(n-b)%5==0&&(n-c)%7==0)break;}if(n>100)printf("-1");else printf("%d ",n);return 0;}31·亲和数#include<stdio.h>int fun(int a){int b=0,i;for(i=1;i<=a/2;i++){if(a%i==0)b+=i;}return b;}int main(){int a,b;scanf("%d %d",&a,&b);if(fun(a)==b&&fun(b)==a)printf("YES");else printf("NO");return 0;}32·高低交换#include<stdio.h>inline int xchg(unsigned char n) {char left=n<<4;char right=n>>4;return left+right;}int main(){int n;scanf("%d",&n);n=xchg(n);printf("%d",n);return 0;33·循环移位#include<stdio.h>int move(int value,int n){if(n==0) return value;else if(n<0){n=-n;value=(value<<n)|(value>>(32-n));}else value=(value>>n)|(value<<(32-n));return value;}int main(){int value,n;scanf("%d %d",&value,&n);value=move(value,n);printf("%d",value);return 0;35·组合数#include<stdio.h>int C(int m,int n){int i,p=1;for (i=1;i<=n;i++)p*=(m+1-i)/(double)i;return p;}int main(){int m,n,t;scanf("%d %d",&m,&n);if(n>m) printf("wrong\n");else {t=C(m,n);printf("%d\n",t);}return 0;}36·积分计算#include<stdio.h>double f(double x){return 1.0/(1.0+x*x);}double jf(double a,double b) {double h,s=0;;int i;h=(b-a)/5000000;for(i=1;i<5000000;i++){s+=(f(a)+f(a+h))*0.5*h;a+=h;}return s;}int main(){double a,b,s;scanf("%lf%lf",&a,&b); s=jf(a,b);printf("%lf",s);return 0;}37·数据加密#include<stdio.h>int fun(int n){return (n+5)%10;}int main(){int a,b[4],i=0;scanf("%d",&a);while(a){b[i]=fun(a%10);a/=10;i++;}a=b[0]*1000+b[1]*100+b[2]*10+b[3]; printf("%d",a);return 0;}38·获取指定二进制位#include <stdio.h>int getbit(int n,int k){int count=0;while(1){count++;if(count==k)break;n/=2;}return n%2;}int main(){int n,k;scanf("%d %d",&n,&k);k=getbit(n,k);printf("%d",k);return 0;}39·ACKERMAN#include<stdio.h>int ack(int m,int n){if(m==0) return n+1;else if(n==0) return ack(m-1,1); else return ack(m-1,ack(m,n-1)); }int main(){int m,n;scanf("%d %d",&m,&n);m=ack(m,n);printf("%d",m);return 0;}40·不会吧，又是A+B#include<stdio.h>int main(){int a1,a2,a3,b1,b2,b3,a,b,c;scanf("%d %d %d %d %d %d",&a1,&a2,&a3,&b1,&b2,&b3); c=(a3+b3)%60;b=(a2+b2+(a3+b3)/60)%60;a=a1+b1+((a3+b3)/60+a2+b2)/60;printf("%d %d %d ",a,b,c);return 0;}41·平均值函数#include<stdio.h>double avg(int A[],int s,int e){int i;double t,sum;for(i=s;i<=e;i++)sum+=A[i];t=sum/(e-s+1);return t;}int main(){int n,s,e,i,A[100];double t;scanf("%d\n",&n);for(i=0;i<n;i++)scanf("%d ",&A[i]);scanf("%d %d",&s,&e);t=avg(A,s,e);printf("%f",t);return 0;}42·插入排序#include<stdio.h>void InsertionSort(int a[],int s,int m) {int t,i,j,k;for(i=0;i<m;i++){for(j=s+1;j<s+m-i;j++){t=a[j];k=j-1;while(t>a[k]){a[k+1]=a[k];k--;if(k==(s-1))break;}a[k+1]=t;}}}int main(){int n,a[100],i,s,m;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&a[i]);scanf("%d %d",&s,&m);InsertionSort(a,s,m);for(i=0;i<n;i++)printf("%d ",a[i]);printf("\n");return 0;}43·一维数组赋值#include<stdio.h>int main(){int A[100],B[100],i,n;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&A[i]);for(i=0;i<n;i++){B[i]=A[i];if(i%2!=0)printf("%d ",B[i]);}return 0;}44·右下角#include<stdio.h>int main(){int n,a[10][10],i,j;scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%d",&a[i][j]);for(i=0;i<n;i++){for(j=0;j<n;j++){if(j<=n-i-2)printf(" "); else printf("%d ",a[i][j]);} printf("\n");}return 0;}45·右上角#include<stdio.h>int main(){int n,a[10][10],i,j;scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%d",&a[i][j]);for(i=0;i<n;i++){for(j=0;j<n;j++){if(j>=i)printf("%d ",a[i][j]); else printf(" ");}printf("\n");}return 0;}46·山迪的麻烦#include<stdio.h>int main(){int n,count=0,i,j,a[100],k;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&a[i]);for(i=1;i<n;i++){k=a[i];for(j=i-1;j>=0&&k<a[j];j--){count++;a[j+1]=a[j];}a[j+1]=k;}printf("%d\n",count);return 0;}47·冒泡排序#include<stdio.h>void BubbleSort(int a[],int s,int m) {int t,i,j;for(i=0;i<m-1;i++){for(j=s;j<s+m-i-1;j++)if(a[j]<a[j+1]){t=a[j];a[j]=a[j+1];a[j+1]=t;}}}int main(){int n,a[100],i,s,m;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&a[i]);scanf("%d %d",&s,&m);BubbleSort(a,s,m);for(i=0;i<n;i++)printf("%d ",a[i]);printf("\n");return 0;}48·恐怖水母#include<stdio.h>int main(){int n,m,i,j,a[100],b[100],t,sum=0; scanf("%d%d",&n,&m);for(i=0;i<n;i++)scanf("%d",&a[i]);for(i=0;i<m;i++)scanf("%d",&b[i]);for(i=0;i<n-1;i++){for(j=0;j<n-1-i;j++)if(a[j]>a[j+1]){t=a[j];a[j]=a[j+1];a[j+1]=t;}}for(i=0;i<m-1;i++){for(j=0;j<m-1-i;j++)if(b[j]>b[j+1]){t=b[j];b[j]=b[j+1];b[j+1]=t;}}for(i=0,j=0;i<n&&j<m;j++){if(a[i]<=a[j]){sum+=b[j];i++;}}printf("%d\n",sum);return 0;}49·左上角#include<stdio.h>int main(){int n,a[10][10],i,j;scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%d",&a[i][j]); for(i=0;i<n;i++){for(j=0;j<n-i;j++)printf("%d ",a[i][j]);printf("\n");}return 0;}50·一维数组加法#include<stdio.h>int main(){int A[100],B[100],C[100],n,i;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&A[i]);for(i=0;i<n;i++)scanf("%d",&B[i]);for(i=0;i<n;i++){C[i]=A[i]+B[i];printf("%d ",C[i]);}return 0;}51·字符串排序#include<stdio.h>#include<string.h>int main(){char str[10][10];int i,j;char t[10];for(i=0;i<10;i++){scanf("%s",str[i]);}for(i=0;i<10;i++){for(j=0;j<10-i;j++){if(strcmp(str[j],str[j+1])>0) {strcpy(t,str[j]);strcpy(str[j],str[j+1]);strcpy(str[j+1],t);}}}for(i=0;i<10;i++)printf("%s ",str[i]);return 0;}52·字符串左中右#include<stdio.h>#include<string.h>void Left(char str[],int n,char dest[]) {int i;for(i=0;i<n;i++)dest[i]=str[i];}void Right(char str[],int n,char dest[]) {int i,m,j=0;m=strlen(str);for(i=m-n;i<=m;i++){。

POJ1386【基础】
题目大意： 如果一个单词的首字母和另一个单词的尾字母相同，我们规定这两个单词可以 前后相连。现在给出一些单词，求是否可以构造一个序列，让所有的单词都可 以前后相连。
输入： 输入包含 T 组测试数据，T 在输入的第一行里给出。每一组测试数据的第一行 包含一个整数 N（1<=N<=100000），表示有多少个单词。接下来有 N 行，每一 行有一个单词，前后没有空格，单词由小写字母组成。两个测试数据之间没有 空行。
输入： 第一行有两个整数 N 和 M。接下来有 M 行，每一行有两个整数 M+1 行，表示 Bessie 依次经过的谷仓的编号。
题解： 这题是求有向图的欧拉回路，做法其实和无向图的没有多大区别。只是 Special Judge 比较蛋疼。还是先深搜后输出点。这一题的代码我用 C++来写 了，才 54 行，好久没有写过那么短的代码了……
POJ2337【基础】
题目大意： 如果一个单词的首字母和另一个单词的尾字母相同，我们规定这两个单词可以 前后相连。现在给出一些单词，求是否可以构造一个序列，让所有的单词都可 以前后相连，并且相连的序列字典序最小。
输入： 第一行有一个整数 t，表示有 t 组测试数据。每一组测试数据的第一行有一个 整数 n（3<=n<=1000），表示有 n 个由小写字母构成的单词。接下来有 n 行， 每一行是一个长度不超过 20 个字符的单词。两个测试数据之间没有空行。
POJ1300【基础】
题目大意： 大厦里有若干间房间，依次从 0 开始编号为 0，1，2，3……，0 号是你的房 间。作为一个管家，你需要找一条路径经过所有开着的门，并满足以下几个要 求： 1、通过一扇开着的门以后马上把它关上； 2、关上的门不可以再打开； 3、最后回到你自己的房间（房间 0）。

此时： 卢有50+5账单为50付完走人 莫有25´2账单为25付完走人 内德有10´3账单为10付完剩20，要买5分的糖 付账后，店主有50+25+10´2，无法找开10，但硬币和为95，能找开纸币
1元。 6.按支付金额大小将三男子编码为A(最多）B（中间） C（最少） 老板娘为X 由（1）可知每个人支付的金额是5的整数倍
C就会按条件①喊叫：‘我看到他们两个人都戴白帽子了’可是C的嘴并 没有动，说明C没有看到自己(指B)戴的是白帽子。”因而B将断定B自己 戴的是黑帽子，这样B就会按条件②动嘴喊叫起来：“我知道自己戴的 是黑帽子，可是B的嘴并没有动，说明A最初的假定错了。同样的推理， C看到B未吭声，即当认识到C自己戴的是黑帽子时，也会按条件②喊 叫，但C的嘴也未动，就更加肯定A最初假定——自己所戴的是“白”帽 子 ——错了。根据这两点A从反面证明自己所戴的帽子也是黑的。
s先生说不知道，p先生就知道自己头上不是0。
p先生知道自己头上不是0还不知道，s先生就知道自己头上不是1。（如 果s先生头上是1，那么p先生就能知道自己头上是2）
s先生知道自己头上不是1还不知道，p先生就知道自己头上不是2。（原 因同上）
p先生知道自己头上不是2还不知道，s先生就知道自己头上不是3。（原 因同上） s先生知道自己头上不是3还不知道，p先生就知道自己头上不是4。（原 因同上） p先生知道自己头上不是4还不知道，s先生就知道自己头上不是5。（原 因同上） s先生知道自己头上不是5就知道了，说明她看到p先生头上写着6。 他便推算出自己头上是7。当然这个p先生也知道。所以p先生就知道 拉。
第5题： a 123
456
789b
在原来的点上增加点a，b。
顺序：3 5 7 8 9 b 6 2 a 1 4

2020年高考必刷卷09数学（理）（本试卷满分150分，考试用时120分钟）注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡的相应位置上。

2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其它答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

第Ⅰ卷（选择题)一、单选题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若集合A={x∈N||x−1|≤1},B={x|y=√1−x2}，则A∩B的真子集的个数为（）A．3B．4C．7D．8【答案】A【解析】【分析】先求出A∩B的交集，再依据求真子集个数公式求出，也可列举求出。

【详解】A={x∈N||x−1|≤1}={0,1,2}，B={x|y=√1−x2}=[−1,1]，A∩B={0,1}，所以A∩B的真子集的个数为22−1=3，故选A。

【点睛】有限集合{a1,a2,⋯a n}的子集个数为2n个，真子集个数为2n−1。

2．若复数22252x2i2x xxx-++---（）为纯虚数，则x的值为（）A ．2．B ．-1.C ．12-．D ．12． 【答案】D【解析】【分析】 由纯虚数的定义可得其实部为0但虚部不为0，解之可得答案．【详解】由纯虚数的定义可得22252020x x x x ⎧-+⎨--≠⎩＝，故x ＝12， 故选D ．【点睛】本题考查纯虚数的定义，涉及一元二次方程与不等式的解法，属基础题．3．若347log log log 2x y z ==<-，则（ ）A ．347x y z <<B ．743z y x <<C ．437y x z <<D ．734z x y <<【答案】B【解析】【分析】令347log log log 2x y z k ===<-,可得3k x =,4k y =,7k z =,进而得到133k x +=,144k y +=,177k z +=,画出3x y =,4x y =,7x y =的图象,利用图象比较大小即可. 【详解】令347log log log 2x y z k ===<-,则3k x =,4k y =,7k z =∴133k x +=,144k y +=,177k z +=,且11k +<-分别画出3x y =,4x y =,7x y =的图象可得,111743k k k +++∴<<,即743z y x <<故选：B.【点睛】本题考查指对互化,考查指数函数图象,考查利用图象比较值的大小.4．“上医医国”出自《国语・晋语八》，比喻高贤能治理好国家．现把这四个字分别写在四张卡片上，其中“上”字已经排好，某幼童把剩余的三张卡片进行排列，则该幼童能将这句话排列正确的概率是（ ）A ．13B ．16C ．14D ．112【答案】A【解析】【分析】先排好医字，共有23C 种排法，再排国字，只有一种方法.【详解】幼童把这三张卡片进行随机排列，基本事件总数n=23C =3，∴该幼童能将这句话排列正确的概率p=13． 故选：A【点睛】有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数：1．基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举；2．注意区分排列与组合，以及计数原理的正确使用．5．埃及金字塔是古埃及的帝王（法老）陵墓，世界七大奇迹之一，其中较为著名的是胡夫金字塔．令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿，还有发生在胡夫金字塔上的数字“巧合”．如胡夫金字塔的底部周长如果除以其高度的两倍，得到的商为3.14159，这就是圆周率较为精确的近似值．金字塔底部形为正方形，整个塔形为正四棱锥，经古代能工巧匠建设完成后，底座边长大约230米．因年久风化，顶端剥落10米，则胡夫金字塔现高大约为（）A．128.5米B．132.5米C．136.5米D．110.5米【答案】C【解析】【分析】设出胡夫金字塔原高，根据题意列出等式，解出等式即可根据题意选出答案。

2020年国家公务员考试⾏测经典逻辑推理试题及答案（共四套）2020年国家公务员考试⾏测经典逻辑推理试题及答案(共四套)2020年国家公务员考试⾏测经典逻辑推理试题及答案(⼀)01.⼀项对N国男⼥收⼊差异的研究结果表明，全职⼯作的妇⼥的收⼊是全职⼯作的男⼈的收⼊的80%。

然⽽，其他调查结果却⼀致显⽰，在N国所有受雇妇⼥的平均年收⼊只是所有受雇男性的平均年收⼊的65%。

下⾯哪⼀点，如果也被调查所证实，最有助于解释上⾯研究结果之间的明显分歧?(A)在N国,所有⼥性雇员的平均年收⼊与所有男性雇员的平均年收⼊的差距在过去的30年中⼀直在逐渐增⼤。

(B)在N国,全职⼯作的妇⼥的平均年收⼊与完全相同的职业和⼯作条件下的全职⼯作的男性的平均年收⼊是⼀样的。

(C)在N国，⼥性⼯作者占据全职的、管理的、监督的、专业的职位的⽐例在增加，这些职位赚的钱通常⽐其他类型的职位赚的钱多。

(D)在N国,妇⼥⼲兼职⼯作的⽐例⽐男性⾼，并且兼职⼯作者赚的钱通常⽐全职⼯作者的少。

(E)在其他妇⼥在劳动⼒中的⽐例与N国相似的10个国家中，全职⼯作的妇⼥的平均年收⼊与全职⼯作的男性的平均年收⼊相⽐，其⽐例从较低的50%到较⾼的90%不等。

02.北京、上海、⼴东、四川和辽宁每队都参加了两次⾜球联赛。

(1)每次联赛只进⾏了四场⽐赛：北京对上海、北京对辽宁、⼴东对四川、⼴东对辽宁(2)只有⼀场⽐赛在两次联赛中胜负情况保持不变。

(3)北京是第⼀次联赛的冠军。

(4)在每⼀次联赛中，输⼀场即被淘汰，只有冠军⼀场都没输。

(5)每场⽐赛都不会有平局的情况请问谁是第⼆次⽐赛是冠军？A.北京B.上海C.⼴东D.四川E.辽宁03.在M市，8⽉中每⼀天电的消耗量与这⼀天湿度的最⼤值成正⽐。

既然今年8⽉的平均湿度峰值⽐去年8⽉的⾼3个百分点，那么就可推出M市今年8⽉的耗电量⼀定⽐去年8⽉的多。

下⾯哪⼀个论述的推理模式与上⾯的论述最相似?(A)在美学院25个班级中，任何⼀个班艺术⽤品的数量都与这个班的学⽣个数成正⽐。

完整版本的poj 题目分类DP:1011 NTA 简单题1013 Great Equipment 简单题1024 Calendar Game 简单题1027 Human Gene Functions 简单题1037 Gridland 简单题1052 Algernon s Noxious Emissions 简单题1409 Communication System 简单题，但是很容易看错~~~1425 Crossed Matchings 简单题1438 Asteroids! 简单题1459 String Distance and Transform Process 简单题1462 Team Them Up! 简单题1556 Heroes Of Might And Magic 简单题，不过背景蛮有意思的……1520 Duty Free Shop 简单题1524 Supermarket 简单题1301 The New Villa 简单题1303 Jury Compromise 其实不是很难，但是很容易错，555……1345 Best Deal 简单题，但是也很容易错……555……1360 Radar Installation 简单题1396 The Umbrella Problem: 2054 简单题1058 Currency Exchange 简单题1076 Gene Assembly 简单题1092 Arbitrage 简单题1093 Monkey and Banana 简单题1094 Matrix Chain Multiplication 简单题1536 Labyrinth 简单题1100 Mondriaan s Dream 简单题，DP可以过，不过据说有复杂的组合公式1103 Hike on a Graph 简单题1134 Strategic Game 简单题1147 Formatting Text 简单题1148 The Game 简单题1161 Gone Fishing 简单题1180 Self Numbers 简单题1192 It s not a Bug, It s a Feature! 简单题1196 Fast Food 简单题1107 FatMouse and Cheese 简单题，不过题目描述有些混乱1136 Multiple 简单题，BFS1276 Optimal Array Multiplication Sequence 简单题1255 The Path 简单题1250 Always On the Run 简单题1213 Lumber Cutting 简单题1206 Win the Bonus 简单题1479 Dweep 无聊题1587 UP 100 无聊题，DP应该可以……但是太烦了……没做……1066 Square Ice 无聊题，目前已知的O(nlogn)算法要用***L……您有没有简单点的O(nlogn)的算法？1245 Triangles 无聊题1022 Parallel Expectations 经典题，想了n久，最后发现可以DP，相当好的一道题1499 Increasing Sequences 经典题{}1039 Number Game 没有完美解决的题，感觉可以直接以所有剩下的数作为状态DP，但是缺乏证明……1227 Free Candies SRbGa的经典题，我看了oibh上的解题报告才做出来的……:( 1234 Chopsticks SRbGa的经典题……图论:1525 Air Raid 简单题，最小路径覆盖1500 Pre-Post-erous! 简单题1501 Knockout Tournament 简单题1508 Intervals 对您来说应该是简单题，但我想了n久……:(，差分限制系统1333 Galactic Import 简单题1304 Tin Cutter 简单题，但是似乎有空间复杂度为O(n)的算法1310 Robot 简单题1311 Network 简单题1344 A Mazing Problem 简单题1395 Door Man 简单题，欧拉回路1372 Networking 简单题1406 Jungle Roads 简单题1053 FDNY to the Rescue! 简单题1055 Oh, Those Achin Feet 不错的简单题1059 What s In a Name 简单题1064 Roads Scholar 简单题1082 Stockbroker Grapevine 简单题1085 Alien Security 简单题，我觉得我当时的算法好巧妙:)1097 Code the Tree 简单题1060 Sorting It All Out 简单题，但是规模要是大些的话……1105 FatMouse s Tour 简单题1119 SPF 简单题1127 Roman Forts 简单题1140 Courses 简单题1157 A Plug for UNIX 蛮不错的简单题1203 Swordfish 简单题1221 Risk 简单题，最短路1197 Sorting Slides 简单题，匹配1268 Is It A Tree? 不错的题，图论1273 It s Ir-Resist-Able! 简单题，图论1298 Domino Effect 简单题，最长路1260 King 简单题，差分限制系统……1291 MPI Maelstrom 不错的题，最长路1266 Gossiping 简单题1285 Shipping Routes 无聊题，最短路1313 Gears on a Board 无聊题1502 Plugged In 无聊题，匹配应该可以，但是太烦了，没做……1568 WishingBone s Room Plan 无聊题，最大最小匹配，不过容易看错题~~~~~~ 1077 Genetic Combinations 无聊题，匹配1364 Machine Schedule 背诵题……匹配……1137 Girls and Boys 背诵题，匹配……1023 University Entrace Examination 经典题，但是和1576重复1576 Marriage is Stable 经典题，感人的背景，经典的算法……1249 Pushing Boxes 经典题，某人的论文写过，求割点和块+BFS可以在O(面积)的时间内做出来，但是这题似乎已经比较老了1141 Closest Common Ancestors 没有完美解决，最简单的算法就能过，但要是规模大了……1084 Channel Allocation 尚未完美解决，我用搜索过的，不过是不是有更好的算法呢……？1231 Mysterious Mountain SRbGa的经典题……1232 Adventure of Super Mario SRbGa的经典题……数学:1007 Numerical Summation of a Series 简单题，还是蛮有意思的1045 HangOver 简单题1049 I Think I Need a Houseboat 简单题1028 Flip and Shift 简单题，可以DP/BFS/……，但是实际上有数学方法可以直接判断出来1026 Modular multiplication of polynomials 简单题，感觉有比较简单的好算法，但想不出来:(1307 Packets 简单题，不过也蛮经典的……1312 Prime Cuts 简单题1334 Basically Speaking 简单题1337 Pi 简单题1342 Word Index 简单题1349 Four Quarters 简单题1350 The Drunk Jailer 简单题1352 Number Base Conversion 简单题1353 Unimodal Palindromic Decompositions 规模不大，所以是简单题……1354 Extended Lights Out 简单题1362 Game Prediction 简单题1365 Mileage Bank 简单题1382 A Simple Task 简单题1383 Binary Numbers 简单题1403 Safecracker 简单题1408 The Fun Number System 简单题1486 Color the Tree 简单题1487 Playing Cards 简单题1489 2^x mod n = 1 简单题，应该有好算法，不过枚举就可以过……1503 One Person "The Price is Right" 简单题，POI Eggs的翻版1512 Water Treatment Plants 简单题，组合计数1526 Big Number 简单题，不过O(1)和O(n)还是有区别的:)1529 Enigmatic Travel 简单题，不过个人感觉题目描述很令人费解1530 Find The Multiple 简单题1537 Playing with a Calculator 简单题1577 GCD & LCM 简单题，分区联赛的题……1005 Jugs 简单题1543 Stripies 简单题1569 Partial Sums 简单题1062 Trees Made to Order 简单题1070 Bode Plot 简单题1073 Round and Round We Go 简单题，142857，我喜欢^_^1078 Palindrom Numbers 简单题1086 Octal Fractions 简单题1199 Point of Intersection 简单题1104 Leaps Tall Buildings 简单题1110 Dick and Jane 简单题1115 Digital Roots 简单题1113 u Calculate e 简单题1152 A Mathematical Curiosity 简单题1154 Niven Numbers 简单题1160 Biorhythms 简单题1163 The Staircases 简单题1177 K-Magic Number 简单题1184 Counterfeit Dollar 简单题1182 Keeps Going and Going and ... 简单题，我喜欢:)1284 Perfection 简单题1272 Numerically Speaking 简单题1269 Coconuts, Revisited 简单题1247 There s Treasure Everywhere! 简单题1241 Geometry Made Simple 简单题1202 Divide and Count 简单题1216 Deck 简单题1218 Ratio 简单题1261 Prime Land 简单题1212 Mountain Landscape 无聊题1410 Number Sequence 无聊题1401 Hilbert Curve Intersections 无聊题1331 Perfect Cubes 无聊题1322 Random Number 无聊题1535 Lucky Ticket 无聊题1539 Lot 无聊题1363 Chocolate 经典题……1366 Cash Machine 经典题！强烈推荐！1149 Dividing up 经典题，应该可以用1366的方法做，但似乎可以利用问题的特殊性用贪心+DP在O(1)的时间内做出来1222 Just the Facts 经典题，没有完美解决，我的做法是O(logn^2)的，据说可能有O(logn)的做法，但我没想到:(1475 Ranklist 没有完美解决，不知道您有没有好方法……1572 Bracelet ~~~题义不明，感觉可能是判定欧拉回路的存在性，但是过不去，555……1133 Smith Numbers 没有完美解决，数学1080 Direct Subtraction 尚未解决，我过的程序是错的，想和您讨论~~~1229 Gift?! SRbGa的经典题……1238 Guess the Number SRbGa的经典题……1239 Hanoi Tower Troubles Again! SRbGa的经典题……字符串处理:1050 Start Up the Startup 简单题1315 Excuses, Excuses! 简单题1151 Word Reversal 简单题，好像是什么Practice的……1170 String Matching 简单题1174 Skip Letter Code 不错的简单题1175 Word Process Machine 简单题1181 Word Amalgamation 简单题1038 T9 无聊题，单词树1330 DNA Translation 无聊题1335 Letter Sequence Analysis 无聊题1099 HTML 无聊题1243 URLs 无聊题1540 Censored! 经典题！强烈推荐！1511 Word Puzzles 没有完美解决的题，可以用后缀树……但是没多大意义……而且我通过的程序是错的……搜索:1002 Fire Net 简单题，CEOI2002的Guard的缩小版，搜索就可以1003 Crashing Balloon 简单题，很faint的题目，想了半天，最后发现最简单的搜索就能过1004 Anagrams by Stack 简单题，同样faint1320 DEL Command 简单题1496 Best Fit 简单题1179 Finding Rectangles 简单题1190 Optimal Programs 简单题1217 Eight 简单题1204 Additive equations 简单题1219 Pizza Anyone? 简单题1036 Enigma 2 无聊题，终于耐心读完题目后发现是简单的搜索+模拟……faint……建议不要看……1089 Lotto 无聊题1054 For the Porsche 无聊题1302 Ships ……题1031 Square Destroyer 变态题，:(:(:(:(，狂剪枝才过的……1297 Hexagon 变态题，标准解法是搜索……1008 Gnome Tetravex 经典题，个人感觉是很不错的卡时搜索，不过似乎IOI不会出这种题型……1380 Microfiches 经典题！强烈推荐！1252 Island of Logic 经典题，不过也够老了……1237 Fans and Gems SRbGa的经典题，变态，但是很有趣:)模拟:1051 A New Growth Industry 简单题1300 Border 简单题1326 M*A*S*H 简单题1494 Climbing Worm 简单题1072 Microprocessor Simulation 简单题1098 Simple Computers 简单题1056 The Worm Turns 简单题1195 Blowing Fuses 简单题1189 Numbers That Count 简单题1144 Robbery 简单题1153 Tournament Seeding 简单题，但是直接计算好像不行，得模拟……:(1167 Trees on the Level 简单题1200 Mining 简单题1278 Pseudo-Random Numbers 简单题1257 Parking Lot 简单题1270 Nonstop Travel 简单题1207 The Knight, the Princess, and the Dragons 无聊题1169 Square Cipher 无聊题1176 Die and Chessboard 无聊题1178 Booklet Printing 无聊题1009 Enigma 无聊题，但是很容易错……:(1012 Mainframe 无聊题，但是很容易错……:(1324 Unix ls 无聊题，输出格式没说清楚~~~~~~~1336 Mark-up 无聊题1277 Transferable V oting 无聊题1279 Cowculations 无聊题1281 Hi-Q 无聊题1282 Call Forwarding 无聊题1065 Robots 变态题，太复杂啦~~~~~~~~~~~1208 Roll the Die! 变态题1388 Exchanges 经典题！强烈推荐！1236 Eat or Not to Eat? SRbGa的经典题……模拟几何:1575 Koch Curve 简单题1010 Area 简单题1565 Input 简单题1081 Points Within 简单题1165 Laser Lines 简单题，但是算法能否再改进呢……？1248 Video Surveillance 简单题，李彭煦的论文中写到过，好像是某年CTSC的……1299 Pendulum 简单题，我蛮喜欢的:)1090 The Circumference of the Circle 无聊题1271 Doing Windows 无聊题1280 Intersecting Lines 无聊题1296 Stars 经典变态题……1030 Farmland 变态题……现在我都为自己当时居然能做出来感到不可思议……1041 Transmitters 变态题……好烦人……现在绝对没有信心再做一遍了……1158 Treasure Hunt 经典题，zig教会我的……1139 Rectangles 没有完美解决其它:1006 Do the Untwist 简单题1014 Operand 简单题1016 Parencodings 简单题1042 W s Cipher 简单题1047 Image Perimeters 简单题1514 Fake Tickets 简单题1029 Moving Tables 简单题，好像是线段树的经典题目之一，但是这题规模比较小，所以不必用。

最优连通子集Description(poj1192)众所周知，我们可以通过直角坐标系把平面上的任何一个点P用一个有序数对(x, y)来唯一表示，如果x, y都是整数，我们就把点P称为整点，否则点P称为非整点。

我们把平面上所有整点构成的集合记为W。

定义1 两个整点P1(x1, y1), P2(x2, y2)，若|x1-x2| + |y1-y2| = 1，则称P1, P2相邻，记作P1~P2，否则称P1, P2不相邻。

定义 2 设点集S是W的一个有限子集，即S = {P1, P2,..., Pn}(n >= 1)，其中Pi(1 <= i <= n)属于W，我们把S称为整点集。

定义 3 设S是一个整点集，若点R, T属于S，且存在一个有限的点序列Q1, Q2, ?, Qk满足:1. Qi属于S（1 <= i <= k）;2. Q1 = R, Qk = T;3. Qi~Qi + 1(1 <= i <= k-1)，即Qi与Qi + 1相邻;4. 对于任何1 <= i < j <= k有Qi ≠ Qj;我们则称点R与点T在整点集S上连通，把点序列Q1, Q2,..., Qk称为整点集S中连接点R与点T的一条道路。

定义4 若整点集V满足：对于V中的任何两个整点，V中有且仅有一条连接这两点的道路，则V称为单整点集。

定义5 对于平面上的每一个整点，我们可以赋予它一个整数，作为该点的权，于是我们把一个整点集中所有点的权的总和称为该整点集的权和。

我们希望对于给定的一个单整点集V，求出一个V的最优连通子集B，满足：1. B是V的子集2. 对于B中的任何两个整点，在B中连通；3. B是满足条件(1)和(2)的所有整点集中权和最大的。

Input第1行是一个整数N（2 <= N <= 1000），表示单整点集V中点的个数；以下N行中，第i行(1 <= i <= N)有三个整数，Xi, Yi, Ci依次表示第i个点的横坐标，纵坐标和权。

121. 已知集合A= x N ------------ N ,用列举法表示集合 A=_ ____________6 x2. 为了保证信息安全传输，有一种称为秘密密钥密码系统，其加密、解密原理如下图： 明文 加密密钥密码 一密文 发送— 解密密钥密码_ 明文， 现在加密密钥为y=log a (x+2),如下所示：明文“ 6”通过加密后得到密文“ 3”，再发送，接受方通过解密密钥解密得明文 “6”，问“接受方接到密文” 4“，则解密后得到明文为 3. 已知A={x|| x-1|<cc>0}, B={x|| x-3|>4} 且A n B= $ 则满足 条件的c 的 集合为4. 设集合 A={5,log 2(a+3)},集合 B={a,b}.若 A n B={2},则 A B 5•点(x,y)在映射f 下的象是(2x-y,2x+y),点(4,6)在映射f 下的原象为八. 2 八. 6.设集合 A {x||x| 4}, B {x|x 4x 3 0}则集合{x|x A 且x A B}=7已知集合A {x| 2 x 4}, B {x|x a},且满足A B的取值范围是8.若P{x|1 x 4},Q {x|x 3或x 1},则P Q .P9.设UR,M{x|x12,xR}, N {1,2,3,4},则(C u M)10.设A {x| a 1x 2 Dx 2B {x | a 2xb 2x C 2 0},则方程(a"2b 1xc 1) (a 2xb 2xc 2)0的解集为的总和等于16040, 11. 已知一个4元集合S 的所有子集的元素和 (空集的元素和认为是零) 则S 的元素之和等于 _______________ .12. 已知集合 A = {x|x 2+ x -6= 0}, B = {x|mx + 1 = 0}.若 B A,则实数 成的集合为 __________________ .13. 设 U 为全集，集合 A {x| 1 x 2}, B {x| x a}，若 A (C U B) ，则a 的取值范围是 ___________ .14.15. m 所能取的一切值构设集合 A = {x || x |<4} ,B = {X |X <1 或 x >3}，则集合{X |X € A 且 x A n B}= 设 T={(x,y)| ax+y-3=0},S={(x,y)| x-y-b=0}.若 S n T={(2,1)},则 a= ______ ,b= 16.设a,b 是非零实数，那么旦a b—可能取的值组成集合的元素是b17. (2) (3) (4) (5) R___Z, R___Q,① ___{0}(1)填空：N___Z, N___Q若 A={x € R|x -3X -4=0},B={X € Z||x|<10},则 A B 正确吗？ 是否对任意一个集合 A ,都有A A ,为什么？ 集合{a,b}的子集有那些？-(1)班同学组成的集合 A ,高一年级同学组成的集合 B ,则A 、B 的关系为U= 1,2,3,4,5,6,7,8 , A C U B 1,8 , C U A B 2,6.口18. 已知 C U AC U B 4,7 ,则集合A=19. 集合P= x, y x y 0 , Q= x, y x y 2 ，则A n B= ______________ *20. 已知集合A=用列举法表示集合A= ___________ .21. 已知U= 1,234,5,6,7,8 , A C u B 1,8 , C U A B 2,6 ,C u A C u B 4,7 ,则集合A= _______________ .22. 非空集合G关于运算㊉满足，①对任意a、b G，都有a+b G ;②存在e G，使对一切e G都有a㊉e=e(^a=a,则称G关于运算㊉的融洽集，现有下列集合和运算：(1)G=非负整数},曲整数的加法(2)G={偶数},③整数的中法(3)G={平面向量},㊉平面向量的加法(4)G={二次三项式},曲多项式加法其中为融洽集的为__________________________ (写出所有符合题意的序号)223. 已知集合A x|xa < 1 , B xx 5x 4 > 0 .若AI B ，则实数a的取值范围是___________ .24. 给定三元集合{1, x, x2 x}，则实数x的取值范围是________________ 。

罗湖逻辑mba试题及答案一、选择题（每题2分，共10分）1. 如果所有苹果都是水果，那么以下哪项陈述是正确的？A. 所有水果都是苹果B. 一些水果可能是苹果C. 没有水果是苹果D. 一些苹果不是水果答案：B2. 以下哪个选项最能代表演绎推理的结论？A. 如果下雨，地面就会湿。

现在地面湿了，所以一定下雨了。

B. 如果下雨，地面就会湿。

现在下雨了，所以地面会湿。

C. 如果地面湿了，那么可能下雨了。

D. 地面湿了，但不一定下雨。

答案：B3. 以下哪个陈述是逻辑上的谬误？A. 因为张三很高，所以他一定是篮球运动员。

B. 张三和李四都是工程师，所以他们一定有相同的技能。

C. 张三比李四高，所以张三一定比所有人都高。

D. 张三和李四都很高，所以他们都是篮球运动员。

答案：A4. 以下哪个选项是有效的逻辑论证？A. 所有猫都有尾巴，所以没有尾巴的都不是猫。

B. 有些猫是黑色的，所以所有猫都是黑色的。

C. 有些猫有尾巴，所以所有猫都有尾巴。

D. 所有猫都有尾巴，所以有些猫有尾巴。

答案：A5. 如果“只有当一个人是医生时，他才能开处方”，那么以下哪项陈述是正确的？A. 如果一个人能开处方，那么他一定是医生。

B. 如果一个人是医生，那么他一定能够开处方。

C. 如果一个人不能开处方，那么他一定不是医生。

D. 如果一个人不是医生，那么他一定能够开处方。

答案：A二、简答题（每题5分，共20分）1. 请解释什么是归纳推理和演绎推理的区别。

答案：归纳推理是从个别事实或实例出发，推广到一般性结论的过程。

而演绎推理则是从一般性原理出发，通过逻辑推导出特定情况下的结论。

2. 什么是逻辑谬误，能否给出一个例子？答案：逻辑谬误是指在推理过程中出现的逻辑错误，导致结论不可靠。

例如，人身攻击谬误：因为张三是个不诚实的人，所以他的论点一定是错误的。

3. 请解释什么是条件命题，并给出一个例子。

答案：条件命题是一种陈述，它表明一个事件的发生是另一个事件发生的条件。

POJ1390Blocks（DP+思维）题解题意：有⼀排颜⾊的球，每次选择⼀个球消去，那么这个球所在的同颜⾊的整段都消去（和消消乐同理），若消去k个，那么得分k*k，问你消完所有球最⼤得分思路：显然这⾥我们直接⽤⼆位数组设区间DP⾏不通，我们不能表⽰出“合并”这种情况。

我们先把所有⼩块整理成连续的⼤块。

我们⽤click（l，r，len）表⽰消去l到r的所有⼤块和r后len块和r颜⾊⼀样的⼩块的最⼤得分。

那么这样我们可以知道，click（l，r，len）只有两种情况：1.r直接和后⾯len全都消去2.r带着len先和前⾯的⼀样的颜⾊的⼀起消代码：#include<cmath>#include<stack>#include<cstdio>#include<vector>#include<cstring>#include <iostream>#include<algorithm>using namespace std;typedef long long ll;const int maxn = 200 + 10;const int INF = 0x3f3f3f3f;const int MOD = 1000000007;int num[maxn], a[maxn], p[maxn], cnt;int dp[maxn][maxn][maxn];//j后还有k个⼀样的⼩块int click(int l, int r, int len){if(l > r) return0;if(dp[l][r][len]) return dp[l][r][len];if(l == r) return dp[l][r][len] = (num[l] + len) * (num[l] + len);dp[l][r][len] = click(l, r - 1, 0) + (num[r] + len) * (num[r] + len);for(int i = l; i < r; i++){if(p[i] != p[r]) continue;dp[l][r][len] = max(dp[l][r][len], click(l, i, num[r] + len) + click(i + 1, r - 1, 0));}return dp[l][r][len];}int main(){int t, ca = 1;scanf("%d", &t);while(t--){int n;scanf("%d", &n);memset(num, 0, sizeof(num));memset(dp, 0, sizeof(dp));for(int i = 1; i <= n; i++) scanf("%d", &a[i]);cnt = 0;a[0] = -INF;for(int i = 1; i <= n; i++){if(a[i] != a[i - 1]){++cnt;num[cnt]++;p[cnt] = a[i];}else{num[cnt]++;}}printf("Case %d: %d\n", ca++, click(1, cnt, 0));}return0; }。

经典数学选修1-1常考题单选题（共5道）1、若命题“p或q”为真，“非p”为真，则[]Ap真q真Bp假q真Cp真q假Dp假q假2、命题“ ？x€ R, ex>cosx+x”的否定是（）A?xO € R, ex0 v cosxO+xOexOB?x € R ex v cosx+xC?x € R ex< cosx+xD?x0 € R, ex0< cosxO+xO3、已知椭圆C: ' 的长轴长为4,若点P是椭圆C上任意u~ b-一点，过原点的直线I与椭圆相交于M N两点，记直线PM PN的斜率分别为KPM KPN当心护心严_十时，则椭圆方程为（）Br~2 y2 ]4、(2015秋?江门期末)对于曲线C:—亠=1，给出下面四个命题:卜一& A-1(1)曲线C不可能表示椭圆；(2)若曲线C表示焦点在x轴上的椭圆，贝U 1v k v ;■(3)若曲线C表示双曲线，则k v 1或k>4；(4)当1v k v 4时曲线C表示椭圆，其中正确的是( )A (2) (3)B (1) (3)C (2) (4)D (3) (4)5、给出以下四个命题：①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行；②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面；③如果两条直线都平行于一个平面，那么这两条直线互相平行；④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直；其中真命题的个数是[]A4B3C2D1简答题(共5道)6 (本小题满分12分)求与双曲线•有公共渐近线，且过点".一-的双曲线的标准方程。

(x)=在(0，+x)上是减函数.X"7、证明:48、已知函数- ，二. -(一：三二).(1)若x= 3是. 的极值点，求- 在，三［1 , a］上的最小值和最大值;(2)若上上；=「门-£：鬥在时是增函数，求实数a的取值范围.9、(本小题满分12分)求与双曲线有公共渐近线，且过点-的双曲线的标准方程。