极值点偏移PPT
- 格式:ppt
- 大小:1.15 MB
- 文档页数:16



极值点偏移问题与拐点偏移问题【考点预测】1.极值点偏移的相关概念所谓极值点偏移,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有对称性。
若函数f (x )在x =x 0处取得极值,且函数y =f (x )与直线y =b 交于A (x 1,b ),B (x 2,b )两点,则AB 的中点为M x 1+x 22,b ,而往往x 0≠x 1+x 22。
如下图所示。
图1 极值点不偏移图2 极值点偏移极值点偏移的定义:对于函数y =f (x )在区间(a ,b )内只有一个极值点x 0,方程f (x )的解分别为x 1、x 2,且a <x 1<x 2<b ,(1)若x 1+x 22≠x 0,则称函数y =f (x )在区间(x 1,x 2)上极值点x 0偏移;(2)若x 1+x 22>x 0,则函数y =f (x )在区间(x 1,x 2)上极值点x 0左偏,简称极值点x 0左偏;(3)若x 1+x 22<x 0,则函数y =f (x )在区间(x 1,x 2)上极值点x 0右偏,简称极值点x 0右偏。
【方法技巧与总结】1.对称变换主要用来解决与两个极值点之和、积相关的不等式的证明问题.其解题要点如下:(1)定函数(极值点为x 0),即利用导函数符号的变化判断函数单调性,进而确定函数的极值点x 0.(2)构造函数,即根据极值点构造对称函数F (x )=f (x )-f (2x 0-x ),若证x 1x 2>x 20,则令F (x )=f (x )-f 2x 0x.(3)判断单调性,即利用导数讨论F (x )的单调性.(4)比较大小,即判断函数F (x )在某段区间上的正负,并得出f (x )与f (2x 0-x )的大小关系.(5)转化,即利用函数f (x )的单调性,将f (x )与f (2x 0-x )的大小关系转化为x 与2x 0-x 之间的关系,进而得到所证或所求.【注意】若要证明f x 1+x 22 的符号问题,还需进一步讨论x 1+x 22与x 0的大小,得出x 1+x 22所在的单调区间,从而得出该处导数值的正负.构造差函数是解决极值点偏移的一种有效方法,函数的单调性是函数的重要性质之一,它的应用贯穿于整个高中数学的教学之中.某些数学问题从表面上看似乎与函数的单调性无关,但如果我们能挖掘其内在联系,抓住其本质,那么运用函数的单调性解题,能起到化难为易、化繁为简的作用.因此对函数的单调性进行全面、准确的认识,并掌握好使用的技巧和方法,这是非常必要的.根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效2.应用对数平均不等式x1x2<x1-x2ln x1-ln x2<x1+x22证明极值点偏移:①由题中等式中产生对数;②将所得含对数的等式进行变形得到x1-x2ln x1-ln x2;③利用对数平均不等式来证明相应的问题.3.比值代换是一种将双变量问题化为单变量问题的有效途径,然后构造函数利用函数的单调性证明题中的不等式即可.【题型归纳目录】题型一:极值点偏移:加法型题型二:极值点偏移:减法型题型三:极值点偏移:乘积型题型四:极值点偏移:商型题型五:极值点偏移:平方型题型六:拐点偏移问题【典例例题】题型一:极值点偏移:加法型例1.(2022•浙江期中)已知函数f(x)=x-ln x-a有两个不同的零点x1,x2.(1)求实数a的取值范围;(2)证明:x1+x2>a+1.例2.(2022•汕头一模)已知函数f(x)=x-ln x-a有两个相异零点x1,x2(x1<x2).(1)求a的取值范围;(2)求证:x1+x2<4a+23.例3.(海淀区校级月考)已知函数f(x)=(x-2)e x+a(x-1)2,a∈R.(Ⅰ)求曲线y=f(x)在点P(1,f(1))处的切线方程;(Ⅱ)若a≥0,求f(x)的零点个数;(Ⅲ)若f(x)有两个零点x1,x2,证明:x1+x2<2.例4.(2022•江门一模)已知函数f(x)=ln|x-1|-ax,a∈R是常数.(Ⅰ)求曲线y=f(x)在点(2,f(2))处的切线方程,并证明对任意a∈R,切线经过定点;(Ⅱ)证明:a<0时,设x1、x2是f(x)的两个零点,且x1+x2>2.题型二:极值点偏移:减法型例5.(2022•七星区校级月考)已知函数f(x)=x ln x-a2x2+1.(1)若f(x)在(0,+∞)上单调递减,求a的取值范围;(2)若f(x)在x=1处的切线斜率是12,证明f(x)有两个极值点x1x2,且3ln2<|ln x2-ln x1|<3.例6.(2022•常熟市月考)设函数f(x)=ln x,g(x)=a(x-1),其中a∈R.(1)若a=1,证明:当x>1时,f(x)<g(x);(2)设F(x)=f(x)-g(x)e x,且0<a<1e,其中e是自然对数的底数.①证明F(x)恰有两个零点;②设x0如为F(x)的极值点,x1为F(x)的零点,且x1>x0,证明:3x0-x1>2.例7.(2022•黄州区校级模拟)已知函数f(x)=ax ln x-(a+1)ln x,f(x)的导数为f (x).(1)当a>-1时,讨论f (x)的单调性;(2)设a>0,方程f(x)=3e-x有两个不同的零点x1,x2(x1<x2),求证:x1+e>x2+1e.例8.(2022•道里区校级二模)已知函数f(x)=mx ln x-(m+1)ln x,f (x)为函数f(x)的导数.(1)讨论函数f (x)的单调性;(2)若当m>0时,函数f(x)与g(x)=3e-x的图象有两个交点A(x1,y1),B(x2,y2)(x1<x2),求证:x2+1e<x1+e.题型三:极值点偏移:乘积型例9.(2021春•汕头校级月考)已知,函数f(x)=ln x-ax,其中a∈R.(1)讨论函数f(x)的单调性;(2)若函数f(x)有两个零点,(i)求a的取值范围;(ii)设f(x)的两个零点分别为x1,x2,证明:x1x2>e2.例10.(2022•攀枝花模拟)已知函数f(x)=ln x+bx-a(a∈R,b∈R)有最小值M,且M≥0.(Ⅰ)求e a-1-b+1的最大值;(Ⅱ)当e a-1-b+1取得最大值时,设F(b)=a-1b-m(m∈R),F(x)有两个零点为x1,x2(x1<x2),证明:x1⋅x22>e3.例11.(2022•张家口二模)已知函数f(x)=e x-a ln xx-a(e是自然对数的底数)有两个零点.(1)求实数a的取值范围;(2)若f(x)的两个零点分别为x1,x2,证明:x1x2>e2e x1+x2.例12.(2022•武进区校级月考)已知函数f (x )=ln x +12x 2-ax .(1)若函数f (x )在x =1处的切线与x 轴平行,求a 的值;(2)若存在t ∈[-1,1],使不等式f (x )≤tx -(a -1)ln x 对于x ∈[1,e ]恒成立,求a 的取值范围;(3)若方程f (x )=12x 2有两个不等的实数根x 1、x 2,试证明x 1x 2>e 2.题型四:极值点偏移:商型例13.已知函数f (x )=x -e x a (a >0)有两个相异零点x 1、x 2,且x 1<x 2,求证:x 1x 2<e a.例14.(2022•新疆模拟)已知函数f(x)=ln x-ax+12x2.(1)当a=52时,求f(x)的单调区间;(2)已知a≥433,x1,x2(x1>x2)为函数f(x)的两个极值点,求y=2(x1-x2)x1+x2-lnx1x2的最大值.例15..(2021春•湖北期末)已知函数f(x)=ae-x+ln x-1(a∈R).(1)当a≤e时,讨论函数f(x)的单调性:(2)若函数f(x)恰有两个极值点x1,x2(x1<x2),且x1+x2≤(2e+1)⋅ln2e2e-1,求x2x1的最大值.例16.(2022•宁德三模)已知函数f(x)=ae-x+ln x-1(a∈R).(1)当a≤e时,讨论函数f(x)的单调性:(2)若函数f(x)恰有两个极值点x1,x2(x1<x2),且x1+x2≤2ln3,求x2x1的最大值.题型五:极值点偏移:平方型例17.(2022•广州一模)已知函数f(x)=x ln x-ax2+x(a∈R).(1)证明:曲线y=f(x)在点(1,f(1))处的切线l恒过定点;(2)若f(x)有两个零点x1,x2,且x2>2x1,证明:x21+x22>4e.例18.(2022•浙江开学)已知a∈R,f(x)=x⋅e-ax(其中e为自然对数的底数).(Ⅰ)求函数y=f(x)的单调区间;(Ⅱ)若a>0,函数y=f(x)-a有两个零点x,x2,求证:x21+x22>2e.例19.(2021秋•泉州月考)已知函数f(x)=ln x+1 ax.(1)讨论f(x)的单调性;(2)若(ex1)x2=(ex2)x1(e是自然对数的底数),且x1>0,x2>0,x1≠x2,证明:x21+x22>2.例20.(2022•开封三模)已知函数f(x)=ln x mx2.(1)讨论f(x)的单调性;(2)若m=2,对于任意x1>x2>0,证明:(x21⋅f(x1)-x22⋅f(x2))⋅(x21+x22)>x1x2-x22.题型六:拐点偏移问题例21.已知函数f(x)=2ln x+x2+x.(1)求曲线y=f(x)在点(1,f(1))处的切线方程.(2)若正实数x1,x2满足f(x1)+f(x2)=4,求证:x1+x2≥2.例22.已知函数f(x)=12a x2-1+1a2x+1a Inx(a∈R).(1)当a>0时,讨论函数f(x)的单调性;(2)当a=12时,设g(x)=f(x)+6x,若正实数x1,x2,满足g(x1)+g(x2)=4,求证:x1+x2≥2.例23.已知函数f(x)=ln x+2x-ax2,a∈R.(Ⅰ)若f(x)在x=1处取得极值,求a的值;(Ⅱ)设g(x)=f(x)+(a-4)x,试讨论函数g(x)的单调性;(Ⅲ)当a=-2时,若存在正实数x1,x2满足f(x1)+f(x2)+3x1x2=x1+x2,求证:x1+x2>12.【过关测试】1.(2022·天津河东·二模)已知函数f x =x2a-2ln x(a∈R且a≠0).(1)a=2,求函数f x 在2,f2处的切线方程.(2)讨论函数f x 的单调性;(3)若函数f x 有两个零点x1、x2x1<x2,且a=e2,证明:x1+x2>2e.2.(2022·河北·沧县中学高二阶段练习)已知函数f x =x+3x+2ln x-a a∈R有两个不同的零点x1,x2.(1)求实数a的取值范围;(2)求证:x1x2>1.3.(2022·江苏泰州·模拟预测)已知函数f x =e x-ax2+bx-1,其中a,b为常数,e为自然对数底数,e =2.71828⋅⋅⋅.(1)当a=0时,若函数f x ≥0,求实数b的取值范围;(2)当b=2a时,若函数f x 有两个极值点x1,x2,现有如下三个命题:①7x1+bx2>28;②2a x1+x2>3x1x2;③x1-1+x2-1>2;请从①②③中任选一个进行证明.(注:如果选择多个条件分别解答,按第一个解答计分)4.(2022·湖北武汉·模拟预测)已知函数f x =x-ln x(1)求证:当x>1时,ln x>2x-1x+1;(2)当方程f x =m有两个不等实数根x1,x2时,求证:x1+x2>m+15.(2022·浙江绍兴·模拟预测)已知函数f x =e x-2x-a+1(其中ex-a+2,g x =x2+a-1≈2.71828是自然对数的底数)(1)试讨论函数f x 的零点个数;(2)当a>1时,设函数h x =f x -g x 的两个极值点为x1、x2且x1<x2,求证:e x2-e x1<4a+2.e x-k(x-1),x>-1,k∈R.6.(2022·安徽淮南·二模(理))已知函数f(x)=1-2x+1(1)若k=0,证明:x∈(-1,0)时,f(x)<-1;(2)若函数f(x)恰有三个零点x1,x2,x3,证明:x1+x2+x3>1.7.(2022·湖南·岳阳一中一模)已知函数f x =a ln x+2-x a∈R.(1)讨论f(x)的单调性和最值;(2)若关于x的方程e x=2m-1m ln mx+2(m>0)有两个不等的实数根x1,x2,求证:e x1+e x2>2 m.8.(2022·山东·青岛二中高三期末)已知函数f x =x1-a ln x,a∈R.(1)讨论f(x)的单调性;(2)若x∈0,12时,都有f x <1,求实数a的取值范围;(3)若有不相等的两个正实数x1,x2满足1+ln x21+ln x1=x2x1,证明:x1+x2<ex1x2.9.(2021·广东·新会陈经纶中学高三阶段练习)已知函数f x =x1-ln x.(1)讨论f x 的单调性;(2)设a,b为两个不相等的正数,且b ln a-a ln b=a-b,证明:2<1a+1b.10.(2022·全国·高三专题练习)已知函数f x =-e x-ax2a∈R.(1)当a=0时,求曲线y=f x 在点1,f1处的切线方程;(2)当a>0时,若函数g x =xe x+f x ,求g x 的单调区间;(3)当a>0时,若函数h x =f x +2e x-ax恰有两个不同的极值点x1、x2,且x1<x2,求证:x1+x22<ln2a.11.(2022·全国·高三专题练习)已知函数f(x)=a-1-xe x(x>0)(e为自然对数的底数,a∈R).(1)求f(x)的单调区间和极值;(2)若存在x1≠x2,满足f x1=f x2,求证:x1+x2>4aa+2.12.(2022·全国·高三专题练习)已知函数f(x)=x-a-1x+a,a∈R.(1)若f(1)=2,求a的值;(2)若存在两个不相等的正实数x1,x2,满足f(x1)=f(x2),证明:①2<x1+x2<2a;②x2x1<a2+1.13.(2022·四川省泸县第二中学模拟预测(文))已知函数f(x)=x-x.e x(1)求f(x)的单调区间;(2)已知a,b∈R,且a≠b,若ae a+b+be a=ae b+be a+b,求证:a+b>0.。



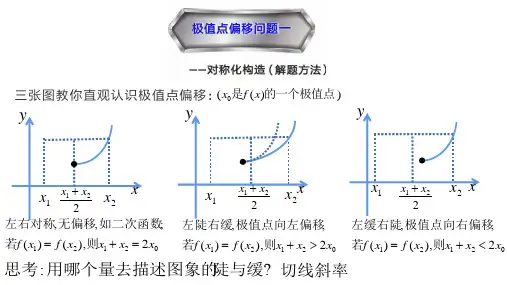



导数及其应用 专题七:极值点偏移问题一、知识储备1、极值点偏移的相关概念所谓极值点偏移,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有对称性。
若函数)(x f 在0x x =处取得极值,且函数)(x f y =与直线b y =交于),(),,(21b x B b x A 两点,则AB 的中点为),2(21b x x M +,而往往2210xx x +≠。
如下图所示。
图1 极值点不偏移 图2 极值点偏移极值点偏移的定义:对于函数)(x f y =在区间),(b a 内只有一个极值点0x ,方程)(x f 的解分别为21x x 、,且b x x a <<<21,(1)若0212x x x ≠+,则称函数)(x f y =在区间),(21x x 上极值点0x 偏移;(2)若0212x x x >+,则函数)(x f y =在区间),(21x x 上极值点0x 左偏,简称极值点0x 左偏;(3)若0212x x x <+,则函数)(x f y =在区间),(21x x 上极值点0x 右偏,简称极值点0x 右偏。
2、对称变换主要用来解决与两个极值点之和、积相关的不等式的证明问题.其解题要点如下:(1)定函数(极值点为0x ),即利用导函数符号的变化判断函数单调性,进而确定函数的极值点x 0.(2)构造函数,即根据极值点构造对称函数0()()(2)F x f x f x x =--,若证2120x x x > ,则令2()()()x F x f x f x=-. (3)判断单调性,即利用导数讨论()F x 的单调性.(4)比较大小,即判断函数()F x 在某段区间上的正负,并得出()f x 与0(2)f x x -的大小关系.(5)转化,即利用函数()f x 的单调性,将()f x 与0(2)f x x -的大小关系转化为x 与02x x -之间的关系,进而得到所证或所求.[提醒] 若要证明122x x f +⎛⎫'⎪⎝⎭的符号问题,还需进一步讨论122x x +与x 0的大小,得出122x x +所在的单调区间,从而得出该处导数值的正负. 二、例题讲解1.(2022·贵州省思南中学高三月考(文))设函数()22ln 1f x x mx =-+.(1)讨论函数()f x 的单调性;(2)当1m =时,若在()f x 定义域内存在两实数1x ,2x 满足12x x <且()()12f x f x =,证明:122x x +>.【详解】(1)依题意,函数()f x 定义域为(0,)+∞,()222(1)2mx f x mx x x-'=-=,当0m ≤时,()0f x '>,()f x 在(0,)+∞上单调递增,当0m >时,由()0f x '=得m x m =,当0mx m <<时,()0f x '>,当m x m >时,()0f x '<,于是得()f x 在(0,)m m 上单调递增,在(,)mm+∞上单调递减,所以,当0m ≤时,()f x 在(0,)+∞上单调递增,当0m >时,()f x 在(0,)m m 上单调递增,在(,)mm+∞上单调递减;(2)分析 :如图:1201x x <<< 要证122x x +> 只需证:122x x -<由于101x <<,则112x <-即只需证1212x x <-< 如图,只需证12(2)()f x f x ->;由于()()12f x f x = 只需证11(2)()f x f x ->此时可构造函数()()(2)F x f x f x =--(即用x 替代了上式1x ) 只需证:在01x <<,()()(2)0F x f x f x =--<。
