大学物理上册期末考试重点例题
- 格式:docx
- 大小:644.58 KB
- 文档页数:20

n 3上海电机学院 200_5_–200_6_学年第_二_学期《大学物理 》课程期末考试试卷 1开课学院: ,专业: 考试形式:闭卷,所需时间 90 分钟考生姓名: 学号: 班级 任课教师一、填充題(共30分,每空格2分) 1.一质点沿x 轴作直线运动,其运动方程为3262xt t m ,则质点在运动开始后4s 内位移的大小为___________,在该时间内所通过的路程为_____________。
2.如图所示,一根细绳的一端固定,另一端系一小球,绳长0.9L m =,现将小球拉到水平位置OA 后自由释放,小球沿圆弧落至C 点时,30OC OA θ=与成,则 小球在C 点时的速率为____________, 切向加速度大小为__________,法向加速度大小为____________。
(210g m s =)。
3.一个质点同时参与两个在同一直线上的简谐振动,其振动的表达式分别为:2155.010cos(5t )6x m 、2113.010cos(5t )6x m 。
则其合振动的频率为_____________,振幅为 ,初相为 。
4、如图所示,用白光垂直照射厚度400d nm 的薄膜,若薄膜的折射率为 21.40n ,且12n n n 3,则反射光中 nm ,波长的可见光得到加强,透射光中 nm 和___________ nm 可见光得到加强。
5.频率为100Hz ,传播速度为sm 300的平面波,波 长为___________,波线上两点振动的相差为3π,则此两点相距 ___m 。
6. 一束自然光从空气中入射到折射率为1.4的液体上,反射光是全偏振光,则此光束射角等于______________,折射角等于______________。
二、选择題(共18分,每小题3分) 1.一质点运动时,0=n a ,ta c (c 是不为零的常量),此质点作( )。
(A )匀速直线运动;(B )匀速曲线运动; (C ) 匀变速直线运动; (D )不能确定 2.质量为1mkg 的质点,在平面内运动、其运动方程为x=3t ,315t y -=(SI 制),则在t=2s 时,所受合外力为( )(A) 7j; (B) j 12- ; (C) j 6- ; (D) j i +6 3.弹簧振子做简谐振动,当其偏离平衡位置的位移大小为振幅的41时,其动能为振动 总能量的( )(A )916 (B )1116 (C )1316 (D )15164. 在单缝夫琅和费衍射实验中波长为λ的单色光垂直入射到单缝上,对应于衍 射角为300的方向上,若单逢处波面可分成3个半波带,则缝宽度a 等于( ) (A.) λ (B) λ (C) 2λ (D) 3λ5. 一质量为M 的平板车以速率v 在水平方向滑行,质量为m 的物体从h 高处直落到车子里,两者合在一起后的运动速率是( ) (A.)M M mv+ (B).M m 2v gh + (C). m 2gh (D).v6. 一平面简谐波在弹性媒质中传播,媒质中的某质元从其平衡位置运动到最大位移处的过程中( )(A) 它的动能转化为势能(B) 它的势能转化为动能(C) 它从相邻的媒质质元获得能量,其能量逐渐增加 (D)它从相邻的媒质质元传出能量,其能量逐渐减少 三、計算題(52分)1、(12分)如图所示,路灯离地面高度为H ,一个身高为h 的人,在灯下水平路面上以匀速度0v 步行,求他的头顶在地面上的影子移动的速度大小。


姓名班级学号………密……….…………封…………………线…………………内……..………………不…………………….准…………………答….…………题…大学基础教育《大学物理(一)》期末考试试题附答案考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、请仔细阅读各种题目的回答要求,在密封线内答题,否则不予评分。
一、填空题(共10小题,每题2分,共20分)1、气体分子的最可几速率的物理意义是__________________。
2、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
3、一质量为0.2kg的弹簧振子, 周期为2s,此振动系统的劲度系数k为_______ N/m。
4、均匀细棒质量为,长度为,则对于通过棒的一端与棒垂直的轴的转动惯量为_____,对于通过棒的中点与棒垂直的轴的转动惯量_____。
5、已知质点的运动方程为,式中r的单位为m,t的单位为s。
则质点的运动轨迹方程,由t=0到t=2s内质点的位移矢量______m。
6、四根辐条的金属轮子在均匀磁场中转动,转轴与平行,轮子和辐条都是导体,辐条长为R,轮子转速为n,则轮子中心O与轮边缘b之间的感应电动势为______________,电势最高点是在______________处。
7、质点在平面内运动,其运动方程为,质点在任意时刻的位置矢量为________;质点在任意时刻的速度矢量为________;加速度矢量为________。
8、一质点作半径为R的匀速圆周运动,在此过程中质点的切向加速度的方向______,法向加速度的大小______。
(填“改变”或“不变”)9、一质点在OXY平面内运动,其运动方程为,则质点在任意时刻的速度表达式为________;加速度表达式为________。


...质点运动学选择题[]1、某质点作直线运动的运动学方程为x=6+3t-5tA、匀加速直线运动,加速度沿x 轴正方向.B、匀加速直线运动,加速度沿x 轴负方向.C、变加速直线运动,加速度沿x 轴正方向.D、变加速直线运动,加速度沿x 轴负方向.3(SI),那么点作dv2,式中的k为大于零的常量.当t0时, []2、某物体的运动规律为kvtdt初速v0,那么速度v与时间 t的函数关系是1122A、vktv0B、vktv022111122C、ktv0ktv,D、0v2v2[]3、质点作半径为R的变速圆周运动时的加速度大小为(v表示任一时刻质点的速率)A、dvdt B、2vRC、dvdt2vRD、(dvdt)24v2R[]4、关于曲线运动表达错误的选项是A、有圆周运动的加速度都指向圆心B、圆周运动的速率和角速度之间的关系是vrC、质点作曲线运动时,某点的速度方向就是沿该点曲线的切线方向D、速度的方向一定与运动轨迹相切[]5、以r表示质点的位失,S表示在t的时间内所通过的路程,质点在t时间内平均速度的大小为A、S;B、tr C、trt;D、rt填空题6、质点的运动方程为2r6ti(3t4)j(SI),那么该质点的轨道方程为;t4s时速度的大小;方向。
7、在xy平面内有一运动质点,其运动学方程为:r10cos5ti10sin5tj〔SI〕,那么t时刻其速度v;其切向加速度的大小a;该质t点运动的轨迹是。
8、在 x轴上作变加速直线运动的质点, 其初速度为v0,初始位置为x0加速度为a=Ct 2(其中C为常量),那么其速度与时间的关系v=,运word格式资料为x=。
9、质点沿x 方向运动,其加速度随时关系为a = 3+2 t(SI) ,如果初始时质点的速度v 0为5 m/s ,那么当t为3s 时,质点的速度v=。
10 2 32t(SI),那么t时刻质点的法向加速度大小为a n =;角加速度=。
11 2 0.2rads ,当t =2 s 时 边缘上某点的速度大小v =;法向加速度大小 a =;切向加速度n 大小 a =;和合加速度大小a =。

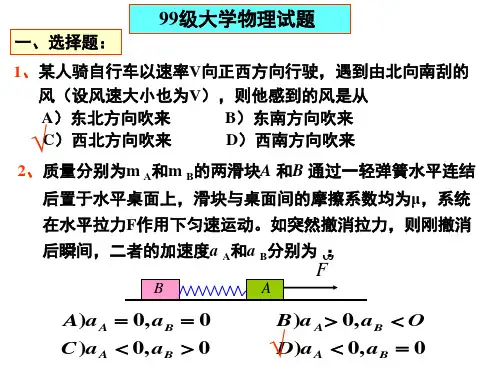
一、选择题:的分布2.如图所示,任一闭合曲面S 内有一点电荷0,。
为S 面上任一点,若将0由闭合曲面内的P 点移到T 点,且OP=OT,(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零 (B)闭合面内的电荷代数和不为零时,闭合面上各点场强一定都不为零练习一1.两个均匀带电的同心球面, 半径分别为R1、R2(R1<R2),小球带电Q,大球带电-Q,下列各图中哪一个正确表示了电场 o R x R 2(0 O R X R 2(D)那么(A) 穿过S 面的电通量改变, 。
点的场强大小不变; (B) 穿过S 面的电通量改变, 。
点的场强大小改变; (C) 穿过S 面的电通量不变, 。
点的场强大小改变; (D) 穿过S 面的电通量不变, 。
点的场强大小不变。
3.在边长为。
的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为(A) q/Eo ; (B) q/2跖; (C) ^/4EO ; (D) q/6£o 。
4.如图所示,a 、c 是电场中某条电场线上的三个点,由此可知 (A) E a >E fc >E c ; (B) E/EovEc ; (C) UplVUc ;(D) UgvUc 。
5. 关于高斯定理的理解有下面几种说法,其中正确的是 (A) 如果高斯面内无电荷,则高斯面上E 处处为零; (B) 如果高斯面上E 处处不为零,则该面内必无电荷; (C) 如果高斯面内有净电荷,则通过该面的电通量必不为零; (D)如果高斯面上E 处处为零,则该面内必无电荷。
6. 对静电场高斯定理的理解,下列四种说法中正确的是(A) 如果通过高斯面的电通量不为零,则高斯面内必有净电荷 (B) 如果通过高斯面的电通量为零,则高斯面内必无电荷 (C) 如果高斯面内无电荷,则高斯面上电场强度必处处为零 (D) 如果高斯面上电场强度处处不为零,则高斯面内必有电荷 答:A7.由真空中静电场的高斯定理= —V q 可知s勺(B)平行。

姓名班级学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…大学基础课《大学物理(一)》期末考试试题 附解析考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、请仔细阅读各种题目的回答要求,在密封线内答题,否则不予评分。
一、填空题(共10小题,每题2分,共20分)1、质量分别为m 和2m 的两物体(都可视为质点),用一长为l 的轻质刚性细杆相连,系统绕通过杆且与杆垂直的竖直固定轴O 转动,已知O 轴离质量为2m 的质点的距离为l ,质量为m 的质点的线速度为v 且与杆垂直,则该系统对转轴的角动量(动量矩)大小为________。
2、一根长为l ,质量为m 的均匀细棒在地上竖立着。
如果让竖立着的棒以下端与地面接触处为轴倒下,则上端到达地面时细棒的角加速度应为_____。
3、四根辐条的金属轮子在均匀磁场中转动,转轴与平行,轮子和辐条都是导体,辐条长为R ,轮子转速为n ,则轮子中心O 与轮边缘b 之间的感应电动势为______________,电势最高点是在______________处。
4、一束平行单色光垂直入射在一光栅上,若光栅的透明缝宽度与不透明部分宽度相等,则可能看到的衍射光谱的级次为____________。
5、一质点作半径为0.1m 的圆周运动,其运动方程为:(SI ),则其切向加速度为=_____________。
6、一质点的加速度和位移的关系为且,则速度的最大值为_______________ 。
7、若静电场的某个区域电势等于恒量,则该区域的电场强度为_______________,若电势随空间坐标作线性变化,则该区域的电场强度分布为 _______________。
8、一长为的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动。

第一章 质点运动学习题1-4一质点在xOy 平面上运动,运动方程为=3t +5, y =21t 2+3t -4.(SI ) (式中t 以 s 计,x ,y 以m 计.)(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,并计算这1秒内质点的位移; (3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,并计算t =4 s 时质点的速度; (5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,并计算t =4s 时质点的加速度。
(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1)质点位置矢量 21(35)(34)2r xi yj t i t t j =+=+++-m(2)将1=t ,2=t 代入上式即有211[(315)(1314)](80.5)2t s r i j m i j m ==⨯++⨯+⨯-=-221[(325)(2324)](114)2t s r i j m i j ==⨯++⨯+⨯-=+m21(114)(80.5)(3 4.5)t s t s r r r i j m i j m i j m ==∆=-=+--=+(3) ∵20241[(305)(0304)](54)21[(345)(4344)](1716)2t s t s r i j m i j mr i j m i j m===⨯++⨯+⨯-=-=⨯++⨯+⨯-=+∴ 1140(1716)(54)(35)m s 404t s t s r r r i j i j v m s i j t --==-∆+--===⋅=+⋅∆- (4) 21d d 1[(35)(34)][3(3)]m s d d 2r t i t t j i t j t t -==+++-=++⋅v 则 14[3(43)](37)t s v i j m s i j -==++⋅=+ 1s m -⋅ (5)∵ 1104(33),(37)t s t s v i j m s v i j m s --===+⋅=+⋅∴ 2241(37)(33)m s 1m s 44t s t s v v v i j i j a j t --==-∆+-+===⋅=⋅∆(6) 2d d[3(3)]1m s d d v a i t j j t t-==++=⋅这说明该点只有y 方向的加速度,且为恒量。

第一章 质点运动学习题1-4一质点在xOy 平面上运动,运动方程为=3t +5, y =21t 2+3t -4.(SI ) (式中t 以 s 计,x ,y 以m 计.)(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,并计算这1秒内质点的位移; (3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,并计算t =4 s 时质点的速度; (5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,并计算t =4s 时质点的加速度。
(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1)质点位置矢量 21(35)(34)2r xi yj t i t t j =+=+++-m(2)将1=t ,2=t 代入上式即有211[(315)(1314)](80.5)2t s r i j m i j m ==⨯++⨯+⨯-=-221[(325)(2324)](114)2t s r i j m i j ==⨯++⨯+⨯-=+m21(114)(80.5)(3 4.5)t s t s r r r i j m i j m i j m ==∆=-=+--=+(3) ∵20241[(305)(0304)](54)21[(345)(4344)](1716)2t s t s r i j m i j mr i j m i j m===⨯++⨯+⨯-=-=⨯++⨯+⨯-=+∴ 1140(1716)(54)(35)m s 404t s t s r r r i j i j v m s i j t --==-∆+--===⋅=+⋅∆- (4) 21d d 1[(35)(34)][3(3)]m s d d 2r t i t t j i t j t t -==+++-=++⋅v 则 14[3(43)](37)t s v i j m s i j -==++⋅=+ 1s m -⋅ (5)∵ 1104(33),(37)t s t s v i j m s v i j m s --===+⋅=+⋅∴ 2241(37)(33)m s 1m s 44t s t s v v v i j i j a j t --==-∆+-+===⋅=⋅∆(6) 2d d[3(3)]1m s d d v a i t j j t t-==++=⋅这说明该点只有y 方向的加速度,且为恒量。

姓名班级学号………密……….…………封…………………线…………………内……..………………不…………………….准…………………答….…………题…2021年大学课程《大学物理(上册)》期末考试试卷附解析考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、请仔细阅读各种题目的回答要求,在密封线内答题,否则不予评分。
一、填空题(共10小题,每题2分,共20分)1、某人站在匀速旋转的圆台中央,两手各握一个哑铃,双臂向两侧平伸与平台一起旋转。
当他把哑铃收到胸前时,人、哑铃和平台组成的系统转动角速度应变_____;转动惯量变_____。
2、质量分别为m和2m的两物体(都可视为质点),用一长为l的轻质刚性细杆相连,系统绕通过杆且与杆垂直的竖直固定轴O转动,已知O轴离质量为2m的质点的距离为l,质量为m的质点的线速度为v且与杆垂直,则该系统对转轴的角动量(动量矩)大小为________。
3、质量为m的物体和一个轻弹簧组成弹簧振子,其固有振动周期为T.当它作振幅为A的自由简谐振动时,其振动能量E=__________。
4、长为的匀质细杆,可绕过其端点的水平轴在竖直平面内自由转动。
如果将细杆置与水平位置,然后让其由静止开始自由下摆,则开始转动的瞬间,细杆的角加速度为_____,细杆转动到竖直位置时角加速度为_____。
5、已知质点的运动方程为,式中r的单位为m,t的单位为s。
则质点的运动轨迹方程,由t=0到t=2s内质点的位移矢量______m。
6、一质点作半径为0.1m的圆周运动,其运动方程为:(SI),则其切向加速度为=_____________。
7、一弹簧振子系统具有1.OJ的振动能量,0.10m的振幅和1.0m/s的最大速率,则弹簧的倔强系数为_______,振子的振动频率为_______。
8、设作用在质量为1kg的物体上的力F=6t+3(SI).如果物体在这一力的作用下,由静止开始沿直线运动,在0到 2.0 s的时间间隔内,这个力作用在物体上的冲量大小I=__________________。
刚体复习重点(一)要点质点运动位置矢量(运动方程) r = r (t ) = x (t )i + y (t )j + z (t )k ,速度v = d r/d t = (d x /d t )i +(d y /d t )j + (d z /d t )k ,动量 P=m v加速度 a=d v/d t=(d v x /d t )i +(d v y /d t )j +(d v z /d t )k曲线运动切向加速度 a t = d v /d t , 法向加速度 a n = v 2/r .圆周运动及刚体定轴转动的角量描述 θ=θ(t ), ω=d θ/d t , β= d ω/d t =d 2θ/d t 2,角量与线量的关系 △l=r △θ, v=r ω (v= ω×r ),a t =r β, a n =r ω2力矩 M r F 转动惯量 2i i J r m =∆∑, 2d mJ r m =⎰ 转动定律 t d L M =M J α= 角动量: 质点p r L ⨯= 刚体L=J ω;角动量定理 ⎰tt 0d M =L -L 0角动量守恒 M=0时, L=恒量; 转动动能2k E J ω= (二) 试题一 选择题(每题3分)1.一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力(答案:C )(A) 处处相等. (B) 左边大于右边.(C) 右边大于左边. (D) 哪边大无法判断. 2.将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为β.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将 (答案:C )(A) 小于β. (B) 大于β,小于2 β. (C) 大于2 β. (D) 等于2 β.3. 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下落,在棒摆动到竖立位置的过程中,下述说法哪一种是正确的?(A) 角速度从小到大,角加速度从大到小. (答案:A )(B) 角速度从小到大,角加速度从小到大.(C) 角速度从大到小,角加速度从大到小.(D) 角速度从大到小,角加速度从小到大.4. 关于刚体对轴的转动惯量,下列说法中正确的是(答案:C )(A) 只取决于刚体的质量,与质量的空间分布和轴的位置无关.(B) 取决于刚体的质量和质量的空间分布,与轴的位置无关.(C) 取决于刚体的质量,质量的空间分布和轴的位置.(D) 只取决于转轴的位置,与刚体的质量和质量的空间分布无关.5. 花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为J 0,角速度为ω0.然后她将两臂收回,使转动惯量减少为J 0/3.这时她转动的角速度变为(答案:D )(A) ω0/3. (B) ()3/1 ω0. (C) 3 ω0. (D) 3ω0.二、填空题1.(本题4分)一飞轮作匀减速运动,在5s 内角速度由40π rad/s 减少到10π rad/s ,则飞轮在这5s内总共转过了 圈,飞轮再经 的时间才能停止转动。
广西大学2020-2021学年第一学期期末复习题《大学物理》第1章质点运动学一、选择题:1.以下五种运动中,加速度a保持不变的运动是(D)(A)单摆的运动。
(B)匀速率圆周运动。
(C)行星的椭圆轨道运动。
(D)抛体运动。
(E)圆锥摆运动。
2.下面表述正确的是(B )(A)质点作圆周运动,加速度一定与速度垂直;(B)物体作直线运动,法向加速度必为零;(C)轨道最弯处法向加速度最大;(D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动,则下列说法正确的是(C)(A)质点的速度不变;(B)质点的加速度不变(C)质点的角速度不变;(D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r ,的端点处,其速度大小为(D)()()(()22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dtrd B dt drA 5.一质点在平面上运动,运动方程为:j t i t r 222+=,则该质点作(B)(A)匀速直线运动(B)匀加速直线运动(C)抛物线运动(D)一般曲线运动6.一质点做曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,s 表示路程,a t 表示切向加速度,对下列表达式,正确的是(B)(A)dtdrv =(B)dtdsv =(C)dtdva =(D)dtvd a t =7.某质点的运动方程为3723+-=t t X (SI),则该质点作[D ](A)匀加速直线运动,加速度沿x 轴正方向;(B)匀加速直线运动,加速度沿x 轴负方向;(C)变加速直线运动.加速度沿x 轴正方向;(D)变加速直线运动,加速度沿x 轴负方向8.一质点沿x 轴运动,其运动方程为()SI t t x 3235-=,当t=2s 时,该质点正在(A )(A)加速(B)减速(C)匀速(D)静止1.D 2.B 3.C 4.D5.B,6B,7A 8A二、填空题1.一质点的运动方程为x =2t ,y =4t 2-6t ,写出质点的运动方程(位置矢量)j t t i t r )64(22-+=,t =1s ,加速度j a8=,轨迹方程为x x y 32-=。
第一章 质点运动学习题1-4一质点在xOy 平面上运动,运动方程为x =3t +5, y =21t 2+3t -4.(SI ) (式中t 以 s 计,x ,y 以m 计.)(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,并计算这1秒内质点的位移; (3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,并计算t =4 s 时质点的速度; (5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,并计算t =4s 时质点的加速度。
(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1)质点位置矢量 21(35)(34)2r xi yj t i t t j =+=+++-v vv v v m(2)将1=t ,2=t 代入上式即有211[(315)(1314)](80.5)2t s r i j m i j m ==⨯++⨯+⨯-=-v v v v v221[(325)(2324)](114)2t s r i j m i j ==⨯++⨯+⨯-=+r r v v vm21(114)(80.5)(3 4.5)t s t s r r r i j m i j m i j m ==∆=-=+--=+r r r v v v v v v(3) ∵20241[(305)(0304)](54)21[(345)(4344)](1716)2t s t s r i j m i j mr i j m i j m===⨯++⨯+⨯-=-=⨯++⨯+⨯-=+r r r v vr r v v v∴ 1140(1716)(54)(35)m s 404t s t s r r r i j i j v m s i j t --==-∆+--===⋅=+⋅∆-v v v v v v v v v v (4) 21d d1[(35)(34)][3(3)]m s d d 2r t i t t j i t j t t -==+++-=++⋅v r r v v v v则 14[3(43)](37)t s v i j m s i j -==++⋅=+r r v v 1s m -⋅(5)∵ 1104(33),(37)t s t s v i j m s v i j m s --===+⋅=+⋅v v v v vv∴ 2241(37)(33)m s 1m s 44t s t s v v v i j i j a j t --==-∆+-+===⋅=⋅∆v v v v v v v v v(6) 2d d [3(3)]1m s d d v a i t j j t t-==++=⋅v vv v v这说明该点只有y 方向的加速度,且为恒量。
1-5 已知一质点做直线运动,其加速度为 a =4+3t (SI ),开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置.解:∵ t tva 34d d +==分离变量,得 t t v d )34(d += 积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-8 一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计, (1) t =2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解: t tt t 18d d ,9d d 2====ωβθω(1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n (2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即βωR R =2亦即t t 18)9(22= 则解得923=t 于是角位移为rad67.29232323=⨯+=+=t θ1-12质点的运动方程为:2,,x at y b ct a b c ==+、、均为常数,当质点的运动方向与x 轴成45°角时,求质点此时运动速率的大小。
解: ()x dx dat a dt dt===v当质点的运动方向与x 轴成45°角时,tan 45tan 451yx y x a a =︒=︒=⨯=v v v v质点此时运动速率为22222x y a a a =+=+=v v v1-13在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小。
解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得t s stl ld d 2d d 2=根据速度的定义,并注意到l ,s 是随t 减少的,∴t s v v t l v d d ,d d 0-==-=船绳 即θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 s v s h s lv v 02/1220)(+==船将船v 再对t 求导,即得船的加速度3202220202002)(d d d d d d s v h s v s l s v slv s v v s t s l t l st v a =+-=+-=-==船船或:1-14质点沿直线运动,初速度v0 ,加速度a=-k为正常数,求:(1)质点完全静止所需时间;(2)这段时间内运动的距离。
解:(1) a=-tvdvdtdvkdtkdtkttk=-=-=--=-=⎰⎰分得:变积分离量得(2)320322323xv dvdt dv dxk dx dt dvv dx kdxkdxv kx x v k=-=-=-=-=--=-=⎰⎰第3章 动量和冲量 动量守恒定律习题3-7 已知一篮球质量m=0.58kg,从h=2.0m 的高度下落,到达地面后,以同样速率反弹,接触地面时间△t=。
求篮球对地面的平均冲力F 球对地。
解:取竖直向上为y 轴正方向,则小球碰撞前 速度为0v =F 球对地小球碰撞后速度为v =由动量定理得0()F mg t mv mv -∆=-地球对mv mv F mg mg t -=+=∆地球对0.589.8388()N =+⨯= mg r根据牛顿第三定律,篮球对地面的平均冲力388F F N =-=-地球球对地对第4章 功和能 机械能守恒定律习题4-5 如图所示,A 球的质量为m ,以速度rv 飞行,与一静止的球B 碰撞后,A 球的速度变为1r v ,其方向与r v 方向成90°角。
B 球的质量为5m ,它被碰撞后以速度2r v 飞行,2r v 的方向与rv 间夹角为arcsin(35)θ=。
求:(1)两球相碰后速度1r v 、2rv 的大小;(2)碰撞前后两小球动能的变化。
解:(1)由动量守恒定律12A A B m v m v m v =+r r r即 1212255cos 5sin mvi mv j mv mv j mv i mv j θθ=-+=-++r r r r r r于是得 2125cos 5sin mv mv mv mv θθ=⎧⎨=⎩21215cos 4335sin 5454v v v v v v vθθ=====⨯⨯=(2)A 球动能的变化222221111317()2224232kA E mv mv m v mv mv ∆=-=-=-B 球动能的变化2222111505()22432kB B E m v m v mv ∆=-=⨯= 碰撞过程动能的变化222212111222232k B E mv m v mv mv ∆=+-=-或如图所示,A 球的质量为m ,以速度u 飞行,与一静止的小球B 碰撞后,A 球的速度变为1v 其方向与u方向成090,B 球的质量为5m ,它被撞后以速度2v 飞行,2v 的方向与u 成θ (53arcsin =θ)角。
求:(1)求两小球相撞后速度12υυ、的大小; (2)求碰撞前后两小球动能的变化。
解 取A 球和B 球为一系统,其碰撞过程中无外力作用,由动量守恒定律得 水平: 25cos mu m υθ= (1) 垂直: 2105sin m m υθυ=- (2) 联解(1)、(2)式,可得两小球相撞后速度大小分别为134u υ=214u υ=碰撞前后两小球动能的变化为 222327214321mu mu u m E KA-=-⎪⎭⎫ ⎝⎛=∆ 2232504521mu u m E KB=-⎪⎭⎫⎝⎛⨯⨯=∆4- 6在半径为R 的光滑球面的顶点处,一物体由静止开始下滑,则物体与顶点的高度差h 为多大时,开始脱离球面? 解:根据牛顿第二定律22cos cos v mg N mRvN mg mRθθ-==- 物体脱离球面的条件是N=0,即2cos 0v mg m Rθ-=由能量守恒212mv mgh =图由图可知cos R hRθ-= 由此解得 3R h =第5章 刚体定轴转动习题5-1 一个转动的轮子,由于轴承摩擦力矩的作用,其转动角速度渐渐变慢,第一秒末的角速度是起始角速度0ω的倍。
若摩擦力不变,求:(1)第二秒末的角速度(用0ω表示);(2)该轮子在静止之前共转了多少转。
解:因为摩擦力矩不变,转动惯量不变,由转动定律可知转动为匀变速转动。
(1) 0(0)t tωωββ=+<1010010.2ωωββωωω=+⨯=-=-第二秒末的角速度200002(0.2)20.6ωωβωωω=+⨯=+-⨯=(2) 2202ωωβθ=+∆r2222000002.522(0.2)rad ωωωθωβω--∆===⨯-轮子在静止之前共转了 002.55(224n ωθωπππ∆===圈)5-4 一力矩M 作用于飞轮上,飞轮的角加速度为1β,如撤去这一力矩,飞轮的角加速度为2β-,求该飞轮的转动惯量。
解:根据转动定律,有 1f M M J β-= 2()f M J β-=- 上面两式相减,得 12MJ ββ=+5-10 一质量为m ,长为l 的均匀细杆放在水平桌面上,可绕杆的一端转动(如图所示),初始时刻的角速度为0ω。