高考数学圆锥曲线精选文档

高中数学知识点 一圆锥曲线部分、平面解析几何的知识结构:炭|»■汕旷崔乂 —■ 才程，人闻性息、考点(限考)概要:1、椭圆：(1)轨迹定义：①定义一：在平面内到两定点的距离之和等于定长的点的轨迹是椭圆，两定点是焦点，两定点间距离是焦距，且定长 2a 大于焦距2c 。

用集合表示为:｛刊昭+昭 =2肚,<2c?,巩出为定点｝②定义二：在平面内到定点的距离和它到一条定直线的距离之比是个常数e ，那么这个点的轨迹叫做椭圆。

其中定点叫焦点，定直线叫准线，常数e 是离心率。

用集合表示为:厂国丽F •诵和廊阿 HSi^HSSJ^Tjj L|闿箫MWBUW 旧展rBe aglr ff<* 人卄武 -TRU ：在虹 L-fttW —ifeBSMKEA■・—奥・/RAgTE Em严闌* IS 幣内CL 耐 严・寰丫Lesgg*&和 <«)MtLlweA^B€ff«^B>g* < lt> 的比较4 山RHHA5il曲测6“旳左丈吞穴育啟/UMfl■相FT?F- = % 0 < f < k F为定点9 £为动点到定言线的距离e越小，椭圆越圆；e越大，椭圆越扁(2)标准方程和性质：2 2①范围：由标准方程^2 爲1知|x| a，|y| b，说明椭圆位于直线x a，a by b所围成的矩形里；②对称性：在曲线方程里，若以y代替y方程不变，所以若点(x, y)在曲线上时，点(x, y)也在曲线上，所以曲线关于x轴对称，同理，以x代替x方程不变，则曲线关于y 轴对称。

若同时以x代替x，y代替y方程也不变，则曲线关于原点对称。

所以，椭圆关于x轴、y轴和原点对称。

这时，坐标轴是椭圆的对称轴，原点是对称中心，椭圆的对称中心叫椭圆的中心；③顶点：确定曲线在坐标系中的位置，常需要求出曲线与x轴、y轴的交点坐标。

在椭圆的标准方程中，令x 0，得y b，则B1(0, b)，B2(0,b)是椭圆与y轴的两个交点。

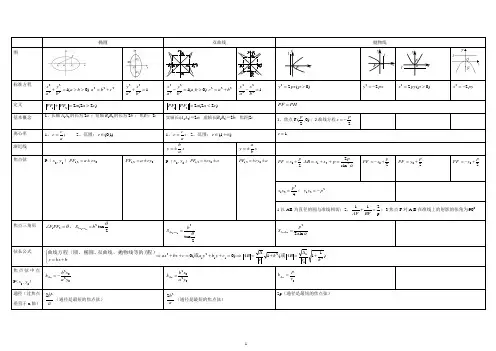
椭圆 双曲线抛物线图标准方程)0(12222>>=+b a b y a x 222c b a += 12222=+b x a y )0,(12222>=-b a b y a x 222b a c += 12222=-bx a y 22(0)y px p => 22y px =- 22(0)x py p => 22x py =-定义 )22(221c a a PF PF >=+)22(2-21c a a PF PF <=PH PF =基本概念 1、长轴A 1A 2的长为2a ；短轴B 1B 2的长为2b ；焦距：2c实轴长:|A 1A 2|＝2a ；虚轴长|B 1B 2|＝2b ；焦距|2c1、焦点F (,0)2p ；2准线方程2px =-离心率 1、ace =; 2、范围：)1,0(∈e 1、ace =; 2、范围：),1(+∞∈e 1e =渐近线x ab y ±= x ba y ±=焦点弦P （00,y x ）02,1ex a PF ±=02,1ey a PF ±=P （00,y x ）a ex PF ±±=02,1 a ey PF ±±=02,120px PF +=α221sin 2p p x x AB =++= 20px PF +-= 20p y PF += 20p y PF +-= 4221p x x =；221p y y -=1以AB 为直径的圆与准线相切；2、p211=+BF AF ；3焦点F 对A,B 在准线上的射影的张角为090 焦点三角形θ=∠21PF F ，2tan221θb S PF F =∆2tan221θb S PF F =∆αsin 22p S OAB=∆弦长公式)11(1)0(0211211212k a AB k a AB c y b y a c bx ax bkx y +∆=+∆=⇒=++=++⇒⎩⎨⎧+=或或程）双曲线、抛物线等的方曲线方程（圆、椭圆、 焦点弦中点P ）（00,y x202y a x b k AB-=202y a x b k AB= 0y p k AB=通径（过焦点垂直于x 轴）a b 22（通径是最短的焦点弦） ab 22（通径是最短的焦点弦） 2p （通径是最短的焦点弦）o Fxy loxyF lxy oF l。

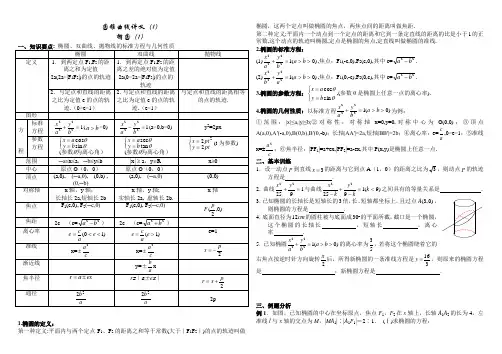
圆锥曲线讲义（1）椭圆（1）一、知识要点: 椭圆、双曲线、抛物线的标准方程与几何性质椭圆 双曲线 抛物线定义 1．到两定点F 1,F 2的距离之和为定值2a(2a>|F 1F 2|)的点的轨迹 1．到两定点F 1,F 2的距离之差的绝对值为定值2a(0<2a<|F 1F 2|)的点的轨迹2．与定点和直线的距离之比为定值e 的点的轨迹.（0<e<1） 2．与定点和直线的距离之比为定值e 的点的轨迹.（e>1）与定点和直线的距离相等的点的轨迹.图形方 程 标准方程 12222=+b y a x (b a >>0) 12222=-b y a x (a>0,b>0) y 2=2px 参数方程 为离心角）参数θθθ(sin cos ⎩⎨⎧==b y a x 为离心角）参数θθθ(tan sec ⎩⎨⎧==b y a x ⎩⎨⎧==pt y pt x 222(t 为参数) 范围 ─a ≤x ≤a ，─b ≤y ≤b |x| ≥ a ，y ∈Rx ≥0 中心 原点O （0，0） 原点O （0，0）顶点(a,0), (─a,0), (0,b) , (0,─b)(a,0), (─a,0) (0,0) 对称轴 x 轴，y 轴； 长轴长2a,短轴长2b x 轴，y 轴; 实轴长2a, 虚轴长2b. x 轴焦点F 1(c,0), F 2(─c,0) F 1(c,0), F 2(─c,0) )0,2(p F 焦距 2c （c=22b a -） 2c （c=22b a +） 离心率 )10(<<=e a ce )1(>=e a ce e=1准线 x=c a 2±x=c a 2±2p x -= 渐近线y=±ab x焦半径 ex a r ±=r =∣a ±e x ∣ 2p x r += 通径a b 22 ab 22 2p1.椭圆的定义：第一种定义:平面内与两个定点F 1、F 2的距离之和等于常数(大于｜F 1F 2｜)的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做焦距.第二种定义:平面内一个动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数,这个动点的轨迹叫椭圆,定点是椭圆的焦点,定直线叫做椭圆的准线. 2.椭圆的标准方程： (1))0(12222>>=+b a b y a x ,焦点：F 1(-c,0),F 2(c,0),其中c=22b a -. (2))0(12222>>=+b a ay b x ,焦点：F 1(0,-c),F 2(0,c),其中c=22b a -. 3.椭圆的参数方程：⎩⎨⎧==θθsin cos b y a x ,(参数θ是椭圆上任意一点的离心率).4.椭圆的几何性质：以标准方程)0(12222>>=+b a by a x 为例：①范围：|x|≤a,|y|≤b;②对称性：对称轴x=0,y=0,对称中心为O(0,0)；③顶点A(a,0),A′(-a,0),B(0,b),B′(0,-b)；长轴|AA′|=2a,短轴|BB′|=2b ；④离心率：e=ac,0<e<1；⑤准线x=±ca 2；⑥焦半径：|PF 1|=a+ex,|PF 2|=a-ex,其中P(x,y)是椭圆上任意一点.二、基本训练1．设一动点P 到直线3x =的距离与它到点A （1，0）的距离之比为3，则动点P 的轨迹方程是 ． 2．曲线192522=+y x 与曲线)9(192522<=-+-k k y k x 之间具有的等量关系是 ． 3．已知椭圆的长轴长是短轴长的3倍，长、短轴都坐标上，且过点(3,0)A ，则椭圆的方程是 ． 4．底面直径为12cm 的圆柱被与底面成30的平面所截，截口是一个椭圆，这个椭圆的长轴长 ，短轴长 ，离心率 ．5．已知椭圆22221(0)x y a b a b+=>>的离心率为35，若将这个椭圆绕着它的右焦点按逆时针方向旋转2π后，所得新椭圆的一条准线方程是163y =，则原来的椭圆方程是 ；新椭圆方程是 ．三、例题分析例1．如图，已知椭圆的中心在坐标原点，焦点F 1，F 2在x 轴上，长轴A 1A 2的长为4，左准线l 与x 轴的交点为M ，|MA 1|∶|A 1F 1|＝2∶1． (Ⅰ)求椭圆的方程；y xOF 1F 2P αβyO x 1l F 2 F 1 A 2 A 1P M l (Ⅱ)若直线l 1：x ＝m (|m |＞1)，P 为l 1上的动点，使∠F 1PF 2最大的点P 记为Q ，求点Q的坐标(用m 表示)．例2．设,A B 是两个定点，且||2AB =，动点M 到A 点的距离是4，线段MB 的垂直平分线l 交MA 于点P ，求动点P 的轨迹方程．例3．已知椭圆22221(0)x y a b a b+=>>，P 为椭圆上除长轴端点外的任一点，12,F F 为椭圆的两个焦点，（1）若α=∠21F PF ，21PF F β∠=，求证：离心率2cos2cosβαβα-+=e ；（2）若θ221=∠PF F ，求证：21PF F ∆的面积为2tan b θ⋅．例4．设椭圆2211x y m +=+的两个焦点是12(,0),(,0)(0)F c F c c ->，且椭圆上存在点P ，使得直线1PF 与直线2PF 垂直．（1）求实数m 的取值范围；（2）设l 是相应于焦点2F 的准线，直线2PF 与l 相交于点Q ，若22||23||QF PF =-，求直线2PF 的方程．例5．点A 、B 分别是椭圆1203622=+y x 长轴的左、右端点，点F 是椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，PF PA ⊥。

【最新整理，下载后即可编辑】圆锥曲线―概念、方法、题型、及应试技巧总结1.圆锥曲线的两个定义：（1）第一定义中要重视“括号”内的限制条件：椭圆中，与两个定点F 1，F 2的距离的和等于常数2a ，且此常数2a 一定要大于21F F ，当常数等于21F F 时，轨迹是线段F 1F 2，当常数小于21F F 时，无轨迹；双曲线中，与两定点F 1，F 2的距离的差的绝对值等于常数2a ，且此常数2a 一定要小于|F 1F 2|，定义中的“绝对值”与2a ＜|F 1F 2|不可忽视。

若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a ﹥|F 1F 2|，则轨迹不存在。

若去掉定义中的绝对值则轨迹仅表示双曲线的一支。

如方程8=表示的曲线是_____（答：双曲线的左支）（2）第二定义中要注意定点和定直线是相应的焦点和准线，且“点点距为分子、点线距为分母”，其商即是离心率e 。

圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化。

如已知点)0,22(Q 及抛物线42x y =上一动点P （x ,y ）,则y+|PQ|的最小值是_____（答2）2.圆锥曲线的标准方程（标准方程是指中心（顶点）在原点，坐标轴为对称轴时的标准位置的方程）：（1）椭圆：焦点在x 轴上时12222=+by a x （0a b >>），焦点在y轴上时2222bx a y +＝1（0a b >>）。

方程22Ax By C +=表示椭圆的充要条件是什么？（ABC ≠0，且A ，B ，C 同号，A ≠B ）。

如（1）已知方程12322=-++ky k x 表示椭圆，则k 的取值范围为____（答：11(3,)(,2)22---）；（2）若R y x ∈,，且62322=+y x ，则y x +的最大值是____，22y x +的最小值是___2）（2）双曲线：焦点在x 轴上：2222by a x - =1，焦点在y 轴上：2222bx a y -＝1（0,0a b >>）。

学前教育理论与实务袁玉长春光华学院．第三章学前教育观第一节学前教育的价值第二节学前教育的发展第三节学前教育的目标第四节科学学前教育观的树立学前儿童的因材施教第五节第一节学前教育的价值一、学前教育在儿童发展中的作用学前教育对于儿童的成长至关重要。

无论是对胎儿，还是对婴儿，或是对幼儿，只要有适宜的教育和训练，就能得到很好的成长与发展。

（一）保证胎儿健康的出生胎儿在5个月，听觉系统的发育已基本完善，6－7个月时能分辨出母亲的情感。

孕妇的情绪会通过神经——体液的变化，去影响胎儿的血液供应、呼吸、胎动等。

（二）保证婴儿及时的成长婴儿期是学前儿童发展的第二个重要时期。

有研究者认为：儿童八个月-2岁这段时期是特别重要的，因为语言、好奇心、智能和社会化的发展等基础都是在此期间奠定的、脑科学研究的人员发现：每个人的学习能力的50%是在生命的头4年发展起来的，早期学习不但不会剥夺童年的换了，而且能够为儿童提供各种发展的良机。

1.母乳喂养有利于婴儿免疫能力的增强。

母乳喂养对婴儿的呼吸道有保护作用，能降低呼吸道的发病率，母乳中含有较多的疾病免疫的因子，有助于刺激婴儿免疫系统的成熟。

母乳最佳喂养方式：产后半小时开始喂奶；出生后4个月内坚持母乳喂养，4-6个月开始添加辅食，具体月龄依婴儿生长情况而定，6个月月龄的婴儿均应添加辅食。

2.母亲注意卫生保健有利于婴儿的生长发育。

在婴儿哺乳期间，母亲吸烟，分泌的乳汁会减少，并增加婴儿的支气管和肺炎发生率。

3.成人重视体育锻炼，有助于婴儿健康成长。

成人注意语言刺激有利于婴儿4.的智力发展。

成人注意激发阅读兴趣有益于5.婴儿良好品行的塑造。

．成人注意音乐刺激有助于婴儿6.的情感陶冶。

（三）保证幼儿迅速的发展1.重视体育锻炼，能促进幼儿身心健康成长。

重视音乐训练，能提高幼儿的智力水平。

2.3.幼儿期教育能为儿童做好入学准备。

研究表明：上过幼儿园的儿童与未上过幼儿园的儿童相比，适应小学生活的能力更强，语文、数学平均成绩更高，当班干部、三好学生的比例更大。

高二数学专题学案圆锥曲线部分高考试题汇编(椭圆部分)1、(2016全国I卷)(20)(本小题满分12分)设圆x2 + y2 + 2x—15 = 0的圆心为4直线l过点B (1,0)且与x轴不重合，l交圆A于C, D两点，过B作AC的平行线交AD于点E.(I)证明|EA| + |EB|为定值，并写出点E的轨迹方程；(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于PQ两点，求四边形MPNQ面积的取值范围.x2 y22、（2015全国I卷）（14）一个圆经过椭圆7十一二1的三个顶点，且圆心在乂轴上，则该圆的标准方程16 4为。

3、（2014全国I卷）20.（本小题满分12分）已知点A（0，-2），椭圆E：上+ y2= 1（a > b > 0）的离心率为3，，F是椭圆a2 b2 2的焦点，直线AF的斜率为233，O为坐标原点.（I）求E的方程；（II）设过点A的直线l与E相交于P, Q两点，当A OPQ的面积最大时，求l的方程.4、（2016山东卷）（21）（本小题满分14分）平面直角坐标系g中，椭圆C：：喙=1（a>b>°）的离心率是浮，抛物线E3x=2'的焦点F是C的一个顶点.（I）求椭圆C的方程；（II）设P是E上的动点，且位于第一象限，E在点P处的切线l与C交与不同的两点A，B，线段AB的中点为D，直线OD与过P且垂直于x轴的直线交于点M.（i）求证：点M在定直线上；（ii）直线l与y轴交于点6，记^PFG的面积为S j ^PDM的面积为S2，求S-的最大值及取得最大值2时点P的坐标.八- x 2 Y 2 一，，〜5、（2015山东卷）（20）（本小题满分13分）平面直角坐标系xOy中，已知椭圆C ：— + ） =1（a > b > 0）a 2 b2的离心率为*，左、右焦点分别是F , F ，以F 为圆心，以3为半径的圆与以F 为圆心，以1为半径的 2 1212圆相交，交点在椭圆C 上. （I ）求椭圆C 的方程；x 2 y 2（H ）设椭圆E ：江+而二1，P 为椭圆C 上的任意一点,过点P的直线厂"m 交椭圆E 于A,B 两点，射线PO 交椭圆E 于点Q.圆锥曲线部分高考试题汇编（双曲线部分）1、（2016全国I 卷）（5）已知方禾m 2+n--就工=1表示双曲线，且该双曲线两焦点间的距离为4,则n的i ）求|OQ | | OP |的值；（ii ）求A ABQ 面积最大值.取值范围是（2、（2015全国I 卷）（5）已知M （x 0 丫0）是双曲线C ： --W= 1上的一点，F 1、F 2是C 上的两个焦点，若西 • MF 2 <0,则y 0的取值范围是（2J3(D )(一二33、（2014全国I 卷）4.已知F 是双曲线C ： x 2 - my 2 = 3m （m > 0）的一个焦点，则点F 到C 的一条渐近线的距离为（ ） A . <3B .3C . <3mD . 3mx 2 y 24、（2016山东卷）（13）已知双曲线E_,： ---= 1 （a >0, b >0）,若矩形ABCD 的四个顶点在E 上， 1a 2b 2AB , CD 的中点为E 的两个焦点，且21AB |=3|BC |,则E 的离心率是.x 2 y 25、（2015山东卷）（15）平面直角坐标系xOy 中，双曲线C : 一--—= 1（a > 0,b > 0）的渐近线与抛物线1a 2 b2C : x 2 = 2py （p > 0）交于点O , A , B ，若A OAB 的垂心为C 的焦点，则C 的离心率为. 2 21x 2 y 2 x 2 y 26、（2014山东卷）（10）已知a > b ，椭圆C 的方程为—+ -- = 1 ,双曲线C 的方程为——^- = 1, C1 a2 b 2 2 a 2 b 2 1与C 的离心率之积为二，则C 的渐近线方程为（）222（A ） x 土 <2y = 0 （B ） J2x 土 y = 0 （C ） x 土2y = 0 （D ） 2x 土 y = 0圆锥曲线部分高考试题汇编（抛物线部分）(A )(-1,3)(B )(-1八”)(C )(0,3)(D )(0,\与)2<2 (C )(-—— 32<31、（2016全国I卷）（10）以抛物线C的顶点为圆心的圆交C于A, B两点，交C的准线于D, E两点.已知| AB | = 4"；2 , | DEI= 2d5，则C的焦点到准线的距离为（）（A）2 （B）4 （C）6 （D）82、（2015全国I卷）（20）（本小题满分12分）x2在直角坐标系xoy中，曲线C：y =—与直线y = kx + a（a >0）交与M,N两点，（I）当k=0时，分别求C在点M和N处的切线方程；（II）y轴上是否存在点R使得当k变动时，总有N OPM =Z OPN ?说明理由。

（完整版）圆锥曲线⾼考真题（1）求M 的⽅程（2）C ，D 为M 上的两点，若四边形ACBD 的对⾓线CD ⊥AB ，求四边形ACBD 的⾯积最⼤值.2.设1F ,2F 分别是椭圆()222210y x a b a b+=>>的左右焦点，M 是C 上⼀点且2MF 与x 轴垂直，直线1MF 与C 的另⼀个交点为N.（1）若直线MN 的斜率为34，求C 的离⼼率；（2）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .3.已知椭圆C ：，直线不过原点O 且不平⾏于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .(1) 证明：直线OM 的斜率与的斜率的乘积为定值；（2）若过点（）,延长线段OM 与C 交于点P ，四边形OAPB 能否平⾏四边⾏？若能，求此时的斜率，若不能，说明理由.4.已知抛物线C ：22y x = 的焦点为F ，平⾏于x 轴的两条直线12,l l 分别交C 于A ，B 两点，交C 的准线于P ，Q 两点.（1）若F 在线段AB 上，R 是PQ 的中点，证明AR ∥FQ ；（2）若△PQF 的⾯积是△ABF 的⾯积的两倍，求AB 中点的轨迹⽅程.5.已知抛物线C ：y 2=2x ，过点（2,0）的直线l 交C 与A ,B 两点，圆M 是以线段AB 为直径的圆．（1）证明：坐标原点O 在圆M 上；（2）设圆M 过点P （4，-2），求直线l 与圆M 的⽅程．6.已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点，线段AB 的中点为()()10M m m >，．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上⼀点，且FP FA FB ++=0u u u r u u u r u u u r ．证明：FA u u u r，FP u u u r ，FB u u u r 成等差数列，并求该数列的公差．7.已知椭圆2222:1(0)x y C a b a b +=>>的离⼼率为，且经过点(0,1)，圆22221:C x y a b +=+。

高中数学圆锥曲线基本知识与典型例题第一部分：椭圆1. 椭圆的概念在平面内与两定点F i、F2的距离的和等于常数(大于|F I F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距____集合p = {M||MF i |+ |MF2|= 2a}, |F I F2|= 2c,其中a>0, c>0，且a, c 为常数：(1) 若业，则集合P为椭圆；⑵若a^c，则集合P为线段；⑶若空，则集合P为空集.2. 椭圆的标准方程和几何性质若/ PF i F 2=5/ PF Z F I ,则椭圆的离心率为例6•写出满足下列条件的椭圆的标准方程：(1) 长轴与短轴的和为 18，焦距为6; ____________________ . (2) 焦点坐标为(,3,0),(,3,0),并且经过点(2，1); _________________ .1(3) 椭圆的两个顶点坐标分别为(3,0) ,(3,0),且短轴是长轴的 丄；3(4) 离心率为—，经过点(2，0); ______________________ .22典型例题例 1.F 1，F 2 是定点，且 |F 1F 2|=6, (A)椭圆 例2.已知 ABC 2X(A)—252y_16(B)直线 的周长是 2X(B)—— 25 16, 2y_ 动点M 满足|MF 1|+|MF 2|=6,则M 点的轨迹方程是() (C)圆(D)线段3,0)，B (3,0)，则动点的轨迹方程是( )y 2A(i(y 2 0) (C)16 2y_ 25 2’ X 1 (D)— 16 例3.若 2X F( c ，0)是椭圆字2 y ab21的右焦点，F 与椭圆上点的距离的最大值为 M ，最小值为m ，则椭圆上与F 点的距离等于(A)( c ，£)ab 2(B)( c,-)a(C)(0 ，土 b) (D) 不存在例 4.设 F i (- c .0)、F 2(C , 0)是椭圆2 2x y=1( a>b>0)的两个焦点，P 是以F I F 2为直径的圆与椭圆的一个交点b(A) i3(B)_6 3(C)(D)2例5 P 点在椭圆—45 2—1 上, F 1、20F 2是两个焦点，若 PF i PF 2，贝U P 点的坐标是X 2例7 F2是椭圆y 1的左、右焦点，点P在椭圆上运动，则| PR | | PF2 |的最大值是________________ 4第二部分：双曲线1. 双曲线的概念平面内动点P与两个定点F i、F2(|F I F2|=2C>0)的距离之差的绝对值为常数2a(2a<2c),则点P的轨迹叫双曲线•这两个定点叫双曲线的焦点，两焦点间的距离叫焦距. _______集合p = {M|||MF i|—|MF2||= 2a} , |F I F2|=2C,其中a、C为常数且a>0, C>0:(1) 当a<C时，P点的轨迹是双曲线；(2) 当a = C时，P点的轨迹是两条射线；(3) 当a>c时，P点不存在.2. 双曲线的标准方程和几何性质例13•根据下列条件，求双曲线方程⑴与双曲线2 x 2 y 1有共冋渐近线，且过点(-3, 2 3)；9162 2⑵与双曲线x y 1有公共焦点，且过点,2).16 42例14设双曲线x 2 十 1上两点A 、B , AB 中点M (1 , 2) ⑴求直线AB 方程；⑵如果线段AB 的垂直平分线与双曲线交于 C 、D 两点，那么A 、B 、C 、D 是否共圆，为什么?典型例题 例8•命题甲：动点P 到两定点A 、B 甲是命题乙的( )(A)充要条件 的距离之差的绝对值等于 2a(a>0);命题乙： 点P 的轨迹是双曲线。

高考数学必做61道圆锥曲线问题——圆锥曲线性质大全.doc
高考数学必做 61 道圆锥曲线问题——圆
锥曲线性质大全
一、神奇曲线，定义统一
01. 距离和差，轨迹椭双
02. 距离定比，三线统一
二、过焦半径，相关问题
03．切线焦径，准线作法
04. 焦点切线，射影是圆
05. 焦半径圆，切于大圆
06. 焦点弦圆，准线定位
07. 焦三角形，内心轨迹
三、焦点之弦，相关问题
08．焦点半径，倒和定值
09．正交焦弦，倒和定值
10. 焦弦中垂，焦交定长
11. 焦弦投影，连线截中
12. 焦弦长轴，三点共线
13. 对焦连线，互相垂直
14. 相交焦弦，轨迹准线
15. 相交焦弦，角分垂直
16. 定点交弦，轨迹直线
17. 焦弦直线，中轴分比。