控制图控制限探讨

控制图1、概念控制图又叫做管制图，是用于分析和判断工序是否处于稳定状态所使用的带有控制界限的一种工序管理图。

控制图是一种对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图，图上有中心线（CL ）、上控制线（UCL ）、下控制线（LCL ），并有按时间顺序抽取的样本计量值的描点序列。

控制图主要用于：过程分析及过程控制。

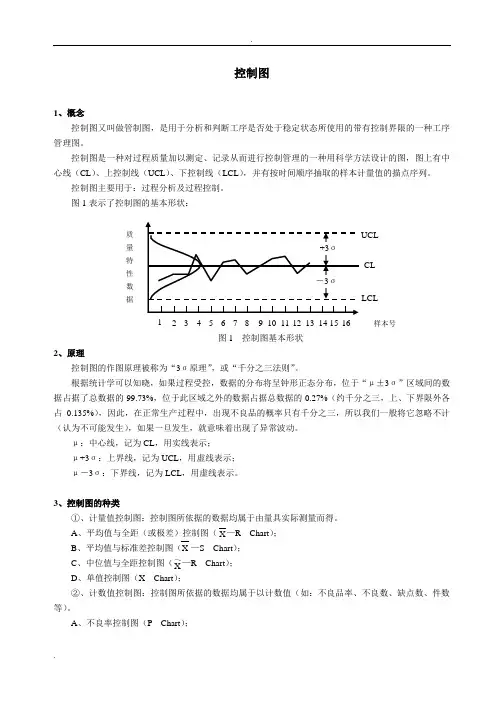
图1表示了控制图的基本形状：2、原理控制图的作图原理被称为“3σ原理”，或“千分之三法则”。

根据统计学可以知晓，如果过程受控，数据的分布将呈钟形正态分布，位于“μ±3σ”区域间的数据占据了总数据的99.73%，位于此区域之外的数据占据总数据的0.27%（约千分之三，上、下界限外各占0.135%），因此，在正常生产过程中，出现不良品的概率只有千分之三，所以我们一般将它忽略不计（认为不可能发生），如果一旦发生，就意味着出现了异常波动。

μ：中心线，记为CL ，用实线表示； μ+3σ：上界线，记为UCL ，用虚线表示； μ－3σ：下界线，记为LCL ，用虚线表示。

3、控制图的种类①、计量值控制图：控制图所依据的数据均属于由量具实际测量而得。

A R Chart ）； B S Chart ）；C Chart ）；D 、单值控制图（X Chart ）；②、计数值控制图：控制图所依据的数据均属于以计数值（如：不良品率、不良数、缺点数、件数等）。

A 、不良率控制图（P Chart ）；质 量 特 性 数 据B、不良数控制图（Pn Chart）；C、缺点数控制图（C Chart）；D、单位缺点数控制图（U Chart）。

4、控制图的用途根据控制图在实际生产过程中的运用，可以将其分为分析用控制图、控制用控制图：①、分析用控制图（先有数据，后有控制界限）：用于制程品质分析用，如：决定方针、制程解析、制程能力研究、制程管制之准备。

分析用控制图的主要目的是：（1）分析生产过程是否处于稳态。

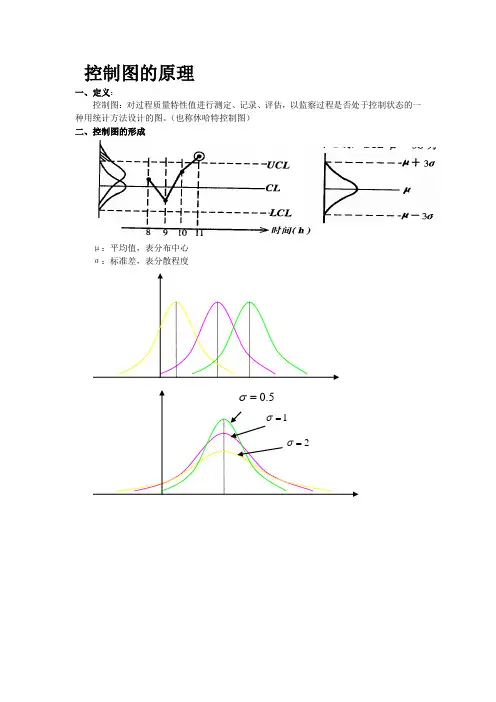
控制图的原理一、定义：控制图：对过程质量特性值进行测定、记录、评估，以监察过程是否处于控制状态的一种用统计方法设计的图。

（也称休哈特控制图）二、控制图的形成σ：标准差，表分散程度σ5.0=σ=1σ2=三、控制图的基本结构1、以随时间推移而变动着的样品号为横坐标，以质量特性值或其统计量为纵坐标；2、三条具有统计意义的控制线：上控制线UCL 、中心线CL 、下控制线LCL ；3、一条质量特性值或其统计量的波动曲线。

四、控制图原理的解释第一种解释：“点出界就判异”小概率事件原理：小概率事件实际上不发生，若发生即判异常。

控制图就是统计假设检验的图上作业法。

第二种解释：“抓异因，弃偶因”控制限就是区分偶然波动与异常波动的科学界限。

休哈特控制图的实质就是区分偶然因素与异常因素的。

五、常规控制图分类上控制限UCL 中心线CL 下控制限LCL样本统计量数值x12始终存在，对质量影响微小，难以消除，是不可避免的如材料成分的微小变化、设备的轻微震动、刃具的正常磨损、夹具的弹性变型等偶然因素有时存在，对质量影响很大，不难消除，是可以避免的如材料成分的显著变化、设备安装不当、零件损坏、人员违反规程操作等异常因素控制图 缺陷数控制图控制图 单位缺陷数控制图 泊松分布计点型控制图 不合格品数控制图 控制图 不合格品率控制图 二项分布 计件型 计数型控制图 单值－移动极差控制图控制图 中位数－极差控制图 控制图均值－标准差控制图控制图 均值－极差控制图 正态分布计量型简记控制图 分布 数据类型 R X -S X -R X -~S R X -p np u c六、按用途分类1、分析用控制图——用于质量和过程分析，研究工序或设备状态；或者确定某一“未知的”工序是否处于控制状态；2、控制用控制图——用于实际的生产质量控制，可及时的发现生产异常情况；或者确定某一“已知的”工序是否处于控制状态。

七、控制图的应用八、Ｘ－Ｒ控制图的绘制 1、确定控制对象（统计量）一般应选择技术上最重要的、能以数字表示的、容易测定并对过程易采取措施的、大家理解并同意的关键质量特性进行控制。

统计学中的控制图应用统计学是一门研究数据收集、分析和解释的学科，它在各个领域都有广泛的应用。

其中，控制图是统计学中的一种重要工具，用于监控和控制过程的稳定性和质量。

本文将介绍控制图的基本原理和应用，并探讨其在实际问题中的重要性。

一、控制图的基本原理控制图是一种图形化的工具，用于显示过程的数据和统计信息。

它通过将过程数据与控制限相比较，帮助我们判断过程的稳定性和质量。

控制限是根据统计学原理计算得出的上下限值，当过程数据超出这些限制时，表明过程存在异常变化。

在控制图中，通常有中心线、上控制限和下控制限。

中心线代表过程的平均水平，上控制限和下控制限分别代表过程的变异范围。

当过程数据在这些限制之间波动时，我们可以认为过程是稳定的。

如果数据超出控制限，我们需要进一步分析问题的原因，并采取相应的措施进行改进。

二、控制图的应用控制图广泛应用于各个行业和领域，包括制造业、服务业、医疗保健等。

它可以帮助我们实时监控过程的稳定性，及时发现问题并采取措施进行纠正。

下面我们将以制造业为例，介绍控制图的应用。

在制造业中，产品质量是一个重要的关注点。

通过使用控制图，我们可以监控产品的关键特性，并及时发现任何异常变化。

例如，在汽车制造过程中，我们可以使用控制图来监控发动机的排放水平。

如果排放水平超出控制限，我们可以迅速发现问题，并检查是否存在零部件的故障或者生产过程中的变化。

这样可以帮助我们及时采取措施，确保产品质量符合标准。

除了产品质量，控制图还可以应用于监控生产过程的稳定性。

在制造业中，生产过程的稳定性对于产品的一致性和效率至关重要。

通过使用控制图，我们可以监控关键过程参数的变化，并及时发现任何异常情况。

例如，在电子芯片制造过程中，我们可以使用控制图来监控温度和湿度等参数。

如果这些参数超出了控制限，我们可以立即采取措施，避免不良产品的产生。

三、控制图的重要性控制图在实际问题中的应用非常重要。

它可以帮助我们实时监控过程的稳定性和质量，并及时采取措施进行改进。

浅谈控制图在工程项目中的应用控制图是一种常用的质量管理工具，可以用于监测和控制工程项目的质量。

它的主要作用是提供关于工程质量的数据，以便管理人员根据这些数据做出相应的决策和改进措施。

本文将从控制图的定义、分类及应用等方面进行浅谈。

一、控制图的定义控制图是一种统计工具，用来分析及显示一项质量特性随时间变化的趋势情况。

它通过收集、显示和分析质量数据，以便管理人员从中获得有关质量改进的信息。

同时，控制图可以帮助判断一个过程是否处于一种可控状态，或者需要进行进一步的改进。

控制图可以分为多种类型，具体如下：1. 均值图：用来监测一个制程中平均值的变化情况。

5. 直方图：用来描述一个样本数据的分布情况。

6. 散点图：用来分析两个变量之间的相互关系。

1. 质量控制：控制图是一种常用的质量控制工具，可以用来监控质量数据，并及时制定改进措施，确保产品或工程符合规定的质量标准。

2. 过程优化：通过分析控制图，可以发现一些制程中的潜在问题，进而进行改进，提高生产效率及质量。

3. 决策支持：控制图提供了可靠的质量数据，这些数据可以用来评估制程的稳定性及可靠性，从而帮助管理人员做出合理的决策。

4. 节约成本：控制图可以帮助控制全过程的质量，减少废品率和返工率等损失，从而节约了公司的成本。

四、注意事项在使用控制图时，需注意以下事项：1. 采集数据应有严格的标准，以确保数据的正确性和准确性。

2. 控制图应合理设置控制限，以保证数据的可控性。

3. 控制图应维护并定期更新，以保持其有效性。

4. 在控制图后发现异常情况时，应立即采取修正措施。

总之，控制图是一种有效的工具，可以用来监控和控制工程项目的质量。

在使用控制图时，应严格遵守标准，确保数据的正确性和可靠性。

同时，应根据实际情况合理设置控制限，及时修正异常情况，从而最大化地发挥控制图的作用。

SPC經典案例剖析---SPC在控制男主人歸家時間上的運用朋友们大家好，这个经典的案例可能读过很多遍了。

现把整篇的文章转载过来并加以分析。

从网上看到一个经典的SPC应用的例子，与大家共赏：俗话说宴无好宴。

朋友邀我去他家做客吃晚饭，进了门迎面遇上他焦急无辜的表情，才知道主题是咨询。

起因是朋友最近回家的时间越来越晚，罪证就在他家门口玄关的那张纸上——朋友的太太是一家美商独资企业的QC主管，在家里挂了一张单值-移动极差控制图，对朋友的抵家时间这一重要参数予以严格监控：设定的上限是晚七点，下限是晚六点，每天实际抵家时间被记录、描点、连线——最近连续七天(扣除双休日)的趋势表明，朋友抵家的时间曲线一路上扬，甚至最近两天都是在七点之后才到家的，证据确凿——按照休哈特控制图的原则和美国三大汽车公司联合编制的SPC(Statistical Quality Control，统计过程控制)手册的解释，连续7点上升已绝对表明过程发生了异常，必须分析导致异常的原因并做出必要的措施(比如准备搓衣板)，使过程恢复正常。

显然，我可能给出的合理解释成了朋友期待的救命稻草，而这顿晚饭就是他在我面前挂着的胡萝卜。

(单值---移动极差图：X-Rs,这个控制图我先来讲它一般的适用场合：(1)对每个产品都进行检验; (2)采用自动化检查和测量的场合; (3)取样费时、费用昂贵的场合; (4)化工等流程性材料及样品均匀的场合。

它的取样信息不多，所以它检出的过程变化的灵敏度也要差一些。

在本例中，这位QC主管显然考虑到老公回家这个重要的参数，是保证他对自己的婚姻忠诚的主要因素，那么根据连续7点呈现上升的趋势，我们很容易就对这个过程判异。

这个判异是根据小概率事件原理：小概率事件在一次试验中发生的概率几乎为零，也就是几乎不可能发生，若发生即判异。

本例中的連續7点呈现上升趋势，是根据判异准则的界内点不随机排列判异。

通常在过程受控的条件下，連續7點不随机排列呈现的概率都很小，若出现我们就可以判断该过程出现了异常因素，导致过程失控。

控制图在质量控制中的应用技巧质量控制是生产过程中至关重要的一环，而控制图则是常用的质量管理工具之一。

控制图能够帮助企业监控生产过程，及时发现问题并采取措施进行调整和改进。

下面将探讨控制图在质量控制中的应用技巧。

1. 控制图的种类在质量控制中，最常用的控制图包括X-Bar控制图、R控制图和S控制图。

X-Bar控制图用来监控过程的平均值；R控制图用来监控过程的变异性；S控制图也用来监控过程的变异性，适合于小样本的情况。

2. 数据的采集在应用控制图时，首先要收集相关的数据。

这些数据可以来自生产过程、质量检测等环节。

数据的准确性对于控制图的应用至关重要，所以要确保数据的采集方法和过程是规范和可靠的。

3. 确定控制限在绘制控制图时，需要确定上限和下限的控制限。

这些控制限可以通过统计算法或经验方法确定。

控制限的设定要考虑到过程的稳定性和容忍度，确保可以及时识别出异常情况。

4. 解读控制图控制图的核心是监控过程的稳定性和偏差。

当数据点超出控制限时，表示过程存在异常。

此时需要及时分析原因，采取措施进行调整，以确保产品质量符合标准。

5. 常见问题的处理在实际应用中，控制图可能会出现一些常见问题，如数据的集中或分散、连续性问题等。

针对这些问题，需要结合实际情况进行分析，找出问题的根源并采取相应的改进措施。

6. 控制图的周期性更新控制图不是一劳永逸的工具，而是需要定期更新和维护的。

通过不断地收集数据，更新控制图，可以及时发现生产过程中的变化，并及时调整控制限以适应新的情况。

7. 培训员工在实际应用控制图时，需要培训相关员工，使其了解控制图的原理和应用方法。

只有员工具备了解相关知识，才能更好地应用控制图来监控和改进生产过程。

8. 持续改进持续改进是质量控制的核心理念之一。

通过应用控制图，可以发现生产过程中的问题，及时进行调整和改进，从而不断提升产品质量和生产效率。

9. 与供应商合作在质量控制中，供应商是一个重要的环节。

TCS 操作控制管理办法 第 页 共 页附件（一）SPC 基础知识——计算均值及控制限1. 选择子组容量、频率、子组数合理子组的确定将决定控制图的效果①在—X -R 控制图中，子组的容量是恒定的。

在过程研究初期n 取4～5，通常取2～5件连续生产的产品。

这样的子组反映的是在很短时间内、非常相似的生产条件下生产出来的产品，因此，子组内的变差主要应是普通原因造成的。

这些条件不满足，就不能有效地区分出变差的特殊原因。

②每隔一定的周期（如15min 或每班两次）抽取子组。

适当时间内抽取足够的子组，才能反映潜在的变化（如换班，人员更换，环境温度变化，材料批次等）。

初期研究中，通常是连续进行分组或在很短时间间隔抽取子组。

对处于稳定状态的过程，抽取子组的周期可以延长。

对正常生产进行监控的子组频率可以是每班两次，每小时1次等。

③足够的子组数可以确保发现变差的主要原因。

一般情况下，一次过程研究的子组数大或等于25，或包含的单值数大或等于100。

2. 建立控制图并记录原始数据3. 计算每个子组的均值（—X ）和极差（R ）123X X X X n++=……＋ R=X max －X mi式中 n －子组容量，图例中n=54. 选择控制图的刻度X 图刻度范围≥子组均值最大值与最小值差的2倍。

R 图刻度，从0到最大值之间范围≥初始阶段最大极差的2倍。

建议R 图的刻度值设置为均值图的2倍（如—X 图上一个刻度代表0.01mm ，R 图上同样的一个刻度代表0.02mm ）。

5. 将均值—X 和极差R 分别画到控制图上将—X 、R 一一对应点到—X 图和R 图上，然后分别用直线将—X 各点，R 各点连接起来。

6、计算控制限① 算平均极差（-R ）及过程平均值（=X ）平均极差-R ＝123R R R K++……＋ 过程均值=X ＝123X X X K++……＋ 式中 K －子组数② 计算控制限控制限显示当仅存在变差的普通原因时，均值和极差的变化范围。

控制图的界限修正控制图的应用?一一控制图的界限修正上海人民电器厂吴士权控制图的控制界限是通过对产品质量特性值实际分布的研究.用测得的质量特性值数据计算出其概率界限.一般取3o作为控制图的控制界限,这就是着名的休氏"千分之三原则.使用-3o作为控制界限的前提是生产过程只受偶然性因素影响,而无系统因素影响.但是实际上,怍控制图时,所收集的子样的均值和标准偏差随着生产过程中五大因素的系统变化会有所波动.不过在通常情况下,这种波动的范围不会超出概率稃限.因此由计算确定的概率界限能有效地警戒质量的异常变化.控制图的这种特点能敏捷地对质量的异常变化作出反映,从而能及时排除异常故障或进行工序调节,有效地贯彻"预防为主"的质量方针.止因为如此,控制图这一统计工具披广泛地应用于工序质量控制中.一,提出控制界限修正的理由建立控制图的规范程序是:首先收集20～50组现场质量特性数据,每组由2～lO个测量数据组成,并根据各组的均值或中位薮,极差R计算出各组均值或中位数的平均值耳或和极差R的平均值,最后以+A或x+mA2R为x控制图的上控制界限UCL或x控制图的上控制界限UC以A莨或mA一R为X一控制图的下控制界限LCL{或x控制图的下控制界限LCL以D4R为R控制图的上控制界限UCL,IDR为R控制图的下控制界限LCL,共同组成控制图的控制界限.有关的系数A,m,D,D4等均可根据所选择的组样本个数11以及样本组大小K和风险率大小Ⅱ从控制图用系数表和有关数理统计表中查取.根据上述方法建立起来的控制界限只考虑到工序能力6o,只要质量波动稳定在6o之～8一内即认为正常.而实际上,我们检验产品质量是否台格的掏;准则是规格的要求.即其测茸值是否在公差范围之内.因而在使用控制图时往往会出现这样的情况:x控制图或-X控制图的点子,常常落在控制界限t某一侧)之外.而其样本的测量值却又都符合产品的技术标准.并有一定公差裕度.对于上述界外点子.一般会判其为失控点子.并要进行异常因的调查和工序调整.尤其是在工序能力指数CP值较高的情况下,而其分布中心和公差中心的偏离系数￡又较大的情况下,这种现象特别严重,因此常常会产生虚假的警报,并要为此花费相当可观的调整工时,影响了工序的正常运行.这种情况同生产者风险Ⅱ过大的情况颇为相似.这样的控制界限,无论从实用性,还是从经济性来说.都显得要求过严完全有理由放弃对这种实际上不需调整的"警戒信号的调整工作.同样.在工序能力指数小于1的情况下,根据上述方法确定的控制界限容易产生判断失误,出现尽管点子都落在控制界限之内,而实际的质量却是已有不少子样不符合规格要求,产生了不少废品.这种警报迟钝的现象同消费者风险p过大情况很相似.因而在确定控制界限时,十分有必要考虑规格界限和工序能力指数之间的关系.避免发生上述二种情况,使得工序控制中应用的控制图控制界限与规格界限柏吻合,保证生产过程中的质量处于稳定的受控状态二,警戒系数的导八在实际工序能力指数cpk大于l时,如果把规格界限(公差,引入控制图控制图的话,则规格界限必然位于控制界限的两侧,并留有一定裕度;其问.控制图的分布中心和上.下控制界限随着生产过程的质量波动会在规格界限之问漂移众所周知.xR控制图或xR控制图分别由控制统计量集中位置的x控制图或x控制图和控制离散程度的极差R控制图组成.其中叔控制图往往会由于工装,刃具,模具等逐渐磨损的系统因素,致使分布中心和公差中心不仅不能重台,而且使其偏离系数逐渐增大,因而经常发现打在控制图上的点子偏向中心线的一侧,被误认为异常.为纠正这种界外的所谓异常点子,叉得花出很大的代价,有时甚至始终无法排除.如果我们仔细分析一下规格标准和控制界限之间的关系,就不难发现,在确定的技术标准下,公差带的宽度是不变的,而分布中心和上,下控制界限划会随着工序的变化,其分布的状态也随之变化=我们作一有公差界限(规格要求)的控制图控制图的应用'l?一一一一.一一一一一一s一圈1带公差界限的控制髓(图lj,并假定分布中心CL与公差中心Tm重台,上,下控制界限之间的区域用】来表示,上控制界限uCL与规格上限su或下控制界限LcL与规格下限s之间的区域用U来表示.规格上,下界限以外的区域用nl来表示.则落入各个区域内点子的统计意义,可用表l来说明.表1各区域内点子的统计意义区域落入该匹域内点子的统计意义该区域为控制区.落入控制区的点子.大概率是受控状态,表示生产过程稳定,工序处于受控状l志其置信度取决于昕选的0值.表明这种情况下生产出来的产品合格率一般能达到帕.7该区域为警戒区.落八警戒区的点子,是异常点子.说明质量的分布状态起了显着变化.(0变【l太.或l|偏离控制中心线.)失控的点子中有町能包含着一定量的不符合技术要求的产品该区域为废品区.落入废品区的点子,大概率为失控程度严重.表示生产过程不稳定,工序处于l¨严重失控状态,废品率明显上升,有叮能出现成批报废.在分布的离散程度具有趋向性地渐渐变小时,其工序能力指数必然会随之变大,因而规格界限与控制界限之间的区域【【会随之扩大.如果我们假定工序能力6o,T,质量的分布界限为3o,而且一?T"t公差的中心值)时,那么,警戒区U的幅度就会显着缩小,而控制区l则必然会相应扩大,由于控制界限仍符台3o原则,因此扩大后的控制区(区域I)的控制界限仍维持着应有的检出能力由此,我们可以引进一个警戒系数的概念,取x控制图的警戒系数为Aw,-X.控制图的警戒系数为A并根据平均极差的大小来确定警戒区的大小.这样能够压缩警戒区的领域,避免产生完全符台技术要求和达到控制精确嚏(3o原则)要求的所谓失控点子.三,控制界限的修正应用警戒系数的概念,可以用下列修正公式来取代标准的控制图公式,将控制界限作一变换.用uRL育和uRL鼢别代替uc和UC,URL嗣nuR【分别是经修正后的一R控制图被一R控制图中的控制图被控制图的9～-控制图的应用?…一...一一～一..'一～上控制界限.用LRLt和LRh分别代替LCLt和LCL,, LRL和LRh分别是经修正后的x—R控制图和曼一R控制图中的控制图控制图上的下控制界限.对一R控制图的x控制图进行修正可得: URL=S一AwRLRLT=SL+AwR对一R控制图的控制图进行修正可得: URLy=S.一ARLRL=SL+A#疑这里的Su为规格的上界限,S为规格的下界限,曩为平均极差.上述公式分别用警戒系数A和A苷来代替控制图确定控制界限时所采用的系数A和m,A,这里的区别在于:A和A.用来决定警戒区区域的大小,而和m,A2则用来决定控锏区区域的大小.一般来说,标准型一R控制图或一R控制图,其收集的数据组越多,则所得控制界限越小,而修正型控制界限却相反,前者以分布中心为准,而后者在保证CP ≥l的条件下,以规格界限为准.在计算标准型控制界限或修正型控制界限时,推荐选用表2所列的有关系数.表2控制界阳用系数表,\系数ADjATT1】AAn\d21.8803.2670.886'07791.880O.7181.O232.5730.5910.7491.1870.58840.729——{2.2820.4860.728O.79606605.S772.il504300.7130.691059760.4832.O040.395O.7010.549063770.419lJ-0761.蛇40.370O.6920.5090.6028l1_373I161.8640351O.6800.昭2062l.330.[841.dO.357O.6730.4120.5981003I}8I12231.770.325O.66603630.61i四,观察与分析生产现场应用控制图的目的在于控制工序的稳定.如果控制图上显示出非管理状态,那必然是工序发生了异常,需要采取措施.经修正控制界限的又控制图及控制图的观察方法基本上与普通的控制图雷同:首先看各点子是否都在控制界限之内,点子越出界外(包括落在线上的)即为异常.接着看界内点子的排列是否有缺陷,即点子应体现只受偶然因素影响,不受系统因素影响.由于经修正后的界限,其实际分布中心往往和所取的控制中心线有偏移,因此在观察10时,就不能刘板地把大多数点子位于中心线一侧作为判断异常的依据.例如以某质量控制点收集的数据作图,.在X控制图上打点的四十个点子中,就有34点在总体中心线CL=的(上方)一侧,若以该批样本数据的均值为中心,则两侧的点子数就基本上相同(19;21),因而采用修正界限的控制图时,一侧性问题,一般可以不予考虑.采用修正型控制界限,由于控制区域扩l夫,使不少原来界外的点子,落入了修正界限之内.能够大幅度地降低调整的工作量.一...～......一......一...一～～～...一～......一...一一～.--一一.-.控制图的庙片j' 五警戒系数的确定表2所列的警戒系数Aw和A拍q依据是什么呢?是休氏区分两类质量因素的理论,即以30作为控制原则.通常又R控制图的X控制界限由公式130f或!A来确定,其中公式A中的系数A=兰d,因此在总体参数u和0未知时,可以通过子样用系数A来估算x控制图的控制界限.由于T±3o=十三√n,因此,当用聂/d来估计o,并用估计时,则得:-,一'±A2R:又id2R现在假定工序能力指数CP值为l,上,下控制界限的区域可以应用3o来对工序进行控制,只要分布的集中位置没有发生显着变化,工序就处于稳定状态.修正型控制界限是建筑在扩大控制区域,而又能维持工序能力指数为1时的警戒区应具有的警戒区域.以X—R控制图的x控制图的界限修正为侧:.=去=击=器～……c】)夸CP=l则R:_『Td:……(2)设CP=1时,两种界限值一致即UCL=URLi (3).+A2R=S一A_RAR=s.一一A2茛.当8=0时,即分布中心和公差中心T重叠时,那么=Tx,ifi.f1.s.一丈=÷T.A=一A (4)用式(2】代入式(4)得:?得A'下一'了/=五3最终得Aw=÷一A2 (5)例如当n=5时,利用公式(5一)可以求出警戒系数Aw.首先从数理统计表中查出n=5时的A和d2,接着把查得的A2=0.577和dz2.326 代入式(5)因此得Aw-主一A壶一o.557a2Z?zb=1.2898—0.557=0.7l28--'0.7l3同样方法可以求出FI=2～lO的各个Aw 系数值.其数值参见表2.据此推广应用,也可以求出一R控制图的文控制图的警戒系数A.设CP=l则UCL=URLr就是文tn3A2R=s一A《RA=S.文一m3A2录当￡+0时则柚R=T—m,A裒:(6)f7)'c=而T::=d得R:代入式(7)b即Ai3一mA…-(8)用这一公式可以求出警戒系数A诺修正控制界限的常用数据可查阅本文表2.从警戒系数A中看出.在两个相邻的样-控皋U图的应用-一.'.一一.'.一一一一一一一一一一....'.一' 书个数之间.样本数人的偶数样串的中位数控制图的警戒系数A反而比其数目大的奇数样本的大.并没像A稍B样,随样本数增大而有规律地减小;因而系数呈参差不齐的锯齿状:(并且随着样本数增大.系数值逐渐趋近)这是由于偶数中位数取中间两个数均值的缘故一六,灵活应用在应用修正型控制图时,如果工序能力指数相当充分,此时町以相应修正警戒系数数值.适当扩大警戒区的区域.减少发生第二种错误的概率.在修正A和Aw时.应似据工序隧力指数的人小,选择相应的修正工序能力指数数值为确保使用的修IF型控I图的经济,有效,适当扩大控制区域,对维持g6ff,J俭出能力具有实用意义=推荐的修正工序能力指数如表3所示表3修正指数参数表工序能指敬cpf修正工序能州数值cp-25i1.1.～.{.1lII.1.Ic¨上L;1.表41学正的警戒系数===■AAn,,,.1.11.!I.g31.1J.21.诳1.I:J1.1{【lIJ.6551.㈨{1.J1ll1.633l】.}127I.II-I.335I).0.虬11.17lI).H7J.1)21【.:川I).)l1.坼【.1{3)『1.HJ21).J711.J3Ll一).21c_857【.1)25.2cII).l={}lI.一f"{I).75}lJ_町3【.1l27r).XO2lJ_0【3J.一i57I1.7I2lc.820.811.85lI.H【lI.I)27I-.2il1.83【.91;H一).77lc_(1HI.|l(J【1.舯1l}.93【lII}.76lI..(;2I-.ll_7¨)【1.8(17l}?93【'为了计算的方便,将修正指数Cp【为1.1,I.2和1.33时的相应修正警戒系数A.w和A面值列一表式(表4)可供使用时参考.如果在使用修正型控制图的过程中,证实工序的分布中心和公差中心一致,则可以进而改用预控图.其效果将会更佳一一般说来,标准型控制图,修正型控制图和预先控制图三者可以根据工序的历史和工序能力的变化情况相互转化:在工序情况不太明嘹的情况下,可以先应用标准型控制图:随着对工序稳定性确认.在充分掌握工序能力指数在1.33以上的历史资料之后.町以修正控制图的控制界限,以减少因虚假警报而调整工序的频次.如果修正界限的控制图使用情况良好,工序一直处于较稳定的状态,则可以进一步改用预先控制图.町以省去计算样组平均值和扳差的麻烦.甚至以在操作人员十分熟悉工序的前提下.作检测不打点,以预控限来监察工序,达到简便地一12控制工序质量的目的.七,结论在xR,R控制图中,X和控制图主要是反映和控制样组分布的集中位置.而R控制图则反映和控制样组分布的离散程度在工序能力指数^=或者等于】.33时.只要分布的离散性没有显着变化,分市的集中位置即使偏离0.其分布晦线仍位丁经修正的控制界限之内因此落在控制界限之内的点子.都能判断为处f受控状态的JE常点子.宴践证明,应用修正控制界限的方法,其控制效果仍旧十分良好,即能在维持其置信度的前提下,允许比标准控制界限有更宽阔的控制区域.从而I丁以大量减少调整工序的时问. 因此无链是一种值得夫力推广应用的经济.fI 效,实用的控制图法。

统计过程控制（SPC）之控制限的建立
定义/说明/要求/目的：
控制限是指：在控制图上的一条线（或多条线），作为判断一个过程是否稳定的基础。

如果存在超出控制限的变差，则证明该过程正遭受特殊原因的影响。

控制限是根据过程数据计算出来的。

极差是指：对过程分布宽度的一种测量。

在一个子组、样本或总体中，指的是最大值与最小值之间的差。

过程分布宽度是指：过程特性的单值的分布的变化程度；通常用过程均值加或减几倍的标准差来表示。

控制限定义了只存在变差的普通原因时，控制统计量能够随机落入的一个数值的范围。

为了进行持续的控制，必须延长控制限。

检查表：。

one point outside control limit -回复标题：理解与处理“一点超出控制限”问题在质量管理领域，控制图是一种强大的工具，用于监控过程的稳定性并识别可能的异常。

然而，当我们在控制图上发现一个点超出了控制限，这可能会引发一系列的问题和挑战。

本文将逐步探讨这个问题，从理解控制限的概念开始，到如何分析和处理这种超出控制限的情况。

一、理解控制限控制限是基于过程的历史数据计算出来的，通常包括上控制限（UCL）和下控制限（LCL）。

它们定义了过程的可接受性能范围，任何在此范围内的数据点都被认为是正常的、预期的变异。

控制限并非基于规格限或者目标值，而是基于过程的内在变异性。

二、识别超出控制限的点当一个数据点出现在控制限之外，我们称其为“超出控制限”。

这种情况可能表明过程发生了某种变化，或者可能是由于随机变异导致的偶然事件。

无论是哪种情况，我们都不能忽视这个信号，因为它可能预示着质量问题或者效率下降。

三、判断是否真正的异常发现一个点超出控制限并不意味着立即需要采取行动。

首先，我们需要判断这个超出是否是真实的异常。

以下是一些可能的判断步骤：1. 检查数据收集和记录的过程是否存在错误。

有时候，超出控制限的点可能是由于测量误差、记录错误或者其他数据收集问题导致的。

2. 确认控制图的设置是否正确。

例如，控制限的计算是否基于足够的历史数据，是否考虑了过程的特殊特性（如季节性、趋势等）。

3. 考虑是否存在特殊原因。

例如，是否有临时的生产条件变化、新的设备或原料、人员变动等可能导致过程变异增加的因素。

如果以上检查都没有发现问题，那么我们可以初步判断这个超出控制限的点是一个真实的异常。

四、分析和处理超出控制限的点一旦确认了超出控制限的点是真实异常，我们就需要进一步分析其原因，并采取相应的措施。

以下是一些可能的步骤：1. 进行详细的过程审查。

这可能包括回顾操作规程、检查设备状态、访谈工作人员等，以找出可能导致变异增加的原因。

团队讨论决定控制图的控制限
在控制图中，中间的一条为中心线（均值线），一般用蓝色的实线绘制，表示允许偏差（或绩效）的平均值，也就是目标值。

在上方的一条称为控制上限，在下方的称为控制下限。

对上下控制界限（Control Limit）的绘制，则一般均用红色的虚线表现，以表示可接受的偏差范围。

至于实际产品质量特性的点连线条则大都用黑色实线绘制。

一般根据控制上限与控制下限来判断过程是否失控，具体方法如下：
（1）如果质量偏差落在控制上限和控制下限的范围内（七点规则的情况除外），则说明项目执行过程是受控的，不需采取纠正措施。

（2）如果质量偏差落在控制上限或控制下限的范围之外，项目执行过程就失控了，必须采取纠正措施。

（3）如果偏差虽然在控制上限与控制下限范围内，但是偏差分布具有非随机的特性，从统计意义上讲项目执行过程也失控了，应该立即采取纠正措施。

质量偏差只要在规格上限和规格下限之内，哪怕是超出了控制上限或控制下限，产品质量仍然是合格的，不需要缺陷补救。

一旦质量偏差突破规格上限或规格下限，产品就是不合格的，需要进行缺陷补救。

规格上限和规格下限通常表现为控制上限和控制下限之外的两条线。

控制图中，任何需要调查分析的观测值都是非随机原因（特殊
原因、异常事件）引起的，例如，7个点在同一侧或呈同向变动、超过控制上限（或控制下限）等。

任何非随机原因引起的偏差都是不可以接受的，都意味着项目执行过程失控。