先行进位加法器教材
- 格式:docx
- 大小:55.18 KB
- 文档页数:11

实验四32位先行进位加法器一、功能概述串行进位加法器延时很大,每级的输出结果都要等上一级的进位到来才可以求和算出结果,这次实验对普通全加器进行改良,改良为先行进位加法器。
先行进位加法器,各级的进位彼此是独立产生,只与输入数据A,B和C_in有关,将各级间的进位级联传播给去掉了,这样就可以减小进位产生的延时。
每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。
通过这种进位方式实现的加法器称为超前进位加法器。
因为各个进位是并行产生的,所以是一种并行进位加法器。
二、实验原理1、设二进制加法器第i位为A i,B i,输出为S i,进位输入为C i,进位输出为C i+1,则有:S i=A i⊕B i⊕C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,则C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1,产生进位C i+1 = 1当A i和B i有一个为1时,P i = 1,传递进位C i+1= C i因此G i定义为进位产生信号,P i定义为进位传递信号。
G i的优先级比P i高,也就是说:当G i = 1时(当然此时也有P i = 1),无条件产生进位,而不管C i是多少;当G i=0而P i=1时,进位输出为C i,跟C i之前的逻辑有关。
下面推导4位超前进位加法器。
设4位加数和被加数为A 和B,进位输入为C in,进位输出为C out,对于第i位的进位产生G i = A i·B i ,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inC1=G0 + P0·C0C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0▪C0C3=G2+ P2·C2= G2+ P2·G1+ P2·P1·G0+P2·P1·P0·C0C4=G3+ P3·C3= G3+ P3·G2+ P3·P2·G1+P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)C out=C4由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi和Cin有关。


实验四32位先行进位加法器一、功能概述串行进位加法器延时很大,每级的输出结果都要等上一级的进位到来才可以求和算出结果,这次实验对普通全加器进行改良,改良为先行进位加法器。
先行进位加法器,各级的进位彼此是独立产生,只与输入数据A,B和C_in有关,将各级间的进位级联传播给去掉了,这样就可以减小进位产生的延时。
每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。
通过这种进位方式实现的加法器称为超前进位加法器。
因为各个进位是并行产生的,所以是一种并行进位加法器。
二、实验原理1、设二进制加法器第i位为A i,B i,输出为S i,进位输入为C i,进位输出为C i+1,则有:S i=A i⊕B i⊕C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,则C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1,产生进位C i+1 = 1当A i和B i有一个为1时,P i = 1,传递进位C i+1= C i因此G i定义为进位产生信号,P i定义为进位传递信号。
G i的优先级比P i高,也就是说:当G i = 1时(当然此时也有P i = 1),无条件产生进位,而不管C i是多少;当G i=0而P i=1时,进位输出为C i,跟C i之前的逻辑有关。
下面推导4位超前进位加法器。
设4位加数和被加数为A 和B,进位输入为C in,进位输出为C out,对于第i位的进位产生G i = A i·B i ,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inC1=G0 + P0·C0C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0▪C0C3=G2+ P2·C2= G2+ P2·G1+ P2·P1·G0+P2·P1·P0·C0C4=G3+ P3·C3= G3+ P3·G2+ P3·P2·G1+P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)C out=C4由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi和Cin有关。

实验四32位先行进位加法器一、功能概述串行进位加法器延时很大,每级的输出结果都要等上一级的进位到来才可以求和算出结果,这次实验对普通全加器进行改良,改良为先行进位加法器。
先行进位加法器,各级的进位彼此是独立产生,只与输入数据A,B 和C_in有关,将各级间的进位级联传播给去掉了,这样就可以减小进位产生的延时。
每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。
通过这种进位方式实现的加法器称为超前进位加法器。
因为各个进位是并行产生的,所以是一种并行进位加法器。
二、实验原理1、设二进制加法器第i位为A i,B i,输出为S i,进位输入为C i,进位输出为C i+1,则有:S i=A i⊕B i⊕C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,则C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1,产生进位C i+1 = 1当A i和B i有一个为1时,P i = 1,传递进位C i+1= C i因此G i定义为进位产生信号,P i定义为进位传递信号。
G i的优先级比P i高,也就是说:当G i = 1时(当然此时也有P i = 1),无条件产生进位,而不管C i是多少;当G i=0而P i=1时,进位输出为C i,跟C i之前的逻辑有关。
下面推导4位超前进位加法器。
设4位加数和被加数为A和B,进位输入为C in,进位输出为C out,对于第i位的进位产生G i = A i·B i,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inC1=G0 + P0·C0C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0▪C0C3=G2 + P2·C2 = G2 + P2·G1 + P2·P1·G0 + P2·P1·P0·C0C4=G3 + P3·C3 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)C out=C4由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi和Cin有关。
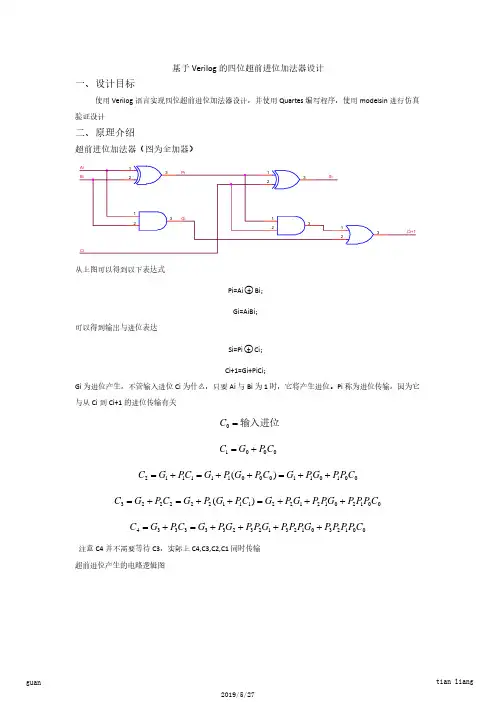


8位超前进位加法器设计说明书超前进位加法器就是使各位的进位直接由加数和被加数来决定,而不需要依赖低位进位。
即有如下逻辑表达式:1)(-++=i i i i i i C B A B A C当第i 位被加数A i 和加数B i 均为1时,有1=i i B A ,不论低位运算结果如何本位必然有进位输出(1=i C ),所以定义i i i B A G =为进位产生函数。
当A i 和B i 中只有一个为1时,有0=i i B A ,1=+i i B A ,使得1-=i i C C ,所以定义i i i B A P +=为进位传递函数。
将P i 和G i 代入全加器的“和”及“进位”表达式有:1-⊕⊕=i i i i C B A Y从而构成超前进位加法器。
VHDL 示例程序如下:(本程序在MAXPLUSII V9.6上编译通过)--*****8位超前进位加法器*****LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE. STD_LOGIC _ARITH.ALL;USE IEEE. STD_LOGIC _UNSIGNED.ALL;ENTITY ADDER8BIT ISPORT(A, B: IN UNSIGNED(7 downto 0);CI,clk: IN STD_LOGIC;Y_OUT: OUT STD_LOGIC_VECTOR(7 downto 0);CO_OUT: OUT STD_LOGIC);END ADDER8BIT;ARCHITECTURE doing OF ADDER8BIT ISSIGNAL CO,Y: STD_LOGIC_VECTOR(7 downto 0);BEGINY(0)<=A(0) xor B(0) xor CI;CO(0)<=(A(0) and B(0)) or (B(0) and CI) or (A(0) and CI);GEN:for i in 1 to 7 GENERATEY(i)<=A(i) xor B(i) xor CO(i-1); --1-⊕⊕=i i i i C B A YCO(i)<=(CO(i-1) and A(i)) or (CO(i-1) and B(i)) or (A(i) and B(i)); -- 1)(-++=i i i i i i C B A B A Cend GENERATE;process(clk)beginif clk'event and clk='1' thenY_OUT<=Y(7) & Y(6) & Y(5) & Y(4) & Y(3) & Y(2) & Y(1) & Y(0);CO_OUT<=CO(7);end if;end process;END doing;附:仿真时序波形。


沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:班级:学号:姓名:指导教师:完成日期:沈阳航空航天大学课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (4)2.1顶层方案图的设计与实现 (4)2.1.1创建顶层图形设计文件 (4)2.1.2器件的选择与引脚锁定 (5)2.1.3编译、综合、适配 (7)2.2功能模块的设计与实现 (7)2.2四位超前进位加法器模块的设计与实现 (7)2.3仿真调试 (9)第3章编程下载与硬件测试 (11)3.1编程下载 (11)3.2硬件测试及结果分析 (11)参考文献 (13)附录(程序清单或电路原理图) (14)第1章总体设计方案1.1设计原理八位超前进位加法器,可以由2个四位超前进位加法器构成。
由第一个四位超前进位加法器的进位输出作为第二个超前进位加法器的进位输入即可实现八位超前进位加法器的设计。
超前进位产生电路是根据各位进位的形成条件来实现的。
只要满足下述条件,就可形成进位C1、C2、C3、C4。
所以:第一位的进位C1=X1*Y1+(X1+Y1)*C0第二位的进位C2=X2*Y2+(X2+Y2)*X1*Y1+(X2+Y2)(X1+Y1)C0第三位的进位C3=X3*Y3+(X3+Y3)X2*Y2+(X3+Y3)*(X2+Y2)*X1*Y1+(X3+Y3)(X2+Y2)(X1+Y1)*C0第四位的进位C4=X4*Y4+(X4+Y4)*X3*Y3+(X4+Y4)*(X3+Y3) * X2*Y2+(X4+Y4)(X3+Y3)(X2+Y2)*X1*Y1+(X4+Y4)(X3+Y3)(X2+Y2)(X1+Y1)*C0 下面引入进位传递函数Pi和进位产生函数Gi的概念。
它们定义为:Pi=Xi+YiGi=Xi*YiP1的意义是:当X1和Y1中有一个为1时,若有进位输入,则本位向高位传递此进位。

数字电路与逻辑设计实验二一、实验目的1.熟悉多路复用器、加法器的工作原理。
2.学会使用VHDL语言设计多路复用器、加法器。
3.掌握generic的使用,设计n-1多路复用器。
4.兼顾速度与成本,设计行波加法器和先行进位加法器。
二、实验内容1.用VHDL语言设计8重3-1多路复用器;2.用VHDL语言设计n-1多路复用器,调用该n-1多路复用器定制为8-1多路复用器。
53.用VHDL语言设计4位行波进位加法器。
4.用VHDL语言设计4位先行进位加法器。
第一部分:8重3-1多路复用器①实验方法1、实验方法采用基于FPGA进行数字逻辑电路设计的方法。
采用的软件工具是Quartus II。
2、实验步骤1、新建,编写源代码。
(1).选择保存项和芯片类型:【File】-【new project wizard】-【next】(设置文件路径+设置project name为multiplexer_3_to_1_st)-【next】(设置文件名multiplexer_3_to_1_st.vhd—在【add】)-【properties】(type=AHDL)-【next】(family=FLEX10K;name=EPF10K10TI144-4)-【next】-【finish】(2).新建:【file】-【new】(第二个AHDL File)-【OK】2、根据题意,写好源代码并保存文件。
3、编译与调试。
确定源代码文件为当前工程文件,点击【processing】-【start compilation】进行文件编译,编译成功。
4、波形仿真及验证。
新建一个vector waveform file。
按照程序所述插入S、I0-I2、Y五个八维向量节点(S、I0-I2为输入节点,Y为输出节点)。
(操作为:右击-【insert】-【insert node or bus】-【node finder】(pins=all;【list】)-【>>】-【ok】-【ok】)。

块内并行4位先行进位逻辑
在数字电路中,块内并行是一种常见的设计思路,尤其在加法器电路中,先行进位逻辑是指在进行加法运算时,进位的计算提前于求和部分。
下面简要介绍一种可能的实现方式,即4位先行进位加法器(4-bit Carry Look-Ahead Adder,CLA)的基本结构:
1.输入:
•两个4位二进制数(A和B)
•输入进位(Cin)
2.输出:
•4位和(Sum)
•输出进位(Cout)
3.块内并行4位先行进位逻辑的主要思路:
•将输入进位(Cin)和每一位的输入(A和B)结合,提前生成每一位的进位,再将这些提前生成的进位和输入进位
相加,得到最终的输出进位。
•这样,通过提前生成进位,可以减少等待进位传播的时间,提高加法器的速度。
4.具体实现:
•使用逻辑门和电路元件,通过逻辑电路设计来实现块内并行4位先行进位逻辑。
实现的方式可能包括AND、OR、
XOR 门等。
请注意,具体的电路设计可能会根据使用的技术(如传统的TTL 逻辑、CMOS 技术等)以及设计的要求而有所不同。
在数字电路设计中,CLA 加法器是常见的一种用于优化进位传播的方式。
如果您需要更详细的信息或具体的电路图,请参考相应的教材、文献或数字电路设计工具的资料。
实验四32 位先行进位加法器一、功能概述串行进位加法器延时很大,每级的输出结果都要等上一级的进位到来才可以求和算出结果,这次实验对普通全加器进行改良,改良为先行进位加法器。
先行进位加法器,各级的进位彼此是独立产生,只与输入数据A, B 和C_in 有关,将各级间的进位级联传播给去掉了,这样就可以减小进位产生的延时。
每个等式与只有三级延迟的电路对应,第一级延迟对应进位产生信号和进位传递信号,后两级延迟对应上面的积之和。
通过这种进位方式实现的加法器称为超前进位加法器。
因为各个进位是并行产生的,所以是一种并行进位加法器。
二、实验原理1、设二进制加法器第i位为A i, B i,输出为S,进位输入为C i, 进位输出为C i+i,则有:S=A i ㊉B i ㊉C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,贝y C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1 ,产生进位C i+i = 1当A i和B i有一个为1时,P i = 1,传递进位C i+i= C i因此G i定义为进位产生信号,P i定义为进位传递信号。
G i的优先级比P i 高,也就是说:当G i = 1时(当然此时也有P i = 1),无条件产生进位,而不管C i 是多少;当G i=0 而P i=1 时,进位输出为C i,跟C i之前的逻辑有关。
下面推导 4 位超前进位加法器。
设 4 位加数和被加数为 A 和B,进位输入为C in,进位输出为C out,对于第i位的进位产生G i = A i •B i,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inG=G o + P o •C oC2=G 1 + P1 •C 1 = G 1 + P1 •G 0 + P1 •P o ?C oC3=G 2 + P2 •C 2 = G2 + P2, G 1 + P2 •P1 •G o +P2 •P1 •P o •C oC4=G 3 + P3 •C 3 = G3 + P3, G 2 + P3 •P2 •G 1 +P3 •P 2 •P1 •G o + P 3 P2 •P1•P o •C o (1-3)C out=C4由此可以看出,各级的进位彼此独立产生,只与输入数据Ai、Bi 和Cin 有关。
2、接口说明序号 接口信号名称方向说明备注1 A[31:0] I 输入数据2 B[31:0] I 输入数据3 S[31:0] O 加法结果4countO最高位进位3、结构框图三、实验方案方案一:分为两个模块:1个4位add_4和1个add_32,其中add_32 调用4个add_4.首先设计4位超前进位加法器:框图如下:设计好四位的之后,开始调用四位的实现32位的方案二:分为五个模块:(1)计算传播值和产生值模块:|L —7 \4位 ^28 4位C^4 4位 - 4位CLACLAA15~12 B 15~12 A11~8 B11~8 A7~4 B 7-4 A3~o B 3~014位L CLAC 12 4位 CLA4位 CLAC4<-l 4位 CLA1 F 1 r卄* g x1 p x1 C 16g x1g x0 Px0C s24位 BCLApgr 5 CLA CLA 9~16g m4 P m4g m7 P m7P m6 gm5 pm54位 BCLAA31~28 B 31~28 A27~24 B 27~24 A23~20 B23~20 A19~16 B 19~161~8gm0 P mO16 位1 f f S7~4gm2Pm24位 BCLAmlPm1* * Si5~i2 g m3P m31 T S3~0模块(2)超前进位模块:cla 模块(3)加法求和模块:sum 模块(4)求和并按输出a,b,c_in 分组:bit_slice 模块(5)32 位超前进位加法器总模块:cla_32 总框图:四、验证方案:对32 位的两个输入赋值:当a=32'b1000_0001_0111_1011_1101_1001_1101_1000;b=32'b0111_1000_ 0001_ 1000_ 1100_ 0111_ 0101_ 0001;c_in=1'b0;结果:s=32'b11111001;_1001 _1001 _0100 _1010 _0001 _0010_当a=32'b1000_0001_1000;0111_ 1011_ 1101_ 1001_ 1101_0001;b=32'b0111_1000_0001_ 1000_ 1100_ 0111_ 0101_c_in=1'b1;结果:s=32'b1111 _1001 _1001 _0100 _1010 _0001 _0010_ 1010; 来对波形进行观察,看波形是否正确。
五、实验代码:方案一:(1)add_32 模块顶层模块:(2) 4位add_4模块方案二:(1) cla_32顶层模块:module cla_32(a,b,c_in,s,count ); input [31:0] a,b;input c_in;output [31:0] s;output count;wire [7:0] gg,gp,gc;wire [3:0] ggg,ggp,ggc;wire gggg,gggp;bit_sliceb1(.a(a[3:0]),.b(b[3:0]),.c_in(gc[0]),.s(s[3:0]),.gp(gp[0]),.gg(gg[0 ])); bit_sliceb2(.a(a[7:4]),.b(b[7:4]),.c_in(gc[1]),.s(s[7:4]),.gp(gp[1]),.gg(gg[1 ])); bit_sliceb3(.a(a[11:8]),.b(b[11:8]),.c_in(gc[2]),.s(s[11:8]),.gp(gp[2]),.gg(g g[2]) );bit_sliceb4(.a(a[15:12]),.b(b[15:12]),.c_in(gc[3]),.s(s[15:12]),.gp(gp[3]),.g g(g g[3]));bit_sliceb5(.a(a[19:16]),.b(b[19:16]),.c_in(gc[4]),.s(s[19:16]),.gp(gp[4]),.g g(g g[4]));bit_sliceb6(.a(a[23:20]),.b(b[23:20]),.c_in(gc[5]),.s(s[23:20]),.gp(gp[5]),.gg(gg[5]));bit_sliceb7(.a(a[27:24]),.b(b[27:24]),.c_in(gc[6]),.s(s[27:24]),.gp(gp[6]), .gg(g g[6]));bit_sliceb8(.a(a[31:28]),.b(b[31:28]),.c_in(gc[7]),.s(s[31:28]),.gp(gp[7]), .gg(g g[7]));clac0(.p(gp[3:0]),.g(gg[3:0]),.c_in(ggc[0]),.c(gc[3:0]),.gp(ggp[0]),.gg (ggg[ 0]));clac1(.p(gp[7:4]),.g(gg[7:4]),.c_in(ggc[1]),.c(gc[7:4]),.gp(ggp[1]),.gg (ggg[1]));assign ggp[3:2]=2'b11;assign ggg[3:2]=2'b00;cla c2(.p(ggp),.g(ggg),.c_in(c_in),.c(ggc),.gp(gggp),.gg(gggg)); assign count=gggg|(gggp&c_in);endmodule2)pg 模块:module pg(a,b,p,g);input [3:0] a,b;output [3:0] p,g;assign p=a A b;assign g=a&b;endmodule(3) cla 模块:module cla(p,g,c_in,c,gp,gg); input [3:0] p,g;input c_in;output [3:0] c;output gp,gg;function [99:0] do_cla;input [3:0] p,g;input c_in;begin:labelinteger i;reg gp,gg;reg [3:0] c;gp=p[0];gg=g[0];c[0]=c_in;for(i=1;i<4;i=i+1)begingp=gp&p[i];gg=(gg&p[i])|g[i]; c[i]=(c[i-1]&p[i-1])|g[i-1]; end do_cla={c,gp,gg};endendfunctionassign {c,gp,gg}=do_cla(p,g,c_in);endmodule( 4) sum 模块:module sum(a,b,c,s );input [3:0] a,b,c;output [3:0] s;wire [3:0] t=a A b;assign s=tAc;endmodule5) bit_slice 模块:module bit_slice(a,b,c_in,s,gp,gg ); input [3:0] a,b;input c_in;output [3:0] s;output gp,gg;wire [3:0]p,g,c;pg i1(a,b,p,g);cla i2(p,g,c_in,c,gp,gg);sum i3(a,b,c,s);endmodule(6)激励代码:module cla32_tb;// Inputsreg [31:0] a;reg [31:0] b;reg c_in;// Outputswire [31:0] s;wire count;// Instantiate the Unit Under Test (UUT) cla_32 uut ( .a(a),.b(b),.c_in(c_in),.s(s),.count(count));initial begin// Initialize Inputsa = 0;b = 0;c_in = 0;// Wait 100 ns for global reset to finish#10a=32'b1000_ 0001 0111 1011_ 1101_ 1001 1101 _1000;b=32'b0111_ 1000 0001 1000_ 1100_ 0111 0101 _0001;c_in=1'b0;#10a=32'b1000_ 0001 0111 1011_ 1101_ 1001 1101 _1000;b=32'b0111_ 1000 0001 1000_ 1100_ 0111 0101 _0001;c_in=1'b1;// Add stimulus here end endmodule 六、波形图说明1、仿真波形2、结果说明对于三个输入:a=32'b1000_0001_0111_1011_1101_1001_1101_1000;b=32'b0111_1000_0001_1000_1100_0111_0101_0001; c_in=1'bO;结果与实验方案的相同,结果仿真正确.七、实验总结 对于这次实验,自己在老师布置完,努力做了几个下午,不 断调试才得到正确结果波形,是非常有收获的。