最新版人教版七年级数学下册知识点及典型试题汇总——适用于期末总复习

新人教版七年级数学下册知识点归纳
本文档旨在为七年级学生提供数学下册知识点的简洁归纳，方便学生进行研究和复。

第一章有理数
有理数基础知识
- 有理数的概念及表示方法
- 有理数的大小关系及比较
- 有理数的加减运算法则
有理数的乘除法
- 正数、负数、0之间的乘除
- 有理数的乘方
- 有理数的开方
第二章代数式
代数式的基本概念
- 代数式的定义及基本元素- 代数式的分类及例子
- 代数式的值及求值
代数式的运算
- 代数式的加减运算
- 代数式的乘除运算
- 代数式的乘方运算
第三章方程与不等式方程的基本概念
- 方程的定义及基本元素- 方程与等式的关系
- 一元一次方程的解法
不等式的基本概念
- 不等式的定义及基本元素
- 不等式的性质及解法
- 一元一次不等式的解法
第四章图形的认识
图形的基本概念
- 点、线、面的区别及联系
- 基本图形的名称及性质
- 平面图形的分类及例子
视图与投影
- 视图的基本概念及种类
- 正视图和俯视图的概念和绘制方法- 投影的基本概念及种类
第五章几何变换
平移
- 平移的定义及性质- 平移的向量表示- 平移的作用及实例
旋转
- 旋转的定义及性质- 旋转的角度表示- 旋转的作用及实例
对称
- 对称的定义及性质- 对称的种类及例子- 对称的作用及实例
以上为新人教版七年级数学下册的知识点归纳。

希望本文档能够帮助同学们更好地掌握数学知识，取得更好的研究成绩。

相交线与平行线一、相交线1、相交线中的角两条直线相交，可以得到四个角，我们把两条直线相交所构成的四个角中，有公共顶点但没有公共边的两个角叫做对顶角。

我们把两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角叫做临补角。

临补角互补，对顶角相等。

直线AB，CD与EF相交（或者说两条直线AB，CD被第三条直线EF所截），构成八个角。

其中∠1与∠5这两个角分别在AB，CD的上方，并且在EF的同侧，像这样位置相同的一对角叫做同位角；∠3与∠5这两个角都在AB，CD之间，并且在EF的异侧，像这样位置的两个角叫做内错角；∠3与∠6在直线AB，CD之间，并侧在EF 的同侧，像这样位置的两个角叫做同旁内角。

2、垂线两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直。

其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

直线AB，CD互相垂直，记作“AB⊥CD”（或“CD⊥AB”)，读作“AB垂直于CD”（或“CD垂直于AB”）。

垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直。

性质2：直线外一点与直线上各点连接的所有线段中，垂线段最短。

简称：垂线段最短。

二、平行线1、平行线的概念在同一个平面内，不相交的两条直线叫做平行线。

平行用符号“∥”表示，如“AB∥CD”，读作“AB平行于CD”。

同一平面内，两条直线的位置关系只有两种：相交或平行。

注意：（1）平行线是无限延伸的，无论怎样延伸也不相交。

（2）当遇到线段、射线平行时，指的是线段、射线所在的直线平行。

2、平行线公理及其推论平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

推论：如果两条直线都和第三条直线平行，那么这两条直线也互相平行。

3、平行线的判定平行线的判定公理：两条直线被第三条直线所截，如果同位角相等，那么两直线平行。

简称：同位角相等，两直线平行。

平行线的两条判定定理：（1）两条直线被第三条直线所截，如果内错角相等，那么两直线平行。

新人教版七年级下册数学知识点整理的两个角叫做同位角，它们的度数相等。

②在两条直线(被截线)的异侧，都在第三条直线(截线)的同一侧，这样的两个角叫做内错角，它们的度数相等。

③在两条直线(被截线)的同一侧，都在第三条直线(截线)的同一侧，这样的两个角叫做同旁内角，它们的度数互补。

7、平移是指在平面内，将一个图形沿着某个方向按照某个距离移动，移动后的图形与原图形形状、大小、方向都相同。

平移的性质：平移不改变图形的形状、大小和方向，只改变图形的位置。

本文介绍了平面几何中的角度和平行线的相关概念和性质。

其中，角度分为同位角、内错角和同旁内角，平行线的判定包括同位角相等、内错角相等、同旁内角互补和平行于同一条直线的两条直线互相平行。

此外，文章还介绍了命题和定理的概念，以及平移变换的性质。

最后，文章对实数进行了分类，包括按定义分类和按性质符号分类。

科学记数法是一种将数表示为(1≤＜10，n为整数)形式的记数方法。

平面直角坐标系由有序数对和两条互相垂直且有公共原点的数轴组成。

其中，有序数对是有顺序的两个数a与b组成的数对，记做（a,b）。

横轴是水平的数轴，也称为x轴或横轴；纵轴是竖直的数轴，也称为y轴或纵轴；两坐标轴的交点为平面直角坐标系的原点。

对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标，记作P(a，b)。

坐标轴上的点不在任何一个象限内，而两条坐标轴将平面分成四个部分，右上部分叫第一象限，按逆时针方向依次叫第二象限、第三象限、第四象限。

坐标轴上的点有特殊的坐标特点，如x轴正半轴上的点的坐标为(a,0)，y轴负半轴上的点的坐标为(0,-b)。

点P(a，b)到x 轴的距离是|b|，到y轴的距离是|a|。

对称点的坐标特点包括：关于x轴对称的两个点，横坐标相等，纵坐标互为相反数；关于y轴对称的两个点，纵坐标相等，横坐标互为相反数；关于原点对称的两个点，横坐标、纵坐标分别互为相反数。

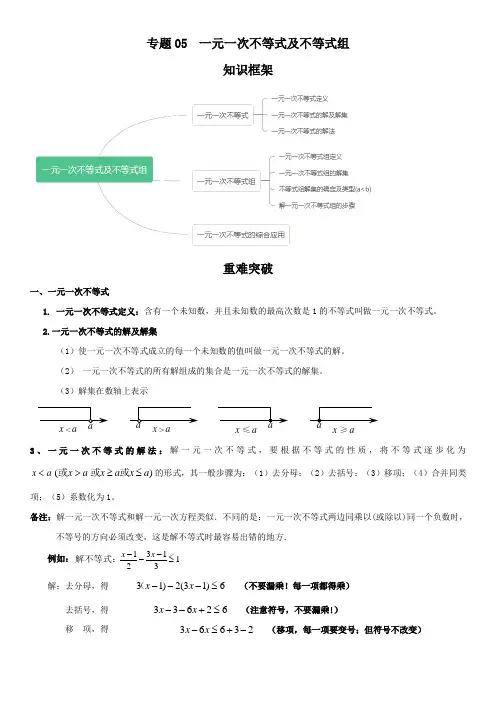
专题05 一元一次不等式及不等式组知识框架重难突破一、一元一次不等式1. 一元一次不等式定义：含有一个未知数，并且未知数的最高次数是1的不等式叫做一元一次不等式。

2.一元一次不等式的解及解集（1）使一元一次不等式成立的每一个未知数的值叫做一元一次不等式的解。

（2） 一元一次不等式的所有解组成的集合是一元一次不等式的解集。

（3）解集在数轴上表示3、一元一次不等式的解法：解一元一次不等式，要根据不等式的性质，将不等式逐步化为x a <(x a >或)x a x a ≥≤或或的形式，其一般步骤为：（1）去分母；（2）去括号；（3）移项；（4）合并同类项；（5）系数化为1。

备注：解一元一次不等式和解一元一次方程类似．不同的是：一元一次不等式两边同乘以(或除以)同一个负数时，不等号的方向必须改变，这是解不等式时最容易出错的地方．例如：131321≤---x x 解不等式： 解：去分母，得 6)13(2)13≤---x x （（不要漏乘！每一项都得乘） 去括号，得 62633≤+--x x （注意符号，不要漏乘!）移 项，得 23663-+≤-x x （移项，每一项要变号；但符号不改变）a a a a < > ≤ ≥合并同类项，得 73≤-x （计算要正确）系数化为1， 得 37-≥x （同除负，不等号方向要改变，分子分母别颠倒了） 例1．（2019·湖南广益实验中学初一期中）下列不等式中，是一元一次不等式的是（ ）A ．1x ＞3B ．x 2＜1C ．x +2y ＞0D ．x ＜2x +1【答案】D【解析】解：A 、1x 是分式，因此1x＞3不是一元一次不等式，故此选项不合题意； B 、x 2是2次，因此x 2＜1不是一元一次不等式，故此选项不合题意；C 、x +2y ＞0含有2个未知数，因此不是一元一次不等式，故此选项不合题意；D 、x ＜2x +1是一元一次不等式，故此选项符合题意；故选：D ．练习1．（2018·六安市裕安中学初一期中）下列不等式中，一元一次不等式有（ ）①2x 32x +> ②130x -> ③ x 32y -> ④x 15ππ-≥ ⑤ 3y 3>- A ．1 个B ．2 个C ．3 个D ．4 个 【答案】B【解析】详解：①不是，因为最高次数是2；②不是，因为是分式；③不是，因为有两个未知数；④是；⑤是.综上，只有2个是一元一次不等式.故选B ．例2．（2019·洋县教育局初二期中）若437m x -+≤是关于x 的一元一次不等式，则m =__________．【答案】3【解析】解：∵437m x -+≤是关于x 的一元一次不等式，∴4-m =1，∴m=3，故答案为：3．练习1.（2019·山东省初二期中）已知12(m+4)x|m|﹣3+6＞0是关于x的一元一次不等式，则m的值为()A．4 B．±4 C．3 D．±3【答案】A【解析】根据题意|m|﹣3=1且m+4≠0解得：|m|=4，m≠﹣4所以m=4．故选：A．例3．（2018·浙江省初二期中）一元一次不等式2（x﹣1）≥3x﹣3的解在数轴上表示为（）A．B．C．D．【答案】B【解析】解: 2（x﹣1）≥3x﹣3去括号, 得2x-2≥3x-3，移项, 合并同类项, 得-x≥-1，得：x≤1故在数轴上表示为:故选B.练习1．（2020·万杰朝阳学校初一期中）如图，张小雨把不等式3x＞2x-3的解集表示在数轴上，则阴影部分盖住的数字是____．【答案】-3【解析】由3x＞2x-3，解得：x＞-3，∴阴影部分盖住的数字是：-3．故答案是：-3．例4．（2020·监利县新沟新建中学初一期中）解不等式：14232-+->-x x ． 【答案】x ＜−2【解析】解：去分母：2（x −1）−3（x ＋4）＞−12，去括号：2x −2−3x −12＞−12，合并同类项：−x ＞2，系数化1：x ＜−2． 练习1．（2018·福建省永春第二中学初一期中）解不等式3(21)x +＜13(43)x --，并把解集在数轴上表示出来．【答案】x ＜2，数轴见解析【解析】去括号，得 6x +3＜13-4+3x ，移项，得 6x -3x ＜13-4-3，即3x ＜6，两边同除以3，得x ＜2，在数轴上表示不等式的解集如下：例5．（2019·重庆市凤鸣山中学初一期中）关于x 的不等式22x a -+≥的解集如图所示，则a 的值是（ ）A ．0B ．2C ．2-D ．4- 【答案】A【解析】解：解不等式22x a -+≥，得22a x- ，∵由数轴得到解集为x ≤-1， ∴212a -=- ，解得：a =0. 故选：A .练习1．（2019·陕西省初二期中）不等式-4x -k ≤0的负整数解是-1，-2，那么k 的取值范围是（ ） A ．812k ≤<B ．812k <≤C ．23k ≤<D ．23k <≤ 【答案】A【解析】解：∵-4x -k ≤0，∴x ≥-4k ， ∵不等式的负整数解是-1，-2，∴-3＜-4k ≤-2， 解得：8≤k ＜12，故选：A ．二、一元一次不等式组1、一元一次不等式组定义： 含有同一个未知数的几个一元一次不等式所组成的不等式组，叫做一元一次不等式组。

人教版七年级下册数学知识点总结归纳七年级下册数学知识点1概率1.一般地，在大量重复试验中，如果事件A发生的频率n/m会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率。

2.随机事件：在一定的条件下可能发生也可能不发生的事件，叫做随机事件。

3.互斥事件：不可能同时发生的两个事件叫做互斥事件。

4.对立事件：即必有一个发生的互斥事件叫做对立事件。

5.必然事件:那些无需通过实验就能够预先确定它们在每一次实验中都一定会发生的事件称为必然事件。

6.不可能事件：那些在每一次实验中都一定不会发生的事件称为不可能事件。

2相交线与平行线1.相交线在同一平面内，两条直线的位置关系有相交和平行两种。

如果两条直线只有一个公共点时，称这两条直线相交。

2.垂线当两条直线相交所成的四个角中，有一个角是直角时，即两条直线互相垂直，其中一条直线叫做另一直线的垂线，交点叫垂足。

3.同位角两条直线a，b被第三条直线c所截(或说a，b相交c)，在截线c的同旁，被截两直线a，b的同一侧的角，我们把这样的两个角称为同位角。

4.内错角两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角。

5.同旁内角两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角。

6.平行线几何中，在同一平面内，永不相交(也永不重合)的两条直线叫做平行线。

平行线的性质：①两直线平行，同位角相等;②两直线平行，内错角相等;③两直线平行，同旁内角互补。

7.平移平移，是指在同一平面内，将一个图形上的所有点都按照某个直线方向做相同距离的移动，这样的图形运动叫做图形的平移运动，简称平移。

3平面直角坐标系1.定义：平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。

水平的数轴称为x轴或横轴，习惯上取向右为正方向;竖直的数轴称为y轴或纵轴，取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点。

2.平面上的任意一点都可以用一个有序数对来表示，记为(a，b)，a是横坐标，b是纵坐标。

2024年人教版七年级数学知识点总结一、有理数1. 有理数的概念：有理数是可以表示为两个整数的比值的数。

2. 有理数的分类：整数、分数、零。

3. 有理数的表示形式及比较大小：分数、小数、整数。

二、整数1. 整数的概念：由整数可以用整数1表示，包含正整数、负整数和零。

2. 整数的运算：加法、减法、乘法、除法的运算法则。

3. 知识点：正负整数的加减法、乘法及除法的运算规则。

三、分数1. 分数的概念：分母为0的数除外，一个不能化为整数的数叫分数。

2. 分数的基本概念：分子、分母、真分数、假分数和带分数。

3. 分数的化简和等值分数：化简分数的方法，等分数的概念。

4. 分数的加减法：同分母的分数相加减，异分母的分数相加减。

5. 分数的乘法：分数与整数相乘，分数之间相乘。

6. 分数的除法：分数与整数相除，分数之间相除。

四、小数1. 小数的概念：有限小数和无限循环小数。

2. 小数的读法和写法：小数的读法，小数的书写规则。

3. 小数的四则运算：小数的加减法，小数的乘法，小数的除法。

4. 小数与分数的相互转换：小数转分数，分数转小数。

五、实数1. 实数的定义：有理数和无理数的统称。

2. 无理数的概念：不能表示为两个整数之比的数，如根号2，根号3等。

六、代数式与方程式1. 代数式的概念：用字母表示数的式子。

2. 方程式的概念：含有等号的代数式叫做方程式。

3. 一元一次方程的解：方程的根、方程的解集。

4. 一元一次方程的应用：利用一元一次方程解决实际问题。

七、比例与百分数1. 比例的概念：两个含有比的式子叫做比例。

2. 比例的性质：比例的基本性质、相等比例的性质。

3. 比例的计算：已知两个相等比例的三个量中的任意两个量，可以求出第三个量。

4. 百分数的概念：以百分号表示的数。

5. 百分数与分数、小数的相互转换。

6. 增长量和减少量的计算：已知原数和增长量（减少量）之比和增长率（减少率），可以求出增加量（减少量）。

八、平面图形的初步认识1. 二维图形的分类：几何图形、点、线段、直线、角、多边形、平行四边形、正方形、长方形、正三角形、等腰三角形。

Ⅶ、假设a＞0,b＜0,a+b＞0,那么a、-a、b、-b的大小关系是〔〕A、-a＜b＜-b＜aB、-a＜-b＜b＜aC、-b＜a＜-a＜bD、-b＜-a＜a＜bⅧ、当-1＜a＜0时，那么有〔〕A、1/a＞aB、∣-a3∣＞-a3C、-a＞a2D、a3＜-a2Ⅸ、如果x＞2,那么以下四个式子中：①x2＞2x②xy＞2y③2x＞x④1/x＜1/2正确的个数是〔〕A、4个B、3个C、2个D、1个Ⅹ、假设x+y＞x-y,y-x＞y，那么以下式子正确的选项是〔〕A、x+y＞0B、y-x＜0C、xy＜0D、y/x＞0Ⅺ、如果关于x的方程x+2m-3=3x+7的解为不大于2的非负数，那么〔〕A、m=6B、m等于5，6，7C、5＜m＜7D、5≤m≤7Ⅻ、-1＜b＜0,0＜a＜1,那么在代数式a-b,a+b,a+b2,a2+b中，对任意的a、b,对应的代数式的值最大的是〔〕A、a+bB、a-bC、a+b2D、a2+b4、运用不等式的性质比较大小：例：ⅰ、制作某产品有两种用料方案：方案1是用5X A型钢板，7X B型钢板；方案2是用3X A型钢板，9X B型钢板。

A型钢板比B型钢板的面积大，从省料的角度考虑，应选哪种方案？〔用求差法比较大小〕ⅱ、设a＞2,b＞3,c＞6,令M=abc,N=ab+bc+ac,那么M、N的大小关系是〔〕<提示：用作商比较法>A、M＞NB、M＜NC、M＝ND、以上三种情况都有可能ⅲ、甲从一个鱼摊上买了三条鱼，平均每条a元，又从另一个鱼摊上买了两条鱼，平均每条b元，后来他又以每条〔a+b〕/2的价格把鱼全部卖出去，结果发现亏了钱，原因是〔〕A、a＞bB、a＜bC、a＝bD、与a、b的大小无关ⅳ、a、b、c、d都是正实数，且a/b＜c/d，比较b/(a+b)和d/(c+d)的大小。

〔提示：用求倒数法〕5、不等式与方程、方程组的结合：2x+y=1+3m例：ⅰ、方程组满足x+y＜0，那么〔〕A、m＞-1B、m＞1C、m＜-1D、m＜1x+2y=1-mⅱ、方程x+2k=4(x+k)+1的解是正数，求k的取值X围。

第五章相交线与平行线平面内，点与直线之间的位置关系分为两种：①点在线上②点在线外同一平面内，两条或多条不重合的直线之间的位置关系只有两种：①相交②平行一、相交线1、两条直线相交，有且只有一个交点。

（反之，若两条直线只有一个交点，则这两条直线相交。

）两条直线相交，产生邻补角和对顶角的概念：邻补角：两角共一边，另一边互为反向延长线。

邻补角互补。

要注意区分互为邻补角与互为补角的异同。

对顶角：两角共顶点，一角两边分别为另一角两边的反向延长线。

对顶角相等。

注：①、同角或等角的余角相等；同角或等角的补角相等；等角的对顶角相等。

反过来亦成立。

②、表述邻补角、对顶角时，要注意相对性，即“互为”，要讲清谁是谁的邻补角或对顶角。

例如：判断对错：因为∠ABC +∠DBC = 180°，所以∠DBC是邻补角。

（）相等的两个角互为对顶角。

（）2、垂直是两直线相交的特殊情况。

注意：两直线垂直，是互相垂直，即：若线a垂直线b，则线b垂直线a 。

垂足：两条互相垂直的直线的交点叫垂足。

垂直时，一定要用直角符号表示出来。

过一点有且只有一条直线与已知直线垂直。

（注：这一点可以在已知直线上，也可以在已知直线外）3、点到直线的距离。

垂线段：过线外一点，作已知线的垂线，这点到垂足之间的线段叫垂线段。

垂线与垂线段：垂线是一条直线，而垂线段是一条线段，是垂线的一部分。

垂线段最短：连接直线外一点与直线上各点的所有线段中，垂线段最短。

（或说直角三角形中，斜边大于直角边。

）点到直线的距离：直线外一点到这条直线的垂线段的长度，叫这点到直线的距离。

注：距离指的是垂线段的长度，而不是这条垂线段的本身。

所以，如果在判断时，若没有“长度”两字，则是错误的。

4、同位角、内错角、同旁内角三线六面八角：平面内，两条直线被第三条直线所截，将平面分成了六个部分，形成八个角，其中有：4对同位角，2对内错角和2对同旁内角。

注意：要熟练地认识并找出这三种角：①根据三种角的概念来区分②借助模型来区分，即：同位角——F型，内错角——Z型，同旁内角——U型。

BC三角形知识点归纳、典型练习题及考点分析一、三角形相关概念 1．三角形的概念由不在同一直线上的三条线段首尾顺次连结所组成的图形叫做三角形 要点：①三条线段；②不在同一直线上；③首尾顺次相接．2．三角形的表示通常用三个大写字母表示三角形的顶点，如用A 、B 、C 表示三角形的三个顶点时，此三角形可记作△ABC ，其中线段AB 、BC 、AC 是三角形的三条边，∠A 、∠B 、∠C 分别表示三角形的三个内角．3．三角形中的三种重要线段三角形的角平分线、中线、高线是三角形中的三种重要线段．（1）三角形的角平分线：三角形一个角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．注意：①三角形的角平分线是一条线段，可以度量，而角的平分线是经过角的顶点且平分此角的一条射线．②三角形有三条角平分线且相交于一点，这一点一定在三角形的内部．③三角形的角平分线画法与角平分线的画法相同，可以用量角器画，也可通过尺规作图来画．（2）三角形的中线：在一个三角形中，连结一个顶点和它的对边中点的线段叫做三角形的中线． 注意：①三角形有三条中线，且它们相交三角形内部一点．②画三角形中线时只需连结顶点及对边的中点即可．（3）三角形的高线：从三角形一个顶点向它的对边作垂线，顶点和垂足间的限度叫做三角形的高线，简称三角形的高．注意：①三角形的三条高是线段②画三角形的高时，只需要向对边或对边的延长线作垂线，连结顶点与垂足的线段就是该边上的高．练习题：1、图中共有（ A ：5 B ：6 C ：7 D ：82、如图，AE ⊥BC ，BF ⊥AC ，CD ⊥AB ，则△ABC 中AC 边上的高是（ ） A ：AE B ：CD C ：BF D ：AF 3、三角形一边上的高（ ）。

A ：必在三角形内部B ：必在三角形的边上C ：必在三角形外部D ：以上三种情况都有可能 4、能将三角形的面积分成相等的两部分的是（ ）。