江苏大学计算机图形学第二次实验报告曲线拟合

计算机图形学实验报告2015-2016学年第一学期班级计自1302 学号姓名一．实验内容与实验步骤1.实验内容实现一个二维或三维裁剪算法，或实现一个Bezier曲线或Bezier曲面算法，并能够实现曲线曲面的形状修改。

2.主要思路每一裁剪窗口边界将二维空间划分成内部和外部的两个半空间。

一旦给所有的的线段端点建立了区域码，就可以快速判断哪条线段完全在裁剪窗口之内，哪条线段完全在窗口之外。

3.部分源代#include"stdafx.h"#include<GL/glut.h>#include<math.h>#include<GL/gl.h>#include<stdio.h>#include<stdlib.h>int flag;void setPixel(GLintx,GLint y){glBegin(GL_POINTS);glVertex2i(x, y);glEnd();}/* Bresenham line-drawing procedure for |m| < 1.0. */void lineBres (float x0, float y0, float xEnd, float yEnd){int dx =fabs(xEnd - x0), dy =fabs(yEnd - y0);int p = 2 * dy - dx;int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);int x, y;/* Determine which endpoint to use as start position. */if (x0 >xEnd) {x = xEnd;y = yEnd;xEnd = x0;}else {x = x0;y = y0;}setPixel (x, y);while (x <xEnd) {x++;if (p < 0)p += twoDy;else {y++;p += twoDyMinusDx;}setPixel (x, y);}}class wcPt2D {public:GLfloat x, y;};inline GLint round (const GLfloat a) { return GLint (a + 0.5); }/* Define a four-bit code for each of the outside regions of a * rectangular clipping window.*/const GLintwinLeftBitCode = 0x1;const GLintwinRightBitCode = 0x2;const GLintwinBottomBitCode = 0x4;const GLintwinTopBitCode = 0x8;inline GLint inside (GLint code) { return GLint (!code); } inline GLint reject (GLint code1, GLint code2){ return GLint (code1 & code2); }inline GLint accept (GLint code1, GLint code2){ return GLint (!(code1 | code2)); }GLubyte encode (wcPt2D pt, wcPt2D winMin, wcPt2D winMax){GLubyte code = 0x00;if (pt.x<winMin.x)code = code | winLeftBitCode;if (pt.x>winMax.x)code = code | winRightBitCode;if (pt.y<winMin.y)code = code | winBottomBitCode;if (pt.y>winMax.y)code = code | winTopBitCode;return (code);}void swapPts (wcPt2D * p1, wcPt2D * p2){wcPt2Dtmp;tmp = *p1; *p1 = *p2; *p2 = tmp;}void swapCodes (GLubyte * c1, GLubyte * c2){GLubytetmp;tmp = *c1; *c1 = *c2; *c2 = tmp;}void lineClipCohSuth (wcPt2D winMin, wcPt2D winMax, wcPt2D p1, wcPt2D p2) {GLubyte code1, code2;GLint done = false, plotLine = false;GLfloat m;while (!done) {code1 = encode (p1, winMin, winMax);code2 = encode (p2, winMin, winMax);if (accept (code1, code2)) {done = true;plotLine = true;}elseif (reject (code1, code2))done = true;else {/* Label the endpoint outside the display window as p1. */if (inside (code1)) {swapPts (&p1, &p2);swapCodes (&code1, &code2);}/* Use slope m to find line-clipEdge intersection. */if (p2.x != p1.x)m = (p2.y - p1.y) / (p2.x - p1.x);if (code1 &winLeftBitCode) {p1.y += (winMin.x - p1.x) * m;p1.x = winMin.x;}elseif (code1 &winRightBitCode) {p1.y += (winMax.x - p1.x) * m;p1.x = winMax.x;}elseif (code1 &winBottomBitCode) {/* Need to update p1.x for nonvertical lines only. */if (p2.x != p1.x)p1.x += (winMin.y - p1.y) / m;p1.y = winMin.y;}elseif (code1 &winTopBitCode) {if (p2.x != p1.x)p1.x += (winMax.y - p1.y) / m;p1.y = winMax.y;}}}if (plotLine)lineBres (round (p1.x), round (p1.y), round (p2.x), round (p2.y)); void myDisplay(){wcPt2DwinMin , winMax , p1 , p2;winMin.x=100; winMin.y=200;winMax.x=400; winMax.y=400;p1.x=50; p1.y=50;p2.x=450; p2.y=450;glClear(GL_COLOR_BUFFER_BIT);glColor3f (1.0f, 0.0f, 0.0f);glRectf(winMin.x ,winMin.y ,winMax.x,winMax.y);glColor3f (1.0f, 1.0f, 1.0f);if (flag){lineClipCohSuth (winMin, winMax,p1,p2);}else{glBegin(GL_LINES);glVertex2i(p1.x,p1.y);glVertex2i(p2.x,p2.y);glEnd();}glFlush();}void Init(){glClearColor(0.0, 0.0, 0.0, 0.0);glMatrixMode (GL_PROJECTION);gluOrtho2D (0.0, 640.0, 0.0, 480.0);}void Reshape(int w, int h){glViewport(0, 0, (GLsizei) w, (GLsizei) h);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);}void keyboard(unsignedchar key, int x, int y) {if (key=='c' || key=='C') flag=true;if (key=='r' || key=='R') flag=false;glutPostRedisplay();}int main(int argc, char *argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);glutInitWindowPosition(100, 100);glutInitWindowSize(640, 480);glutCreateWindow("Cohen-Sutherland直线裁减算法，C 键裁减，R键复原"); Init();glutDisplayFunc(myDisplay);glutReshapeFunc(Reshape);glutKeyboardFunc(keyboard);glutMainLoop();return 0;}二．实验结果三．实验总结这次实验我的收获主要有两个方面：一是编程水平的提高，还有一个是对计算机图形学理论知识的巩固。

计算机图形学实验报告
实验目的：通过本次实验，深入了解并掌握计算机图形学的基本原理和相关技术，培养对图形处理的理解和能力。

实验内容：
1. 图像的基本属性
- 图像的本质及表示方法
- 像素和分辨率的概念
- 灰度图像和彩色图像的区别
2. 图像的处理技术
- 图像的采集和处理
- 图像的变换和增强
- 图像的压缩和存储
3. 计算机图形学的应用
- 图像处理在生活中的应用
- 计算机辅助设计中的图形学应用
- 三维建模和渲染技术
实验步骤和结果：
1. 在计算机图形学实验平台上加载一张测试图像，分析其像素构成
和基本属性。

2. 运用图像处理技术，对测试图像进行模糊、锐化、色彩调整等操作，观察处理后的效果并记录。

3. 学习并掌握计算机图形学中常用的处理算法，如卷积、滤波等，
尝试应用到测试图像上并进行实验验证。

4. 探讨计算机图形学在数字媒体制作、虚拟现实、计算机辅助设计
等领域的应用案例，并总结其在实践中的重要性和价值。

结论：
通过本次实验，我对计算机图形学有了更深入的了解，掌握了图像
处理技术的基本原理和应用方法。

计算机图形学作为一门重要的学科，对多个领域有着广泛的应用前景，有助于提高数字媒体技术、虚拟现
实技术等领域的发展水平。

希望在未来的学习和工作中能进一步深化
对计算机图形学理论和实践的研究，不断提升自己在这一领域的专业
能力和创新意识。

计算机图形学 实验报告实验一:二维线画图元的生成实验目的：掌握直线段的生成算法，并用C/WIN-TC/VC++实现算法，包括中点法生成直线，微分数值法生成直线段等。

实验内容：用不同的方法生成斜率不同的直线段，比较各种方法的效果。

Bresenham 算法的思想Bresenham 画法与中点法相似，都是通过每列象素中确定与理想直线最近的像素来进行直线的扫描的转换的。

通过各行、各列的象素中心构造一组虚拟网格线的交点，然后确定该列象素中与此交点最近的像素。

该算法的巧妙之处在于可以采用增量计算，使得对于每一列，只需要检查一个误差项的符号，就可以确定该列的所有对象。

1.1方法一：直线的中点算法 算法的主要思想：讨论斜率k ∈[1,+∞)上的直线段的中点算法。

对直线01p p ，左下方的端点为0p （x0，y0），右上方的端点为1p （x1，y1）。

直线段的方程为： y m x B =+⇔yy x B x y y x x B x∆=+⇔∆=∆+∆∆ (,)0F x y xy yx xB ⇔=∆-∆-∆= 现在假定已求得像素（,,i r i x y ），则如图得,,11(,]22i i r i r x x x ∈-+ 由于直线的斜率k ∈[1,+∞)，故m=1/k ∈(0,1],则1,,13(,]22i i r i r x x x +∈-+ 在直线1i y y =+上，区间,,13(,]22i r i r x x -+内存在两个像素NE 和E 。

根据取整原则，当11(,)i i x y ++在中点M 11(,)2i i x y ++右方时，取像素NE ，否则取像素E ，即,11,,1()()01()()0i r i i r i r i x E F M x x x NE F M x +++⎧⇔≤=⎨+⇔>⎩i i 点当(,y +1)在左方时点当(,y +1)在右方时若取2()i d F M =，则上式变为 ,1,,()01(0i r i i r i r i x E d x x NE d +⎧≤=⎨+>⎩点当点)当计算i d 的递推公式如下：,11,12[(2)()]0122(,2)0122[(2)(1)]2i i r i i i i i i i rx y y x xB d d F x y d x y y x xB ++⎧∆+-∆+-∆⎪≤⎪=++=⎨>⎪∆+-∆++-∆⎪⎩=202()i i i i d xd d x y d +∆≤⎧⎨+∆-∆>⎩算法的初始条件为：00,00,0(,)(0,0)12(,1)22r r x y x y d F x y x y =⎧⎪⎨=++=∆-∆⎪⎩ 相应的程序示例：建立成员函数：void MidPointLine4(CDC*pDC,int x0,int y0,int x1,int y1,int color) { /*假定x0<x1,直线斜率m>1*/int dx,dy,incrE,incrNE,d,x,y; dx=x1-x0; dy=y1-y0; d=2*dx-dy; incrE=2*dx;incrNE=2*(dx-dy); x=x0;y=y0;pDC->SetPixel(x,y,color); while (x<x1) {if (d<=0) d+=incrE; else{ d+=incrNE; x++; } y++;p->SetPixel(x,y,color);} }编写OnDraw 函数：void CMy1_1View::OnDraw(CDC* pDC) { CMy1_1Doc* pDoc = GetDocument(); ASSERT_VALID(pDoc); // TODO: add draw code for native data here MidPointLine4(pDC,200,200,300,300,RGB(0,0,0)); MidPointLine4(pDC,300,200,400,300,RGB(0,0,0)); MidPointLine4(pDC,400,200,500,300,RGB(0,0,0)); }编译运行程序得到如下结果：1.2方法二：直线的数值微分法 算法的主要思想：由于课本上已经给出了斜率m ∈[-1,1]上的算法，故此处给出斜率m ∈[1，+∞〕上的算法，m ∈(-∞,-1]上的可同理推导。

数值分析课程设计报告学生姓名学生学号所在班级指导教师一、课程设计名称函数逼近与曲线拟合二、课程设计目的及要求实验目的：⑴学会用最小二乘法求拟合数据的多项式，并应用算法于实际问题。

⑵学会基本的矩阵运算，注意点乘和叉乘的区别。

实验要求：⑴编写程序用最小二乘法求拟合数据的多项式，并求平方误差，做出离散函数（ ）和拟合函数的图形；⑵用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差，并用MATLAB 的内部函数plot 作出其图形，并与（1）结果进行比较。

三、课程设计中的算法描述用最小二乘法多项式曲线拟合，根据给定的数据点，并不要求这条曲线精确的经过这些点，而是拟合曲线无限逼近离散点所形成的数据曲线。

思路分析：从整体上考虑近似函数)(x p 同所给数据点）（i i y x ,误差i i i y x p r -=)(的大小，常用的方法有三种：一是误差i i i y x p r -=)(绝对值的最大值i mi r ≤≤0max ，即误差向量的无穷范数；二是误差绝对值的和∑=mi i r 0，即误差向量的1范数；三是误差平方和∑=mi i r 02的算术平方根，即类似于误差向量的2范数。

前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑2范数的平方，此次采用第三种误差分析方案。

算法的具体推导过程： 1.设拟合多项式为：2.给点到这条曲线的距离之和，即偏差平方和：3.为了求得到符合条件的a 的值，对等式右边求 偏导数，因而我们得到了：4.将等式左边进行一次简化，然后应该可以得到下面的等式5.把这些等式表示成矩阵的形式，就可以得到下面的矩阵：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====n i i n i n i i k n i k i ni k ini k i n i k i ni in i ini k ini iy y y a a x xx x xxx x 11i 110121111112111a n6. 将这个范德蒙得矩阵化简后得到⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n k k n n k k y y y a a a x x x x x x 21102211111 7.因为Y A X =*,那么X Y A /=,计算得到系数矩阵，同时就得到了拟合曲线。

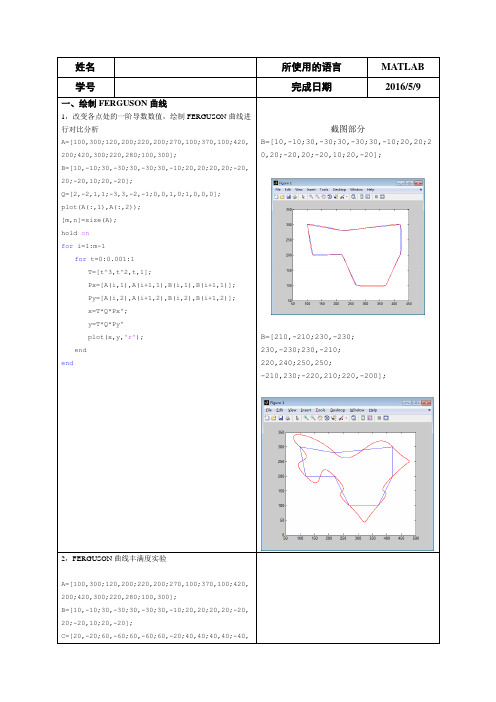
姓名所使用的语言MATLAB 学号完成日期2016/5/9 一、绘制FERGUSON曲线1，改变各点处的一阶导数数值，绘制FERGUSON曲线进行对比分析A=[100,300;120,200;220,200;270,100;370,100;420, 200;420,300;220,280;100,300];B=[10,-10;30,-30;30,-30;30,-10;20,20;20,20;-20, 20;-20,10;20,-20];Q=[2,-2,1,1;-3,3,-2,-1;0,0,1,0;1,0,0,0];plot(A(:,1),A(:,2));[m,n]=size(A);hold onfor i=1:m-1for t=0:0.001:1T=[t^3,t^2,t,1];Px=[A(i,1),A(i+1,1),B(i,1),B(i+1,1)];Py=[A(i,2),A(i+1,2),B(i,2),B(i+1,2)];x=T*Q*Px';y=T*Q*Py'plot(x,y,'r');endend截图部分B=[10,-10;30,-30;30,-30;30,-10;20,20;2 0,20;-20,20;-20,10;20,-20];B=[210,-210;230,-230;230,-230;230,-210;220,240;250,250;-210,230;-220,210;220,-200];2，FERGUSON曲线丰满度实验A=[100,300;120,200;220,200;270,100;370,100;420, 200;420,300;220,280;100,300];B=[10,-10;30,-30;30,-30;30,-10;20,20;20,20;-20, 20;-20,10;20,-20];C=[20,-20;60,-60;60,-60;60,-20;40,40;40,40;-40,40;-40,40;40,-40];D=[40,-40;120,-120;120,-120;120,-40;80,80;80,80 ;-80,80;-80,80;80,-80];Q=[2,-2,1,1;-3,3,-2,-1;0,0,1,0;1,0,0,0];plot(A(:,1),A(:,2));[m,n]=size(A);hold onfor i=1:m-1for t=0:0.001:1T=[t^3,t^2,t,1];Px=[A(i,1),A(i+1,1),B(i,1),B(i+1,1)];Py=[A(i,2),A(i+1,2),B(i,2),B(i+1,2)];x=T*Q*Px';y=T*Q*Py';Px1=[A(i,1),A(i+1,1),C(i,1),C(i+1,1)];Py1=[A(i,2),A(i+1,2),C(i,2),C(i+1,2)];x1=T*Q*Px1';y1=T*Q*Py1';Px2=[A(i,1),A(i+1,1),D(i,1),D(i+1,1)];Py2=[A(i,2),A(i+1,2),D(i,2),D(i+1,2)];x2=T*Q*Px2';y2=T*Q*Py2';plot(x,y,'r');plot(x1,y1,'r');plot(x2,y2,'r');endend二、绘制Bezier曲线1、二次Bernstein基函数性质分析三次Bernstein基函数性质分析2、绘制任意二次三点Bezier曲线x=[100 150 200 ];y=[100 50 100 ];plot(x,y,'k','LineWidth',1); k=length(x);for i=1:k-2for t=0:0.005:1Bx=(t^2-2*t+1)*x(1)+(-2*t^2+2*t)*x(2)+... (t^2)*x(3);By=(t^2-2*t+1)*y(1)+(-2*t^2+2*t)*y(2)+... (t^2)*y(3);hold onplot(Bx,By,'r','LineWidth',2);endend3、绘制三次七点Bezier曲线clear allhold onB1=[100,300;120,200;220,200;270,100];B2=[270,100;370,100;420,200;420,300]plot(B1(:,1),B1(:,2),'-b');plot(B2(:,1),B2(:,2),'-b');for t=0:0.001:1P=[t*t*t t*t t 1];Q=[-1,3,-3,1;3,-6,3,0;-3,3,0,0;1,0,0,0];P1=P*Q*B1;plot(P1(:,1),P1(:,2),'.b','markersize',10); P1=P*Q*B2;plot(P1(:,1),P1(:,2),'.b','markersize',10); end三、绘制B样条曲线1、绘制均匀二次三点B样条曲线x=[100 150 200 250 300 350 400 450 500];y=[100 50 100 50 150 50 100 50 100];plot(x,y,'k','LineWidth',1);k=length(x);B=1/2;for i=1:k-2for t=0:0.005:1Bx=B*(t^2-2*t+1)*x(i)+B*(-2*t^2+2*t+1)*x(i+1)+. ..B*(t^2)*x(i+2);By=B*(t^2-2*t+1)*y(i)+B*(-2*t^2+2*t+1)*y(i+1)+. ..B*(t^2)*y(i+2);hold onplot(Bx,By,'r','LineWidth',2);endend2、绘制三次B样条曲线x=[100 120 220 270 370 420 420 ];y=[300 200 200 100 100 200 300 ];plot(x,y,'k','LineWidth',1);k=length(x);B=1/6;for i=1:k-3for t=0:0.005:1Bx=B*(-t^3+3*t^2-3*t+1)*x(i)+B*(3*t^3-6*t^2-0*t +4)*x(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*x(i+2)+B*(1*t^3-0*t^2-0* t+0)*x(i+3);By=B*(-t^3+3*t^2-3*t+1)*y(i)+B*(3*t^3-6*t^2-0*t +4)*y(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*y(i+2)+B*(1*t^3-0*t^2-0* t+0)*y(i+3);hold onplot(Bx,By,'r','LineWidth',2);endend3、在同一控制顶点下(四个控制定点)绘制三次Bezier曲线和三次B样条曲线hold onx=[220 270 300 320 340 360 370 420 ];y=[200 100 150 150 150 150 100 200 ];plot(x,y,'-b','LineWidth',2);plot(x,y,'*r','LineWidth',3);k=length(x); B=1/6;for i=1:k-3for t=0:0.001:1Bx=B*(-t^3+3*t^2-3*t+1)*x(i)+B*(3*t^3-6*t^2-0*t+4)*x(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*x(i+2)+B*(1*t^3-0*t^2-0*t+0)*x(i+3);By=B*(-t^3+3*t^2-3*t+1)*y(i)+B*(3*t^3-6*t^2-0*t+4)*y(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*y(i+2)+B*(1*t^3-0*t^2-0*t+0)*y(i+3);plot(Bx,By,'r','LineWidth',2);endend四、有理曲线绘制各种参数图形绘制有理二次Bezier曲线x=[100 150 200 250 300 350 400 450 500];y=[100 50 100 50 150 50 100 50 100];plot(x,y,'k','LineWidth',1);k=length(x);B=1/2;for i=1:k-2for t=0:0.005:1Bx=(B*(t^2-2*t+1)*x(i)+B*(-2*t^2+2*t+1)*x(i+1)+...B*(t^2)*x(i+2))/(B*(t^2-2*t+1)+B*(-2*t^2+2*t+1)+...B*(t^2));By=(B*(t^2-2*t+1)*y(i)+B*(-2*t^2+2*t+1)*y(i+1)+...B*(t^2)*y(i+2))/(B*(t^2-2*t+1)+B*(-2*t^2+2*t+1)+...B*(t^2));hold onplot(Bx,By,'r','LineWidth',2);endend各种参数图形均匀有理B样条曲线绘制有理三次B样条曲线hold onx=[220 270 300 320 340 370 420 ];y=[200 100 140 150 130 100 200 ];plot(x,y,'-b','LineWidth',2);k=length(x); B=1/6;for i=1:k-3for t=0:0.001:1Bx=(B*(-t^3+3*t^2-3*t+1)*x(i)+B*(3*t^3-6*t^2-0*t+4)*x(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*x(i+2)+B*(1*t^3-0*t^2-0*t+0)*x(i+3))/(B*(-t^3+3*t^2-3*t+1)+B*(3*t^3-6*t^2-0*t+4)+...B*(-3*t^3+3*t^2+3*t+1)+B*(1*t^3-0*t^2-0*t+0));By=(B*(-t^3+3*t^2-3*t+1)*y(i)+B*(3*t^3-6*t^2-0*t+4)*y(i+1)+...B*(-3*t^3+3*t^2+3*t+1)*y(i+2)+B*(1*t^3-0*t^2-0*。

计算机图形学实验报告2计算机图形学实验报告实验⼆、三维⽹格模型光顺⼀、实验⽬的与基本要求：（1）掌握Obj⽂件的读⼊；（2）利⽤给定的数据结构类，建⽴读⼊⽹格模型数据结构；（3）利⽤OpenGL类库，对三维模型进⾏绘制；（4）利⽤OpenGL类库，增加采⽤⿏标交互⽅式对三维模型进⾏旋转、放缩、平移等操作；（5）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；⼆、实验设备（环境）及要求1. 操作系统：Windows XP 或Windows 72. 编程环境：Microsoft Visual Studio 2010，OpenGL 库函数3. 界⾯框架：Win32，MFC，QT选择其中⼀种三、实验内容与步骤实验分为以下⼏个步骤：（1）掌握Obj⽂件的读⼊顶点和⾯的个数；（2）建⽴数组存储点的坐标及⾯上的点数；（3）存储顶点的邻接⾯数，并记录每个顶点周围的邻接点（4）计算每个⾯的法向利⽤OpenGL类库，增加采⽤⿏标交互⽅式对三维模型进⾏旋转、放缩、平移等操作；（5）利⽤⾯法向及顶点坐标进⾏绘制⼏何体（6）实现⿏标对物体旋转、平移、缩放的算法（7）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；四、实现过程说明及成果展⽰：（1）掌握Obj⽂件的读⼊顶点和⾯的个数；由于obj⽂件的存储形式是v x1 x2 x3;…f v1 v2 v3;…这种形式，所以在记录点和⾯的数量时，只需按⾏读取，然后再判断⾸字母是v/f即可实现代码如下：（2）建⽴数组存储点的坐标及⾯上的点数；数组的⼤⼩由点数和⾯数决定，点数组和⾯数组均由0开始记录，故后⾯再⽤⾯对应点的时候，由于⾯上点是从1开始记录，故需要减1然后使⽤，代码如下：（3）存储顶点的邻接⾯数，并记录每个顶点周围的邻接点记录点邻接⾯的是新建⼀个数组，在读⾯的时候，将该⾯的序号存⼊对应点的数组中，然后再在每个⾯上取⼀点，记录到点的邻接点数组中，在每个⾯上取得的点为向外右⼿⽅向的下⼀个点，实现代码如下：（4）计算每个⾯的法向计算⾯的法向⽅式为⾯上右⼿⽅向上的两向量的叉乘得到，即所⽤代码为：（8）利⽤⾯法向及顶点坐标进⾏绘制⼏何体⽤法向绘制的⽅式是先⽤glNormal3fv(v)指出⾯的法向;再⽤glVertex3f传⼊⾯上点的坐标；由于我将glNormal3fv(v）中写在算法向所以我直接对此直接调⽤即可，代码如下：（9）实现⿏标对物体旋转、平移、缩放的算法平移：利⽤Transform函数和键盘事件来改变参数，w,s,a,d分别控制绘制的kitty猫的上下左右的移动：实现代码如下：旋转：利⽤gllookat();函数设定了观察⾓度，并⽤⿏标事件改变参数，⽤实现观察视⾓的变化实现物体的旋转，代码如下：缩放：运⽤glScalef⽅法和键盘事件改变参数，实现物体的放⼤和缩⼩，代码如下：（10）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；Laplacian⽅法的原理是利⽤⽬标点与其所有邻接点平均后的点的差向量，对⽬标点的坐标进⾏变换的过程，具体⽅法是：①建⽴每个点的邻接顶点数组，存储每个点的邻接点②对每个顶点的邻接点进⾏求平均，即将邻接点的坐标求和后除以邻接点个数，从⽽得到邻接平均点③得到优化向量优化向量= 邻接平均点-⽬标点④设定优化度参数λ，得到优化后的新坐标新坐标= ⽬标点+ λ*优化向量在程序中，对于第num个顶点，我设定的变量为邻接平均点v0优化向量l新坐标数组vNewArr具体代码如下：五、结果展⽰及说明计算⾯法向后直接绘制（未光顺）：光顺进⾏⼀次后光顺多次后利⽤点绘制结果为旋转后缩放后平移后六、⼼得体会(1)计算⾯法向时法向量的⽅向没有运⽤右⼿⽅向，导致有的⾯法向向⾥，从⽽出现雪花(2)在运⽤Laplacian算法进⾏求邻接平均点时未初始化邻接平均点数组，导致平均点的累加从⽽出现越光顺越粗糙的现象(3)在obj⽂件中⾯对应顶点数和顶点数组的标号相差1.在运⽤的时候需减1，⾯从1开始记顶点，顶点数组从0开始记顶点七、实验代码#define GLUT_DISABLE_ATEXIT_HACK#include#include#include#include#include#include#include#includeusing namespace std;int v_num = 0; //记录点的数量int f_num = 0; //记录⾯的数量int vn_num = 0;//记录法向量的数量int vt_num = 0;GLfloat **vArr; //存放点的⼆维数组GLfloat **vNewArr;//存放点的⼆维数组int **fvArr; //存放⾯顶点的⼆维数组GLfloat **fnArr;//存放⾯法向量的⼆维数组int **ftArr;int **vfArr;//存放顶点临接的⾯数的数组int **nextVArr;//存放下⼀个临界顶点的数组GLfloat **vnArr;//存放点法向量的⼆维数组string s1, s2, s3, s4;GLfloat f2, f3, f4;int num1, num2, num3;typedef GLfloat point3[3];point3 x, y,l;//平⾯上的两个向量x,y和拉普拉斯向量lstatic GLfloat theta[] = { 0.0,0.0,0.0 };static GLint axis = 2;static GLdouble viewer[] = { 0.0, 0.0, 5.0 }; /* initial viewer location */ static GLdouble Tran[] = { 0.0,0.0,0.0 }; static GLdouble sca = 1.0;void getLineNum(string addrstr) //获取点和⾯的数量{ifstream infile(addrstr.c_str()); //打开指定⽂件if (!infile) {cout <<"open error!"<< endl;}string sline;//每⼀⾏int i = 0, j = 0;while (getline(infile, sline)) //从指定⽂件逐⾏读取{if (sline[0] == 'v'){v_num++;}if (sline[0] == 'f'){f_num++;}}}int readfile(string addrstr) //将⽂件内容读到数组中去{//getLineNum(addrstr);//new⼆维数组vArr = new GLfloat*[v_num];for (int i = 0; i < v_num; i++) {vArr[i] = new GLfloat[3];}vNewArr = new GLfloat*[v_num];for (int i = 0; i < v_num; i++) {vNewArr[i] = new GLfloat[3]; }vnArr = new GLfloat*[vn_num];for (int i = 0; i < vn_num; i++) {vnArr[i] = new GLfloat[3];}vfArr = new int*[v_num];for (int i = 0; i < v_num; i++) {vfArr[i] = new int[10];for (int j = 0; j < 10; j++) { vfArr[i][j] = -1;}}nextVArr = new int*[v_num];for (int i = 0; i < v_num; i++) {nextVArr[i] = new int[10];for (int j = 0; j < 10; j++) { nextVArr[i][j] = -1; }}fvArr = new int*[f_num];fnArr = new GLfloat*[f_num];ftArr = new int*[f_num];for (int i = 0; i < f_num; i++) {fvArr[i] = new int[3];fnArr[i] = new GLfloat[3];ftArr[i] = new int[10];}ifstream infile(addrstr.c_str()); if (!infile) { cout <<"open error!"<< endl;exit(1);}string sline;//每⼀⾏int ii = 0, jj = 0, kk = 0, mm = 0;while (getline(infile, sline)){if (sline[0] == 'v')//存储点{istringstream sin(sline);sin >> s1 >> f2 >> f3 >> f4;vArr[ii][0] = f2;vArr[ii][1] = f3;vArr[ii][2] = f4;ii++;}if (sline[0] == 'f') //存储⾯{istringstream in(sline);GLfloat a;in >> s1>>num1>>num2>>num3;//去掉f fvArr[kk][0] = num1;fvArr[kk][1] = num2;fvArr[kk][2] = num3;for (int i = 0; i < 10; i++) {if (vfArr[num1-1][i] == -1) {vfArr[num1-1][i] = kk;nextVArr[num1-1][i] = num2;break;}}for (int j = 0; j < 10; j++) {if (vfArr[num2-1][j] == -1) {vfArr[num2-1][j] = kk;nextVArr[num2-1][j] = num3;break;}}for (int i = 0; i < 10; i++) {if (vfArr[num3-1][i] == -1) {vfArr[num3-1][i] = kk;nextVArr[num3-1][i] = num1;break;}}kk++;}}return 0;}//计算⾯法向void nomal(point3p) {/*⽮量的归⼀化*///double sqrt();float d = 0.0;int i;for (i = 0; i < 3; i++)d += p[i] * p[i];d = sqrt(d);if (d > 0.0)for (i = 0; i < 3; i++)p[i] /= d;}void getFaceNormal(point3A, point3B, point3C) { x[0] = C[0] - A[0]; x[1] = C[1] - A[1];x[2] = C[2] - A[2];y[0] = A[0] - B[0];y[1] = A[1] - B[1];y[2] = A[2] - B[2];point3 v;v[0] = x[1] * y[2] - x[2] * y[1];v[1] = x[2] * y[0] - x[0] * y[2];v[2] = x[0] * y[1] - x[1] * y[0];nomal(v);glNormal3fv(v);}void Laplacian() {for (int num = 0; num < v_num; num++) {int m = 0;//求得点的邻接⾯数for (int i = 0; i < 10; i++) {if (nextVArr[num][i] != -1) {m++;}else {break;}}point3 v0;for (int i = 0; i < 3; i++) {v0[i] = 0;}for (int i = 0; i < m; i++) {v0[0] += vArr[nextVArr[num][i] - 1][0];v0[1] += vArr[nextVArr[num][i] - 1][1];v0[2] += vArr[nextVArr[num][i] - 1][2];}if (m != 0) {for (int i = 0; i < 3; i++)v0[i] /= m;}l[0] = v0[0] - vArr[num][0];l[1] = v0[1] - vArr[num][1];l[2] = v0[2] - vArr[num][2];vNewArr[num][0] = vArr[num][0] + l[0] * 0.3;vNewArr[num][1] = vArr[num][1] + l[1] * 0.3;vNewArr[num][2] = vArr[num][2] + l[2] * 0.3;}for (int i = 0; i < v_num; i++) {vArr[i][0] = vNewArr[i][0];vArr[i][1] = vNewArr[i][1];vArr[i][2] = vNewArr[i][2];}}void init(void){getLineNum("H:\\kitten_noisy.obj");readfile("H:\\kitten_noisy.obj");double viewer[] = { 0.0, 0.0, 8.0 }; /* initial viewer location */GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat mat_shininess[] = { 50.0 };//材料的镜⾯指数，其值越⼤越精细GLfloat light_position[] = { 1.0, 1.0f, 1.0, 0.0 };GLfloat white_light[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat lmodel_ambient[] = { 0.1, 0.1, 0.1, 1.0 };glClearColor(0.0, 0.0, 0.0, 0.0);glShadeModel(GL_SMOOTH);glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);glLightfv(GL_LIGHT0, GL_POSITION, light_position);//光源位置glLightfv(GL_LIGHT0, GL_DIFFUSE, white_light);//漫反射光源glLightfv(GL_LIGHT0, GL_SPECULAR, white_light);//镜⾯反射光源glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);//环境光源// glEnable(glMaterialf);glEnable(GL_LIGHTING);//启动光照glEnable(GL_LIGHT0);//启⽤0度光源glEnable(GL_DEPTH_TEST);//启动深度测试/*glShadeModel(GL_SMOOTH); // Enable Smooth ShadingglClearColor(0.0f, 0.0f, 0.0f, 0.5f); // ⿊⾊背景glClearDepth(1.0f);// 深度缓冲区设置glEnable(GL_DEPTH_TEST); // 允许深度测试glDepthFunc(GL_LEQUAL);// 定义深度测试类型glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST); // Really Nice Perspective Calculation */}。

数值分析课程设计报告学生学生学号所在班级指导教师一、课程设计名称函数逼近与曲线拟合二、课程设计目的及要求实验目的：⑴学会用最小二乘法求拟合数据的多项式，并应用算法于实际问题。

⑵学会基本的矩阵运算，注意点乘和叉乘的区别。

实验要求：⑴编写程序用最小二乘法求拟合数据的多项式，并求平方误差，做出离散函数（x x ,x x ）和拟合函数的图形；⑵用MATLAB 的部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差，并用MATLAB 的部函数plot 作出其图形，并与（1）结果进行比较。

三、课程设计中的算法描述用最小二乘法多项式曲线拟合，根据给定的数据点，并不要求这条曲线精确的经过这些点，而是拟合曲线无限逼近离散点所形成的数据曲线。

思路分析：从整体上考虑近似函数)(x p 同所给数据点）（i i y x ,误差i i i y x p r -=)(的大小，常用的方法有三种：一是误差i i i y x p r -=)(绝对值的最大值i mi r ≤≤0max ，即误差向量的无穷数；二是误差绝对值的和∑=mi i r 0，即误差向量的1数；三是误差平方和∑=mi i r 02的算术平方根，即类似于误差向量的2数。

前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑2数的平方，此次采用第三种误差分析方案。

算法的具体推导过程： 1.设拟合多项式为：y =x 0+x 1x +x 2x 1+⋯+x x x x2.给点到这条曲线的距离之和，即偏差平方和：x 2=∑[x x −(x 0+x 1x +⋯+x x x x x )]2xx =13.为了求得到符合条件的a 的值，对等式右边求x x 偏导数，因而我们得到了：−2∑[x −(x 0+x 1x +⋯+x x x x x)]xx =1x =0−2∑[x −(x 0+x 1x +⋯+x x x x x)]xx =1=0⋯⋯−2∑[x −(x 0+x 1x +⋯+x x x x x )]xxxx =1=04.将等式左边进行一次简化，然后应该可以得到下面的等式x 0x +x 1∑x x +⋯+x x ∑x x xxx =1xx =1x 0∑x x +x 1∑x x 2+⋯+∑x x x +1xx =1xx =1xx =1x 0∑x x x+x 1∑x xx +1+⋯+x x ∑x x 2xxx =1xx =1xx =15.把这些等式表示成矩阵的形式，就可以得到下面的矩阵：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====n i i n i n i i k n i k i ni k ini k i n i k i ni in i ini k ini iy y y a a x xx x xxx x 11i 110121111112111a n6. 将这个德蒙得矩阵化简后得到⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n k k n n k k y y y a a a x x x x x x 21102211111 7.因为Y A X =*,那么X Y A /=,计算得到系数矩阵，同时就得到了拟合曲线。

插值与曲线拟合实验报告实验目的：1. 了解插值和曲线拟合的原理和方法；2. 掌握梯形公式的应用；3. 掌握拉格朗日插值多项式和牛顿插值多项式的构造方法；4. 掌握用MATLAB进行数据拟合的方法。

实验仪器：1. 计算机；2. MATLAB软件。

实验原理：插值：给定一组数据点，插值就是在这些数据点之间插入某些值，以尽量接近原函数的方式得到一个新的函数。

插值方法有很多种，其中比较常用的是拉格朗日插值多项式和牛顿插值多项式。

拉格朗日插值多项式：以一种通用的方式构造多项式，使其通过给定的一组数据点。

构造方法是依据n个数据点(x1,y1),(x2,y2),…,(xn,yn)构造n-1次函数L(x)，使得L(xi)=yi且有L(xj)=0（j不等于i）。

该多项式的形式为：L(x)=y1*L1(x)+y2*L2(x)+…+yn*Ln(x)其中，Lk(x)的构造方法是：Lk(x)=(x-x1)(x-x2)…(x-xk-1)(x-xk+1)…(x-xn) /(xk-x1)(xk-x2)…(xk-xk-1)(xk-xk+1)…(xk-xn)牛顿插值多项式：采用递推公式构造，其形式为：其中，f(x0,x1)表示在x0和x1之间的斜率，f(x0,x1,x2)表示在x0、x1和x2之间的曲率，以此类推。

曲线拟合：给定一组数据点，拟合就是寻找一个函数或者曲线，以最优化的方式拟合这些数据点，从而对未知的数据点进行预测。

拟合方法有很多种，其中比较常用的是线性方程、最小二乘法和多项式拟合。

最小二乘法：使用这种方法时，需要有一个数学模型，以此作为拟合函数。

当给定输入-输出数据时，使用最小二乘法以最小化误差平方和的方式来确定函数中未知的参数。

在MATLAB中使用polyfit函数实现多项式拟合。

实验结果：选择数据点如下：x = [1,2,3,4,5];y = [0.7652, 0.6347, 0.4496, 0.2499, 0.0621];使用梯形公式计算插值结果为 0.3865；使用拉格朗日插值多项式计算插值结果为 0.3865；使用牛顿插值多项式计算插值结果为 0.3865。

计算机科学与通讯工程学院实验报告课程计算机图形学实验题目曲线拟合学生姓名学号专业班级指导教师日期成绩评定表评论内容详细内容权重得分方案论证与综合剖析的正确、20%论证剖析合理性算法设计算法描绘的正确性与可读性20%编码实现源代码正确性与可读性30%程序书写表记符定义标准，程序书写风20%标准格标准报告质量报告清楚，提交准时10%总分指导教师署名曲线拟合实验内容绘制三次Bezier曲线〔1〕给定四个点P1—P4，以此作为控制极点绘制一段三次Bezier曲线。

〔2〕给定四个点P1—P4，以此作为曲线上的点绘制一段三次Bezier曲线。

绘制三次B样条曲线给定六个点P1—P6，以此作为控制极点绘制一条三次B样条曲线。

实验环境软硬件运转环境：WindowsXP开发工具：visualstudio2021问题剖析绘制三次Bezier曲线Bezier曲线是用N+1个极点〔控制点〕所组成的N根折线来定义一根N阶曲线。

本次实验中的三次Bezier曲线有4个极点，设它们分别为P0，P1，P2，P3，那么关于曲线上各个点Pi〔x,y〕知足以下关系：P(t)=[(-P0+3P1-3P2+3P3)t3+(3P0-6P1+3P2)t2+(-3P0+3P2)t+(P0+4P1+P2)]/6X(t)=[(-X0+3X1-3X2+3X3)t3+(3X0-6X1+3X2)t2+(-3X0+3X2)t+(X0+4X1+X2)]/6Y(t)=[(-Y0+3Y1-3Y2+3Y3)t3+(3Y0-6Y1+3Y2)t2+(-3Y0+3Y2)t+(Y0+4Y1+Y2)]/6此中P0、P1、P2、P3为四个的点，坐标分别为(X0、Y0)、(X1、Y1)、(X1、Y2)、(X3、Y3)。

因此只需确立控制点的坐标，该曲线可经过编程即可绘制出来。

绘制三次B样条曲线三次B样条函数绘制曲线的圆滑连结条件为：关于6个极点，取P1、P2、P3、P44个极点绘制在第一段三次样条曲线，再取P2、P3、P4、P5这4个极点绘制在第二段三次样条曲线，总计可绘制3段圆滑连结的三次样条曲线。

曲线拟合报告近年来，曲线拟合技术在各个领域得到广泛应用。

曲线拟合是将一组数据点用一个数学函数近似表示的过程。

在实际问题中，我们常常遇到需要通过已有的数据点来预测未知数值的情况，而曲线拟合恰好可以满足这个需求。

本报告将探讨曲线拟合的原理、应用以及其潜在的局限性。

一、曲线拟合的原理曲线拟合的核心思想是通过寻找一个能够最好地描述已知数据点的数学函数来实现。

常用的曲线拟合方法包括线性拟合、多项式拟合、指数拟合等。

其中，线性拟合是最简单的一种拟合方法，它假设数据点之间存在线性关系，通过最小二乘法求解出最佳的拟合直线。

在线性拟合的基础上，多项式拟合提供了更广泛的拟合能力。

多项式拟合可以通过增加拟合函数中的项数来适应不同的数据特征，这使得它在实际应用中更具灵活性。

然而，多项式拟合的缺点是容易出现过拟合现象，即在拟合函数中引入过多的项，导致对噪声数据的过分拟合。

二、曲线拟合的应用曲线拟合在科学研究和工程实践中有着广泛的应用。

以生物医学领域为例，研究人员经常需要通过拟合实验数据来找到疾病发展趋势、寻找治疗方法等。

曲线拟合技术可以帮助他们更好地了解疾病的发展规律，为治疗方案的设计提供科学依据。

此外，曲线拟合还在金融领域、气象学、地球物理学等多个领域得到了广泛应用。

例如，在金融领域，曲线拟合可以用于预测股市趋势、分析市场波动性等。

在气象学中，曲线拟合可以用于天气的预测和气候模型的建立。

这些应用都依赖于曲线拟合技术提供的模型和预测能力。

三、曲线拟合的局限性虽然曲线拟合是一种强大的数学工具，但它也存在一些局限性。

首先，曲线拟合的有效性通常取决于已知数据点的质量和数量。

如果数据点存在较大的误差或者缺乏充分的样本点，拟合结果可能会不准确。

因此，在进行曲线拟合之前，我们需要对数据进行预处理和筛选，以提高拟合结果的可靠性。

其次，曲线拟合可能会受到噪声数据的干扰。

数据集中的随机噪声对拟合结果可能产生较大影响，甚至导致过拟合。

为了解决这个问题，我们可以采用平滑技术或者正则化方法来降低噪声对拟合结果的影响。