第13章动荷载作业参考解答

第十五章动荷载一、教学目标和教学内容1、教学目标通过本章学习，唤起学生对动荷载问题的注意。

让学生知道动荷载问题的两个方面，目前应当掌握在较简单的工程问题中，动荷载引起杆件的应力、应变和位移的计算。

对于材料在动荷载下的力学行为，以后根据工作的需要再进一步补充学习。

让学生掌握动荷载问题的基本知识，如杆件作等加速运动时的应力计算，作等速旋转圆盘的应力分析，简单的自由落体冲击和水平冲击，以及循环应力问题的有关概念。

能够深刻认识动荷系数概念，并能够熟练地进行杆件作等加速运动时的应力计算，作等速旋转圆盘的应力分析，完成简单的自由落体冲击和水平冲击的计算。

2、教学内容介绍杆件作等加速运动拉伸、压缩及弯曲时的应力计算。

介绍等角速度旋转的动荷应力计算。

讲解简单冲击时，能量守恒的基本方程，分别导出自由落体冲击和水平冲击时的动荷系数公式，及杆件经受冲击时的应力计算公式。

二、重点难点重点：建立三类动荷载概念。

掌握杆件作等加速运动时的应力计算。

作等速旋转圆盘的应力分析。

简单的自由落体冲击和水平冲击问题的计算难点：对动静法和动荷系数的理解。

对于动荷载问题与静荷载问题的联系与区别。

在简单冲击问题中，被冲击杆件冲击点的相应静荷位移的理解和计算，特别是水平冲击时的静荷位移的理解和计算。

三、教学方式采用启发式教学，通过提问，引导学生思考，让学生回答问题。

四、建议学时3学时五、实施学时六、讲课提纲(一)概念（动荷载的概念）1、静荷载：作用在构件上的荷载由零开始，逐渐（平缓、慢慢）地增长到最终值，以致在加载过程中，构件各点的加速度很小，可以不计；荷载加到最终值保持不变或变动的不显著的荷载，称之为静荷载。

2、动荷载：如果构件本身处于加速度运动状态（高层、超高层建筑施工时起吊重物；这些建筑物中运行的电梯—惯性力问题）；或者静止的构件承受处于运动状态的物体作用（落锤打桩，锤头猛烈冲击砼桩顶—冲击问题）；地震波引起建筑物晃动(构件在振动状态下工作—振动问题)；机械零件在周期性变化的荷载下工作(交变应力疲劳问题)，则构件受到荷载就是动荷载。

大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。

解：(1) 取整体(2) 2-4 在简支梁，力的大小等于20KN ，如图所示。

若解：(1)(2)求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

解：(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解：（1）取铰链B (2) 取铰链C 由前二式可得：F FF ADF2-9 三根不计重量的杆AB，AC，AD在A点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。

试求在与O D平行的力F作用下，各杆所受的力。

已知F=0.6 kN。

解：(1)间汇交力系；(2)解得：AB、AC3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。

求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) (b) (c) 3-2 M ，试求A 和C解：(1) 取 (2) 取 3-3 Nm ，M 2解：(1)(2) 3-5 大小为AB 。

各杆 解：(1)(2)可知：(3) 研究OA 杆，受力分析，画受力图：列平衡方程：AB A3-7 O1和O2圆盘与水平轴AB固连，O1盘垂直z轴，O2盘垂直x轴，盘面上分别作用力偶（F1，F’1），（F2，F’2）如题图所示。

动载荷一、概念题1. 动载荷下,动应力不超过比例极限,则材料服从( 胡克定律 ),且具有相同的( 弹性模量 )2. 动载荷下,构件的强度条件是( []σσ≤max St )3. 在突加载荷下(相当于物体自由下落冲击,h=0情况), 构件的动应力是相应静应力的( 2倍 )4. 提高构件抗冲击能力的主要措施是(增大静位移,避免增加静应力。

如安葬橡皮座垫等)二、计算题1起重机吊索的横截面面积,已知Q=40kN,上升的加速度a=5m/S 2,吊索的[]σ=80MPa.。

重物的平衡方程Q g a F a g Q Q F Y Ndd Nd )/1(,0)/(,0+==-+=∑[]2755,/mm A A F Nd d ≥≤=σσ2重为Q 的重物自高度H 下落至梁上，梁的EI 和W 均已知,求梁的最大正应力.ZZ Z s t n a x W Wl W l W W M 92*3/2max ===σ C 点的静挠度,查表7-1,st d st h K EI Wl l l l EIl l l W ∆++==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=∆211,2434323632*3*3222⎥⎦⎤⎢⎣⎡++==3max 22431192Wl EIh W WlK z st d d σσ3.速度为v ，重为W 的重物，沿水平方向冲击梁的截面C ，试求梁的最大动应力。

设已知梁的E 、I Z 和W Z l 。

Zstnax W WL=σ,梁的自由端C 点静挠度,查表7-1,EI Wl St 33=ΛglEIWW v K glW EIl v g vK Z st d d st d 33max max 2===∆=σσ。

理论力学14章作业题解思考题14-1 确定自由度。

解 (a) k=2 ； (b) k=2； (c) 只滚不滑 k=2，又滚又滑 k=314-1 一台秤构造如图。

已知：BC//OD ，且BC=OD ，BC=AB/10。

设秤锤重P 1=10N ，试求秤台上的重物P 2。

解：（1）分析虚位移 秤杆AC 作转动，有10=C A r r d d /。

秤台作平动，有E C r r d d =，故有E C A r r r d d d 1010==。

（2）建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有：01021=+-P P ，N P 1002=。

Cr d Er14-5 OA=l ，OC=R满足的条件。

解： （用虚位移原理求解）(1) 运动分析（虚位移关系分析）A 处虚位移关系用合成运动的理论分析。

A 为动点，OC 为动系。

r e A r r r r r r d d d +=f d d cos A e r r =另外：R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知：AC=BC=EC=GC=DE=DG=l ，荷载F 2。

求平衡时的F 1。

解 用解析法，1个自由度，选q 为广义坐标。

建立坐标，如图。

(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解：(1) 接触D 处水平约束，代之约束力。

第13章 动 载 荷＊教学提示：本章讨论三类动载问题：等加速直线运动时构件的惯性力和应力计算；等角速转动时构件的应力计算；冲击载荷作用下的应力计算。

最后讨论了提高杆件抗冲击载荷能力的措施。

教学要求：掌握动载荷的概念、动应力的计算方法；了解提高杆件抗冲击载荷能力的常规措施；重点掌握用动静法求解构件的动应力问题。

13.1 载荷和动应力的概念前几章讨论了杆件在静载荷作用下的强度和刚度问题。

静载荷是指从零缓慢地增加到某一定值后保持不变且杆内各质点不产生加速度，或加速度很小可以忽略不计的载荷。

杆件在静载荷作用下产生的应力和变形分别称为静应力和静变形。

在工程实际中，除了受静载荷作用的构件外，还将遇到许多运动构件，这些构件在高速运行时，常常出现不可忽略的动力效应——附加在运动构件上的力效应。

若载荷使杆件内各质点产生的加速度较显著，或者载荷随时间而变化，则这样的载荷称为动载荷。

例如：高速旋转的飞轮，由于向心加速度使其内部各质点产生很大的离心惯性力，从而可能导致飞轮的破裂；涡轮机的长叶片，由于旋转时的惯性力所引起的拉应力可以达到相当大的数值，可能使得叶片被拉断而引发严重事故。

当具有一定速度的物体冲击静止的杆件时，该物体的速度在很短的时间内急剧变化，产生很大的负值加速度，故物体对静止的杆件施加很大的作用力。

比如，气锤在锻造坯件时，由于锤头和锻坯这两个物体在碰撞瞬间所产生的冲击载荷，能使锤杆内的应力较之静荷应力有几倍甚至几十倍的增长。

这种在动载荷作用下，杆件产生的应力和变形分别称为动应力和动变形。

试验证明，在动载荷作用下，若杆件的动应力不超过材料的比例极限，胡克定律仍然有效，而且材料的弹性常数也与静载荷作用下的数值相同。

本章着重讨论惯性力和冲击载荷等问题。

13.2 惯性力的问题13.2.1 等加速直线运动时构件的应力计算当构件各点的加速度为已知时或可以求出时，可以采用动静法求解构件的动应力问题。

这类问题称为惯性力问题。

绪论部分荷载：直接施加在结构上的力，在工程上统称荷载。

结构：在建筑物中承受和传递荷载而起骨架作用的部分。

构件：组成结构的每一个部分。

平衡状态：建筑的结构及组成结构的各构件，都相对于地面保持着静止状态，这种状态在工程上称为平衡状态。

要保证构件的正常工作，必须同时满足三个要求：1）在荷载作用下构件不发生破坏，即应具有足够的强度2）在荷载作用下构件所产生的变形在工程的允许范围内，即应具有足够的刚度3）承受荷载作用时，构件在其原有形状下应保持稳定，即应具有足够的稳定性※构件的强度、刚度和稳定性统称为构件的承载能力建筑力学的任务是：研究和分析作用在结构（或构件）上力与平衡的关系，结构（或构件）的内力、应力、变形的计算方法以及构件的强度、刚度与稳定条件，为保证结构（或构件）既安全可靠又经济合理提供计算理论依据。

杆系结构：由杆件组成的结构。

建筑力学：是由研究建筑结构的力学计算理论和方法的一门科学。

第一章静力学的基本概念力的定义：力是物体间的相互机械运动。

用一个带有箭头的有向线段来表示一个力（注意作用点的位置）物体在受到力的作用后，产生的效应可以分成两种：外效应，也称为运动效应，使物体的运动状态发生改变。

内效应，也称为变形效应，使物体的形状发生变化。

力的三要素：大小、方向、作用点力的大小反应物体之间的相互机械作用的强弱程度力的方向包含力的作用线在空间的方位和指向力的作用点是指力在物体的作用位置当接触面面积很小时，则可以将微小面积抽象为一个点，这个点称为力的作用点。

该作用力称为集中力；反之，如果接触面积较大而不能忽略时，则力在整个接触面上分布作用，此时的作用力称为分布力。

分布力的大小用单位面积上的力的大小来度量，称为荷载集度。

力是矢量，记作F刚体：在外力的作用下，不发生形变的物体。

平衡：在外力作用下，物体相对于地球保持静止或匀速直线运动状态，我们就称物体在外力作用下保持平衡。

力系分类汇交力系：力系中各力作用线汇交于一点力偶系：力系中各力可以组成若干力偶或力系由若干力偶组成平行力系：力系中各力作用线相互平行一般力系：力系中各力作用线既不完全交于一点，也不完全相互平行等效力系：若某一力系对物体产生的效应，可以用另一个力系来代替，则这两个力系称为等效力系。

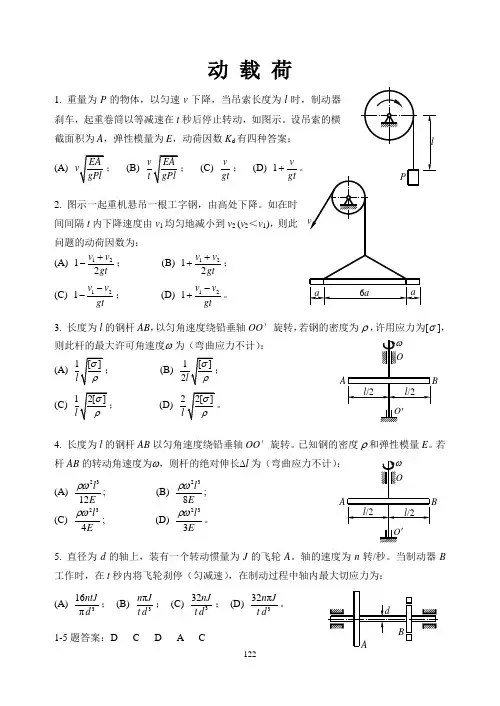
动载荷1. 重量为P的物体，以匀速v下降，当吊索长度为l刹车，起重卷筒以等减速在t截面积为A，弹性模量为E，动荷因数K d有四种答案：(A) (B) (C)vgt；(D) 1vgt+2. 图示一起重机悬吊一根工字钢，由高处下降。

如在时间间隔t内下降速度由v1均匀地减小到v2 (v2＜v1)，则此问题的动荷因数为：(A) 1212v vgt+-；(B) 1212v vgt++；(C) 121v vgt--；(D) 121v vgt-+。

3. 长度为l的钢杆AB，以匀角速度绕铅垂轴OO′旋转，若钢的密度为ρ，许用应力为[σ ]，则此杆的最大许可角速度ω 为（弯曲应力不计）：(A) (B)(C) (D)4. 长度为l的钢杆AB以匀角速度绕铅垂轴OO′旋转。

已知钢的密度ρ和弹性模量E。

若杆AB的转动角速度为ω，则杆的绝对伸长∆l为（弯曲应力不计）(A)2312lEρω; (B)238lEρω;(C)234lEρω; (D)233lEρω。

5. 直径为d的轴上，装有一个转动惯量为J的飞轮A。

轴的速度为n转/秒。

当制动器B 工作时，在t秒内将飞轮刹停（匀减速），在制动过程中轴内最大切应力为：(A)316πntJd；(B)3πn Jt d；(C)332nJt d；(D)332πn Jt d。

1-5题答案：D C D A C1221236. 图示钢质圆盘有一偏心圆孔。

圆盘以匀角速度ω 旋转，密度为ρ。

由圆盘偏心圆孔引起的轴内横截面上最大正应力max σ为： (A)213()8d a d ρδω； (B)213()4d a d ρδω；(C) 2134()d a d ρδω； (D) 2138()d a d ρδω。

答：C7. 材料密度为ρ，弹性模量为E 的圆环，平均直径为D ，以角速度ω 作匀速转动，则其平均直径的增量∆D = 。

答：32Δ4D D Eρω=8. 杆AB 单位长度重量为q ，截面积为A ，弯曲截面系数为W ，上端连有重量为P 的重物，下端固定于小车上。