当前位置：文档之家 › 相似三角形的判定(复习)

相似三角形的判定(复习)

  • 格式：ppt
  • 大小：1.27 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

相似三角形的性质和判定复习优秀课件

相似三角形的性质和判定复习优秀课件

①相似三角形的对应角 相等 ,对应边 成比例 。
②相似三角形对应高的比,对应中线的比,对应角平分线
的比都等于相似比。
③相似三形的周长的比等于 相似比 。
④相似三角形面积的比等于相似比的平方 。
2、三角形相似的判定方法： ①定理 两角对应相等的两个三角形相似 。
②定理两边对应成比例且夹角相等的两个三。角相似
AB BO CD DO
答：球能碰到墙面离 地5.4m高的地方．
2.如图，把△ABC沿AB边平移到 △A′B′C′的位置，它们的重叠部分（即 图中的阴影部分）的面积是△ABC的面 积一半，若AB=2，则求此三角形平移 的距离AA′。
C C' M
A A'
B B'
• 3（2010·珠海)如图，在平行四边ABCD中，过点 A作AE⊥BC，垂足为E，连结DE，F为线段DE 上一点，且∠AFE＝∠B.
连接BF交DC与点E,则图中相似三角形共有( D )
A. 0对 B. 1对 C. 2对 D.3对 A
D
F
E
B
(第2题)
C
3、三角形的三条中位线所构成的三角形与原三角 形的周长之比是_1_︰_2____，面积之比是_1_︰__4___。
4.如图，P 是 Rt△ABC 斜边 AB 上任意 一点(A、B 两点除外)，过 P 点作一直线， 使截得的三角形与 Rt△ABC 相似，这样
• (1)求证：△ADF∽△DEC.
• (2)若AB＝4，AD＝3 3，AE＝3 ，求AF的长．
思路与方法点拨
• 1.寻求相似三角形时要注意挖掘图形中的隐含条件， 如公共角、对顶角等。
• 2. “两角对应相等的两个三角形相似.”在证明三角 形相似中用得较多，在证明过程中应注意结合图形 和已知条件去找相等的角。

相似三角形的判定复习

相似三角形的判定复习

综合训练
名师名题37页第12题
1.在平行四边形ABCD中，过点A作AE⊥BC, 垂足为E，连接DE,F为线段DE上一点，且 ∠AFE= ∠ B. 求证：(1)△ADF∽ △DEC (2)若AB=8，AD=6 3 ，AF= 4 3 ，求AE的长。
⌒ 2.如图，AB是⊙O 的直径，点E是AD上的一点，
C
B
基础训练
1.下列说法正确的是( A.相似形是全等形. B.全等形是相似形. C.不全等的图形不是相似形. D.不相似的图形可能是全等形. )
基础训练
2、在Rt △ABC 和Rt △A’B’C’中， ∠C＝∠C’ ＝90°，下列条件中不能判定 这两个三角形相 似的是（ ） A、 ∠A＝55°，∠A’＝35° B、 AC＝9,BC＝12,A’C’＝6 ,B’C’=8 C 、 AC＝3,BC＝4,A’C’ ＝6， A’B’ =8 D、 AB＝10,AC＝8, A’B’ =15,B’C’=9
基础训练
3.在△ABC 中，D是AB的中点，且DE∥BC，
DE 求 的值。 BC
基础训练
4、如图，在△ABC中，AC＞AB, D在AC边上 （点D不与A、C重合），连接BD.若再增加个 条件就能使△ABD∽△ACB,则这个条件可以 是 .
基础训练
5.如图，△ABC 中，AB=9，AC=6，点E在AB上， 且AE=3，点F在AC上，连接EF，若△AEF与 △ABC 相似，则AF= .
△ABC∽△A'B'C'
A
方法5：两角对应相等，两三角形相似。 ∠A= ∠A' ∠B= ∠B' △ABC∽△A'B'C'
B
C
直角三角形相似的判定: 斜边和一对直角边对应成比 例，两直角三角形相似。

第12讲相似三角形的判定复习课件(共46张PPT)

第12讲相似三角形的判定复习课件(共46张PPT)
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
4．如图4－12－5，AB是半圆O的直径， D，E是半圆上任意两点，连结AD，DE，AE 与BD相交于点C，要使△ADC与△ABD类似， 可以添加一个条件．下列添加的条件其中错误
的是 A．∠ACD＝∠DAB B．AD＝DE C．AD2＝BD·CD D．AD·AB＝AC·BD
大师导航 归类探究 自主招生交流平台 思维训练
第四章 类似三角形
第12讲 类似三角形的判定
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
部分数学符号的来历 数学运算中经常使用符号，如＋，－，×，÷，＝，＞， ＜，∽，≌，()， 等，你知道它们都是谁首先使用，何时 被人们公认的吗？ 加减号“＋”“－”：1489 年德国数学家魏德曼在他的著 作中首先使用了这两个符号，但正式为大家公认是从 1514 年荷 兰数学家荷伊克开始．乘号“×”：英国数学家奥屈特于 1631 年提出用“×”表示相乘；另一乘号“·”是数学家赫锐奥特首 创的．除号“÷”：最初这个符号是作为减号在欧洲大陆流行， 奥屈特用“∶”表示除或比，也有人用分数线表示比，后来有 人把二者结合起来就变成了“÷”．瑞士的数学家拉哈的著作中 正式把“÷”作为除号．等号“＝”：最初是 1540 年由英国牛
D.147
大师导航 归类探究 自主招生交流平台 思维训练
【解析】 ∵∠C＝∠E，∠ADC＝∠BDE， ∴△ADC∽△BDE，∴DDEC＝ABDD， 又∵AD∶DE＝3∶5，AE＝8， ∴AD＝3，DE＝5， ∵BD＝4，∴D5C＝34，∴DC＝145.
∵AC⊥BC，∴∠ACB＝90°，
又∵BE是∠ABC的平分线， ∴FG＝FC，
例2答图

九年级数学《相似三角形的判定-总复习课》课件

九年级数学《相似三角形的判定-总复习课》课件

(2)若∠A=∠A′，可添加条件____
复习目标
1 熟练掌握三角形相似的判定方法，理解各判定 方法的区别与联系。
2 能够从题目的条件和结论出发，选取合适的判 定方法解决三角形相似问题。
尝试思考题
1 你能记得多少种判定三角形相似的方法？ 2 三1 定义： 对应角相等，对应边成比例。 2 平行线法 ：平行于三角形一边的直线和其他两边（或 两边的延长线）相交，所构成的三角形与原三角形相似。 3 两角法：两角对应相等，两三角形相似。 4 两边一夹角法 ：两边对应成比例且夹角相等，两三角 形相似。 5三边法：三边对应成比例，两三角形相似。 6直角三角形相似的判定定理： 斜边和一条直角边对应成比例的两直角三角形相似。
相似三角形的判定
导新定向
1.如图1，在□ABCD中，G是BC延长线上一点，AG与BD交
于点E,与DC交于点F，则图中相似三角形共有（
）
A 3对 B 4对 C 5对 D 6对
A
D
EF
B
图1 C
G
AB BC
2.要判定△ABC∽△A'B'C',已知条件, A，B，= B，C， (1)还要添加条件____或____.
（３）如图③，在矩形ABCD中，已知ＡＢ＝ 2 3 ，BC=3，
M是AD边上一点，将矩形ABCD沿CM折叠，点D落在AB边上 的点E处，求证：点E恰好是四边形ABCM的边AB上的一个
“强相似点”。
（４）如图③，将矩形ABCD沿CM折叠，使点D落在AB边上 的点E处，若点E恰好是四边形ABCM的边AB上的一个强相 似点，试确定E点位置．
（1）如图①， ∠A=∠B=∠DEC=45°， 试判断点E是否是四 边形ABCD的边AB上 的相似点，并说明理由； （2）如图②，在矩形ABCD中，A、B、C、D四点均在正方 形网格（网格中每个小正方形的边长为1）的格点（即每 个小正方形的顶点）上，试在图②中画出矩形ABCD的边 AB上的强相似点；

相似三角形判定复习

相似三角形判定复习

一.填空选择题: 填空选择题: 1.(1)△ ABC中,D、 分别是AB AC上的点 AB、 上的点， 1.(1)△ ABC中,D、E分别是AB、AC上的点，且 B，那么△ ABC， ∠AED=∠ B，那么△ AED ∽ △ ABC，从而
AD (AC)
=
DE BC
(2) △ ABC中，AB的中点为E，AC的中点为D， ABC中 AB的中点为 的中点为E AC的中点为 的中点为D 连结ED ED， AED与 ABC的相似比为 连结ED， 则△ AED与△ ABC的相似比为 A 1:2 A ______.
A1 A
B
C
B1
C1
对于直角三角相似的判定除了上述三种方法外， 对于直角三角相似的判定除了上述三种方法外， 还有什么定理？ 还有什么定理？ 定理：如果一个直角三角形的斜边和一条 定理：如果一个直角三角形的斜边和一条 直角三角形 直角边与另一个直角三角形的斜边和一条直角 边对应成比例， 边对应成比例，那么这两个直角三角形相似
相似三角形的判定的复习
我们学习了判定一般三角形相似的哪几种方法？ 我们学习了判定一般三角形相似的哪几种方法？ • 定理1：对应角相等两三角形相似 定理1 • 定理2：两边对应成比例且夹角相等， 定理2 两边对应成比例且夹角相等， 两三角形相似 • 定理3：三边对应成比例，两三角形相 定理3 三边对应成比例， 似
2、如图，已知BC∥B'C'，AC∥A'C' 如图，已知BC∥B'C'， BC∥B'C' 求证： ABC∽△ 求证：△ABC∽△A'B'C' A A’ ’ O 2 1 4 C’ 3 C ’ B’ ’ B
∴△ABC∽△A’B’C’ ∽ ’ ’ ’ 证明： 证明：∵BC∥B’C’ ∥ ’ ’ ∴∠3＝ ∴∠ ＝∠4， ， B’C’/BC ＝ ’ ’ OC’/OC ’ ∵AC∥A’C’ ∥ ’ ’ ∴∠1＝ ∴∠ ＝∠2 OC’ ∴ A’C’/AC ＝ ’ ’ ’ ∴∠ACB＝∠A’C’B’ ∴∠ ＝ ’ ’ ’ ’ B’C’/BC A’ ’ ’ ＝

相似三角形的判定(复习)

相似三角形的判定(复习)

（ 1） 、相似三角形与全等三角形 全等三角形 定义 能够完全重合的两个三角形 相似三角形 对应角相等，对应边成比例的两个三角形
图形性 质
形状、大小完全一样 表示方 法 性质 相似比 区别与 联系 △ABC≌△A B C
， ， ，
形状一样、大小未必一样 △ABC∽△A B C
， ， ，
对应角相等，对应边相等
A E
P
D
B
C
7
中国领先的中小学教育品牌
【课后作业】
一、填空题 1．如图所示，△ABC 的高 AD，BE 交于点 F，则图中的相似三角形共有______对．
2．如图所示，□ABCD 中，G 是 BC 延长线上的一点，AG 与 BD 交于点 E，与 DC 交于点 F，此图中的相 似三角形共有______对．
C.
15 12 cm或 cm 4 5
D.
5 cm 12
4
中国领先的中小学教育品牌
2、子母型
例题 1、 如图,D 为△ABC 的边 AB 上一点,且∠ABC=∠ACD,AD=3 cm,AB=4 cm,则 AC 的长为_______________.
例题 2、如图，AD⊥BC 于 D，若
AC CD ,则△ABC 是_________________三角形 BC AC
E
AB BC AC ，试说明∠BAD=∠CAE。 AD DE AE
A E
B
D C
（2） 、相似三角形的判定方法填空
判定 方法 1
∵___________ ∴△ABC∽△ADE
判定 方法 2
∵________________ ∴△ABC∽△A B C
， ， ，
判定 方法 3

相似三角形判定复习精选课件

相似三角形判定复习精选课件
S 和 平行四边A形BCD
A
，SABF
D
OE
B
F
C
Rt△ABC中， ∠ACB＝90 °，CD⊥AB于D （1）写出图中所有的相似三角形，并选择其中一对 说明理由 （2）若AD＝4cm, BD＝1cm,请你求出CD的长度
C
∟
B
A
D
如图，已知：DE ∥BC，DC和BE相交于P点，连结 AP交DE于M，延长AP交BC于点N ，求证： DM=ME，BN=NC。
4
方法3：三组对应 边的比相等，两个
三角形相似
5
方法4：两组对应 边比相等且夹角相
等，
两个三角形相似
相似三角形的判定定理：
定理1：三组对应边的比相等，两三角形相似。
AB BC CA A 'B 'B 'C 'C 'A '
△ABC∽△A'B'C'
定理2：两组对应边的比相等且夹角相等，
两三角形相似。
AB A' B '
网格问题
单击此处添加正文，文字是您思想的提炼，为了演示发布的良好效果，请言简意赅地 述您的观点。
如图，小正方形的边长均为1，则下列图中
的三角形(阴影部分)与△AABC相似的是
A
B C (A)
(B)
(C)
(D)
尝试
在正方形方格中, △ABC的顶点A、B、
C在单位正方形的顶点上 ，请在图中
画一个△A1B1C1 使
形与原三角形相似，这样的直线
最多能画出多少条?画出满足条件
的A图形. A
A
A
D B
ED CB
D
E CB E

相似三角形知识点归纳

相似三角形知识点归纳

相似三角形知识点归纳1.相似三角形的定义：如果两个三角形的对应角相等，则这两个三角形是相似的。

记作△ABC∽△DEF。

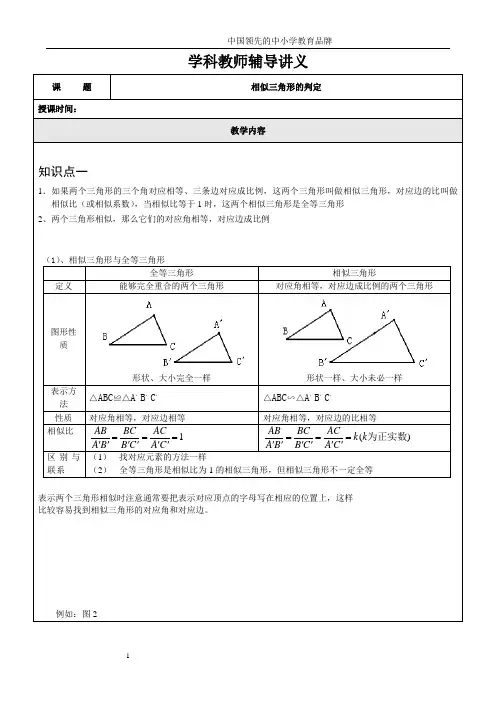
2.相似三角形的判定条件：(1)AA相似判定法：如果两个三角形的两个角相等，则这两个三角形是相似的。

(2)SAS相似判定法：如果两个三角形的对应两边成比例并且夹角相等，则这两个三角形是相似的。

(3)SSS相似判定法：如果两个三角形的对应三条边成比例，则这两个三角形是相似的。

3.相似三角形的性质：(1)对应边成比例：在相似三角形中，对应边的长度之比相等。

即AB/DE=BC/EF=AC/DF。

(2)对应角相等：在相似三角形中，对应角的度数相等。

即∠A=∠D，∠B=∠E，∠C=∠F。

(3) 对应角的正弦值成比例：在相似三角形中，如果一个角和其对边的正弦值成比例，则另一个角和其对边的正弦值也成比例。

即sin∠A/sin∠D = sin∠B/sin∠E = sin∠C/sin∠F。

(4)图形相似：除了三角形外，相似三角形所在的图形也是相似的。

4.角平分线的性质：(1)在相似三角形中，角平分线之间的关系相等。

即角平分线所分的两个角对应的另外两个角也是相等的。

(2)在相似三角形中，角平分线和对应边长成比例。

即角平分线与对应边所分出的线段之比相等。

5.高度的性质：(1)在相似三角形中，高度之间的关系成比例。

即两个相似三角形的高度之比等于对应边长之比。

(2)在相似三角形中，高度与底边成比例。

即两个相似三角形的高度和底边之比等于对应边长之比。

6.面积的性质：(1)在相似三角形中，面积之间的关系成比例。

即两个相似三角形的面积之比等于对应边长之比的平方。

(2)在相似三角形中，面积与任意一边平方成比例。

即两个相似三角形的面积和任意一边的平方之比等于对应边长之比。

7.相似三角形的应用：(1)根据相似三角形的性质，可以通过测量一个三角形和两条边的比例，计算出另一个三角形的边长和面积。

(2)在地图上，可以利用相似三角形的性质，测量无法直接测量的远距离。

相似三角形复习

相似三角形复习
AC BC = AD CD
E
C
Rt△ACD∽Rt△CBD △ ∽ △
A D B
AE AD = CF CD
AC=AE BC=CF
……
需证∠ 需证∠DAE=∠DCF ∠
需证△ 需证△ADE∽△CDF ∽ 结论1 结论
需证 ∠ADE=∠CDF ∠
CD⊥AB ⊥
DE⊥DF ⊥ 结论2 结论
练习2：如图， 、 分别是 分别是△ 的高， 练习 ：如图，AD、CF分别是△ABC的高，在AB上截取 的高 上截取 AE=AD，EG∥BC交AC于G，求证：EG=CF ， ∥ 交 于 ，求证：
③∠F=∠C, ∠
AF AE = AC AB
则△ABC∽△AEF ( 错 ) △ ∽
B D
(2)如图 △ABC和△CDB中, 如图:△ 如图 和 中 ∠ABC=∠CDB=90° ∠ °
BC 2 = AC • BD
则Rt△ABC∽Rt△CDB （ 对 ） △ ∽ △
A
C
是边AB上一点 例1。已知△ABC中，P是边 上一点，连结 。已知△ 中 是边 上一点，连结CP ①∠ACP满足什么条件时，△ACP∽△ABC？ 满足什么条件时， ∽ ？ 满足什么条件时 满足什么条件时， ②AC：AP满足什么条件时，△ACP∽△ABC？ ： 满足什么条件时 ∽ ？
结论） （结论）
引申：证明一个结论，可以从条件出发，围绕条件找条件， 引申：证明一个结论，可以从条件出发，围绕条件找条件，直
到找到所需的条件。也可以从结论开始分析， 到找到所需的条件。也可以从结论开始分析，证此结论需要什么 条件，从题中证出所需条件，从而找到解题思路。 条件，从题中证出所需条件，从而找到解题思路。
指出下列判断是否正确,为什么 指出下列判断是否正确 为什么? 为什么

相似三角形的判定复习课(共23张ppt)

相似三角形的判定复习课(共23张ppt)

AC=AN•cos∠BAO= t；
∴OC=OA-AC=6-t，∴N（6-t， t）．
∴NM=
=
；
又：AM=6-t，AN= t（0＜t≤6）；
①当MN=AN时，
= t，即：t2-8t+12=0，t1=2，t2=6（舍去）；
②当MN=MA时，
=6-t，即： t2-12t=0，t1=0（舍去），t2= ；
解：（1）由题意，A（6，0）、B（0，8）， 则OA=6，OB=8，AB=10； 当t=3时，AN= t=5= AB，即N是线段AB的中点； ∴N（3，4）． 设抛物线的解析式为：y=ax（x-6），则： 4=3a（3-6），a=- ； ∴抛物线的解析式：y=- x（x-6）=- x2+ x．
（2）在此运动的过程中，△MNA的面积是否存在最大值？若 存在，请求出最大值；若不存在，请说明理由；
解得DM= ；
②DM与BE是对应边时，DM=
∴DM2+DN2=MN2=1， 即DM2+4DM2=1，
DN，
解得DM= ．
∴DM为 或 时，△ABE与以D、M、N为顶点的三角形相似． 故选C．
2、如图，已知在△ABC中，AD是BC边上的中线，以AB为 直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长 线于点N，过点B作BG⊥MN于G． （1）求证：△BGD∽△DMA； （2）求证：直线MN是⊙O的切线
证明：（1）∵MN⊥AC于点M，BG⊥MN于G， ∴∠BGD=∠DMA=90°． ∵以AB为直径的⊙O交BC于点D， ∴AD⊥BC，∠ADC=90°， ∴∠ADM+∠CDM=90°， ∵∠DBG+∠BDG=90°，∠CDM=∠BDG， ∴∠DBG=∠ADM． 在△BGD与△DMA中，∠BGD=∠DMA=90°， ∠DBG=∠ADM． ∴△BGD∽△DMA；

复习相似三角形的判定方法

复习相似三角形的判定方法
1m 0.8m
D C B
E
CE=3.2m,AB=29m
某一时刻测得1m的杆子在阳光下的影长 为2m,若测量树杆AB的高度,但其影子恰 好落在土坡的坡面CD和地面BC上,量得 CD=2m,BC=10m,CD与地面成45°,求 线杆的高度. 3
A
AB=5+
墙
2
1m
2
m
2m
D
B
C
E
F
需要测出哪些线段？ 需测出：BC、DE、BD 此时如果测得DE＝120米， BC＝60米，BD＝50米，求 两岸间的大致距离AB．
B C A
D
E
请同学们自已解答 并进行交流
练习：旗杆靠近一个建筑物,在某一时刻旗杆影 子中的一部分 映在建筑物的墙上.测得旗杆 AB在地面上的影长BC为20m,在墙上的影长 CD为4m,同时又测得竖立于地面的1m长的标 杆影长为0.8m, 求出旗杆的高度. A
F
A
B
C
D
E
需要测量哪些线段？比例式如何构成？
利用物理学中“入射角=反射角”，构成三角形相 似
人的视线(AB)刚好看见平面镜里旗杆的顶点F
F
法线 A
C
B（平面镜）
E
需要测量哪些线段？比例式如何构成？
例2:如图，如何估算河的宽度，
例2:如图，可以在河对岸选定一个目标作为点A，再在
河的这一边选点B和C，使AB⊥BC，然后，再选点E，使 EC⊥BC，用视线确定BC和AE的交点D． 需要测出哪些线段？ BD、CD、CE 此时如果测得BD＝120米，DC＝60米，EC＝50米，求 两岸间的大致距离AB．
胡夫金字塔是埃及现存规模最大的金字塔，被喻为“世界 古代七大奇观之一”。塔的４个斜面正对东南西北四个方向， 塔基呈正方形，每边长约２３０多米。据考证，为建成大金字 塔，共动用了１０万人花了２０年时间.原高１４６．５９米， 但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所 降低 。

初三数学相似三角形的判定复习

初三数学相似三角形的判定复习

A D EB CE DB CA'AAB C 'B 'C'AAB C 'B 'C'AAB C 'B 'C一对一辅导教案学生姓名 学校年级初三学科数学 授课教师上课时间第（ ）次课 共（ ）次课课时：3 课时教学课题相似三角形的判定教学目标 熟悉并掌握相似三角形的判定。

教学重点与难点 熟练应用相似三角形的判定教学过程：（一）三角形相似的判定：（1）平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.基本图形：推理格式：在△ABC 中，∵ DE//BC ，∴ △ADE ∽△ABC. （2）如果两个三角形三组对应边．．．的比相等，那么这两个三角形相似. 基本图形：推理格式：在△ABC 和△'C 'B 'A 中，'A 'C CA 'C 'B BC 'B 'A AB == ，∴△ABC ∽△'C 'B 'A . （3）如果两个三角形的两组对应边．．．的比相等，并且相应的夹角相等，那么这两个三角形相似。

基本图形：推理格式：在△ABC 和△'C 'B 'A 中，'C 'A AC 'B 'A AB = ，∠A=∠'A ，∴ABC ∆∽△'C 'B 'A . （4）如果一个三角形的两个角与另一个三角形的两个角对应．．相等，那么这两个三角形相似。

基本图形：推理格式：在△ABC 和△'C 'B 'A 中，∵∠A=∠'A ，∠B=∠'B ，∴△ABC ∽△'C 'B 'A .例. 如图，BC ⊥AF ，FD ⊥AB ，垂足分别为C 、D ，那么图中有_________对相似三角形.FCEA D B（二）相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CB ADE （不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行） （不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD一、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

相似三角形的判定复习

相似三角形的判定复习

6. 已知:P是正方形ABCD的边 BC上 的点,且BP=3PC,Q是CD的中点. 求证:△ADQ∽△QCP.
A
D
QB PCFra bibliotek相似三角形判定方法的 选用，要根据所给的条件或 图中隐含的条件而定，应选 取最简单的判定方法．
（复习）
知识网络： 定义 基本图形
相 判定 两角对应相等 似 两边对应成比例且夹角相等 三 三边对应成比例 角 形 性质 对应角相等，对应边相等
Rt△相似的判定（５种）
例题经典： 例１．下列条件中，不能判定△ABC与
△A′B′C′相似的是（ ）
A．∠A=45°.∠C=26°.∠A′=45°.∠B′=109° B.AB=1.5,AC=14/15,∠A=36°,A′B′=2.1,A′C′ =1.5,∠A′=36° C.AB=1.AC=3/2.BC=2,A′B′=6,A′C′=9,B′C′=12. D.AB=2,BC=1,∠C=90°,A′B′= ∠C′=90° ,B′C′= 2 ,
4. 如图,点C、D在线段AB上,△PCD 是等边三角形. a. 当AC、CD、DB满足怎样的关 系时,△ACP∽△PDB? b. 当△ACP∽△PDB时,∠APB 等于多少度? P B
A
C
D
5. 已知:A′B′∥AB, B A B′
B′C′∥BC .
求证:△A′B′C′∽△ABC.
C
A′ O
C′
2 2
２．如图， ABCD中，G是BC延长 线一点，AG与BD交于E，与DC交 于F，则图中相似三角形共有（ ） A．3对 B.4对 C.5对 D.6对 A
E
F
D G
B
C
3. 已知△ABC,P是AB边上一点,连 结CP . a.∠ABC 满足什么条件,△ACP∽△ABC. b. AC:AP满足什么条件,△ACP∽△ABC. A P B C

相似三角形的判定及有关性质复习 课件

相似三角形的判定及有关性质复习 课件

(4)直角三角形相似的判定定理 定理1：如果两个直角三角形有一个锐角相等，那么它 们相似. 定理2：如果两个直角三角形的两条直角边对应成比例， 那么它们相似. 定理3：如果一个直角三角形的斜边和一条直角边与另 一个直角三角形的斜边和一条直角边对应成比例，那 么它们相似.
4.相似三角形的性质
性质定理1：相似三角形对应角相等，对应边成比例. 性质定理2：相似三角形对应边上的高、中线和它们的 周长的比都等于相似比. 性质定理3：相似三角形的面积比等于相似比的平方. 性质定理4：相似三角形外接圆或内切圆的直径比、周 长比等于相似比，外接圆或内切圆的面积比等于相似 比的平方.
题型一 构造法 添加辅助线是平面几何解决问题最常用的手段，添加辅 助线的目的是构造平行线、或三角形、或三角形的相似等 结构.
例 1 如图，梯形 ABCD 中，AB∥CD，CE 平分∠BCD，CE⊥AD 于 E，DE＝2AE， 若△CED 的面积为 1，求四边形 ABCE 的面积.
解 延长 CB，DA 交于点 F，又 CE 平分∠BCD，CE⊥AD. ∴△FCD 为等腰三角形，E 为 FD 的中点. ∴S△FCD＝12FD·CE＝12×2ED×CE＝2S△CED＝2，EF＝2AE. ∴FA＝AE＝14FD.又∵AB∥CD，∴∠FBA＝∠FCD， ∠FAB＝∠D，∴△FBA∽△FCD.∴SS△△FFCBDA＝FFAD2＝142＝116， ∴S△FBA＝116×S△FCD＝18. ∴S 四边形 ABCE＝S△FCD－S△CED－S△FBA＝2－1－18＝78.
1.平行线等分线段定理 (1)定理：如果一组平行线在一条直线上截得的线段相等，那 么在任一条(与这组平行线相交)直线上截得的线段也相等 推论1：经过三角形一边的中点且与另一边平行的直线必平 分第三边. 推论2：经过梯形一腰的中点且与底边平行的直线必平分另 一腰. (2)中位线定理 三角形中位线定理：三角形的中位线平行于第三边，并且等 于它的一半. 梯形中位线定理：梯形的中位线平行于两底，并且等于两底 和的一半.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C
2、如图，G是ABCD的CD延长线上一点，连结 BG交对角线AC于E，交AD于F，则：
(1)图中与△AEF相似的三角形是_△__C__E_B_．
(2)图中与△ABC相似的三角形是_△__C_D__A_．
G
A
F
D (3)图中与△GFD相似的
E
B
C
三角形是_△__G__B_C_、__△__B_F_A_．
思考其他证明方法？
∵
D
,
11 已知△ABC 中∠C＝90°，D、E分别是AB、 AC上的点且AD·AB= AE·AC
求证：ED⊥AB
B
D
A
EC
12.如图AB=4,AC=5,CD=3,BE=6 求证： △ADE∽△ABC

C
E
A
B
直角三角形相似的模糊辨析
❖ 已知：如图，∠ABC=∠CDB=90, AC=a,BC=b, 当BD与a、b之间满足怎样的关系式时，
∠∠AA´´==112200ºº，，AA´´BB´´==33厘厘米米，，AA´´CC´´==66厘厘米米；； ⑵⑵AABB==44厘厘米米，，BBCC==66厘厘米米，，AACC==88厘厘米米，，
AA´´BB´´==1122厘厘米米，，BB´´CC´´==1188厘厘米米，，AA´´CC´´==2244厘厘米米
BC OB
还证有 明其方法他吗的？∴∴∠△AA``BB`C`C`=`∽∠△ABCA,BCAA`BB `
=
B`C` BC
10.如图 ，D、E、F分别是△ABC的三边的中点.
求证: △ DEF∽△ABC.
A F
分析:1找两对角对应相等
2.三边对应成比例 E 3.两边对应成比例且 夹角相等.
B
D
C
证
明
:
6．如图3：若∠1=∠C，则△ ∽△___
A
D 1
C 图3
BB
A
D
C
图4
7．在△ABC中，∠BAC=90°，AD是BC边上 的高，图中相似的三角形有：__________.
8.已知△ABC,P是AB边上的一点,连结CP.
A
①∠1满足什么条件时 , △ACP∽△ABC ？
P
② AC满足什么 条件时 , △ACP∽△ABC ？
(4)两个角对应相等的两个三角形相似 （5）两边对应成比例并且夹角对应成比例的两个三角形相似
3.相似三角形的性质 相似三角形的对应角相等，对应边成比例。
我能行
知识运用
1.根据条件指出下列图形中的相似三角形，并 写出理由。
A
B
E
A D
C
D
条件:∠B=∠D
B
C
∠ACD=∠ABC
A 2D 1
B
四边形ABCD中,AD∥BC,∠A=90°， BD⊥DC
（6）有一个角相等的两个直角三角形是相似三角形（×） （7）有一个锐角相等的两个直角三角形是相似三角形（√） （8）所有的正三角形都相似（ √）
（9）两个等腰三角形只要有一个角对应相等就相似（×）
55..依依据据下下列列各各组组条条件件，，判判定定△△AABBCC与与△△AA´´BB´´CC´´是是不不是是相相似似，，并并 说说明明为为什什么么：： ⑴⑴∠∠AA==112200ºº，，AABB==77厘 厘米米，，AACC==1144厘厘米米，，
AP
解：①∵∠A=∠A
B
C
∴当∠1=∠B时 ，△ACP∽△ABC
②∵∠A=∠A
∴当AC:AP = AB:AC 时，△ACP∽△ABC
变式1
如图，已知在△ABC中，P是AB上一点，连结CP， 添加一个什么条件，使△ACP∽△ ABC？写出所 有的可能，并选择其中一个结论说明理由．
Ａ
Ｐ
Ｂ
Ｃ
变式2
如图，已知在△ABC中，Ｄ是AＣ上一点，过 Ｄ画线段ＤＥ使Ｅ在△ABC的边上，并且点Ｄ、 Ｅ和△ABC的一个顶点组成的小三角形与 △ABC相似，你能想出一种不同的画法？
Ａ
Ｄ ●
Ｂ
Ｃ
9.已知：如图A`B`∥ AB，B`C`∥ BC
求证： △A`B`C`∽ △ ABC
分析:三角形相似需要等角和比例线段
平行线能给相似提供哪些条件? A 你想选用哪种判定方法?
A`
证明：∵ A`B`∥ AB
O
C`
B`
B
C∴∠A`B`O=∠ABO,
A`B ` AB
=
OB` OB
同理:∠C`B`O=∠CBO,B`C`= OB`
(1)△ABC∽△CDB?
A
(2)△ABC∽△BDC?
C
(3)图中的两个三角形相似？
Tips:
如果结论中已经出现了“∽” 符号，则隐含了对应线段；如果
B
D
只是用文字表示，则对应关系没
有给出，需要自行找对应。
直角三角形相似的提高运用
❖ 已知：如图，AC⊥BD于C, AB·EC=BA C·DE. 求证:(1)DF⊥AB;(2)EF·DF=BF·AF.
3.如图，AD⊥BC于点D， CE⊥AB于点 E ， 且交AD于F，你能从中找出几对相似三角形？
A
E F
B
C
D
4.判断下列说法是否正确 （1）两个顶角相等的等腰三角形是相似三角形 （√ ） （2）两个等腰直角三角形是相似三角形（√ ） （3）底角相等的两个等腰三角形是相似三角形 （√ ）
（4）两个直角三角形一定是相似三角形（ ×） （5）一个钝角三角形和一个锐角三角形有可能 相似（×）
相似三角形的判定（复习）
四皓中学 王化贤
知识回顾
1、什么是相似三角形？
三角对应相等，三边对应成比例的两个三角形相似。
2、学过的判定两个三角形相似的方法有哪些？ （1）定义：
（2）预备定理：平行于三角形一边的直线，和其他两边（或 延长线），所得三角形和原三角形相似。
（3）三组边的比对应相等的两个三角形相似。
1、要准确地把等 积式变成有用的比 例式
F E
2、能由比例式判
断出相似，也要能
由相似得到有用的 B
C
D
比例式
判定定理2、3的提高运用
❖ 如图，在△ABC中，∠C=60°，BE⊥ AC于E， AD⊥ BC于D。求证： ∠ CED＝ ∠ CBA
1、通过相似三角形证对应 角相等是获得等角的一条 重要途径 2、根据要证相等的角，找 到所在的一组相似三角形 3、利用判定2、3关键要 找准对应边，并熟悉对应 边成比例的两种表达方式