集合复习课
- 格式:doc
- 大小:91.00 KB
- 文档页数:3







《集合》复习课教学设计教学目标:(1)掌握集合、交集、并集、补集的概念及有关性质;(2)掌握集合的有关术语和符号;(3)运用性质解决一些简单的问题。
教学重点:集合的相关运算。
教学难点:集合知识的综合运用。
教学过程:一、复习回顾:1.提问:什么叫集合?元素?集合的表示方法有哪些?2.提问:什么叫交集?并集?补集?符号语言如何表示?图形语言如何表示?3.提问:什么叫子集?真子集?空集?相等集合?有何性质?4.交集、并集、补集的有关运算结论有哪些?5.集合问题的解决方法:Venn图示法、数轴分析法。
二、讲授新课:(一)集合的基本运算:例1:设U=R,A={x|-5<x<5},B={x|0≤x<7},求A∩B、A∪B、CUA、CUB、(CU A)∩(CUB)、(CUA)∪(CUB)、CU(A∪B)、CU(A∩B)。
(学生画图→在草稿上写出答案→订正)说明:不等式的交、并、补集的运算,用数轴进行分析,注意端点。
例2:全集U={x|x<10,x∈N+},A⊆U,B⊆U,且(CUB)∩A={1,9},A∩B={3},(CU A)∩(CUB)={4,6,7},求A、B。
说明:列举法表示的数集问题用Venn图示法、观察法。
(二)集合性质的运用:例3:A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}, 若A∪B =A,求实数a的值。
说明:注意B为空集可能性;一元二次方程已知根时,用代入法、韦达定理,要注意判别式。
例4:已知集合A={x|x>6或x<-3},B={x|a<x<a+3},若A∪B=A,求实数a的取值范围。
(三)巩固练习:1.已知A={x|-2<x<-1或x>1},A∪B={x|x+2>0},A∩B={x|1<x≦3},求集合B。
2.P={0,1},M={x|x⊆P},则P与M的关系是。
3.已知50名同学参加跳远和铅球两项测验,分别及格人数为40、31人,两项均不及格的为4人,那么两项都及格的为人。



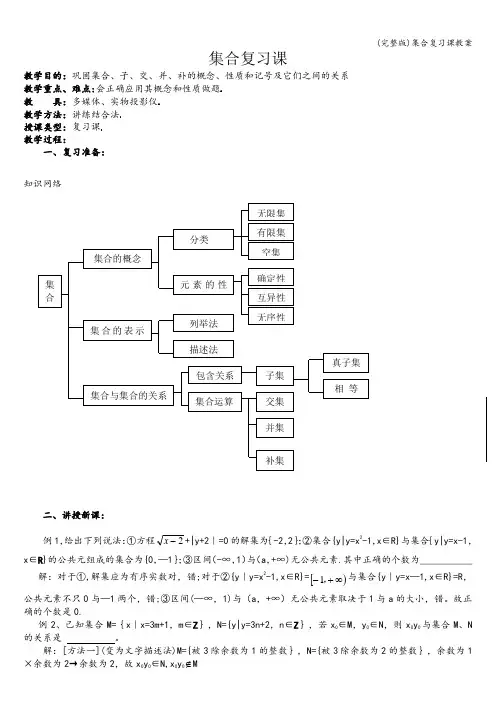
集合复习课教学目的:巩固集合、子、交、并、补的概念、性质和记号及它们之间的关系 教学重点、难点:会正确应用其概念和性质做题 教 具:多媒体、实物投影仪 教学方法:讲练结合法 授课类型:复习课 教学过程:一、复习准备:知识网络二、讲授新课:例1,给出下列说法:①方程2-x +|y+2|=0的解集为{-2,2};②集合{y|y=x 2-1,x ∈R}与集合{y|y=x-1,x ∈R }的公共元组成的集合为{0,—1};③区间(-∞,1)与(a ,+∞)无公共元素.其中正确的个数为___________解:对于①,解集应为有序实数对,错;对于②{y |y=x 2-1,x ∈R}=[)∞+-,1与集合{y |y=x —1,x ∈R}=R ,公共元素不只0与—1两个,错;③区间(—∞,1)与(a ,+∞)无公共元素取决于1与a 的大小,错。
故正确的个数是0.例2、已知集合M={x |x=3m+1,m ∈Z },N={y|y=3n+2,n ∈Z },若x 0∈M ,y 0∈N ,则x 0y 0与集合M 、N 的关系是 。
解:[方法一](变为文字描述法)M={被3除余数为1的整数},N={被3除余数为2的整数},余数为1×余数为2→余数为2,故x 0y 0∈N,x 0y 0∉M[方法二](变为列举法)M={…,—2,1,4,7,10,13,},N={…,-1,2,5,8,11,……}M 中一个元素与N 中一个元素相乘一定在N 中,故x 0y 0∈N ,x 0y 0∉M[方法三](直接验证)设x 0=3m+1,y 0=3n+2,则x 0y 0=9mn+6m+3n+2=3(3mn+2m+n )+2, 故x 0y 0∈N,x 0y 0∉M例3,已知集合A={x |22-+x ax =1}是单元素集,用列举法表示a 的取值集合B解:B 表示方程22-+x ax =1有等根或仅有一个实数根时a 的取值集合。
⑴有等根时有:x 2-x-2—a=0①且x 2-2≠0②;①△=1—4(—a —2)=0,a=—9/4,此时x=1/2适合条件②,故a=-9/4满足条件;⑵仅有一个实数根时,x+a 是x 2—2的因式,而22-+x ax =)2)(2(+-+x x a x ,∴a=±2.当a=2时,x=1+2,满足条件;当a=—2时,x=1—2也满足条件总之,B={-9/4,—2,2}例4,设M={z|z=x 2—y 2,x 、y ∈Z },⑴试验证5和6是否属于M ?⑵关于集合M,还能得到什么结论.解:⑴5=32-22∈M,6=x 2—y 2=(x-y)(x+y),x 、y 不会是整数,故6∉M⑵可以得到许多结论,如:①因2n+1=(n+1)2—n 2,故一切奇数属于M ;②M 为无限集;③因4n=(n+1)2—(n-1)2,故4的倍数属于M;④对于a 、b ∈M,则ab ∈M (证明:设a=x 12-x 22,b=y 12-y 22,则ab=(x 1y 1+x 2y 2)2—(x 1y 2+x 2y 1)2∈M 。
高中数学集合复习教案一、教学目标1. 理解集合的概念,掌握集合的表示方法。
2. 能够运用集合的基本运算(并集、交集、补集)解决实际问题。
3. 理解集合的性质,如无序性、确定性、互异性。
4. 能够运用集合的知识解决数学问题,提高逻辑思维能力。
二、教学内容1. 集合的概念与表示方法集合的定义集合的表示方法(列举法、描述法)2. 集合的基本运算并集:两个集合的并集包含所有属于两个集合的元素。
交集:两个集合的交集包含属于两个集合的元素。
补集:一个集合的补集是除去该集合之外的所有元素构成的集合。
3. 集合的性质无序性:集合中的元素没有先后顺序。
确定性:集合中的元素是明确的,没有重复。
互异性:集合中的元素彼此不同。
4. 集合的应用运用集合的基本运算解决实际问题。
运用集合的性质解决数学问题。
三、教学重点与难点1. 重点:集合的概念与表示方法,集合的基本运算,集合的性质。
2. 难点:集合的应用,解决实际问题。
四、教学方法1. 采用讲解法,引导学生理解集合的概念和表示方法。
2. 采用示例法,通过具体例子讲解集合的基本运算。
3. 采用练习法,让学生通过练习题巩固集合的知识。
4. 采用讨论法,引导学生运用集合的知识解决实际问题。
五、教学准备1. 教案、教材、PPT。
2. 练习题及答案。
3. 教学工具(黑板、粉笔)。
六、教学过程1. 导入:通过简单的例子引入集合的概念,激发学生的兴趣。
2. 讲解:讲解集合的概念、表示方法、基本运算和性质。
3. 练习:让学生完成一些练习题,巩固所学知识。
4. 应用:引导学生运用集合的知识解决实际问题。
5. 总结:对本节课的内容进行总结,强调重点和难点。
七、课堂练习1. 选择题:下列哪个选项是集合的表示方法?A. {1, 2, 3}B. {1, 2, 3, 4}C. {1, 2, 3} U {4, 5, 6}D. {1, 2, 3} ∩{4, 5, 6}2. 填空题:设A = {1, 2, 3},B = {3, 4, 5},求A ∪B 的结果是______。
集合复习课
教学目标:1)巩固学过的有关集合的基本知识
2)利用所学进行相关题型的解答
3)规范解题格式
教学重点:集合的性质、运算
教学难点:分类讨论
教学过程:
1、 知识点回顾
1) 集合的性质:确定性、无序性、互异性
确定性:指出了集合规则的明确性,能够判断元素是否属于集合。
标准明确。
无序性:说明了集合只是元素的集中,元素与元素是平等的,并没有轻重之分。
互异性:因为集合时我们研究对象的全体,因此没有必要重复研究。
2) 集合的表示方法:列举法、描述法、韦恩图法
列举法:将元素一一列举出来。
描述法:将元素的共同特征表述。
韦恩图:利用封闭的曲线。
尤其注意描述法的不惟一性、描述法与列举法的互换。
3) 元素与集合的关系是属于或者不属于的关系,符号:∉∈/;
集合与集合的关系是包含,真包含,不包含等,符号:⊄⊂⊆//
注意包含关系、真包含、相等之间的关系。
4) 集合的运算:交、并、补
相关性质:
1.交集的运算性质
A ∩
B B ∩A ,A ∩B A ,A ∩B B ,A ∩A A ,A ∩Φ Φ、
2.并集的运算性质
A ∪
B B ∪A ,A ∪B A ,A ∪B B ,A ∪A A ,A ∪Φ A
3.补集的运算性质
CS(CSA)=A ,CSΦ=S ,A ∩CSA =Φ, A ∪CSA =S
CS(A ∩B)=(CSA)∪(CSB),
CS(A ∪B)=(CSA)∩(CSB)
注意:
2、 相关题型
1) 集合本身相关:
例1:集合}0,,62|),{(2
≠∈++==x R x x x y y x M ,点,),(M y x P ∈则点Q (|x|,-y )是第几象限的点。
例2:区别以下集合
}1
1|{},1|),{(},1|{},1|{222+==+==+==+==x y x D x y y x C x y y B a x x A 例3:设集合},12|{},,2|{Z k k x x B Z k k x x A ∈+==∈==,若B A a ∈∈,,
试判断a+b 与A ,B 的关系。
例4:若},33,)1(,2{22++++=a a a a A 且A ∈1,求实数a 的值。
例5:设},,,|{22Z y x y x a a M ∈-==求证;
1)一切奇数属于M
2)偶数4k-2不属于M
3)属于M 的两个整数,其积仍属于M 。
例6:已知集合},012|{2R x x ax x A ∈=++=。
1) 若A 中只有一个元素,求a 的值,并求出这个元素。
2) 若A 中至少有一个元素,求a 的取值范围。
2)集合与集合的关系
例1:设集合},12|{},,12|{Z k k x x B Z k k x x A ∈+==∈-==,判断A 、B 的关系。
(若题目改变,Z k ∈,换成N k ∈,……)
例2:非空集合},223|{}5312|{≤<⊆-≤≤+x x a x a x 则a 的取值范围。
例3:集合A=},21|{2R a a a x x ∈-+=与集合}2|{x x
y x B -==的关系。
例4:已知}|,|,0{},,,{y x N y x xy x M =-=,若M N N M ⊆⊆,,求)11()11()11(2008
200822y x y x y x ++++++ 的值。
例5:设},,14|{},,12|{Z k k x x B Z k k x A ∈±==∈-=求证A=B 。
3)集合的基本运算
例1:设},,,{},0|{},03|{2
32r q p S rx qx x x N px x x M ==+-==-+= 且},1,0,3,2{},3{--=-=N M N M 求集合S 。
例2:已知集合},,1{},,3,1{2
x B x A ==若},3,1{x B A = ,求x 的值。
例3:已知集合 }082|{},065|{},019|{2222=-+==+-==-+-=x x x C x x x B a ax x x A 满足φφ=≠C A B A ,,求实数a
例4:设集合}1|),{(},52|),{(2
+==++==ax y y x B x x y y x A ,问:
1) a 为何值时,集合B A 有两个元素?
2) A 为何值时,集合B A 至多有一个元素?
4)综合
例1:已知集合M 有3个真子集,N 有7个真子集,则N M N M ,的可能个
数。
例2:设全集U={1,2,3,4,5},},2,1{=B C A U 则集合A C B U 的个数。
例3:设全集U=R ,}028|{},012|{222=-++==-+=b bx x x B ax x x A ,
若},2{=B C A U 求a ,b 的值。
例5:已知A={x|x>a},B=}032|{22<--a ax x x ,求B A B A ,
3、作业。