2019马尾区变化情况

福州市城乡建设委员会关于全市农村污水治理工作5月份进展情况的通报【法规类别】污染防治【发布部门】福州市城乡建设委员会【发布日期】2017.06.06【实施日期】2017.06.06【时效性】现行有效【效力级别】XP10福州市城乡建设委员会关于全市农村污水治理工作5月份进展情况的通报各县（市）区人民政府：根据市政府办公厅印发的《福州市农村生活污水治理行动实施方案（2017-2019年）》（榕政办[2017]106号），2017年全市要完成19个乡镇污水处理设施建设、71921户（其中省级65383户）三格化粪池新建改造、661个行政村污水治理任务，并要求各县（市）完成1个以上农村污水处理PPP工程包项目落地等任务。

现将5月份相关情况通报如下：一、基本情况1、乡镇污水处理设施建设任务进展情况截至5月底，19个乡镇污水处理设施建设项目完成年度投资1.16亿元，占年度投资计划的39.3%，其中9个项目完工（福清市新厝镇，长乐市玉田镇、罗联乡，罗源县中房镇、鉴江镇、碧里乡，闽清县梅溪镇，永泰县清凉镇、东洋乡），8个项目正在建设（闽侯县竹岐乡、鸿尾乡、尚干镇，闽清县白中镇、三溪乡、省璜镇，永泰县塘前乡、葛岭镇），2个项目正在开展前期工作（罗源县西兰乡、洪洋乡）。

2、三格化粪池新建改造任务工作进展71921户三格化粪池新建改造任务，5月底已建成7287户，完工率10.1%。

其中，马尾区任务数1688户建成4户，福清市任务数10547户建成1835户，长乐市任务数9707户建成107户，闽侯县任务数6353户建成270户，连江县任务数7200户建成1870户，罗源县任务数8893户建成287户，闽清县任务数10495户建成1814户，永泰县任务数11650户建成1100户。

晋安区（任务数3388户）和仓山区（任务数2000户）均没有建成项目。

福州市电动自行车管理办法（2019年修订）第一条为了加强电动自行车管理，维护道路交通秩序，保障道路交通安全畅通，根据《中华人民共和国道路交通安全法》《福建省非机动车管理办法》等规定，结合我市道路交通实际，制定本办法。

第二条本办法适用于本市行政区域内电动自行车的销售、登记和通行管理。

第三条本市电动自行车管理遵循严格管理的原则，并对五城区内的电动自行车实行总量控制。

本办法所称五城区是指鼓楼区、台江区、仓山区、晋安区、马尾区。

第四条本办法所称的电动自行车，是指以蓄电池作为辅助能源，具有两个车轮，能实现人力骑行、电动或电助动功能且符合相关国家安全技术标准的特种自行车。

第五条市、县（市）区人民政府公安交通、市场监督、环境保护、城管执法、交通运输等有关部门，依据下列职责共同做好电动自行车管理工作：（一）公安机关交通管理部门负责电动自行车登记上牌、道路行驶管理;（二）市场监督主管部门负责编制并公布符合现行国家标准的电动自行车目录,依法对销售电动自行车实施监督管理;（三）环境保护部门依法对从事电动自行车废铅酸蓄电池收集、贮存、转移、利用、经营活动的单位实施监督管理;（四）城管执法部门负责电动自行车在城市道路、公共场所停放管理，查处占道销售电动自行车的违法行为;（五）交通运输主管部门负责查处电动自行车非法营运行为。

第六条各级人民政府应当通过报刊、广播、电视、网络等媒体，宣传电动自行车规范骑行、规范停放等有关管理规定，增强市民道路交通安全意识。

第七条本市电动自行车实行合格产品目录管理。

市市场监督主管部门应当根据现行国家标准编制《福州市合格电动自行车产品目录》，报经市政府审定后公布。

在本市销售和登记报牌的电动自行车产品应当符合《福州市合格电动自行车产品目录》。

电动自行车产品目录登记具体办法由市市场监督主管部门制定。

第二章销售管理第八条销售电动自行车应当经市场监督主管部门注册登记。

禁止销售不符合现行国家标准的电动自行车。

黄庆飞、福州市马尾区人民政府二审行政判决书【案由】行政行政行为种类行政监督【审理法院】福建省福州市中级人民法院【审理法院】福建省福州市中级人民法院【审结日期】2020.11.27【案件字号】（2020）闽01行终603号【审理程序】二审【审理法官】俞淑娟郑鋆张厚磊【审理法官】俞淑娟郑鋆张厚磊【文书类型】判决书【当事人】黄庆飞;福州市马尾区人民政府【当事人】黄庆飞福州市马尾区人民政府【当事人-个人】黄庆飞【当事人-公司】福州市马尾区人民政府【代理律师/律所】黄胜利福建坤广律师事务所【代理律师/律所】黄胜利福建坤广律师事务所【代理律师】黄胜利【代理律所】福建坤广律师事务所【法院级别】中级人民法院【原告】黄庆飞【被告】福州市马尾区人民政府【本院观点】《中华人民共和国政府信息公开条例》第十条规定，行政机关制作的政府信息，由制作该政府信息的行政机关负责公开。

【权责关键词】行政复议合法违法质证证据不足行政复议缺席判决维持原判改判撤销原判发回重审政府信息公开【指导案例标记】0【指导案例排序】0【本院认为】本院认为，《中华人民共和国政府信息公开条例》第十条规定，行政机关制作的政府信息，由制作该政府信息的行政机关负责公开。

行政机关从公民、法人和其他组织获取的政府信息，由保存该政府信息的行政机关负责公开；行政机关获取的其他行政机关的政府信息，由制作或者最初获取该政府信息的行政机关负责公开。

法律、法规对政府信息公开的权限另有规定的，从其规定。

第三十六条第（四）项规定，对政府信息公开申请，行政机关经检索没有所申请公开信息的，告知申请人该政府信息不存在。

本案中，上诉人申请公开的《股权转让协议》并非被上诉人福州市马尾区人民政府制作，且被上诉人福州市马尾区人民政府经检索亦未查询到上诉人所申请公开的信息，被上诉人在尽到合理的查找和检索义务后，作出被诉《政府信息公开申请办理告知书》，告知上诉人未查询到所申请公开的信息，并建议其向福州市马尾区市场监督管理局咨询并无不当。

2019-2020学年福建省福州市马尾区八年级（上）期中生物试卷1.下列各项中，属于腔肠动物和扁形动物的共同特征的是（）A. 两侧对称B. 有口无肛门C. 有刺细胞D. 营寄生生活2.蛔虫是常见的肠道寄生虫。

下列哪项特征与它的寄生生活无关（）A. 体表有角质层B. 有口有肛门C. 生殖器官发达D. 消化管结构简单3.鲍鱼是营养丰富的海鲜，它的贝壳可以做中药。

你推测它应该属于（）A. 线形动物B. 软体动物C. 节肢动物D. 腔肠动物4.下列动物中，都属于节肢动物的是（）A. 螃蟹、苍蝇B. 蚯蚓、蜘蛛C. 乌贼、金龟子D. 钉螺、水蛭5.蝗虫和蚯蚓的共同特征是（）A. 身体分节B. 体表具有外骨骼C. 具有刚毛D. 体内有脊柱6.下列动物中，生长发育过程中都有蜕皮现象的一组是（）A. 蚯蚓、蜘蛛、蜈蚣B. 蜘蛛、螃蟹、河蚌C. 水蚤、鼠妇、龙虾D. 蜜蜂、蜻蜓、沙蚕7.下列动物都属于昆虫的一组是（）A. 蜘蛛、螳螂、蛤蜊B. 蜻蜓、蟑螂、蝗虫C. 沼虾、蚂蚁、水蚤D. 蜈蚣、瓢虫、水蛭8.下列动物中，都属于脊椎动物的一组是（）A. 蜜蜂、蜂鸟B. 蜗牛、黄牛C. 甲鱼、带鱼D. 鲸鱼、章鱼9.鲨鱼属于鱼类，下列动物中与它亲缘关系最近的是（）A. 海马B. 海豚C. 海龟D. 海葵10.鲫鱼流出鳃的水和进入鳃的水相比，水中溶解的气体成分的变化情况是（）A. 两者所含气体成分含量相同B. 流出的水中氧气含量减少，二氧化碳增加C. 流出的水中氧气含量增加，二氧化碳含量减少D. 流出的水中氧气含量增加，二氧化碳含量增加11.鲫鱼的下列形态特点与游泳无直接关系的是（）A. 身体呈流线型B. 体表有黏液C. 体色背深腹浅D. 鱼鳍的形状12.青蛙必须生活在潮湿的环境中，最主要的原因是（）A. 皮肤裸露B. 幼体用鳃呼吸C. 生殖发育离不开水D. 肺不发达，需要皮肤辅助呼吸13.有一动物体表覆盖有鳞片，体内受精，受精卵有卵壳保护。

警示教育大会讲话稿农机购置补贴工作暨农机系统廉政警示教育报告会讲话稿下午,还要邀请专家作廉政警示教育专题报告.下面,根据会议安排,就农机购置补贴廉政风险防控工作,谈四点意见.一、肯定成绩,正视不足2019年,是十二五收官之年,全省农机化发展仍然保持持续健康快速的良好态势,全面完成了十二五规划确定的主要目标,农机装备水平和装备结构、农机作业水平和作业质量、农机服务水平和服务机制都有了新的提升,为我省粮食增产、农业增效、农民增收发挥了重要作用.农机购置补贴政策作为一项重要的强农惠农富农政策,为农机化的发展起到了决定性的引导作用、撬动作用,在全社会引起了积极的反响,也得到了农业部和省委、省政府的充分肯定.上个月,方春明副省长在全省2019年农机购置补贴实施专报上作出重要批示,充分肯定了我省购机补贴实施成效.我省也有望连续第四年续被评为农业部强农惠农富农政策落实（农机购置补贴）延伸绩效管理优秀单位.这是全省各级农机、财政部门共同努力的结果；是不折不扣执行农业部、财政部以及省实施指导意见要求的结果；也是各地各有关部门严明纪律,严格程序,高效规范实施的结果；更是树立廉政风险防控意识、安全廉洁的结果.去年一年,从转作风、防风险的角度看,全省农机、财政系统及相关部门在实施购机补贴政策的全过程中,更加突出体现了王学军书记提出的严、细、深、实、快的五字要求：一是严字当头.对补贴实施工作高标准严要求,对违规问题严肃处理,实行零容忍.全年共处理违规企业16家,包括福田、洋马等10家生产企业,以及6家经销企业,并在全省通报了怀远县和界首市农机购置补贴有关问题查处情况.各级农机化主管部门在补贴实施过程中,严密关注补贴机具价格和市场供需变化,针对发现的补贴率过高产品进行及时分析、汇总、上报和调整.二是细处入手.在政策落实过程中,坚持一手抓顶层设计、体系构建,一手抓关键问题、具体细节.借助第三方技术团队,通过大数据分析,详细核查补贴辅助管理系统数据,发现并组织各地整改了927条录入错误数据,查处了存在跨年度重复补贴问题的机具.三是深入教育.深入开展全省农机购置补贴反腐倡廉警示教育活动.省、市、县各级农机部门参与购机补贴的同志,多次接受廉政警示教育.2019年,在全省农机购置补贴工作会议上,就购机补贴廉政风险防控进行了专题培训；在全省农机系统预防职务犯罪案例分析报告会上,省侦查逻辑办案研究会柴学友会长结合职务犯罪案例,作了反腐倡廉教育报告.四是实处着力.改进工作作风,心无旁骛抓落实；推进绩效管理,攻坚克难尽职责.2019年,创新性绩效管理考评方式,引入了第三方,建立农机购置补贴政策落实第三方评估机制,督促各地全面落实各项指标任务.通过信息公开,强化社会监督,推进政策落实.全年开展了3次市、县级农机购置补贴信息公开检查,县级专栏建设率97.7%,上年度享受补贴的购置者信息表公开率达93.1%.五是快而有序.实施过程全面监控,实施进度及时通报,适时开展督查调度.我省总体实施、结算进度较快,截至2019年1月底,农机购置补贴资金实施比例99%,结算比例98.8%,年度财政资金基本执行完成.在肯定成绩的同时,我们也要看到,购机补贴工作量大面广,政策性强,环节多,横向上涉及多部门、多主体,以及各地的差异性,纵向上涉及上层顶层设计的不断完善和最基层一线农民需求的不断变化.虽然自上而下,都高度重视购机补贴工作,都摆上了重中之重的位置,但在具体实施的过程中,仍然存在很多的不足,既有客观上的原因,也有主观上的原因,但在购机补贴政策已实施完善10年多的情况下,应该说还是主观原因偏多.比如,一些县在制定方案时不认真研究分析,方案不够精准,致使操作性不强,市级在审核时把关不严,指导不够；有些地方在政策理解、方法措施上不到位,安排资金在比例上没有突出重点机具和敞开机具,造成被动；有些地方没有严格按照操作流程,有些环节缺失；有些地方把一站式服务和有些涉及收费的项目混搭,容易造成群众误解；有的农机购置补贴信息公开专栏公开的内容不全面,公开的格式不规范,有的站甚至被当地政府部门关停还无动于衷；有的地方规定动作做得不到位,增加的环节随意性大、不规范等等.对此,要引起我们高度重视,在今后的工作中予以改进和完善.二、以案为鉴,警钟长鸣近年来,我国经济发展进入新常态,党风廉政建设和反腐败工作不断深入推进,有权必有责、失责必追究.为此,我们必须始终保持清醒头脑.2019年,从全国来看,农机购置补贴领域违纪违法问题呈明显下降趋势,但少数省份仍发生了一些违纪违法问题,一些农机管理干部也因此受到党纪国法的处理.为进一步强化警示教育,经总结梳理,主要有以下一些问题：(一)违规审批农机购置补贴问题.福建省福州市马尾区农机管理站副站长付晓华在负责对国家农业机械购置补贴申请的审核、上报过程中,明知申请人福州某生态农业科技有限公司不属于补贴对象,仍两次审核通过该公司借当地农户个人名义提交的共计102万余元的农机购置补贴申请并上报,致使国家利益及公共财产遭受重大损失.2019年12月,付晓华受到留党察看一年和行政撤职处分.(二)违规向农机购置农户收取培训费问题.青海省贵德县农机管理站在向农机购置农户相关补贴手续时,违规向部分农户收取培训费.2019年11月24日,贵德县监察局报经县政府同意,分别给予县农机管理站原站长谢文合、原副站长崔成刚、现任站长杨明德行政记大过处分.(三)截留私分补贴款问题.今年1月,江苏省纪委通报：泰州市姜堰区华港镇里华村村委会副主任李正国和村委委员吕小粉在帮助4户村民贷款购买插秧机过程中,截留私分国家农机补助款1.32万元.其中,李正国分得9200元,吕小粉分得4000元.李正国受到党内严重警告处分,吕小粉受到党内警告处分.(四)骗取深松补贴款问题.今年2月,山东省纪委通报：莒南县大店镇农机管理站原站长崔元军采取虚报手段,骗取农机深松整地补贴款28.87万元.莒南县纪委给予崔元军开除党籍处分,司法机关已依法追究其刑事责任.(五)利用职权为他人谋取农机补贴问题.今年1月,xq生产建设兵团纪委通。

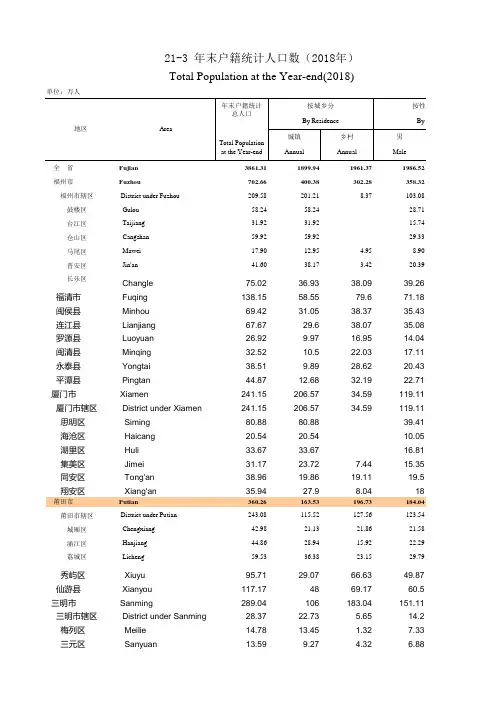
福清市 Fuqing138.1558.5579.671.18闽侯县 Minhou69.4231.0538.3735.43连江县 Lianjiang67.6729.638.0735.08罗源县 Luoyuan26.929.9716.9514.04闽清县 Minqing32.5210.522.0317.11永泰县 Yongtai38.519.8928.6220.43平潭县 Pingtan44.8712.6832.1922.71厦门市 Xiamen241.15206.5734.59119.11厦门市辖区 District under Xiamen241.15206.5734.59119.11思明区 Siming80.8880.8839.41海沧区 Haicang20.5420.5410.05湖里区 Huli33.6733.6716.81集美区 Jimei31.1723.727.4415.35同安区 Tong'an38.9619.8619.1119.5翔安区 Xiang'an35.9427.98.0418 莆田市 Putian360.26163.53196.73184.04 莆田市辖区 District under Putian243.08115.52127.56123.54 城厢区 Chengxiang42.9821.1321.8621.58 涵江区 Hanjiang44.8628.9415.9222.29 荔城区 Licheng59.5336.3823.1529.79秀屿区 Xiuyu95.7129.0766.6349.87仙游县 Xianyou117.174869.1760.5三明市 Sanming289.04106183.04151.11三明市辖区 District under Sanming28.3722.73 5.6514.2梅列区 Meilie14.7813.45 1.327.33三元区 Sanyuan13.599.27 4.32 6.88永安市 Yong'an 33.1418.214.9517.03 明溪县 Mingxi 11.9 3.778.13 6.17 清流县 Qingliu 15.6 4.6610.958.16 宁化县 Ninghua 37.769.1628.6119.8 大田县 Datian 41.5413.7227.8222.56 尤溪县 Youxi 45.311.8233.4824.31 沙县 Shaxian 27.219.4717.7413.98 将乐县 Jiangle 18.73 5.3813.349.72 泰宁县 Taining 13.86 3.5710.37.17 建宁县 Jianning 15.62 3.5412.088.01 泉州市 Quanzhou755.12379.03376.09391.12 泉州市辖区 District under Quanzhou 138.4389.1549.2869.54 鲤城区 Licheng 26.5626.5613 丰泽区 Fengze 27.2227.2213.17洛江区 Luojiang 20.21 5.9114.2910.51 泉港区 Quangang 42.0720.0322.0421.6 石狮市 Shishi 34.5525.668.8917.57 晋江市 Jinjiang 117.6366.8250.8160.15 南安市 Nan'an 165.5289.3376.1987.08 惠安县 Hui'an 103.9947.9756.0252.49 安溪县 Anxi 121.9529.0192.9465.04 永春县 Yongchun 60.5528.9231.6332.01 德化县 Dehua 34.8611.5923.2718.49 漳州市 Zhangzhou 520.8256.03264.77267.12 漳州市辖区 District under Zhangzhou 80.4662.2818.1839.54 芗城区 Xiangcheng 46.8939.417.4923.04 龙文区 Longwen 16.2112.99 3.228.03 龙海市 Longhai 89.7939.7550.0445.11 云霄县 Yunxiao 46.7118.8427.8724.6 漳浦县 Zhangpu 94.0349.4444.5948.34 诏安县 Zhao'an 68.2525.5242.7335.61 长泰县 Changtai 21.2711.2610.0110.79 东山县 Dongshan 22.08139.0811.11 南靖县 Nanjing 36.2415.0821.1618.54 平和县 Pinghe 62.3922.7739.6233.18 华安县 Hua'an 16.957.998.968.78 南平市 Nanping319.83113.89205.94164.98 南平市辖区 District under Nanping 85.9137.7848.1444.04 延平区 Yanping 50.0324.6625.3825.67 建阳区 Jianyang 35.8813.1222.7618.37 邵武市 Shaowu 30.612.9417.6515.64 武夷山市 Wuyishan 24.5910.4914.1112.48 建瓯市Jian’ou55.2817.637.6828.52顺昌县 Shunchang23.58.4615.0412.1浦城县 Pucheng439.8433.1622.16光泽县 Guangze16.32 4.5111.818.5松溪县 Songxi16.85 4.8711.988.78政和县 Zhenghe23.787.4116.3812.75龙岩市 Longyan318.67144.31174.36165.32龙岩市辖区 District under Longyan105.5758.0147.5753.9新罗区 Xinluo55.1340.2114.9227.54永定区 Yongding50.4417.832.6526.36漳平市 Zhangping29.7311.7517.9815.62长汀县 Changting55.1422.9632.1829.15上杭县 Shanghang53.122.6130.527.31武平县 Wuping40.2916.4323.8620.89连城县 Liancheng34.8412.5622.2918.44宁德市 Ningde353.78130.21223.57185.39宁德市辖区 District under Ningde50.7123.6527.0625.74蕉城区 Jiaocheng50.7123.6527.0625.74福安市 Fu'an67.2526.0241.2235.39福鼎市 Fuding60.1220.4239.731.17霞浦县 Xiapu54.8619.5235.3328.86古田县 Gutian42.9913.7429.2522.7屏南县 Pingnan19.12 6.3412.7810.22寿宁县 Shouning26.568.9917.5714.21周宁县 Zhouning21.197.3613.8311.4柘荣县 Zherong10.98 4.17 6.81 5.7235.76 66.96 33.99 32.59 12.88 15.41 18.08 22.17 122.04 122.04 41.47 10.49 16.86 15.82 19.46 17.94 176.22 119.5521.4022.5729.73 45.84 56.67 137.93 14.177.456.727.4417.9618.98 20.99 13.2496.77.61364 68.8913.5614.059.69 20.47 16.98 57.48 78.4451.5 56.91 28.54 16.38 253.67 40.93 23.858.17 44.68 22.11 45.69 32.64 10.48 10.97 17.71 29.218.17 154.85 41.88 24.36 17.51 14.95 12.11 26.767.828.06 11.03 153.3551.67 27.59 24.08 14.11 25.98 25.79 19.3916.4 168.39 24.97 24.97 31.86 28.9526 20.298.91 12.369.85.25。

2019年福州市气候公报FUZHOU CLIMATE BULLETIN福州市气象局二O二O年一月第一章基本气候概况2019年福州市年平均气温显著偏高，年雨量和年日照时数正常。

影响较重的气象灾害有5月31日到6月2日暴雨天气和8月初到12月初的干旱；气象灾害总体较轻，总体气候属较好年景。

一、气温2019年，全市年平均气温20.7℃，比常年平均高0.8℃，异常度为1.55，属显著偏高（图1）。

各季全市平均气温情况见表1，其中冬季显著偏高，早春季和秋季偏高，雨季和夏季正常。

从各月平均气温来看（图2），1月显著偏高，4月、8～10月和12月偏高，其余月份正常。

表12019年福州市各季平均气温（℃）季节平均气温距平异常度评价冬季13.2 1.5 1.65显著偏高春季早春季17.4 1.3 1.35偏高雨季23.9-0.4-0.64正常夏季28.20.50.9正常秋季20.91.0 1.24偏高注：按照福建天气、气候特征，季节划分为：冬季（上年12月～当年2月）、早春季（3～4月）、雨季（5～6月）、夏季（7～9月）、秋季（10～11月），下同。

各县（市）区年平均气温为19.8～21.3℃，距平为0.2～1.2℃，其中罗源和福清正常，福州市区偏高，其余县（市）区属显著偏高～异常偏高。

各县（市）区年最低气温为1.8～6.3℃，闽清和永泰出现在12月8日，福图11981~2019年福州市逐年平均气温图22019年福州市逐月平均气温清出现在1月27日，其余县（市）区出现在1月23日。

各县（市）区年最高气温为37.7～39.7℃，福州市区出现在9月9日，其余县（市）区出现在8月11日前后（见附表）。

二、雨量全市平均年雨量1424.6毫米，比常年平均少5.1%，属正常（图3）。

各季雨量分布见表2，其中冬季、早春季和雨季正常，夏季偏少，秋季异常偏少。

各月雨量分布十分不均，其中1月和8～11月偏少～异常偏少，3月和6月偏多，7月显著偏多，其余月份正常（见图4）。

三角函数一．选择题（共12小题）1．（2022•鼓楼区校级三模）若，且，则＝（）A．B．C．2D．−22．（2022•鼓楼区校级模拟）已知角θ的大小如图所示，则＝（）A．﹣5B．5C．D．3．（2022•福州模拟）某智能主动降噪耳机工作的原理是利用芯片生成与噪音的相位相反的声波，通过两者叠加完全抵消掉噪音（如图）．已知噪音的声波曲线y＝A sin（ax+p）（其中A＞0，a＞0，0≤φ＜2π）的振幅为1，周期为π，初相为，则用来降噪的声波曲线的解析式为（）A．y＝sin2x B．y＝cos2x C．y＝﹣sin2x D．y＝﹣cos2x4．（2022春•福州期中）已知α为锐角，且sin（α﹣）＝，则cos（﹣α）＝（）A．B．﹣C．D．﹣5．（2022•鼓楼区校级三模）已知函数的图象过点，现将y＝f（x）的图象向左平移个单位长度得到的函数图象也过点P，则（）A．ω的最小值为2B．ω的最小值为6C．ω的最大值为2D．ω的最大值为66．（2021秋•鼓楼区校级期末）已知角α的终边在射线y＝﹣2x（x≥0）上，则2sinα+cosα的值为（）A．B．C．﹣D．﹣7．（2021秋•鼓楼区校级期末）函数f（x）的部分图象如图所示，则f（x）可能是（）A．B．C．D．8．（2021秋•福州期末）已知函数f（x）＝sin（ωx﹣φ）的部分图象如图所示，则f（x）的单调递增区间为（）A．B．C．D．9．（2021秋•仓山区校级期末）与﹣2022°终边相同的最小正角是（）A．138°B．132°C．58°D．42°10．（2022春•马尾区校级月考）已知弧长为的弧所对的圆心角为，则该弧所在的扇形面积为（）A．B．C．D．11．（2021秋•鼓楼区校级期末）已知，tanα＝3，，则tan（α﹣β）＝（）A．B．C．2D．12．（2021秋•鼓楼区校级期末）下列函数中，周期为π的是（）A．y＝B．y＝tan2xC．y＝sin x cos x D．y＝sin|x|二．填空题（共4小题）13．（2022•福州模拟）已知2sin（α﹣）＝cosα，则tanα＝．14．（2022春•福州期中）如图，半圆O的半径为1，A为直径所在直线上的一点，且OA＝，B为半圆弧上的动点．将线段AB绕点A顺时针旋转得到线段AC，则线段OC长度的最大值是．15．（2022春•仓山区校级期中）在平面直角坐标系中，O（0，0），P（8，6），将向量OP按顺时针方向旋转后，得向量，则点Q的坐标是．16．（2021秋•福州期末）函数f（x）＝sin（ωx+φ）（ω＞0，|φ|＜）的部分图像如图所示，BC∥x轴，则ω＝，φ＝．三．解答题（共5小题）17．（2021秋•福州期末）已知角α的顶点与坐标原点重合，始边与x轴的非负半轴重合，终边过点P（，）．（1）求cos（α+π）的值；（2）若tanβ＝﹣2，求tan（α﹣β）的值．18．（2021秋•鼓楼区校级期末）已知角α的顶点为坐标原点，始边为x轴的非负半轴，终边经过点P（1，﹣m﹣1），且cos．（1）求实数m的值；（2）若m＞0，求的值．19．（2021秋•鼓楼区校级期末）设函数．（1）求f（x）的单调增区间；（2）求f（x）在[0，π]上的最大值与最小值．20．（2021秋•福州期末）已知函数f（x）＝．（1）求f（x）的最小正周期；（2）将y＝f（x）的图象上的各点______得到y＝g（x）的图象，当x∈时，方程g（x）＝m有解，求实数m的取值范围．在以下①、②中选择一个，补在（2）中的横线上，并加以解答，如果①、②都做，则按①给分．①向左平移个单位，再保持纵坐标不变，横坐标缩短到原来的一半．②纵坐标保持不变，横坐标伸长到原来的2倍，再向右平移个单位．21．（2021秋•仓山区校级期末）在①f（x）是偶函数；②（，0）是f（x）的图象在y轴右侧的第一个对称中心；③f（x）相邻两条对称轴之间距离为．这三个条件中任选两个，补充在下面问题的横线上，并解答．已知函数f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜π），满足_____．（1）求函数f（x）的解析式；（2）将函数y＝f（x）的图象向右平移个单位，再将所得的图象上每一点的纵坐标不变，横坐标变为原来的2倍后所得到的图象对应的函数记作y＝g（x）；若函数F（x）＝f（x）+k•g（x）在（0，nπ）内恰有2021个零点，求实数k与正整数n的值．2022年新高二数学人教新版（2019）专题复习《三角函数》参考答案与试题解析一．选择题（共12小题）1．（2022•鼓楼区校级三模）若，且，则＝（）A．B．C．2D．−2【考点】两角和与差的三角函数．【专题】计算题；方程思想；综合法；三角函数的求值；数学运算．【分析】由已知可得＝﹣，可求tan＝﹣3，进而可求值．【解答】解：，可得＝﹣，所以＝﹣，解得tan＝﹣3或tan＝﹣，又，∴∈（，），∴tan＝﹣3，故＝＝﹣2．故选：D．【点评】本题考查二倍角的正弦公式，属中档题．2．（2022•鼓楼区校级模拟）已知角θ的大小如图所示，则＝（）A．﹣5B．5C．D．【考点】二倍角的三角函数．【专题】函数思想；定义法；三角函数的求值；数学运算．【分析】由已知求得tan（）＝﹣5，得到，再由倍角公式及同角三角函数基本关系式化弦为切求解．【解答】解：∵θ+的终边过P（﹣1，5），∴tan（）＝﹣5，即，∴，∴＝＝＝＝．故选：A．【点评】本题考查任意角的三角函数的定义，考查倍角公式及同角三角函数基本关系式的应用，是基础题．3．（2022•福州模拟）某智能主动降噪耳机工作的原理是利用芯片生成与噪音的相位相反的声波，通过两者叠加完全抵消掉噪音（如图）．已知噪音的声波曲线y＝A sin（ax+p）（其中A＞0，a＞0，0≤φ＜2π）的振幅为1，周期为π，初相为，则用来降噪的声波曲线的解析式为（）A．y＝sin2x B．y＝cos2x C．y＝﹣sin2x D．y＝﹣cos2x【考点】由y＝Asin（ωx+φ）的部分图象确定其解析式．【专题】数形结合；综合法；三角函数的图象与性质；数学运算．【分析】由已知可得A＝1，T＝π，p＝，由此即可求出a的值，由此即可求解．【解答】解：由已知可得A＝1，T＝π，p＝，则a＝2，所以y＝﹣sin（2x+）＝﹣cos2x，故选：D．【点评】本题考查了三角函数的图象及其求解解析式问题，考查了学生的运算能力，属于基础题．4．（2022春•福州期中）已知α为锐角，且sin（α﹣）＝，则cos（﹣α）＝（）A．B．﹣C．D．﹣【考点】两角和与差的三角函数．【专题】转化思想；综合法；三角函数的图象与性质；数学运算．【分析】由题意，利用同角三角函数的基本关系、诱导公式，求得cos（﹣α）的值．【解答】解：∵α为锐角，且sin（α﹣）＝，∴α﹣为锐角，cos（α﹣）＝＝，则cos（﹣α）＝cos（α﹣）＝，故选：C．【点评】本题主要考查同角三角函数的基本关系、诱导公式的应用，属于基础题．5．（2022•鼓楼区校级三模）已知函数的图象过点，现将y＝f（x）的图象向左平移个单位长度得到的函数图象也过点P，则（）A．ω的最小值为2B．ω的最小值为6C．ω的最大值为2D．ω的最大值为6【考点】函数y＝Asin（ωx+φ）的图象变换．【专题】计算题；转化思想；综合法；三角函数的求值；三角函数的图象与性质；逻辑推理；数学运算．【分析】直接利用函数的图象的平移变换的应用求出结果．【解答】解：函数的图象过点，所以f（0）＝sinφ＝，故φ＝；当函数f（x）的图象向左平移个单位，得到，由于函数的图象经过点（0，）；所以，故ω的最小值为2．故选：A．【点评】本题考查的知识要点：三角函数关系式的变换，函数的图象的平移变换，主要考查学生的运算能力和数学思维能力，属于基础题．6．（2021秋•鼓楼区校级期末）已知角α的终边在射线y＝﹣2x（x≥0）上，则2sinα+cosα的值为（）A．B．C．﹣D．﹣【考点】任意角的三角函数的定义．【专题】函数思想；定义法；三角函数的求值；数学运算．【分析】由已知可得α为第四象限角，且，结合平方关系求解sinα与cosα的值，则答案可求．【解答】解：∵角α的终边在射线y＝﹣2x（x≥0）上，∴α为第四象限角，由，解得sinα＝，cosα＝，∴2sinα+cosα＝，故选：D．【点评】本题考查三角函数的化简求值，考查任意角的三角函数的定义，是基础题．7．（2021秋•鼓楼区校级期末）函数f（x）的部分图象如图所示，则f（x）可能是（）A．B．C．D．【考点】由y＝Asin（ωx+φ）的部分图象确定其解析式．【专题】数形结合；数形结合法；三角函数的图象与性质；数学抽象．【分析】根据函数f（x）＝A sin（ωx+φ）的部分图象，求出A、T和ω、φ的值．【解答】解：设函数f（x）＝A sin（ωx+φ），由f（x）的部分图象知，A＝2，＝﹣＝，解得T＝π，所以ω＝＝2，又函数的图象过点（，2），即2×+φ＝+2kπ，k∈Z，解得φ＝﹣+2kπ，k∈Z，令k＝0，得φ＝﹣，所以f（x）＝2sin（2x﹣）．故选：A．【点评】本题考查了函数f（x）＝A sin（ωx+φ）的图象与性质的应用问题，是基础题．8．（2021秋•福州期末）已知函数f（x）＝sin（ωx﹣φ）的部分图象如图所示，则f（x）的单调递增区间为（）A．B．C．D．【考点】由y＝Asin（ωx+φ）的部分图象确定其解析式；正弦函数的单调性．【专题】计算题；方程思想；综合法；三角函数的图象与性质；数学运算．【分析】由图可得T＝2，可求ω，又函数过点（，1），可求φ，从而可求函数解析式，可求单调递增区间．【解答】解：由图形可知＝﹣＝1，所以T＝2，所以＝2，所以ω＝π，所以f（x）＝sin（πx﹣φ），又函数f（x）过点（，1），所以sin（﹣φ）＝1，所以﹣φ＝+2kπ，k∈Z，所以φ＝﹣2kπ，所以f（x）＝sin（πx﹣），由2kπ﹣≤πx﹣≤2kπ+，可得2k﹣≤x≤2k+，k∈Z，所以f（x）的单调递增区间为[2k﹣，2k+]，k∈Z，故选：D．【点评】本题考查由函数图象求解析式，求单调递增区间，属基础题．9．（2021秋•仓山区校级期末）与﹣2022°终边相同的最小正角是（）A．138°B．132°C．58°D．42°【考点】终边相同的角．【专题】计算题；转化思想；综合法；三角函数的求值；数学运算．【分析】利用终边相同的角的定义得到α＝﹣2022°+k•360°，k∈Z，然后令﹣2022°+k•360°＞0，求出k的值，代入求出此时的α即可．【解答】解：与﹣2022°终边相同的角为α＝﹣2022°+k•360°，k∈Z，由题意﹣2022°+k•360°＞0，解得k＞5.61，k∈Z，所以k的最小值为6，此时α＝﹣2022°+6×360°＝138°，故与﹣2020°终边相同的最小正角是138°．故选：A．【点评】本题考查了终边相同的角的应用，解题的关键是掌握终边相同角的表示，属于基础题．10．（2022春•马尾区校级月考）已知弧长为的弧所对的圆心角为，则该弧所在的扇形面积为（）A．B．C．D．【考点】扇形面积公式．【专题】计算题；对应思想；综合法；三角函数的求值；数学运算．【分析】由已知利用弧长公式先求出圆半径，由此能求出这条弧所在的扇形面积．【解答】解：∵弧长为的弧所对的圆心角为，∴圆半径r＝＝2，∴这条弧所在的扇形面积为S＝lr＝×2＝．故选：B．【点评】本题考查扇形面积的求法，考查弧长公式、扇形面积等基础知识，考查运算求解能力，是基础题．11．（2021秋•鼓楼区校级期末）已知，tanα＝3，，则tan（α﹣β）＝（）A．B．C．2D．【考点】两角和与差的三角函数．【专题】函数思想；分析法；三角函数的求值；数学运算．【分析】运用三角函数的同角公式,可得sin(α+β)的值，结合正切函数的两角差公式，分别求得tanβ、tan(α﹣β)的值，即可求解．【解答】解：∵tanα＞0，，∴，，∵，∴，由三角函数的同角公式可得，＝，∴tan(α+β)＝，∵＝，∴＝，故选：B．【点评】本题考查两角和与差的三角函数，考查计算能力，需要学生熟练掌握公式，属于基础题．12．（2021秋•鼓楼区校级期末）下列函数中，周期为π的是（）A．y＝B．y＝tan2xC．y＝sin x cos x D．y＝sin|x|【考点】三角函数的周期性．【专题】函数思想；分析法；三角函数的图象与性质；数学运算．【分析】根据三角函数的周期公式，即可得到结论．【解答】解：函数的周期，选项A，ω＝1，，故A选项错误，选项B，ω＝2，，故B选项错误，选项C，y＝sin x cos x＝，即ω＝2，，故C选项正确，选项D，当x＞0时，y＝sin x，当x＜0时，y＝sin(﹣x)＝﹣sin x，函数不是周期函数，故D选项错误，故选：C．【点评】本题主要考查三角函数的图象和性质，比较基础，属于基础题．二．填空题（共4小题）13．（2022•福州模拟）已知2sin（α﹣）＝cosα，则tanα＝1+．【考点】两角和与差的三角函数；同角三角函数间的基本关系．【专题】计算题；转化思想；转化法；三角函数的求值；数学运算．【分析】由已知利用两角差的正弦公式，同角三角函数基本关系式即可求解．【解答】解：因为2sin（α﹣）＝cosα，所以2（sinα﹣cosα）＝sinα﹣cosα＝cosα，可得sinα＝（1+）cosα，则tanα＝＝1+．故答案为：1+．【点评】本题主要考查了两角差的正弦公式，同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．14．（2022春•福州期中）如图，半圆O的半径为1，A为直径所在直线上的一点，且OA＝，B为半圆弧上的动点．将线段AB绕点A顺时针旋转得到线段AC，则线段OC长度的最大值是3．【考点】三角函数的恒等变换及化简求值．【专题】计算题；函数思想；综合法；三角函数的图象与性质；数学运算．【分析】以O点为坐标原点，建立如图所示平面直角坐标系，设∠AOB＝θ，则B（cosθ，sinθ），即可表示出C点坐标，从而得到，再根据向量模的坐标计算、三角恒等变换公式及正弦函数的性质计算可得．【解答】解：如图以O点为坐标原点，建立平面直角坐标系，设∠AOB＝θ，则，则，过点C、B分别作CD⊥x轴、BE⊥x轴，交x轴于点D、E，显然△CAD与△ABE全等，所以CD＝AE，AD＝BE，从而得到，即，所以＝，所以当，即时，，故答案为：3．【点评】本题考查了三角函数的性质，属于中档题．15．（2022春•仓山区校级期中）在平面直角坐标系中，O（0，0），P（8，6），将向量OP按顺时针方向旋转后，得向量，则点Q的坐标是（−，﹣7）．【考点】弧长公式．【专题】计算题；对应思想；向量法；平面向量及应用；数学运算．【分析】由题意可设＝（10cosθ，10sinθ），其中cosθ＝，sinθ＝，将向量按逆时针旋转后，得向量，由三角函数的公式即可求得点Q坐标．【解答】解：∵点O（0，0），P（8，6），∴＝（8，6），故可设＝（10cosθ，10sinθ），其中cosθ＝，sinθ＝，∵将向量按逆时针旋转后，得向量，设Q（x，y），则x＝10cos（θ﹣）＝10（cosθcos+sinθsin）＝﹣，y＝10sin（θ﹣）＝10（sinθcos﹣cosθsin）＝﹣7，∴点Q坐标是（−，﹣7）故答案为：（−，﹣7）．【点评】本题考查平面向量的坐标运算，涉及三角函数公式的应用，属中档题．16．（2021秋•福州期末）函数f（x）＝sin（ωx+φ）（ω＞0，|φ|＜）的部分图像如图所示，BC∥x轴，则ω＝2，φ＝．【考点】由y＝Asin（ωx+φ）的部分图象确定其解析式．【专题】计算题；数形结合；数形结合法；三角函数的图象与性质；数学运算．【分析】由周期求出ω，由五点法作图求出φ的值，即可得解．【解答】解：因为BC∥x轴，所以f（x）的图象的一条对称轴方程为x＝（+）＝，﹣＝＝×，所以ω＝2．由2×+φ＝π+kπ，k∈Z，且0＜φ＜π，得φ＝．故答案为2，．【点评】本题考查了由y＝A sin（ωx+φ）的部分图象确定其解析式，考查了数形结合思想，属于基础题．三．解答题（共5小题）17．（2021秋•福州期末）已知角α的顶点与坐标原点重合，始边与x轴的非负半轴重合，终边过点P（，）．（1）求cos（α+π）的值；（2）若tanβ＝﹣2，求tan（α﹣β）的值．【考点】两角和与差的三角函数．【专题】计算题；转化思想；综合法；三角函数的求值；数学运算．【分析】角α的终边过点P（，），可求cosα，tanα，可求（1）（2）的值．【解答】解：角α的终边过点P（，）．∴cosα＝，tanα＝＝，（1）cos（α+π）＝﹣cosα＝﹣；（2）tan（α﹣β）＝＝＝﹣2．【点评】本题考查三角函数的定义，以及三角恒等变换，属基础题．18．（2021秋•鼓楼区校级期末）已知角α的顶点为坐标原点，始边为x轴的非负半轴，终边经过点P（1，﹣m﹣1），且cos．（1）求实数m的值；（2）若m＞0，求的值．【考点】任意角的三角函数的定义．【专题】函数思想；定义法；三角函数的求值；数学运算．【分析】（1）由已知借助于余弦函数的定义列式求解m值；（2）由（1）可得sinα，cosα的值，结合三角函数的诱导公式可得的值．【解答】解：（1）由题意可得，∴，整理得（m+1）2＝4，解得m＝1或m＝﹣3；（2）∵m＞0，∴由（1）可得m＝1，则，∴．【点评】本题考查任意角的三角函数的定义，考查诱导公式的应用，是基础题．19．（2021秋•鼓楼区校级期末）设函数．（1）求f（x）的单调增区间；（2）求f（x）在[0，π]上的最大值与最小值．【考点】三角函数的最值．【专题】整体思想；转化法；三角函数的求值；数学运算．【分析】（1）利用三角函数的恒等变换化简函数的解析式，再利用正弦函数的单调性求出函数的递增区间即可；（2）根据x的范围，求出x+的范围，求出函数的最大值和最小值即可．【解答】解：（1）＝＝，令，得，所以f（x）的单调增区间为；（2）由x∈[0，π]，得，所以当，即时，f（x）取最大值2；当，即x＝π时，f（x）取最小值．【点评】本题主要考查三角函数的恒等变换，正弦函数的单调性，最值问题，是基础题．20．（2021秋•福州期末）已知函数f（x）＝．（1）求f（x）的最小正周期；（2）将y＝f（x）的图象上的各点______得到y＝g（x）的图象，当x∈时，方程g（x）＝m有解，求实数m的取值范围．在以下①、②中选择一个，补在（2）中的横线上，并加以解答，如果①、②都做，则按①给分．①向左平移个单位，再保持纵坐标不变，横坐标缩短到原来的一半．②纵坐标保持不变，横坐标伸长到原来的2倍，再向右平移个单位．【考点】函数y＝Asin（ωx+φ）的图象变换；三角函数中的恒等变换应用；三角函数的周期性．【专题】转化思想；综合法；三角函数的图象与性质；数学运算．【分析】（1）由题意利用三角恒等变换化简f（x）的解析式，再利用正弦函数的周期性，得出结论．（2）由题意利用函数y＝A sin（ωx+φ）的图象变换规律，求得g（x）的解析式，再利用余弦函数的定义域和值域，求得g（x）的范围，可得m的范围．【解答】解：（1）∵函数f（x）＝sin2x+2cos2x+2＝sin2x+2•+2＝sin2x+cos2x+3＝2sin（2x+）+3，故函数的周期为＝π．（2）将f（x）＝2sin（2x+）+3的图象按照变换①：向左平移个单位，再保持纵坐标不变，可得y＝2sin（2x++）+3＝2cos2x+3的图象，再横坐标缩小为原来的一半可得g（x）＝2cos4x+3的图象，当x∈[，]时，4x∈[﹣，π]，cos4x∈[﹣1，1]，g（x）∈[1，5]，若方程g（x）＝m有解，则m∈[1，5]．将f（x）＝2sin（2x+）+3的图象按照变换②：纵坐标保持不变，横坐标伸长到原来的2倍，可得y＝2sin（x+）+3的图象，再向右平移个单位，可得g（x）＝2sin x+3的图象．当x∈[，]时，sin x∈[﹣，]，g（x）∈[2，+3]．若方程g（x）＝m有解，则m∈[2，+3]．【点评】本题主要考查三角恒等变换，函数y＝A sin（ωx+φ）的图象变换规律，正弦函数的周期性，余弦函数的定义域和值域，属于中档题．21．（2021秋•仓山区校级期末）在①f（x）是偶函数；②（，0）是f（x）的图象在y轴右侧的第一个对称中心；③f（x）相邻两条对称轴之间距离为．这三个条件中任选两个，补充在下面问题的横线上，并解答．已知函数f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜π），满足_____．（1）求函数f（x）的解析式；（2）将函数y＝f（x）的图象向右平移个单位，再将所得的图象上每一点的纵坐标不变，横坐标变为原来的2倍后所得到的图象对应的函数记作y＝g（x）；若函数F（x）＝f（x）+k•g（x）在（0，nπ）内恰有2021个零点，求实数k与正整数n的值．【考点】函数y＝Asin（ωx+φ）的图象变换；由y＝Asin（ωx+φ）的部分图象确定其解析式．【专题】分类讨论；转化法；三角函数的图象与性质；数学运算．【分析】（1）根据三角函数的图象和性质，求出ω和φ的值即可，（2）根据函数图象变换关系，求出g（x）以及F（x）的解析式，根据函数零点性质建立方程进行讨论求解即可．【解答】解：（1）①f（x）是偶函数；②（，0）是f（x）的图象在y轴右侧的第一个对称中心；③f（x）相邻两条对称轴之间距离为．若选择①②，由①f（x）＝sin（ωx+φ）是偶函数，∴φ＝．即f（x）＝sin（ωx+）＝cosωx，由②（，0）是f（x）的图象在y轴右侧的第一个对称中心；则ω＝，得ω＝2，即f（x）＝cos2x．选择①③：由①f（x）＝sin（ωx+φ）是偶函数，∴φ＝．即f（x）＝sin（ωx+）＝cosωx，由③知：f（x）相邻两条对称轴之间距离为．∴，即T＝π，则＝π，则ω＝2，则f（x）＝cos2x．若选②③：③知：f（x）相邻两条对称轴之间距离为．∴，即T＝π，则＝π，则ω＝2，则f（x）＝sin（2x+φ），由②（，0）是f（x）的图象在y轴右侧的第一个对称中心；∴2×+φ＝π，得φ＝，则f（x）＝sin（2x+）＝cos2x，综上f（x）＝cos2x．（2）依题意，将函数y＝f（x）的图象向右平移个单位，得y＝cos2（x﹣）＝cos（2x﹣）＝sin2x，再将所得的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍得到y＝sin x，可得g（x）＝sin x，所以F（x）＝cos2x+k sin x＝﹣2sin2x+k sin x+1，当k＝0时，F（x）＝cos2x，则F（x）在（0，nπ）内的零点个数为偶数个，F（x）在（0，nπ）内恰有2021个零点，为奇数个零点，故k≠0，令F（x）＝0，可得2sin2x﹣k sin x﹣1＝0，令t＝sin x∈[﹣1，1]，则2t2﹣kt﹣1＝0，Δ＝k2+8＞0，则关于t的二次方程2t2﹣kt﹣1＝0必有两个不等的实根，t1，t2，且t1t2＝﹣，则t1，t2异号，（i）当0＜|t1|＜1，且0＜|t2|＜1时，则方程sin x＝t1和sin x＝t2在区间（0，nπ）（n∈N*）均有偶数个根，从而2sin2x﹣k sin x﹣1＝0在区间（0，nπ）（n∈N*）有偶数个根，不符合题意；（ii）当0＜|t1|＜1，且|t2|＞1时，则方程sin x＝t1在区间（0，nπ）有偶数个根，sin x＝t2无解，从而方程2sin2x ﹣k sin x﹣1＝0在（0，nπ）有偶数个根，不合题意．同理，当0＜|t2|＜1且|t1|＞1时，从而方程2sin2x﹣k sin x﹣1＝0在（0，nπ）有偶数个根，不合题意．（iii）当t1＝1，t2＝﹣＜0，当x∈（0，2π）时，sin x＝t1只有一根，sin x＝t2有两根，所以关于x的方程2sin2x﹣k sin x﹣1＝0在（0，2π）有三个根，由于2021＝3×673+2，则方程2sin2x﹣k sin x﹣1＝0在（1346π，1347π）只有一个根，在区间（1347π，1348π）上无实解，方程sin x＝t2在区间（1346π，1347π）上无实解，在区间（1347π，1348π）上有两个根．所以关于x的方程2sin2x﹣k sin x﹣1＝0在区间（0，1347π）上有2020个根．在区间（0，1348π）上有2022个根．不合题意．（iⅤ）当t1＝﹣1时，则t2＝，当x∈（0，2π）时，sin x＝t1只有一根，sin x＝t2有两根，所以关于x的方程2sin2x ﹣k sin x﹣1＝0在（0，2π）上有三个根，由于2021＝3×673+2，则方程2sin2x﹣k sin x﹣1＝0在（0，1347π）上有3×673＝2019个根．由于方程sin x＝t1在区间（1346π，1347π）上无实数根，在区间（1347π，1348π）上只有一个实数根．由于方程sin x＝t2在区间（1346π，1347π）上有两个实数根，在区间（1347π，1348π）上只有一个实数根．因此关于x的方程2sin2x﹣k sin x﹣1＝0在（0，1347π）上有2021个根，在区间（0，1348π）上有2022个根，因此2×（﹣1）2﹣k（﹣1）﹣1＝1+k＝0．所以解得k＝﹣1．n＝1347．【点评】本题主要考查三角函数关系式的变换，三角函数图象和性质的应用，函数的零点和函数的图象的关系，主要考查学生的运算能力和转换能力及思维能力，综合性较强，运算量较大，属于难题．考点卡片1．终边相同的角【知识点的认识】终边相同的角：k•360°+α（k∈Z）它是与α角的终边相同的角，（k＝0时，就是α本身），凡是终边相同的两个角，则它们之差一定是360°的整数倍，应该注意的是：两个相等的角终边一定相同，而有相同的终边的两个角则不一定相等，也就是说，终边相同是两个角相等的必要条件，而不是充分条件．还应该注意到：A＝{x|x＝k•360°+30°，k∈Z}与集合B＝{x|x＝k•360°﹣330°，k∈Z}是相等的集合．相应的与x轴正方向终边相同的角的集合是{x|x＝k•360°，k∈Z}；与x轴负方向终边相同的角的集合是{x|x＝k•360°+180°，k∈Z}；与y轴正方向终边相同的角的集合是{x|x＝k•360°+90°，k∈Z}；与y轴负方向终边相同的角的集合是{x|x＝k•360°+270°，k∈Z}【命题方向】下列角中终边与330°相同的角是（）A．30°B．﹣30°C．630°D．﹣630°【分析】直接利用终边相同的角判断即可．解：因为330°的终边与﹣30°的终边相同，所以B满足题意．故选B．【点评】本题考查终边相同的角的表示方法，考查基本知识的熟练程度．【解题方法点拨】终边相同的角的应用（1）利用终边相同的角的集合S＝{β|β＝2kπ+α，k∈Z}判断一个角β所在的象限时，只需把这个角写成[0，2π）范围内的一个角α与2π的整数倍的和，然后判断角α的象限．（2）利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k赋值来求得所需角．2．弧长公式【知识点的认识】弧长、扇形面积的公式设扇形的弧长为l，圆心角大小为α（rad），半径为r，则l＝rα，扇形的面积为S＝lr＝r2α．【命题方向】已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是（）A．2 B．C．2sin1 D．sin2【分析】解直角三角形AOC，求出半径AO，代入弧长公式求出弧长的值．解：如图：∠AOB＝2，过点0作OC⊥AB，C为垂足，并延长OC交于D，∠AOD＝∠BOD＝1，AC＝AB＝1，Rt△AOC中，AO＝＝，从而弧长为α•r＝，故选B．【点评】本题考查弧长公式的应用，解直角三角形求出扇形的半径AO的值，是解决问题的关键．【解题方法点拨】弧长和扇形面积的计算方法（1）在弧度制下，计算扇形的面积和弧长比在角度制下更方便、简捷．（2）从扇形面积出发，在弧度制下使问题转化为关于α的不等式或利用二次函数求最值的方法确定相应最值．（3）记住下列公式：①l＝αR；②S＝lR；③S＝αR2．其中R是扇形的半径，l是弧长，α（0＜α＜2π）为圆心角，S是扇形面积．3．扇形面积公式【知识点的认识】弧长、扇形面积的公式设扇形的弧长为l，圆心角大小为α（rad），半径为r，则l＝rα，扇形的面积为S＝lr＝r2α．【命题方向】扇形的周长为6cm，面积是2cm2，则扇形的圆心角的弧度数是（）A．1 B．4 C．1或4 D．2或4【分析】设出扇形的圆心角为αrad，半径为Rcm，根据扇形的周长为6 cm，面积是2 cm2，列出方程组，求出扇形的圆心角的弧度数．解：设扇形的圆心角为αrad，半径为Rcm，则，解得α＝1或α＝4．选C．【点评】本题考查扇形面积公式，考查方程思想，考查计算能力，是基础题．【解题方法点拨】弧长和扇形面积的计算方法（1）在弧度制下，计算扇形的面积和弧长比在角度制下更方便、简捷．（2）从扇形面积出发，在弧度制下使问题转化为关于α的不等式或利用二次函数求最值的方法确定相应最值．（3）记住下列公式：①l＝αR；②S＝lR；③S＝αR2．其中R是扇形的半径，l是弧长，α（0＜α＜2π）为圆心角，S是扇形面积．4．任意角的三角函数的定义【知识点的认识】任意角的三角函数1定义：设α是一个任意角，它的终边与单位圆交于点P（x，y），那么sin α＝y，cos α＝x，tan α＝．2．几何表示：三角函数线可以看作是三角函数的几何表示，正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是（1，0）．【命题方向】已知角α的终边经过点（﹣4，3），则cosα＝（）A．B．C．﹣D．﹣【分析】由条件直接利用任意角的三角函数的定义求得cosα的值．解：∵角α的终边经过点（﹣4，3），∴x＝﹣4，y＝3，r＝＝5．∴cosα＝＝＝﹣，故选：D．【点评】本题主要考查任意角的三角函数的定义，两点间的距离公式的应用，属于基础题．【解题方法点拨】利用三角函数的定义求三角函数值的方法利用三角函数的定义，求一个角的三角函数值，需确定三个量：（1）角的终边上任意一个异于原点的点的横坐标x；（2）纵坐标y；（3）该点到原点的距离r．若题目中已知角的终边在一条直线上，此时注意在终边上任取一点有两种情况（点所在象限不同）．5．三角函数的恒等变换及化简求值【概述】三角函数的恒等变化主要是指自变量x数值比较大时，如何转化成我们常见的数值比较小的而且相等的三角函数，主要的方法就是运用它们的周期性．【公式】①正弦函数有y＝sin（2kπ+x）＝sin x，sin（+x）＝sin（﹣x）＝cos x②余弦函数有y＝cos（2kπ+x）＝cos x，cos（﹣x）＝sin x③正切函数有y＝tan（kπ+x）＝tan x，tan（﹣x）＝cot x，④余切函数有y＝cot（﹣x）＝tan x，cot（kπ+x）＝cot x．【例题解析】例：sin60°cos（﹣45°）﹣sin（﹣420°）cos（﹣570°）的值等于解：，，，，∴原式＝．先利用诱导公式把sin（﹣420°）和cos（﹣570°）转化成﹣sin60°和﹣cos30°，利用特殊角的三角函数值求得问题的答案．这其实也就是一个化简求值的问题，解题时的基本要求一定要是恒等变换．【考点点评】本考点是三角函数的基础知识，三角函数在高考中占的比重是相当大的，所有有必要认真掌握三角函数的每一个知识点，而且三角函数的难度相对于其他模块来说应该是比较简单的．6．同角三角函数间的基本关系【知识点的认识】1．同角三角函数的基本关系（1）平方关系：sin2α+cos2α＝1．（2）商数关系：＝tanα．2．诱导公式公式一：sin（α+2kπ）＝sin α，cos（α+2kπ）＝cos_α，其中k∈Z．公式二：sin（π+α）＝﹣sin_α，cos（π+α）＝﹣cos_α，tan（π+α）＝tan α．公式三：sin（﹣α）＝﹣sin_α，cos（﹣α）＝cos_α．公式四：sin（π﹣α）＝sin α，cos（π﹣α）＝﹣cos_α．公式五：sin（﹣α）＝cosα，cos（﹣α）＝sinα．公式六：sin（+α）＝cosα，cos（+α）＝﹣sinα3．两角和与差的正弦、余弦、正切公式（1）C（α﹣β）：cos（α﹣β）＝cosαcosβ+sinαsinβ；（2）C（α+β）：cos（α+β）＝cosαcosβ﹣sinαsinβ；（3）S（α+β）：sin（α+β）＝sinαcosβ+cosαsinβ；（4）S（α﹣β）：sin（α﹣β）＝sinαcosβ﹣cosαsinβ；（5）T（α+β）：tan（α+β）＝．（6）T（α﹣β）：tan（α﹣β）＝．4．二倍角的正弦、余弦、正切公式（1）S2α：sin 2α＝2sin_αcos_α；（2）C2α：cos 2α＝cos2α﹣sin2α＝2cos2α﹣1＝1﹣2sin2α；（3）T2α：tan 2α＝．【解题方法点拨】诱导公式记忆口诀：对于角“±α”（k∈Z）的三角函数记忆口诀“奇变偶不变，符号看象限”，“奇变偶不变”是指“当k为奇数时，正弦变余弦，余弦变正弦；当k为偶数时，函数名不变”．“符号看象限”是指“在α的三角函数值前面加上当α为锐角时，原函数值的符号”．7．三角函数中的恒等变换应用【知识点的认识】1．同角三角函数的基本关系（1）平方关系：sin2α+cos2α＝1．（2）商数关系：＝tanα．2．诱导公式公式一：sin（α+2kπ）＝sin α，cos（α+2kπ）＝cosα，tan（α+2kπ）＝tanα，其中k∈Z．公式二：sin（π+α）＝﹣sinα，cos（π+α）＝﹣cosα，tan（π+α）＝tan α．公式三：sin（﹣α）＝﹣sinα，cos（﹣α）＝cosα，tan（﹣α）＝﹣tanα．公式四：sin（π﹣α）＝sin α，cos（π﹣α）＝﹣cosα，tan（π﹣α）＝﹣tanα．公式五：sin（﹣α）＝cosα，cos（﹣α）＝sin α，tan（﹣α）＝cotα．公式六：sin（+α）＝cosα，cos（+α）＝﹣sinα，tan（+α）＝﹣cotα．3．两角和与差的正弦、余弦、正切公式（1）C（α﹣β）：cos （α﹣β）＝cosαcosβ+sinαsinβ；（2）C（α+β）：cos（α+β）＝cosαcosβ﹣sinαsinβ；（3）S（α+β）：sin（α+β）＝sinαcosβ+cosαsinβ；（4）S（α﹣β）：sin（α﹣β）＝sinαcosβ﹣cosαsinβ；（5）T（α+β）：tan（α+β）＝．（6）T（α﹣β）：tan（α﹣β）＝．4．二倍角的正弦、余弦、正切公式（1）S2α：sin 2α＝2sinαcosα；（2）C2α：cos 2α＝cos2α﹣sin2α＝2cos2α﹣1＝1﹣2sin2α；（3）T2α：tan 2α＝．。

第三章位置与坐标单元测试(A卷）（北师大版）参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．（2019春•孝义市期中）根据下列表述，能确定位置的是（）A．孝义市府前街B．南偏东45°C．美莱登国际影城3排D．东经116.4°，北纬39.9°【答案】解：A、孝义市府前街，具体位置不能确定，故本选项错误；B、南偏东45°，具体位置不能确定，故本选项错误；C、美莱登国际影城3排，具体位置不能确定，故本选项错误；D、东经116.4°，北纬39.9°，位置很明确，能确定位置，故本选项正确．故选：D．【点睛】本题考查了坐标确定位置，理解位置的确定需要两个条件是解题的关键．2．（2019春•长春期中）在平面直角坐标系中，点A（2，﹣6）在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】解：点A（2，﹣6）在第四象限，故选：D．【点睛】本题主要考查了平面直角坐标系中，各象限内点的坐标的符号的确定方法，关键是根据各象限内点的坐标特征解答．3．（2019春•偏关县期中）如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，﹣1）和（﹣3，1），那么“卒”的坐标为（）A．（﹣2，﹣1）B．（﹣2，﹣2）C．（2，﹣1）D．（2，1）【答案】解：如图所示：“卒”的坐标为（﹣2，﹣2），故选：B．【点睛】此题考查坐标确定位置，解题的关键就是确定坐标原点和x，y轴的位置．4．（2019春•裕华区校级期中）在平面直角坐标系中，点P（4，﹣3）到x轴的距离（）A．4 B．3 C．5 D．﹣3【答案】解：在平面直角坐标系中，点P（4，﹣3）到x轴的距离为3．故选：B．【点睛】本题考查了点的坐标，点的纵坐标的绝对值是点到x轴的距离，横坐标的绝对值是点到y轴的距离．5．若点P（a，b）在第二象限，则点P到x轴，y轴的距离分别是（）A．a，b B．b，a C．﹣a，b D．b，﹣a【答案】解：∵点P（a，b）在第二象限，∴a＜0，b＞0，∴点P到x轴、y轴的距离分别是b，﹣a．故选：D．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．6．（2019春•南海区期中）在平面直角坐标系中，点A与点B关于原点对称，点A坐标为（1，﹣2），则点B坐标为（）A．（1，2）B．（﹣1，﹣2）C．（﹣1，2）D．（1，﹣2）【答案】解：∵点A与点B关于原点对称，点A坐标为（1，﹣2），∴点B坐标为：（﹣1，2）．故选：C．【点睛】此题主要考查了关于原点对称点的性质，正确把握横纵坐标的符号是解题关键．7．（2019春•马尾区期中）若x轴的负半轴上的点P到y轴的距离为3，则点P的坐标为（）A．（3，0）B．（0，﹣3）C．（﹣3，0）D．（0，3）【答案】解：∵x轴的负半轴上的点P到y轴的距离为3，∴点P的坐标为（﹣3，0），故选：C．【点睛】本题主要考查了点的坐标，坐标平面内的点与有序实数对是一一对应的关系．8．（2019春•海淀区校级期中）已知点P位于第四象限，且距离x轴4个单位长度，距离y轴3个单位长度，则点P的坐标是（）A．（﹣4，3）B．（4，﹣3）C．（3，﹣4）D．（﹣3，4）【答案】解：∵点P位于第四象限，且距离x轴4个单位长度，距离y轴3个单位长度，∴点P的纵坐标为﹣4，横坐标为3，即点P的坐标为（3，﹣4），故选：C．【点睛】本题主要考查点的坐标，解题的关键是掌握到x轴的距离即为纵坐标的绝对值、到y轴的距离即为横坐标的绝对值及四个象限内点的坐标的符号特点．9．（2019春•南昌期中）在平面直角坐标系中，有C（1，2）、D（1，﹣1）两点，则点C可看作是由点D （）A．向上平移3个单位长度得到B．向下平移3个单位长度得到C．向左平移1个单位长度得到D．向右平移1个单位长度得到【答案】解：∵C（1，2）、D（1，﹣1），∴点C可看作是由点D向上平移3个单位长度得到，故选：A．【点睛】本题考查了坐标与图形变化﹣平移，熟练掌握平移的规律是解题的关键．10．（2019春•南海区期中）点A的坐标为（1，2），把点A向右平移2个单位，再向下平移1个单位后得到A′，则点A′的坐标为（）A．（0，4）B．（3，1）C．（﹣1，3）D．（2，0）【答案】解：∵点A（1，2）先向右平移2个单位，再向下平移1个单位得对应点A′，∴点A′坐标是：（3，1）．故选：B．【点睛】本题考查点坐标的平移变换，关键是要懂得左右平移点的纵坐标不变，而上下平移时点的横坐标不变，平移中，对应点的对应坐标的差相等．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．二．填空题（共8小题，满分24分，每小题3分）11．（2019春•资阳区校级期中）如图，是象棋盘的一部分．若“帅”位于点（1，﹣2）上，则“炮”位于点（﹣2，1）上．【答案】解：依题意，坐标系的原点是从下数第3行与从左数第4列的交点，故炮的坐标为（﹣2，1）．故答案是：（﹣2，1）．【点睛】考查类比点的坐标及学生解决实际问题和阅读理解的能力．解决此类问题需要先确定原点的位置，再求未知点的位置，或者直接利用坐标系中的移动法则“右加左减，上加下减”来确定坐标．12．（2019春•黄石港区校级期中）已知点P（m，1）在第二象限，则点Q（﹣m，3）在第一象限．【答案】解：∵点P（m，1）在第二象限，∴m＜0，∴﹣m＞0，∴点Q（﹣m，3）在第一象限．故答案为：一．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．13．（2019春•海淀区校级期中）点A（﹣1，﹣3）关于x轴对称点的坐标是（﹣1，3），关于原点对称的点坐标是（1，3）．【答案】解：点A（﹣1，﹣3）关于x轴对称点的坐标是：（﹣1，3），关于原点对称的点坐标是：（1，3）．故答案为：（﹣1，3），（1，3）．【点睛】此题主要考查了关于x轴以及关于y轴对称点的性质，正确记忆对应点符号关系是解题关键．14．（2019春•岳麓区校级期中）已知点A（2a﹣4，a+2）在x轴上，则a的值为﹣2．【答案】解：∵点A（2a﹣4，a+2）在x轴上，∴a+2＝0，解得a＝﹣2，故答案为：﹣2．【点睛】本题考查了点的坐标，熟记x轴上点的纵坐标为0是解题的关键．15．（2019春•广安区校级期中）将点D（2，3）先向左平移6个单位，再向下平移3个单位，得到点D′，则点D′的坐标为（﹣4，0）．【答案】解：D′的横坐标为2﹣6＝﹣4，纵坐标为3﹣3＝0，∴点D′的坐标为（﹣4，0）．故答案为：（﹣4，0）．【点睛】本题考查了坐标与图形变化﹣平移；用到的知识点为：左右平移只改变点的横坐标，左减右加；上下平移只改变点的纵坐标，上加下减．16．（2019春•偏关县期中）已知点M（3，﹣2）与点N（a，b）在同一条平行于x轴的直线上，且点N到y轴的距离等于4，则点N的坐标是（4，﹣2）或（﹣4，﹣2）．【答案】解：∵点M（3，﹣2）与点N（a，b）在同一条平行于x轴的直线上，∴b＝﹣2，∵N到y轴的距离等于4，∴a＝±4，∴点N的坐标为（4，﹣2）或（﹣4，﹣2）．故答案为：（4，﹣2）或（﹣4，﹣2）．【点睛】本题考查了点的坐标，主要利用了平行于x轴的直线上点的坐标特征，点到y轴的距离等于横坐标的绝对值．17．（2019春•西城区校级期中）线段AB平移后得到线段CD，已知A（2，3）的对应点为C（﹣1，4），则B（3，2）的对应点D的坐标为（0，3）．【答案】解：由题意：点A（2，3）向左平移3个单位，再向上平移1个单位得到点C（﹣1，4），∴点B（3，2）向左平移3个单位，再向上平移1个单位得到点D，∴D（0，3），故答案为（0，3）．【点睛】此题主要考查了点的平移规律，关键是掌握平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．18．（2019春•颍泉区校级期中）已知线段AB∥y轴，且AB＝3，若点A的坐标为（1，﹣2）．则点B的坐标是（1，1）或（1，﹣5）【答案】解：∵AB∥y轴，点A的坐标为（1，﹣2），∴点B的横坐标为1，∵AB＝3，∴点B在点A的上方时，点B的纵坐标为1，点B的坐标为（1，1），点B在点A的下方时，点B的纵坐标为﹣5，点B的坐标为（1，﹣5），综上所述，点B的坐标为（1，1）或（1，﹣5）．故答案为：（1，1）或（1，﹣5）．【点睛】本题考查了坐标与图形性质，主要利用了平行于y轴的点的横坐标相同的性质，要注意分情况讨论，作出图形更形象直观．三．解答题（共5小题，满分46分）19．（9分）（2019春•江城区期中）在平面直角坐标系中画出以A（4，2），B（2，0），C（﹣3，0）为顶点的三角形．【答案】解：建立直角坐标系，描点如下：【点睛】本题考查平面直角坐标系中点的特点；牢记平面直角坐标系中坐标轴上，各象限内点的特点是解题的关键．20．（9分）（2019春•宽城区期中）王霞和爸爸妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出坐标原点O和x轴，y轴．只知道游乐园D 的坐标为（1，﹣2）（1）请画出x轴，y轴，并标出坐标原点O．（2）写出其他各景点的坐标．【答案】解：（1）建立的平面直角坐标系如图所示：（2）由图知，望春亭的坐标为（﹣3，﹣1），湖心亭的坐标为（﹣4，2），音乐台的坐标为（﹣1，4），牡丹23亭的坐标为（2，3）【点睛】本题主要考查了坐标确定位置，在解题时要能确定出原点的位置是本题的关键．21．（9分）（2019春•江城区期中）如图，三角形ABC沿x轴正方向平移2个单位长度，再沿y轴负方向平移1个单位长度得到三角形EFG．（1）写出三角形EFG的三个顶点坐标；（2）求三角形EFG的面积．【答案】解：（1）如图：E（4，1），F（0，﹣2），G（5，﹣3）．（2）S△EFG＝4×5﹣3×4×﹣1×5×﹣4×1×＝20﹣6﹣2.5﹣2＝9.5．【点睛】此题主要考查了坐标与图形的变化﹣﹣平移，关键是正确确定组成图形的关键点平移后的对应点位置．22．（9分）（2019春•黄石港区校级期中）已知P（a+1，b﹣2），Q（4，3）两点．（1）若P，Q两点关于x轴对称，求a+b的值（2）若点P到y轴的距离是3，且PQ∥x轴，求点P的坐标．【答案】解：（1）∵P，Q两点关于x轴对称，∴a+1＝4，b﹣2＝﹣3，∴a＝3，b＝﹣1，∴a+b＝3﹣1＝2；（2）∵点P到y轴的距离是3，∴点P的横坐标为3或﹣3，又∵PQ∥x轴，∴点P的纵坐标为3，∴P（3，3）或（﹣3，3）．【点睛】此题主要考查了关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，﹣y）．23．（10分）（2019春•集美区校级期中）已知△A′B′C′是△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：△ABC A（a，0）B（3，0）C（5，5）△A′B′C′A′（4，2）B′（7，b）C′（c，7）（1）观察表中各对应点坐标的变化；（2）确定a＝0b＝2c＝9并在平面直角坐标系中画出△ABC；求出△ABC的面积．【答案】解：（1）∵B（3，0），B′（7，b）∴对应点向右平移了4个单位长度，∵A（0，0），A′（4，2），∴对应点向上平移了2个单位长度，所以点A、B、C分别向右平移了4个单位长度，然后向上平移了2个单位长度后分别得到了点A′、B′、C′；（2）∵B（3，0），B′（7，b）∴对应点向右平移了4个单位长度，∴a＝0，∵A（0，0），A′（4，2），∴对应点向上平移了2个单位长度，∴b＝2，∴c＝9．如图所示：△ABC即为所求；S三角形A′B′C′＝S三角形ABC＝×3×5＝．故答案为：029．【点睛】此题主要考查了平移的性质以及三角形面积求法，正确得出对应点坐标是解题关键.。