扩散参数。

水分子扩散系数
（原创实用版）
目录
1.水分子扩散系数的定义
2.水分子扩散系数的测量方法
3.水分子扩散系数的影响因素
4.水分子扩散系数的应用
正文
水分子扩散系数是指水分子在单位时间内，通过单位面积的膜的扩散通量与水分子浓度的比值。

这个系数是描述水分子在各种材料中的扩散能力的重要参数，其值越大，表示水分子在这些材料中的扩散速度越快。

测量水分子扩散系数的方法通常有几种，其中最常用的是使用膜渗透法。

在这个方法中，我们将水分子通过一个半透膜，然后测量水分子通过这个膜的时间。

通过这个时间，我们可以计算出水分子的扩散速度，从而得出水分子扩散系数。

水分子扩散系数的大小受到许多因素的影响，包括温度、压力、材料的性质以及水分子的浓度等。

一般来说，温度越高，水分子的扩散系数越大；压力越大，水分子的扩散系数也越大。

此外，材料的性质也会影响水分子的扩散系数，例如，一些材料可能对水分子有阻隔作用，从而降低水分子的扩散系数。

水分子扩散系数在许多领域都有应用，包括环境科学、生物医学和材料科学等。

第1页共1页。

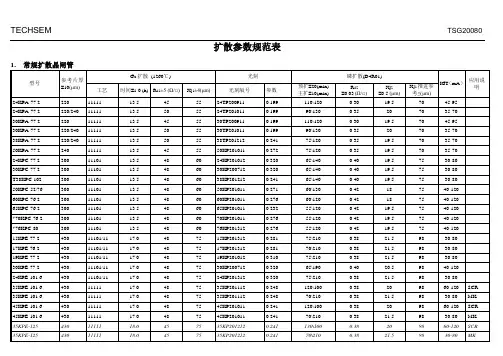
扩散参数规范表
4.整流管产品工艺代码：ZP-4
工艺代码：ZP-2
注：①上述标准有效期至2015年5月30日。

上述工艺参数供参考,其它按工艺文件要求执行。

有效期到后，更新版本或由副总工程师签字延期。

②参考时间应以设定中心值为准，如实际超出上述偏差时，经工程师确认，方可在公差范围内调整。

否则必须评审确定。

③镓扩散时间，不得随意调整。

如必须修正时，应由工程师确认，并附说明，指明磷扩散工艺时间参考。

④带*型号产品待试验验证，批量投入工程师指令流程。

拟制：审核：批准：
发放范围：晶圆制造部镓扩散（检验员共用）、磷扩散（检验员共用）各1份，共2份。

sd模型扩散参数-概述说明以及解释1.引言1.1 概述SD模型（System Dynamics Model）是一种用于模拟和研究动态系统行为的建模方法。

通过对系统内各个变量之间的关系进行建模，SD模型可以帮助我们更好地理解和预测系统的行为，从而为决策提供科学依据。

在SD模型中，扩散参数是一个重要的概念。

它描述了系统中物质、信息或者经济资源等在不同部分之间的流动程度。

换句话说，扩散参数可以理解为描述不同部分之间互相影响程度的量度。

在现实生活中，很多系统都可以通过SD模型来进行建模，比如生态系统、经济系统、社会系统等等。

而在这些系统中，扩散参数的选择和设定是至关重要的。

因为扩散参数的大小和影响程度将直接决定系统中各个部分之间的相互作用强度，从而对系统整体行为产生重要影响。

在编写SD模型时，我们需要通过实证研究或者专家经验来确定扩散参数的数值。

在实际操作中，常常会面临到参数求解的复杂性和不确定性。

因此，为了提高模型的可靠性和准确性，我们需要结合实际情况，合理选择和设定扩散参数，以使模型具有更好的描述和预测能力。

总之，扩散参数是SD模型中的一个重要概念，它描述了系统中不同部分之间的互相影响程度。

在建立SD模型时，正确选择和设定扩散参数是确保模型准确性和可靠性的关键步骤。

通过深入理解和运用扩散参数，我们可以更好地研究和分析系统的行为特征，为决策提供科学指导。

1.2 文章结构文章结构部分的内容包括对整篇文章的结构进行介绍和说明，让读者能够清晰了解文章的组织和内容布局。

下面是关于"文章结构"部分的内容示例：2. 文章结构本文按照以下结构进行组织和阐述。

首先，引言部分会提供一个概述，介绍本研究的背景和研究目的。

然后，正文部分将详细讨论SD模型的扩散参数，分为三个要点进行阐述。

最后，结论部分对文章进行总结，分析了研究结果的影响，并提出了一些建议。

引言部分旨在为读者提供对SD模型扩散参数的整体了解。

大气扩散模型参数符号解释
Us （Vs ）——烟气出口流速（m/s ）； Q H ——烟囱的热排放率（KJ 千焦），Q H 越高烟云抬升的浮力就越大，大多
数烟云抬升模式认为其中α=1/4～1，常取α为2/3；
D （d ）——烟气出口内径（m ）；
ū——烟囱出口处的平均风速（m/S ）；
T s ——烟囱出口温度（K ）；
T a ——环境大气温度（K ），取当地近5年平均值； t —气体扩散时间，气体由泄露源泄漏时刻t=0； x,y,z —以泄漏源为坐标原点，空间任意一点的坐标； C —空间中任一点的气体浓度；
k —气体扩散系数；
Q —气体由扩散源扩散时施放的气体总量；
μ--平均风速； σ--用浓度标准偏差表示y 轴上的扩散参数； H —气体扩散的有效高度； x —下风方向到泄漏点源的距离； y —侧风方向离泄漏源点的距离； z —垂直向上方向离泄漏源点的距离； l-距离泄漏源的距离； p 0－泄漏源的总浓度；
m-放射性气体排出的速度； s-放射性气体排除后向四周扩散的速度； α H Q ∝ ∆H。

液体扩散系数
液体扩散系数是一种量化了液体扩散形态与行为的参数。

它描述了液体在单位
高度变化时受到的动力效率，表示液体在不同状态下的流动性。

液体扩散系数的量化值可以帮助科学家以准确的速度和浓度来映射液体的流动性，从而实现对液体运动性的高效跟踪。

液体扩散系数最常用于分析液体的湮没趋势，如饮用水和油气的成层流动性以
及重金属的渗透性。

这个系数被用于描述液体如何通过外表面运动，以及液体渐变如何影响流动。

例如，特定类型气体体系中温度升高后，运动性会增加，液体扩散系数也会随之增加。

测量液体扩散系数，可以计算出它在特定体系中的运动性变化百分比。

进行液体扩散分析时需要对流动性能进行详细分析，以准确测量液体扩散系数，并利用这个数值更加精准的控制液体的流动性能。

随着互联网的发展，液体扩散系数的研究也得到了大幅度的推进。

越来越多的
科学家正探索如何利用液体扩散系数的力量来改善现有的液体技术。

例如，许多液体分析软件正在使用液体扩散系数，让实验人员可以更加精确的控制液体流动性能，作出更有效的调节。

在液体扩散系数在其中发挥作用的同时，新技术也可以让工程师以更快的速度进行持续分析和研究，从而推动液体的进步。

液体扩散系数是一个非常强大的参数，它可以有效地帮助科学家研究液体的流
动性，控制液体的行为，改善液体技术，并加速液体产业的发展。

在互联网的促进下，科学家也正逐渐发掘液体扩散系数所蕴含的潜力，以进一步让其服务于液体技术领域。

扩散系数和粘度的关系
扩散系数和粘度是液体流动过程中的两个重要参数。

扩散系数是描述液体中的分子扩散过程的参数，而粘度则是描述液体流动过程中的阻力的参数。

一般来说，扩散系数与粘度之间存在一定的关系，但是这种关系并不是十分显著。

在一般情况下，扩散系数随着粘度的升高而升高。

这是因为，当粘度升高时，液体流动的阻力也会升高，分子扩散过程就会变得更加困难。

但是，这种关系并不是线性的，而是呈指数级别的关系。

此外，扩散系数与粘度还可能存在其他的关系。

例如，在某些特定的温度范围内，扩散系数可能随着粘度的升高而降低。

这是因为在这个温度范围内，液体的分子运动可能会受到某些因素的限制，导致分子扩散速率降低。

另外，扩散系数和粘度之间的关系还可能受到液体的种类、浓度、温度等因素的影响。

因此，在研究扩散系数和粘度之间的关系时，需要注意这些因素的影响。

总的来说，扩散系数和粘度之间存在一定的关系，但是这种关系并不是十分明显，并且可能受到许多因素的影响。

因此，在研究扩散系数和粘度之间的关系时，需要注意这些因素的影响。

扩散过程；高方阻工艺；电池性能参数。

祝飞属于恒定表面浓度的扩散，浓度沿纵深的浓度分布为余误差型。

磷源在扩散温度下分解并沉积在硅面上向内部扩散。

此时表面浓度为P在Si中的固溶度，结深随时间逐渐推进，扩散层方阻随通源时间变小。

⏹停源再分布过程，理论上是恒定杂质总量的扩散，但实际上还需考虑到此时：硅面上还有已沉积但未扩散的磷；炉内仍有残留磷源；表面高磷浓度薄层被氧化为PSG。

这个过程中表面浓度可能会降低，结深继续向纵深推进，不排除方阻有逐渐变大的可能。

这有效降低了表面杂质复合中心，提高了表面少子寿命，增加了短波响应，从而有效的提高I SC和V OC，从而提高N cell。

⏹高方阻的问题：高方阻还意味着表面薄层电阻的明显增加，这将增大R S，降低FF。

所以高方阻工艺的关键是使得I SC和V OC的提高大于FF的损失。

⏹高方阻扩散要求：（1）保证方阻均匀性是一切的前提，其影响因素为：设备因素包括温度、尾气负压、排风；工艺因素包括预沉积氧化层的厚度、磷源浓度等。

要求极差值小于8，通过实验确定各参数。

（2）高方阻的扩散方案：原则是降低掺杂量，如降温、减小源的浓度等，但需配合diffusion time和drive in time的调整。

通过DOE（Desire of experiments）确定具体参数。

（3）在原有制程工艺上进行试生产，若看到I SC和V OC的提升，尤其是V OC的提高，则证明高方阻扩散成功。

⏹高方阻镀膜要求：（1）若表面钝化效果糟糕，则高方阻造成的I SC提升会因此而再次损失。

（2）为了配合高方阻对短波响应的提升，PECVD镀膜时要考虑对n和d做出调整，从而减少短波反射。

（3）用椭圆偏振光法（即椭偏仪）可以测量膜厚和折射率，本质是通过检测、分析入射光和反射光的偏振状态，是间接获得结果的一种非接触测量方法。

需DOE实验确定具体参数。

⏹高方阻印刷要求：按原有的印刷工艺，对N cell进行确认，若有提高，则只需调节烧结工艺；若没有提高或者提高很少，则需变更正电极网版的设计，原则一是“细线密栅”，二是不增加遮光面积。

用烟羽图象分析估算湍流和扩散参数用烟羽图象分析估算湍流和扩散参数本文通过对大型风洞中烟羽的瞬时和时间平均图象的分析,估算了下风向上的单粒子和双粒子扩散率.在图象法相同的风洞条件下.我们又对甲烷示踪气进行释放和采样,直接测得单粒子的扩散速率(即时间平均情形).用烟羽图象法估算和示踪法直接测量所得的扩散率之相关为09其均方根误差为7.6舾,实测与估算值之比的几何平均为1.09.利用单,双粒子扩散的估算值可以计算下列湍流参数;侧向风速方差&;,拉格朗B时间尺度,涡旋扩散率,涡旋耗散率e.以及掘风向湍强.以上诸参数值与流场直接测量值相当吻合.本文详缨介绍r泅羽图象方法,并表明这是一种准确,实用和经济的方法.一,引言在许多风洞和现场测试中,都希望不采用快速响应测风仪器或示踪气体采样的方法就能估算出湍流和扩散参数.在对于缺少电源和采样器难于布置的复杂地形区尤为如此.遇有这些情况下,采用烟羽法不仅可估算扩散参数,还能求得湍流参数.此法之所以实用,N0IJpo于1979,1980年早已加以阐述.其原理是:运用Gifford婀羽理论(1959),分析瞬时和时均烟流的冒像,可分别确定噼时及平均烟浇的扩散参数8翱.然后将扩散参数估计值仪入各种相应的湍泷参数公式,可得出湍流参数的储葬值.日"(1966)和Byzovaet口t(1970)己有过类似的做法.为了证实烟剐方法的准确性羊}1可用性, 1981年元月我们在美国国家环保局流休栏式组(子北卡研究三角带)的大型风洞中做了一次烟羽试验.这次试验的情况和特征详见Snydert979年文.本文介绍这个试验的结果和有关拉格朗B时间尺度f,侧向风速均方根值6,涡旋扩散率K,涡旋耗散率e和湍流强度i.二,实验方法本实验按以下顺序进行.首先在风洞内制造油雾烟流,甩并排安置在风洞侧面几米远的两个照相机摄影.一个相机用4分钟曝光,另一个在这4分钟内每隔15秒一次,以/60秽的速囊快拍,4分钟的时间是通过反复试验选完的,以产生在均匀照明条件下有清晰边界的平均烟羽图像.在风洞风速保持为1.Om/s,烟的释放速率维持不变条件下重复三次试验.图1显示了这些瞬时和时均烟羽照片的实例.然后以同样的风澜条件,在风洞中相同位置上释放甲烷示踪气体.利用火焰电离气相色谱仪顺烟羽中心线下风向几个不同距离处沿垂向测量甲烷的4分钟浓度分布.这些浓度值用来计算时均扩散参数Br…这是下标.意为观侧值.过些值可用以同时均烟羽图像分析求稼的扩散参数进行比较圈!典型的瞬间(z/6os)和时均(i丑n)魍羽影像此项试验后,用热膜探头对风漏内水平和垂直气流方向的风速进行详尽的测量.释放点砼的垂直和水平方向时均流速和湍强分别见图2和圈3.这些图表明在横剖面上的湍流近于均匀.图4显示了风洞轴向上的速度和湍强分布.湍强从源处(:0)的0.125皿遵tmt'sl图2风j胃内z=O,Y芒O处垂直方向上的风速与湍流强度分布图3风洞内源高70c111,x=O处侧风向水平剖面的风速与湍强分布圈4风漏内z兰70era.Y=O处风速与湍强沿轴线的分布蠢暑下降到可见烟流末端(x=an)的O.075处.端流在可见烟流长度中降低了约40西,这卑均匀湍流的假定有了矛盾.然而,可以接受这种假定下所得的结果.在下风向2'和4'处测得的欧拉单点风速自相关图形见瞬5依据B!]zova等人(1970)的方法,我们取欢拉^TDI.一Ma韶0='BnaIOIl2～一9涧'})图5下风向x=0,2和4m.Y兰O,z=70cm位置的自相关图时间尺度,为0.5f.,这里fo是自相关值首次达到负值经过的时间.估计的平均值为0.74秒.在=0处测得的侗风向速度的均方根值为9.1厘米-秒～.这些值将用来计算"观测舶湍流参数同时与用烟流分析法得到并在均匀湍流理论假定下导出的对应值进行比较.三,烟羽分析Gifford烟羽理论(195g)认为时均烟羽在下风向距离处的扩散参数.与时均烟流的几何形状有如下关系:蘸(1)其中z是可见烟羽的半宽度,z_是最大烟流半宽度,e是自然对数的底.该公式是在烟粒子的时均侧风向分布为高斯型,烟羽可见边缘为一条烟粒子积分视线浓度的等值线假定(Roberts,1923)下得到的.运用(1)式时,靠肉眼从图片上直接分辨烟羽可见边缘通常是困难的.尤其是在接近下风向末端时.为避免这个阊题,利用微密39^星N度计扫描图象底片,给出光学密度值作为离主轴的侧风向距离的函数下风向0.5和2处的扫描实例见图6()和6(&).用高斯分布检验这些数据,发现如果假定光学密度与可见烟粒子浓度的积分线成线性关系,则.酎风向的粒子分布的确是高斯型的.这就验证了烟流理论的第一个假定.用微密度计在离源0.25,0.51.0,2一和3.5处扫描结果的高斯分布图形见图7.这些曲线可由下式来表示:图6(a)对应于源后下风0.5米处的光学密度射面.实线为最佳拟台的高斯曲线EN图6(b)对应于源后下风向2米处的光学密度削面.实线为最佳拟台高斯曲线p=poe一./(2)其中p是光学密度.z是俱4风向距离,po是某一给定的下风向距离上最大光学密度, B是扩散参数.图7各种下风向距离处实舅光学密摩的高斯拟台寝1各种下风向置嵩的光学密度饲风商赞的塞斯参敷X(cm)P0即(七m)Zz(cm)z:E(cm)—__251.1885.653.94.8J500.91223.087.27.21O0O.614102.0812.311.11500.d90229.5914.013.72000.462249.6615.715.0_250099d16.3913.315.0L'3∞0.40,0,1'拈$9r乱7131r3500.385528.2712.311.1Ze是光学密度为0.30点处的垂向距离,ZE!是ZE的最小二秉估计值表1列出了p0和fJ随下风向距离变化的函数值.羽当拾定光学密度值p时,烟羽宽度zF可以(2)式得到.该步骤中作了光学密度线即是等积分烟流粒子浓度线的假定,这一假定类似于Robert的阻光定律,也是Gifford烟羽理论的第二假定(1959).以上分析中采用了随意选定的p值0.30,所得的z日值也同其平滑值z一起列在表1中,是由个满足z日的二次多项式得出.这里所用的二次式为:Z日=2.0+0.116一2.58x10—(3)该式可求得源的下风向2.25米处的最大半宽z,为15.13厘米.将上述z,和z值代入(1)式,求得o,把o的值与由甲烷示踪烟流实验的直接观铡的扩散值一同绘于图8.表2列出了a,和o.值,这里下标0表示观测值.图8中所显示的扩散观测值与计算值相当吻台.它们的相关系数为0.99,均方根误差为7.6嘧,D,a/a,的几何平均值为1.09.这些结果证实了Giffoocd(1959)的烟羽公式.§最曩垂图8烟羽分析和甲烷示踪气推求的单粒子扩散参散估计囊2扩做参量随下风向噩鼻变化囊x(cm)d晡口Z口1JOr252.21.51.6503.83.02.34.Il006.96.13.38.4I5010.37.96.612.420013.79.010.3l5.125016.59.513.6l7.230019.511.3l5.919.435021.910.3I9.321.7表中.l为沿烟羽轴线的瞬时扩散.口M为烟羽的弯曲程度,GT为烟羽的总扩散.aTO是甩甲烷示踪气实验得到的烟羽总扩散.以上数值的单位均为cm,平均风速为1=/s.如同我们在下一节将要见到的,拉格朗日时间尺度可由相对或瞬时的扩敲估计值D一来确定.a1值由一系列瞬时快照(1/6os)得到.而用微密度计扫描这些底片相当困难,所以这些瞬间烟羽快照的每一条中心线是用手工来数字化的,并将烟流中心线的方差o:作为下风向距离的函数来计算.这些值代表烟羽的弯曲程度.ar由下面的关系得到:a}=oi+D:(4)Df,D.和of的值列于表2.aJ和a,对应于xl构图形如图9所示.此图形类似于由大烟羽所得到的图形(Nappo,1980),并且清楚地表明在1O0和300厘米之间存在一个加速的相对扩散区域.图9表明,相对扩散与T3/2成正化.这与Batchelor的理论预澳j相一致.单粒子扩散在于r<时与成正比,这里是拉格朗日时间尺度.当扩散时间短的时候,Batchetor(1950)的相对扩散理论预测扩散与r成正比,这与图9所示的相接近.其间的差异是由于源处有直径约O.8厘米的烟粒子初始分离现象.下风嵯鼻(ciII1图9烟羽分析推求的单粒子和糨对的扩散参数四,结果扩散理论涉及到大气扩散对大气湍流的影响.如果能独立地估丝'那么同样的理论就可用于计笋堂叁邀由此可得以下结果,并综合于表3.41裹5用■羽圈象洼和直接风塌薯量采樽的赭藏参敢1.一向风速的均方根值.侧向风速分量的均方根值,0y,已由fo,扩散公式得到.即在短的扩散时闯内,符台以下公式:o}=oST(5)当用25厘米处的o值(表2)及相应的传输时问为0.25秒时,可计算出口为8.8cm/s. 如前所述的,的直接测量值为9.1cm/s.2.拉格朗日时间尺度}~Smitb改进的粒子扩散理论(1068)和Gfford~格朗日动力扩散理论,可以推出瞬时或相对的扩散参数a的同样的表达式, 即:o÷.盟(6)0【式中y用前面实验得到的值8.8cm/s,0r在25~m处的值见表2,的计算值为3.2秒.欧拉时间尺度fj由速度测量得到为0.74秒.采用关系或f一9,而中性条件下B一4,则的"观测值为3.0秒.3.涡旋扩散率涡旋扩散率数,由下列公式给出:K=a}(7)采用0y和的烟羽估算值.可确定出为248cm/s.用o和的实铡值得到的为250cm/s.4.涡旋耗散率￡Batcbelor(1952)用涡旋耗赦率e表示相对扩散参数a,采用以下公式:oi—c】sTS(8)这里c:=O.4.当传输时间取为3秒和口{值由表2为253cm,可求得B为23.4cm /s3.B~zova等人(197o)给出e的关系式为:8=oU(2c.)(9)这里C】一0.6,用a和的实测值,则可算出￡的观测值为23.Ocm/s.5.湍流强度由口/给定的湍流强度很容易从a的试验值计算得到,i=8.8晒.而由直接量铡得到一9.1嘶.五,结论上述结果表明,烟羽分析法是一种获取现场及实验室瞬问和时间平均大气扩散估算的准确,经济而有效的方法.运用均匀湍流扩散理论的结果,这些数据能估算出湍流参数值,而这些在其他情形下(例如在水里)是不容易得到的.这些工作是在美国国家海洋气象局和美国能源部的合作下完成的.如果没有美国国家环保局流体模式组RobertLawson和Ro—getThompsom的帮助,这项研究是无法进行的.特此致谢.参考文(略).宁奇伟译自~Atmospheric Environmont~V o.18.№.2, 1984.施鲁怀校。

溶质扩散系数
溶质扩散系数是描述溶质在溶体中传输的一个关键参数，它表示在只有扩散作用的情况下，溶质扩散的速率与浓度梯度的比值。

这个参数对于理解溶质在溶液中的行为，以及预测其在多孔介质中的迁移和扩散非常重要。

溶质扩散系数主要受溶质本身的性质影响，如分子量、分子尺寸、溶解度、扩散层厚度等。

此外，溶液的温度、压力、盐度、pH值等也会影响溶质的扩散系数。

在实际应用中，溶质扩散系数对于许多领域都非常重要，例如在化学反应工程、环境科学、石油工业、食品工业等领域的传质和传热过程中，都需要用到这个参数。

因此，对于这些领域的科学家和技术人员来说，了解和掌握溶质扩散系数的测量方法和影响因素是非常必要的。

大气扩散参数表格篇一：点源大气扩散模式计算参数点源大气扩散模式计算的参数选取邓新民【摘要】就实际环评工作中点源大气扩散模式计算参数选取的有关问题提出了一些新的看法。

关键词点源，扩散模式，参数中图法分类 X823PARAMETER SELECTION IN THE ATMOSPHERE DIFFUSION MODEL OF POINT SOURCEDeng Xinmin（Department of Meteorology，CIM）ABSTRACT Based on the actual environmental assessment，several methods on how to select parameters in the atmosphere diffusion model of point source are presented．Key Words Point source，Diffusion model，Parameters1 引言建设项目环境影响评价是我国环境保护的一项基本制度，大气环境影响评价是建设项目环境影响评价的重要内容，而大气环境影响预测与评价则是大气环境影响评价的重要内容或核心问题。

所谓大气环境影响预测与评价，就是计算或估计建设项目所排放的大气污染物在评价区域内对大气环境质量的影响。

在绝大多数情况下，影响预测采用模式计算的方法，通常用《环境影响评价技术导则大气环境》（HJ／T 2．2-93）（下称导则）推荐的模式或相关模式［1］。

环评实践表明，一般地讲，模式的选用通常是正确的，也符合建设项目实际。

因此，模式的参数选取是否恰当，就成为影响评价是否正确、是否符合实际的关键因素。

在我们看来，参数选取至少应满足以下条件：其一，满足计算公式本身所要求的条件；其二，参数的选取和计算结果要有典型性和代表性；其三，要符合实际情况。

但在实际的环评工作中，参数的选取或未引起足够注意，或存在这样那样问题。

大气扩散参数的计算
大气扩散参数的计算是指对于某一特定气体在大气中的传输过程，根据气象条件和物理参数计算出其在大气中扩散的程度以及扩散速度等参数。

这些参数包括气体浓度、风速、风向、大气稳定度、地形高度等，通过计算可以得到大气扩散模型，用于评估气体在大气中的扩散效果以及其对周围环境造成的影响。

大气扩散参数的计算在环境保护、工业污染治理等领域具有重要意义，可以辅助决策者制定科学、合理的环保政策和治理方案。

- 1 -。

横向扩散参数幂函数表达式数据随着信息时代的到来，我们生活中产生的数据越来越多。

为了更好地处理和分析这些数据，人们提出了各种数学模型和函数表达式。

其中，横向扩散参数幂函数表达式是一种常用的数学模型，它可以描述数据的扩散和传播规律。

横向扩散参数幂函数表达式是一种形式简单、计算方便的函数表达式。

它的一般形式为y = a * x^b，其中a和b是参数，x是自变量，y是因变量。

这个函数表达式可以用来描述各种数据的增长和传播规律，例如人口增长、病毒传播、信息扩散等。

我们来看一个实际的例子，以更好地理解横向扩散参数幂函数表达式。

假设有一种病毒在某个地区爆发，初始感染人数为100人，每天感染人数增加50%，那么感染人数的变化可以用横向扩散参数幂函数表达式来描述。

其中，a = 100，b = 0.5，x表示天数，y表示感染人数。

根据函数表达式y = 100 * x^0.5，我们可以计算出不同天数下的感染人数。

通过观察数据，我们可以发现感染人数以指数形式增长，呈现出横向扩散的特点。

横向扩散参数幂函数表达式在实际应用中具有广泛的用途。

以人口增长为例，人口增长可以用横向扩散参数幂函数表达式来描述。

在人口增长模型中，a表示初始人口数，b表示人口增长率，x表示时间，y表示人口数量。

根据国际经验，人口增长率通常在0.01到0.02之间。

通过调整参数a和b的值，我们可以预测未来几年甚至几十年的人口数量。

除了人口增长，横向扩散参数幂函数表达式还可以用来描述信息传播和市场扩张等现象。

以信息传播为例，假设有一条热点新闻，在发布后的第一天传播到1000人，每天传播人数增加50%，那么信息传播的规律可以用横向扩散参数幂函数表达式来描述。

其中，a = 1000，b = 0.5，x表示天数，y表示传播人数。

通过计算函数表达式y = 1000 * x^0.5，我们可以得到不同天数下的传播人数。

通过观察数据，我们可以发现传播人数也呈现出指数增长的趋势，符合横向扩散的特点。

稳定扩散参数数量级稳定扩散是指在一定条件下，系统内的某种物质或信息能够保持稳定地传播和扩散的现象。

在现实生活中，稳定扩散的例子比比皆是，比如空气中的气味、水中的颜色等。

而在科学研究和工程领域，稳定扩散更是一个重要的概念，它涉及到许多领域，如物理学、化学、生物学、地球科学等。

稳定扩散参数量级的研究和评估对于深入理解稳定扩散现象至关重要。

在了解稳定扩散参数量级之前，我们首先要了解什么是扩散。

扩散是指物质在不同浓度之间由高浓度向低浓度自发移动的过程。

这种移动是由于分子的热运动所引起的，是一种熵增的过程。

而稳定扩散则是指在一定条件下，扩散过程能够保持稳定和持续进行的现象。

稳定扩散参数量级的研究，就是希望能够找到一种方法或指标，来描述和评估系统中的稳定扩散现象。

稳定扩散的参数量级一般可以通过实验和理论计算相结合的方式来进行评估。

在实验方面，可以通过观察系统中物质浓度随时间和空间的变化规律来进行评估。

而在理论计算方面，可以通过建立数学模型和方程来描述扩散过程，并通过求解这些方程来得到稳定扩散的参数量级。

这些参数包括扩散系数、浓度梯度、扩散速率等。

在评估稳定扩散参数量级时，我们可以首先从简单的情况开始，比如一维扩散。

一维扩散是指物质只能沿着一个方向进行扩散，这样的情况下可以比较容易地得到稳定扩散参数的量级。

然后可以逐步引入更复杂的情况，比如二维和三维的扩散，以及非均匀介质中的扩散等。

这样逐步深入，可以更全面地理解稳定扩散参数量级的意义和应用。

总结回顾一下，稳定扩散参数量级的评估是一个重要且复杂的课题。

它涉及到实验观测、理论计算以及数学模型的建立等多个方面。

通过逐步从简到繁地探讨稳定扩散参数量级的评估方法，我们可以更加深入地理解稳定扩散现象。

在实际应用中，对于稳定扩散参数的合理评估，可以帮助我们更好地理解和预测系统中的扩散过程，为相关领域的研究和工程实践提供重要的参考。

个人观点和理解上，稳定扩散参数量级的评估是一个非常有挑战性和有价值的研究课题。