2014青岛一模数学理

山东省青岛市2014届高三4月统一质量检测考试理科数学试卷（带解析）1R ()C B = ）A ．{|01}x x ≤≤ BC【答案】A 【解析】R ()C B =考点：集合的运算,简单不等式的解法. 2．已知1i12ib a -=+） A【答案】A 【解析】考点：复数的四则运算，复数的相等.3） A【答案】D 【解析】考点：等差数列、等比数列.4为（）A【答案】D【解析】考点：正弦型函数，三角函数诱导公式.5）A【答案】C【解析】考点：直线与圆的位置关系，平面向量的坐标运算.6）A【答案】C【解析】考点：算法与程序框图7）A【答案】B【解析】考点：定积分，二项式定理.8．取值范围是（ ）A【答案】A 【解析】所示.考点：简单线性规划的应用，直线的斜率计算公式.9．则三棱锥的外接球的表面积为（ ）【答案】B【解析】所以，考点：垂直关系，球的表面积10．）【答案】B【解析】试题分析：由题意可得，是偶函数，考点：函数的奇偶性、周期性，函数的图象，函数的零点.11的焦点坐标为 . 【解析】考点：抛物线的几何性质.12最大为 .【答案】70【解析】试题分析：由已知，考点：回归直线方程及其应用13为 .【解析】43，3,>=考点：平面向量的数量积、夹角、模，平行四边形的面积.14．在某班进行的演讲比赛中，共有5位选手参加，其中.生不能连着出场，且女生甲不能排在第一个，那么出场顺序的排法种数为 .【答案】60【解析】试题分析：①若第一个出场的是男生，则第二个出场的是女生，以后的顺序任意排，方法有．考点：排列组合.15则甲是乙成立的充分不必要条件；④是表示双曲线”的充分必要条件．其中所有真命题的序号是 .【答案】①②④【解析】在区间1内有零点，即试题分析：函数2a2<对于②已知不相交，则甲⇒乙，反之，乙推不出甲，②是真命题；由以，成立；反之，.故答案为①②④.考点：充要条件，函数零点存在定理，绝对值不等式的性质，双曲线.16（1（2）已的三个内对的边分别若锐足【答案】（1（2【解析】试题分析：（1（2解得本题，巧妙地利用“整体观”.试题解析：（1分分分（2分分分分考点：三角函数式的化简，三角函数的性质，正弦、余弦定理的应用，三角形面积公式. 17的活（1（2）设其中来自【答案】（1【解析】试题分析：（1计算即得； （2解答本题，关键是概率的计算过程，综合应用事件的互斥、独立关系，避免各种情况的遗漏. 试题解析：（14分 （2分11分 分考点：古典概型，互斥事件、独立事件概率的计算，随机变量的分布列及数学期望..【答案】证明：（1）见解析；（2【解析】试题分析：证明：（1应用“向量法”解题；解答本题的关键是确定“垂直关系”，这也是难点所在，平时学习中，应特别注意转化意识的培养，能从“非规范几何体”，探索得到建立空间直角坐标系的条件.试题解析：证明：（1）连结和交于，连结，1分3分4分（2,AE AD A=ACBEF分1(0,1,2)=-分2(22,1,2=-分 12||||n n⋅分考点：直线与平面、平面与平面垂直，二面角的定义及计算，空间向量的应用.19．已知数的和，（1（2【答案】（1（2【解析】试题分析：（1准确判断；（2）由（1，计算等比数列的和。

青岛1中2013-2014学年度第一学期期末考试高三数学（理科）第Ⅰ卷（选择题 共60分）一、选择题1、已知复数z 满足(1)2i z +=，则z 等于（ ）A 、1i +B 、1i -C 、1i -+D 、1i --2、函数21112xy +⎛⎫= ⎪⎝⎭值域为（ ）A 、（—∞，1）B 、1,12⎛⎫ ⎪⎝⎭C 、1[,1)2D 、1[,)2+∞ 3、在棱长为2的正方体1111ABCD A B C D -中，点O 为底面ABCD 的中心，在正方体1111ABCD A B C D -内随机取一点P ，则点P 到点O 的距离大于1的概率为（ ）A 、12πB 、112π-C 、6πD 、16π- 4、若5250125(1)(1)(1)(1)x a a x a x a x +=+-+-++-，则0a 等于（ ） A 、32 B 、1 C 、—1 D 、—325、等差数列{}n a 满足：296a a a +=，则9S =（ ）A 、—2B 、0C 、1D 、26、设,a b R ∈，则()|sin |f x x x a b =++是奇函数的充要条件是（ ）A 、220a b +=B 、0ab =C 、0b a= D 、220a b -=7、要得到函数cos(2)3y x π=+的图像，只需将函数1sin 2cos 222y x x =+的图像（ ） A 、向左平移8π个单位 B 、向右平移8π个单位 C 、向右平移3π个单位 D 、向左平移4π个单位 8、抛物线22x y =和直线4y x =+所围成的封闭图形的面积是（ ）A 、16B 、18C 、20D 、229、圆22221x y +=与直线sin 10(,)2x y k k Z πθθπ+-=≠+∈的位置关系是（ ）A 、相离B 、相切C 、相交D 、不能确定10、已知函数(1)y f x =+是定义在R 上的偶函数，且()f x 在[1，+∞）上单调递减，则不等式(21)(2)f x f x ->+的解集为（ ）A 、{|3}x x <B 、1{|3}2x x <<C 、1{|3}3x x -<<D 、1{|3}3x x << 11、已知点P 是双曲线221169x y -=右支上一点，12F F 、分别为双曲线的左右焦点，I 为12PF F ∆的内心，若1212IPF IPF IF F S S S λ∆∆∆=+成立，则λ的值为（ ）A 、58 B 、45 C 、43 D 、3412、已知函数32()31f x x x =-+，21,0()468,0x x g x xx x x ⎧+>⎪=⎨⎪---≤⎩，关于方程[]()0g f x a -=（a 为正实数）的根的叙述有下列四个命题（ ）①存在实数a ，使得方程恰有3个不同的实根；②存在实数a ，使得方程恰有4个不同的实根；③存在实数a ，使得方程恰有5个不同的实根；④存在实数a ，使得方程恰有6个不同的实根；A 、0B 、1C 、2D 、3第Ⅱ卷（选择题 共60分）二、填空题13、设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，则((2))f f 的值为__________ 14、当实数,x y 满足约束条件0220x y x x y a ≥⎧⎪≤⎨⎪++≤⎩（a 为常数）时3z x y =+有最大值为12，则实数a 的值为_____________15、已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是_________cm ²16、过抛物线22(0)y px p =>的焦点F 的直线l 与抛物线在第一象限的交点为A ，与抛物线准线的交点为B ，点A 在抛物线准线上的射影为C ，若AF FB =，12BA BC ⋅=，则p 的值为_________三、解答题17、在ABC ∆中，角A 、B 、C 所对的边分别为a b c 、、，且1cos 4A =（1）求2sin cos 22B C A +-的值；（Ⅱ）若3a =，求bc 的最大值18、三棱柱111ABC A B C -，∠BCA=90°，AC=BC=2，1A 在底面ABC 上的射影恰为AC 的中点D ，又知11BA AC ⊥（1）求证：1AC ⊥平面1A BC（2）求锐二面角1A A B C --的余弦值19、某地发生特大地震并引发海啸，使当地的自来水受到了污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质，已知每投放质量为m 的药剂后，经过x 天该药剂在水中释放的浓度y （毫克/升）满足()y mf x =，其中2(04)4()6(4)2x x f x x x ⎧+<≤⎪⎪=⎨⎪>⎪-⎩，当药剂在水中释放的浓度不低于4（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于4（毫克/升）且不高于10（毫克/升）时，称为最佳净化（1）如果投放的药剂质量为6m =，试问自来水达到有效净化一共可持续几天？（2）如果投放的药剂质量为m ，为了使在6天（从投放药剂算起包括6天）之内的自来水达到最佳净化，试确定应该投放的药剂质量m 的范围20、已知函数2(),ax f x x e a R -=⋅∈（1）当1a =时，求()f x 的图像在1x =-处的切线方程；（2）讨论()f x 的单调性21、设数列{}n a 的前n 项和为n S ，已知1a a =，122,*n n n a S n N +=-∈（1）设2n n n b S =-，求数列{}n b 的通项公式（2）若1n n a a +≤，*n N ∈，求a 的取值范围22、已知椭圆2222:1(0)x y E a b a b+=>>的左右焦点分别为12F F 、，离心率2e =，点(0,1)D 在椭圆E 上（1）求椭圆E 的方程（2）设过点2F 且不与坐标轴垂直的直线交椭圆E 于A 、B 两点，线段AB 的垂直平分线与x 轴交于(,0)G t ，求点G 横坐标t 的取值范围（3）试用t 表示△GAB 的面积，并求△GAB 面积的最大值。

青岛市高三统一质量检测理科综合物理本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 15页。

满分 300分。

考试时间 150分钟。

答题前考生务必用 0.5毫米黑色签字将自己的姓名、座号、考生号、县区和科类填写在试卷和答题卡规定的位置。

考试结束后,将本试卷和答题卡一并交回。

第Ⅰ卷 (必做,共 107分注意事项:1.第Ⅰ卷共 20小题,共 107分。

2.每小题选出答案后,用 2B 铅笔把答题纸上对应题目的答案标号涂黑。

如需改动,用橡皮擦干净后,再选涂其他答案标号。

不涂在答题卡上,只答在试卷上无效。

二、选择题(共 7小题,在每小题所给出的四个选项中,有的只有一项选项正确,有的有多0分。

14C .着陆器着陆时的速度大约是 3.6m/sD .着陆器着陆后,对月面的压力是 2×104 N15.如图所示,截面为三角形的钢坯 A 、 B 叠放在汽车的水平底板上, 汽车底板和钢坯表面均粗糙, 以下说法正确的是A .汽车、钢坯都静止时,汽车底板对钢坯 A 有向左的静摩擦力B .汽车、钢坯都静止时,钢坯 A 对 B 无摩擦力作用C .汽车向左加速时,汽车与钢坯相对静止,钢坯 A 受到汽车底板对它的静摩擦力D .汽车向左启动前后,汽车与钢坯相对静止,钢坯 A 对 B 的弹力不变16.两个固定的等量异种点电荷所形成电场的等势面如图中虚线所示,一带电粒子以某一速度从图中 a 点进入电场,其运动轨迹为图中实线所示,若粒子只受静电力作用,则下列关于带电粒子的判断正确的是A .带正电B .速度先变大后变小C .电势能先变大后变小D .经过 b 点和 d 点时的速度大小相同17.如图所示为某住宅区的应急供电系统,由交流发电机和副线圈匝数可调的理想降压变压器组成.发电机中矩形线圈所围的面积为 S ,匝数为 N ,电阻不计,它可绕水平轴OO ′ 在磁感应强度为 B 的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接降压变压器,滑动触头 P 上下移动时可改变输出电压, R 0表示输电线的电阻.以线圈平面与磁场平行时为计时起点,下列判断正确的是A .若发电机线圈某时刻处于图示位置,变压器原线圈的电流瞬时值为零B .发电机线圈感应电动势的瞬时值表达式为e = NBSω sin ωtC .当用电量增加时,为使用户电压保持不变,滑动触头 P 应向上滑动D .当滑动触头 P 向下移动时,变压器原线圈两端的电压将升高18. 2013年 6月 13日 13时 18分, “神舟 10号”载人飞船成功与“天宫一号”目标飞行器交会对接. 如图所示, “天宫一号” 对接前从圆轨道Ⅰ变至圆轨道Ⅱ, 已知地球半径为 R , 轨道Ⅰ距地面高度 h 1,轨道Ⅱ距地面高度 h 2,则关于“天宫一号”的判断正确的是 A .调整前后线速度大小的比值为 21h R h R ++ B .调整前后周期的比值为 3231 ( (h R h R ++ C .调整前后向心加速度大小的比值为 (2221h R h R ++ D .需加速才能从轨道Ⅰ变至轨道Ⅱ 19.物体静止在水平地面上,在竖直向上的拉力 F 作用下向上运动.不计空气阻力,物体的机械能 E 与上升高度 h 的大小关系如图所示, 其中曲线上点 A 处的切线斜率最大, h 2 ~ h 3的图线为平行于横轴的直线.则下列判断正确的是123A .在 h 1 处物体所受的拉力最大B .在 h 2 处物体的速度最大C . h 2 ~ h 3过程中拉力的功率为零D . 0~ h2过程中物体的加速度先增大后减小20.如图,光滑斜面 PMNQ 的倾角为θ,斜面上放置一矩形导体线框 abcd ,其中 ab 边长为l 1, bc 边长为 l 2,线框质量为 m 、电阻为 R ,有界匀强磁场的磁感应强度为 B ,方向垂直于斜面向上, e f为磁场的边界,且 e f∥ MN .线框在恒力 F 作用下从静止开始运动,其 ab 边始终保持与底边 MN 平行, F 沿斜面向上且与斜面平行. 已知线框刚进入磁场时做匀速运动,则下列判断正确的是A .线框进入磁场前的加速度为 mm g F θsin - B .线框进入磁场时的速度为 212 sin (l B Rmg F θ-C .线框进入磁场时有a → b → c → d 方向的感应电流D .线框进入磁场的过程中产生的热量为(F − mg sin θ l 1第Ⅱ卷 (必做 157 分+选做 36分,共 193分注意事项:1.第Ⅱ卷共 18大题。

山东省2014青岛一模第二套语文 (2)英语 (10)数学(文科) (22)数学（理科） (30)文科综合 (39)理科综合 (55)高三自评试卷语 文本试卷分第Ⅰ卷和第Ⅱ卷两部分，共8页，满分150分。

考试时间150分钟。

考试结束后，将答题卡交回。

注意事项：1．答题前，考生务必用0.5毫米黑色签字笔将姓名、准考证号、县区和科类填写在答题卡和试卷规定的位臵上。

2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

答案不能答在试卷上。

3．第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位臵，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

第Ⅰ卷（共36分）一、（15分，每小题3分）1．下列词语中加点的字，读音全都正确的一项是A ．埋．怨（mán ） 果脯．（p ǔ） 盥．洗室（guàn ） 长吁．短叹（x ū） B ．角．逐（jué） 迸．发（bèng ） 狙．击手（j ū） 瓜熟蒂．落（tì） C ．择．菜（zhái ） 折．本（shé） 剖．腹产（p āo ） 因噎．废食（y ē） D ．湖泊．（p ō） 铜臭．（xiù） 入场券．（quàn ） 着．手成春（zhuó） 2.下列词语中，没有错别字的一组是A ．发轫 掉书袋 步入正轨 轻歌曼舞B ．泄秘 绵里针 趋之若鹜 天随人愿C ．临摹 壁上观 竹报平安 凭心而论D ．装潢 主旋律 稍纵既逝 一副春联3.下列各句中，加点词语使用正确的一句是A ．孔子带领弟子到处漂泊，甚至在陈国、蔡国的旷野荒郊饥饿彷徨，饱经艰险，虽然满腹经纶，却找不到安身之地，实在令人恻然．．鼻酸。

B ．一次偶然的机会,少年海涅在皇家花园的“叹息小径”上读到《堂吉诃德》，这次阅读为他打下了他精神世界的底子，导致．．他日后多次重读这部巨著。

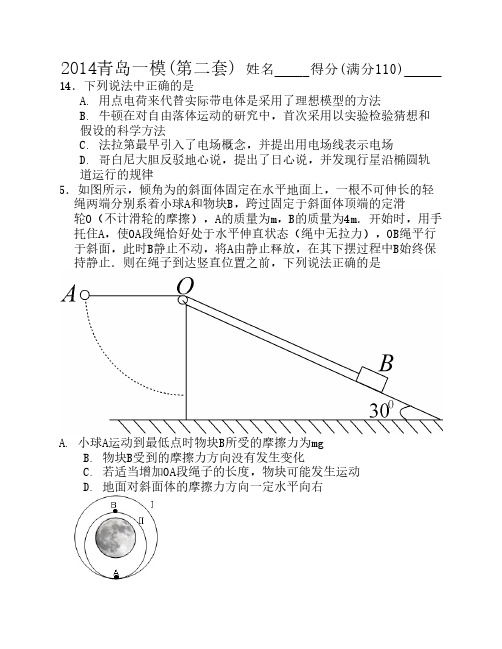
2014青岛一模(第二套) 姓名 得分(满分110) 14．下列说法中正确的是A. 用点电荷来代替实际带电体是采用了理想模型的方法B. 牛顿在对自由落体运动的研究中，首次采用以实验检验猜想和假设的科学方法C. 法拉第最早引入了电场概念，并提出用电场线表示电场D. 哥白尼大胆反驳地心说，提出了日心说，并发现行星沿椭圆轨道运行的规律15．如图所示，倾角为的斜面体固定在水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的定滑轮O（不计滑轮的摩擦），A的质量为m，B的质量为4m．开始时，用手托住A，使OA段绳恰好处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动，将A由静止释放，在其下摆过程中B始终保持静止．则在绳子到达竖直位置之前，下列说法正确的是A. 小球A运动到最低点时物块B所受的摩擦力为mgB. 物块B受到的摩擦力方向没有发生变化C. 若适当增加OA段绳子的长度，物块可能发生运动D. 地面对斜面体的摩擦力方向一定水平向右16．2013年12月6日17时47分，在北京飞控中心工作人员的精密控制下，嫦娥三号开始实施近月制动，进入100公里环月轨道Ⅰ，2013年12月10日晚21:20分左右，嫦娥三号探测器将再次变轨，从100公里的环月圆轨道Ⅰ，降低到近月点（B点）15公里、远月点（A点）100公里的椭圆轨道Ⅱ，为下一步月面软着陆做准备．关于嫦娥三号卫星下列说法正确的是A．卫星在轨道Ⅱ上A点的加速度小于在B点的加速度B．卫星沿轨道Ⅰ运动的过程中，卫星中的科考仪器处于失重状态C．卫星从轨道Ⅰ变轨到轨道Ⅱ，在A点应加速D．卫星在轨道Ⅱ经过A点时的动能小于在轨道Ⅱ经过B点时的动能17．用220V的正弦交流电通过理想变压器对一负载供电，变压器输出电压是380V，通过负载的电流图象如图所示，则A．变压器原线圈中电流的频率为50HzB．变压器的输入功率38WC．变压器原、副线圈的匝数比是19:11D．负载电流的函数表达式i=0.1sin50πt (A)18．如图所示，有一块无限大的原来不带电的金属平板MN，现将一个带电量为+Q的点电荷放置于板右侧，并使金属板接地；金属平板与电量为+Q的点电荷之间的空间电场分布与等量异种电荷之间的电场分布类似，则金属板MN为等势面且电势为零．已知BCDE在以电荷+Q为圆心的圆上，电荷+Q离金属板MN的距离AQ为d，B点为AQ的中点，则下列说法正确的是+QNMBCDEAA．C点和E点的场强相同B．B点的场强大于D点的场强C．D点电势低于零电势D．带负电点电荷在B点的电势能大于在D点电势能19．如图所示在粗糙的桌面上有一个质量为M的物块，通过轻绳跨过定滑轮与质量为m的小球相连，不计轻绳与滑轮间的摩擦，在小球下落的过程中，下列说法正确的是A．小球的机械能守恒B．物块与小球组成的系统机械能守恒C．若小球匀速下降，小球减少的重力势能等于物块M与桌面间摩擦产生的热量D．若小球加速下降，小球减少的机械能大于物块M与桌面间摩擦产生的热量1415161718192020．如图所示，在边长为L的正方形区域内有垂直于纸面向里的匀强磁场，有一带正电的电荷，从D点以v 0的速度沿DB方向射入磁场，恰好从A点射出，已知电荷的质量为m，带电量为q，不计电荷的重力，则下列说法正确的是A．匀强磁场的磁感应强度为 B ．电荷在磁场中运动的时间为C ．若电荷从CD 边界射出，随着入射速度的减小， 电荷在磁场中运动的时间会减小D ．若电荷的入射速度变为2v 0，则粒子会从AB中射出选择题得分21．（18分）（1）某同学验证动能定理的实验装置如图所示．水平桌面上固定一倾斜的气垫导轨；导轨上A点处有一带长方形遮光片的滑块，其总质量为M，左端由跨过轻质光滑定滑轮的细绳与一易拉罐相连，易拉罐和里面的细沙总质量为m；遮光片两条长边与导轨垂直；导轨上B点有一光电门，可以测量遮光片经过光电门时的挡光时间为t，d 表示遮光片的宽度，L表示A、B两点间的距离．滑块与导轨间没有摩擦，用g表示重力加速度．AB遮光片光电门Mm定滑轮L①该同学首先用游标卡尺测量了遮光片的宽度，如右图所示，遮光片的宽度d = cm．②该同学首先调整导轨倾角，易拉罐内盛上适量细沙，用轻绳通过滑轮连接在滑块上．让滑块恰好在A点静止．剪断细绳后，滑块开始加速下滑，则其受到的合外力为．③为验证从A →B过程中小车合外力做功与动能滑块变化的关系，需要验证的关系式为_______________________(用题目中所给的物理量符号表示)．（2）某同学为描绘某元件的伏安特性曲线，在实验室中做了以下实验：①用多用电表欧姆档粗略测量该元件的电阻，选用×10档，测量结果如图所示，则测得的电阻为Ω；②实验室中有如下器材：A．电流表A1(量程0.6 A，内阻约0.6Ω)B．电流表A2(量程30mA，内阻约2Ω)C．电压表V(量程3 V，内阻约3kΩ)D．滑动变阻器R1 (10Ω，0.3A)E．滑动变阻器R2 (1000Ω，0.1A)F．电源E (电动势3V，内阻约0.1Ω)UIⅠⅡOG．开关S及导线若干请同学们选择合适的仪器，在虚线框内画出实验电路图，要求闭合开关前滑动变阻器放置在合适位置；③如图中Ⅰ、Ⅱ图线，一条为元件真实的U—I图线，另一条是本次实验中测得的U—I图线，其中是本次实验中测得的图线．实验题得分 .22．（18分）如图所示，一质量为m的物块在与水平方向成θ的力F的作得分:用下从A点由 静止开始沿水平直轨道运动，到B点后撤去力F， 物体飞出后越过“壕沟”落在平台 EG段．已知物块的质量m=1kg，物块与水平直轨道间的动摩擦因数为μ=0.5，AB段长 L=10m，BE 的高度差h =0.8m，BE的水平距离 x =1.6m．若物块可看做质点，空气阻力不 计，g取10m/s2．（1）要越过壕沟，求物块在B点最小速度v的大小；（2）若θ=370，为使物块恰好越过“壕沟”，求拉力F的大小；（3）若θ大小不确定，为使物块恰好越过“壕沟”，求力F的最小值（结果可保留根号）．得分:23.（20分）如图所示，两条平行的金属导轨相距L = lm，金属导轨的倾斜部分与水平方向的夹角为37°，整个装置处在竖直向下的匀强磁场中．金属棒MN和PQ的质量均为m=0.2kg，电阻分别为R MN =1Ω和R PQ = 2Ω ．MN置于水平导轨上，与水平导轨间的动摩擦因数μ=0.5，PQ置于光滑的倾斜导轨上，两根金属棒均与导轨垂直且接触良好．从t=0时刻起，MN棒在水平外力F1的作用下由静止开始以a =1m/s2的加速度向右做匀加速直线运动，PQ则在平行于斜面方向的力F2作用下保持静止状态．t=3s时，PQ棒消耗的电功率为8W，不计导轨的电阻，水平导轨足够长，MN始终在水平导轨上运动．求：（1）磁感应强度B的大小；（2）t=0～3 s时间内通过MN棒的电荷量；（3）求t =6s时F2的大小和方向；（4）若改变F1的作用规律，使MN棒的运动速度v与位移s满足关系：，PQ棒仍然静止在倾斜轨道上．求MN棒从静止开始到s=5m的过程中，系统产生的热量．36.（12分）（1）（4分）下列各种说法中正确的是得分:A．物体吸收热量，内能一定增加B．液体与大气相接触，表面层内分子所受其他分子的作用表现为相互吸引C．判断物质是晶体还是非晶体，可以从该物质是否有规则的几何外形来判断D．气体的压强与单位体积内的分子数和温度有关（2）如图所示，有两个不计质量的活塞M、N将两部分理想气体封闭在绝热气缸内，温度均是270C．M活塞是导热的，N活塞是绝热的，均可沿气缸无摩擦地滑动，已知活塞的横截面积均为S=2cm2，初始时M活塞相对于底部的高度为Ｈ=27cm，N活塞相对于底部的高度为h=18cm．现将一质量为m=400g的小物体放在M活塞的上表面上，活塞下降．已知大气压强为p0=1.0×105Pa,①求下部分气体的压强多大；②现通过加热丝对下部分气体进行缓慢加热，使下部分气体的温度变为1270C，求稳定后活塞M、N距离底部的高度．2014青岛一模（第二套）一、选择题(全对6分，部分3分，错选0分)：14. AC 15. AD 16. ABD 17. A 18. BD 19. CD 20. A二、实验填空题21.(1) 1.14(3分) ②mg(2分) ③(3分)(2) ①130(3分) ② 如图(4分) ③Ⅰ(3分)二、非选择题：22.(18分)（1）解： ……. (2分)……. (1分) ……. (2分)（2） ……. (2分) a=0.8m/s2 ……. (1分)对物块受力分析，由牛顿第二定律可得：……. (2分)代入数据可得： F = 5.27N……. (1分)(3) 由数学知识可知： ……. (3分)代入数据得： …. (2分)23.(20分)解：（1） ……. (1分)……. (1分) …. (1分)……. (1分)代入数据得：B = 2T ………. (1分) (2) ……. (1分) ………. (2分)代入数据可得: q = 3C………. (1分)(3) ……. (1分) ……. (1分)……. (1分) ……. (1分)规定沿斜面向上为正方向，对PQ进行受力分析可得:代入数据：F2=-5.2N （负号说明力的方向沿斜面向下）………. (1分)（4）MN棒做变加速直线运动，当s=5m时，因为速度v与位移s成正比，所以电流I、安培力也与位移s成正比，安培力做功W安=-…………. (3分)36.解：（1）(4分) BD（2）(8分)①对两个活塞和重物作为整体进行受力分析得： ……. (2分) ………. (1分)②对下部分气体进行分析，由理想气体状态方程可得：………. (1分) 得：h2=20cm………. (1分)对上部分气体进行分析，根据玻意耳定律定律可得：…………………. (1分)得：L = 7.5cm …………………. (1分)故此时活塞M距离底端的距离为H2 = 20+7.5=27.5cm …………………. (1分).…………………. (3分)。

青岛市高三统一质量检测理科综合本试卷分第Ⅰ卷和第Ⅱ卷两部分，共15页。

满分300分。

考试时间150分钟。

答题前考生务必用0.5毫米黑色签字将自己的姓名、座号、考生号、县区和科类填写在试卷和答题卡规定的位置。

考试结束后，将本试卷和答题卡一并交回。

相对原子质量：H 1 C 12 N 14 O 16 S 32第Ⅰ卷（必做，共107分）注意事项：1．第Ⅰ卷共20小题，共107分。

2．每小题选出答案后，用2B铅笔把答题纸上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上无效。

一、选择题（共13小题，每小题5分，共65分。

每小题只有一项是符合题意。

）1．下列有关细胞结构和功能的叙述中，正确的是A．脱氧核糖核酸等大分子物质均可以通过核孔进入细胞质B．葡萄糖、乳酸、氨基酸依次是光合作用、细胞呼吸、基因表达的产物C．将有大液泡的植物细胞置于蔗糖溶液中不一定能发生质壁分离D．大肠杆菌的部分蛋白质在内质网上加工2．下列关于细胞生命历程的叙述，错误的是A．血红蛋白和生长激素的合成都能够体现“基因选择性表达”B．细胞凋亡可清除被病原体感染的细胞C．细胞的正常基因突变成为原癌基因是细胞癌变的原因D．衰老细胞核体积增大，物质运输的功能降低3．下列有关实验或调查的叙述，不正确的是A．研究遗传病发病率需在人群中随机抽样调查，研究遗传方式需分析患者家系系谱图B．统计显微镜下各期细胞数占计数细胞总数的比例，能比较细胞周期各期时间的长短C．选取经低温诱导的洋葱根尖制成的临时装片，在显微镜下观察不到联会现象D．加入无水乙醇越多，叶绿体色素提取液的绿色越深4．下面左图为某二倍体动物精原细胞分裂过程中细胞内的同源染色体对数的变化曲线，右图表示该动物的一个细胞分裂示意图。

下列叙述错误的是A．CD段含有4个染色体组，12个DNA分子B．FG段可发生基因重组C．若染色体②上有基因B，⑤的相同位点上有基因b，则其原因是在AB段发生了基因突变D．右图中细胞是次级精母细胞，处于曲线图的HI段5．下列有关生物进化的叙述正确的是A．从根本上讲，若没有突变，进化将不可能发生B．迁入、迁出不会造成种群基因频率的改变C．自然选择是定向的，而基因频率的改变是不定向的D．物种之间的共同进化都是通过物种之间的生存斗争实现的6．不同浓度的生长素影响某植物乙烯生成和成熟叶片脱落的实验结果如图所示。

理科数学 2013.12本试卷分第I 卷和第Ⅱ卷两部分，共4页。

满分150分。

考试时间120分钟。

考试结束后，将本试卷和答题卡—并交回。

注意事项：1．答题前，考生务必用0.5毫米黑色签字笔将姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。

2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．第II 卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、 修正带。

不按以上要求作答的答案无效。

4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。

参考公式：S 是锥体的底面积，，h 是锥体的高。

R 是球的半径。

第I 卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． (1)，则A B =(A){}|12x x << (B){}|12x x -<< (D){}|11x x -<< (2)若函数21,1()ln ,1x x f x x x ⎧+≤=⎨>⎩则(())f e （e 为自然对数的底数）=(A)0 (B)1 (C)2 (D)2ln(1)e +(3)已知α为第二象限角，且，则tan()πα+的值是(4)则“函数()x f x a =”在R 上是增函数”是“函数()ag x x =”“在(0,)+∞上是增函数”的(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件(5)(6)(7)的图象向右平移(0)m m >个单位长度后，所得到的图象关于 y m(8)设数列{}n a 是由正数组成的等比数列，n S 为其前n 项和，已知2431,7a a S == ，则5S =(A)(9)已知,,a b c R ∈，给出下列命题：①若a b >，则22ac bc >；②若ab ≠0，③若0,a b n N *>>∈，则n n a b >； ④若log 0(0,1)a b a a <>≠，则a ，b 中至少有一个大于1．其中真命题的个数为 (A)2 (B)3 (C)4 (D)1 (10)已知某几何体的三视图如右图所示，其中，主（正）视图， 左（侧）视图均是由直角三角形与半圆构成，俯视图由圆 与内接直角三角形构成，根据图中的数据可得此几何体的体积为( )(B)(C)(A) (B) (C) (D)(11)若ABC ∆外接圆的半径为1，圆心为O ．且，则CA CB 等于(D)3 (12)设函数[)()1,,1,f x n x n n n N =-∈+∈，则方程2()log f x x =的根有(A)1个 (B) 2个 (C)3个 (D)无数个第II 卷（共90分）二、填空题：本大题共4小题，每小题4分，共16分．(13)已知向量(1,2)a =，向量(,2)b x -，且()a a b ⊥-，则实数x 等于______________.． ，若目标函数(0,0)z abx y a b =+>> 的最大值为8，则a+b 的最小值为_____________．(16)若二次函数2()(0)f x ax bx c a =++≠的图象和直线y=x 无交点，现有下列结论： ①方程[()]f f x x =一定没有实数根；②若a>0，则不等式[()]f f x x >对一切实数x 都成立； ③若a<0，则必存在实数0x ，使00[()]f f x x >;④函数2()(0)g x ax bx c a =-+≠的图象与直线y=-x 一定没有交点，其中正确的结论是____________（写出所有正确结论的编号）． 三、解答题：本大题共6小题，共74分． (17)（本小题满分12分）在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且角A 、B 、C 成等差教列． ( I)c 的值； ( II)设sin sin t A C =，求f 的最大值． (18)（本小题满分12分）已知函数()22,xxf x k k R -=+∈ . ( I)若函数()f x 为奇函数，求实数k 的值；( II)若对任意的[)0,x ∈+∞，都有()2xf x ->成立，求实数k 的取值范围．(19)（本小题满分12分）在四棱锥P-ABCD 中，侧面PCD ⊥底面ABCD ，PD ⊥CD ，底面ABCD 是直角梯形，AB ∥DC ，90,1,2ADC AB AD PD CD ∠===== ADC -900,AB= AD= PD=1.CD=2.(I)求证：BC ⊥平面PBD ：(II)设E 为侧棱PC 上异于端点的一点，PE PC λ=，试确定λ的值，使得二面角E-BD -P 的大小为45 ．(20)（本小题满分12分）已知等差数列{}n a 满足：11(),1n n a a n N a *+>∈=，该数列的前三项分别加上l ，l ，3后顺次成为等比数列{}n b 的前三项． (I)求数列{}n a ，{}n b 的通项公式； ( II)求c 的最小值．(21)（本小题满分13分）某建筑公司要在一块宽大的矩形地面（如图所示）上进 行开发建设，阴影部分为一公共设施不能建设开发，且要求 用栏栅隔开（栏栅要求在直线上），公共设施边界为曲线 2()1(0)f x ax a =->的一部分，栏栅与矩形区域的边界交于点M 、N ，切曲线于点P ，设(,())P t f t ．( I)将OMN ∆（O 为坐标原点）的面积S 表示成f 的函数S(t)； (II)S(t)取得最小值，求此时a 的值及S(t)的最小值．(22)（本小题满分13分）已知函数()ln r x x =，函数 ( I)试求f (x)的单调区间。

2014年山东省青岛市初中学业水平考试数学模拟试题（一）（考试时间：90分钟；满分：120分）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！一、选择题（本题满分24分，共有8道小题，每小题3分）下列每小题四个结论，中只有一个是正确的．不选、选错或选出的标号超过一个的不得分．1、如果□×1)52(=-，则□内应填的实数是（ ）A 、52 B 、25 C 、25- D 、52-2、如右图所示零件的左视图是（ ）A B C D3、下列图形中，既不是轴对称图形，又不是中心对称图形的是（ ）A BC D4、青岛市深入实施环境污染整治，全市经济开发区的40家化工企业中已关停，整改32家，每年排放的污水减少了167 000吨．将167 000用科学记数法且保留两个有效数字表示为（ ）A 、1.6×105B 、1.7×105C 、1.70×105D 、0.17×106则这15名同学每天使用零花钱的众数和中位数分别是（ ）A 、3，3B 、2，3 C 、2，2 D 、3，56、如图，现有一圆心角为90°，半径为8cm 的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（ ）A 、4cmB 、3cmC 、2cmD 、1cm7、反比例函数x y 6=与xy 3=在第一象限的图像如右图所示，作一条平行于x 轴的直线分别交双曲线与A、B ，连接OA 、OB ，则△AOB 的面积为（ ）A 、23B 、2C 、3D 、18、如图，在平面直角坐标系中，对△ABC 进行循环往复的轴对称或中心对称变换，若原来点A 坐标是（a ，b ），则经过第2011次变换后所得的A 点坐标是（ ）A 、（a ，b ）B 、（a ，—b ）C 、（—a ，b ）D 、（—a ，—b ）二、填空题（本题满分18分，共有6道小题，每小题3分）9、计算：__________212)3(|2|0=+---π 10、某城市在一次关于城市规划的民意调查中，从全部300万市民中随机调查了20000人，其中15000人同意此方案，则由此可以估计该城市中同意此方案的人大约有________万人11、某城市居民最低生活保障在2009年是240元，经过连续两年的增加，到2011年提高到345.6元，则该城市两年最低生活保障的平均年增长率是_________ 12、如图，△ABC 内接于圆O ，AC 是圆O 的直径，∠ACB=50°，点D 是弧BAC 上一点，则∠D=_____________13、如图，在Rt △ABC 中，∠ACB=90°，∠A=30°，BC=2．将△ABC 绕点C 按顺时针方向旋转n 度后得到△EDC ，此时点D 在AB 边上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积分别为_______________ 14、如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△112C D B 的面积为1S ，△223C D B 的面积为2S ，…，△n n n C D B 1+的面积为n S ，则________=n S 。

2014年山东省青岛市高考数学一模试卷（理科）一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 若集合A ＝{x|0≤x ≤2}，B ＝{x|x 2>1}，则A ∩B ＝（ ）A {x|0≤x ≤1}B {x|x >0或x <−1}C {x|1<x ≤2}D {x|0<x ≤2} 2. 已知向量a →=(−1,2)，b →=(3, m)，m ∈R ，则“m =−6”是“a → // (a →+b →)”的（ ） A 充要条件 B 充分不必要条件 C 必要不充分条件 D 既不充分也不必要条件 3. 如图是一容量为100的样本的重量的频率分布直方图，则由图可估计样本重量的中位数为( )A 11B 11.5C 12D 12.5 4. 双曲线x 24−y 25=1的渐近线方程为( )A y =±√52x B y =±2√55x C y =±54x D y =±32x5. 执行如图所示的程序框图，则输出的结果是（ ）A 5B 7C 9D 116. 函数y =2cos 2(x +π2)图象的一条对称轴方程可以为（ ）A x =π4B x =π3C x =34π D x =π7. 过点P(1, √3)作圆O:x 2+y 2=1的两条切线，切点分别为A 和B ，则弦长|AB|=( ) A √3 B 2 C √2 D 48. 已知实数x ，y 满足约束条件{x >04x +3y ≤4y ≥0，则w =y+1x 的最小值是（ ）A −2B 2C −1D 19. 由曲线xy =1，直线y =x ，y =3所围成的平面图形的面积为（ ） A 329 B 2−ln3 C 4+ln3 D 4−ln310. 在实数集R 中定义一种运算“*”，对任意a ，b ∈R ，a ∗b 为唯一确定的实数，且具有性质：(1)对任意a ∈R ，a ∗0=a ；(2)对任意a ，b ∈R ，a ∗b =ab +(a ∗0)+(b ∗0)． 关于函数f(x)=(e x )∗1e x的性质，有如下说法：①函数f(x)的最小值为3；②函数f(x)为偶函数；③函数f(x)的单调递增区间为(−∞, 0]． 其中所有正确说法的个数为（ ） A 0 B 1 C 2 D 3二、填空题：本大题共5小题，每小题5分，共25分． 11. 已知a+2i i=b +i(a, b ∈R)，其中i 为虚数单位，则a +b ＝________．12. 已知随机变量ξ服从正态分布N(0, 1)，若P(ξ>1)=a ，a 为常数，则P(−1≤ξ≤0)=________． 13. 二项式(x +1x 2)6的展开式中，常数项为________． 14. 如图所示是一个四棱锥的三视图，则该几何体的体积为________；15. 已知函数f(x)={−x 2+x ，x ≤1，log 13x ，x >1，g(x)=|x −k|+|x −1|，若对任意的x 1，x 2∈R ，都有f(x 1)≤g(x 2)成立，则实数k 的取值范围为________．三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤.16. 在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且2cosAcosC(tanAtanC −1)=1． （1）求B 的大小； （2）若a +c =3√32，b =√3，求△ABC 的面积．17. 2013年6月“神舟”发射成功．这次发射过程共有四个值得关注的环节，即发射、实验、授课、返回．据统计，由于时间关系，某班每位同学收看这四个环节的直播的概率分别为34、13、12、23，并且各个环节的直播收看互不影响．（1）现有该班甲、乙、丙三名同学，求这3名同学至少有2名同学收看发射直播的概率； （2）若用X 表示该班某一位同学收看的环节数，求X 的分布列与期望．18. 如图几何体中，四边形ABCD 为矩形，AB =2BC =4，BF =CF =AE =DE ，EF =2，EF // AB ，AF ⊥CF ． （1）若G 为FC 的中点，证明：AF // 面BDG ； （2）求二面角A −BF −C 的余弦值．19. 已知{a n }是等差数列，首项a 1=3，前n 项和为S n ．令c n =(−1)n S n (n ∈N ∗)，{c n }的前20项和T 20=330．数列{b n }是公比为q 的等比数列，前n 项和为W n ，且b 1=2，q 3=a 9． （I ）求数列{a n }、{b n }的通项公式；（II ）证明：(3n +1)W n ≥nW n+1(n ∈N ∗)． 20. 已知椭圆C 1的中心为原点O ，离心率e =√22，其一个焦点在抛物线C 2:y 2=2px 的准线上，若抛物线C 2与直线l ：x −y +√2=0相切．（1）求该椭圆的标准方程；（2）当点Q(u, v)在椭圆C 1上运动时，设动点P(2v −u, u +v)的运动轨迹为C 3．若点T 满足：OT →=MN →+2OM →+ON →，其中M ，N 是C 3上的点，直线OM 与ON 的斜率之积为−12，试说明：是否存在两个定点F 1，F 2，使得|TF 1|+|TF 2|为定值？若存在，求F 1，F 2的坐标；若不存在，说明理由．21. 已知函数f(x)=ax +lnx ，函数g(x)的导函数g′(x)=e x ，且g(0)g′(1)=e ，其中e 为自然对数的底数． （1）求f(x)的极值；（2）若∃x ∈(0, +∞)，使得不等式g(x)<√x成立，试求实数m 的取值范围；（3）当a =0时，对于∀x ∈(0, +∞)，求证：f(x)<g(x)−2．2014年山东省青岛市高考数学一模试卷（理科）答案1. C2. A3. C4. A5. C6. D7. A8. D9. D 10. C11. 1 12. 12−a13. 15 14. 415. k ≤34或k ≥5416. 解：（1）由2cosAcosC(tanAtanC −1)=1得：2cosAcosC(sinAsinCcosAcosC −1)=1， ∴ 2(sinAsinC −cosAcosC)=1，即cos(A +C)=−12， ∴ cosB =−cos(A +C)=12，又0<B <π， ∴ B =π3；（2）由余弦定理得：cosB =a 2+c 2−b 22ac=12，∴(a+c)2−2ac−b 22ac=12， 又a +c =3√32，b =√3，∴274−2ac −3=ac ，即ac =54，∴ S △ABC =12acsinB =12×54×√32=5√316． 17. 解：（1）设“这3名同学至少有2名同学收看发射直播”为事件A ，则P(A)=C 32(34)2×(1−34)+C 33(34)3=2732．…（2）由条件可知X 可能取值为0，1，2，3，4． P(X =0)=(1−34)×(1−13)×(1−12)×(1−23)=136；P(X =1)=34×(1−13)×(1−12)×(1−23)+(1−34)×13×(1−12)×(1−23)+(1−34)×(1−13)×12×(1−23)+(1−34)×(1−13)×(1−12)×23=1372；P(X =2)=34×13×(1−12)×(1−23)++(1−34)×13×12×(1−23)+(1−34)P(X =4)=34×13×12×23=112；∴ X 的分布列X 的期望E(X)=0×136+1×1372+2×718+3×2372+4×112=94．…18. （1）证明：连接AC 交BD 于O 点，则O 为AC 的中点， 连接OG ，因为点G 为FC 中点，所以OG 为△AFC 的中位线， 所以OG // AF…∵ AF ⊄面BDG ，OG ⊂面BDG ， 所以AF // 面BDG ．…（2）解：取AD 中点M ，BC 的中点Q ，连接MQ ， 则MQ // AB // EF ，所以MQFE 共面，作FP ⊥MQ 于P ，EN ⊥MQ 于N ，则EN // FP 且EN =FP ， ∵ AE =DE =BF =CF ，AD =BC ，∴ △ADE 和△BCF 全等， ∴ EM =FQ ，∴ △ENM 和△FPQ 全等，∴ MN =PQ =1∵ BF =CF ，Q 为BC 中点，∴ BC ⊥FQ ， 又BC ⊥MQ ，FQ ∩MQ =Q ，∴ BC ⊥面MQFE ， ∴ PF ⊥BC ，∴ PF ⊥面ABCD ，…以P 为原点，PF 为z 轴建立空间直角坐标系如图所示， 则A(3, 1, 0)，B(−1, 1, 0)，C(−1, −1, 0)， 设F(0, 0, ℎ)，则AF →=(−3,−1,ℎ)，CF →=(1,1,ℎ)， ∵ AF ⊥CF ，∴ AF →⋅CF →=0⇒−3−1+ℎ2=0⇒ℎ=2 设面ABF 的法向量n 1→=(x 1,y 1,z 1)， ∵ AF →=(−3,−1,2)，BF →=(1,−1,2)∴ 由{n 1→⋅BF →=0˙⇒{−3x 1−y 1+2z 1=0x 1−y 1+2z 1=0，令z 1=1，得n 1→=(0,2,1)… 设面CBF 的法向量n 2→=(x 2,y 2,z 2)， ∵ BF →=(1,−1,2)，BC →=(0,−2,0)，∴ 由{n 2→⋅BC →=0˙⇒{x 2−y 2+2z 2=0−2y 2=0，令z 2=1，得n 2→=(−2,0,1)…∴ cos <n 1→，n 2→>=|n 1→|⋅|n 2→|˙=√5×√5=15设二面角A −BF −C 的平面角为θ，则cosθ=cos(π−<n 1→，n 2→>)=−cos <n 1→，n 2→>=−15．…19. （I ）解：设等差数列的公差为d ，∵ c n =(−1)n S n ， ∴ T 20=−S 1+S 2−S 3+S 4+...+S 20=330， ∴ a 2+a 4+a 6+...+a 20=330， ∴ 10(3+d)+10×92×2d =330，解得d =3，∴ a n =3+3(n −1)=3n ，… ∴ q 3=a 9=27，q =3， ∴ b n =2⋅3n−1．… （II ）证明：由(I)知，W n =2(1−3n )1−3=3n −1，要证(3n +1)W n ≥nW n+1，只需证(3n +1)(3n −1)≥n(3n+1−1)， 即证：3n ≥2n +1．… 当n =1时，3n =2n +1，下面用数学归纳法证明：当n ≥2时，3n >2n +1，（1）当n =2时，左边=9，右边=5，左>右，不等式成立， （2）假设n =k(k ≥2)，3k >2k +1，则n =k +1时，3k+1=3×3k >3(2k +1)=6k +3>2(k +1)+1， ∴ n =k +1时不等式成立． 根据（1）（2）可知：当n ≥2时，3n >2n +1， 综上可知：3n ≥2n +1对于n ∈N ∗成立，∴ (3n +1)W n ≥nW n+1(n ∈N ∗)．…20. 解：（1）由{y 2=2pxx −y +√2=0⇒y 2−2py +2√2p =0，∵ 抛物线C 2:y 2=2px 与直线l ：x −y +√2=0相切， ∴ △=4p 2−8√2p =0⇒p =2√2…∴ 抛物线C 2的方程为：y 2=4√2x ，其准线方程为：x =−√2， ∴ c =√2． ∵ 离心率e =√22， ∴ e =ca =√22， ∴ a =2，b 2=a 2−c 2=2， 故椭圆的标准方程为x 24+y 22=1．…（2）设M(x 1, y 1)，N(x 2, y 2)，P(x ′, y ′)，T(x, y) 则{x′=2v −uy′=u +v ⇒{u =13(2y′−x′)v =13(x′+y′)，∵ 当点Q(u, v)在椭圆C 1上运动时，动点P(2v −u, u +v)的运动轨迹C 3， ∴ u 24+v 22=1⇒[13(2y′−x′)]2+2[13(x′+y′)]2=4，∴ x ′2+2y ′2=12，∴ C 3的轨迹方程为：x 2+2y 2=12…由OT →=MN →+2OM →+ON →得(x, y)=(x 2−x 1, y 2−y 1)+2(x 1, y 1)+(x 2, y 2)=(x 1+2x 2, y 1+2y 2)，∴ x =x 1+2x 2，y =y 1+2y 2．设k OM ，k ON 分别为直线OM ，ON 的斜率，由题设条件知k OM ⋅k ON =y 1y 2x 1x 2=−12，因此x 1x 2+2y 1y 2=0，…∵ 点M ，N 在椭圆x 2+2y 2=12上，∴ x 12+2y 12=12，x 22+2y 22=12，故x 2+2y 2=(x 12+4x 22+4x 1x 2)+2(y 12+4y 22+4y 1y 2)=(x 12+2y 12)+4(x 22+2y 22)+4(x 1x 2+2y 1y 2)=60+4(x 1x 2+2y 1y 2)．∴ x 2+2y 2=60，从而可知：T 点是椭圆x 260+y 230=1上的点，∴ 存在两个定点F 1，F 2，且为椭圆x 260+y 230=1的两个焦点，使得|TF 1|+|TF 2|为定值，其坐标为F 1(−√30,0)，F 2(√30,0)． …21. 解：（1） 函数f(x)的定义域为(0, +∞)，f′(x)=a +1x (x >0)． 当a ≥0时，f ′(x)>0，∴ f(x)在(0, +∞)上为增函数，f(x)没有极值； 当a <0时，f′(x)=a(x+1a)x，若x ∈(0,−1a)时，f ′(x)>0；若x ∈(−1a，+∞)时，f ′(x)<0， ∴ f(x)存在极大值，且当x =−1a 时，f(x)极大=f(−1a )=ln(−1a )−1；综上可知：当a ≥0时，f(x)没有极值；当a <0时，f(x)存在极大值，且当x =−1a 时，f(x)极大=f(−1a )=ln(−1a )−1； （2）∵ 函数g(x)的导函数g ′(x)=e x ， ∴ g(x)=e x +c ， 又∵ g(0)g ′(1)=e ，∴ (1+c)e =e ⇒c =0，∴ g(x)=e x ， ∵ ∃x ∈(0, +∞)，使得不等式g(x)<√x成立，∴ ∃x ∈(0, +∞)，使得m <x −e x √x +3成立，令ℎ(x)=x −e x √x +3，则问题可转化为：m <ℎ(x)max ，对于ℎ(x)=x −e x √x +3，x ∈(0, +∞)，由于ℎ′(x)=1−e x (√x 2√x )，当x∈(0, +∞)时，∵ e x>1，√x+2√x ≥2√√x2√x=√2，∴ e x(√x2√x)>1，∴ ℎ′(x)<0，从而ℎ(x)在(0, +∞)上为减函数，∴ ℎ(x)<ℎ(0)=3，∴ m<3；（3）当a=0时，f(x)=lnx，令φ(x)=g(x)−f(x)−2，则φ(x)=e x−lnx−2，∴ φ′(x)=e x−1x，且φ′(x)在(0, +∞)上为增函数，设φ′(x)=0的根为x=t，则e t=1t，即t=e−t，∵ 当x∈(0, t)时，φ′(x)<0，φ(x)在(0, t)上为减函数；当x∈(t, +∞)时，φ′(x)>0，φ(x)在(t, +∞)上为增函数，∴ φ(x)min=φ(t)=e t−lnt−2=e t−lne−t−2=e t+t−2，∵ φ′(1)=e−1>0，φ′(12)=√e−2<0，∴ t∈(12，1)，由于φ(t)=e t+t−2在t∈(12，1)上为增函数，∴ φ(x)min=φ(t)=e t+t−2>e12+12−2>√2.25+12−2=0，∴ f(x)<g(x)−2．。

青岛市第一学期学分认定考试高三数学（理）试题2014.01本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分.共150分.考试时间120分钟. 注意事项：1.用0.5毫米黑色签字笔（中性笔）将有关信息填在答题卡规定的位置上，按要求贴好条形码.2.第I 卷答案请用2B 铅笔把答题纸上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试题卷上.3.第II 卷必须用0.5毫米黑色签字笔（中性笔）作答，答案必须写在答题纸各题目指定区域；如需改动，先划掉原来的解答，然后再写上新的解答；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.参考公式：2341=4==;=33S R V R V S h V S h ππ球球锥体底柱体底；；第I 卷（选择题 共60分）一、选择题：本题共12小题，每小题5分，共60分；在每小题给出的四个选项中只有一个是符合题目要求的.1.设集合{}{}{}24=lg 1x A x R B x R y x =∈≤∈=-，集合，则下列说法正确的是 A.[]1,2A B ⋂= B.()()102U U x C A C B x R x ⎧-⎫⋃=∈≥⎨⎬-⎩⎭C.()(],1U A C B ⋃==-∞D.()U C A B B ⋂= 2.已知命题22:2:23p x R q a y x ax ∃∈===-+；命题是函数在区间[)1,+∞递增的充分但不必要条件.给出下列结论：①命题“p q ∧”是真命题；②命题“p q ⌝∧”是真命题；③命题“p q ⌝∨”是真命题；④命题“p q ∨⌝”是假命题 其中正确说法的序号是A.②④B.②③C.②③④D.①②③④3.已知()()41,3,log a 2a b a b b =-=-⊥，若，则向量a b 与的夹角是A.60B.30C.120D.150 4.设变量,x y 满足约束条件22x y x x y ≤⎧⎪≤⎨⎪+≥⎩则目标函数2z x y =+的最小值为A.6B.4C.3D.25.函数()ln 1f x x =-的图象大致形状是6.函数()()sin 0,2f x A x A πωϕϕ⎛⎫=+>< ⎪⎝⎭其中的图象如图所示，为了得到()sin3g x x =的图象，只需将()f x 的图象A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 7.函数()()2113x m f x --+⎛⎫= ⎪⎝⎭的单调增区间与值域相同，则实数m 的取值为A.13B.3C.1-D.18.若,αβ为两个不同的平面，m ，n 为不同直线，下列推理:①若,,,m n m n αβαβ⊥⊥⊥⊥则直线；②若直线//m n m n αβ⊥⊥平面，直线直线，则直线平面；③若直线m//n ，,m n αβαβ⊥⊂⊥，则平面平面；④若平面//,m n m αββα⊥⊂⊥平面，直线平面，则直线直线n ；其中正确说法的序号是A.②③④B.①③④C.①②③④D.①②④ 9.以抛物线220y x =的焦点为圆心，且与双曲线221169x y -=两条渐近线都相切的圆的方程为A.2220640x y x +-+=B.2220360x y x +-+=C.2210160x y x +-+=D.221090x y x +-+=10.已知()621ax+（a 是正整数）的展开式中，8x 的系数小于120，则实数a 的值为 A.4 B.3 C.2 D.1 11.若在区间()1,1-内任取实数a ，在区间（0，1）内任取实数b ，则直线()()220121ax by x y -=-+-=与圆相交的概率为 A.38 B.516 C.58 D.31612.设函数()f x 的定义域为R ，()0111103xx x f x x R x ≤≤⎧⎪=∈⎨⎛⎫--≤<⎪⎪⎝⎭⎩，且对任意的都有()()11f x f x +=-，若在区间[]()()1,5g x f x mx m -=--上函数，恰有6个不同零点，则实数m 的取值范围是 A.11,46⎛⎤⎥⎝⎦ B.11,34⎛⎤ ⎥⎝⎦ C.10,5⎛⎤ ⎥⎝⎦ D.10,6⎛⎤ ⎥⎝⎦第II 卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分.13.由2,1,2,0y x x x y ====所围成的封闭图形的面积为__________.14.设袋中有黑球、白球共9个（有不同编号），从中任取3个球，若其中含有白球的概率为2021，则袋中白球的个数为________.15.一个几何体的三视图如右图所示，则这个几何体的表面积为________.16.设曲线()()1*11n y x n N +=∈在点，处的切线与x 轴的交点的横坐标为123999,lg n n n x a x a a a a =+++⋅⋅⋅+令，则的值为_________.三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤.17.（本小题满分12分）已知()()()22sin .cos 223sin ,,,f x x x x a b c ππ=---分别为△ABC 中中角A ，B ，C 的对边，角A 为锐角且()0f A（I ）求角A 的大小；（II ）若2,23a b ==，求△ABC 的面积S.某品牌电视机代理销售商根据近年销售和利润情况得出某种型号电视机的利润情况有如下规律：每台电视机的最终销售利润与其无故障使用时间T （单位：年）有关.若1T ≤，则每台销售利润为0元；若1<T ≤3，则每台销售利润为100元；若3T >，则每台销售利润为200元.设每台该种电视机的无故障使用时间1,1T ≤<T ≤3,T >3这三种情况发生的概率分别为12312,,,,P P P P P 又知是方程21060x x a -+=，且23P P =.（1）求123,,,P P P 的值；（II ）记ξ表示销售两台这种电视机的销售利润总和，写出ξ的所有结果，并求ξ的分布列； （III ）求销售两台这种型号电视机的销售利润总和的期望值.已知四边形ABCD 满足1//,2AD BC BA AD DC BC a ====，E 是BC 的中点，将△BAE 沿AE 翻折成11,B AE B AE AECD ∆⊥使面面，F 为1B D 的中点.（I ）求四棱锥1B AECD -的体积；（II ）证明：1//B E ACF 面；（III ）求面11ADB ECB 与面所成二面角的余弦值.设数列{}n b 的前n 项和为{}*,22n n n n S n N b S a ∈=-对任意，都有；数列为等差数列，且5714,20a a ==（I ）求数列{}n b 的通项公式；（II ）若{}7,1,2,3,,.2n n n n n n c a b n T c n T =⋅=⋅⋅⋅<设为数列的前项和求证：.21.（本小题满分12分）已知()()323,ln f x x ax x g x x b =-+=+ （I ）若曲线()()()1f x h x g x x x=+=在处的切线是0x y +=，求实数a 和b 的值； （III ）若()3x f x =是的极值点，求()[]02f x 在，上的最大最小值.22.（本小题满分14分） 已知()2212121x F F C y a a+=>1、分别是椭圆：的左、右焦点，O 为坐标原点.（I ）若椭圆2212131y x C C -=与双曲线：的离心率互为倒数，求此时实数a 的值；（II ）若直线()101l F 经过点和点，，且原点到直线2l 又另一条直线m ，斜率为1，与椭圆1C E F OE OF ⊥交于，两点，且，求直线m 的方程； （III ）若在直线2x =上存在点P ，使线段121PF M MF PF ⊥的中点满足.求a 的取值范围.。