分式的乘除练习题及答案

分式的乘除乘方专题练习例1、下列分式abc 1215，a b b a --2)(3，)(222b a b a ++，b a b a +-22中最简分式的个数是( ). A.1 B.2 C.3 D.4例23234)1(x y y x • aa a a 2122)2(2+⋅-+ x y xy 2263)3(÷ 41441)4(222--÷+--a a a a a1.约分把一个分式的分子与分母的公因式约去，叫做约分.约分的依据是分式的基本性质. 若分式的分子、分母是多项式，必须先把分子、分母分解因式，然后才能约去公因式. 分子与分母没有公因式的分式，叫做最简分式，又叫做既约分式.分式的运算结果一定要化为最简分式.2.分式的乘法3.分式的除法 例3、 若432z y x ==,求222z y x zx yz xy ++++的值.例4、计算（1）3322）（cb a - （2）43222)()()(x y x y y x -÷-⋅-（3）2332)3()2(c b a bc a -÷- （4）232222)()()(x y xy xy x y y x -⋅+÷-分式的乘方求n 个相同分式的积的运算就是分式的乘方，用式子表示就是(ba )n .分式的乘方，是把分子、分母各自乘方.)56(3)1(122ab cd c b a -÷-、计算： （2）432643xy y x ÷-（3）（xy －x 2）÷x y xy -（4）2223ba a ab -+÷b a b a -+3 （5）3224)3()12(y x y x -÷-（6）322223322322)2()2()34(cb ab ac b a b a ab c +-÷-⋅2、如果32=b a ，且a ≠2，求51-++-b a b a 的值、 计算（1）)22(2222a b ab b a a b ab ab a -÷-÷+-- （2）(2334b a )2·(223a b -)3·(a b 3-)2（3）(22932x x x --+)3·（-xx --13）22、先化简，再求值：(b a ab 22+)3÷2223)b a ab (-·[)(21b a -]2，其中a=-21,b=323、（1）先化简后求值：2(5)(1)5a a a a-+-÷（a 2+a ），其中a=－13．（2）先化简，再求值：21x x x -+÷1x x +，其中x=1．4．已知m+1m=2，计算4221m m m ++的值．7．（宁夏）计算：（9a 2b －6ab 2）÷（3ab ）=_______．8．（北京）已知x －3y=0，求2222x y x x y +-+·（x －y ）的值． 9．（杭州）给定下面一列分式：3x y ，－52x y ，73x y ，－94x y，…（其中x ≠0）． （1）把任意一个分式除以前面一个分式，你发现了什么规律？（2）根据你发现的规律，试写出给定的那列分式中的第7个分式．．11．（结论开放题）请你先化简，再选取一个使原式有意义而你又喜爱的数代入求值：322m m m m --÷211m m -+．12．（阅读理解题）请阅读下列解题过程并回答问题：计算：22644x x x--+÷（x+3）·263x x x +-+． 解：22644x x x --+÷（x+3）·263x x x +-+ =22644x x x--+·（x 2+x －6）① =22(3)(2)x x --·（x+3）（x －2）② =22182x x -- ③ 上述解题过程是否正确？如果解题过程有误，请给出正确解答．13.已知a 2+10a+25=－│b －3│，求代数式42()b a b -·32232a ab a b b +-÷222b a ab b -+的值．（一）、填空题1.把一个分式的分子与分母的 约去，叫做分式的约分.2.在分式xyxy y x 222+中，分子与分母的公因式是 . 3.将下列分式约分： (1)258x x = (2)22357mn n m -= (3)22)()(a b b a --= 4.计算2223362c ab b c b a ÷= . 5.计算42222ab a a ab ab a b a --÷+-= . 6.计算(-y x )2·(-32yx )3÷(-y x )4= . （二）、解答题7.计算下列各题316412446222+⋅-+-÷+--x x x x x x x y x y xy x -+-24422 ÷(4x 2-y 2)(3) 4344516652222+-÷-++⋅-+-a a a a a a a a (4)22222xa bx x ax a ax -÷+-8、某厂每天能生产甲种零件a 个或乙种零件b 个，且a ∶b=2∶3.甲、乙两种零件各一个配成一套产品，30天内能生产的产品的最多套数为多少？1、已知x 2+4y 2-4x+4y+5=0，求22442y xy x y x -+-·22y xy y x --÷(y y x 22+)2的值.2、已知a b c =1，求a a ba b b cb c a c c ++++++++111的值。

分式乘除法计算练习题及答案x?2x2?6x?93xy28z2问题1 计算：．； 2x?3x?44zy名师指导这道例题就是直接应用分式的乘法法则进行运算．值得注意的是运算结果应约分到不好约分为止，同时还应注意在计算时跟整式运算一样，先确定符号，再进行相关计算，求出结果.这道例题中分式的分子、分母是多项式，应先把分子、分母中的多项式分解因式，再进行约分.解题示范3xy28z224xy2z2解：6xy；z2y4yz2x?2x2?6x?9x?222x?3． 2x?3x?4x?3x?2归纳提炼类比分数的乘法运算不难理解，分式的乘法运算就是根据分式乘法法则，将各式分子、分母分别相乘后再进行约分运算，值得注意的地方有三点：一是要确定好运算结果的符号；二是计算结果中分子和分母能约分则要约分；三是有时计算结果的分母不一定是单一的多项式，而是多个多项式相乘，这时也不必把它们展开. a2b?2axa?2a2?4??问题计算：；． a?3a2?6a?93cd6cd名师指导分式除法运算，根据分式除法法则，将分式除法变为分式乘法运算，注意点同分式乘法．解题示范a2b?2axa2b6cd6a2bcdab；解：3cd6cd3cd2ax6acdxxa?2a2?4a?222a?3． ?2a?3a?6a?9a?3a?2a3b?a2b2a2?ab?2问题已知：a?2b?2?2的值．2a?2ab?ba?b名师指导完成这类求值题时，如果把已知条件直接代入，计算将会较为繁杂，容易导致错误产生．解决这种问题，一般应先将代数式进行化简运算，然后再把已知条件代入化简后的式子中进行计算，这样的处理方式可以使运算量少很多．解题示范解：化简代数式得，a3b?a2b2a2?ab?222a?2ab?ba?ba2b ?2aa2b2 ?2aab．把a?2b?2ab，所以原式?·2xy． x?y2y22．计算：?3xy?．x33．计算：?9ab____． b3x2yxy?．．计算：a3am2?4m?3?25．若m等于它的倒数，则分式的值为m?2m?3mA．－1B．3C．－1或D．?6．计算?21 x?y的结果是 xA．2B．x2?yC．x2D．x7．计算32的结果是A．3a2－1 B．3a2－C．3a2＋6a＋ D．a2＋2a＋1 8．已知x等于它的倒数，则x2?x?6x?3x?3x2?5x?6的值是A．－ B．－C．－1 D．09．计算a2?1a2?aa2?2a?1÷a?1．10．观察下列各式：x?1x2?x?1x3?x2?x?1x4?x3?x2?x?1你能得到一般情况下?的结果吗？根据这一结果计算：1?2?22?23??22006?22007．） xn?1?n?2?x?1，22008ax??17．B．A分数乘除法计算题专项练习1一、直接写出得数57?34＝79?97＝5?43＝7?152＝?354＝1＝ 191591120?38＝ 10?32＝=7×1= 1＋17= 1953×0=?778=3?9= 134?5 =4÷34=10÷10%= 12÷23=1.8×15926=?10?5= 1715×60=二、看谁算得又对又快58?167?141135248?6?351926?3855?511 12?35?32533545×4÷×48?3＋8?458÷71521÷ 10 ÷×姓名：6÷310－310÷ 13353×4÷[523713133－]÷314÷ 16718×14＋34×7114×57÷14×5 736× ×9+2312×3.2＋5.6×0.5＋1.2×50%211?3?2?5955711[2－]×12三、解方程78x＝218239x?4＝15x＋215x＝23 56x=308x－113=6x＋5×4.4=40÷x ＝5122x＋215x＝20四、求下面各比的比值1052:8467:46.7106345：0.610：140 19:12五、化简下面各比65:1 123: 1.1:114.9:0.152：15:0.12六、列式计算1．4个131的和除以8，商是多少？．112减去2乘23的积，差是多少？3．一个数的比它的34多，求这个数。

初中数学分式的加减乘除化简计算题一、计算题1.解方程: 1.311221x x =-++； 2.21212339x x x -=+--. 2.计算: 1.322222a b b b a a ⎛⎫⎛⎫⎛⎫-÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭； 2.3222()x y x x y xy x y ⎛⎫⎛⎫-÷+ ⎪ ⎪-⎝⎭⎝⎭. 3.计算：22214().244x x x x x x x x +---÷--+ 4.计算：2111()().111x x x x x x +⋅+++-+ 5.计算：(1)2161;3962x x x x -+---+ (2)22944(3).33a a a a a a --+-+÷+-- 6.先化简,再求值：24()224a a a a a a ÷----,其中3a =. 7.1. ()3123a b c-- 2. ()32322a b a b---⋅ 3. ()()232322ab ca b ---÷ 4. ()()2252310310--⨯÷⨯ 8.解方程:1.54410 1236x x x x -+=--- 2. 2 -?24124x x x +=+- 9.先化简,再求值: 13(a+)?(a-2+)22a a ++其中a 满足20.a -= 10.已知234a b c ==,求325a b c a b c-+++的值.11.已知关于x 的方程4333k x x x-+=--有增根,试求k 的值.参考答案1.答案：1.方程两边同乘()21x +，得3222x =+-， 解得32x =，检验:当32x =时，()210x +≠， 所以原分式方程的解为32x =. 2.方程两边同乘()()33x x +-，得32612x x -++=，解得3x =， 检验:当3x =时，()()330x x +-=，所以3x =不是原分式方程的解， 所以原分式方程无解.解析：2.答案：1.322322322332232232228448484a b b a b b a b a a b a a b a a b a b b ⎛⎫⎛⎫⎛⎫⎛⎫-÷-=-÷=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2.原式()()()()()233222221x y x y x x x y x y x y x y y +-==-+- 解析：3.答案：解：22214()244x x x x x x x x+---÷--+ 221[](2)(2)4x x x x x x x +-=-⋅--- 22(2)(2)(1)[](2)(2)4x x x x x x x x x x +--=-⋅--- 2224(2)4x x x x x x x --+=⋅-- 24(2)4x x x x x -=⋅-- 21.(2)x =- 解析：4.答案：解：原式221(1)x x x x +=⋅++11[](1)(1)(1)(1)x x x x x x +-++-+- 21(1)(1)x x x x x =+++- 22(1)(1)(1)(1)x x x x x x x -=++-+- (1)(1)(1)x x x x +=+- .1x x =- 解析：5.答案：解：(1)原式2(3)122(3)(3)2(3)(3)x x x x x +=-+-+-(1)(3)2(3)(3)x x x x ---+- 2692(3)(3)x x x x -+-=+- 2(3)2(3)(3)x x x -=-+- 3.2(3)x x -=-+ (2)原式22299(2)()33(3)a a a a a a ---=-÷++-+ 2(2)(3)3(2)a a a a a ---+=⋅+- .2a a =- 解析： 6.答案：24()224a a a a a a ÷---- (2)42(2)(2)a a a a a a a +-=÷-+- (2)2(2)(2)a a a a a a -=÷-+- 22a a a a+=⋅-22a a +=- 当3a =时,原式32532+==-. 解析： 7.答案：1. ()()()633312336939=b ab c a b c a c ----==原式 2. 92366898=b a b a b a b a ---⋅==原式 3. ()()4622466324767=224a c a b c a b a b c b ------÷==原式 4. ()()104661=9109101010---⨯÷⨯==原式 解析： 8.答案：1.方程两边同乘3(2)x -,得()354? 4x 103(2)x x -=+--. 解这个方程,得2x =.检验:当2x =时, 3(2)x -0=,所以2x =是原方程的增根,原方程无解.2.方程的两边同乘以()()22?x x +-,得()()2(2)422? x x x -+=+-, 解得3x =.检验:当3x =时, 240x -≠,所以3x =是原方程的解.解析：9.答案：解:原式2(2)1432+2a a a a a ++-+=÷+ 2(1)2=2(1)(1)a a a a a ++⋅++-\ 11a a +=- 当20a -=,即2a =时,原式 3.=解析：10.答案：解:令=k 234a b c ==,则2,3,4.a k b k c k === ∴原式322354202023499k k k k k k k k ⨯-⨯+⨯===++解析：11.答案：解方程233x m x x -=--得6x m =--它的解是正数60m ∴-->解得1k = 解析：。

初中数学分式的化简与乘除法练习题一、单选题 1.计算()22ba a -的结果为( ) A.b B.b -C.abD.b a2.化简221121a a a a a a ++÷--+的结果是( ) A.1a a + B.1a a - C.11a - D.1a a- 3.化简22164244244a a a a a a a --+÷++++，其结果是( ) A.2-B.2C. ()222a -+ D.()222a +4.下列计算正确的有( )①22a a b b ⎛⎫= ⎪⎝⎭；②333622y y x x -⎛⎫= ⎪⎝⎭；③23546x x y y ⎛⎫= ⎪⎝⎭；④222()()a b a b a b a b --⎛⎫= ⎪++⎝⎭；⑤222224x x x y x y ⎛⎫= ⎪++⎝⎭. A.1个B.2个C.3个D.4个5.计算222105a b a bab a b+-的结果为( ) A.2a b - B.a a b - C.b a b -D.2a a b -6.计算221()222a b a b a b-÷⋅-+的结果是( )A.2()4a b -B.21()a b -C.24()a b - D.2()a b + 7.计算32()a b-的结果是( ) A.332a b - B.336a b - C.338a b- D.338a b8.化简1()x y y x x y x y-÷-⋅+-的结果是( ) A.221x y - B.y x x y -+ C.221y x - D.x y x y -+9.计算322222x y y y x x ⎛⎫⎛⎫⎛⎫÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭)的结果是( )A.368x yB.368x y -C.2516x yD.2516x y-10.计算24a a b ⎛⎫ ⎪+⎝⎭的结果是( )A.2228a a b+ B. 22216a a b+ C.228()a a b + D.2216()a ab + 11.下列运算结果正确的是( )A.4453m n m n m n=B. 2223344x x y y ⎛⎫= ⎪⎝⎭C. 2222241a a a a b ⎛⎫= ⎪--⎝⎭D.a c ac b d bd÷= 12.计算3222n m mm n n -⋅÷的结果是( )A.22m nB.23m n -C.4nm- D.n - 13.计算a ba b a÷⋅的结果是( ) A.a B.2a C.21aD.2b a14.计算()x y x x y x x y++÷⋅+,其结果是( ) A.x y + B.2x x y + C.1y D.11y+15.计算623993m mm m m ⋅÷+--,其结果是( ) A.21(3)m + B.21(3)m -+ C.21(3)m - D.219m -+ 16.计算221()222a ba b a b-÷⋅-+,其结果是( )A.2()4a b -B.21()a b -C.24()a b - D.2()a b + 二、解答题17.化简：22266(3)(2)443x x x x x x x x-+-÷+⋅⋅--+-. 18.计算: ()322a b ab b a ⎛⎫⎛⎫-⋅-÷- ⎪ ⎪⎝⎭⎝⎭19.计算: 2322222a b ab b c cac ⎛⎫-÷⋅ ⎪⎝⎭ 20.先化简，在求值：2223()()()x y x x y xy x y -÷+⋅-,其中1, 1.2x y =-=- 三、计算题21.()222191691a a a a a a --÷+⨯++-四、填空题22.计算:322x y ⎛⎫-= ⎪⎝⎭.23.化简293242a a a a-+÷--的结果为 . 24.计算:22536c bab a c= . 25.化简422222()()a a b a a b b a b b a-+÷⋅-的结果是 . 参考答案1.答案：A 解析：原式22ba b a ==故选A. 2.答案：D解析：原式()()211111a a a a a a a-+-==-+。

分式的乘除法练习及答案分式的乘除法练及答案运算法则：1）分式乘法法则：$\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}$2）分式的除法法则：$\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{ad}{bc}$3）分式的乘方法则：$\frac{a}{n} \cdot \frac{n}{b} = \frac{a}{b}$1.下列各式的约分正确的是（）A。

$\frac{2}{2(a-c)^2} = \frac{1}{a-c}$B。

$\frac{abc}{233+(a-c)^3} = \frac{abc}{233+a^3-3a^2c+3ac^2-c^3}$C。

$\frac{2}{a-b} = \frac{2}{a-b}$D。

$\frac{2a-c}{1-4a+c^2+2a^2} = \frac{2a-c}{(1+2a)(1-c)}$2.在等式$\frac{a^2+aM}{a+1} = \frac{a^2-1}{a}$中，M的值为（）A。

$a$B。

$a+1$C。

$-a$D。

$a-1$3.XXX在下面的计算题中只做对了一道题，你认为他做对的题目是（）A。

$\frac{111b}{1bab} \div 2 = \frac{1}{b}$B。

$\frac{2}{2} \div \frac{2}{2} = 1$C。

$\frac{2}{2} \cdot \frac{2}{2} = 1$D。

$(x-y) \div \frac{1}{2} = 2(x-y)$4.将分式$\frac{2}{x+1}+\frac{x}{x+1}$化简得，$x$满足的条件是$x \neq -1$5.化简1）$\frac{-x^2}{2b} = -\frac{x^2}{2b}$2）$\frac{2y}{3a} \cdot \frac{a}{2} = \frac{y}{3}$6.计算frac{2b^2-3ab^2x^2}{2} \div \frac{-3ab}{1+3ax} =\frac{2b(1-3ax)}{9a}$frac{x^2-y^2}{x^2+xy-a-2} \div \frac{x+y}{2y-a} \cdot \frac{2a^2+2a}{2a^2+2a} = \frac{(x-y)(2a+y)}{(x+2y-a)(2a+2y)}$frac{4m^2-4m+1}{4m^2-1} \div \frac{2}{2} = \frac{2m-1}{2m+1}$frac{(4x-y)}{2x-ym+1} \cdot \frac{m-1}{m+1} \div \frac{-4}{(7n^2-4x^2)(-8x^2)} = \frac{(4x-y)(m-1)(7n^2-4x^2)}{2(m+1)x^2}$frac{2xy}{-ynm} \div \frac{5}{4x^2} = -\frac{8x^3}{5nymy}$frac{a^2-14}{a^2+4a-1} \div (a+1) \cdot \frac{2a-1}{a+4} = \frac{2a-1}{a^2+4a-1}$。

分式及分式的运算15．1.1 从分数到分式1．下列各式不是分式的是( )A.x yB.y π＋yC.x 2D.1＋x a 2．若分式x ＋1x －1有意义，则x 的取值范围是( ) A ．x ≠1 B ．x ≠－1 C ．x ＝1 D ．x ＝－13．如果分式|x |－1x －1的值为零，那么x 的值为( ) A ．1 B ．－1 C ．0 D ．±14．某人种了x 公顷的棉花，总产量为y 千克，则棉花的单位面积产量为________千克/公顷．5．当x ＝________时，分式x 2－9x －3的值为零． 6．x 取何值时，下列分式有意义？(1)x ＋22x －3； (2)6（x ＋3）|x |－12；(3)x ＋6x 2＋1； (4)x （x －1）（x ＋5）.15．1.2 分式的基本性质1．下列分式是最简分式的是( )A.x －13x －3B.3（x 2－y 2）x －yC.x －12x ＋1D.2x 4－2x2．分式x 5y 与3x 2y 2的最简公分母是( ) A ．10xy B ．10y 2 C ．5y 2 D ．y 23．根据分式的基本性质填空：(1)a ＋b ab ＝（ ）a 2b； (2)x 2＋xy x 2＝x ＋y （ ）； (3)a －2a 2－4＝1（ ）. 4．下列式子变形：①b a ＝b ＋1a ＋1；②b a ＝b －1a －1；③b －2a ＝2b －42a ；④a 2＋a a 2－1＝a a －1.其中正确的有________(填序号)．5．约分：(1)－4x 2y 6xy 2＝________； (2)a 2＋2a a 2＋4a ＋4＝________． 6．通分：(1)x ac ，y bc ； (2)24－x 2，x x ＋2； (3)1x 2－6x ＋9，13x －9.15．2 分式的运算15．2.1 分式的乘除第1课时 分式的乘除1．计算a bc ·c 2a 2的结果是( ) A.c 2a 2b B.c ab C.c 2ab D.a 2bc2．计算2x 3÷1x的结果是( ) A ．2x 2 B ．2x 4 C ．2x D ．43．化简：(1)a 2＋ab a －b ÷ab a －b＝________； (2)2x ＋2y 5a 2b ·10ab 2x 2－y 2＝________． 4．计算：(1)x x 2－1÷1x ＋1； (2)x 2－9x 2＋6x ＋9·3x 3＋9x 2x 2－3x.5．先化简，再求值：x －2x ＋3·x 2－9x 2－4x ＋4，其中x ＝－1.第2课时 分式的乘方1．计算⎝⎛⎭⎫x2y 3的结果是( )A.x 38y 3B.x 36y 3C.x 8y 3D.x 38y2．计算a 2·⎝⎛⎭⎫1a 3的结果是( )A ．aB ．a 5 C.1a D.1a 53．已知⎝⎛⎭⎫x3y 22·⎝⎛⎭⎫－y3x 2＝6，则x 4y 2的值为( )A ．6B ．36C ．12D ．34．计算：(1)⎝⎛⎭⎫3b2a 2＝________；(2)a 2b ·b2a ＝________；(3)⎝⎛⎭⎫－y 2ax 2÷y 24x ＝________．5．计算：(1)⎝⎛⎭⎫－3ac 2b 2； (2)a －b b ·ba 2－b 2；(3)－a 32b ÷⎝⎛⎭⎫－a 2b 3·b 2.6.先化简，再求值：a －a 2a 2－1÷a a －1·⎝ ⎛⎭⎪⎫a ＋1a －12，其中a ＝2.15．2.2 分式的加减第1课时 分式的加减1．计算x －1x ＋1x的结果是( ) A.x ＋2x B.2x C.12D ．1 2．化简4x x －2－x 2－x的结果是( ) A.3x x －2 B.5x 2－x C.5x x －2 D.3x 2－x3．计算：(1)1a 2－1＋a a 2－1＝________； (2)1a －1－1a （a －1）＝________． 4．计算：(1)5a ＋3b a 2－b 2－2a a 2－b 2； (2)m m ＋n ＋m m －n －m 2m 2－n 2.5．先化简：x 2＋x x 2＋2x ＋1＋1－x x 2－1，然后从－1≤x ≤2的范围内选取一个合适的整数作为x 的值代入求值．第2课时 分式的混合运算1．化简⎝⎛⎭⎫1＋1x －2·x 2－2x x －1的结果为( ) A ．4x B ．3x C ．2x D ．x2．化简：(1)⎝ ⎛⎭⎪⎫a ＋1a －1＋11－a ÷a 1－a＝________； (2)x 2－4x 2－2x ＋1·x －1x －2－x x －1＝________． 3．计算：(1)a 2－16a ＋64a －8÷⎝⎛⎭⎫1－8a ； (2)⎝ ⎛⎭⎪⎫x 2－1x 2－2x ＋1＋x ＋1x －1·1－x 1＋x；(3)⎝⎛⎭⎫x －1x ÷⎝⎛⎭⎫2x －1＋x 2x ； (4)⎝⎛⎭⎫b 2a 2÷⎝⎛⎭⎫b a －14a ·23b .4．先化简，后求值：⎝⎛⎭⎫1x －1－1x ＋1÷x x 2－1，其中x ＝2.分 式15．1.1 从分数到分式1．C 2.A 3.B 4.y x5.－3 6．解：(1)要使x ＋22x －3有意义，得2x －3≠0.解得x ≠32.∴当x ≠32时，x ＋22x －3有意义． (2)要使6（x ＋3）|x |－12有意义，得|x |－12≠0.解得x ≠±12.∴当x ≠±12时，6（x ＋3）|x |－12有意义． (3)要使x ＋6x 2＋1有意义，得x 2＋1≠0.∴当x 为任意实数时，x ＋6x 2＋1都有意义． (4)要使x （x －1）（x ＋5）有意义，得(x －1)(x ＋5)≠0.∴当x ≠1且x ≠－5时，x （x －1）（x ＋5）有意义． 15．1.2 分式的基本性质1．C 2.B 3.(1)a 2＋ab (2)x (3)a ＋2 4.③④5．(1)－2x 3y (2)a a ＋26．解：(1)最简公分母为abc ，则x ac ＝bx abc ，y bc ＝ay abc. (2)最简公分母为(2＋x )(2－x )，则24－x 2＝2（2＋x ）（2－x ），x x ＋2＝x （2－x ）（2＋x ）（2－x ）＝2x －x 2（2＋x ）（2－x ）. (3)最简公分母为3(x －3)2，则1x 2－6x ＋9＝33（x －3）2，13x －9＝x －33（x －3）2. 15．2 分式的运算15．2.1 分式的乘除第1课时 分式的乘除1．B 2.B 3.(1)a ＋b b (2)4b a （x －y ）4．解：(1)原式＝x （x ＋1）（x －1）·(x ＋1)＝x x －1. (2)原式＝（x ＋3）（x －3）（x ＋3）2·3x 2（x ＋3）x （x －3）＝3x .5．解：x ＝－1时，原式＝x －2x ＋3·（x －3）（x ＋3）（x －2）2＝x －3x －2＝43. 第2课时 分式的乘方1．A 2.C 3.A 4.(1)9b 4a 2 (2)ab 3 (3)1a 2x5．解：(1)原式＝9a 2c 24b 2. (2)原式＝a －b b ·b （a ＋b ）（a －b ）＝1a ＋b. (3)原式＝－a 32b ·⎝⎛⎭⎫－b 3a 6·b 2＝b 34a 3. 6．解：原式＝a （1－a ）（a ＋1）（a －1）·a －1a ·（a ＋1）2（a －1）2＝－a ＋1a －1＝a ＋11－a .当a ＝2时，原式＝2＋11－2＝－3.15．2.2 分式的加减第1课时 分式的加减1．D 2.C 3.(1)1a －1(2)1a 4．解：(1)原式＝5a ＋3b －2a （a ＋b ）（a －b ）＝3（a ＋b ）（a ＋b ）（a －b ）＝3a －b. (2)原式＝m （m －n ）＋m （m ＋n ）（m ＋n ）（m －n ）－m 2（m ＋n ）（m －n ）＝m 2（m ＋n ）（m －n ）＝m 2m 2－n 2. 5．解：原式＝x （x ＋1）（x ＋1）2－x －1（x ＋1）（x －1）＝x x ＋1－1x ＋1＝x －1x ＋1.∵－1≤x ≤2且x 为整数，∴取x ＝0或2.当x ＝2时，原式＝13. 第2课时 分式的混合运算1．D 2.(1)－1 (2)2x －13．解：(1)原式＝（a －8）a －82÷a －8a ＝(a －8)·a a －8＝a . (2)原式＝⎣⎢⎡⎦⎥⎤（x －1）（x ＋1）（x －1）2＋x ＋1x －1 ·1－x 1＋x ＝⎝ ⎛⎭⎪⎫x ＋1x －1＋x ＋1x －1 ·1－x 1＋x＝2（x ＋1）x －1 ·1－x 1＋x ＝－2. (3)原式＝x 2－1x ÷2x 2－1－x 2x ＝（x ＋1）（x －1）x ·x （x ＋1）（x －1）＝1. (4)原式＝b 24a 2·a b －16ab ＝3b 2－212ab.4．解：原式＝x ＋1－x ＋1（x ＋1）（x －1）·（x ＋1）（x －1）x ＝2x .当x ＝2时，原式＝1.。

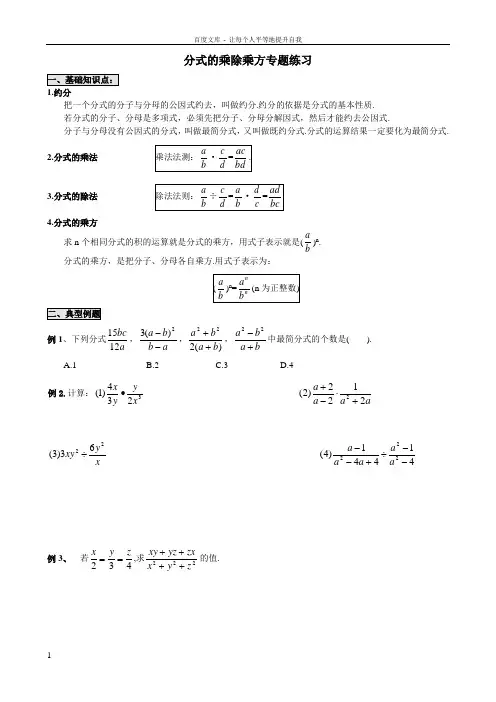
分式的乘除乘方专题练习1.约分把一个分式的分子与分母的公因式约去，叫做约分.约分的依据是分式的基本性质.若分式的分子、分母是多项式，必须先把分子、分母分解因式，然后才能约去公因式.分子与分母没有公因式的分式，叫做最简分式，又叫做既约分式.分式的运算结果一定要化为最简分式.2.分式的乘法3.分式的除法4.分式的乘方 求n 个相同分式的积的运算就是分式的乘方，用式子表示就是(b a )n . 分式的乘方，是把分子、分母各自乘方.用式子表示为：例1、下列分式abc 1215，a b b a --2)(3，)(222b a b a ++，b a b a +-22中最简分式的个数是( ). A.1 B.2 C.3 D.4例2.计算：3234)1(x y y x • a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷ 41441)4(222--÷+--a a a a a例3、 若432z y x ==,求222z y x zx yz xy ++++的值.例4、计算（1）3322）（cb a - （2）43222)()()(x y x y y x -÷-⋅-（3）2332)3()2(c b a bc a -÷- （4）232222)()()(x y xy xy x y y x -⋅+÷-)56(3)1(122ab cd c b a -÷-、计算： （2）432643xy yx ÷-（3）（xy －x 2）÷x y xy - （4）(广州中考题)2223b a a ab -+÷b a b a -+3 （5）3224)3()12(y x y x -÷- （6）322223322322)2()2()34(c b ab a c b a b a ab c +-÷-⋅2、 (浙江中考题)如果32=b a ，且a ≠2，那么51-++-b a b a = . 3、已知x 2+4y 2-4x+4y+5=0，求22442yxy x y x -+-·22y xy y x --÷(y y x 22+)2的值.1、 计算（1）)22(2222a b ab b a a b ab ab a -÷-÷+-- （长沙中考题） （2）(2334b a )2·(223ab -)3·(a b 3-)2（3）(22932x x x --+)3·（-xx --13）2 (南昌中考题)2、先化简，再求值：(b a ab 22+)3÷2223)b a ab (-·[)(21b a -]2，其中a=-21,b=323、（1）先化简后求值：2(5)(1)5a a a a-+-÷（a 2+a ），其中a=－13．（2）先化简，再求值：21x x x -+÷1x x +，其中．4．已知m+1m=2，计算4221m m m ++的值．5、（科外交叉题）•已知两块大小相同的正方体铜块和正方体铁块的重量分别为x 牛和y 牛，当把它们放在同一水平桌面上时，•铁块对桌面的压强是铜块对桌面的压强的多少倍？（提示：物体的压强公式为压强=压力面积，即P=F S ）6、一艘轮船从甲地顺流行至乙地，然后再从乙地逆流返回甲地，已知水流速度为3km/h ，去时所需时间是回来所需时间的34，求轮船在静水中的速度．（•只列方程不必求解） 7．（宁夏）计算：（9a 2b －6ab 2）÷（3ab ）=_______．8．（北京）已知x －3y=0，求2222x y x x y+-+·（x －y ）的值．9．（杭州）给定下面一列分式：3x y ，－52x y ，73x y ，－94x y，…（其中x ≠0）． （1）把任意一个分式除以前面一个分式，你发现了什么规律？（2）根据你发现的规律，试写出给定的那列分式中的第7个分式．10．（规律探究题）计算：222200420032004200220042004+．11．（结论开放题）请你先化简，再选取一个使原式有意义而你又喜爱的数代入求值：322m m m m --÷211m m -+．12．（阅读理解题）请阅读下列解题过程并回答问题：计算：22644x x x --+÷（x+3）·263x x x +-+． 解：22644x x x--+÷（x+3）·263x x x +-+ =22644x x x --+·（x 2+x －6）① =22(3)(2)x x --·（x+3）（x －2）② =22182x x -- ③ 上述解题过程是否正确？如果解题过程有误，请给出正确解答．13.已知a 2+10a+25=－│b －3│，求代数式42()b a b -·32232a ab a b b +-÷222b a ab b-+的值．（一）、填空题1.把一个分式的分子与分母的 约去，叫做分式的约分.2.在分式xyxy y x 222+中，分子与分母的公因式是 . 3.将下列分式约分：(1)258x x = (2)22357mn n m -= (3)22)()(a b b a --= 4.计算2223362cab b c b a ÷= . 5.计算42222a b a a ab ab a b a --÷+-= . 6.计算(-y x )2·(-32yx )3÷(-y x )4= . （二）、解答题7.计算下列各题(1)316412446222+⋅-+-÷+--x x x x x x x (2)y x y xy x -+-24422÷(4x 2-y 2)(3)4344516652222+-÷-++⋅-+-a a a a a a a a (4)22222x a bx x ax a ax -÷+-8.当x=-3时，求xx x x x x 43342323-++-的值9.已知x+y 1=1,y+z 1=1,求证z+x1=1.10、某厂每天能生产甲种零件a 个或乙种零件b 个，且a ∶b=2∶3.甲、乙两种零件各一个配成一套产品，30天内能生产的产品的最多套数为多少？1、已知a b c =1，求a a ba b b cb c a c c ++++++++111的值。

分式的乘除练习题及答案问题1计算：（1）22238()4xy zz y-g；（2）2226934x x xx x+-+--g．名师指导（1）这道例题就是直接应用分式的乘法法则进行运算．值得注意的是运算结果应约分到不好约分为止，同时还应注意在计算时跟整式运算一样，先确定符号，再进行相关计算，求出结果.（2）这道例题中分式的分子、分母是多项式，应先把分子、分母中的多项式分解因式，再进行约分.解题示范解：（1）2222223824()644xy z xy zxyz y yz-=-=-g；（2）22222692(3)(2)(3)3 343(2)(2)(3)(2)(2)2x x x x x x x xx x x x x x x x x+-++-+--===---+--+--g g．归纳提炼类比分数的乘法运算不难理解，分式的乘法运算就是根据分式乘法法则，将各式分子、分母分别相乘后再进行约分运算，值得注意的地方有三点：一是要确定好运算结果的符号；二是计算结果中分子和分母能约分则要约分；三是有时计算结果的分母不一定是单一的多项式，而是多个多项式相乘，这时也不必把它们展开.问题2计算：（1）2236a b axcd cd-÷；（2）2224369a aa a a--÷+++．名师指导分式除法运算，根据分式除法法则，将分式除法变为分式乘法运算，注意点同分式乘法．解题示范解：（1）22226636326a b ax a b cd a bcd ab cd cd cd ax acdx x -÷=-=-=-g；（2）2222242(3)(2)(3)33693(2)(2)(3)(2)(2)2a a a a a a a a a a a a a a a a a ---+-++÷===+++++-++-+g ．问题3 已知：2a =，2b =322222222a b a b a ab a ab b a b+-÷++-的值． 名师指导完成这类求值题时，如果把已知条件直接代入，计算将会较为繁杂，容易导致错误产生．解决这种问题，一般应先将代数式进行化简运算，然后再把已知条件代入化简后的式子中进行计算，这样的处理方式可以使运算量少很多．解题示范解：化简代数式得，322222222a b a b a ab a ab b a b +-÷++- 22()()()()()a b a b a b a b a b a a b ++-=+-g 222()()()()a b a b a b a a b a b +-=+- ab =．把2a =2b =ab ，所以原式22(222=+=-=．归纳提炼许多化简求值题，有的在题目中会明确要求先化简，再求值，这时必须按要求的步骤进行解题．但有的在题目中未必会给出明确的要求或指示，与整式中的求代数式值的问题一样，分式中的求值题一般也是先化简，然后再代入已知条件，这样可以简化运算过程．【自主检测】1．计算：2()xy x -·xy x y-=___ _____． 2．计算：23233y xy x -÷____ ____．3．计算：3()9a ab b-÷=____ ____． 4．计算：233x y xy a a÷=____ ____． 5．若m 等于它的倒数，则分式mm m m m 332422--÷--的值为 （ ） A ．－1 B ．3 C ．－1或3 D ．41-6．计算2()x yx xy x ++÷的结果是（ ） A ．2()x y + B ．y x +2 C ．2x D ．x7．计算2(1)(2)3(1)(1)(2)a a a a a -++++g 的结果是（ ） A ．3a 2－1 B ．3a 2－3 C ．3a 2＋6a ＋3 D ．a 2＋2a ＋18．已知x 等于它的倒数，则263x x x ---÷2356x x x --+的值是（ ） A ．－3 B ．－2 C ．－1 D ．09．计算22121a a a -++÷21a aa -+．10．观察下列各式：2324325432(1)(1)1(1)(1)1(1)(1)1(1)(1)1x x x x x x x x x x x x x x x x x x -÷-=+-÷-=++-÷-=+++-÷-=++++L L（1）你能得到一般情况下(1)(1)n x x -÷-的结果吗？（2）根据这一结果计算：2320062007122222++++++L ．【自主评价】一、自主检测提示8．因为x 等于它的倒数，所以1x =±，2263356x x x x x x ---÷--+(3)(2)(2)(3)33x x x x x x -+--=--g (2)(2)x x =+-224(1)43x =-=±-=-．10．根据所给一组式子可以归纳出：122(1)(1)1n n n x x x x x x ---÷-=+++++L ．所以232006200720082008122222(21)(21)21++++++=--=-L ．二、自我反思1．错因分析2．矫正错误3．检测体会4．拓展延伸参考答案1．2x y - 2． 292x y- 3． 213b - 4．9x 5．C 6．C 7．B8．A 9．1a 10．（1）121n n x x x --++++L ，（2）200821-。

分式的乘除计算题精选（含答案）一．解答题（共21小题）1．•．2．÷．3．．4．．5．．6．．7．．8．9．10．11．（ab3）2•．12．××．13．．14．÷•．15．．16．．17．．18．．19．（1）；（2）．20．．21．÷•．分式的乘除计算题精选（含答案）参考答案与试题解析一．解答题（共21小题）1．（2014•淄博）计算：•．考点：分式的乘除法．专题：计算题．分析：原式约分即可得到结果．解答：解：原式=•=．点评：此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．2．（2014•长春一模）化简：÷．考点：分式的乘除法．专题：计算题．分析：原式利用除法法则变形，约分即可得到结果．解答：解：原式=•=．点评：此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．3．（2012•漳州）化简：．考点：分式的乘除法．专题：计算题．=•，然后约分即可．解答：解：原式=•=x．点评：本题考查了分式得乘除法：先把各分式的分子或分母因式分解，再把除法运算转化为乘法运算，然后进行约分得到最简分式或整式．4．（2012•南昌）化简：．考点：分式的乘除法．专题：计算题．分析：根据分式的乘法与除法法先把各分式的分子因式分解，再把分式的除法变为乘法进行计算即可．解答：解：原式=÷=×=﹣1．点评：本题考查的是分式的乘除法，即分式乘除法的运算，归根到底是乘法的运算，当分子和分母是多项式时，一般应先进行因式分解，再约分．5．（2012•大连二模）计算：．考点：分式的乘除法．分析：首先将除法运算化为乘法运算，要注意先把分子、分母能因式分解的先分解，然后约分．解答：解：原式=y（x﹣y）÷=y（x﹣y）•=y．点评：此题考查了分式的除法．此题难度不大，注意把分子分母中能够分解因式的部分首先因式分解，然后约分，化为最简分式．考点：分式的乘除法．专题：计算题．分析：本题考查的是分式的乘除法运算，按运算顺序，先算括号里面的，再做乘法运算，要注意先把分子、分母能因式分解的先分解，然后约分．解答：解：原式=÷（2分）=•（5分）=（6分）点评：在完成此类化简题时，应先将分子、分母中能够分解因式的部分进行分解因式．有括号的先算括号里面的．通过分解因式，把分子分母中能够分解因式的部分，分解成乘积的形式，然后把除法转化成乘法，再约去．7．（2010•密云县）化简：．考点：分式的乘除法．分析：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母．然后将各分式的分子、分母分解因式，进而可通过约分、化简得出结果．解答：解：原式==．点评：在完成此类化简题时，应先将分子、分母中能够分解因式的部分进行分解因式．有些需要先提取公因式，而有些则需要运用公式法进行分解因式．通过分解因式，把分子分母中能够分解因式的部分，分解成乘积的形式，然后找到其中的公因式约去．8．（2010•从化市一模）化简：考点：分式的乘除法．分析：本题考查的是分式的乘法运算，做乘法运算时要注意先把分子、分母能因式分解的先分解，然后约分．解答：解：（3分）=（6分）=．（9分）点评：在完成此类化简题时，应先将分子、分母中能够分解因式的部分进行分解因式，然后找到其中的公因式约去．9．（2009•清远）化简：考点：分式的乘除法．专题：计算题．分析：本题可先将分式的除法运算转化为乘法运算，然后将各分式的分子、分母分解因式，进而可通过约分、化简得出结果．解答：解：原式==．点评：分式的除法计算首先要转化为乘法运算，然后对式子进行化简，化简的方法就是把分子、分母进行分解因式，然后进行约分．分式的乘除运算实际就是分式的约分．10．（2007•双柏县）化简：考点：分式的乘除法．分析：在完成此类化简题时，应先将分子、分母中能够分解因式的部分进行分解因式．有些需要先提取公因式，而有些则需要运用公式法进行分解因式．通过分解因式，把分子分母中能够分解因式的部分，分解成乘积的形式，然后找到其中的公因式约去．解答：解：原式=÷=•=x．11．（2002•汕头）计算：（ab3）2•．考点：分式的乘除法．专题：计算题．分析：根据积的乘方，等于把积中的每一个因式分别乘方，再把所得的幂相乘计算即可得出结果．解答：解：原式=a2b6•=﹣b5．点评：本题考查积的乘方的性质，熟练掌握性质是解题的关键，难度适中．12．化简：××．考点：分式的乘除法．分析：直接利用分式的乘法运算法则化简求出即可．解答：解：××=．点评：此题主要考查了分式的乘法运算，正确化简求出是解题关键．13．计算：．考点：分式的乘除法．专题：计算题．分析：将原式的第一项的分子分母分解因式，且分子提取﹣1，第三项利用分式的乘方法则：给分式的分子分母分别平方，并把结果相除，然后根据除以一个数等于乘以这个数的倒数把原式化为积的形式，约分后即可得到结果．解答：解：原式===．点评：此题考查了分式的乘除法以及分式的乘方运算．学生在做此类题若出现多项式时，一般将14．计算：÷•．考点：分式的乘除法．专题：计算题．分析：原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分即可得到结果．解答：解：原式=÷•=••=．点评：此题考查了分式的乘除法，分式乘除法的关键是约分，约分的关键是找公因式．15．计算题：．考点：分式的乘除法．专题：计算题．分析：把除法运算转化为乘法运算和把25x2﹣9因式分解得到原式=••，然后约分即可．解答：解：原式=••=x2．点评：本题考查了分式的乘除法：先把分子或分母因式分解，再把除法运算转化为乘法运算，然后进行约分得到最简分式或整式．16．计算：．考点：分式的乘除法．注意除以一个分式等于乘以这个分式的倒数．解答：解：原式==．点评：本题考查分式的乘除法运算，分式的乘除混合运算一般是统一为乘法运算，如果有乘方，还应根据分式乘方法则先乘方，即把分子、分母分别乘方，然后再进行乘除运算．17．化简：．考点：分式的乘除法．分析：首先把分子、分母能因式分解的先分解，然后约分即可．解答：解：原式=•，=．点评：此题主要考查了分式的乘法，应先将分子、分母中能够分解因式的部分进行分解因式，然后找到其中的公因式约去．18．化简：．考点：分式的乘除法．专题：计算题．分析：原式利用除法法则变形，约分即可得到结果．解答：解：原式=﹣••=﹣．点评：此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．19．分式化简，（1）；（2）．考点：分式的乘除法．专题：计算题．分析：先把幂去掉，再把除号变成乘号，约去同类项得出结果．解答：解：（1）原式=﹣×==．（2）原式==．点评：根据分式的性质分母分子分别相乘约去同类项，特别注意负号．20．．考点：分式的乘除法．分析：先把分式的分子和分母用平方差公式和完全平方公式进行因式分解，再约去公因式，然后把除法运算转化为乘法运算，化简即可得出结果．解答：解：原式==•（x+3）（x﹣3）=3x+9．点评：本题考查分式的乘除法，由于式子比较复杂，同学们在解答的时候要细心．21．计算：÷•．考点：分式的乘除法．专题：计算题．分析：原式利用除法法则变形，约分即可得到结果．解答：解：原式=••=﹣=．点评：此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．。

分式乘除运算（习题）复习巩固1.下列各式：①115x -；②43x π-；③222x y -；④m n m n -+；⑤25x x．其中属于分式的是______________．（填序号）2.下列运算正确的是（）A ．11b b a a +-+-=B ．2x y x y x+=+C ．x y y x x y y x--=++D ．1x y x y --=-+3.下列各分式中，属于最简分式的是（）A ．34()85()x y x y -+B ．22y x x y -+C ．2222x y x y xy ++D ．222()x y x y -+4.下列结论：①无论x 取何值，分式221x x +都有意义；②当1x =-时，分式2121x x x +++的值为0；③若使1121x x x x ++÷--有意义，则x 的取值范围是x ≠2且x ≠1．其中正确的是_______．（填序号）5.若分式211x x --的值为0，则x =___________．6.化简下列分式：（1）22214ac a bc -；（2）2242a a a --；（3）2324x x x x+-；（4）222x x y xy --；（5）222612633x xy y xy y -+-．7.计算：（1）22322358154m ab m b a -÷；（2）22225593x y xy x y x y -⋅-；（3）2224123a b a b a ab a b --÷++；（4）222692693x x x x x x-+-÷-+；（5）2222222xy x y x xy y xy x y-⋅-+-；（6）22244442824a a a a a a a a -++÷⋅--+．8.把分式222xy x y +中x ，y 的值都扩大为原来的2倍，则分式的值（）A ．不变B ．扩大为原来的2倍C ．扩大为原来的4倍D ．缩小为原来的129.甲、乙两个工程队合修一条公路，已知甲工程队每天修2(1)a -米（其中a >1），乙工程队每天修2(1)a -米，则甲工程队修900米所用时间是乙工程修600米所用时间的_____倍．复习巩固1.①④⑤2.D 3.C 4.①5.-16.（1）7c ab -；（2）2a a +-；（3）12x -；（4）x y -；（5）22x y y -.7.（1）76a m -；（2）215y x xy +；（3）4a b a +；（4）2x -；（5）2()x y x y +--；（6）22(2)a a -+.8.A 9.3322a a -+。

第十九讲 分式的乘除【要点梳理】 要点一、分式的乘除法1.分式的乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母.用字母表示为：a c acb d bd⋅=，其中a b c d 、、、是整式，0bd ≠.2.分式的除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘.用字母表示为：a c a d adb d bc bc÷=⋅=，其中a b c d 、、、是整式，0bcd ≠.要点诠释：（1）分式的乘除法都能统一成乘法，然后约去公因式，化为最简分式或整式.（2）分式与分式相乘，若分子和分母是多项式，则先分解因式，看能否约分，然后再乘. （3）整式与分式相乘，可以直接把整式（整式可以看作分母是1的代数式）和分式的分子相乘作为分子，分母不变.当整式是多项式时，同样要先分解因式，便于约分. （4）分式的乘除法计算结果，要通过约分，化为最简分式或整式.要点二、分式的乘方分式的乘方运算法则：分式的乘方是把分子、分母分别乘方，用字母表示为：nn n a a b b⎛⎫= ⎪⎝⎭（n 为正整数）. 要点诠释：（1）分式乘方时，一定要把分式加上括号.不要把n n n a a b b ⎛⎫= ⎪⎝⎭写成nn a a b b ⎛⎫= ⎪⎝⎭（2）分式乘方时，要首先确定乘方结果的符号，负数的偶次方为正，负数的奇次方为负.（3）在一个算式中同时含有分式的乘方、乘法、除法时，应先算乘方，再算乘除，有多项式时应先分解因式，再约分.（4）分式乘方时，应把分子、分母分别看作一个整体.如()222222a b a b a b b b b ---⎛⎫=≠ ⎪⎝⎭.【典型例题】 类型一、分式的乘法例1、计算：(1)422449158a b xx a b；(2)222441214a a a a a a -+--+-． 【思路点拨】(1)中分子、分母都是单项式，直接用分式乘法法则计算，结果要通过约分化简；(2)中分子、分母都是多项式，要先把可分解因式的分子、分母分解因式，然后用乘法法则化简计算． 【答案与解析】解：(1)422449158a b x x a b 422449315810a b x bx a b x==． (2)222441214a a a a a a -+--+-22(2)1(1)(2)(2)a a a a a --=-+-22(2)(1)(1)(2)(2)a a a a a --=-+-222(1)(2)2a a a a a a --==-++-．【总结升华】分式的乘法运算的实质就是运用分式的基本性质把分式约分化简的过程，熟练之后也可先约分后运用乘法法则计算． 举一反三： 【变式】计算．（1）26283m x xm ；（2）22122x x x x+-+ 【答案】解：（1）原式22621283242m x mx xx m mx ===；（2）原式22112(2)2x x x x x x+==-+-；类型二、分式的除法例2、 计算：(1)222324a b a bc cd-÷；(2)2222242222x y x y x xy y x xy -+÷+++． 【思路点拨】(1)先运用法则将分式的除法转化为乘法，然后约分化简；(2)先运用分式的除法法则将分式的除法转化为乘法，同时将分子、分母分解因式，然后约分化简． 【答案与解析】解：(1)222324a b a b c cd -÷22222244236a bcd a b cd c a b c a b ==--23dc=-． (2) 2222242222x y x y x xy y x xy-+÷+++2(2)(2)2()()2x y x y x x y x y x y+-+=++22(2)24x x y x xyx y x y --==++．【总结升华】分式的除法和实数的除法一样，均是转化为乘法来完成的． 举一反三： 【变式】化简：．【答案】 解：原式=•=．类型三、分式的乘方例3、（2014秋•华龙区校级月考）下列计算正确的是（ ）A. B.C. D.【思路点拨】把四个选项先利用分式的乘方法则，将分子分母分别乘方，然后利用积与幂的乘法法则，积的乘方的运算法则，积的乘方等于积中每一个因式分别乘方并把结果相乘，幂的乘方法则是底数不变，指数相乘，即可计算出结果，得到计算正确的选项．【答案】C．【解析】解：A、，本选项错误；B、，本选项错误；C、，本选项正确；D、，本选项错误．所以计算结果正确的是C．【总结升华】此题考查了分式的乘方法则，考查了积的乘方及幂的乘方法则，完全平方公式的运用，是一道基础题．类型四、分式的乘除法、乘方的混合运算例4、计算：（1）（2016春•淅川县期中）（﹣2ab﹣2c﹣1）2÷×（）3；（2）22 2223()a b aba abb b a⎛⎫-⎛⎫÷+⎪ ⎪-⎝⎭⎝⎭．【思路点拨】先算乘方，再算乘、除.【答案与解析】解：（1）（﹣2ab﹣2c﹣1）2÷×（）3 =﹣••=﹣．（2）222223()a b ab a ab b b a ⎛⎫-⎛⎫÷+ ⎪ ⎪-⎝⎭⎝⎭ 2222232()1()[()]()a b ab b a a b b a -=+-22222332()()1()()a b a b a b b a a b a b +-=+-211()a a b a ab==++．【总结升华】（1）题中有除法和乘方运算，应先算乘方，要特别注意符号的处理．（2）本题是乘除混合运算，首先把除法运算转化为乘法运算，再用乘法运算法则计算． 举一反三：【变式】计算：(1)332212b b a a ab ⎛⎫⎛⎫⎛⎫-÷-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；(2)2222()m n n m m nm n mn m --+⎛⎫÷⎪-⎝⎭． 【答案】解： (1)332212b b a a ab ⎛⎫⎛⎫⎛⎫-÷-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23263382633312212b b b a a b a b a a a ba b ⎛⎫⎛⎫=-÷-÷==⎪ ⎪⎝⎭⎝⎭． (2)2222()m n n m m n m n mn m --+⎛⎫÷ ⎪-⎝⎭22222()()()()m n m n m n m m nm n m n m n mn +---==-+．【巩固练习】 一.选择题 1.计算261053ab cc b 的结果是( )A ．24a cB ．4aC ．4a cD ．1c2. （2016•迁安市一模）化简：（a ﹣2）•的结果是（ ）A ．a ﹣2B ．a+2C ．D ．3．（2015•蜀山区一模）化简的结果是（ ）A.12B.1a a + C. D.4．分式32)32(ba 的计算结果是（ ） A ．3632b aB ．3596b aC ．3598b aD ．36278b a5．下列各式计算正确的是（ ）A ．yx y x =33B ．326m m m =C ．b a ba b a +=++22D ．b a a b b a -=--23)()(6．22222nm m n m n ⋅÷-的结果是（ ）A ．2n m -B ．32nm -C ．4mn -D ．－n二.填空题7.1a c b c÷⨯_____； 2233y xy x -÷_____．8．389()22x yy x⋅-=______；=+-÷-x y x x xy x 33322______． 9．（2015•泰安模拟）化简的结果是 ．10.如果两种灯泡的额定功率分别是21U P R =，225U P R=，那么第一只灯泡的额定功率是第二只灯泡额定功率的________倍.11．3322()a bc =____________；=-522)23(z y x ____________． 12．222222.2ab b a b a ab b a ab+-=++-______． 三.解答题13. （2016•黄石）先化简，再求值：÷•，其中a=2016.14.阅读下列解题过程，然后回答后面问题计算：2111ab c d b c d÷⨯÷⨯÷⨯解：2111ab c d b c d÷⨯÷⨯÷⨯＝2a ÷1÷1÷1① ＝2a ． ②请判断上述解题过程是否正确？若不正确，请指出在①、②中，错在何处，并给出正确的解题过程．15．小明在做一道化简求值题：22222().,x xy y x yxy x xy x-+--÷他不小心把条件x 的值抄丢了，只抄了y ＝－5，你说他能算出这道题的正确结果吗？为什么？【答案与解析】 一.选择题 1.【答案】C ； 【解析】 ∵2261061045353ab c ab c ac b c b c==，∴ 选C 项． 2.【答案】B ；【解析】原式=（a ﹣2）•=a+2，故选B ．3.【答案】B ；【解析】解：原式=×=．故选B.4.【答案】D ；【答案】23663333228()3327a a a b b b==. 5.【答案】D ；【解析】3322()()()()a b a b a b b a a b --==---. 6.【答案】B ；【解析】222222222223n n m n m m m m n n m m n n-÷⋅=-⋅⋅=-.二.填空题7.【答案】2abc；292x y -；【解析】2111a a ac b c b c c bc÷⨯=⨯⨯=.22223933322y x x xy xy x y y -÷=-⨯=-. 8.【答案】218x-；－1； 【解析】328918()22x y y x x⋅-=-；22233()3133()x xy x y x x y x x x x x y --+-÷=⨯=---. 9.【答案】；【解析】解：原式=••=．10.【答案】5；【解析】222122555U U U RP P R R R U ÷=÷=⨯=. 11.【答案】9368a b c；1010524332x y z -；【解析】3399323636228()a a a bc b c b c==；25101052510510533243()2232x x x y z y z y z -=-=-. 12.【答案】ba； 【解析】()()()()()2222222.2b a b a b a b ab b a b ba ab b a ab a a b aa b ++-+-=⋅=++--+. 三.解答题13.【解析】 解：原式=••=（a ﹣1）•=a+1当a=2016时，原式=2017． 14.【解析】解：第①步不正确，因为乘除运算为同级运算时，应从左到右依次计算.应为：22111111111a b c d a b c d b b c c d d ÷⨯÷⨯÷⨯=⨯⨯⨯⨯⨯⨯=2222a b c d.15.【解析】解：22222().x xy y x yxy x xy x-+--÷＝()()22xyx yx x y xx y ---⨯⨯- ＝5y -=这道题的结果与x 的值无关，所以他能算出正确结果是5.。

5.3 分式的乘除知识点 1 分式的乘法1．计算6ab 5c 2·10c 3b的结果是( ) A.4a c 2 B ．4a C.4a c D.1c2．计算8x x －y ·y －x 8y的结果是( ) A.y x B ．－x y C.x y D ．－y x3．2017·海宁期末 计算：－3xy 24z ·－8z y＝________． 4．计算：(1)4x 3y ·y 2x 2； (2)2x y 2·2y x；(3)1a 2－a ·a －1a.知识点 2 分式的除法5．计算b 3a ÷2a b的结果是( ) A.b 26a 2 B.b 3a 2 C.b 25a 2 D.236．计算a －1a ÷a －1a 2的结果是( ) A.1a B ．a C ．a －1 D.1a －17．已知a 米布料能做b 件上衣，2a 米布料能做3b 条裤子，则一件上衣的用料是一条裤子用料的________倍．8．计算：(1)4x 3y ÷2x 3y ； (2)x x 2－1÷1x ＋1.知识点 3 分式的乘除混合运算9．计算x ÷x y ·1x的结果是( )A ．1B ．xy C.y x D.x y10．计算下列四个算式：①a y ·x b ；②n m ·2m n ；③4x ÷2x ；④a b 2÷2a 2b 2，其结果是分式的是( ) A ．①③ B ．①④C ．②④D ．③④11．计算：(1)3x 2y 4·⎝⎛⎭⎫－4x 3y 3÷(－2x 2y )；(2)x 2－1x 2－4x ＋4÷(1－x )·2－x x 2＋x；(3)a 2－25a 2＋10a ＋25÷a ＋5a 2－a ·a 2＋5a 5－a.12．若3－2x x －1÷( )＝1x －1，则( )中的式子为( ) A ．－3 B ．3－2xC ．2x －3 D.13－2x13．一箱苹果的售价为a 元，箱子与苹果的总质量为m 千克，箱子的质量为n 千克，则买x 千克苹果需付________元．14．2018•丰台区一模 如果m 2＋2m ＝1，那么m 2＋4m ＋4m ÷m ＋2m 2的值为________． 15．计算：x 2－y 2x ＋y ·2x ＋2y x 2＋xy÷()x －y .16．若x ＝2019，计算x 2－2x ＋1x 3－x ÷x －1x 2＋x的值．若把x ＝2019换成x ＝20945，你还能迅速得出结果吗？为什么？17．某水果超市运来凤梨和西瓜两种水果，已知凤梨总重(m －2)2千克，西瓜总重(m 2－4)千克，其中m ＞2，售完后，两种水果都卖了540元．(1)请用含m 的代数式分别表示这两种水果的单价；(2)凤梨的单价是西瓜单价的多少倍？18．已知x 为整数，且分式2x －2x 2－1的值是整数，求x 的所有可能值．19．阅读下面的解题过程：已知x x 2＋1＝13，求x 2x 4＋1的值． 解：由 x x 2＋1＝13知x ≠0，所以x 2＋1x ＝3，即x ＋1x＝3， 所以x 4＋1x 2＝x 2＋1x 2＝⎝⎛⎭⎫x ＋1x 2－2＝32－2＝7. 故x 2x 4＋1的值为17. 该题的解法叫做“倒数法”，请你利用“倒数法”解决下面的题目：已知：x x 2－3x ＋1＝15，求x 2x 4＋x 2＋1的值．教师详解详析1．C2．B [解析] 8x x －y ·y －x 8y ＝8x x －y·－（x －y ）8y ＝－x y . 3．6xy [解析] －3xy 24z ·－8z y＝6xy .故答案为6xy . 4．解：(1)原式＝23x. (2)原式＝4y. (3)原式＝1a （a －1）•a －1a＝1a 2. 5．A6．B [解析] a －1a ÷a －1a 2＝a －1a ·a 2a －1＝a . 7．1.5 [解析] 由题意可得a b ÷2a 3b ＝a b ·3b 2a＝1.5. 8．解：(1)原式＝4x 3y ·y 2x 3＝23x 2. (2)原式＝x ()x ＋1（x －1）·(x ＋1)＝x x －1. 9．C10．B [解析] ①a y ·x b ＝ax by ；②n m ·2m n＝2； ③4x ÷2x＝2； ④a b 2÷2a 2b 2＝12a. 11．(1)2x (2)1x 2－2x (3)－a 2（a －1）a ＋512．B [解析] ∵3－2x x －1÷( )＝1x －1，∴3－2x x －1÷1x －1＝3－2x x －1·(x －1)＝3－2x ， ∴( )中的式子为3－2x .故选B.13.ax m －n [解析] 苹果的质量为(m －n )千克，每千克苹果的售价为a m －n元，所以买x 千克苹果需付x ·a m －n ＝ax m －n (元)． 14．1 [解析] m 2＋4m ＋4m ÷m ＋2m 2＝（m ＋2）2m ·m 2m ＋2＝m 2＋2m . 因为m 2＋2m ＝1，所以m 2＋4m ＋4m ÷m ＋2m 2的值为1. 15．解： 原式＝（x ＋y ）（x －y ）x ＋y ·2（x ＋y ）x （x ＋y ）·1x －y ＝2x. 16．解：x 2－2x ＋1x 3－x ÷x －1x 2＋x ＝（x －1）2x （x ＋1）（x －1）·x （x ＋1）x －1＝1. ∴当x ＝2019时，原式＝1.若把x ＝2019换成20945，能迅速得出结果为1.∵计算结果与x 的值无关，∴x 的取值只要能使原式有意义，原式都等于1.17．解：(1)根据题意，得凤梨的单价为540（m －2）2元/千克；西瓜的单价为540m 2－4元/千克． (2)540（m －2）2÷540m 2－4＝540（m －2）2·（m ＋2）（m －2）540＝m ＋2m －2. 所以凤梨的单价是西瓜单价的m ＋2m －2倍． 18．解：2x －2x 2－1＝2x ＋1. 由题意知x ＋1＝1或x ＋1＝2或x ＋1＝－1或x ＋1＝－2，∴x ＝0，1，－2，－3.又∵x 2－1≠0，∴x ＝1舍去，故x 的所有可能值为0，－2，－3.19．解：由x x 2－3x ＋1＝15知x ≠0， ∴x 2－3x ＋1x＝5， ∴x ＋1x－3＝5， ∴x ＋1x＝8， ∴x 4＋x 2＋1x 2＝x 2＋1x 2＋1＝⎝⎛⎭⎫x ＋1x 2－1＝63， ∴x 2x 4＋x 2＋1＝163.。

分式加减乘除运算练习题1.当$x\neq 2$时，分式$\dfrac{x^3}{x-2}$有意义；当$x=2$时，分式无意义。

2.当$x=-1$时，分式$\dfrac{2x-5}{1-x^2}$的值为零；当$x=1$时，分式的值等于零。

3.如果$\dfrac{1-x}{a^2-ab+b^2}=\dfrac{2}{a^5b^3}$，则$\dfrac{2a^2b}{bc^2a+b^2}$的值为$8$。

4.分式$\dfrac{2}{23abbc^2aca+bb}$、$\dfrac{x+1}{x^2-1}$的最简公分母是$23abbc^2aca(x^2-1)$。

5.若分式$\dfrac{5\pi-3}{2x}$的值为负数，则$x$的取值范围是$x\in(-\infty,-\dfrac{5\pi}{6})\cup(0,\dfrac{3}{5})$。

6.已知$x=2009$，$y=2010$，则$\dfrac{x+y}{x^4-y^4}$的值为$\dfrac{1}{xxxxxxx}$。

7.在分式$\dfrac{x+y}{x+y-4xy}$中，共有$2$个分式。

8.下列判断中，正确的是B、C、D。

9.下列各式正确的是B、C。

10.最简分式是A。

11.约分正确的是B、C、D。

12.约分正确的是A、C。

13.计算正确的是A、B、C。

2xy-x^2-y^2=1/y-x将分式中的x和y都扩大3倍，得到：6x+3y)/(18xy) = 1/(3y-3x)答案为D，缩小6倍。

变形后得到：x-y/(x+y) = -x-y/(x+y)答案为A。

变形后得到：x-y)/(x+y) = (x-y)/(x+y)答案为B。

根据题意，xy=x-y，可以得到y=-x/(x+1)。

将其代入分式中，得到：1/y - 11/x = 1/(-x/(x+1)) - 11/x = -(x+1)/(11x)答案为A，-1/11.由x/x=1得到x不等于0.因此，分式可以化简为：111+2+3)/x = 116/x答案为C，5/6x。